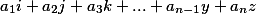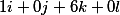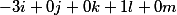| Каждое уравнение или переносится на новую строку или разделяется точкой с запятой |
| Исходная система уравнений |
| Фундаментальная система решений (ФСР) данной системы уравнений |
| База системы/знаменатель |
Попробуем решить систему уравнений, типа
Решение подобных систем неразрывно связывают с формулой приведения матрицы к треугольному виду. Это наглядно, красиво и никогда не дает сбоев. Есть только одно но, нужно делать очень много ручной работы и использовать понятия ранга матрицы
Нет никаких сомнений подвергать выверенную веками технологию, но есть не менее красивое решение используя векторное произведение. Информации по ним на январь 2019 года в интернете нет, поэтому скромно назовемся первооткрывателем.
Это решение конечно же не оптимально (по быстродействию), так как при вычислении векторного произведения, надо вычислять определитель матрицы, а это так или иначе вычисление треугольной матрицы.
Но решение красиво и наглядно, кроме этого легко видеть критерий при котором система не имеет решений.
В чем же суть методики?
Решая эту систему как произведение двух векторов, мы получим
А следоватетельно, корни системы равны
Для тех кто не верит, это легко проверяется подстановкой
Такой же нехитрый прием используется и при системах где количество переменных может быть и пять и десять.
Рассмотрим, как же решаются такие системы с помощью векторных произведений.
Итак, у нас есть исходная система
Приведем её вот в такой вид
У нас получилось 6 столбцов.
На этом этапе не будем вводить новых сущностей и не используем в своей работе понятия ранга матрицы. Мы просто видим что уравнений 3, а переменных 5-ть. Следовательно общее решение будет использовать 5-3=2 независимых переменных.
На этом же шаге, мы можем определить, какие же из переменных будут свободными. Так как фантазии ноль, то те из переменных, которые будут правее всех, те и станут свободными.
То есть свободными у нас будут две переменных
А теперь за три шага определяем фундаментальное решение исходной системы
Шаг1.
Шаг 2.
Шаг 3.
Нет необходимости подробно рассказывать откуда мы берем данные. Это очевидно
Интереснее то, что мы с этими “векторами” делать будем.
Разделим их на -81
получаем следующие три вектора
Таким образом фундаментальное решение принимает вид
Великолепно! Не правда ли….
Хочется еще что то решить…. Еще один пример
Это интересное уравнение, так вектора в любом сочетании будут давать ноль.
Это говорит нам о том, что одно из уравнений “лишнее”. Согласимся с этим и уберем его. Например последнее.
Тогда нам надо выбрать две свободных переменных, пусть это будут переменные с индексами 2 и 4.
Тогда вектора находятся как
Разделим на -3 и наше общее решение будет иметь вид
Не каждому сразу становиться ясно откуда у нас появляются нули и единицы в нашем стройном вектором ряде. Это связано с тем, что мы свободные переменные выбрали как нашей душе угодно, а не самые крайние правые.
Если бы мы взяли переменные с индексами 3 и 4 как свободные то решение бы мы переписали так как нам бы выдала машина.
В начале статьи мы упомянули о критерии неразрешимости той или иной системы уравнений. В классической версии для этого исползуется правило Кронекера-Копелли, здесь же просто анализируется результат векторного произведения.
Если результирующий вектор имеет вид
где 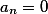
Примеры, неразрешимых систем уравнений
Если результирующий вектор имеет все нулевые коэффициенты ( мы такой пример рассмотрели выше), то это говорит о том, что или как минимум одно из уравнений есть линейное представление другого, и/или одна из переменных пропорциональна другой.
Калькулятор, представленный здесь, дает Вам возможность самому проанализировать исходную систему, за Вас он лишь сделает точные расчеты, по тем данным, что Вы ему введете.
Вот один из примеров


Калькулятор онлайн.
Решение систем линейных алгебраических уравнений (СЛАУ)
Метод Гаусса, матричный метод, метод Крамера, исследование на совместность (теорема Кронекера-Капелли),
определение количества решений, нахождение нормальной фундаментальной системы решений.
С помощью данной математической программы вы можете решить и исследовать систему линейных алгебраических уравнений (СЛАУ).
Программа не только даёт ответ задачи, но и приводит подробное решение с пояснениями шагов решения.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и
экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре.
А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее
сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным
решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень
образования в области решаемых задач повышается.
Правила ввода чисел
Числа можно вводить целые и дробные.
Дробные числа можно вводить в 3-х различных видах:
- в виде десятичных дробей,
- в виде обыкновенных дробей,
- в виде периодических десятичных дробей.
Ввод дробного числа в виде десятичной дроби.
При вводе десятичной дроби, целую часть от дробной части можно отделять точкой или запятой :
Ввод: -2.34
Результат: ( -2{,}34 )
Ввод: -1,15
Результат: ( -1{,}15 )
Ввод дробного числа в виде обыкновенной дроби.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3
Результат: $$ -frac{2}{3} $$
Целая часть отделяется от дроби знаком амперсанд: &
Ввод: 5&8/3
Результат: $$ 5frac{8}{3} $$
Помните, что на ноль делить нельзя!
Ввод дробного числа в виде периодической десятичной дроби.
В периодических десятичных дробях период заключается в скобки.
Ввод: 0,(72)
Результат: $$ frac{8}{11} $$
Ввод: -2,3(4)
Результат: $$ -2frac{31}{90} $$
Наши игры, головоломки, эмуляторы:
Немного теории.
Системы линейных алгебраических уравнений
Основные определения
Система (m) линейных алгебраических уравнений с (n) неизвестными (сокращенно СЛАУ) представляет собой систему вида
( left{ begin{array}{l}
a_{11}x_1 + a_{12}x_2 + cdots + a_{1n}x_n = b_1 \
a_{21}x_1 + a_{22}x_2 + cdots + a_{2n}x_n = b_2 \
cdots \
a_{m1}x_1 + a_{m2}x_2 + cdots + a_{mn}x_n = b_m
end{array} right. tag{1} )
Уравнения системы называют алгебраическими потому, что левая часть каждого из них есть многочлен от (n) переменных
( x_1 , ldots x_n ), а линейными потому, что эти многочлены имеют первую степень.
Числа (a_{ij} in mathbb{R} ) называют коэффициентами СЛАУ. Их нумеруют двумя индексами: номером уравнения (i) и номером
неизвестного (j). Действительные числа ( b_1 , ldots b_m ) называют свободными членами уравнений.
СЛАУ называют однородной, если ( b_1 = b_2 = ldots = b_m = 0 ). Иначе её называют неоднородной.
Решением СЛАУ, да и вообще всякой системы уравнений, называют такой набор значений неизвестных ( x_1^circ, ldots , x_n^circ ),
при подстановке которых каждое уравнение системы превращается в тождество. Любое конкретное решение СЛАУ также называют её частным решением.
Решить СЛАУ — значит решить две задачи:
— выяснить, имеет ли СЛАУ решения;
— найти все решения, если они существуют.
СЛАУ называют совместной, если она имеет какие-либо решения. В противном случае её называют несовместной. Однородная СЛАУ
всегда совместна, поскольку нулевой набор значений её неизвестных всегда является решением.
Если СЛАУ (1) имеет решение, и притом единственное, то её называют определенной, а если решение неединственное — то неопределенной.
При (m=n), т.е. когда количество уравнений совпадает с количеством неизвестных, СЛАУ называют квадратной.
Формы записи СЛАУ
Кроме координатной формы (1) записи СЛАУ часто используют и другие её представления.
Рассматривая коэффициенты (a_{ij}) СЛАУ при одном неизвестном (x_j) как элементы столбца, а (x_j) как коэффициент, на который умножается
столбец, из (1) получаем новую форму записи СЛАУ:
( begin{pmatrix}
a_{11} \
a_{21} \
vdots \
a_{m1}
end{pmatrix} x_1 + begin{pmatrix}
a_{12} \
a_{22} \
vdots \
a_{m2}
end{pmatrix} x_2 + ldots + begin{pmatrix}
a_{1n} \
a_{2n} \
vdots \
a_{mn}
end{pmatrix} x_n = begin{pmatrix}
b_1 \
b_2 \
vdots \
b_m
end{pmatrix} )
или, обозначая столбцы соответственно ( a_1 , ldots , a_n , b ),
( x_1 a_1 + x_2 a_2 + ldots + x_n a_n = b tag{2} )
Таким образом, решение СЛАУ (1) можно трактовать как представление столбца (b) в виде линейной комбинации столбцов ( a_1, ldots, a_n ).
Соотношение (2) называют векторной записью СЛАУ.
Обратим внимание на то, что слева в каждом уравнении системы (1) стоит сумма попарных произведений — так же, как и в произведении двух матриц.
Если взять за основу произведение матриц, то СЛАУ (1) можно записать так :
( begin{pmatrix}
a_{11} & a_{12} & cdots & a_{1n} \
a_{21} & a_{22} & cdots & a_{2n} \
vdots & vdots & ddots & vdots \
a_{m1} & a_{m2} & cdots & a_{mn}
end{pmatrix} begin{pmatrix}
x_1 \
x_2 \
vdots \
x_n
end{pmatrix} = begin{pmatrix}
b_1 \
b_2 \
vdots \
b_m
end{pmatrix} )
или (Ax=b), где (A) — матрица размера (m times n); (x) — столбец неизвестных; (b) — столбец свободных членов:
( A = begin{pmatrix}
a_{11} & a_{12} & cdots & a_{1n} \
a_{21} & a_{22} & cdots & a_{2n} \
vdots & vdots & ddots & vdots \
a_{m1} & a_{m2} & cdots & a_{mn}
end{pmatrix} ,; )
( X = begin{pmatrix}
x_1 \
x_2 \
vdots\
x_n
end{pmatrix} ,; )
( B = begin{pmatrix}
b_1 \
b_2 \
vdots \
b_m
end{pmatrix} )
Поскольку (A ;,; X) и (B) являются матрицами, то запись СЛАУ (1) в виде (AX=B) называют матричной. Если (B=0), то СЛАУ
является однородной и в матричной записи имеет вид (AX=0).
Приведенные рассуждения показывают, что задачи :
а) решения СЛАУ (1)
б) представления столбца в виде линейной комбинации данных столбцов
в) решения матричных уравнений вида (AX=B)
являются просто различной формой записи одной и той же задачи.
Критерий совместности СЛАУ
“Триединство” форм записи СЛАУ позволяет легко получить критерий совместности СЛАУ. Напомним, что содержательный смысл это понятие имеет
для неоднородных СЛАУ (однородные СЛАУ всегда совместны).
Матрицу
( A = begin{pmatrix}
a_{11} & a_{12} & cdots & a_{1n} \
a_{21} & a_{22} & cdots & a_{2n} \
vdots & vdots & ddots & vdots \
a_{m1} & a_{m2} & cdots & a_{mn}
end{pmatrix} )
называют матрицей (коэффициентов) СЛАУ (1), а матрицу
( (A|B) = left( begin{array}{cccc|c}
a_{11} & a_{12} & cdots & a_{1n} & b_1 \
a_{21} & a_{22} & cdots & a_{2n} & b_2 \
vdots & vdots & ddots & vdots & vdots \
a_{m1} & a_{m2} & cdots & a_{mn} & b_m
end{array} right) )
расширенной матрицей СЛАУ (1). Расширенная матрица полностью характеризует СЛАУ. Это означает, что по этой матрице однозначно
(если сохранить обозначения для неизвестных) восстанавливается сама СЛАУ.
Теорема Кронекера-Капелли. Для совместности СЛАУ (AX=B) необходимо и достаточно, чтобы ранг её матрицы (A) был равен рангу
её расширенной матрицы ( (A|B) ).
Формулы Крамера
Теорема. СЛАУ с квадратной невырожденной матрицей имеет решение, и притом единственное, которое определяется по
формулам Крамера :
$$ x_i = frac{Delta_i}{|A|} ;,quad i=overline{1,n} tag{3} $$
где (Delta_i) — определитель матрицы, получающейся из матрицы (A) заменой (i)-го столбца на столбец свободных членов.
Следствие. Однородная СЛАУ с квадратной невырожденной матрицей имеет единственное решение — нулевое.
Если матрица СЛАУ не является квадратной невырожденной, то формулы Крамера не работают и приходится использовать другие методы
нахождения решений.
Однородные системы
Следующая теорема описывает важнейшее свойство множества решений однородной системы (m) линейных алгебраических уравнений с (n) неизвестными.
Теорема. Если столбцы ( X^{(1)}, X^{(2)}, ldots , X^{(s)} ) — решения однородной СЛАУ (AX=0), то любая их линейная комбинация
также является решением этой системы.
Следствие. Если однородная СЛАУ имеет ненулевое решение, то она имеет бесконечно много решений.
Естественно попытаться найти такие решения ( X^{(1)}, ldots , X^{(s)} ) системы (AX=0), чтобы любое другое решение этой системы
представлялось в виде их линейной комбинации и притом единственным образом. Оказывается, что это всегда возможно и приводит к следующему определению.
Определение. Любой набор из (k=n-r) линейно независимых столбцов, являющихся решениями однородной СЛАУ (AX=0), где
(n) — количество неизвестных в системе, а (r) — ранг её матрицы (A), называют фундаментальной системой решений этой однородной СЛАУ.
При исследовании и решении однородных систем линейных алгебраических уравнений будем использовать следующую терминологию. Если в матрице
(A) однородной СЛАУ (AX=0) фиксировать базисный минор, то ему соответствуют базисные столбцы и, следовательно, набор неизвестных, отвечающих
этим столбцам. Указанные неизвестные называют базисными, или зависимыми, а остальные неизвестные — свободными, или
независимыми.
Теорема. Пусть дана однородная СЛАУ (AX=0) с (n) неизвестными и ( text{rang}A = r ). Тогда существует набор из (k=n-r)
решений ( X^{(1)}, ldots , X^{(k)} ) этой СЛАУ, образующих фундаментальную систему решений.
Если в фундаментальной системе решений все значения независимых неизвестных равны нулю, кроме одного, которое равно единице, то такую систему решений
называют фундаментальной нормальной системой решений.
Следствие. С помощью нормальной фундаментальной системы решений однородной СЛАУ множество всех решений можно описать формулой :
$$ X = c_1X^{(1)} + ldots + c_kX^{(k)} $$
где постоянные ( c_i ;, quad i=overline{1,k} ), принимают произвольные значения.
Следствие. Для существования ненулевого решения у однородной квадратной СЛАУ необходимо и достаточно, чтобы её матрица была вырождена.
Неоднородные системы
Рассмотрим произвольную СЛАУ (AX=B). Заменив столбец (B) свободных членов нулевым, получим однородную СЛАУ (AX=0), соответствующую
неоднородной СЛАУ (AX=B). Справедливо следующее утверждение о структуре произвольного решения неоднородной СЛАУ.
Теорема. Пусть столбец (X^circ) — некоторое решение СЛАУ (AX=B). Произвольный столбец (X) является решением этой СЛАУ тогда и
только тогда, когда он имеет представление (X = X^circ + Y ), где (Y) — решение соответствующей однородной СЛАУ (AY=0).
Следствие. Пусть (X’) и (X”) — решения неоднородной системы (AX=B). Тогда их разность ( Y = X’ – X” ) является
решением соответствующей однородной системы (AY=0).
Эта теорема сводит проблему решения СЛАУ к случаю однородной системы: чтобы описать все решения неоднородной СЛАУ, достаточно энать одно
её решение (частное решение) и все решения соответствующей однородной СЛАУ.
Чтобы решить неоднородную систему, надо, во-первых, убедиться, что она совместна (например, по теореме Кронекера-Капелли), а во-вторых,
найти частное решение (X^circ) этой системы, чтобы свести её к однородной системе.
Теорема о структуре общего решения СЛАУ. Пусть (X^circ) — частное решение СЛАУ (AX=B) и известна фундаментальная система
решений ( X^{(1)}, ldots , X^{(k)} ) соответствующей однородной системы (AX=0). Тогда любое решение СЛАУ (AX=B) можно представить в виде
$$ X = X^circ + c_1 X^{(1)} + c_2 X^{(2)} + ldots + c_k X^{(k)} $$
где ( c_i in mathbb{R} ;, quad i=overline{1,k} ).
Эту формулу называют общим решением СЛАУ.
ФРС. Фундаментальное решение системы уравнений
| Каждое уравнение или переносится на новую строку или разделяется точкой с запятой |
| Исходная система уравнений |
| Фундаментальная система решений (ФСР) данной системы уравнений |
| База системы/знаменатель |
Попробуем решить систему уравнений, типа
Решение подобных систем неразрывно связывают с формулой приведения матрицы к треугольному виду. Это наглядно, красиво и никогда не дает сбоев. Есть только одно но, нужно делать очень много ручной работы и использовать понятия ранга матрицы
Нет никаких сомнений подвергать выверенную веками технологию, но есть не менее красивое решение используя векторное произведение. Информации по ним на январь 2019 года в интернете нет, поэтому скромно назовемся первооткрывателем.
Это решение конечно же не оптимально (по быстродействию), так как при вычислении векторного произведения, надо вычислять определитель матрицы, а это так или иначе вычисление треугольной матрицы.
Но решение красиво и наглядно, кроме этого легко видеть критерий при котором система не имеет решений.
В чем же суть методики?
Решая эту систему как произведение двух векторов, мы получим
А следоватетельно, корни системы равны
Для тех кто не верит, это легко проверяется подстановкой
Такой же нехитрый прием используется и при системах где количество переменных может быть и пять и десять.
Рассмотрим, как же решаются такие системы с помощью векторных произведений.
Итак, у нас есть исходная система
Приведем её вот в такой вид
У нас получилось 6 столбцов.
На этом этапе не будем вводить новых сущностей и не используем в своей работе понятия ранга матрицы. Мы просто видим что уравнений 3, а переменных 5-ть. Следовательно общее решение будет использовать 5-3=2 независимых переменных.
На этом же шаге, мы можем определить, какие же из переменных будут свободными. Так как фантазии ноль, то те из переменных, которые будут правее всех, те и станут свободными.
То есть свободными у нас будут две переменных
А теперь за три шага определяем фундаментальное решение исходной системы
Шаг1.
Шаг 2.
Шаг 3.
Нет необходимости подробно рассказывать откуда мы берем данные. Это очевидно
Интереснее то, что мы с этими “векторами” делать будем.
Разделим их на -81
получаем следующие три вектора
Таким образом фундаментальное решение принимает вид
Великолепно! Не правда ли….
Хочется еще что то решить…. Еще один пример
Это интересное уравнение, так вектора в любом сочетании будут давать ноль.
Это говорит нам о том, что одно из уравнений “лишнее”. Согласимся с этим и уберем его. Например последнее.
Тогда нам надо выбрать две свободных переменных, пусть это будут переменные с индексами 2 и 4.
Тогда вектора находятся как
Разделим на -3 и наше общее решение будет иметь вид
Не каждому сразу становиться ясно откуда у нас появляются нули и единицы в нашем стройном вектором ряде. Это связано с тем, что мы свободные переменные выбрали как нашей душе угодно, а не самые крайние правые.
Если бы мы взяли переменные с индексами 3 и 4 как свободные то решение бы мы переписали так как нам бы выдала машина.
В начале статьи мы упомянули о критерии неразрешимости той или иной системы уравнений. В классической версии для этого исползуется правило Кронекера-Копелли, здесь же просто анализируется результат векторного произведения.
Если результирующий вектор имеет вид
где 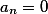
Примеры, неразрешимых систем уравнений
Если результирующий вектор имеет все нулевые коэффициенты ( мы такой пример рассмотрели выше), то это говорит о том, что или как минимум одно из уравнений есть линейное представление другого, и/или одна из переменных пропорциональна другой.
Калькулятор, представленный здесь, дает Вам возможность самому проанализировать исходную систему, за Вас он лишь сделает точные расчеты, по тем данным, что Вы ему введете.
Вот один из примеров
Фундаментальная система решений (конкретный пример)
Вы можете заказать подробное решение вашей задачи здесь!!!
Чтобы понять, что такое фундаментальная система решений вы можете посмотреть видео-урок для этого же примера кликнув здесь. Теперь перейдем собственно к описанию всей необходимой работы. Это поможет вам более детально разобраться в сути данного вопроса.
Как найти фундаментальную систему решений линейного уравнения?
Возьмём для примера такую систему линейных уравнений:

Найдём решение этой линейной системы уравнений методом Гаусса. Для начала нам надо выписать матрицу коэффициентов системы.

Преобразуем эту матрицу к треугольной. Первую строку переписываем без изменений. И все элементы, что стоят под $a_{11}$, надо сделать нулями. Что бы сделать ноль в место элемента $a_{21}$, надо от второй строки вычесть первую, и разность записать во второй строке. Что бы сделать ноль в место элемента $a_{31}$, надо от третьей строки вычесть первую и разность записать в третьей строке. Что бы сделать ноль в место элемента $a_{41}$, надо от четвёртой строки вычесть первую умноженную на 2 и разность записать в четвёртой строке. Что бы сделать ноль в место элемента $a_{31}$, надо от пятой строки вычесть первую умноженную на 2 и разность записать в пятой строке.

Первую и вторую строку переписываем без изменений. И все элементы, что стоят под $a_{22}$, надо сделать нулями. Что бы сделать ноль в место элемента $a_{32}$, надо от третьей строки вычесть вторую умноженную на 2 и разность записать в третьей строке. Что бы сделать ноль в место элемента $a_{42}$, надо от четвёртой строки вычесть вторую умноженную на 2 и разность записать в четвёртой строке. Что бы сделать ноль в место элемента $a_{52}$, надо от пятой строки вычесть вторую умноженную на 3 и разность записать в пятой строке.

Видим, что последние три строки – одинаковые, поэтому если от четвёртой и пятой вычесть третью, то они станут нулевыми.

По этой матрице записываем новую систему уравнений.

Видим, что линейно независимых уравнений у нас, только три, а неизвестных пять, поэтому фундаментальная система решений будет состоять из двух векторов. Значит, нам надо перенести две последние неизвестные вправо.

Теперь, начинаем выражать те неизвестные, что стоят в левой части через те, что стоят в правой части. Начинаем с последнего уравнения, сначала выразим $x_3$, потом полученный результат подставим во второе уравнение и выразим $x_2$, а потом в первое уравнение и тут выразим $x_1$. Таким образом мы все неизвестные, что стоят в левой части, выразили через неизвестные, что стоят в правой части.

После чего вы вместо $x_4$ и $x_5$, можем подставлять любые числа и находить $x_1$, $x_2$ и $x_3$. Каждая такая пятёрка чисел будет корнями нашей изначальной системы уравнений. Что бы найти векторы, что входят в ФСР нам надо вместо $x_4$ подставить 1, а вместо $x_5$ подставить 0, найти $x_1$, $x_2$ и $x_3$, а потом наоборот $x_4=0$ и $x_5=1$.
Какие именно векторы создают фундаментальную систему решений данной системы уравнений?

Для лучшего понимания хода роботы можете посмотреть видео-урок по данном задании.
Материалы по теме:
- Метод Гаусса (конкретный пример)
- Матрицы и определители
- Три метода решения определителя (детерминанта) матрицы!
- Сложение и вычитание матриц
![]() Загрузка…
Загрузка…
Содержание:
- Однородные СЛАУ
- Фундаментальная система решений
Однородные СЛАУ
Определение
Однородной СЛАУ называется система, все правые части которой равны нулю одновременно.
Однородная СЛАУ, записанная в
матричном виде, $A X=Theta$ всегда совместна,
так как $X=Theta$ всегда является ее решением.
Заметим, что если $x_{1}, x_{2}$ – это два решения однородной
СЛАУ, то их линейная комбинация также будет решением однородной СЛАУ:
$$Y=lambda_{1} x_{1}+lambda_{2} x_{2}$$
$$A Y=Aleft(lambda_{1} x_{1}+lambda_{2} x_{2}right)=lambda_{1} A x_{1}+lambda_{2} A x_{2}=lambda_{1} Theta+lambda_{2} Theta=Theta$$
Теорема
Если однородная квадратная СЛАУ имеет ненулевое решение, то
определитель матрицы системы равен нулю.
Пример
Задание. Выяснить, имеет ли однородная СЛАУ
$left{begin{array}{l}
3 x-2 y=-1 \
x+3 y=7
end{array}right.$ ненулевые решения.
Решение. Вычислим определитель матрицы системы:
$$Delta=left|begin{array}{rr}
3 & -2 \
1 & 3
end{array}right|=9-(-2)=9+2=11 neq 0$$
Так как определитель не равен нулю, то система имеет только нулевое решение $x=y=0$
Ответ. Система имеет только нулевое решение.
Фундаментальная система решений
Рассмотрим множество всех столбцов, которые являются решениями исходной системы.
Определение
Фундаментальной системой решений (ФСР) однородной СЛАУ называется базис этой системы столбцов.
Количество элементов в ФСР равно количеству неизвестных системы минус ранг матрицы системы.
Любое решение исходной системы есть линейная комбинация решений ФСР.
Теорема
Общее решение неоднородной СЛАУ равно сумме частного решения неоднородной СЛАУ и
общего решения соответствующей однородной СЛАУ.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти общее решение и ФСР однородной системы
$left{begin{array}{l}
x_{1}+x_{2}-3 x_{4}-x_{5}=0 \
x_{1}-x_{2}+2 x_{3}-x_{4}=0 \
4 x_{1}-2 x_{2}+6 x_{3}+3 x_{4}-4 x_{5}=0 \
2 x_{1}+4 x_{2}-2 x_{3}+4 x_{4}-7 x_{5}=0
end{array}right.$
Решение. Приведем систему к ступенчатому виду с помощью
метода Гаусса. Для этого записываем
матрицу системы (в данном случае, так как система однородная, то ее правые части равны нулю, в этом случае столбец
свободных коэффициентов можно не выписывать, так как при любых элементарных преобразованиях в правых частях будут
получаться нули):
$$A=left(begin{array}{rrrrr}
1 & 1 & 0 & -3 & -1 \
1 & -2 & 2 & -1 & 0 \
4 & -2 & 6 & 3 & -4 \
2 & 4 & -2 & 4 & -7
end{array}right)$$
с помощью элементарных преобразований приводим данную матрицу к ступенчатому виду. От второй строки отнимаем
первую, от третьей – четыре первых, от четвертой – две первых:
$$A simleft(begin{array}{rrrrr}
1 & 1 & 0 & -3 & -1 \
0 & -2 & 2 & 2 & 1 \
0 & -6 & 6 & 15 & 0 \
0 & 2 & -2 & 10 & -5
end{array}right)$$
Обнуляем элементы второго столбца, стоящие под главной диагональю, для этого от третьей строки отнимаем три
вторых, к четвертой прибавляем вторую:
$$A simleft(begin{array}{rrrrr}
1 & 1 & 0 & -3 & -1 \
0 & -2 & 2 & 2 & 1 \
0 & 0 & 0 & 9 & -3 \
0 & 0 & 0 & 12 & -4
end{array}right)$$
От четвертой строки отнимем $frac{4}{3}$ третьей и третью
строку умножим на $frac{1}{3}$ :
$$A simleft(begin{array}{rrrrr}
1 & 1 & 0 & -3 & -1 \
0 & -2 & 2 & 2 & 1 \
0 & 0 & 0 & 3 & -1 \
0 & 0 & 0 & 0 & 0
end{array}right)$$
Нулевые строки можно далее не рассматривать, тогда получаем, что
$$A simleft(begin{array}{rrrrr}
1 & 1 & 0 & -3 & -1 \
0 & -2 & 2 & 2 & 1 \
0 & 0 & 0 & 3 & -1
end{array}right)$$
Далее делаем нули над главной диагональю, для этого от первой строки отнимаем третью, а
ко второй строке прибавляем третью:
$$A simleft(begin{array}{rrrrr}
1 & 1 & 0 & -6 & 0 \
0 & -2 & 2 & 5 & 0 \
0 & 0 & 0 & 3 & -1
end{array}right)$$
то есть получаем систему, соответствующую данной матрице:
$$left{begin{array}{l}
x_{1}+x_{2}-6 x_{4}=0 \
-2 x_{2}+2 x_{3}+5 x_{4}=0 \
3 x_{4}-x_{5}=0
end{array}right.$$
Или, выразив одни переменные через другие, будем иметь:
$$left{begin{array}{l}
x_{1}=-x_{2}+6 x_{4} \
x_{2}=x_{2} \
x_{3}=x_{2}-frac{5}{2} x_{4} \
x_{4}=x_{4} \
x_{5}=3 x_{4}
end{array}right.$$
Здесь $x_{2}, x_{4}$ – независимые (или свободные)
переменные (это те переменные, через которые мы выражаем остальные переменные), $x_{1}, x_{3}, x_{5}$ – зависимые (связанные) переменные
(то есть те, которые выражаются через свободные). Количество свободных переменных равно разности общего количества переменных $n$ (в рассматриваемом примере $n=5$ , так как система зависит от
пяти переменных) и ранга матрицы $r$ (в этом
случае получили, что $r=3$ – количество
ненулевых строк после приведения матрицы к ступенчатому виду):
$n-r=5-3=2$
Так как ранг матрицы $r=3$ , а количество неизвестных
системы $n=5$ , то тогда количество решений в ФСР
$n-r=5-3=2$ (для проверки, это число должно равняться количеству свободных переменных).
Для нахождения ФСР составляем таблицу, количество столбцов которой соответствует количеству неизвестных (то есть
для рассматриваемого примера равно 5), а количество строк равно количеству решений ФСР (то есть имеем две строки).
В заголовке таблицы выписываются переменные, свободные переменные отмечаются стрелкой. Далее свободным переменным
придаются любые, одновременно не равные нулю значений и из зависимости между свободными и связанными переменными
находятся значения остальных переменных. Для рассматриваемой задачи эта зависимость имеет вид:
$$left{begin{array}{l}
x_{1}=-x_{2}+6 x_{4} \
x_{3}=x_{2}-frac{5}{2} x_{4} \
x_{5}=3 x_{4}
end{array}right.$$
Тогда придавая в первом случае, например, независимым переменным значения
$x_{2}=1$ , $x_{4}=0$ получаем, что $left{begin{array}{l}
x_{1}=-1+6 cdot 0=-1 \
x_{3}=1-frac{5}{2} cdot 0=1 \
x_{5}=3 cdot 0=0
end{array}right.$ . Полученные значения записываем в первую
строку таблицы. Аналогично, беря $x_{2}=0$ , $x_{4}=2$, будем иметь, что
{x_{1}=12, x_{3}=-5, x_{5}=6} , что и определяет второе решение ФСР.
В итоге получаем следующую таблицу:
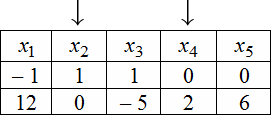
Эти две строчки и есть фундаментальным решением заданной однородной СЛАУ. Частное решение системы:
$$X_{1}=left(begin{array}{r}
-1 \
1 \
1 \
0 \
0
end{array}right), X_{2}=left(begin{array}{r}
12 \
0 \
-5 \
2 \
6
end{array}right)$$
Общее решение является линейной комбинацией частных решений:
$$X=C_{1} X_{1}+C_{2} X_{2}=C_{1}left(begin{array}{r}
-1 \
1 \
1 \
0 \
0
end{array}right)+C_{2}left(begin{array}{r}
12 \
0 \
-5 \
2 \
6
end{array}right)$$
где коэффициенты $C_{1}, C_{2}$ не равны нулю одновременно. Или запишем общее решение в таком виде:
$left{begin{array}{l}
x_{1}=-C_{1}+12 C_{2} \
x_{2}=C_{1} \
x_{3}=C_{1}-5 C_{2} \
x_{4}=2 C_{2} \
x_{5}=6 C_{2}
end{array}right.$
$C_{1}, C_{2} neq 0$
Придавая константам $C_{1}, C_{2}$ определенные значения
и подставляя их в общее решение, можно будет находить частные решения однородной СЛАУ.
Читать дальше: примеры решения СЛАУ.


i%20+%20(%201%20)j%20+%20(%207%20)k)

i%20+%20(%20-162%20)j%20+%20(%20-486%20)k%20+%20(%20-81%20)l)
i%20+%20(%20162%20)j%20+%20(%20405%20)k%20+%20(%20-81%20)l)
i%20+%20(%20243%20)j%20+%20(%20324%20)k%20+%20(%20-81%20)l)
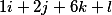
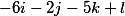
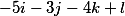


i%20+%20(%20-0%20)j%20+%20(%200%20)k%20+%20(%200%20)l)
i%20+%20(%20-0%20)j%20+%20(%20-0%20)k%20+%20(%200%20)l)

i%20+%20(%20-0%20)j%20+%20(%20-3%20)k)
i%20+%20(%20-0%20)j%20+%20(%20-3%20)k)
i%20+%20(%2027%20)j%20+%20(%20-3%20)k)