Материал из Викиконспекты
Перейти к: навигация, поиск
| Определение: |
| Фундаментальный цикл графа относительно остова (англ. fundamental cycle) — простой цикл , полученный путем добавления к остову ребра |
Пример фундаментального цикла в графе. Красным выделен фундаментальный цикл, полученный добавлением ребра
| Теорема: |
|
Множество всех фундаментальных циклов относительно любого остова графа образует базис циклического пространства этого графа. |
| Доказательство: |
|
Рассмотрим остов графа и фундаментальные циклы относительно остова . В каждом цикле есть ребро , которое принадлежит ровно одному из . Поэтому сумма различных фундаментальных циклов относительно остова не является пустым графом, из чего следует, что линейно независимы. Докажем, что любой цикл из циклического пространства графа является суммой фундаментальных циклов. Пусть — цикл циклического пространства графа , ребра принадлежащие и не принадлежащие . Рассмотрим граф . Каждое из ребер встречается ровно в двух слагаемых — и . Значит содержит только ребра из . Так как простые циклы, то степени всех их вершин четны, степени вершин тоже четны по лемме, значит степени всех вершин четны. Если непустой граф, то в есть цикл, значит цикл есть и в . Значит пустой граф, откуда следует что . |
См. также
- Остовные деревья
- Циклическое пространство графа
Источники информации
- Харари Фрэнк Теория графов = Graph theory/Пер. с англ. и предисл. В. П. Козырева. Под ред. Г.П.Гаврилова. Изд. 2-е. — М.: Едиториал УРСС, 2003. — 296 с. — ISBN 5-354-00301-6
|
Абстрактный цикл. |
Базовые понятия и утверждения
Пусть
– произвольный граф. На множестве циклов
графавведем бинарное отношение, которое
назовемотношением равенстваи
определим следующим условием: будем
считать, что два цикла равны, если
множества их ребер совпадают.
Это бинарное отношение, будучи отношением
эквивалентности, разбивает множество
циклов данного графа на классы
эквивалентности. Далее в этом параграфе,
говоря о циклах графа, будем иметь в
виду, если не оговорено противное, классы
эквивалентности, а не отдельных их
представителей. Эти классы эквивалентности
назовем абстрактными циклами. Любой
абстрактный циклзадается множеством своих ребер.
Пример 1. Граф,
представленный диаграммой на рис. 3.72,
имеет следующие абстрактные циклы:
|
|
|
Рис. |
,
,
,
,
,
.
Обобщенным цикломбудем называть
абстрактный цикл или объединение
непересекающихся абстрактных циклов.
В число обобщенных циклов включим также
цикл без ребер; назовем его пустым циклом
и обозначим символом.
На множестве всех обобщенных циклов
графа
введем две операции:
а) операцию
сложения по модулю 2: суммой обобщенных
циклови
назовем обобщенный цикл
с множеством ребер
(здесь
и
– множества ребер обобщенных циклов
и
соответственно);
б) операцию умножения на 0 и 1:
;
.
Например, для обобщенных циклов графа
из примера 1 имеем:
,
,
.
Множество всех обобщенных циклов графа
с операциями сложения по модулю 2 и
умножения на 0 и 1 образуют линейное
пространство (убедиться в выполнении
восьми аксиом линейного пространства
несложно).
Операция
естественным образом распространяется
на любое конечное число обобщенных
циклов.
Линейной комбинацией обобщенных
цикловназовем выражение
,
где.
Говорят, что система обобщенных циклов
зависима, если найдется набор чисел
,
не все из которых равны 0, такой, что.
В противном случае систему обобщенных
цикловназываютнезависимой.
Система обобщенных циклов
графа
образуетбазис линейного пространства
циклов, если она удовлетворяет двум
условиям:
1)
линейно независима;
2) любой обобщенный цикл
графа
может быть представлен в виде линейной
комбинации обобщенных циклов.
Базис линейного пространства циклов
называют фундаментальной системой
циклов.
Из курса линейной алгебры нам известно,
что в линейном пространстве может быть
несколько базисов, но все они состоят
из одного числа векторов линейного
пространства (напомним, что это число
называют размерностью линейного
пространства).
Представляют интерес два вопроса: 1) из
скольких циклов состоит фундаментальная
система циклов произвольного графа и
2) как найти фундаментальную систему
циклов графа?
Ответ на первый вопрос дает следующее
утверждение: число циклов в любой
фундаментальной системе циклов графа
равно его цикломатическому числу.
Приведем алгоритм построения
фундаментальной системы циклов
произвольного графа.
1-й шаг.Находим в графекакой-либо обобщенный цикл
и удаляем из него ребро
(«разрываем»
цикл). Получаем граф.
-й
шаг.В графе,
построенном на ()-м
шаге, находим какой-либо обобщенный
цикли удаляем из него произвольное ребро
.
Получаем граф.
Если в графе
циклов нет, то
– искомая фундаментальная система
циклов. Если в графеобобщенные циклы остались, то повторяем
-й
шаг.
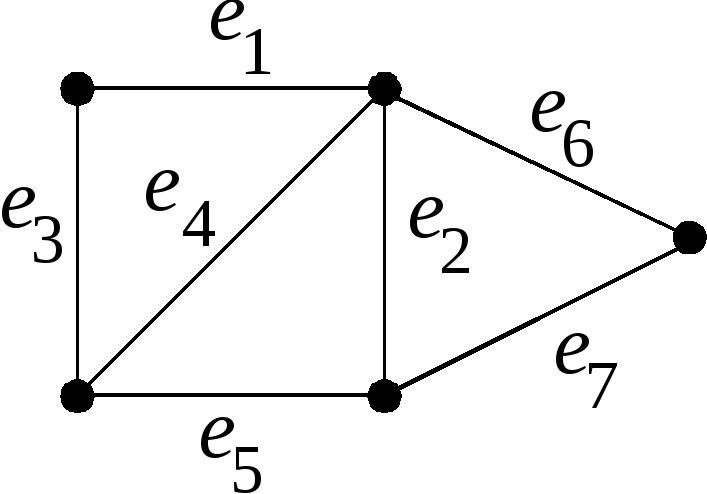
Пример 2.Построим
фундаментальную систему циклов графаиз примера 1.
1-й шаг.Возьмем цикли удалим из него одно ребро, пусть это
будет ребро.
Получим граф(рис. 3.73).
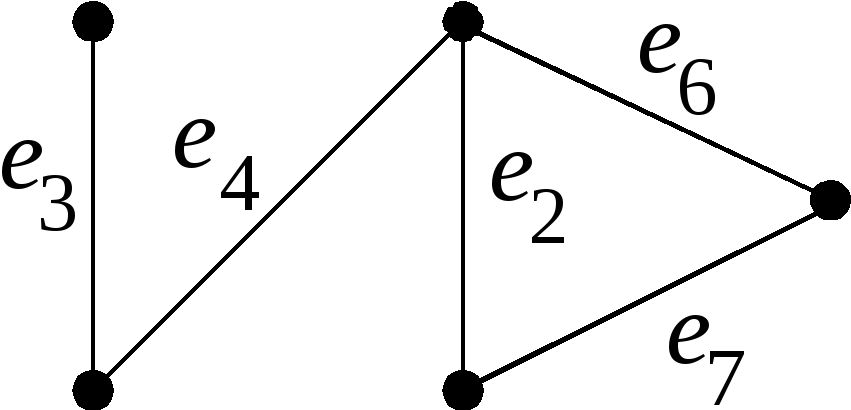
2-й шаг.В
графевозьмем цикл
и удалим из него одно ребро, пусть это
будет ребро.
Получим граф(см. рис. 3.73).
3-й шаг.В
графевозьмем цикл
и удалим из него одно ребро, пусть это
будет ребро.
Получим граф(рис. 3.73), в котором нет циклов.
|
|
|
|
|
|
|
|
|
Рис. |
Следовательно,
– фундаментальная система циклов (или,
что то же самое, базис пространства
циклов) графа.
Все остальные обобщенные циклы графа
– линейные комбинации базисных циклов.Например,.
Заметим, что действия по алгоритму не
строго детерминированы: на каждом шаге
мы имели несколько вариантов выбираемого
цикла и удаляемого из него ребра. Если
бы наш выбор был иным, то мы нашли бы
другую фундаментальную систему циклов.
Однако число циклов в этой другой
фундаментальной системе тоже было бы
равно трем. Например,
также является фундаментальной системой
циклов графа.
13
Соседние файлы в папке discretka_2
- #
- #
- #
- #
- #
- #
- #
- #
- #
Симметрическая разность двух циклов в эйлеровом подграфе
Базис циклов неориентированного графа — множество простых циклов, которые образуют базис пространства циклов графа. Таким образом, это минимальный набор циклов, который позволяет любой эйлеров подграф представить как симметрическую разность базисных циклов.
Фундаментальный базис циклов может быть образован из любого остовного дерева леса-каркаса заданного графа путём выбора циклов, которые имеют ровно одно ребро, не принадлежащее дереву. Также, если задать рёбрам графа положительные веса, базис циклов минимального веса может быть построен в полиномиальное время.
В планарных графах множество циклов ограниченных граней (то есть циклы-границы ограниченных граней — одна, внешняя, грань бесконечна) вложенного в плоскость графа образуют базис циклов. Минимальный по весу базис циклов планарного графа соответствует дереву Гомори — Ху[en] двойственного графа.
Определения[править | править код]
Остовное дерево заданного графа 


Базис циклов — это базис векторного пространства и каждый базисный вектор соответствует простому циклу. Базис состоит из множества циклов, которые можно комбинировать, чтобы с помощью симметрической разности получить любой эйлеров подграф и этот набор циклов является минимальным набором, обладающих указанным свойством. Любой базис циклов заданного графа имеет то же самое число элементов базиса и это число равно размерности пространства циклов. Это число называется контурным рангом или ‘цикломатическим числом графа и оно равно 



Специальные базисы циклов[править | править код]
Изучались некоторые специальные типы базисов циклов, среди них — фундаментальные базисы циклов, слабые фундаментальные базисы циклов, разреженные (или 2-) базисы циклов и целые базисы циклов[3].
Порождённые циклы[править | править код]
Любой граф имеет базис циклов в котором каждый цикл является порождённым циклом. В вершинно 3-связном графе всегда существует базис, состоящий из периферийных циклов, циклов, удаление которых не приводит к разделению на несвязные части[4][5]. В любом графе, не получаемом добавлением ребра к циклу, периферийный цикл должен быть порождённым циклом.
Фундаментальные циклы[править | править код]
Если 











Можно задать фундаментальный базис циклов, не опираясь на дерево, для которого циклы фундаментальны. В том и только в том случае существует дерево, для которого заданный базис циклов является фундаментальным, когда любой цикл содержит ребро, не входящее ни в один другой цикл базиса. Отсюда следует, что набор циклов является фундаментальным базисом циклов в том и только в том случае, когда он имеет то же свойство и правильное число циклов в базисе[6].
Слабо фундаментальные циклы[править | править код]
Базис циклов называется слабо фундаментальным, если его циклы можно упорядочить так, что каждый цикл содержит ребро, не принадлежащее ни одному предыдущему циклу. Фундаментальный базис циклов является автоматически слабо фундаментальным (для любого упорядочения циклов)[7]. Если любой базис циклов графа слабо фундаментален, это же верно для любого минора графа. Опираясь на это свойство, класс графов (и мультиграфов), для которых любой базисный цикл слабо фундаментален, можно описать с помощью пяти запрещённых миноров — графа квадратной пирамиды, мультиграфа, образованного удвоением всех рёбер цикла с четырьмя вершинами, двух мультиграфов, образованных удвоением пары рёбер тетраэдра и мультиграфа, образованного утроением рёбер треугольника[8].
Циклы граней[править | править код]
Если связный конечный планарный граф вложен в плоскость, каждая грань вложения окружена циклом рёбер. Одна грань будет неограничена (она содержит точки, произвольно далёкие от вершин графа), остальные грани будут ограничены. Согласно формуле Эйлера, существует ровно 
Симметрическая разность любого набора циклов граней является границей соответствующего набора граней и различные наборы ограниченных граней имеют различные границы, так что нельзя представить тот же самый набор, как симметрическую разность циклов более чем одним способом. Это означает, что циклы граней линейно независимы. Поскольку это линейно независимое множество имеет достаточно большой размер, оно обязательно образует базис циклов[9]. Этот базис всегда является слабо фундаментальным базисом циклов и является фундаментальным в том и только в том случае, когда вложение графа является внешнепланарным.
Для графов, правильно вложенных в другие поверхности таким образом, что все грани топологически являются дисками, в общем случае необязательно существует базис циклов, состоящий только из циклов граней. Циклы граней этих вложений дают подходящее подмножество всех эйлеровых подграфов. Группа гомологий 

Целые базисы[править | править код]
Используя теорию гомологий, пространство циклов графа можно интерпретировать как группу гомологий 




Минимальный вес[править | править код]
Если рёбрам графа приданы некоторые веса, вес подграфа можно вычислить как сумму весов рёбер. Базис пространства циклов с наименьшим весом обязательно будет базисом циклов — по теореме Веблена[11], любой эйлеров подграф, не являющийся сам по себе простым циклом, может быть разложен на несколько простых циклов, которые обязательно будут иметь меньший вес.
Согласно стандартным свойствам базисов векторных пространств и матроидах, базис циклов минимального веса не только минимизирует сумму весов циклов базиса, он также минимизирует любую другую монотонную комбинацию весов цикла. Например, он минимизирует вес самого длинного цикла базиса[12].
Алгоритмы полиномиального времени[править | править код]
В любом векторном пространстве и, в более общем случае, в любом матроиде базис с минимальным весом можно найти с помощью жадного алгоритма, который рассматривает возможные элементы базиса по одному в отсортированном порядке их весов и включает элемент в базис, если он линейно независим от отобранных до этого элементов. Проверку на линейную независимость можно провести с помощью исключений Гаусса. Однако неориентированный граф может иметь экспоненциально много простых циклов, так что получить и проверить все эти циклы становится невыполнимой задачей.
Хортон (Horton 1987) предложил первый алгоритм полиномиального времени для поиска базиса с минимальным весом в графах, у которых все веса больше нуля. Его алгоритм использует тот же подход «получить и проверить», но число просматриваемых циклов ограничивается небольшим множеством размера 
Если использовать алгоритм Дейкстры для поиска каждого кратчайшего дерева путей, а затем использовать исключение Гаусса для шагов проверки базового жадного алгоритма, получим алгоритм полиномиального времени для базиса циклов минимального веса.
Последующие исследования дали улучшенные алгоритмы для этой задачи[14][15][16][17], уменьшающие временную сложность худшего случая[en] для нахождения базиса циклов минимального веса до 


NP-трудность[править | править код]
Поиск фундаментального базиса минимального возможного веса тесно связан с задачей поиска остовного дерева, которое минимизирует средние попарные расстояния — обе задачи NP-трудны[19]. Поиск минимального по весу слабого фундаментального базиса также NP-труден[7] и аппроксимация MAXSNP-трудна[en][20]. Если разрешены отрицательные веса и циклы с отрицательным весом, то поиск базиса циклов минимального веса (без ограничений) также NP-труден, поскольку он может быть использован для поиска гамильтонова цикла — если граф гамильтонов, и задать всем рёбрам вес −1, базис циклов минимального веса будет содержать как минимум один гамильтонов цикл.
В планарных графах[править | править код]
Базис циклов с минимальным весом для планарного графа не обязательно совпадает с базисом, образованном границами граней — он может содержать циклы, не соответствующие граням, а также некоторые грани могут отсутствовать в качестве циклов в базисе с минимальным весом. Однако существует базис циклов минимального веса, в котором никакие два цикла не пересекают друг друга — для любых двух циклов в этом базисе либо циклы заключают непересекающиеся подмножества граней, либо один из двух циклов заключает внутри себя другой. Это множество циклов соответствует в двойственном графе данного планарного графа множеству разрезов, которые образуют дерево Гомори–Ху[en] двойственного графа, минимальный по весу базис пространства разрезов[21]. Основываясь на этой двойственности, явное представление базиса циклов минимального веса для планарного графа можно построить за время 
Приложения[править | править код]
Базисы циклов используются для решения задач периодического планирования, таких как задача планирования систем общественного транспорта. В этой задаче циклы базиса соответствуют переменным целочисленного программирования, используемого для решения задачи[23].
В теориях структурной жёсткости[en] и кинематики базисы циклов используются для построения системы неизбыточной системы уравнений, которую можно решить с целью проверки жёсткости структуры. В этой задаче базис циклов минимального или близкого к минимальному веса приводит к более простым системам уравнений[24].
В распределённых вычислениях базисы циклов используются для анализа числа необходимых шагов, чтобы алгоритм стабилизировался[25].
В биоинформатике базисы циклов используются для определения гаплотипа информации из данных генотипа[26]. Базис циклов также используется для анализа третичной структуры[en] РНК[27].
Базис циклов минимального веса графа ближайших соседей точек, взятых с трёхмерной поверхности, можно использовать для реконструкции поверхности[28].
Примечания[править | править код]
- ↑ Diestel, 2012.
- ↑ 1 2 Gross, Yellen, 2005.
- ↑ 1 2 3 4 Liebchen, Rizzi, 2007.
- ↑ Diestel, 2012, pp. 32, 65.
- ↑ Tutte, 1963. Смотрите, в частности, теорему 2.5.
- ↑ Cribb, Ringeisen, Shier, 1981.
- ↑ 1 2 Rizzi, 2009.
- ↑ Hartvigsen, Zemel, 1989.
- ↑ 1 2 Diestel, 2012, стр. 105—106.
- ↑ Mac Lane, 1937.
- ↑ Veblen, 1912.
- ↑ Chickering, Geiger, Heckerman, 1995.
- ↑ Horton, 1987.
- ↑ Berger, Gritzmann, de Vries, 2004.
- ↑ Mehlhorn, Michail, 2006.
- ↑ Kavitha, Mehlhorn, Michail, Paluch, 2008.
- ↑ Kavitha, Liebchen, Mehlhorn, Michail, Rizzi, Ueckerdt, Zweig, 2009.
- ↑ Amaldi, Iuliano, Rizzi, 2010.
- ↑ Deo, Prabhu, Krishnamoorthy, 1982.
- ↑ Galbiati, Amaldi, 2004.
- ↑ Hartvigsen, Mardon, 1994.
- ↑ Borradaile, Sankowski, Wulff-Nilsen, 2010.
- ↑ Liebchen, 2007.
- ↑ Cassell, De Henderson, Kaveh, 1974.
- ↑ Boulinier, Petit, Villain, 2004.
- ↑ Aguiar, Istrail, 2012.
- ↑ Lemieux, Major, 2006.
- ↑ Gotsman, Kaligosi, Mehlhorn, Michail, Pyrga, 2007.
Литература[править | править код]
- Reinhard Diestel. 1.9 Some linear algebra // Graph Theory. — Springer, 2012. — Т. 173. — С. 23–28. — (Graduate Texts in Mathematics).
- David M. Chickering, Dan Geiger, David Heckerman. On finding a cycle basis with a shortest maximal cycle // Information Processing Letters. — 1995. — Т. 54, вып. 1. — С. 55–58. — doi:10.1016/0020-0190(94)00231-M.
- J. D. Horton. A polynomial-time algorithm to find the shortest cycle basis of a graph // SIAM Journal on Computing. — 1987. — Т. 16, вып. 2. — С. 358–366. — doi:10.1137/0216026.
- S. Mac Lane. A combinatorial condition for planar graphs // Fundamenta Mathematicae. — 1937. — Т. 28. — С. 22–32.
- Oswald Veblen. An application of modular equations in analysis situs // Annals of Mathematics. — 1912. — Т. 14, вып. 1. — С. 86–94. — JSTOR 1967604.
- Franziska Berger, Peter Gritzmann, Sven de Vries. Minimum cycle bases for network graphs // Algorithmica. — 2004. — Т. 40, вып. 1. — С. 51–62. — doi:10.1007/s00453-004-1098-x.
- Kurt Mehlhorn, Dimitrios Michail. Implementing minimum cycle basis algorithms // ACM Journal of Experimental Algorithmics. — 2006. — Т. 11. — doi:10.1145/1187436.1216582.
- Telikepalli Kavitha, Kurt Mehlhorn, Dimitrios Michail, Katarzyna E. Paluch. An
algorithm for minimum cycle basis of graphs // Algorithmica. — 2008. — Т. 52, вып. 3. — С. 333–349. — doi:10.1007/s00453-007-9064-z.
- Telikepalli Kavitha, Christian Liebchen, Kurt Mehlhorn, Dimitrios Michail, Romeo Rizzi, Torsten Ueckerdt, Katharina A. Zweig. Cycle bases in graphs: Characterization, algorithms, complexity, and applications // Computer Science Review. — 2009. — Т. 3, вып. 4. — С. 199–243. — doi:10.1016/j.cosrev.2009.08.001.
- W. T. Tutte. How to draw a graph // Proceedings of the London Mathematical Society. — 1963. — Т. 13. — С. 743–767. — doi:10.1112/plms/s3-13.1.743.
- D. W. Cribb, R. D. Ringeisen, D. R. Shier. Proceedings of the Twelfth Southeastern Conference on Combinatorics, Graph Theory and Computing, Vol. I (Baton Rouge, La., 1981). — 1981. — Т. 32. — С. 221–229. — (Congressus Numerantium).
- David Hartvigsen, Eitan Zemel. Is every cycle basis fundamental? // Journal of Graph Theory. — 1989. — Т. 13, вып. 1. — С. 117–137. — doi:10.1002/jgt.3190130115.
- David Hartvigsen, Russell Mardon. The all-pairs min cut problem and the minimum cycle basis problem on planar graphs // SIAM Journal on Discrete Mathematics. — 1994. — Т. 7, вып. 3. — С. 403–418. — doi:10.1137/S0895480190177042.
- Edoardo Amaldi, Claudio Iuliano, Romeo Rizzi. Integer Programming and Combinatorial Optimization: 14th International Conference, IPCO 2010, Lausanne, Switzerland, June 9-11, 2010, Proceedings. — Springer, 2010. — Т. 6080. — С. 397–410. — (Lecture Notes in Computer Science). — doi:10.1007/978-3-642-13036-6_30.
- Giulia Galbiati, Edoardo Amaldi. Approximation and Online Algorithms: First International Workshop, WAOA 2003, Budapest, Hungary, September 16-18, 2003, Revised Papers. — Berlin: Springer, 2004. — Т. 2909. — С. 151–164. — (Lecture Notes in Computer Science). — doi:10.1007/978-3-540-24592-6_12.
- Narsingh Deo, G. M. Prabhu, M. S. Krishnamoorthy. Algorithms for generating fundamental cycles in a graph // ACM Transactions on Mathematical Software. — 1982. — Т. 8, вып. 1. — С. 26–42. — doi:10.1145/355984.355988.
- Glencora Borradaile, Piotr Sankowski, Christian Wulff-Nilsen. Proc. 51st Annual IEEE Symposium on Foundations of Computer Science (FOCS 2010). — IEEE Computer Soc., Los Alamitos, CA, 2010. — С. 601–610. — doi:10.1109/FOCS.2010.63.
- Christian Liebchen, Romeo Rizzi. Classes of cycle bases // Discrete Applied Mathematics. — 2007. — Т. 155, вып. 3. — С. 337–355. — doi:10.1016/j.dam.2006.06.007.
- Christian Liebchen. Periodic timetable optimization in public transport // Operations Research Proceedings. — 2007. — Т. 2006. — С. 29–36. — doi:10.1007/978-3-540-69995-8_5.
- A. C. Cassell, J. C. De Henderson, A. Kaveh. Cycle bases for the flexibility analysis of structures // International Journal for Numerical Methods in Engineering. — 1974. — Т. 8, вып. 3. — С. 521–528. — doi:10.1002/nme.1620080308.
- Christian Boulinier, Franck Petit, Vincent Villain. Proceedings of the Twenty-third Annual ACM Symposium on Principles of Distributed Computing (PODC ’04). — New York, NY, USA: ACM, 2004. — С. 150–159. — doi:10.1145/1011767.1011790.
- Derek Aguiar, Sorin Istrail. HapCompass: A Fast Cycle Basis Algorithm for Accurate Haplotype Assembly of Sequence Data // Journal of Computational Biology. — 2012. — Т. 19, вып. 6. — С. 577–590. — doi:10.1089/cmb.2012.0084.
- Sébastien Lemieux, François Major. Automated extraction and classification of RNA tertiary structure cyclic motifs // Nucleic Acids Research. — 2006. — Т. 34, вып. 8. — С. 2340–2346. — doi:10.1093/nar/gkl120.
- Sébastien Lemieux, François Major. Automated extraction and classification of RNA tertiary structure cyclic motifs // Nucleic Acids Research. — 2006. — Т. 34, вып. 8. — С. 2340–2346. — doi:10.1093/nar/gkl120.
- Craig Gotsman, Kanela Kaligosi, Kurt Mehlhorn, Dimitrios Michail, Evangelia Pyrga. Cycle bases of graphs and sampled manifolds // Computer Aided Geometric Design. — 2007. — Т. 24, вып. 8—9. — С. 464–480. — doi:10.1016/j.cagd.2006.07.001.
- Jonathan L. Gross, Jay Yellen. 4.6 Graphs and Vector Spaces // Graph Theory and Its Applications. — 2nd. — CRC Press, 2005. — С. 197–207. — ISBN 9781584885054.
- Romeo Rizzi. Minimum weakly fundamental cycle bases are hard to find // Algorithmica. — 2009. — Т. 53, вып. 3. — С. 402–424. — doi:10.1007/s00453-007-9112-8.
Фундаментальные циклы
Компактное представление пространства дает его базис. Если выписать все
простые циклы графа 
базисом, так как некоторые из этих циклов могут быть суммами других
(см. пример на рис. 7.1). Построить базис пространства ![C[G]](https://intuit.ru/sites/default/files/tex_cache/40f7582c1aef765b7b3649cd37f50564.png)
какой-нибудь каркас 
– все ребра
графа 

ребро 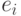
(простой)
цикл 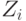
циклов,
они называются фундаментальными циклами относительно
каркаса 
Теорема 2. Множество всех фундаментальных циклов относительно
любого каркаса 

пространства циклов этого графа.
Доказательство. Зафиксируем некоторый каркас 
фундаментальные циклы 
этого
каркаса. В каждом из этих циклов имеется ребро 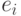
принадлежащее
данному циклу и не принадлежащее никакому из остальных. Поэтому при
сложении этого цикла с другими фундаментальными циклами данное
ребро не “уничтожится” – оно будет присутствовать в
суммарном графе.
Следовательно, сумма различных фундаментальных циклов никогда не будет
пустым графом, то есть фундаментальные циклы линейно независимы.
Покажем теперь, что любой квазицикл графа 
фундаментальных циклов. Действительно, пусть 
квазицикл.
Пусть 
ребра 
не принадлежащие 
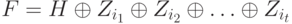
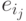

слагаемых этой
суммы – в 

при сложении все
эти ребра уничтожатся. Все остальные ребра, присутствующие
в графах-слагаемых, принадлежат 
– подграф
графа 
значит, 
тоже квазицикл. Но в 
единственная возможность: 

Из этой теоремы следует, что размерность пространства циклов графа равна
числу ребер, не входящих в его каркас. Так как каркас содержит
ребер, где 
размерность
равна 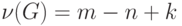
графа.
Построение базы циклов
Базис пространства циклов графа коротко называют базой циклов.
На основании теоремы 2 можно предложить достаточно простой способ построения
базы циклов графа. Сначала находится какой-нибудь каркас, затем для
каждого ребра, не принадлежащего каркасу, отыскивается тот единственный
цикл, который это ребро образует с ребрами каркаса. Таким образом, любой
алгоритм построения каркаса может быть использован для нахождения базы
циклов.
Поиск в глубину особенно удобен благодаря основному свойству DFS-дерева
(теорема 1 из
“Поиск в глубину”
) – каждое обратное ребро относительно этого дерева
является продольным. Это означает, что из двух вершин такого ребра одна
является предком другой в DFS-дереве. Каждое такое ребро в процессе поиска
в глубину встретится дважды – один раз, когда активной вершиной будет
предок, другой раз, когда ею будет потомок. В этом последнем случае
искомый фундаментальный цикл состоит из рассматриваемого обратного ребра
и участка пути в DFS-дереве, соединяющего эти две вершины. Но этот путь так
или иначе запоминается в процессе обхода в глубину, так как он необходим
для последующего возвращения. Если, например, для хранения открытых вершин
используется стек, то вершины этого пути находятся в верхней части стека.
В любом случае этот путь легко доступен и цикл находится без труда.
Запишем процедуру построения фундаментальных циклов на базе алгоритма
поиска в глубину с построением DFS-дерева. Переменная 
счетчик
циклов, 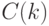
составляющих цикл
с номером 
Алгоритм 1. Построение базы циклов.
- пометить все вершины как новые
-
for
do if
новая then
Procedure
- открыть вершину
-
while
открытая do
-
if имеется неисследованное
ребро -
then пометить ребро
как исследованное -
if вершина
новая
-
then открыть
вершину -
else
-
else закрыть вершину
Procedure
- Создать список
из одного элемента
-
repeat
- добавить
к списку
-
until
Хотя сам поиск в глубину выполняется за линейное от числа вершин и ребер
время, решающее влияние на трудоемкость этого алгоритма оказывает
необходимость запоминать встречающиеся циклы. Подсчитаем суммарную длину
этих циклов для полного графа с 
случае является простым путем, относительно него будет
цикла
длины 
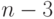
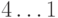
длины 
длин всех фундаментальных циклов будет равна
Таким образом, на некоторых графах число операций этого алгоритма будет
величиной порядка 
- Download source – 9.7 KB
1. Introduction
Graphs can be used in many different applications from electronic engineering describing electrical circuits to theoretical chemistry describing molecular networks. It can be necessary to enumerate cycles in the graph or to find certain cycles in the graph which meet certain criteria. In this article, I will explain how to in principle enumerate all cycles of a graph but we will see that this number easily grows in size such that it is not possible to loop through all cycles. However, the ability to enumerate all possible cycles allows one to use heuristical methods like Monte Carlo or Evolutionary Algorithms to answer specific questions regarding cycles in graphs (e.g., finding the smallest or largest cycle, or cycles of a specific length) without actually visiting all cycles.
Here, I will address undirected unweighted graphs (see Figure 1a for an example) but the algorithm is straightforwardly transferable to weighted graphs.
2. Fundamentals
In this section, all tools which are absolutely necessary to understand the following sections will be explained.
a) Representation of a Graph
The first topic is the representation of a given graph (e.g., as shown in Fig. 1a) in the program code. A common and practical approach is the adjacency matrix (A). It consists of NxN elements, where N is the number of nodes in the graph. Each Element (A_{ij}) equals 1 if the two nodes (i) and (j) are connected and zero otherwise. The adjacency matrix for the Graph shown in Fig. 1a is shown in Fig. 1b. As we are dealing with undirected graphs, the adjacency matrix is symmetrical, i.e., just the lower or upper half is needed to describe the graph completely because if node A is connected to node B, it automatically follows that B is connected to A. Additionally also, the diagonal elements are neglected which were only needed to indicate that one node is connected with itself. Consequently, this would automatically be a fundamental node of the whole graph because it cannot be divided further.
The code provides a class HalfAdjacencyMatrix used to represent a graph. As described, it just stores one half of the matrix and additionally neglects the diagonal elements.
The class can also be used to store a cycle, path or any kind of substructure in the graph. In that case, there might be nodes which do not belong to the substructure and therefore have no edges. The adjacency matrix might also contain two or more disjoint substructures (see below).
Fig. 1: An undirected graph (a) and its adjacency matrix (b).
b) Combining Two Paths / Cycles
To determine a set of fundamental cycles and later enumerate all possible cycles of the graph, it is necessary that two adjacency matrices (which might contain paths, cycles, graphs, etc.), can be merged.
This will be done in the following by applying the logical XOR operator on each edge of the two adjacency matrices. In the following two examples are presented how the XOR-operator can be used to yield merged paths and cycles.
Fig. 2: Illustration of the XOR operator applied to two distinct paths (a) and to two distinct cycles (b) within an arbitrary graph.
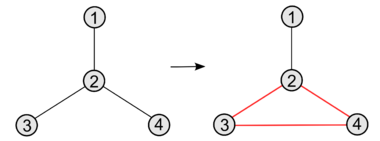
In Fig. 2a, the XOR operator is applied to two paths both emerging from the root element in the given graph. The result is a closed cycle B-C-D-B where the root element A was excluded. This scheme will be used to yield a fundamental cycle from two paths of a graphs spanning tree as described in Sec. 3.
Two cycles are combined in Fig. 2b yielding a new cycle. This scheme will be used in Sec. 4 to form new cycles from the cycle base of the graph.
The implementation of the XOR-operator (operator^) is straightforward. The function loops over each bit present in the two matrices and applies XOR to each bit (edge), individually. The class additionally provides operator^= for convenience.
inline HalfAdjacencyMatrix operator^(const HalfAdjacencyMatrix& rhs) const { if(m_nNodes != rhs.m_nNodes) throw std::runtime_error("HalfAdjacencyMatrix::operator^(): The two matrices MUST be of the same size!"); HalfAdjacencyMatrix result(m_nNodes); for(size_t i = 0; i < m_aBits.size(); ++i) { if((m_aBits[i] || rhs.m_aBits[i]) && (m_aBits[i] != rhs.m_aBits[i])) { result.m_aBits[i] = 1; ++result.m_nEdges; } } return result; }
3. Finding a Fundamental Cycle Set
a) Spanning Trees
The algorithm described here follows the algorithm published by Paton [1]. The central idea is to generate a spanning tree from the undirected graph. After the spanning tree is built, we have to look for all edges which are present in the graph but not in the tree. Adding one of the missing edges to the tree will form a cycle which is called fundamental cycle. Note that a graph can have many different spanning trees depending on the chosen root node and the way the tree was built. Consequently, each spanning tree constructs its own fundamental cycle set. All fundamental cycles form a cycle basis, i.e., a basis for the cycle space of the graph. As the basis is complete, it does not matter which spanning tree was used to generate the cycle basis, each basis is equally suitable to construct all possible cycles of the graph. Two possible spanning trees of the exemplary graph shown in Fig. 1a are shown in Fig. 3 which were built using the depth-first (a) and the breadth-first search (b), respectively.
Note that Paton prefers depth-first search over breadth-first search because using depth-first search each node just differs by one edge from the main branch. This can be utilized to construct the fundamental cycles more efficiently. For simplicity, I use the XOR operator to combine two paths of the spanning tree and thus both, depth-first and breadth-first search are equally efficient.
Fig. 3: Generation of a minimal spanning tree of the undirected graph in Fig. 1a. Depth-first search (a) is illustrated vs. breadth-first search (b). All edges which are missing in the tree but present in the graph are shown as red dashed lines.
b) Size of the Cycle Base
As stated in the previous section, the fundamental cycles in the cycle base will vary depending on the chosen spanning tree. However, the number of fundamental cycles is always the same and can be easily calculated:
For any given undirected graph having (V) nodes and (E) edges, the number of fundamental cycles (N_{text{FC}}) is:
$N_{text{FC}} = E – V + 1 quad$
assuming that the graph is fully connected in the beginning [2]. This number is also called “cycle rank” or “circuit rank” [3].
c) Pseudo-Code
V: All Vertices
E: All Edges
pick start Vertex v in V
T = {v} // Spanning tree
Q = {v} // Process Queue
while not Q.empty:
i := Q.top
for j < |V|
if (i,j) in E
if j in T
// Fundamental Cycle Found!
pi := T.pathFromRootToElement(i)
pj := T.pathFromRootToElement(j)
cycle := merge pi and pj
else
Q.push(j)
insert j to T and set i as parent of j
The above psudo code finds a set of fundamental cycles for the given graph described by V and E.
There are a few things to address here:
- How to pick the start vertex
v?
As discussed earlier, the spanning tree will depend on the chosen start vertexvand therefore also the fundamental cycle set. However as the cycle bases are all equivalent, it does not matter which vertex is chosen, thus in this implementation, just the first node in the graph is picked. - How are the two paths,
piandpjmerged?
The simplest method to merge the two paths is the XOR operator:
Here, one directly gets rid of all the edges which are present in both paths, i.e., A-C and C-F in the given example. Note that the edge E-D (red dotted line) is not present in the tree and must be added to yield the fundamental cycle.
d) Implementation
The implementation follows a standard depth-search algorithm. As soon as a node is found which was already visited, a cycle of the graph was found. By combining the paths to the current node and the found node with the XOR operator, the cycle represented by an adjacency matrix is obtained and stored in the class for later usage.
void Graph::computeFundamentalCycles() { if(!m_aFundamentalCycles.empty()) return; std::unique_ptr<TreeNode[]> aTree(new TreeNode[m_aNodes.size()]); std::stack<size_t> nodeStack; nodeStack.push(0); HalfAdjacencyMatrix adjMat = m_adjMat; for(size_t i = 0; i < m_aNodes.size(); ++i) { aTree[i].parent = &aTree[i]; aTree[i].index = i; } while(nodeStack.size() > 0) { size_t currentNodeIndex = nodeStack.top(); nodeStack.pop(); TreeNode& currentTreeNode = aTree[currentNodeIndex]; for(size_t j = 0; j < m_aNodes.size(); ++j) { if(!adjMat.isConnected(currentNodeIndex, j)) continue; if(aTree[j].parent != &aTree[j]) { HalfAdjacencyMatrix pi(m_aNodes.size()), pj(m_aNodes.size()); unique_tree_path(&aTree[currentNodeIndex], pi); unique_tree_path(&aTree[j], pj); pi.connect(currentNodeIndex, j); m_aFundamentalCycles.push_back(pi ^ pj); } else { aTree[j].parent = ¤tTreeNode; nodeStack.push(j); } adjMat.disconnect(currentNodeIndex, j); } } }
4. Iterating Through All Possible Cycles
In this last section, we use the set of fundamental cycles obtained as a basis to generate all possible cycles of the graph. As the set of fundamental cycles is complete, it is guaranteed that all possible cycles will be obtained.
a) How to Combine Fundamental Cycles?
To combine two cycles again, the XOR operator can be used. Assume the three fundamental cycles (A-B-E-F-C-A; B-D-E-B; D-E-F-D) illustrated with red dotted lines are found by our algorithm as complete basis:
As an example, combining the two cycles B-D-E-B and D-E-F-D using XOR will erase the edge D-E and yields the circle B-D-F-E-B (blue lines).
However, it is not sufficient to just combine pairs of circles because then the encircling cycle (A-B-D-F-C-A) would not be found which is only obtained if all three fundamental cycles are combined, erasing the edges B-E, D-E and E-F. In general, it is necessary to iterate through all possible tuples of fundamental cycles starting with pairs and ending with the (N_text{FC})-tuple (total number of fundamental cycles).
b) How to Represent a Tuple of Fundamental Cycles?
Straightforwardly, tuples of fundamental cycles can be represented in the code by a bitstring of length (N_text{FC}). For the example graph, the bitstring would therefore be of length 3 yielding the following possible combinations of the three fundamental cycles (FCs):
| Bitstring | XOR Combination | Cycle |
| 100 | FC1 | A-B-E-F-C-A |
| 010 | FC2 | B-D-E-B |
| 001 | FC3 | D-E-F-D |
| 110 | FC1 ^ FC2 | A-B-D-E-F-C-A |
| 101 | FC1 ^ FC3 | A-B-E-D-F-C-A |
| 011 | FC2 ^ FC3 | B-D-F-E-B |
| 111 | FC1 ^ FC2 ^ FC3 | A-B-D-F-C-A |
Within the representation of bitstrings, all possible cycles are enumerated, i.e., visited, if all possible permutations of all bitstrings with (2 le k le N_text{FC}), where (k) is the number of 1s in the string, are enumerated.
E.g., if a graph has four fundamental cycles, we would have to iterate through all permutations of the bitstrings, 1100, 1110 and 1111 being 11 iterations in total.
c) Combinatorics
Let’s talk about some math at this point to see how this approach scales. Starting with pairs, we have to know how many permutations of 2 ones in a bitstring of (N_text{FC}) are possible. This number is directly given by the binomial coefficient of (N_text{FC}) choose 2″. In general, if we want to know how many permutations of (k) ones in a bitstring of length (N_text{FC}) are possible, this number is given by the binomial coefficient of (N_text{FC}) choose (k)“. To get the total number of combinations of fundamental cycles, the binomial coefficients starting from (k=2) to (k=N_text{FC}) have to be summed up yielding the following equation:
$sum_{k=2}^{N=N_text{FC}}binom{N}{k} =
sum_{k=0}^{N}binom{N}{k} – binom{N}{1} – binom{N}{0} = 2^N – N – 1$
The code therefore scales exponential with the number of fundamental cycles in the graph. Exponential scaling is always a problem because of the vast number of iterations, it is usually not possible to iterate through all combinations as soon as (N) grows in size. To get an impression of the scaling, we estimate that one iteration needs 10ms to be computed. Then one would need 10 seconds for (N=10) but approximately 11 years for (N=35). One can easily see that the time needed for one iteration becomes negligible as soon as (N) becomes large enough yielding an unsolvable problem.
Note that this is only true if one would really want to enumerate each and every possible cycle. However, for most questions, it is sufficient to just be in principle able to visit every cycle without doing so, e.g. heuristical algorithms, Monte Carlo or Evolutionary algorithms. In general, it is therefore a good idea to rethink the question, asked to the graph, if an enumeration of all possible cycles of a graph is necessary.
d) Cycle Validation
Now that we know how to combine the different fundamental cycles, there is still one problem left which is related to the XOR operator: Combining two disjoint cycles with an XOR operation will again lead two disjoint cycles. Therefore, each combination must be validated to ensure that one joint cycle is generated.
Let’s start with how to check if a pair of fundamental cycles generates one adjoint cycle. This is rather straightforward because we just have to apply the AND operator and check if there are edges belonging to both cycles. This check can be integrated into the XOR operation directly: If one or more edges are cleaved by the operation, then the two cycles have at least one edge in common and generate a new valid cycle.
For higher tuples, the validation unfortunately is not that simple: Consider merging three cycles, then it is necessary that at least two edges are cleaved during the XOR operation. However, this test is not sufficient because two of the three cycles could have two edges in common and the third cycle is disjoint. One option would be to keep track of all pairs and check if edges are cleaved between a valid pair and the third cycle but this would result in two major disadvantages:
- All possible pairs of fundamental cycles have to be computed before triples can be computed. As soon if we have to deal with quadruples, quintuples or higher tuples all “lower” tuples have to be computed before the higher tuples can be evaluated. Thus random accessing any possible bitstring is not possible anymore.
- Recall that given by the combinatorics this method would require a vast amount of memory to store valid combinations.
Therefore, I will use a very simple approach which might not be the most efficient one: For each (k)-tuple combination where (k>2) a depth search algorithm will be used to check if the merged substructure in the CycleMatrix (typedef HalfAdjacencyMatrix) is completely connected. This is straightforwardly implemented as just the visited edges have to be counted. If this number is equal to the total number of edges, then the tuple formed one adjoined cycle.
bool validateCycleMatrix(const CycleMatrix& m) { size_t pathLength = 0; for (size_t i = 0; i < m_aNodes.size(); ++i) { for (size_t j = 0; j < m_aNodes.size(); ++j) { if (m.isConnected(i, j)) { ++pathLength; std::set<size_t> aVisited; aVisited.insert(i); validateCycleMatrix_recursion(m, pathLength, j, i, aVisited); return pathLength + 1 == m.getNumEdges(); } } } throw std::runtime_error("Graph::validateCycleMatrix(): Given Cycle Matrix does not contain any edges!"); }
The method validateCycleMatrix just takes the CycleMatrix which is to be validated. Then it looks for the first present edge and starts a depth search (which is related to the same algorithm already used to determine the spanning tree) recursively using validateCycleMatrix_recursion. The cycle is valid if the number of edges visited by the depth search equals the number of total edges in the CycleMatrix.
void validateCycleMatrix_recursion(const CycleMatrix& m, size_t& pathLength, const size_t i, size_t previousNode, std::set<size_t>& aVisited) const { if (pathLength > 500) throw runtime_error ("Graph::validateCycleMatrix_recursion(): Maximum recursion level reached."); for (size_t j = 0; j < m_aNodes.size(); ++j) { if (m.isConnected(i, j) && j != previousNode) { auto ppVisited = aVisited.find(j); if (ppVisited != aVisited.end()) { return; } ++pathLength; aVisited.insert(i); validateCycleMatrix_recursion(m, pathLength, j, i, aVisited); return; } } throw std::runtime_error("Graph::validateCycleMatrix_recursion(): Found a dead end!"); }
e) Implementation
In the following, all steps necessary to enumerate all cycles of the graph are summarized in one single function which tries to save all cycles in the class; if possible. The code also offers an iterator (CycleIterator) which follows an C++ input iterator. Note that this function’s purpose is mainly to illustrate how to put all ends described in the previous sections together and it will literally take for ages if the cycle rank of the given graph is large enough.
void computeAllCycles() { if(m_aFundamentalCycles.empty()) computeFundamentalCycles(); m_aCycles = m_aFundamentalCycles; std::vector<bool> v(m_aFundamentalCycles.size()); for(size_t r = 2; r <= m_aFundamentalCycles.size(); ++r) { std::fill_n(v.begin(), r, 1); std::fill_n(v.rbegin(), v.size() - r, 0); do { CycleMatrix M(m_aNodes.size()); size_t nEdges = 0; for (size_t i = 0; i < m_aFundamentalCycles.size(); ++i) if (v[i]) { M ^= m_aFundamentalCycles[i]; nEdges += m_aFundamentalCycles[i].getNumEdges(); } if(r == 2) { if(nEdges > M.getNumEdges()) m_aCycles.push_back(M); } else { if(validateCycleMatrix(M)) m_aCycles.push_back(M); } } while (std::prev_permutation(v.begin(), v.end())); } }
5. Outlook
The code can straightforwardly be extended to carry weights for each edge and the use of bitstrings to represent each cycle allows one to directly use a genetic algorithm to find longest paths or shortest paths fulfilling certain constraints without actually visiting all possible cycles.
6. Code
The assigned code contains all described classes and functions. There is also an example code which enumerates all cycles of the graph in Fig. 1a. The function CreateRandomGraph generates a random graph with a given connection probability for each edge. The code is tested using VC++ 2017 (on Windows) and GCC 6.4.0 (on Linux). Note that the code uses some C++11 features and therefore must be compiled using -std=c++11 or higher (GCC).
7. History
June 2018 – Version 2
Unfortunately, there was a code error in the original post where a debug code remained in the uploaded version. The following code lines were replaced in the function “Graph::computeAllCycles()” and “Graph::CycleIterator::next()“:
if (r < 5) std::fill_n(v.begin() + r + 1, 5 - r - 1, 0); std::fill_n(v.rbegin(), v.size() - r, 0);
September 2018 – Version 3
I uploaded a patch for an error in the validateCycleMatrix method: In line number 666, the line:
return pathLength == m.getNumEdges();
was replaced by:
return pathLength + 1 == m.getNumEdges();
This change was necessary as the deep search algorithm used to validate the CycleMatrix determines the cycle length but does not account for the last edge closing the cycle which connects the last visited node with the starting node. Thus, the total number of edges in the CycleMatrix has to be equal to the path length as obtained by the deep search algorithm plus one.
An additional test with a slightly larger graph than in Fig. 1a is added to test the patch.
The code was changed in both, the article and the download source.
References
- [1] Paton, Keith (1969), “An Algorithm for Finding a Fundamental Set of Cycles of a Graph”, Scientific Applications 12:514
- [2] Berge, Claude (2001), “Cyclomatic number”, The Theory of Graphs, Courier Dover Publications, pp. 27–30
- [3] Circuit rank. In Wikipedia. Retrieved January 07, 2018, from https://en.wikipedia.org/wiki/Circuit_rank
This member has not yet provided a Biography. Assume it’s interesting and varied, and probably something to do with programming.






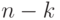
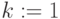
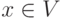 do if
do if 
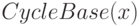
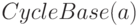

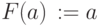
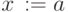

 новая
новая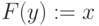

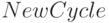


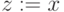

 к списку
к списку