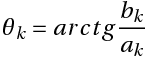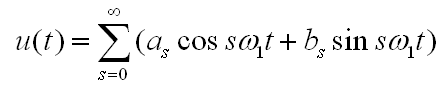Ряды Фурье – способ представления сложной функции суммой более простых, хорошо известных.
Синус и косинус – это периодические функции. Еще они образуют ортогональный базис. Это свойство можно объяснить по аналогии с осями XX и YY на координатной плоскости. Точно так же, как мы можем описать координаты точки относительно осей, мы можем описать любую функцию относительно синусов и косинусов. Тригонометрические функции хорошо изучены и их легко применять в математике.
Представить синусы и косинусы можно в виде таких волн:
Синие – это косинусы, красные – синусы. Еще такие волны называют гармониками. Косинусы – четными, синусы – нечетными. Термин гармоника пришел еще из античности и связан с наблюдениями о взаимосвязи высот звуков в музыке.
Что такое ряд Фурье
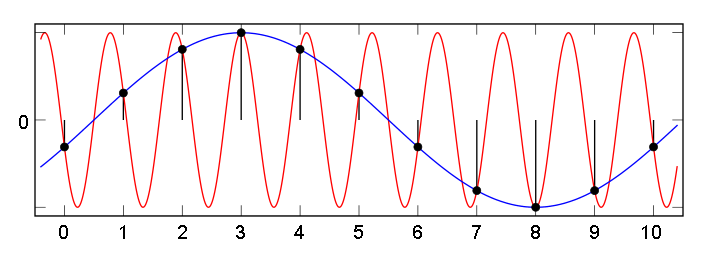
Такой ряд, где в качестве простейших используются функции синуса и косинуса, называется тригонометрическим. Назван он в честь своего изобретателя Жана Батиста Жозефа Фурье, в конце XVIII–начале XIX в. доказавшего, что любую функцию можно представить в виде комбинации таких гармоник. И чем больше их взять, тем точнее это представление будет. Для примера картинка ниже: можно заметить, что с большим количеством гармоник, т. е. членов ряда Фурье, красный график становится все ближе к синему – исходной функции.
Практическое применение в современном мире
А вообще нужны ли эти ряды сейчас? Где они могут применяться практически и использует ли их кто-то кроме математиков-теоретиков? Оказывается, Фурье потому и знаменит на весь мир, что практическая польза его рядов буквально неисчислима. Их удобно применять там, где есть какие-либо колебания или волны: акустика, астрономия, радиотехника и т. д. Самый простой пример его использования: механизм работы фотоаппарата или видеокамеры. Если объяснять вкратце, эти устройства записывают не просто картинки, а коэффициенты рядов Фурье. И работает это везде – при просмотре картинок в интернете, фильма или прослушивании музыки. Именно благодаря рядам Фурье вы сейчас можете прочитать эту статью со своего мобильного телефона. Без преобразования Фурье нам не хватило бы никакой пропускной способности интернет-соединений, чтобы просто посмотреть видео на YouTube даже в стандартном качестве.
На этой схеме двухмерное преобразование Фурье, которое используется для разложения изображения на гармоники, т. е. базисные составляющие. На этой схеме черным закодировано значение -1, белым 1. Вправо и вниз по графику увеличивается частота.
Разложение в ряд Фурье
Наверное, вы уже устали читать, поэтому перейдем к формулам.
Для такого математического приема, как разложение функций в ряд Фурье, придется брать интегралы. Много интегралов. В общем виде ряд Фурье записывают в виде бесконечной суммы:
f(x)=A+∑n=1∞(ancos(nx)+bnsin(nx))f(x) = A + displaystylesum_{n=1}^{infty}(a_n cos(nx)+b_n sin(nx))
где
A=12π∫−ππf(x)dxA = frac{1}{2pi}displaystyleintlimits_{-pi}^{pi} f(x)dx
an=1π∫−ππf(x)cos(nx)dxa_n = frac{1}{pi}displaystyleintlimits_{-pi}^{pi} f(x)cos(nx)dx
bn=1π∫−ππf(x)sin(nx)dxb_n = frac{1}{pi}displaystyleintlimits_{-pi}^{pi} f(x)sin(nx)dx
Если мы каким-то образом сможем посчитать бесконечное количество ana_n и bnb_n (они и называются коэффициентами разложения Фурье, AA – это просто постоянная этого разложения), то полученный ряд в результате будет на 100% совпадать с исходной функцией f(x)f(x) на отрезке от −π-pi до πpi. Такой отрезок обусловлен свойствами интегрирования синуса и косинуса. Чем больше nn, для которого мы рассчитаем коэффициенты разложения функции в ряд, тем точнее будет это разложение.
Возьмем простую функцию y=5xy=5x
A=12π∫−ππf(x)dx=12π∫−ππ5xdx=0A = frac{1}{2pi}displaystyleintlimits_{-pi}^{pi} f(x)dx = frac{1}{2pi}displaystyleintlimits_{-pi}^{pi} 5xdx = 0
a1=1π∫−ππf(x)cos(x)dx=1π∫−ππ5xcos(x)dx=0a_1 = frac{1}{pi}displaystyleintlimits_{-pi}^{pi} f(x)cos(x)dx = frac{1}{pi}displaystyleintlimits_{-pi}^{pi} 5xcos(x)dx = 0
b1=1π∫−ππf(x)sin(x)dx=1π∫−ππ5xsin(x)dx=10b_1 = frac{1}{pi}displaystyleintlimits_{-pi}^{pi} f(x)sin(x)dx = frac{1}{pi}displaystyleintlimits_{-pi}^{pi} 5xsin(x)dx = 10
a2=1π∫−ππf(x)cos(2x)dx=1π∫−ππ5xcos(2x)dx=0a_2 = frac{1}{pi}displaystyleintlimits_{-pi}^{pi} f(x)cos(2x)dx = frac{1}{pi}displaystyleintlimits_{-pi}^{pi} 5xcos(2x)dx = 0
b2=1π∫−ππf(x)sin(2x)dx=1π∫−ππ5xsin(2x)dx=−5b_2 = frac{1}{pi}displaystyleintlimits_{-pi}^{pi} f(x)sin(2x)dx = frac{1}{pi}displaystyleintlimits_{-pi}^{pi} 5xsin(2x)dx = -5
И так далее. В случае с такой функцией мы можем сразу сказать, что все an=0a_n=0, коэффициенты bnb_n придется вычислять. Если мы возьмем первые четыре члена разложения в ряд Фурье для функции y=5xy=5x, получим:
5x≈10⋅sin(x)−5⋅sin(2⋅x)+103⋅sin(3⋅x)−52⋅sin(4⋅x)5x approx 10 cdot sin(x) – 5 cdot sin(2 cdot x) + frac{10}{3} cdot sin(3 cdot x) – frac{5}{2} cdot sin (4 cdot x)
График получившейся функции будет выглядеть следующим образом:
Получившееся разложение в ряд Фурье приближается к нашей исходной функции. Если мы возьмем большее количество членов ряда, например, 15, то увидим уже следующее:
Чем больше членов разложения в ряд, тем выше точность.
Если мы немного изменим масштаб графика, сможем заметить еще одну особенность преобразования: ряд Фурье – это периодическая функция с периодом 2π2pi.
Таким образом, можно представлять любую функцию, которая является непрерывной на отрезке [−π;π][-pi;pi]. Все это нужно для того, чтобы облегчить анализ каких-то явлений, которые описываются сложными функциями. Не всегда возможно аналитически (т. е. по формуле) посчитать производную, а в случае с набором синусов и косинусов такой проблемы не возникнет. Собственно разложение в ряд Фурье показывает, что зачастую задачи можно решать аналитически на упрощенных моделях, одним из примеров которых и является ряд Фурье.
Тест по теме «Ряды Фурье»
Ряд
Фурье
Ряд
Фурье
функции x(t)
представляется в виде :
где
коэффициенты
Фурье
a0,
an
и bn
определяются формулами
При
расчете коэффициентов ряда Фурье
необходимо выбрать начальный момент
времени t0
периода интегрирования. Как правило,
значение t0
выбирают так, чтобы упростить вычисления.
Обычно, исходя из этого условия, принимают
t0=-Т/2
. Формулы приобретают следующий вид:
Разложение
в ряд Фурье четных и нечетных функций
Если
функция x(t),
описывающая сигнал, является четной,
то есть
x(t)=x(-t),
то коэффициенты an=0,
n=0,1,2,…,
и в разложении остаются только постоянная
и косинусоидальные составляющие:
Если
функция x(t),
описывающая сигнал, является нечетной,
то есть
x(t)=-x(t),
то коэффициенты an=0,
n=0,1,2,…,
и в разложении остаются только
синусоидальные составляющие:
Получила
распространение и другая форма записи
тригонометрического ряда Фурье:
где
амплитуда An
и фаза n-ой
гармонической составляющей связаны с
коэффициентами an
и bn
соотношениям:
или
Пример
1.
Найти
разложение в ряд Фурье для функции
заданной
в интервале [−π,
π].
Решение.
Найдем
сначала a0:
Далее
вычислим коэффициенты an:
Заметим,
что
Поскольку
cos (n
− 1)π
= (−1)n
−1,
то для коэффициентов an
получаем выражение
Видно,
что an
= 0
для нечетных n.
Для четных n,
когда n
= 2k
(k
= 1,2,3,…),
мы имеем
Вычислим
теперь коэффициенты bn.
Начнем с b1:
Остальные
коэффициенты bn
при n
> 1
равны нулю. Действительно,
Таким
образом, формула разложения заданной
функции в ряд Фурье имеет вид
График
функции и варианты разложения для n
= 2
и n
= 8
показаны на рисунке 1.
Рисунок
1.
Пример
2.
Разложить
в ряд Фурье функцию с периодом
,
заданную на интервале
формулой

Построим
график функции (рис. 2).
y
1
-3
-2
-
2
3
x
Рисунок
2
Решение.
Функция удовлетворяет условиям Дирихле.
Применяя формулы (2) и (3), находим
коэффициенты Фурье
,
,
.
Разложение
в ряд Фурье
имеет вид
.
Индивидуальное
задание.
Разложить
в ряд Фурье функцию, построить график
функции.
На
отрезке
разложить в ряд Фурье функции:
-
-
-
; -
; -
; -
;
-
; -
; -
; -
; -
; -
; -
; -
; -
; -
;
-
;
-
;
-
;
-
Разложить
функцию
в тригонометрический ряд Фурье на
отрезке [-1;1] ;
21.
Разложить
функцию
в тригонометрический ряд Фурье на
отрезке [-1/2;1/2] ;
22.
Разложить
функцию
в тригонометрический ряд Фурье на
отрезке [-/2;
/2]
;
23.
Разложить
функцию
в тригонометрический ряд Фурье на
отрезке [-1/2;1/2] ;
24.
Разложить
функцию
в тригонометрический ряд Фурье на
отрезке
[-1;1]
в комплексной форме;
25.
Разложить
функцию в
тригонометрический ряд Фурье на отрезке
[-3;3] в комплексной форме;
26.
Разложить
функцию
в тригонометрический ряд Фурье на
отрезке [1;3] ;
27.
Разложить
функцию
в тригонометрический ряд Фурье на
отрезке [5;15] ;
28.
Разложить
функцию
в тригонометрический ряд Фурье на
отрезке [0;1] ;
29.
Разложить функцию
заданную на отрезке
и продолженную на отрезок
четным образом в тригонометрический
ряд Фурье
Преобразование
Фурье
Представим
интеграл Фурье
в
виде:

(1)

(2)
Функция
F(),
определенная формулой (1), называется
косинусом-преобразованием Фурье для
f(x).
Формула
(2) задает обратное косинус – преобразование
Фурье, позволяющее по F(a
) находить f(x).
Аналогично,
если f(x) –
нечетная
функция, то A(a
) = 0, тогда
формулы (3) и (4) задают соответственно
прямое и обратное синус-преобразование
Фурье

(3)

(4)
Если
интеграл Фурье в комплексной форме
представить в виде

(5)
то
функция S(a )
также
называется спектральной и S(a
) = 2p C(a
).
Преобразованием
Фурье называется функция
определенная
формулой (6)

(6)
а
функция f(x)
, определенная
формулой (7) называется обратным
преобразованием Фурье

(7)
Преобразование
Фурье отличается от спектральной функции
только множителем
(
также называется спектральной функцией).
Если
функция f(x)
– оригинал
с показателем роста
,
то функция g(x), определенная формулой
,
где
называется
затухающим оригиналом. Тогда для функции
g(x) существует и преобразование Фурье
и преобразование Лапласа и они связаны
между собой формулой
(8)
Пример
1.
Для
функции
найти
косинус преобразование Фурье.
Решение
Тогда
косинус – преобразование Фурье функции
имеет вид
Пример
2
Найти
преобразование Фурье для функции
Решение.
Данная
функция является затухающим оригиналом,
т.к. функция
–
оригинал с показателем роста
и
где
Воспользуемся
формулой (8), связывающей преобразование
Фурье с преобразованием Лапласа. Найдем
для функции
преобразование
Лапласа по таблице
Тогда
Получили
преобразование Фурье заданной функции:
Индивидуальные
задания.
Найти
синус и косинус – преобразование Фурье
для функции:
Найти
преобразование Фурье следующих функций:
на отрезке [ 0;6];
на отрезке [0;4];
на отрезке [0;10];
на отрезке [0;9];
на отрезке [0;10];
на отрезке [0;9];
на отрезке [0;8];
на отрезке [0;9].
и)
к)
;
л)
;
м)
;
н)
;
о)
п)
р)
с)
т)
у)
ф)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Некоторые способы приближения функций:
При изучении функций применяются различные методы представления данной функции при помощи более простых функций, свойства которых являются известными.
Вопрос о том, какими «базовыми» функциями 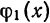
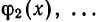


измерять «близость» функций.
Так, например, при вычислении значений функции 
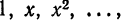

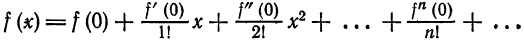
Различаются три основных способа приближения (аппроксимации) функций.
Локальное приближение — это такой вид приближения функции 
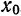
(имеющих производные любого порядка) служат ряды Тейлора.
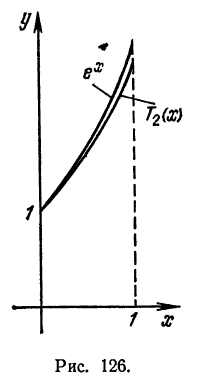
На рис. 126 представлены графики функций 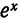
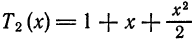
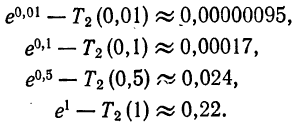
Равномерное приближение — это такой способ аппроксимации функции 
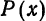
Например, многочлен 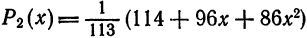
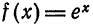
показывают, что
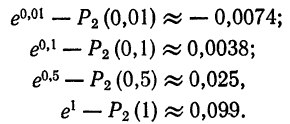
График многочлена 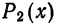
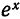
В случаях локальной и равномерной аппроксимаций в качестве
оценки «близости» двух функций 
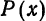
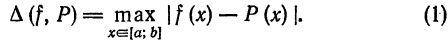
Аппроксимация такого вида называется поточечной или аппроксимацией в обычном смысле.
Приближение в среднем (приближение по среднему квадратическому отклонению). Если данная функция 
такой функции на отрезке. На рис. 127 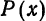


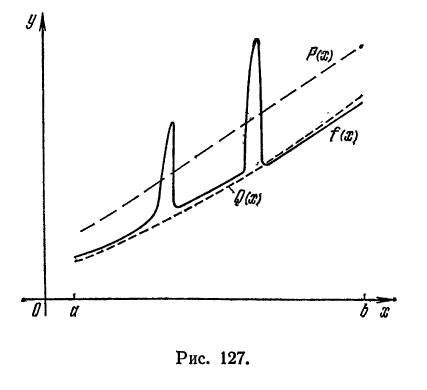
как лучшее приближение для 
Определение:
Средним квадратическим отклонением функций 
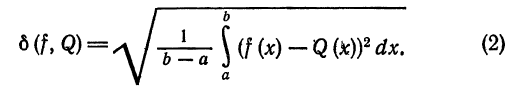
Нахождение наилучших приближений в среднем, т.е, оцененных по среднему квадратическому отклонению играет большую роль в-решении многих технических задач.
Пример:
Найти поточечное и среднее квадратиченское: отклонения функции 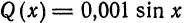
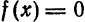
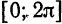
Решение:
По формуле (1) находим поточечное отклонение
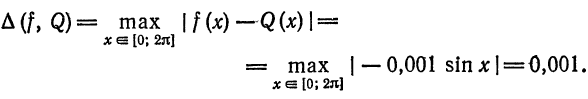
Среднее квадратическое отклонение вычислим по формуле (2):
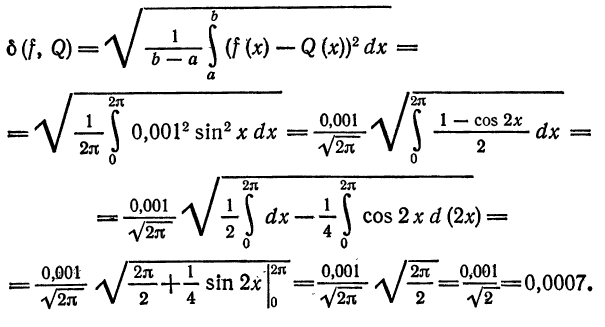
Для среднего квадратического отклонения и потокчечного отклонения двух функций на отрезке имеет место следующее утверждение: среднее квадратическое отклонение двух функций не превосходит поточечного отклонения на том же отрезке:
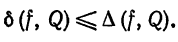
В самом деле,
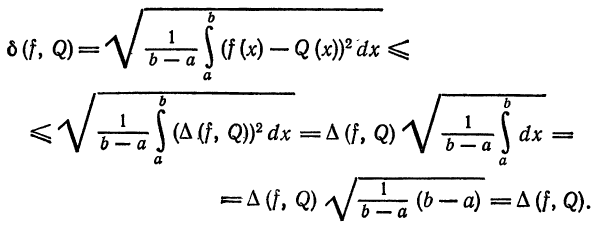
Ортогональные системы функций. Обобщенные многочлены Фурье
Часто в качестве базовых функций, при помощи которых строятся приближения для рассматриваемых функций, служат так называемые ортогональные системы функций.
Определение:
Система отличных от нулей функций
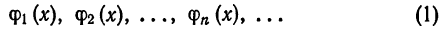
называется ортогональной на отрезке [a ; b], если для любых 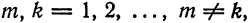
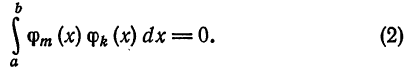
Если к тому же
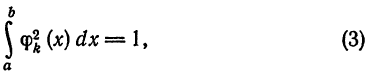
для всех 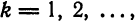
Любую ортогональную систему функций (1) можно ортонормировать. Для этого достаточно каждую функцию 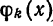
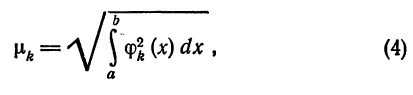
т. е. взять функции
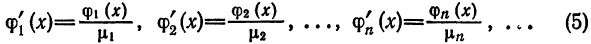
В самом деле, для функций 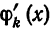
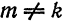
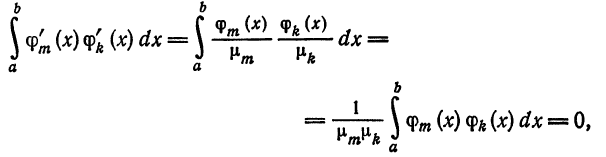
т. е. система (5) также ортогональна. Кроме того,
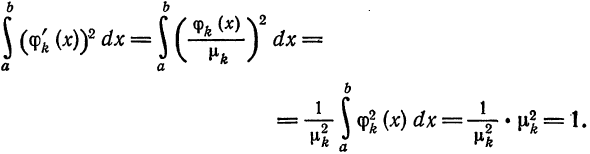
Следовательно, система (5) ортонормирована.
Числа 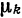
Пример:
Покажем, что система тригонометрических функций
является ортогональной системой функций на отрезке
Для этого надо показать, что интегралы
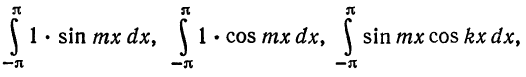
при любых 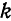
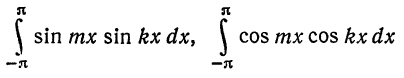
при 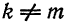
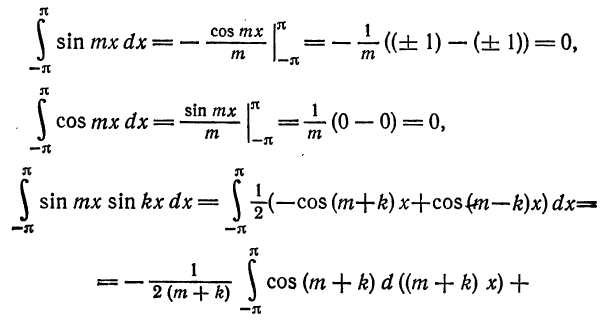
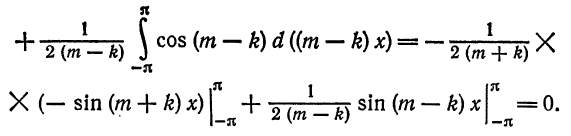
При помощи формул
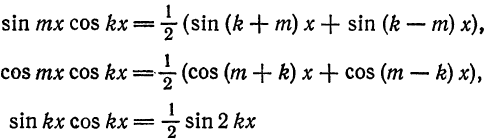
аналогично доказывается, что остальные интегралы также равны нулю.
Пример:
Можно показать, что следующие многочлены, известные под названием многочленов Лежандра, составляют ортогональную систему на отрезке
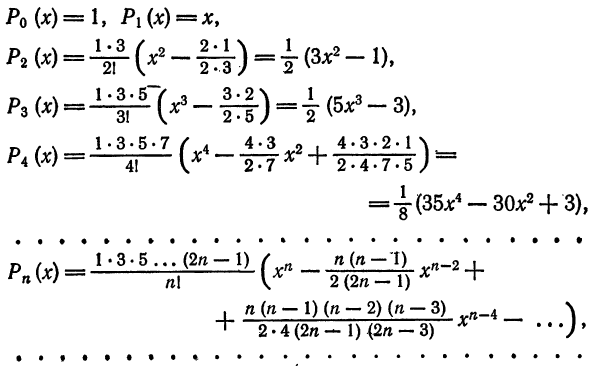
Легко видеть, что подсистема любой ортогональной системы функции также ортогональна на том же отрезке. В самом деле, если равенства (2) выполняются для всех функций системы, то они выполняются и для всех функций некоторой ее подсистемы. Учитывая это замечание и ортогональность системы (6), можем указать новые примеры ортогональных систем функций.
Пример:
Система функций
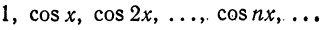
ортогональна на отрезке 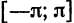

ортогональна на отрезке 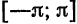
Определение:
Выражение
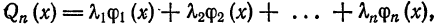
где 
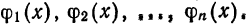
Например, выражение
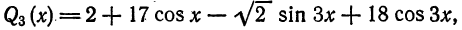
является обобщенным многочленом относительно системы (6).
Определение:
Пусть дана ортогональная система (1) на отрезке
[a ; b]. Величины
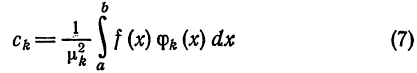
называются обобщенными коэффициентами Фурье для функции 
Если система (1) ортонормирована, то в силу
формул (4) и (3) 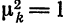
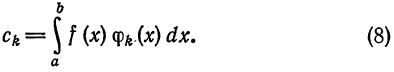
Определение:
Обобщенный многочлен
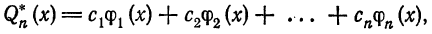
взятый с соответствующими, обобщенными коэффициентами Фурье, называется обобщенным многочленом Фурье n-го порядка для функции 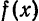
Пример:
Составить обобщенный многочлен Фурье второго порядка для функции 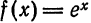
Решение. Пусть
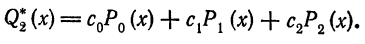
Имеем:
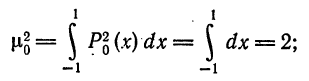
тогда
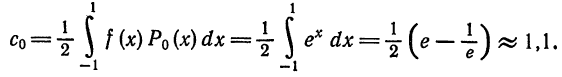
Далее,
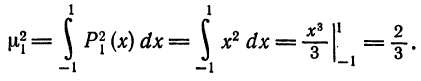
Следовательно,
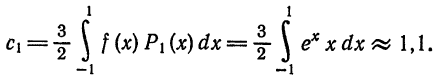
Аналогично,
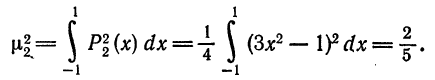
Следовательно,
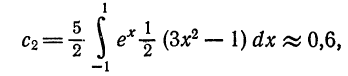
т. e.
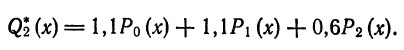
Роль обобщенных многочленов Фурье в теории приближения функций выражается в следующей теореме.
Теорема:
Для каждого n среди всех обобщенных многочленов n-го порядка
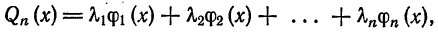
где
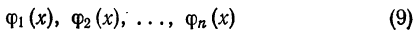
— ортонормированием система функций на [а; b], наилучшее среднее квадратическое приближение функции 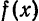
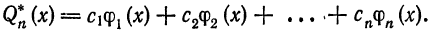
Доказательство:
Имеем:
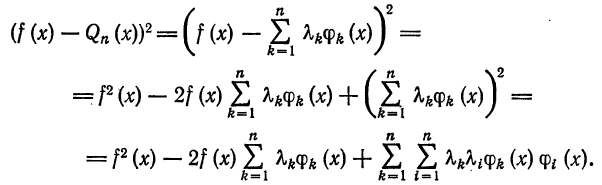
Интегрируя полученное равенство почленно и учитывая соотношения (2), (3) и (8), найдем:
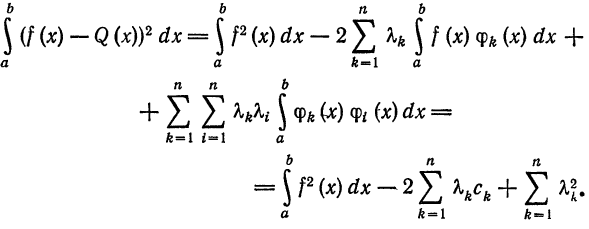
В полученном выражении добавим и вычтем 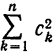
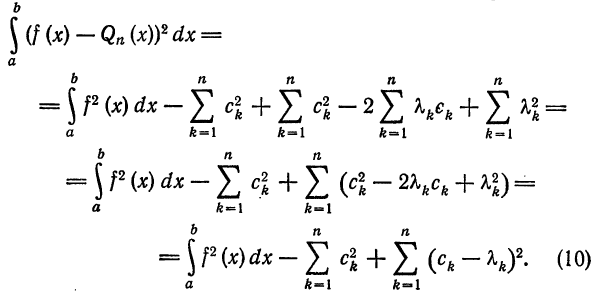
Первые два члена выражения из правой части равенства (10) не зависят от взятого обобщенного много члена 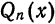
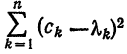
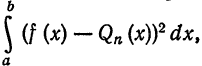
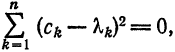

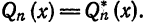
Аналогично доказывается эта теорема для любой ортогональной системы (1), только вместо равенства (8) надо будет использовать равенство (7).
Таким образцом, для функции 
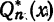
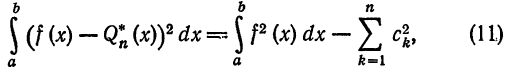
или
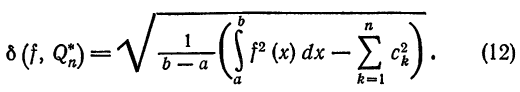
Обобщенные ряды Фурье
Пусть дана бесконечная ортогональная на отрезке [а; b] система функций
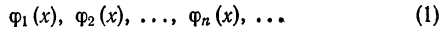
Определение:
Ряд
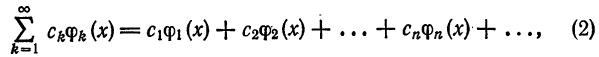
где
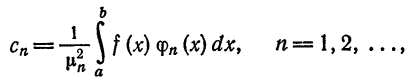
называется обобщенным рядом Фурье для функции 
Обращаем внимание на то, что коэффициенты 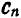
Таким образом, при заданной системе ортогональных функций каждая функция 
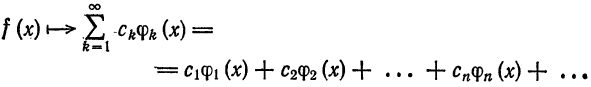
Частичные суммы ряда (2) совпадают с обобщенными многочленами Фурье 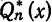
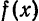
Из формулы (12) §2 видно, что при возрастании n среднее квадратическое отклонение 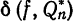
Определение:
Обобщенный ряд Фурье (2) называется сходящимся в среднем к функции 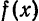
Из формулы (11) § 2 видно, что необходимым и достаточным условием сходимости в среднем ряда (2) к порождающей функции 
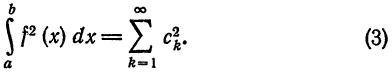
Это равенство известно под названием равенства Ляпунова — Парсеваля или уравнения замкнутости. Равенство Ляпунова — Парсеваля имеет место, в частности, для тригонометрических ортогональных систем из примеров 1, 3, 4 § 2 и любой ограниченной на [а; b] функции 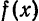
рода. В § 1 мы показали, что среднее квадратическое отклонение 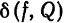
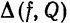
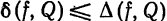


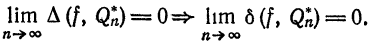
Обратное утверждение, вообще говоря, не имеет места, так как ряд (2) может сходиться в среднем к функции 
Во многих инженерно-технических приложениях основную ценность представляют именно приближения в среднем для рассматриваемых функций. Аппаратом для получения таких приближений служат обобщенные ряды Фурье и их частичные суммы — обобщенные
многочлены Фурье.
Докажем теорему об единственности представления функции в виде обобщенного ряда.
Теорема:
Если функция 
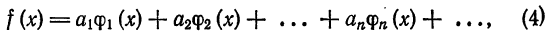
то этот ряд совпадает с обобщенным рядом Фурье для функции 
Докажем теорему в предположениях, что выражение (4) можно почленно интегрировать.
Для определения коэффициента 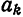
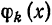
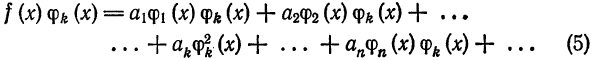
Интегрируя (5) получим
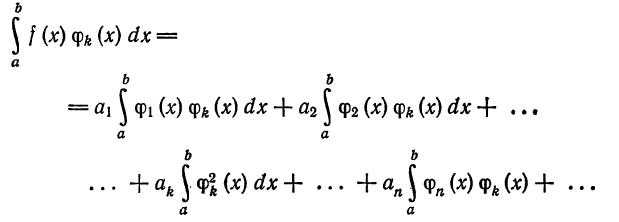
Так как система 
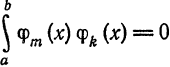
Следовательно,
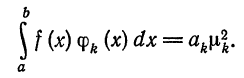
Отсюда
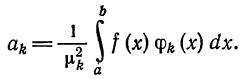
Учитывая формулу (7) § 2, имеем 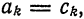
функций. В частности, если в качестве «базовых» функций взять тригонометрическую систему из примера 1 § 2, получим разложение (на отрезке 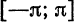
функции по многочленам Лежандра; если взять систему функций примеров 3 и 4 § 2, то получим соответственно разложение (на 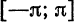
Разложение функций в ряды Фурье по тригонометрическим системам играет большую роль как в
математике, так и в ее приложениях (особенно в электротехнике), поэтому мы остановимся на них подробнее.
Тригонометрические ряды Фурье
Разложение функций в ряд Фурье на отрезке 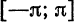
изменяющийся по сложному закону 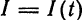
синусоидальные токи 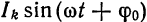
аппаратом для исследования таких задач служат ряды Фурье относительно тригонометрической системы ортогональных функций на отрезке 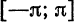
Обобщенные многочлену Фурье, обобщенные коэффициенты Фурье, обобщенные ряды Фурье для функции 
Многочленом Фурье (или тригонометрическим многочленом) n-го порядка функции 
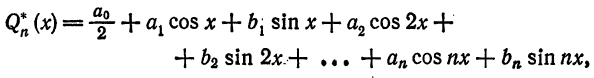
где 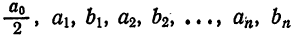
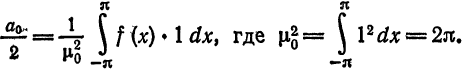
Следовательно, 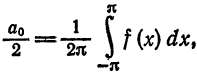
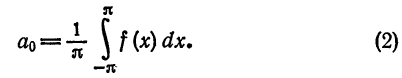
Для коэффициентов 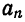
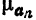
§ 2 получим
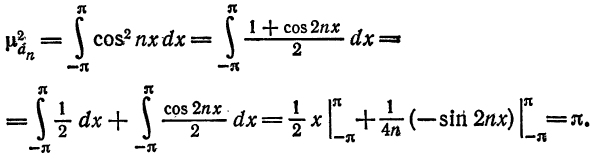
Следовательно,
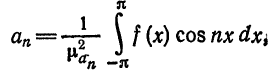
или
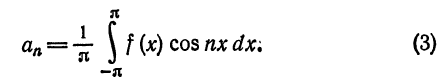
Аналогично показывается, что 
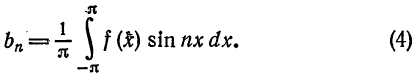
Таким образом, каждой функции 
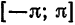
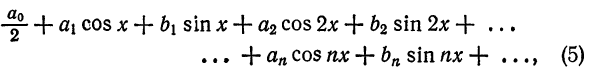
т. е.
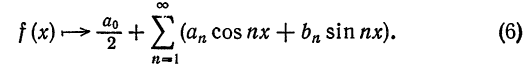
Определение:
Ряд
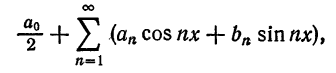
где
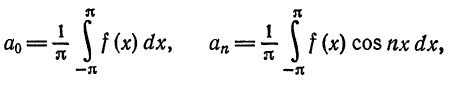
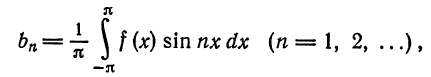
называется рядом Фурье (или тригонометрическим рядом) для функции 
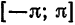
Пример:
Составить ряд Фурье для функции 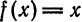
Решение По формуле (2) имеем
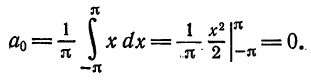
По формуле (3); получаем
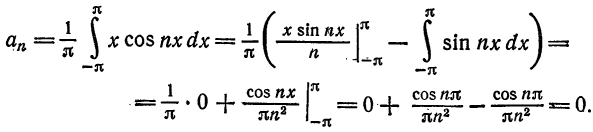
Далее, по формуле (4)
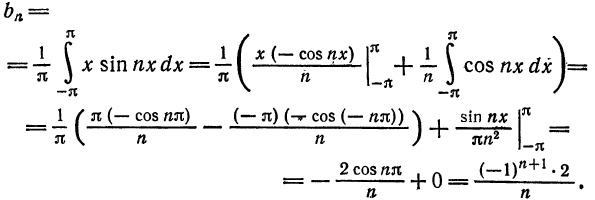
Следовательно,
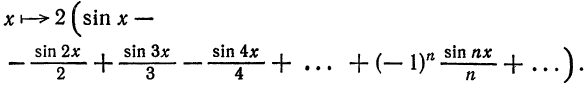
Ряд (5) может сходиться к функции 
равенства только в том случае, если ряд сходится поточечно к функции 
Для формулировки условий сходимости ряда (5) к функции введем понятие кусочно-непрерывных функций.
Функция 
Функция 
Приводим достаточное условие сходимости в среднем ряда Фурье к порождающей функции.
Теорема:
Ряд Фурье (5) сходится в среднем к порождающей функции 

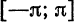
Следующие теоремы Дирихле представляют собой достаточные условия поточечной сходимости ряда к порождающей функции, за исключением, быть может, точек разрыва и границ отрезка.
Теорема:
Если функция 




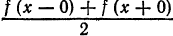
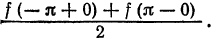
Функция 
Теорема:
Если функция 



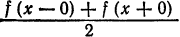
Сформулированные теоремы мы принимаем без доказательства.
Таким образом, если функция 
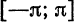
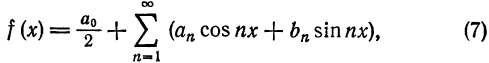
причем коэффициенты 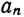
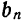

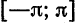
Пример:
Так как функция 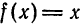
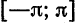
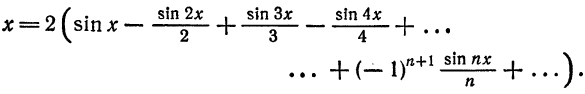
Заметим, что значение полученного ряда в концах интервала равно
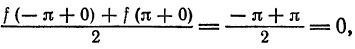
следовательно, сумма ряда равна значению порождающей функции 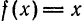
Заметим, что.большинство функций, которые встречаются в математике и ее приближениях, являются
кусочно-дифференцируемыми, а часто просто дифференцируемыми функциями, поэтому для них ряд Фурье сходится к порождающей функции в обычном смысле.
Скорость сходимости ряда Фурье к порождающей функции зависит от свойств данной функции. Оказывается, что чем выше «степень гладкости» данной функции, т. е. чем более высокого порядка непрерывные производные она имеет, тем больше скорость сходимости ее ряда Фурье.
Приводим, также без доказательства, следующую оценку скорости сходимости ряда Фурье.
Теорема:
Если 
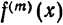
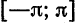
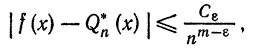
где 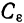
Разложение функций в ряд Фурье на произвольном отрезке
Пусть функция 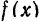
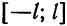
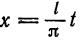
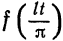
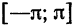
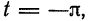
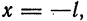
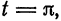

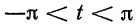
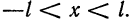
Предположим, например, что исходная функция 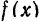
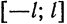
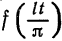
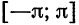
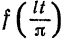
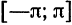
концов отрезка 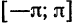
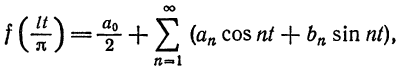
где
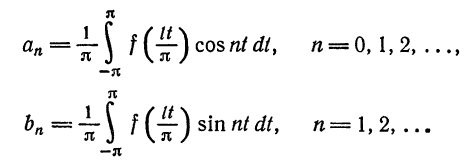
Перейдем теперь к переменной 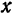
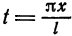
и при этом
Итак,
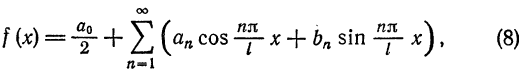
где
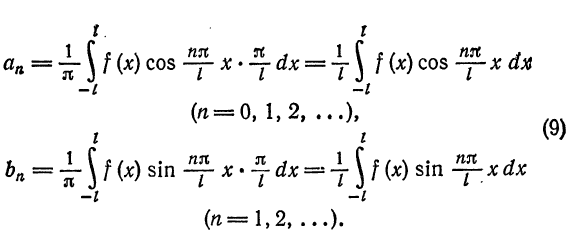
Таким образом, функцию
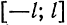
Пример:
Разложить функцию 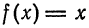
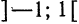
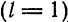
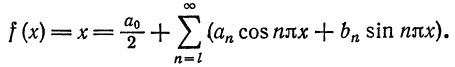
Вычислим коэффициенты ряда по формулам (9):
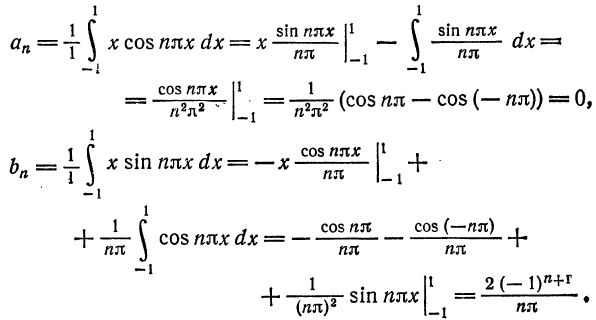
Таким образом,
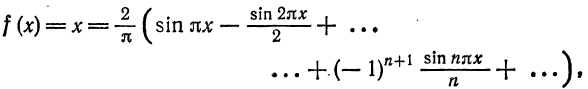
для
Разложение в ряд Фурье периодических функций
Если данная функция 
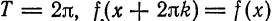
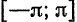
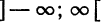
В самом деле; сумма тригонометрического ряда Фурье
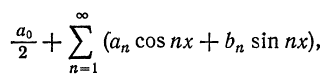
если она существует, является периодической функцией с периодом 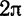
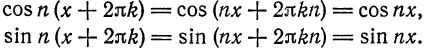
Аналогично, если функция 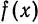
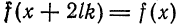
Так как для периодической функции периода T интегралы по любым отрезкам длины T равны между собой
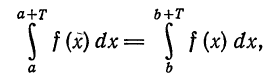
то для вычисления коэффициентов Фурье периодической функции можно интегрировать по любому отрезку
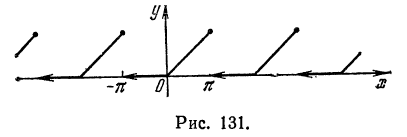
длины T. Так, если функция имеет период 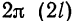
(2) — (4) (в формулах (9)) вместо 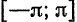
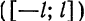
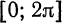
Пример:
Разложить в ряд Фурье периодическую функцию 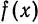
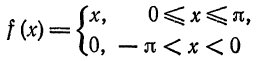
и 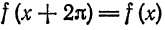
Решение:
Данная функция кусочно-дифференцируема, следовательно,
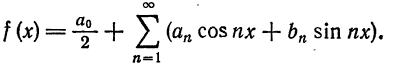
При этом
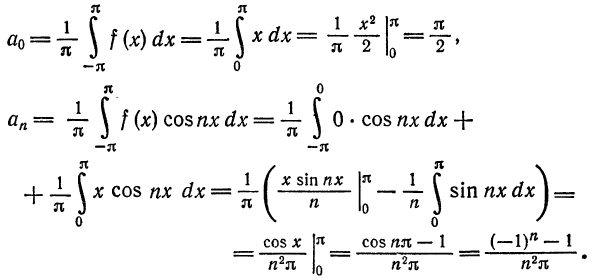
Отсюда 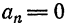
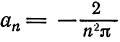
Аналогичными вычислениями находим
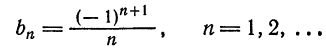
Следовательно,
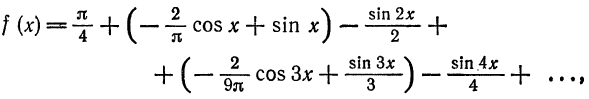
или
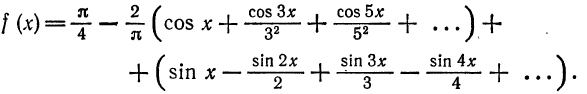
В точках 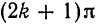
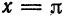
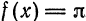
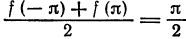
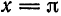
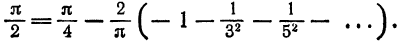
Отсюда
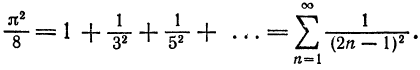
О том, что ряд 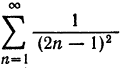
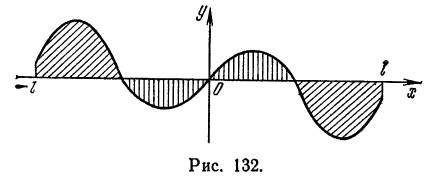
Разложение в ряд Фурье четных и нечетных функций
Сделаем два замечания, необходимых для дальнейшего.
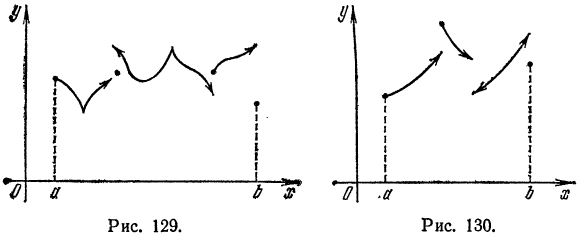
1) Рассмотрим нечетную на отрезке 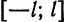
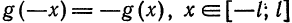
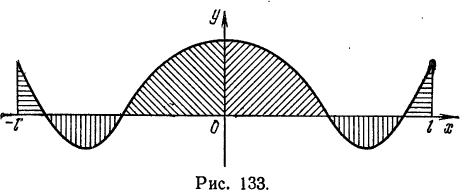
Из геометрических соображений ясно (см., например, рис. 132), что
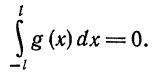
2) Если функция 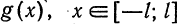
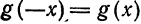
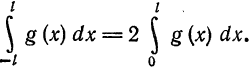
Рассмотрим разложение в ряд Фурье нечетных функций.
Пусть 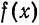
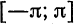
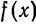
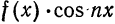
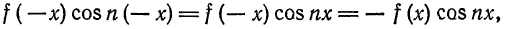
а произведение 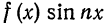
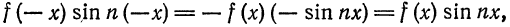
то для коэффициентов ряда Фурье получим:
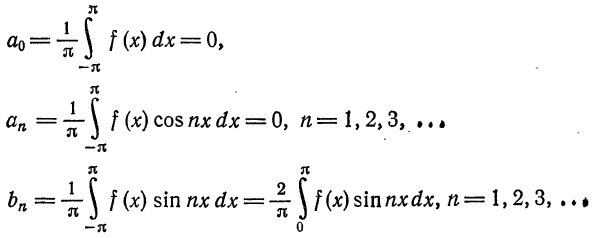
Отсюда следует, что разложение нечетной функция 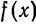
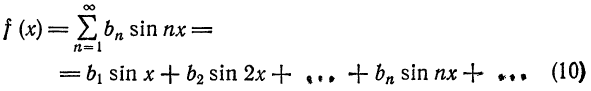
Аналогично, для четных функций 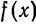
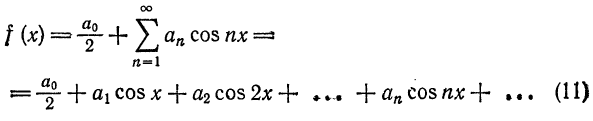
Таким образом, если функция f(x)] нечетная, то ее ряд Фурье содержит только члены с синусами; если 
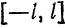
Разложение произвольных функций в ряды Фурье
Пусть дана кусочно-дифференцируемая функция 
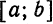
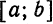

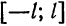
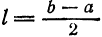

Если перенести начало координат в точку 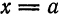
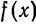
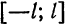
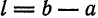

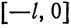
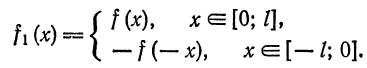
Функция 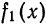
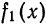
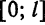

Продолжая «четным образом» функцию 
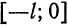
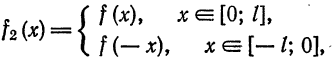
которая является четной, аналогично получим разложение данной функции в ряд Фурье только по косинусам.
Таким образом, любая функция 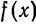
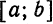
Заметим, что возможность таких разложений была указана в § 3 из общих соображений относительно обобщенных рядов Фурье.
Практический гармонический анализ
Теория разложения функций в тригонометрические ряды Фурье называется также гармоническим анализом. Под практическим гармоническим анализом понимается представление конкретных функций, возникающих при решении практических задач, в виде ряда
Фурье, коэффициенты которого, как правило, вычисляются приближенным образом. В большинстве случаев функции, описывающие исследуемый процесс, даны в виде экспериментальных данных или графиков, которые вычерчиваются самопишущим прибором. В таких случаях коэффициенты Фурье вычисляются при помощи приближенных методов интегрирования. Для приближенного вычисления интегралов
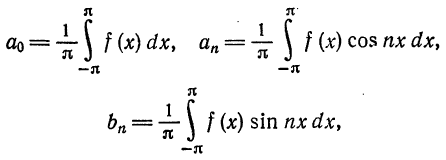
применяется какой-либо из методов численного интегрирования. Применим, например, формулу прямоугольников (1) § 8 гл. 8. Разделим отрезок 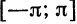
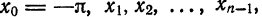
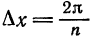

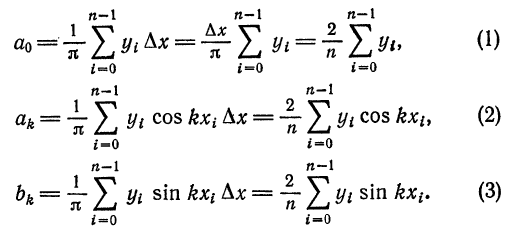
Для облегчения ручных вычислений коэффициентов Фурье разработаны различные схемы и шаблоны, в более сложных случаях вычисления проводятся на ЭВМ
Пример:
Найти тригонометрический многочлен второго порядка для функции, заданной графически на рис. 134.
Решение:
Делим отрезок 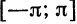
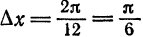
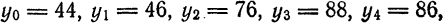
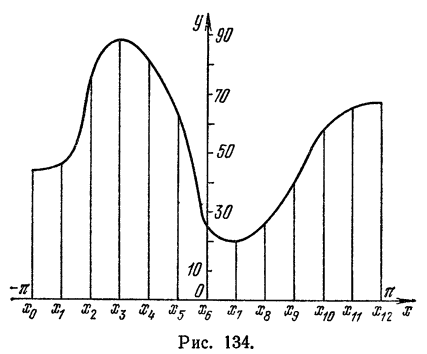
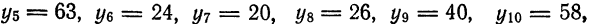
Тогда по формуле (1)
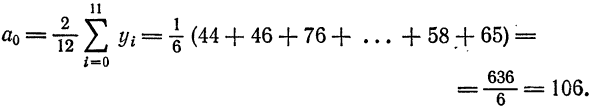
По формуле (2) имеем
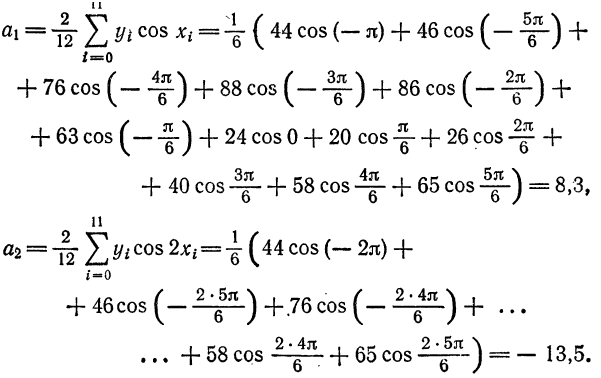
По формуле (3) вычислим 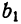
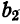
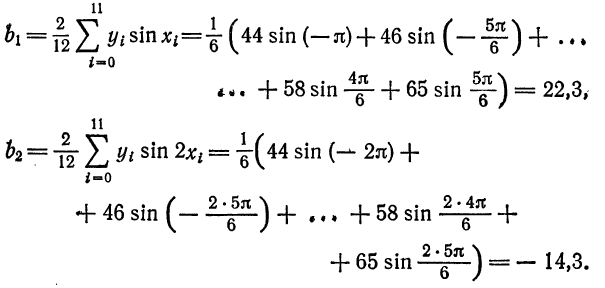
Таким образом,
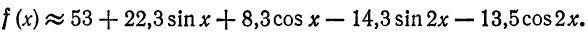
Если функция 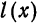
В электротехнике и радиотехнике нередко встречаются периодические функции, имеющие точки разрыва первого рода внутри отрезка 
Пример:
Разложить в ряд Фурье кривую двухполупериодного выпрямленного синусоидального тока
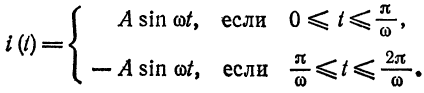
Решение:
Данная функция может быть представлена в виде 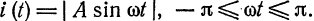
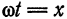
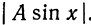
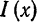
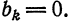
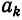
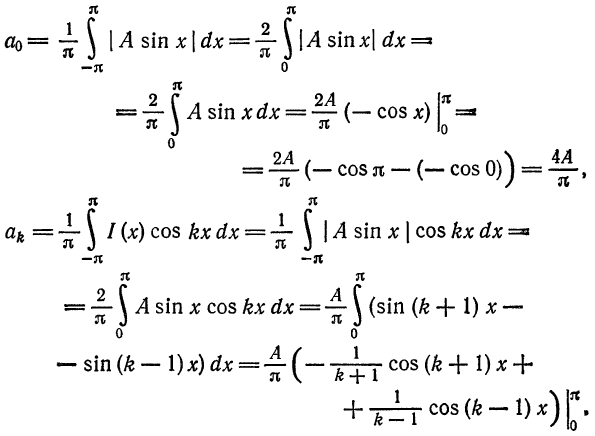
При 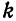
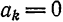
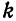
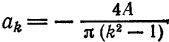
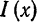
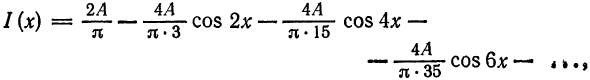
а исходная функция, следовательно, — в ряд Фурье
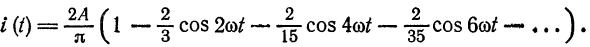
Пример:
Разложить в ряд Фурье кривую однополупериодного выпрямленного синусоидального тока
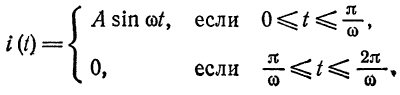
Решение:
Положим 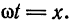
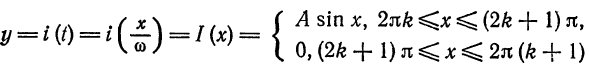
(рис. 136). Имеем:
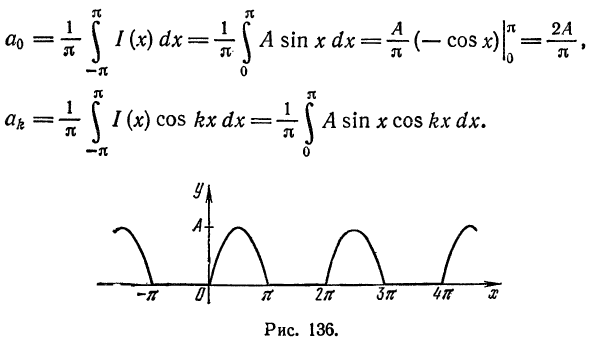
Из примера 2 известно, что при 
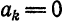
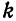
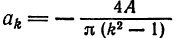
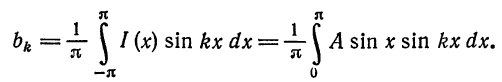
Если 
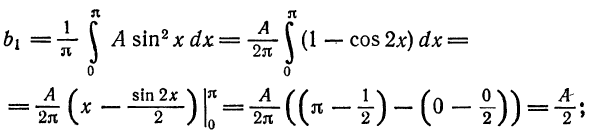
если 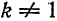
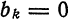
Функция 
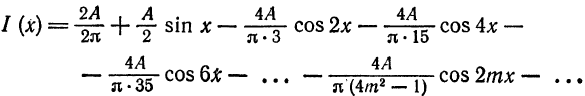
Следовательно,
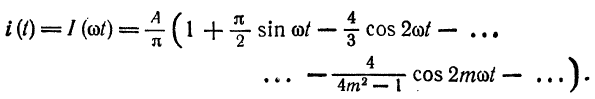
Пример:
Разложить в ряд Фурье периодическую функцию 

Решение:
Функция 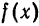
Вычислим ее коэффициенты Фурье. Так как 
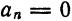
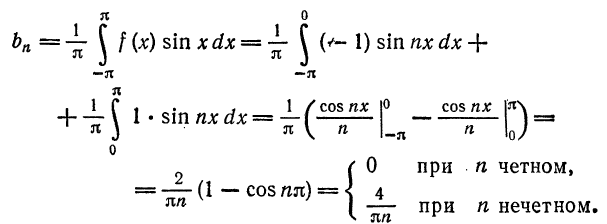
Следовательно,
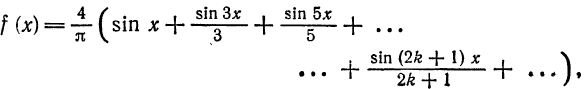
где
Пример:
Разложить в ряд Фурье периодическую функцию 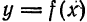
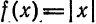
(рис. 138).
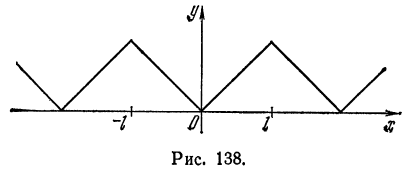
Решение:
Так как рассматриваемая функция четная, то 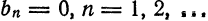
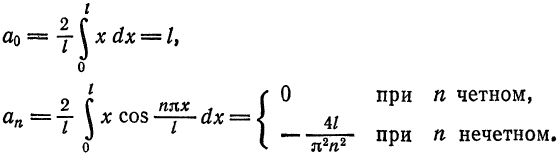
Следовательно, на отрезке
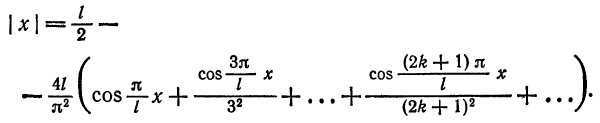
Пример:
Разложить функцию 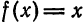
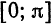
Решение:
Продолжая эту функцию нечетным образом на 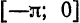
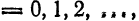
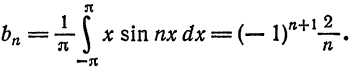
Следовательно, во всех точках промежутка 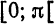
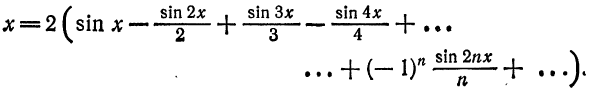
В точке 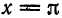
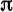
Пример:
Разложить функцию 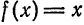
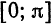
Решение:
Продолжая эту функцию четным образом на 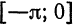
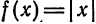
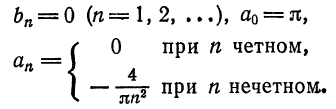
Следовательно, на отрезке
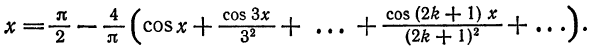
Дополнение к рядам Фурье
Смотрите также:
Решение задач по математическому анализу
Решение рядов Фурье
Тригонометрические ряды
Определение:
Функция f(x), определенная на неограниченном множестве D, называется периодической, если существует число 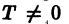
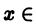
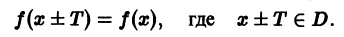
Наименьшее из таких чисел Т называется периодом функции f(х).
Пример:
Функция
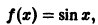
определенная на интервале 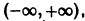

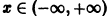
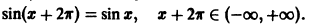
Таким образом, функция sinx имеет период 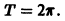
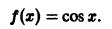
Пример:
Функция
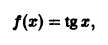
определенная на множестве D чисел
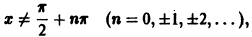
является периодической, так как существует число 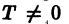

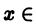
Определение:
Функциональный ряд вида
называется тригонометрическим рядом, а постоянные 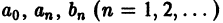
Частичные суммы Sn(x) тригонометрического ряда (1) являются линейными комбинациями функций из системы функций

которая называется тригонометрической системой. Так как членами этого ряда являются периодические функции с периодом 2

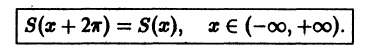
Определение:
Разложить периодическую функцию f(x) с периодом Т = 2
Ортогональность тригонометрической системы
Определение:
Функции f(х) и g(х), непрерывные на отрезке [а, b], называются ортогональными на этом отрезке, если выполнено условие
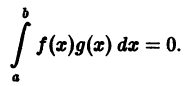
Например, функции 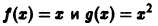
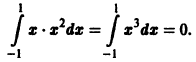
Определение:
Конечная или бесконечная система функций
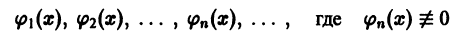
(n = 1, 2,…), интегрируемых на отрезке [а, b], называется ортогональной системой на отрезке [а, b], если для любых номеров тип таких, что 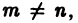
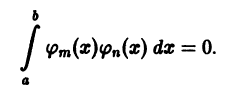
Теорема:
Тригонометрическая система
ортогональна на отрезке
При любом целом 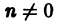
С помощью известных формул тригонометрии
для любых натуральных 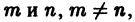
Наконец, в силу формулы
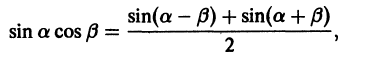
для любых целых m и n получаем
При m = n имеем
Тригонометрический ряд Фурье
Поставим себе задачей вычислить коэффициенты 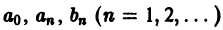
Теорема:
Пусть равенство
имеет место для всех значений х, причем ряд в правой части равенства сходится равномерно на отрезке 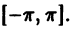
Из равномерной сходимости ряда (1) вытекает непрерывность, а значит, и интегрируемость функции fх). Поэтому равенства (2) имеют смысл. Более того, ряд (1) можно почленно интегрировать. Имеем
откуда и следует первая из формул (2) для n = 0.
Умножим теперь обе части равенства (1) на функцию cos mх, где m — произвольное натуральное число:
Ряд (3), как и ряд (1), сходится равномерно. Поэтому его можно интегрировать почленно,
Все интегралы в правой части, кроме одного, который получается при n = m, равны нулю в силу ортогональности тригонометрической системы. Поэтому
Аналогично, умножая обе части равенства (1) на sin mx; и интегрируя от 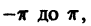
Пусть дана произвольная периодическая функция f(x) периода 2
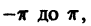
Определение:
Тригонометрический ряд

коэффициенты 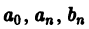
называется тригонометрическим рядом Фурье функции f(x), а коэффициенты 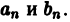
Каждой интегрируемой на отрезке 
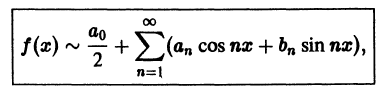
т.е. тригонометрический ряд, коэффициенты которого определяются по формулам (2). Однако если от функции f(х) не требовать ничего, кроме интегрируемости на отрезке 
Замечание:
Часто требуется разложить в тригонометрический ряд функцию f(x), определенную только на отрезке 


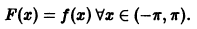
Эту функцию F(x) называют периодическим продолжением функции f(x). При этом функция F(x) не имеет однозначного определения в точках
Ряд Фурье для функции F(x) тождествен ряду Фурье для функции f(х). К тому же, если ряд Фурье для функции f(x) сходится к ней, то его сумма, являясь периодической функцией, дает периодическое продолжение функции f(x) с отрезка 

Достаточные условия разложимости функции в ряд Фурье
Приведем достаточный признак сходимости ряда Фурье, т. е. сформулируем условия на заданную функцию, при выполнении которых построенный по ней ряд Фурье сходится, и выясним, как при этом ведет себя сумма этого ряда. Важно подчеркнуть, что хотя приведенный ниже класс кусочно-монотонных функций и является достаточно широким, функции, ряд Фурье для которых сходится, им не исчерпываются.
Определение:
Функция f(x) называется кусочно-монотонной на отрезке [a, b], если этот отрезок можно разбить конечным числом точек 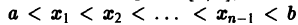
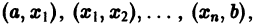
Пример:
Функция
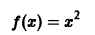
является кусочно-монотонной на интервале 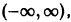
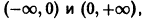
Пример:
Функция
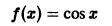
кусочно-монотонна на отрезке 
Теорема:
Функция f(x), кусочно-монотонная и ограниченная на отрезке [a, b], может иметь на нем только точки разрыва первого рода.
Пусть, например, 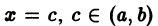
Это означает, что точка с есть точка разрыва первого рода (рис. 2).
Теорема:
Если периодическая функция f(x) с периодом 2
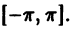
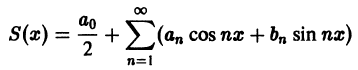
этого ряда выполняются равенства:
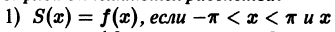
Пример:
Функция f(х) периода 2
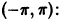
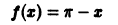
(рис. 3), удовлетворяет условиям теоремы. Поэтому ее можно разложить в ряд Фурье. Находим для нее коэффициенты Фурье:
Ряд Фурье для данной функции имеет вид
Пример:
Разложить функцию в ряд Фурье (рис. 4) на интервале
Данная функция удовлетворяет условиям теоремы. Найдем коэффициенты Фурье. Используя свойство аддитивности определенного интеграла, будем иметь
Следовательно, ряд Фурье имеет следующий вид:
На концах отрезка 
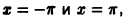
Замечание:
Если в найденном ряде Фурье положить х = 0, то получим
Разложение в ряд Фурье четных и нечетных функций
Функция f(x), определенная на отрезке [-l, l], где l > 0, называется четной, если
График четной функции симметричен относительно оси ординат.
Функция f(x), определенная на отрезке l), где l > 0, называется нечетной, если
График нечетной функции симметричен относительно начала координат.
Пример:
а) Функция
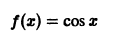
является четной на отрезке 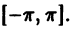
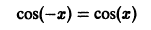
для всех
б) Функция
где 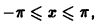
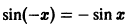
для всех
в) Функция
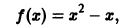
где 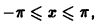
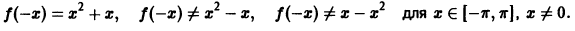
Пусть функция f(х), удовлетворяющая условиям теоремы 1, является четной на отрезке 
т. е. f(x) cos nх является четной функцией, а f(x) sin nх — нечетной. Поэтому коэффициенты Фурье четной функции f(х) будут равны
Следовательно, ряд Фурье четной функции имеет вид
Если f(x) — нечетная функция на отрезке 
Таким образом, ряд Фурье нечетной функции имеет вид
Пример:
Разложить в ряд Фурье на отрезке 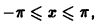
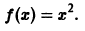
Так как эта функция четная и удовлетворяет условиям теоремы 1, то ее ряд Фурье имеет вид
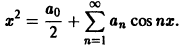
Находим коэффициенты Фурье. Имеем
Применяя дважды интегрирование по частям, получим, что
Значит, ряд Фурье данной функции выглядит так:
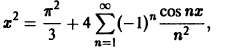
или, в развернутом виде,
Это равенство справедливо для любого 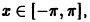
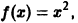
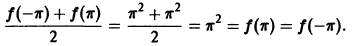
Графики функции 
Замечание:
Этот ряд Фурье позволяет найти сумму одного из сходящихся числовых рядов, а именно, при х = 0 получаем, что
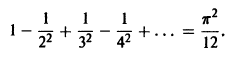
Пример 2. Разложить в ряд Фурье на интервале 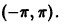
Функция f(x) удовлетворяет условиям теоремы 1, следовательно ее можно разложить в ряд Фурье, который в силу нечетности этой функции будет иметь вид
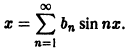
Интегрируя по частям, находим коэффициенты Фурье
Следовательно, ряд Фурье данной функции имеет вид
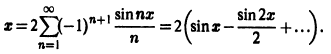
Это равенство имеет место для всех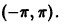
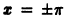
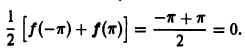
Вне отрезка 
Разложение функции, заданной на отрезке, в ряд по синусам или по косинусам
Пусть ограниченная кусочно-монотонная функция f(х) задана на отрезке 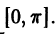
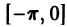
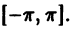
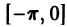

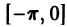
Итак, каждую ограниченную кусочно-монотонную функцию /(х), определенную на отрезке 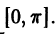
Пример:
Функцию
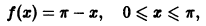
разложить в ряд Фурье: а) по косинусам; б) по синусам.
Данная функция при ее четном и нечетном продолжениях в отрезок 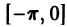
а) Продолжим f(x) в отрезок 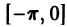
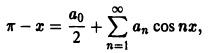
где коэффициенты Фурье равны соответственно
б) Продолжим f{x) в отрезок 
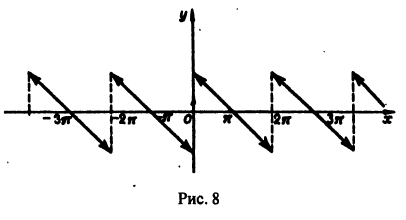
Ряд Фурье для функции с произвольным периодом
Пусть функция f(x) является периодической с периодом 
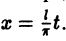
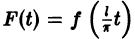
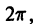
и ее можно разложить на отрезке 
Возвращаясь к переменной х, т. е. положив 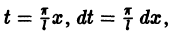
Все теоремы, справедливые для рядов Фурье периодических функций с периодом 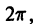
Пример:
Разложить в ряд Фурье периодическую функцию с периодом 2 l, заданную на отрезке 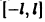
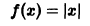
Так как данная функция четная, то ее ряд Фурье имеет вид
Подставляя в ряд Фурье найденные значения коэффициентов Фурье, получим
Отметим одно важное свойство периодических функций.
Теорема:
Если функция f(x) имеет период Т и интегрируема, то для любого числа а выполняется равенство
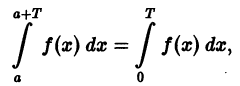
т. е. интеграл no отрезку, длина которого равна периоду Т, имеет одно и то же значение независимо от положения этого отрезка на числовой оси.
В самом деле,
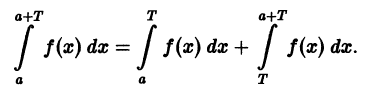
Делаем замену переменной во втором интеграле, полагая х = t + T, dx = dt. Это дает
и следовательно,
Геометрически это свойство означает, что в случае 
В частности, для функции f(x) с периодом Т = 
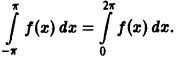
Пример:
Функция
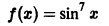
является периодической с периодом Т = 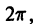
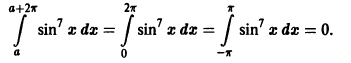
Доказанное свойство, в частности, показывает, что коэффициенты Фурье периодической функции f(x) с периодом 2 l можно вычислять по формулам
где a — произвольное действительное число (отметим, что функции 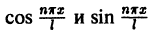
Пример:
Разложить в ряд Фурье заданную на интервале 0 < х < 

с периодом 
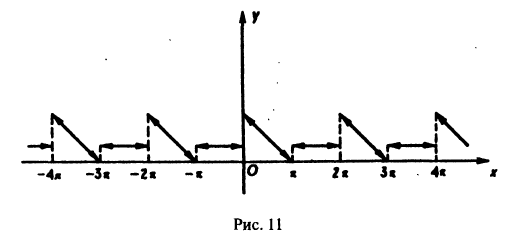
Найдем коэффициенты Фурье данной функции. Положив в формулах (1) и (2) а = 0, 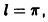
Следовательно, ряд Фурье будет выглядеть так:
В точке х = 
Комплексная запись ряда Фурье
В этом параграфе используются некоторые элементы комплексного анализа (см. главу XXX, где все, производимые здесь действия с комплексными выражениями, строго обоснованы).
Пусть функция f(x) удовлетворяет достаточным условиям разложимости в ряд Фурье. Тогда на отрезке 
Используя формулы Эйлера (см. ***)
найдем, что
Подставляя эти выражения в ряд (1) вместо cos nх и sin nх, будем иметь
Введем следующие обозначения
Тогда ряд (2) примет вид
Преобразуем правую часть этого равенства следующим образом
Последнее равенство можно записать так:
Таким образом, ряд Фурье (1) представлен в комплексной форме (3).
Найдем выражения коэффициентов 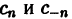
Аналогично находим
Окончательно формулы для 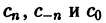
Коэффициенты Cn называются комплексными коэффициентами Фурье функции f(x).
Для периодической функции f(x) с периодом 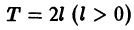
где коэффициенты Cn вычисляются по формулам
Сходимость рядов (3) и (4) понимается так: ряды (3) и (4) называются сходящимися для данного значения х, если существуют пределы
Пример:
Разложить в комплексный ряд Фурье функцию периода
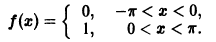
Данная функция удовлетворяет достаточным условиям разложимости в ряд Фурье. Пусть
Найдем комплексные коэффициенты Фурье этой функции. Имеем
или, короче,
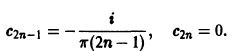
Подставляя значения Сn в ряд (3), окончательно получим
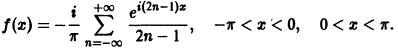
Заметим, что этот ряд можно записать и так:
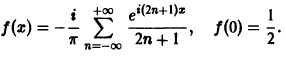
Ряды Фурье по общим ортогональным системам функций
Ортогональные системы функций
Обозначим через 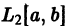
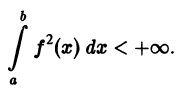
В частности, все функции f(х), непрерывные на отрезке 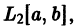
Определение:
Система функций 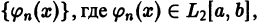
Условие (1) предполагает, в частности, что ни одна из функций 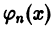
Введем обозначение
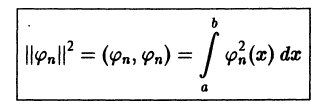
и назовем величину 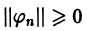
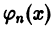
Если в ортогональной системе 
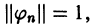

Если система 
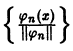
Пример:
Тригонометрическая система
ортогональна на отрезке 
является ортонормированной системой функций на 
Пример:
Косинус-система
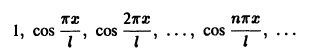
и синус-система
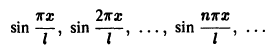
являются ортогональными на отрезке [0, l] , но не ортонормированными 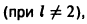
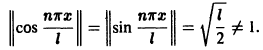
Пример:
Многочлены, определяемые равенством
(n = 0, 1, 2, …), называются многочленами (полиномами) Лежандра. При n = 0 имеем
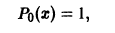
при n = 1 получаем
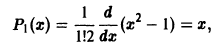
при n = 2 имеем
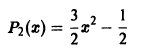
и т.д.
Можно доказать, что функции
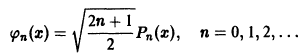
образуют ортонормированную систему функций на отрезке [-1, 1].
Покажем, например, ортогональность полиномов Лежандра. Пусть m>n. В этом случае, интегрируя n раз по частям, находим
поскольку для функции 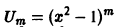
Определение:
Система функций 
Здесь предполагается, что весовая функция р(х) определена и положительна всюду на интервале (а, b) за возможным исключением конечного числа точек, где р(х) может обращаться в нуль.
Пример:
Система функций Бесселя 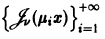
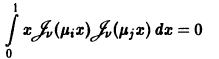
для 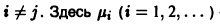
Пример:
Рассмотрим многочлены Чебышева—Эрмита, которые могут быть определены при помощи равенства
Выполнив дифференцирование в формуле (3), находим
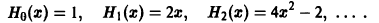
Можно показать, что многочлены Чебышева — Эрмита ортогональны на интервале 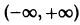
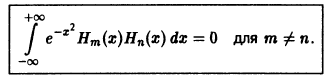
Пусть 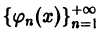
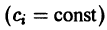
Умножая обе части последнего равенства на 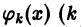

Эта операция имеет, вообще говоря, чисто формальный характер. Тем не менее, в некоторых случаях, например, когда ряд (4) сходится равномерно, все функции 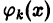
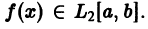
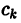
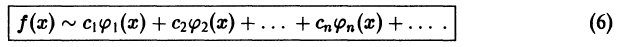
Ряд, стоящий в правой части, называется рядом Фурье функции f(x) относительно системы 
Сходимость в среднем
Определение:
Последовательность 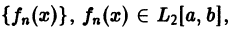
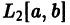
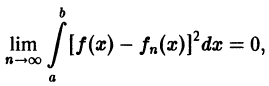
или, что то же, 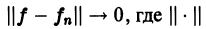
Теорема:
Если последовательность 
Пусть последовательность 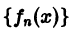
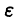
откуда вытекает наше утверждение.
Обратное утверждение неверно: последовательность 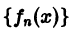
Пример:
Рассмотрим последовательность
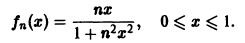
Легко видеть, что
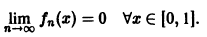
Но эта сходимость не равномерна: существует 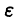
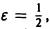
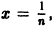
Таким образом, за счет увеличения n сделать неравенство 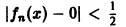
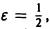
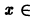
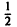
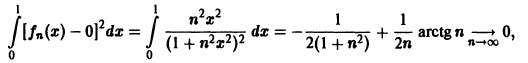
так что последовательность 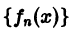
Минимальное свойство коэффициентов Фурье. Неравенство Бесселя. Равенство Парсеваля
Пусть 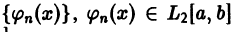
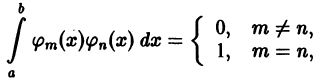
и пусть 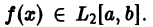
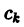

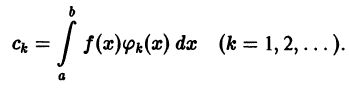
Рассмотрим линейную комбинацию
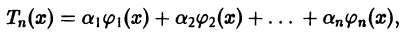
где 
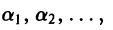

принимает минимальное значение. Запишем его подробнее
Интегрируя почленно, в силу ортонормированности системы 
Первые два слагаемых в правой части равенства (7) не зависят от 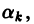
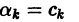
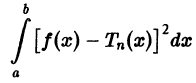
называют средним квадратичным приближением функции f(x) линейной комбинацией Тn(х). Таким образом, среднее квадратичное приближение функции 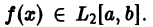
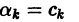
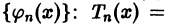
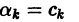
Равенство (9) называется тождеством Бесселя. Так как его левая часть неотрицательна, то из него следует неравенство Бесселя
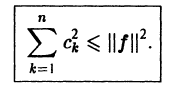
Поскольку n здесь произвольно, то неравенство Бесселя можно представить в усиленной форме
т. е. для всякой функции 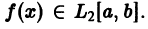

ортонормирована на отрезке 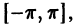
справедливое для любой функции f(x) с интегрируемым квадратом.
Если 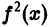
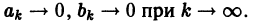
Равенство Парсеваля
Для некоторых систем 
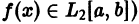
называется равенством Парсеваля—Стеклова {условием полноты).
Тождество Бесселя (9) позволяет записать условие (12) в равносильной форме
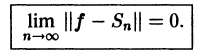
Тем самым выполнение условия полноты означает, что частичные суммы Sn(х) ряда Фурье функции f(x) сходятся к функции f(x) в среднем, т. е. по норме пространства
Определение:
Ортонормированная система 
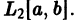
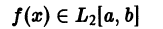
можно с любой точностью приблизить в среднем линейной комбинацией вида
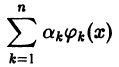
с достаточно большим числом слагаемых, т. е. если для всякой функции 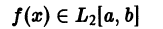
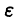
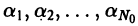
Из приведенных рассуждений следует
Теорема:
Если ортонормированная система 
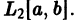
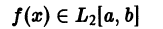
Можно показать, что тригонометрическая система
полна в пространстве 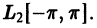
Теорема:
Если функция 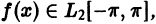
Замкнутые системы. Полнота и замкнутость систем
Определение. Ортонормированная система функций 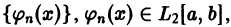
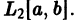
В пространстве 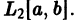
Ряды Фурье основные определения и свойства с подробным объяснением и теорией
При изучении разнообразных периодических процессов, т. е. процессов, которые через определенный промежуток времени повторяются (встречаются в радиотехнике, электронике, теории упругости, теории и практике автоматического регулирования и т. д.), целесообразнее разлагать периодические функции, описывающие эти процессы, не в степенной ряд, а в так называемый тригонометрический ряд.
Напомним, что функция у = f(x), определенная на множестве D, называется периодической (см. п. 14.3) с периодом Т > 0, если при каждом х € D значение 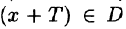
Для построения графика периодической функции периода Т достаточно построить его на любом отрезке длины Т и периодически продолжить его во всю область определения.
Отметим основные свойства периодической функции.
- Алгебраическая сумма периодических функций, имеющих один и тот же период Т, есть периодическая функция с периодом Т.
- Если функция f(x) имеет период Т , то функция f(ax) имеет период действительно,
- Если функция f(х) имеет период T и интегрируема на отрезке
при любых
Пусть, например, 0 < а < b < Т, тогда
С другой стороны,
Но
Подставляем полученный результат в (66.2) и, сравнивая с (66.1), имеем
В частности,
Простейшими периодическими функциями являются тригонометрические функции sinх и cosх. Период этих функций равен 
Простейшим периодическим процессом (движением) является простое гармоническое колебание (движение), описываемое функцией
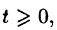
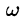
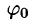
Функцию такого вида (и ее график) называют простой гармоникой. Основным периодом функции (66.3) является 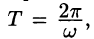
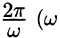

Проведем преобразование функции (66.3):
где 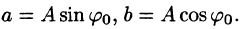
Сложное гармоническое колебание, возникающее в результате наложения конечного (или бесконечного) числа простых гармоник, также описывается функциями вида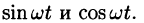
или, что равносильно, функция
задает сложное гармоническое колебание. Так как период первой гармоники есть
период функции 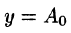
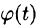

Понятно, что при наложении простых гармоник получаем периодическую функцию, описывающую сложное периодическое колебание (периодический процесс).
Возникает вопрос: всякую ли периодическую функцию, описывающую периодический процесс, можно представить в виде суммы простых гармоник вида (66.3) или (66.4)? Если да, то как найти неизвестные параметры (коэффициенты) каждой из этих гармоник? Ответим сначала на второй вопрос, а потом и на первый.
Тригонометрический ряд Фурье
С помощью так называемого тригонометрического ряда любую (практически) периодическую функцию можно представить в виде ряда, членами которого являются простые гармоники.
Тригонометрическим рядом называется функциональный ряд вида
где действительные числа 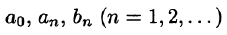
Ряд (66.5) можно записать в виде
Действительно, положив 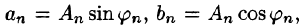
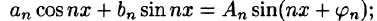
Свободный член ряда записан в виде 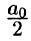
Приведем формулы, которые понадобятся нам в дальнейшем. Считая m и n целыми положительными, находим:
Замечанья.
1. Формулы (66.7)-(66.11) показывают, что семейство функций
обладает свойством ортогональности: интеграл от произведения любых двух функций этого семейства на интервале, имеющем длину 
2.Формулы (66.7)-(66.11) справедливы и в случае, когда область интегрирования есть отрезок 
Пусть f(х) — произвольная периодическая функция с периодом 
Так как функция f(х) (и сумма ряда) имеет период 


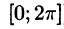
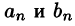
Интегралы от всех, кроме нулевого, членов ряда равны нулю в силу формул (66.7) и (66.8). Отсюда
Умножив обе части равенства (66.12) на cos mar и проинтегрировав полученный ряд в пределах от 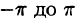
В силу формул (66.7), (66.9) и (66.10) из последнего равенства при m = п получаем:
Отсюда
Аналогично, умножив равенство (66.12) на sinmx и проинтегрировав почленно на отрезке 
Числа 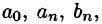
Для интегрируемой на отрезке 
и говорят: функции f(x) соответствует (поставлен в соответствие) ее ряд Фурье. Если ряд Фурье сходится, то его сумму обозначим S(x).
Разложение в ряд Фурье периодических функций
Разложение в ряд Фурье
Теорема Дирихле
Выясним условия, при которых знак соответствия (~) можно заменить знаком равенства (=), т. е. условия, при которых ряд Фурье функции f(х) сходится и имеет своей суммой как раз функцию f(х).
Будем рассматривать функции f(x), имеющие период 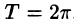
Сформулируем теорему, представляющую достаточное условие разложимости функции в ряд Фурье.
Теорема Дирихле:
Пусть 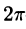

- f(х) кусочно-непрерывна, т. е. непрерывна или имеет конечное число точек разрыва I рода;
- f(x) кусочно-монотонна, т. е. монотонна на всем отрезке, либо этот отрезок можно разбить на конечное число интервалов так, что на каждом из них функция монотонна.
Тогда соответствующий функции f(х) ряд Фурье сходится на этом отрезке и при этом:
- В точках непрерывности функции сумма ряда S(x) совпадает с самой функцией: S(x) = f(x);
- В каждой точке
разрыва функции сумма ряда равна
т. е. равна среднему арифметическому пределов функции /(х) справа и слева;
- В точках
(на концах отрезка) сумма ряда равна
Таким образом, если функция f(х) удовлетворяет условиям 1 и 2 теоремы (условия Дирихле), то на отрезке 
причем коэффициенты вычисляются по формулам (66.13)-(66.15). Это равенство может нарушиться только в точках разрыва функции f(х) и на концах отрезка 
В силу периодичности исходной функции и суммы ряда Фурье может быть получено указанное разложение во всей области определения функции.
Замечания:
1.Если функция f(x) с периодом 
(Интегралы 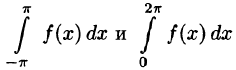
2.Условиям Дирихле удовлетворяют большинство функций, которые встречаются в математике и ее приложениях. Существуют функции, не удовлетворяющие условиям Дирихле, но при этом разложимые в ряд Фурье, т. е. теорема Дирихле дает лишь достаточное условие разложимости, но не необходимое.
Пример:
Разложить в ряд Фурье функцию f(x) периода 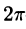

Решение:
На рисунке 260 изображен график функции f(х). Эта функция удовлетворяет условиям Дирихле, значит, она разложима в ряд Фурье. Находим коэффициенты ряда:
Аналогично находим
Исходной функции f(x) соответствует ряд Фурье
Функция f(х) непрерывна во всех внутренних точкой отрезка 
В точках 
Графики функций f(х) и S(х) показаны на рис. 260.
Разложение в ряд Фурье четных и нечетных функций
Если разлагаемая на отрезке 
Если функция f(x) четная, то ее ряд Фурье имеет вид
где
Если функция f(x) нечетная, то ее ряд Фурье имеет вид
где
Как известно (см. п. 39.4), если функция f(x) интегрируема на симметричном отрезке [—а; а], то
Если функция f(x) — четная, то f(х) cos nx — четная функция 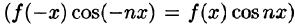
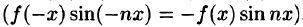
Если же f(х) — нечетная функция, то, очевидно, функция f(х) cosnx — нечетная, a f(x) sinnx — четная.
С учетом формулы (67.5) из формул (66.13)-(66.15) получаем формулы (67.1)-(67.4).
Ряды (67.1) и (67.3) называются неполными тригонометрическими рядами, или рядами по косинусам и по синусам соответственно.
Пример:
Разложить в ряд Фурье функцию
Решение:
На рисунке 261 изображен график заданной функции. Условиям Дирихле функция у = х удовлетворяет. Эта функция — нечетная. Следовательно,
Ряд Фурье содержит только синусы:
При этом
Разложение в ряд Фурье функций произвольного периода
Разлагать в ряд Фурье можно и периодические функции с периодом, отличным от 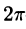
Пусть функция f(x), определенная на отрезке [-l; l], имеет период 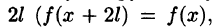
Сделав подстановку 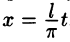
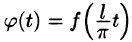

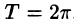
Действительно, если 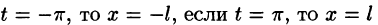
Разложение функции 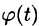

где
Возвращаясь к переменной х и заметив, что 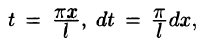
где
Ряд (67.6) с коэффициентами, вычисляемыми по формулам (67.7), называется рядом Фурье для функции f(x) с периодом Т = 2l.
Замечание:
Все теоремы, имеющие место для рядов Фурье 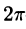
где
если f(x) — нечетная функция, то
где
Пример:
Разложить функцию f(x) = х на интервале (—4; 4) в ряд Фурье.
Решение:
Данная функция нечетная, удовлетворяет условиям Дирихле. По формулам (67.10) и (67.11), при l = 4, имеем:
где
Вычисляем 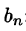
Таким образом,
для -4 < x < 4.
Представление непериодической функции рядом Фурье
Пусть у = f(х) — непериодическая функция, заданная на всей числовой оси 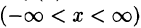
Такая функция не может быть разложена в ряд Фурье, т. к. сумма ряда Фурье есть функция периодическая и, следовательно, не может быть равна f(x) для всех x.
Однако непериодическая функция f(x) может быть представлена в виде ряда Фурье на любом конечном промежутке [a; b], на котором она удовлетворяет условиям Дирихле. Для этого можно поместить начало координат в середину отрезка [a; b] и построить функцию 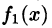
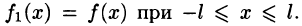
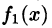
Разлагаем функцию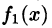
Пусть теперь непериодическую функцию f(х) требуется разложить в ряд Фурье на отрезке [0; l]. (Это частный случай: начало координат перенесено в точку х = а отрезка [а; b]; область определения функции f(x) будет иметь вид [0; l], где l = |b- а|.)
Такую функцию можно произвольным образом доопределить на отрезке [-l;0], а затем осуществить ее периодическое продолжение с периодом Т = 2l. Разложив в ряд Фурье на отрезке [—l,l] полученную таким образом периодическую функцию 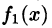
В частности, функцию f(x) можно доопределить на отрезке [—l; 0] четным образом (т. е. чтобы при 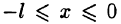
Если же функцию f(x) продолжить на отрезок [-l; 0] нечетным образом (см. рис. 264), то она разлагается в ряд, состоящий только из синусов (см. формулы (67.10) и (67.11)).
Ряд косинусов и ряд синусов для функции f(x), заданной на отрезке [0; l], имеют одну и ту же сумму. Если 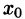
Замечание:
Все, что было сказано о разложении в ряд Фурье функции f(x) на отрезке [0;l], переносится практически без изменения на случай, когда функция задана на отрезке 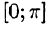
Пример:
Разложить в ряд косинусов функцию
Решение:
Продолжим функцию f(x) на отрезок 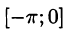
с периодом 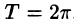
Таким образом,
где
Комплексная форма ряда Фурье
Ряды Фурье часто применяются в комплексной форме записи. Преобразуем ряд (66.12) и его коэффициенты (66.13)-(66.15) к комплексной форме. Для этого используем формулы Эйлера, выражающие косинус и синус через показательную функцию:
(из формулы Эйлера 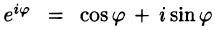
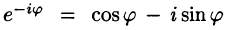
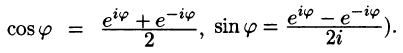
где обозначено
Найдем выражения для комплексных коэффициентов 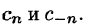
т. е.
Таким образом, формулу (67.12) можно записать в виде
Коэффициенты этого ряда, согласно формулам (67.13)-(67.15), можно записать в виде
Равенство (67.16) называется комплексной формой ряда Фурье функции f(x), а числа 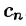
Если функция f(x) задается на отрезке [—l; l], то комплексная форма ее ряда Фурье имеет вид
Как видим, комплексная форма ряда Фурье (и коэффициентов) более компактна, чем обыкновенный ряд Фурье.
В электротехнике и радиотехнике члены ряда 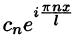
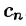
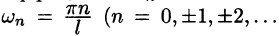
Совокупность величин 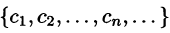
Графически амплитудный спектр изображается в виде вертикальных отрезков длиной 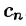
Пример:
Построить ряд Фурье в комплексной форме для 2-периодической функции
Решение:
На рисунке 266 изображен график функции f(х). По формулам (67.18) находим (l = 1):
Следовательно, для всех точек непрерывности функции f(х) справедливо равенство
Интеграл Фурье
Как известно, всякую (периодическую или непериодическую) функцию f(х), удовлетворяющую на отрезке [—l; l] условиям теоремы Дирихле, можно разложить в ряд Фурье
где
Это разложение будет справедливым на всей числовой оси Ох в том случае, когда f(x) — периодическая функция с периодом Т = 2l.
Рассмотрим случай, когда f(x) — непериодическая функция, заданная на бесконечном промежутке
Будем предполагать, что на любом конечном промежутке [—l; l] функция f(x) удовлетворяет условиям теоремы Дирихле и что сходится следующий несобственный интеграл:
Говорят: f(х) абсолютно интегрируема на всей числовой оси.
Подставляя в ряд (68.1) значения коэффициентов 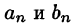
т. e.
Будем теперь неограниченно увеличивать l. Первое слагаемое в правой части равенства (68.3) при 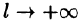
Рассмотрим второе слагаемое в равенстве (68.3). Величина 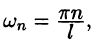
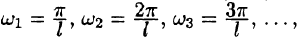
Итак,
Полученная сумма напоминает интегральную сумму для функции
(доказывается, что так оно и есть), поэтому, переходя в равенстве (68.3) к пределу при 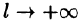
или
Формула (68.4) называется формулой Фурье, а интеграл в правой части формулы — интегралом Фурье для функции f(x). Формула Фурье имеет место в точках непрерывности функции f(х); в точках разрыва данной функции интеграл Фурье равен среднему арифметическому ее односторонних пределов:
Формулу (68.4) можно переписать в другом виде (в виде однократного интеграла):
т. е.
где
Как видно, есть аналогия между рядом Фурье и интегралом Фурье: в обоих случаях функция f(x) раскладывается на сумму гармонических составляющих. Однако, ряд Фурье суммируется по индексу п, принимающему дискретные значения п = 1,2,3,…, в интеграле Фурье производится интегрирование по непрерывной переменной 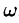
Некоторые сведения, связанные с интегралом Фурье, изложим в виде замечаний.
Замечания:
1.Если функция f(x) — четная, то формула Фурье (68.5) принимает вид
в случае нечетной функции —
2.Если функция f(x) задана лишь на промежутке 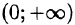
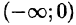
3.Формулу Фурье (68.5) можно представить в симметричной форме записи, если положить в формулах (68.6) и (68.7)
В случае четной функции
в случае нечетной функции
Функции 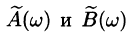
4.Интеграл Фурье (68.4) в комплексной форме имеет вид
интеграл Фурье (68.5) имеет вид
где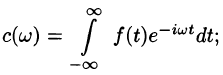
где
Пример:
Представить интегралом Фурье функцию
Решение:
Функция удовлетворяет условиям представимости интегралом Фурье, абсолютно интегрируема на промежутке
Функция нечетная, применим формулу (68.7):
Следовательно,
Замечание. Интересно отметить, что если х = 1, то
С другой стороны, 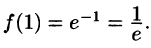
Иными словами, при помощи представления функций интегралом Фурье иногда можно вычислить величины несобственных интегралов.
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
Ряд Фурье́ — представление функции 

Этот ряд может быть также записан в виде
где
— амплитуда
-го гармонического колебания,
— круговая частота гармонического колебания,
— начальная фаза
-го колебания,
—
-я комплексная амплитуда
В более общем виде, рядом Фурье элемента некоторого пространства функций называется разложение этого элемента по полной системе ортонормированных функций или другими словами по базису, состоящему из ортогональных функций. В зависимости от используемого вида интегрирования говорят о рядах Фурье — Римана, Фурье — Лебега и т. п.[1]
Существует множество систем ортогональных многочленов и других ортогональных функций (например, функции Хаара, Уолша и Котельникова), по которым может быть произведено разложение функции в ряд Фурье.
Разложение функции в ряд Фурье является мощным инструментом при решении самых разных задач благодаря тому, что ряд Фурье прозрачным образом ведёт себя при дифференцировании, интегрировании, сдвиге функции по аргументу и свёртке функций.
Существуют многочисленные обобщения рядов Фурье в различных разделах математики. Например, любую функцию на конечной группе можно разложить в ряд, аналогичный ряду Фурье, по матричным элементам неприводимых представлений этой группы (теорема полноты).
История[править | править код]
Ряд Фурье назван в честь французского математика Жана-Батиста Жозефа Фурье (1768—1830), внесшего важный вклад в изучение тригонометрических рядов после предварительных исследований Леонарда Эйлера, Жана Лерона д’Аламбера и Даниила Бернулли[2]. Фурье представил ряд с целью решения уравнения теплопроводности в металлической пластине, написав свои первоначальные результаты в своем «Воспоминании о распространении тепла в твердых телах» («Трактат о распространении тепла в твердых телах») и опубликовав в Аналитической теории тепла (Théorie analytique de la chaleur) в 1822 году. В Воспоминании приведен анализ Фурье, в частности ряд Фурье. Благодаря исследованиям Фурье был установлен факт того, что произвольная (непрерывная)[3] функция может быть представлена тригонометрическим рядом. Первое объявление об этом великом открытии было сделано Фурье в 1807 году перед Французской академией[4]. Ранние идеи разложения периодической функции на сумму простых осциллирующих функций относятся к 3 веку до нашей эры, когда древние астрономы предложили эмпирическую модель движения планет, основанную на семействах и эпициклах.
Уравнение теплопроводности является уравнением в частных производных. До работы Фурье в общем случае не было известно решение уравнения теплопроводности, хотя были известны конкретные решения, если бы источник тепла вел себя простым образом, в частности, если источником тепла была волна синуса или косинуса. Эти простые решения теперь иногда называют собственными решениями. Идея Фурье состояла в том, чтобы смоделировать сложный источник тепла как суперпозицию (или линейную комбинацию) простых синусоидальных и косинусных волн и записать решение как суперпозицию соответствующих собственных решений. Эта суперпозиция или линейная комбинация называется рядом Фурье.
С современной точки зрения, результаты Фурье несколько неформальны из-за отсутствия точного понятия функции и интеграла в начале девятнадцатого века. Позднее Петер Густав Лежён Дирихле[5] и Бернхард Риман[6][7][8] выразили результаты Фурье с большей точностью и формальностью.
Хотя первоначальной мотивацией было решение уравнения теплопроводности, позже стало очевидно, что те же методы можно применять к широкому кругу математических и физических задач, особенно тех, которые включают линейные дифференциальные уравнения с постоянными коэффициентами, для которых собственные решения являются синусоидами. Ряд Фурье имеет много применений в области электротехники, вибрации анализа, акустики, оптики, обработки сигналов, обработки изображений, квантовой механики, эконометрики[9], теории перекрытия-оболочки[10] и т. д.
Тригонометрический ряд Фурье[править | править код]
Тригонометрическим рядом Фурье функции ![{displaystyle fin {mathcal {L}}([-pi ,pi ])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92aa58d626b8727d9d8907f6d7187afba35d3ac7)
![{displaystyle ([-pi ,pi ])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/29ff6ff22577090b4ccc15d2d0644494c12a43a2)
(1)
где
Числа 




![{displaystyle fin {mathcal {L}}([-pi ,pi ])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92aa58d626b8727d9d8907f6d7187afba35d3ac7)




![[-pi,pi]](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb064fd6c55820cfa660eabeeda0f6e3c4935ae6)


Ряд (1) для функции 
![{displaystyle {mathcal {L}}_{2}([-pi ,pi ])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dccc9dba55628dc13689087f3a616e08cff40331)

,
то их среднеквадратичное отклонение от функции 
.
Несмотря на среднеквадратичную сходимость, ряд Фурье функции, вообще говоря, не обязан сходиться к ней поточечно.
Часто при работе с рядами Фурье бывает удобнее в качестве базиса использовать вместо синусов и косинусов экспоненты мнимого аргумента. Мы рассматриваем пространство ![{displaystyle {mathcal {L}}^{2}([-pi ,pi ],mathbb {C} )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/acab138aad0d81ddb7f1b8fb5ab32358305f1fb2)
.
Мы также рассматриваем систему функций
-
.
Как и прежде, эти функции являются попарно ортогональными и образуют полную систему, и, таким образом, любая функция ![{displaystyle fin {mathcal {L}}^{2}([-pi ,pi ],mathbb {C} )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9dd9f8be496e976aa4264b3208bbbd1ad98fe36)
,
где ряд в правой части сходится к 
![L^2([-pi,pi],mathbb{C})](https://wikimedia.org/api/rest_v1/media/math/render/svg/31dbda1e2403eda880c8a98c040056904747f933)
.
Коэффициенты 
Для вещественнозначной функции коэффициенты 

Обобщения[править | править код]
Ряды Фурье в гильбертовом пространстве[править | править код]
Описанную выше конструкцию можно обобщить со случая пространства ![L^2[-pi,pi]](https://wikimedia.org/api/rest_v1/media/math/render/svg/20068d1913d7c592e020af9f2b46f4654ae2fc27)

и 



Домножим это выражение на 


Числа
называются координатами, или коэффициентами Фурье элемента 

называется рядом Фурье элемента 

Ряд Фурье любого элемента 



-
.
Если эти условия не выполняются, то сумма ряда Фурье элемента 

Двойственность Понтрягина[править | править код]
При обобщении теории рядов Фурье на случай гильбертовых пространств теряются свойства, выражающие связь рядов Фурье со свёрткой — то, что коэффициенты Фурье свертки функций являются почленными произведениями их коэффициентов Фурье, и наоборот, коэффициенты Фурье произведения представляются сверткой коэффициентов Фурье сомножителей. Эти свойства являются ключевыми для приложений теории Фурье к решению дифференциальных, интегральных и других функциональных уравнений. Поэтому большой интерес представляют такие обобщения теории рядов Фурье, при которых эти свойства сохраняются. Таким обобщением является теория двойственности Понтрягина. Она рассматривает функции, заданные на локально-компактных абелевых группах. Аналогом ряда Фурье такой функции будет функция, заданная на двойственной группе.
Сходимость ряда Фурье[править | править код]
Обзор результатов о сходимости ряда Фурье[править | править код]
Обозначим через 

.
Далее обсуждается сходимость последовательности функций 



![[-pi,pi]](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb064fd6c55820cfa660eabeeda0f6e3c4935ae6)
- Если
, то последовательность
сходится к функции
в смысле
. Кроме того,
являются наилучшим (в смысле расстояния в
) приближением функции
тригонометрическим многочленом степени не выше
.
- Сходимость ряда Фурье в заданной точке
— локальное свойство, то есть, если функции
и
совпадают в некоторой окрестности
, то последовательности
и
либо одновременно расходятся, либо одновременно сходятся, и в этом случае их пределы совпадают. (Принцип локализации).
- Если функция
дифференцируема в точке
, то её ряд Фурье в этой точке сходится к
. Более точные достаточные условия в терминах гладкости функции
задаются признаком Дини.
- Функция, непрерывная в точке
, может иметь расходящийся в ней ряд Фурье. Однако, если он сходится, то непременно к
. Это следует из того, что для непрерывной в
функции
последовательность
сходится по Чезаро к
.
- Если функция
разрывна в точке
, но имеет пределы в этой точке справа и слева
то при некоторых дополнительных условиях
сходятся к
. Подробнее см. модифицированный признак Дини.
- Теорема Карлесона: если
, то её ряд Фурье сходится к ней почти всюду. Это верно и если
. Однако, существуют функции из
, ряд Фурье которых расходится во всех точках (пример такой функции построен Колмогоровым[11]).
- Зафиксируем точку
. Тогда множество всех непрерывных функций, ряд Фурье которых сходится в этой точке, является множеством первой категории в пространстве
. В некотором смысле это означает, что «типичная» непрерывная функция имеет расходящийся ряд Фурье.
Убывание коэффициентов Фурье и аналитичность функции[править | править код]
Существует фундаментальная связь между аналитичностью функции и скоростью убывания её коэффициентов Фурье. Чем «лучше» функция, тем быстрее её коэффициенты стремятся к нулю, и наоборот. Степенное убывание коэффициентов Фурье присуще функциям класса 
См. также[править | править код]
- Преобразование Фурье
- Быстрое преобразование Фурье
- Тригонометрический ряд
- Признак Жордана
- Признак Дини
- Числовой ряд
- АТС-теорема
- Натуральный звукоряд
- Явление Гиббса[en]
Примечания[править | править код]
- ↑ Математический энциклопедический словарь. — М.: «Сов. энциклопедия », 1988. — С. 619.
- ↑ Fetter, Alexander L. Theoretical Mechanics of Particles and Continua / Alexander L. Fetter, John Dirk Walecka. — Courier, 2003. — P. 209—210. — ISBN 978-0-486-43261-8. Архивная копия от 18 апреля 2021 на Wayback Machine
- ↑ Stillwell, John (англ.) (рус.. Logic and the philosophy of mathematics in the nineteenth century // Routledge History of Philosophy / Ten, C. L.. — Routledge, 2013. — Т. Volume VII: The Nineteenth Century. — С. 204. — ISBN 978-1-134-92880-4. Архивная копия от 16 мая 2020 на Wayback Machine
- ↑ Florian Cajori. A History of Mathematics. — Macmillan, 1893. — С. 283.
- ↑ Lejeune-Dirichlet, Peter Gustav (англ.) (рус.. Sur la convergence des séries trigonométriques qui servent à représenter une fonction arbitraire entre des limites données (фр.) // Journal für die reine und angewandte Mathematik. — 1829. — Vol. 4. — P. 157—169. — arXiv:0806.1294.
- ↑ Ueber die Darstellbarkeit einer Function durch eine trigonometrische Reihe (неопр.). Habilitationsschrift, Göttingen; 1854. Abhandlungen der Königlichen Gesellschaft der Wissenschaften zu Göttingen, vol. 13, 1867. Published posthumously for Riemann by Richard Dedekind. Архивировано 20 мая 2008 года.
- ↑ Mascre, D. & Riemann, Bernhard (1867), Posthumous Thesis on the Representation of Functions by Trigonometric Series, in Grattan-Guinness, Ivor, Landmark Writings in Western Mathematics 1640–1940, Elsevier, 2005, <https://books.google.com/books?id=UdGBy8iLpocC>
- ↑ Remmert, Reinhold. Theory of Complex Functions: Readings in Mathematics (англ.). — Springer, 1991. — P. 29. Архивная копия от 16 мая 2020 на Wayback Machine
- ↑ Nerlove, Marc; Grether, David M.; Carvalho, Jose L. Analysis of Economic Time Series. Economic Theory, Econometrics, and Mathematical Economics (англ.). — Elsevier, 1995. — ISBN 0-12-515751-7.
- ↑ Flugge, Wilhelm. Statik und Dynamik der Schalen (нем.). — Berlin: Springer-Verlag, 1957. Архивная копия от 14 мая 2020 на Wayback Machine
- ↑ В. М. Тихомиров, В. В. Успенский. Пеpвые филдсовские лауpеаты и советская математика 30-х годов. I. — Матем. просв., сер. 3, 2, МЦНМО, М., 1998, 21-40.
Литература[править | править код]
- Жук В. В., Натансон Г. И. Тригонометрические ряды Фурье и элементы теории аппроксимации. — Л.: Изд-во Ленингр. ун-та, 1983. — 188 с.
- Рудин У. Основы математического анализа. — 1976.
- Пискунов Н. С. Дифференциальное и интегральное исчисления для ВТУЗов. — М.: «Наука», 1964. — Т. 2.
- Зигмунд А. Тригонометрические ряды. — М.: «Мир», 1965. — Т. 1.
- Харди Г. Х., Рогозинский В. В.ruen. Ряды Фурье. — М.: Физматгиз, 1959.
Ссылки[править | править код]
- Представление периодических сигналов. Ряд Фурье.
- Некоторые свойства разложения периодических сигналов в ряд Фурье.
Практическое применение преобразования Фурье для анализа сигналов. Введение для начинающих
Время на прочтение
9 мин
Количество просмотров 255K
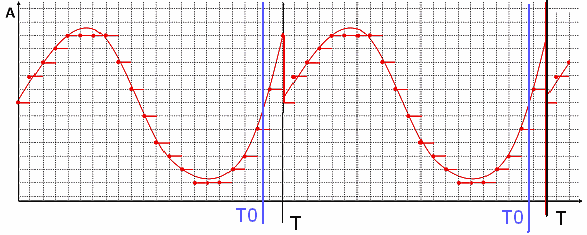
1. Преобразование Фурье и спектр сигнала
Во многих случаях задача получения (вычисления) спектра сигнала выглядит следующим образом. Имеется АЦП, который с частотой дискретизации Fd преобразует непрерывный сигнал, поступающий на его вход в течение времени Т, в цифровые отсчеты — N штук. Далее массив отсчетов подается в некую программку, которая выдает N/2 каких-то числовых значений (программист, который утянул из инета написал программку, уверяет, что она делает преобразование Фурье).
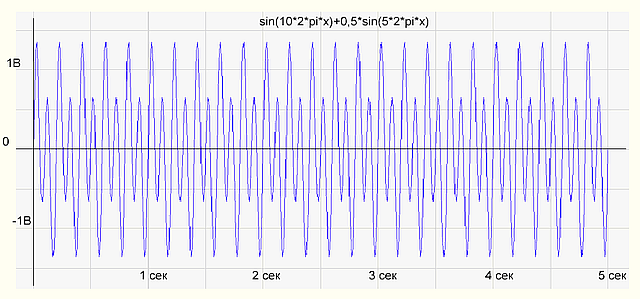
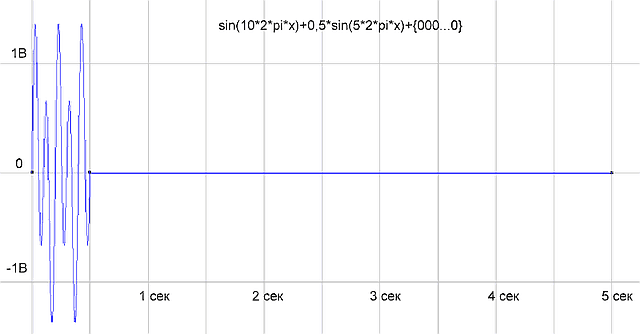
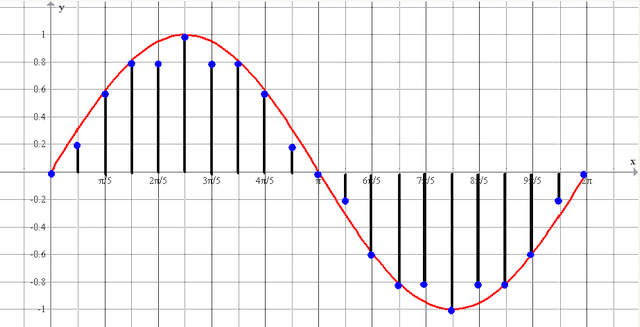
Чтобы проверить, правильно ли работает программа, сформируем массив отсчетов как сумму двух синусоид sin(10*2*pi*x)+0,5*sin(5*2*pi*x) и подсунем программке. Программа нарисовала следующее:
рис.1 График временной функции сигнала
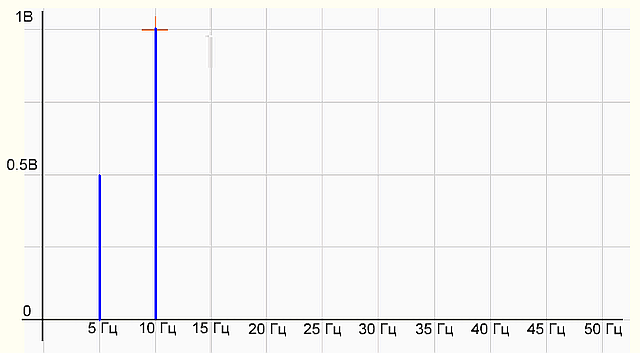
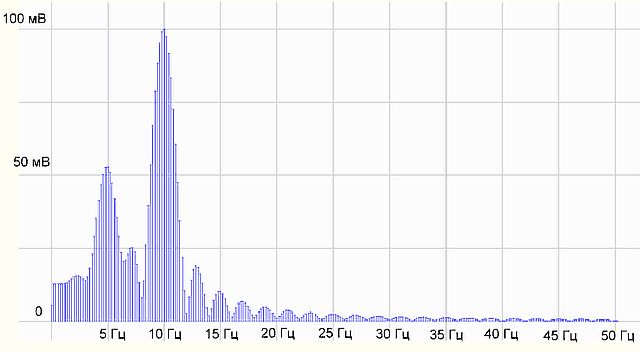
рис.2 График спектра сигнала
На графике спектра имеется две палки (гармоники) 5 Гц с амплитудой 0.5 В и 10 Гц — с амплитудой 1 В, все как в формуле исходного сигнала. Все отлично, программист молодец! Программа работает правильно.
Это значит, что если мы подадим на вход АЦП реальный сигнал из смеси двух синусоид, то мы получим аналогичный спектр, состоящий из двух гармоник.
Итого, наш реальный измеренный сигнал, длительностью 5 сек, оцифрованный АЦП, то есть представленный дискретными отсчетами, имеет дискретный непериодический спектр.
С математической точки зрения — сколько ошибок в этой фразе?
Теперь
начальство решило
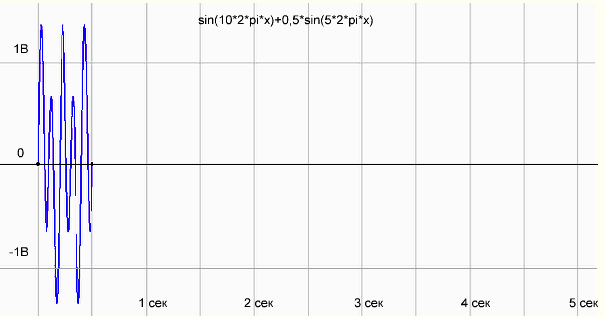
мы решили, что 5 секунд — это слишком долго, давай измерять сигнал за 0.5 сек.
рис.3 График функции sin(10*2*pi*x)+0,5*sin(5*2*pi*x) на периоде измерения 0.5 сек
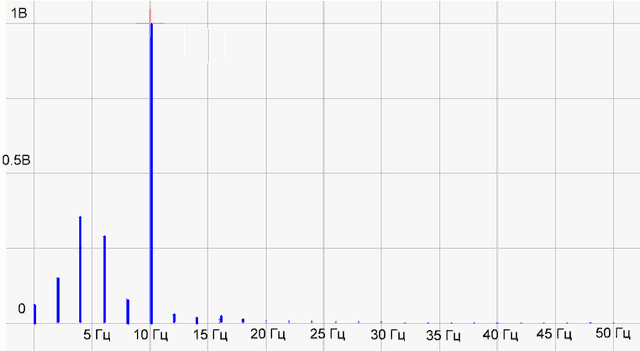
рис.4 Спектр функции
Что-то как бы не то! Гармоника 10 Гц рисуется нормально, а вместо палки на 5 Гц появилось несколько каких-то непонятных гармоник. Смотрим в интернетах, что да как…
Во, говорят, что в конец выборки надо добавить нули и спектр будет рисоваться нормальный.
рис.5 Добили нулей до 5 сек
рис.6 Получили спектр
Все равно не то, что было на 5 секундах. Придется разбираться с теорией. Идем в Википедию — источник знаний.
2. Непрерывная функция и представление её рядом Фурье
Математически наш сигнал длительностью T секунд является некоторой функцией f(x), заданной на отрезке {0, T} (X в данном случае — время). Такую функцию всегда можно представить в виде суммы гармонических функций (синусоид или косинусоид) вида:
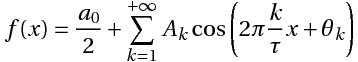
k — номер тригонометрической функции ( номер гармонической составляющей, номер гармоники)
T — отрезок, где функция определена (длительность сигнала)
Ak — амплитуда k-ой гармонической составляющей,
θk- начальная фаза k-ой гармонической составляющей
Что значит «представить функцию в виде суммы ряда»? Это значит, что, сложив в каждой точке значения гармонических составляющих ряда Фурье, мы получим значение нашей функции в этой точке.
(Более строго, среднеквадратичное отклонение ряда от функции f(x) будет стремиться к нулю, но несмотря на среднеквадратичную сходимость, ряд Фурье функции, вообще говоря, не обязан сходиться к ней поточечно. См. https://ru.wikipedia.org/wiki/Ряд_Фурье.)
Этот ряд может быть также записан в виде:
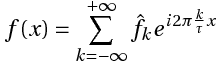
где 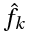
или
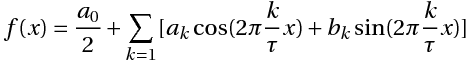
Связь между коэффициентами (1) и (3) выражается следующими формулами:
и
Отметим, что все эти три представления ряда Фурье совершенно равнозначны. Иногда при работе с рядами Фурье бывает удобнее использовать вместо синусов и косинусов экспоненты мнимого аргумента, то есть использовать преобразование Фурье в комплексной форме. Но нам удобно использовать формулу (1), где ряд Фурье представлен в виде суммы косинусоид с соответствующими амплитудами и фазами. В любом случае неправильно говорить, что результатом преобразования Фурье действительного сигнала будут комплексные амплитуды гармоник. Как правильно говорится в Вики «Преобразование Фурье (ℱ) — операция, сопоставляющая одной функции вещественной переменной другую функцию, также вещественной переменной.»
Итого:
Математической основой спектрального анализа сигналов является преобразование Фурье.
Преобразование Фурье позволяет представить непрерывную функцию f(x) (сигнал), определенную на отрезке {0, T} в виде суммы бесконечного числа (бесконечного ряда) тригонометрических функций (синусоид иили косинусоид) с определёнными амплитудами и фазами, также рассматриваемых на отрезке {0, T}. Такой ряд называется рядом Фурье.
Отметим еще некоторые моменты, понимание которых требуется для правильного применения преобразования Фурье к анализу сигналов. Если рассмотреть ряд Фурье (сумму синусоид) на всей оси Х, то можно увидеть, что вне отрезка {0, T} функция представленная рядом Фурье будет будет периодически повторять нашу функцию.
Например, на графике рис.7 исходная функция определена на отрезке {-T2, +T2}, а ряд Фурье представляет периодическую функцию, определенную на всей оси х.
Это происходит потому, что синусоиды сами являются периодическими функциями, соответственно и их сумма будет периодической функцией.
рис.7 Представление непериодической исходной функции рядом Фурье
Таким образом:
Наша исходная функция — непрерывная, непериодическая, определена на некотором отрезке длиной T.
Спектр этой функции — дискретный, то есть представлен в виде бесконечного ряда гармонических составляющих — ряда Фурье.
По факту, рядом Фурье определяется некоторая периодическая функция, совпадающая с нашей на отрезке {0, T}, но для нас эта периодичность не существенна.
Далее.
Периоды гармонических составляющих кратны величине отрезка {0, T}, на котором определена исходная функция f(x). Другими словами, периоды гармоник кратны длительности измерения сигнала. Например, период первой гармоники ряда Фурье равен интервалу Т, на котором определена функция f(x). Период второй гармоники ряда Фурье равен интервалу Т/2. И так далее (см. рис. 8).
рис.8 Периоды (частоты) гармонических составляющих ряда Фурье (здесь Т=2π)
Соответственно, частоты гармонических составляющих кратны величине 1/Т. То есть частоты гармонических составляющих Fk равны Fk= кТ, где к пробегает значения от 0 до ∞, например к=0 F0=0; к=1 F1=1T; к=2 F2=2T; к=3 F3=3T;… Fk= кТ (при нулевой частоте — постоянная составляющая).
Пусть наша исходная функция, представляет собой сигнал, записанный в течение Т=1 сек. Тогда период первой гармоники будет равен длительности нашего сигнала Т1=Т=1 сек и частота гармоники равна 1 Гц. Период второй гармоники будет равен длительности сигнала, деленной на 2 (Т2=Т/2=0,5 сек) и частота равна 2 Гц. Для третьей гармоники Т3=Т/3 сек и частота равна 3 Гц. И так далее.
Шаг между гармониками в этом случае равен 1 Гц.
Таким образом сигнал длительностью 1 сек можно разложить на гармонические составляющие (получить спектр) с разрешением по частоте 1 Гц.
Чтобы увеличить разрешение в 2 раза до 0,5 Гц — надо увеличить длительность измерения в 2 раза — до 2 сек. Сигнал длительностью 10 сек можно разложить на гармонические составляющие (получить спектр) с разрешением по частоте 0,1 Гц. Других способов увеличить разрешение по частоте нет.
Существует способ искусственного увеличения длительности сигнала путем добавления нулей к массиву отсчетов. Но реальную разрешающую способность по частоте он не увеличивает.
3. Дискретные сигналы и дискретное преобразование Фурье
С развитием цифровой техники изменились и способы хранения данных измерений (сигналов). Если раньше сигнал мог записываться на магнитофон и храниться на ленте в аналоговом виде, то сейчас сигналы оцифровываются и хранятся в файлах в памяти компьютера в виде набора чисел (отсчетов).
Обычная схема измерения и оцифровки сигнала выглядит следующим образом.
рис.9 Схема измерительного канала
Сигнал с измерительного преобразователя поступает на АЦП в течение периода времени Т. Полученные за время Т отсчеты сигнала (выборка) передаются в компьютер и сохраняются в памяти.
рис.10 Оцифрованный сигнал — N отсчетов полученных за время Т
Какие требования выдвигаются к параметрам оцифровки сигнала? Устройство, преобразующее входной аналоговый сигнал в дискретный код (цифровой сигнал) называется аналого-цифровой преобразователь (АЦП, англ. Analog-to-digital converter, ADC) ( Wiki).
Одним из основных параметров АЦП является максимальная частота дискретизации (или частота семплирования, англ. sample rate) — частота взятия отсчетов непрерывного во времени сигнала при его дискретизации. Измеряется в герцах. (( Wiki))
Согласно теореме Котельникова, если непрерывный сигнал имеет спектр, ограниченный частотой Fмакс, то он может быть полностью и однозначно восстановлен по его дискретным отсчетам, взятым через интервалы времени 
А что будет, если мы будем брать отсчеты с меньшей частотой, чем требуется по теореме Котельникова?
В этом случае возникает эффект «алиасинга» (он же стробоскопический эффект, муаровый эффект), при котором сигнал высокой частоты после оцифровки превращается в сигнал низкой частоты, которого на самом деле не существует. На рис. 11 красная синусоида высокой частоты — это реальный сигнал. Синяя синусоида более низкой частоты — фиктивный сигнал, возникающий вследствие того, за время взятия отсчета успевает пройти больше, чем пол-периода высокочастотного сигнала.
Рис. 11. Появление ложного сигнала низкой частоты при недостаточно высокой частоте дискретизации
Чтобы избежать эффекта алиасинга перед АЦП ставят специальный антиалиасинговый фильтр — ФНЧ (фильтр нижних частот), который пропускает частоты ниже половины частоты дискретизации АЦП, а более высокие частоты зарезает.
Для того, чтобы вычислить спектр сигнала по его дискретным отсчетам используется дискретное преобразование Фурье (ДПФ). Отметим еще раз, что спектр дискретного сигнала «по определению» ограничен частотой Fмакс, меньшей половине частоты дискретизации Fd. Поэтому спектр дискретного сигнала может быть представлен суммой конечного числа гармоник, в отличие от бесконечной суммы для ряда Фурье непрерывного сигнала, спектр которого может быть неограничен. Согласно теореме Котельникова максимальная частота гармоники должна быть такой, чтобы на нее приходилось как минимум два отсчета, поэтому число гармоник равно половине числа отсчетов дискретного сигнала. То есть если в выборке имеется N отсчетов, то число гармоник в спектре будет равно N/2.
Рассмотрим теперь дискретное преобразование Фурье (ДПФ).
Сравнивая с рядом Фурье
видим, что они совпадают, за исключением того, что время в ДПФ имеет дискретный характер и число гармоник ограничено величиной N/2 — половиной числа отсчетов.
Формулы ДПФ записываются в безразмерных целых переменных k, s, где k – номера отсчетов сигнала, s – номера спектральных составляющих.
Величина s показывает количество полных колебаний гармоники на периоде Т (длительности измерения сигнала). Дискретное преобразование Фурье используется для нахождения амплитуд и фаз гармоник численным методом, т.е. «на компьютере»
Возвращаясь к результатам, полученным в начале. Как уже было сказано выше, при разложении в ряд Фурье непериодической функции (нашего сигнала), полученный ряд Фурье фактически соответствует периодической функции с периодом Т. (рис.12).
рис.12 Периодическая функция f(x) с периодом Т0, с периодом измерения Т>T0
Как видно на рис.12 функция f(x) периодическая с периодом Т0. Однако из-за того, что длительность измерительной выборки Т не совпадает с периодом функции Т0, функция, получаемая как ряд Фурье, имеет разрыв в точке Т. В результате спектр данной функции будет содержать большое количество высокочастотных гармоник. Если бы длительность измерительной выборки Т совпадала с периодом функции Т0, то в полученном после преобразования Фурье спектре присутствовала бы только первая гармоника (синусоида с периодом равным длительности выборки), поскольку функция f(x) представляет собой синусоиду.
Другими словами, программа ДПФ «не знает», что наш сигнал представляет собой «кусок синусоиды», а пытается представить в виде ряда периодическую функцию, которая имеет разрыв из-за нестыковки отдельных кусков синусоиды.
В результате в спектре появляются гармоники, которые должны в сумме изобразить форму функции, включая этот разрыв.
Таким образом, чтобы получить «правильный» спектр сигнала, являющегося суммой нескольких синусоид с разными периодами, необходимо чтобы на периоде измерения сигнала укладывалось целое число периодов каждой синусоиды. На практике это условие можно выполнить при достаточно большой длительности измерения сигнала.
Рис.13 Пример функции и спектра сигнала кинематической погрешности редуктора
При меньшей длительности картина будет выглядеть «хуже»:
Рис.14 Пример функции и спектра сигнала вибрации ротора
На практике бывает сложно понять, где «реальные составляющие», а где «артефакты», вызванные некратностью периодов составляющих и длительности выборки сигнала или «скачками и разрывами» формы сигнала. Конечно слова «реальные составляющие» и «артефакты» не зря взяты в кавычки. Наличие на графике спектра множества гармоник не означает, что наш сигнал в реальности из них «состоит». Это все равно что считать, будто число 7 «состоит» из чисел 3 и 4. Число 7 можно представить в виде суммы чисел 3 и 4 — это правильно.
Так и наш сигнал… а вернее даже не «наш сигнал», а периодическую функцию, составленную путем повторения нашего сигнала (выборки) можно представить в виде суммы гармоник (синусоид) с определенными амплитудами и фазами. Но во многих важных для практики случаях (см. рисунки выше) действительно можно связать полученные в спектре гармоники и с реальными процессами, имеющими циклический характер и вносящими значительный вклад в форму сигнала.
Некоторые итоги
1. Реальный измеренный сигнал, длительностью T сек, оцифрованный АЦП, то есть представленный набором дискретных отсчетов (N штук), имеет дискретный непериодический спектр, представленный набором гармоник (N/2 штук).
2. Сигнал представлен набором действительных значений и его спектр представлен набором действительных значений. Частоты гармоник положительны. То, что математикам бывает удобнее представить спектр в комплексной форме с использованием отрицательных частот не значит, что «так правильно» и «так всегда надо делать».
3. Сигнал, измеренный на отрезке времени Т определен только на отрезке времени Т. Что было до того, как мы начали измерять сигнал, и что будет после того — науке это неизвестно. И в нашем случае — неинтересно. ДПФ ограниченного во времени сигнала дает его «настоящий» спектр, в том смысле, что при определенных условиях позволяет вычислить амплитуду и частоту его составляющих.
Использованные материалы и другие полезные материалы.
FourierScope — программа для построения радио сигналов и их спектрального анализа.
Graph — программа с открытым кодом, предназначенная для построения математических графиков.
ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ – КАК ЭТО ДЕЛАЕТСЯ
Дискретное преобразование Фурье (ДПФ)
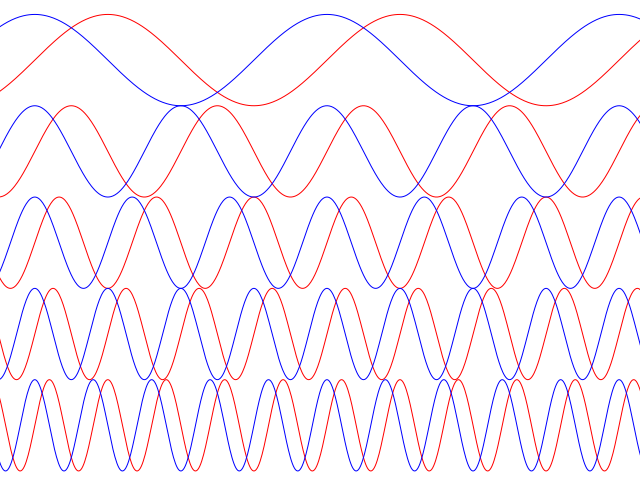
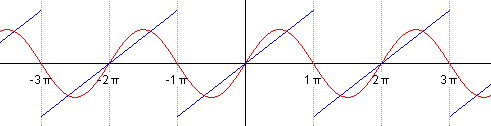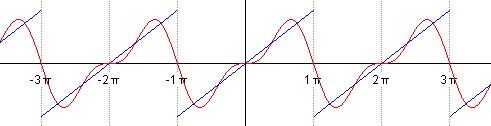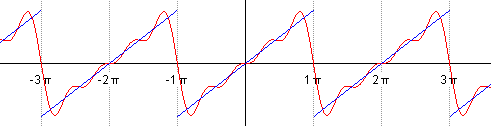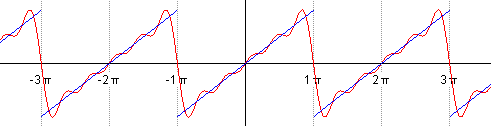
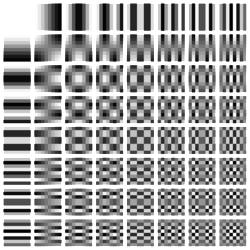
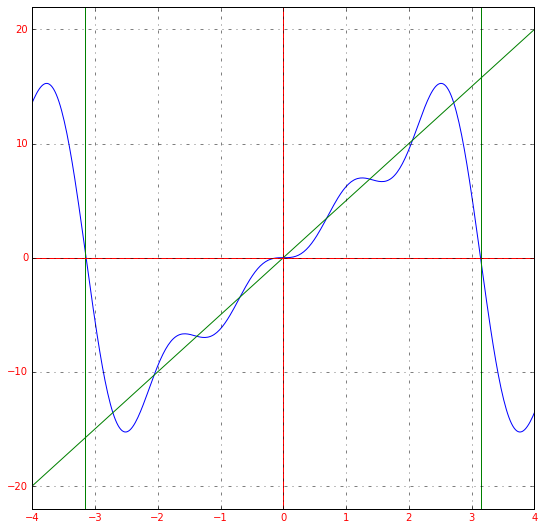
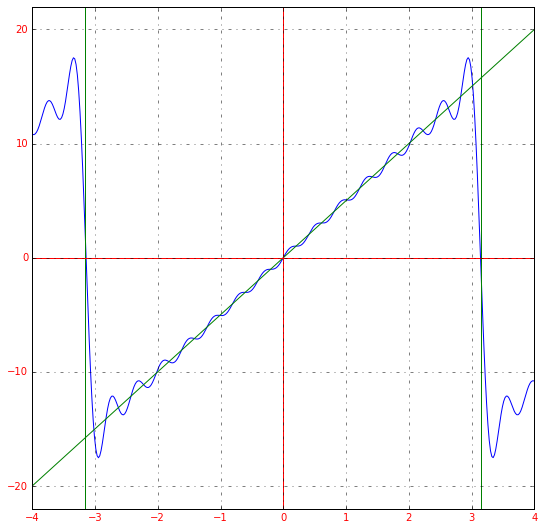
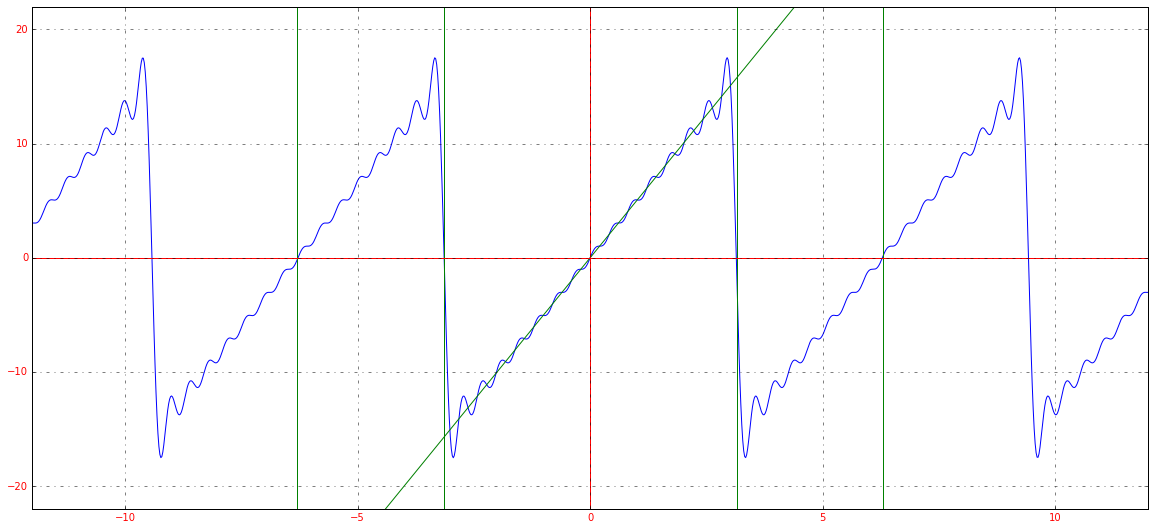










































 ;
; ;
;





















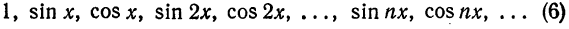
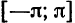
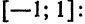
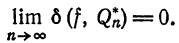
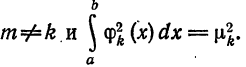
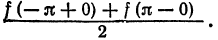
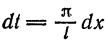
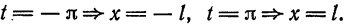
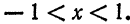
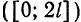
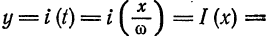
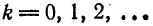
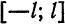
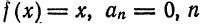










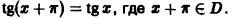
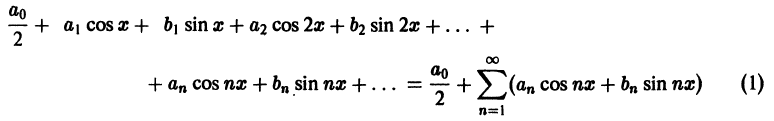
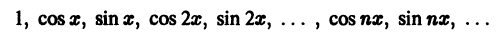
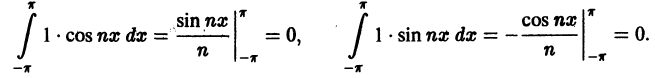
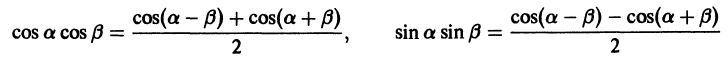
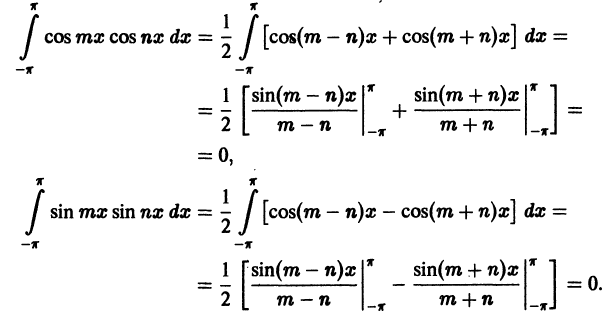
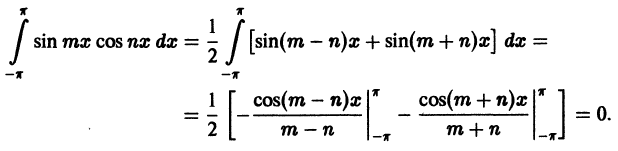
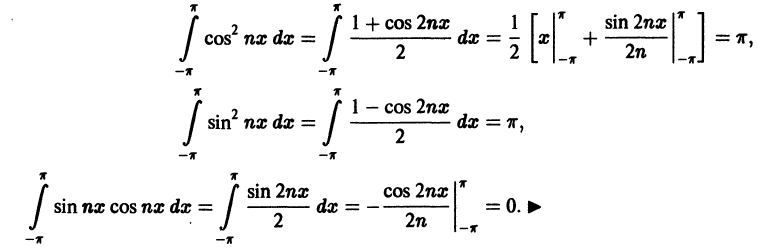
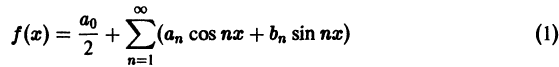
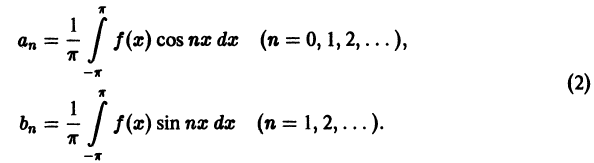
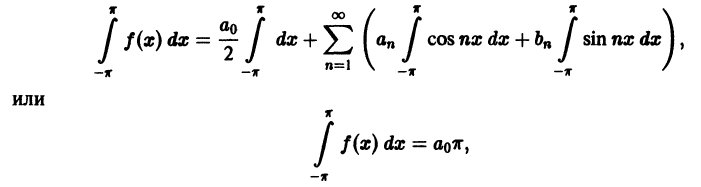
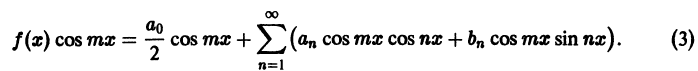
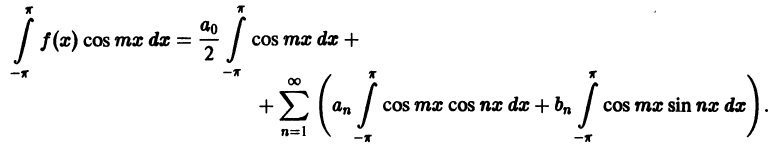
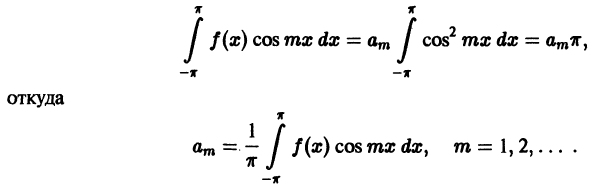
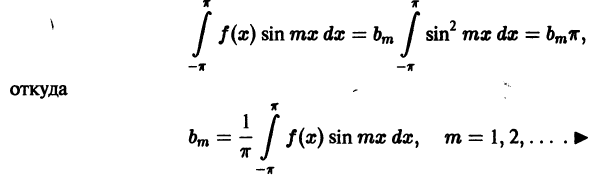
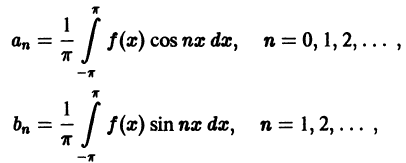
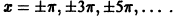
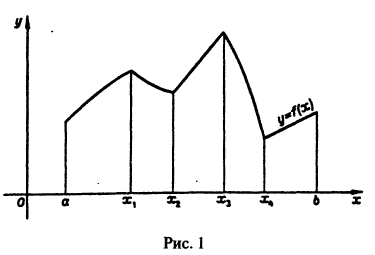
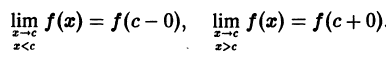
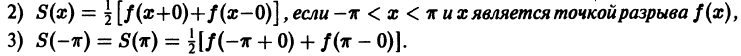
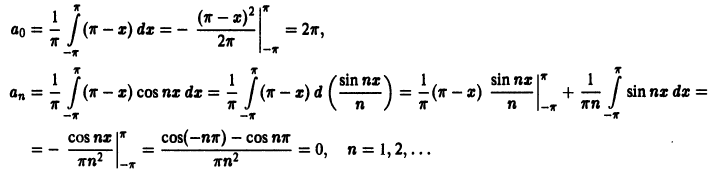
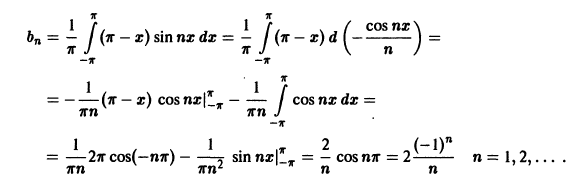
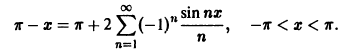
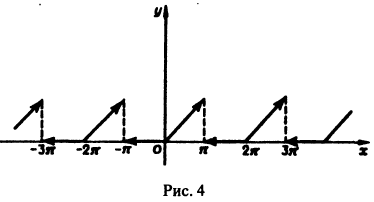
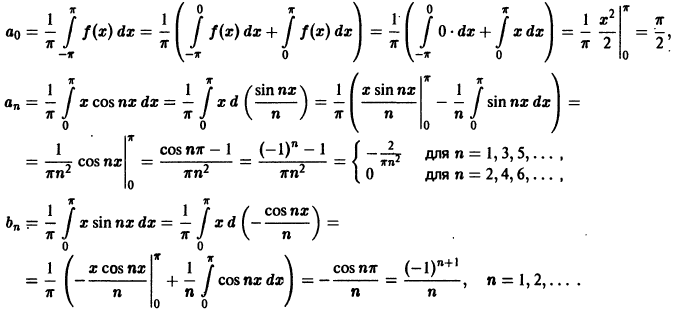
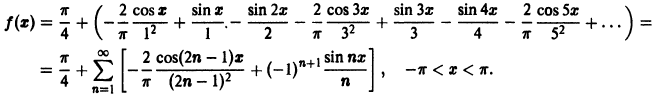
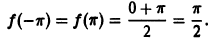
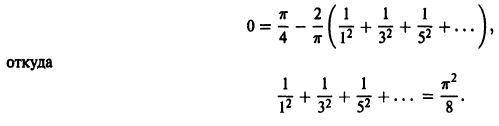
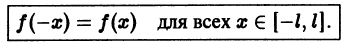
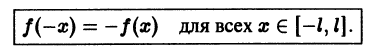
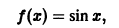
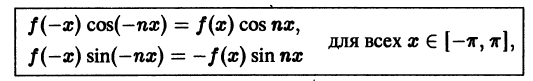
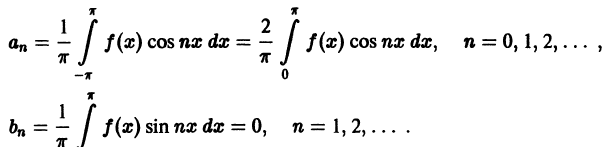
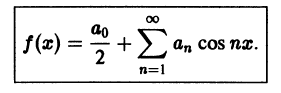
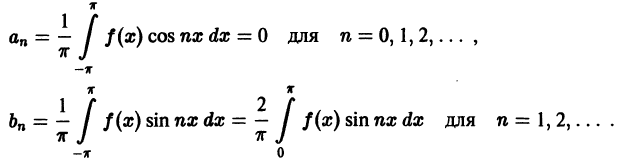
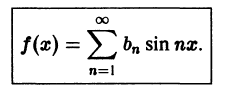
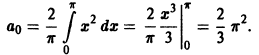
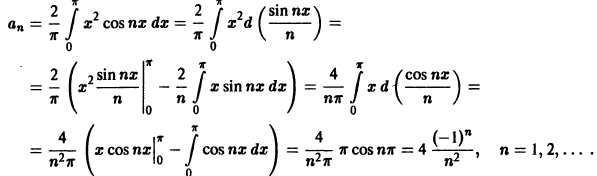
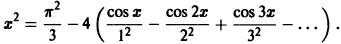
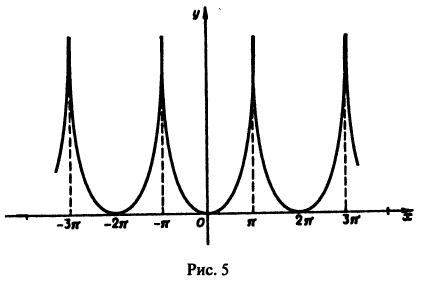
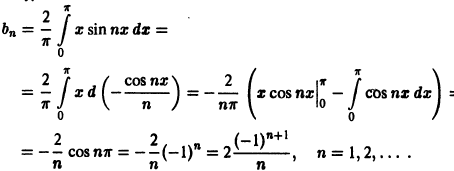
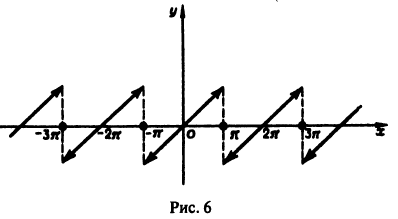
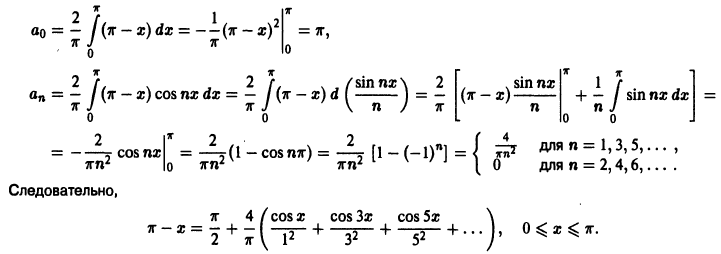
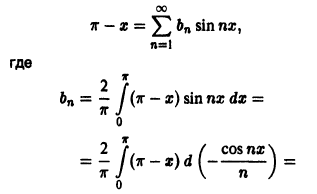
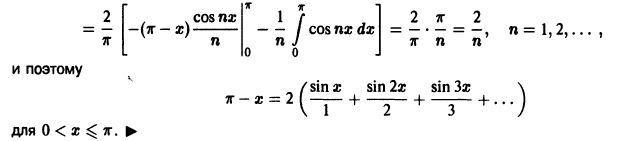
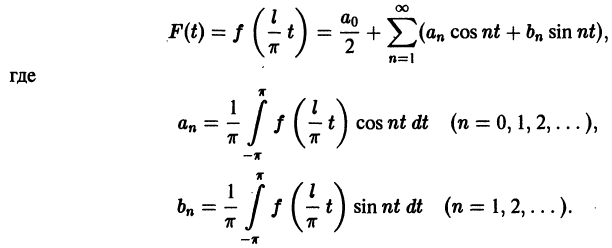
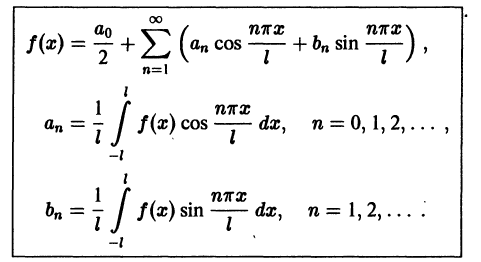
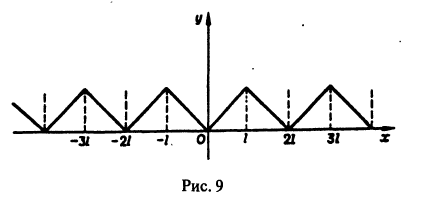
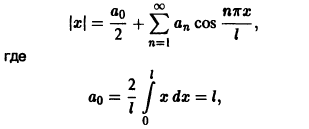
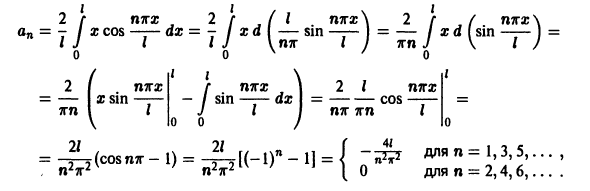
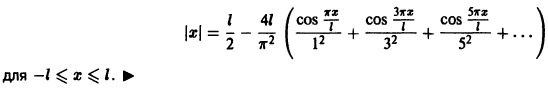
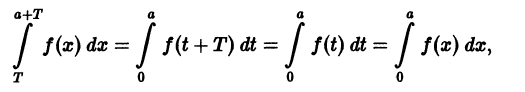
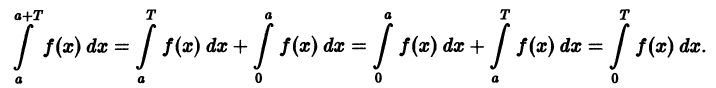
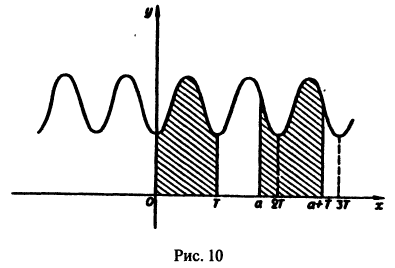
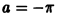
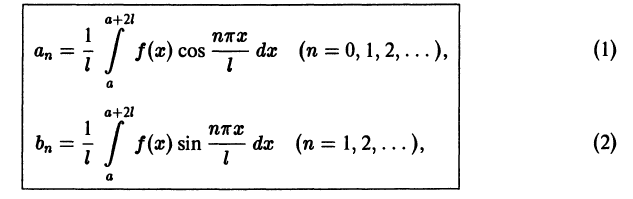
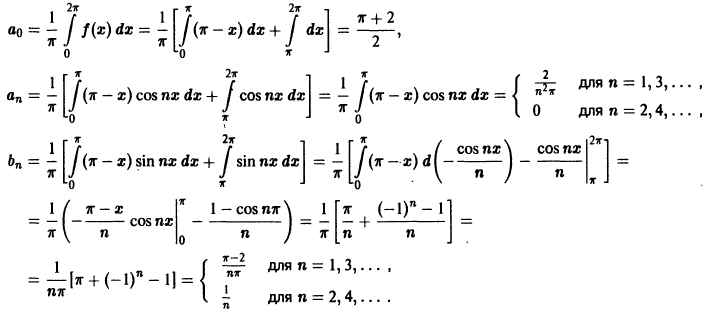
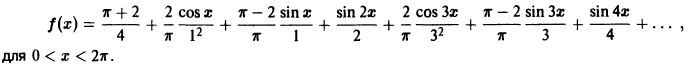
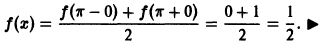
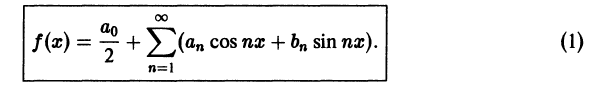
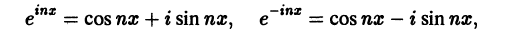
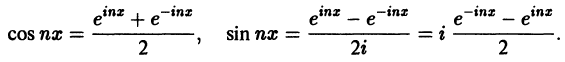
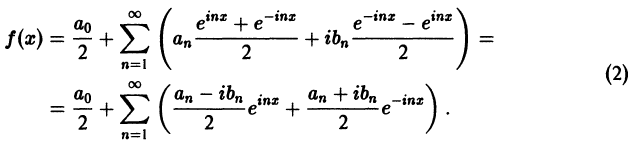
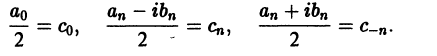
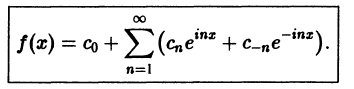
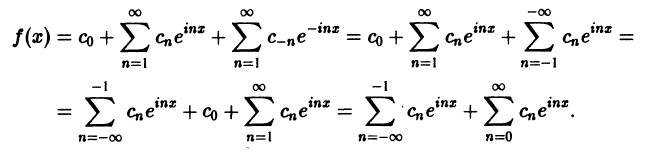
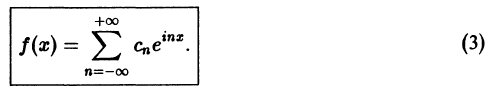
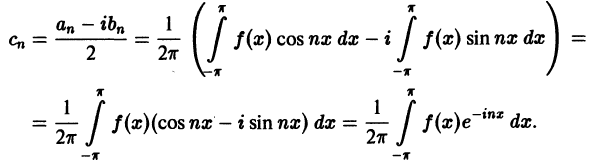
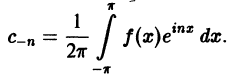
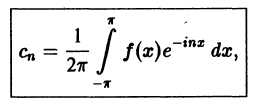
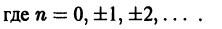

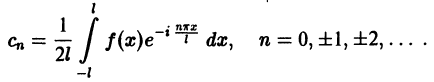
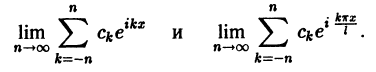
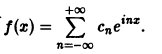
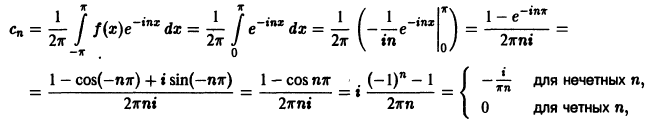
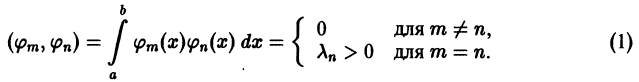
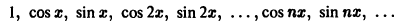
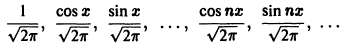

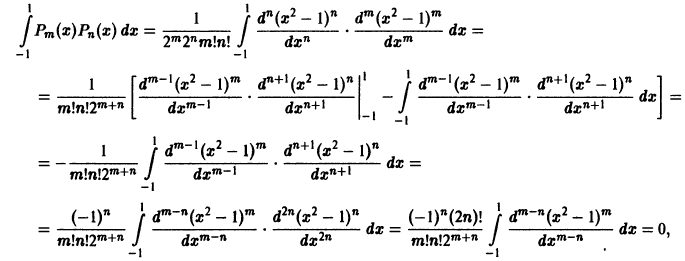
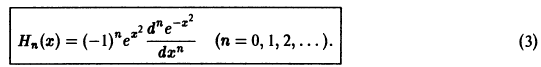
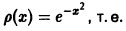
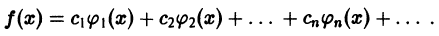
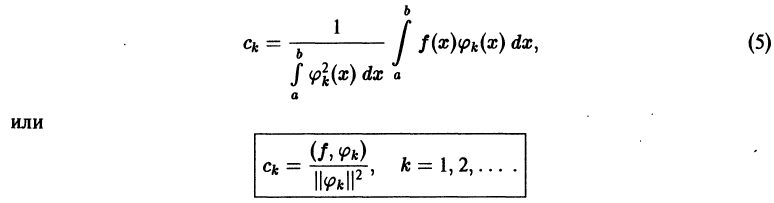
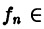
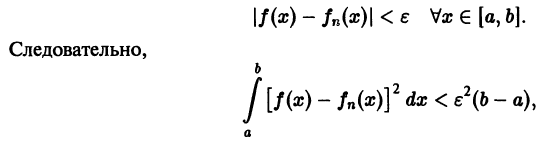
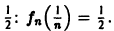
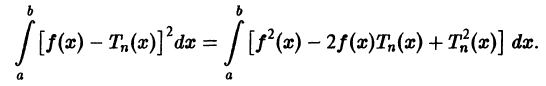
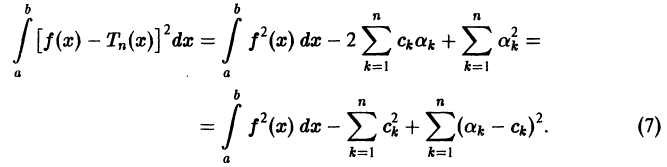
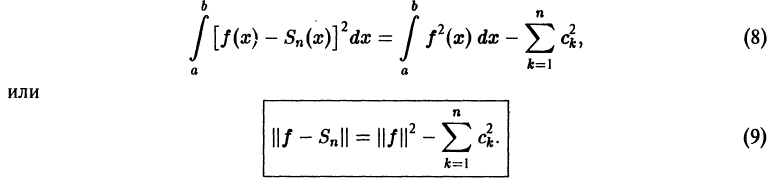

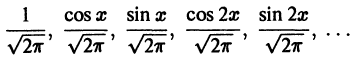
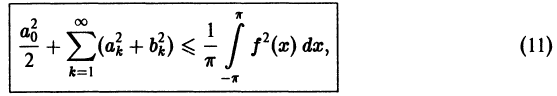

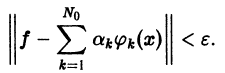
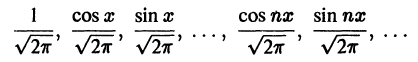
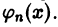
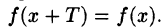
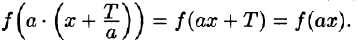
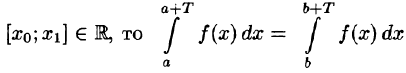
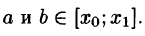
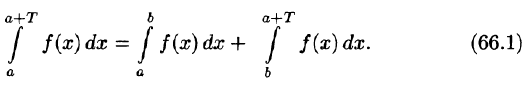
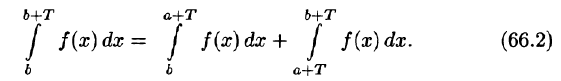
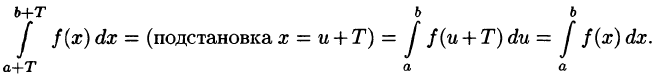
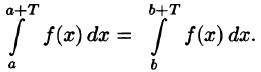
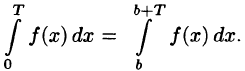
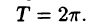

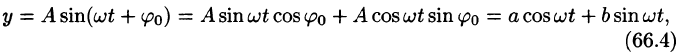
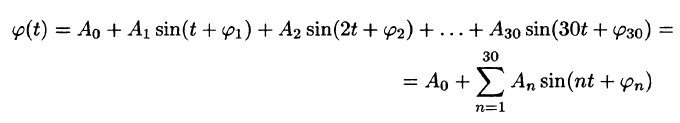
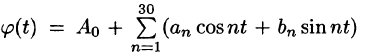
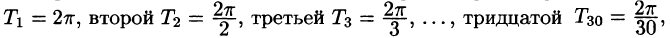
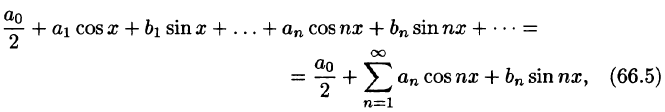
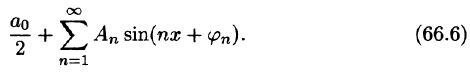
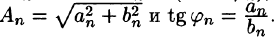
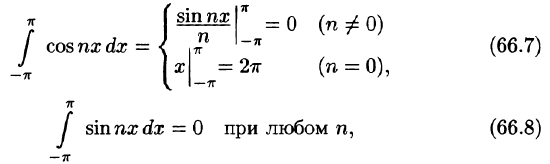
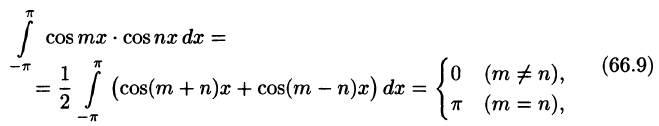
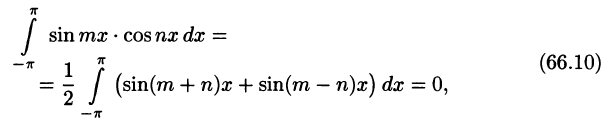
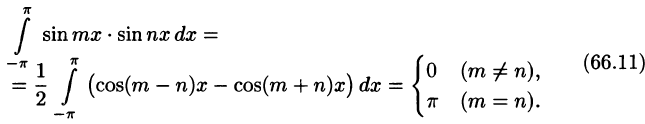
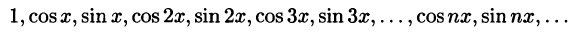
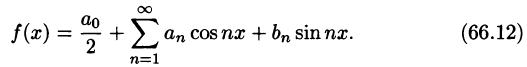
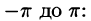
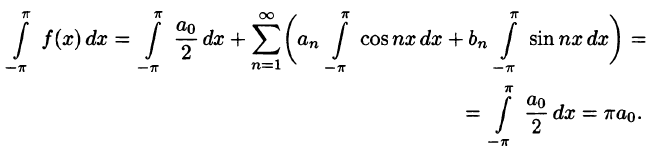
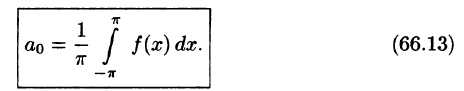
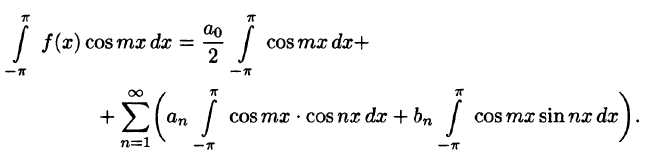
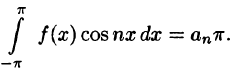
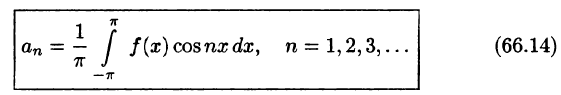
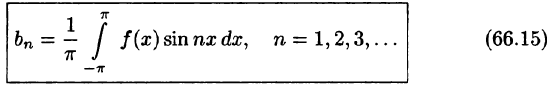
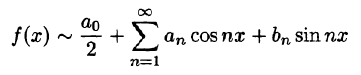
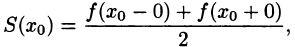 т. е. равна среднему арифметическому пределов функции /(х) справа и слева;
т. е. равна среднему арифметическому пределов функции /(х) справа и слева;  (на концах отрезка) сумма ряда равна
(на концах отрезка) сумма ряда равна 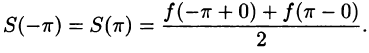
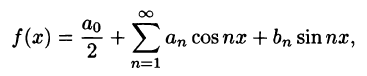
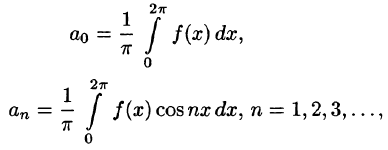
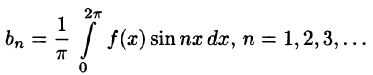
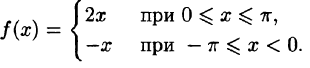
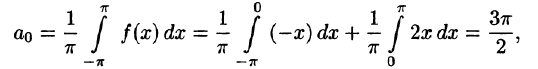
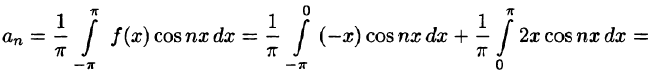
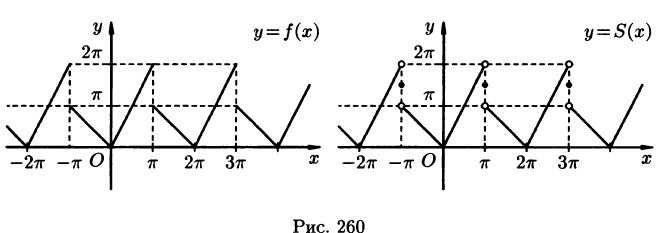
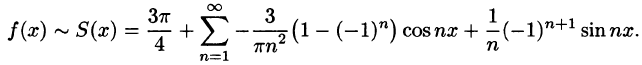
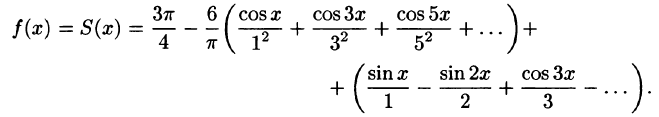
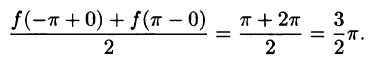
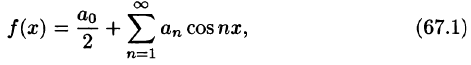
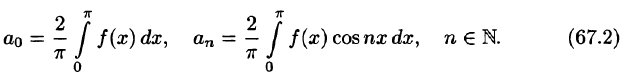

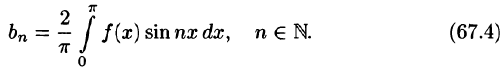
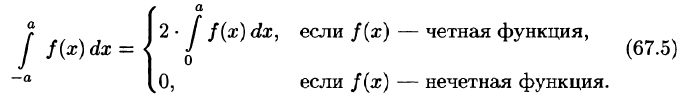
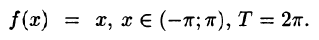
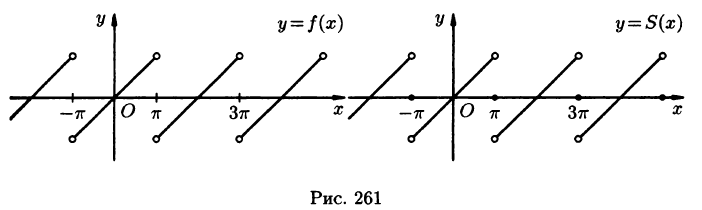
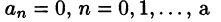
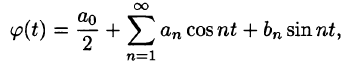
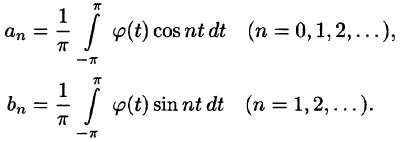
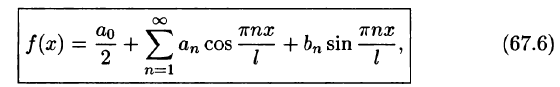
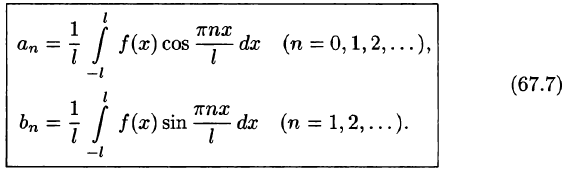
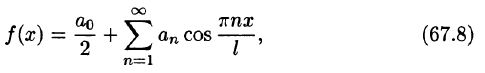
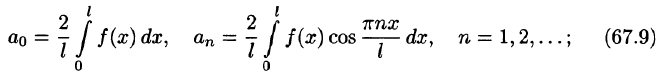
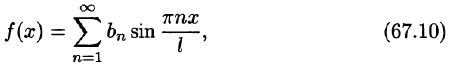
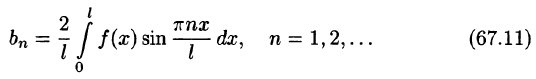
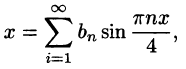
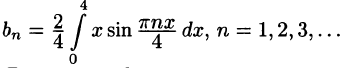
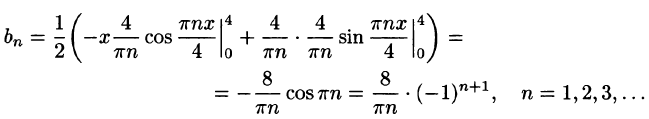
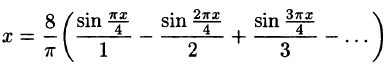
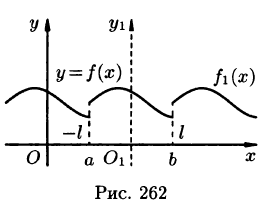
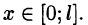
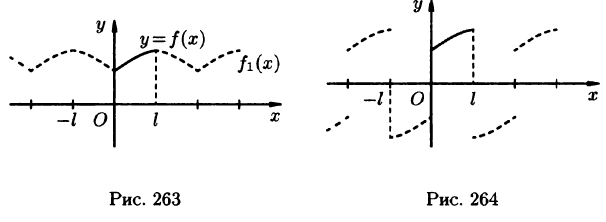
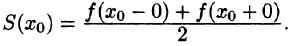
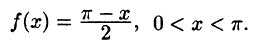
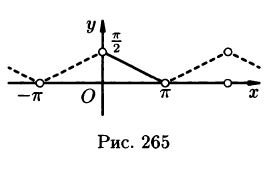
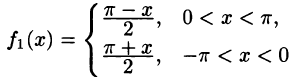
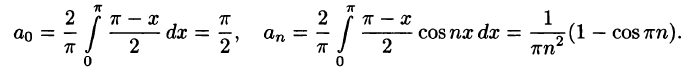
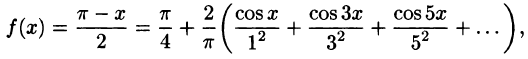
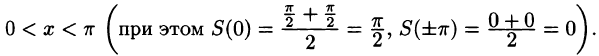
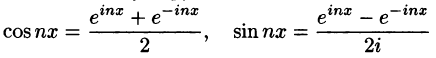
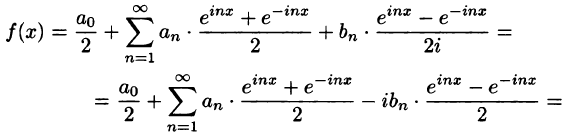
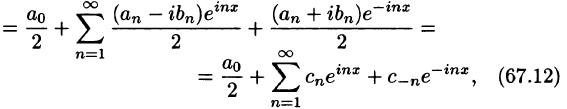
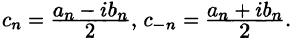
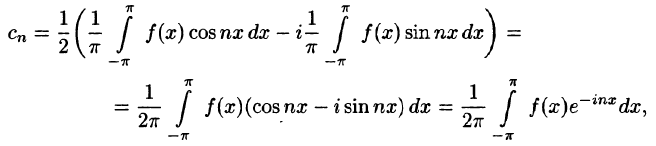
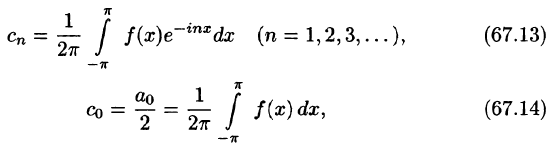
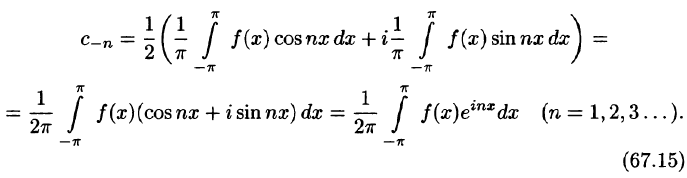
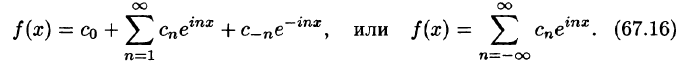
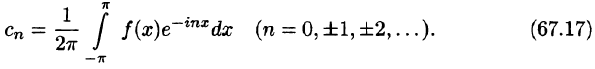
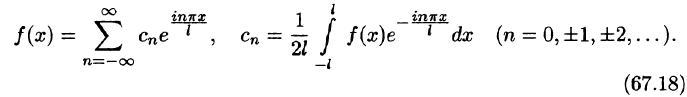
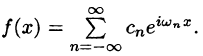
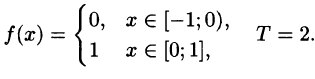
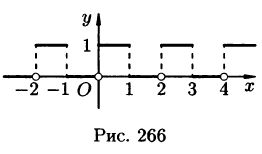
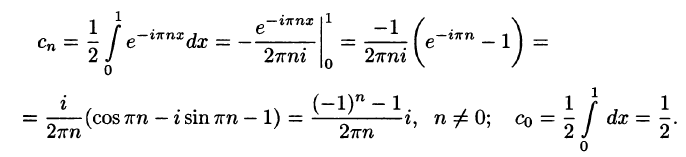
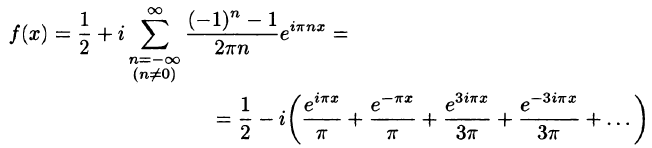
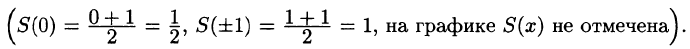
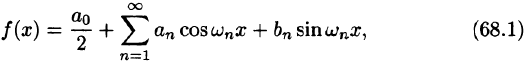
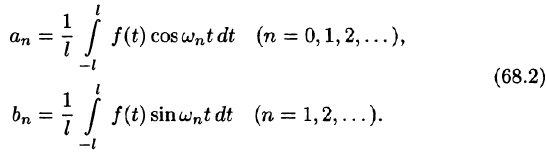
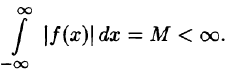
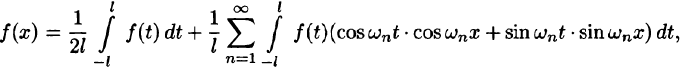
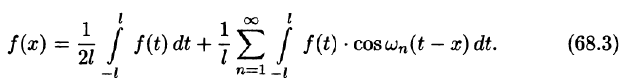
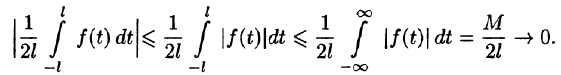
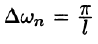
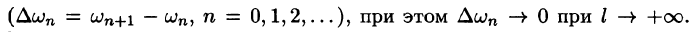
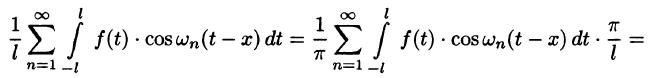
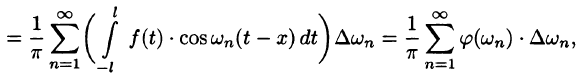
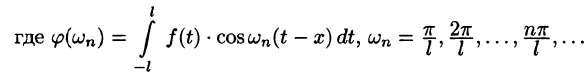
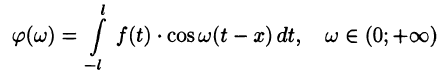
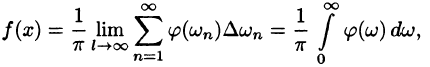
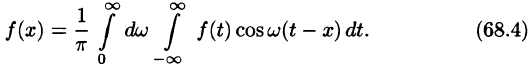
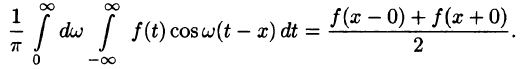
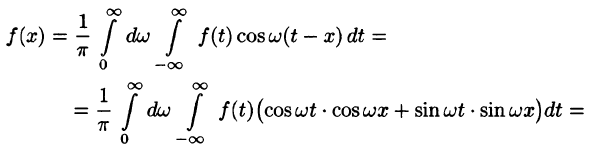
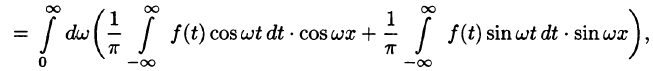
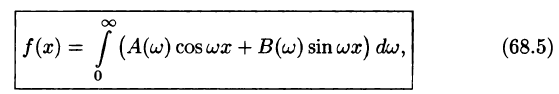
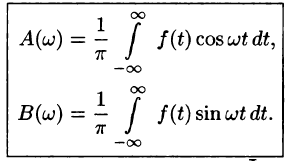
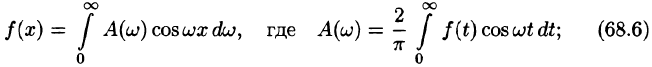
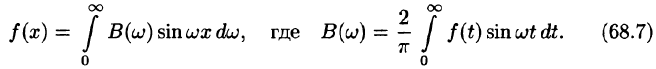
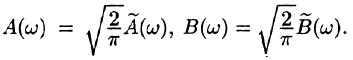
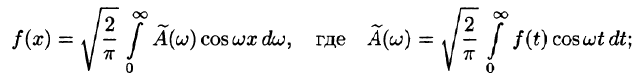
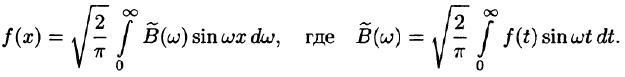
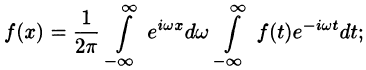
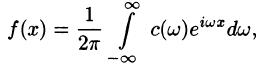
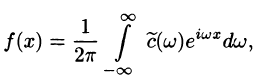
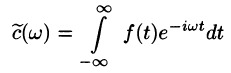
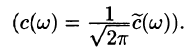
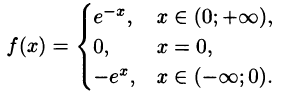
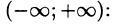
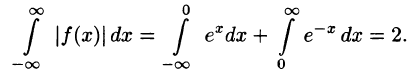
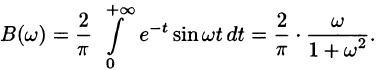
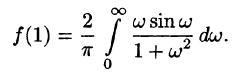
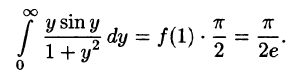































![fin L_2([-pi,pi])](https://wikimedia.org/api/rest_v1/media/math/render/svg/a98b9866136e1b2964922c7dcfc2cbe624f051be)









![fin L_p([-pi,pi]), p>1](https://wikimedia.org/api/rest_v1/media/math/render/svg/4dac0ede6f46583238f3753a37400b84d3b708b3)
![L_1([-pi,pi])](https://wikimedia.org/api/rest_v1/media/math/render/svg/b93096ec2dab6eecb12e20fc91df465356e074f0)

![C([-pi,pi])](https://wikimedia.org/api/rest_v1/media/math/render/svg/a7f1487c87ed13f3571e53d5f9b5a98f6cb5a270)