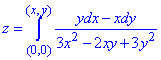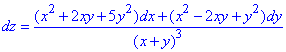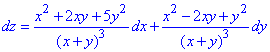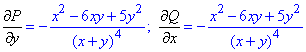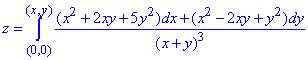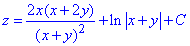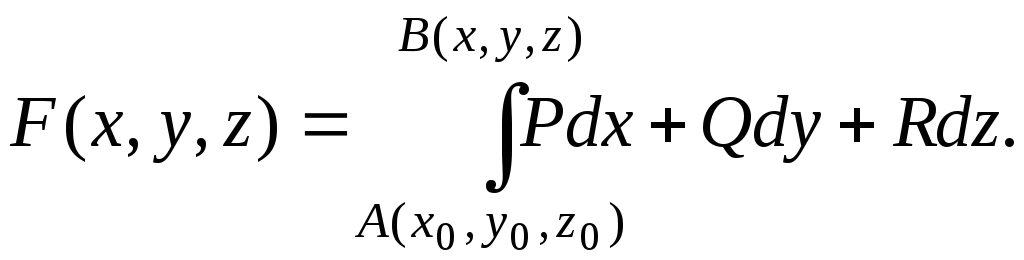Как найти функцию если известен ее дифференциал

Сегодня научим Вас возобновлять функцию через интеграл от ее полного дифференциала.
Алгоритм который описывает что за чем нужно делать детально расписан в приведенной дальше статье.
Формула Ньютона-Лейбница для криволинейного интеграла от полного дифференциала имеет вид
(1)
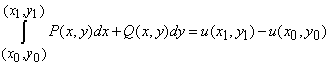
где P(x, y) частичная производная функции u по переменной y,
Q(x, y) частичная производная функции u по переменной x.
Для ее использования необходимо лишь убедиться, что частичные производные P(x, y), Q(x, y) равны между собой

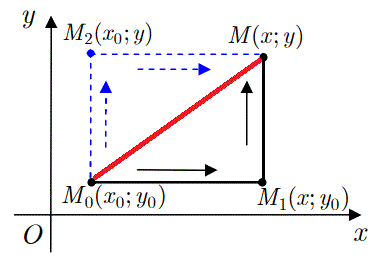
Криволинейный интеграл 2 рода (1) упрощается, если контур интегрирования от точки M₀(x₀,y₀) к M(x, y) по прямой заменить ломаной, что состоит из прямых параллельных к осям координат M₀M₁ но M₁M или M₀M₂ но M₂M.
С одной стороны это позволяют свойства криволинейных интегралов.
Из другой такой способ имеет практическую выгоду.

На практике можем превратить в нуль один из дифференциалов под интегралом, если интегрировать вдоль прямых параллельных осям, в замен придется интегрировать вдоль двух отрезков прямых, тоесть вычислять сумму двух интегралов. Детальнее об этом можете почитать в статье об интегрировании полных дифференциалов.

Пример 1 Найти функцию z, если известен полный дифференциал функции
dz=(ydx-xdy)/(3x²-2xy+3y²)

Решение: Разделяем слагаемые при dx, dy, но выписываем для функции z дифференциалы P, Q:

Найдем частичные производные первого порядка функций P(x, y), Q(x, y):

Из равенства частичных производных 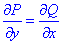делаем вывод, что выражение dz является полным дифференциалом.
Функцию z найдем с помощью криволинейного интегралу 2-го рода:

Приведенный криволинейный интеграл от точки (0,0) к точке (x, y) будем вычислять вдоль прямых x=0 и y=y0.
Так как криволинейный интеграл не зависит от контура интегрирования, то кривую интегрирования будем строить в виде ломанной из двух прямых, которые параллельны осям и соединяют крайние точки.
Это делается с целью избавиться от одного из дифференциалов на каждом из промежутков интегрирования.
В этом случае ломаную можно выбрать из следующих прямых

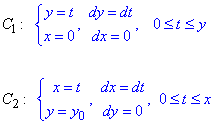
Здесь также записано почему ровные соответствующие дифференциалы.
Вычислим криволинейный интеграл 2 рода для возобновления функции z через полный дифференциал:

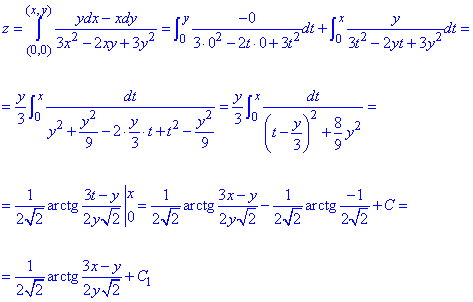
Внимательно разберите интегрирование.

Пример 2 Найти функцию z, если

Решение: Имеем дифференциал:

Здесь обозначено 

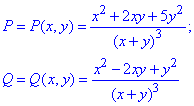
Найдем частичные производные первого порядка функций P(x, y) но Q(x, y):

Как видим условие равенства частных производных выполняется 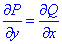, поэтому выражение dz является полным дифференциалом.
Функцию z найдем с помощью криволинейного интеграла 2-го рода:

Полученный криволинейный интеграл от точки (1,0) к точке (x,y) будем вычислять вдоль прямых y=1 и x=x0.
То есть

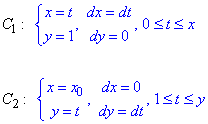
Возобновим функцию z за ее полным дифференциалом с помощью криволинейного интегралу второго рода

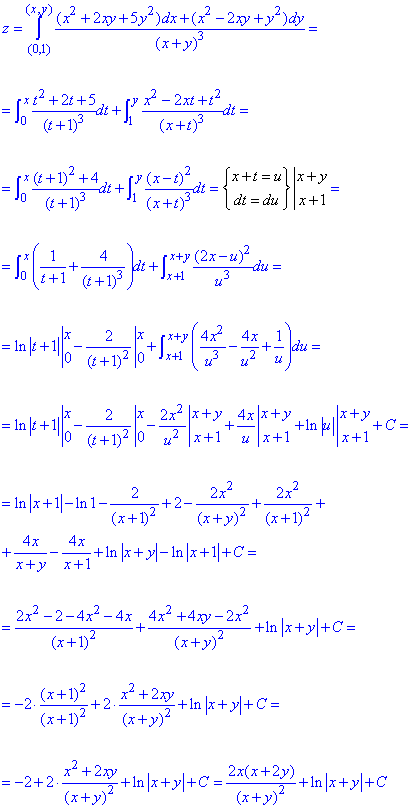
При интегрировании выполнили замену переменных
Выписываем конечное значение интеграла 

Впереди Вас ожидают новые решения на криволинейные, поверхностные, тройные и другие интегралы.

Теорема
1.
Пусть функции
непрерывны
в ограниченной правильной области
.
Для того, чтобы выражение

было полным дифференциалом некоторой
функции
необходимо
и достаточно, чтобы в области

выполнялось условие

(1)

При
этом сама функция восстанавливается
по полному дифференциалу с помощью
криволинейного интеграла 2^го

рода:

(2)

Доказательство.
Необходимость.
Если
,
то (по определению)

и
.
Теорема о равенстве смешанных производных
доказывает равенство (1).

Достаточность.
Равенство (1)
обеспечивает независимость
от
пути (теорема из §7). В доказательстве
леммы 2, §7, мы уже построили функцию

такую, что
.
Эта функция имеет вид (2);
криволинейный интеграл можно свести к
определённому, например, таким образом:

.

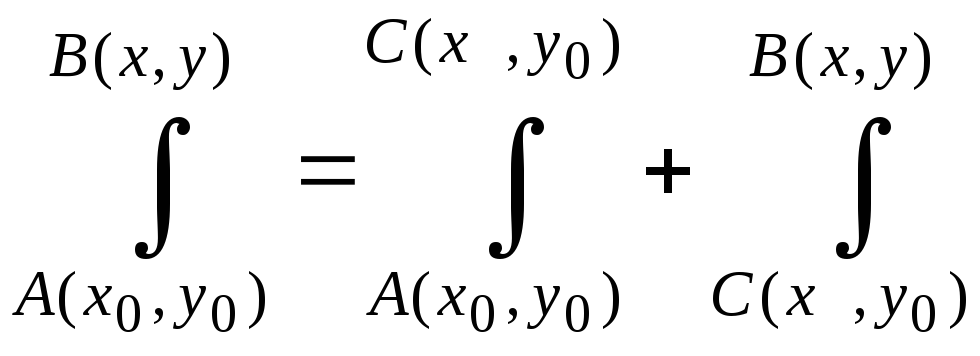
Тогда
получим выражение функции двух переменных
через её частные производные первого
порядка:

Замечание
1.
Условие правильности области было
введено лишь для упрощения доказательства
формулы Грина. На самом же деле всё
доказанное в этом и предыдущем параграфах
имеет место для т.н. односвязной области:

плоская
область

называется односвязной, если каков бы
не был замкнутый контур
,
ограниченная этим контуром часть
плоскости целиком принадлежит

(другими словами, область не содержит
“дыр”).

Всё
доказанное можно свести в такую теорему.

Теорема
2.
Пусть функции
непрерывны
в ограниченной замкнутой односвязной
области
.
Тогда следующие четыре утверждения
равносильны:

1)

2)

по любому контуру
.

3)
интеграл

не зависит от пути в
;

4)
выражение

является полным дифференциалом некоторой
функции.

Действительно,
из 1) следует 2) в силу формулы Грина.
Далее из 2) следует 3) (лемма 1), а из 3)
следует 4) в силу леммы 2. И, наконец, из
4) следует 1) в силу теоремы о равенстве
смешанных производных.

Замечание
2.
Примем без доказательства, что выражение

является полным дифферен-циалом некоторой
функции
,
если выполняются равенства:

(3)

Как
и в двумерном случае, эта функция
восстанавливается криволинейным
интегралом 2^го
рода:

Если
в качестве пути

выбрать ломанную, звенья которой
параллельны осям координат, то получим
выражение

через определённые интегралы:

Пример2.
Убедиться, что выражение

является
полным дифференциалом некоторой функции
и найти эту функцию.

Решение.
Выпишем

и

и найдём их производные:

Равенства
(3)
выполняются,
значит, данное выражение – это полный
дифференциал некоторой функции. Эта
функция имеет вид (в качестве пути
интегрирования выберем начало координат):

Соседние файлы в папке Лекции по мат.анализу

• #
• #
• #
• #
• #
• #
• #

Бессонный С. С. Частные случаи дифференциальных уравнений в полных дифференциалах // Молодой ученый. — 2018. — №29. — С. 1-3. — URL https://moluch.ru/archive/215/52109/ (дата обращения: 01.04.2020).

Отсутствие общего метода отыскания интегрирующего множителя, если неизвестно общее решение исходного уравнения, приводит к необходимости исследования решений отдельных типов дифференциальных уравнений, сводящихся к уравнениям в полных дифференциалах.

Рассмотрим уравнение следующего вида:

(1)

Оно является уравнением в полных дифференциалах при условии, что его левая часть является полным дифференциалом некоторой функции Это возможно при выполнении условия

(2)

Затем необходимо проинтегрировать любое из двух уравнений (3), причем интегрировать первое уравнение нужно по x, а второе по y.

Причем интегрируя первое уравнение по х будем считаем y константой и вместо постоянной интегрирования C, необходимо ставить C(y) — неизвестную функция зависящую от y.

интегрируя второе уравнение по y будем считаем x константой и вместо постоянной интегрирования C, необходимо ставить C(x) — неизвестную функция зависящую от x.

Подставляя, полученное в результате интегрирования по x первого из уравнений (3), выражение во второе из уравнений (3) находят C(y). В случае интегрирования по y второго из уравнений (3) получившееся выражение подставляют в первое из уравнений (3) и находят C(x).

Отсюда следует что общий интеграл исходного уравнения в полных дифференциалах представляется в виде:

Рассмотрим применение данного метода на следующем примере:

Пример № 1. Решить уравнение

(5)

Удостоверимся в том, что представленное дифференциальное уравнения является уравнением в полных дифференциалах. [1, c. 25]

Для этого сначала представим его в стандартном виде

(6)

И проверим выполняется ли условие (2) для уравнения (5)

Делаем вывод о том, что дифференциальное уравнение (5) является уравнением в полных дифференциалах.

Найдем функцию удовлетворяющую следующим условиям

(8)

Для этого проинтегрируем по x первое из уравнений (8), принимая y за константу, а значение постоянной интегрирования С за С(y) — неизвестную функцию, зависящую от y.

Подставляя во второе из уравнений (8) найдем C(y)

Общее решение уравнения (5) имеет вид

Найдем решение уравнения (5) другим методом, который называется методом выделения полного дифференциала. Данный метод также применяется для отыскания интегрирующего множителя.

И сразу получаем решение

На данном примере видно, что удобней и быстрей применить метод выделения полного дифференциала и сразу записать общий интеграл исходного уравнения. Однако этот метод хорошо работает только в случаях, когда коэффициенты при дифференциалах являются интегрируемыми в квадратурах функциями.

Пример № 2. Привести к уравнению в полных дифференциалах

Найдем интегрирующий множитель. В данной ситуации мы имеем дело с частным случаем, когда интегрирующий множитель зависит только от x.

Умножив уравнение (14) на полученное значение получим искомое уравнение в полных дифференциалах

Приведенные выше примеры демонстрируют простоту нахождения общих интегралов дифференциальных уравнений в полных дифференциалах, при условии правильного определения оптимального метода в каждом конкретном случае.

Литература:

1. Филиппов, А. Ф. Сборник задач по дифференциальным уравнениям. / А. Ф. Филиппов. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2000. — 176 с.

Основные термины (генерируются автоматически): уравнение, полный дифференциал, интегрирующий множитель, исходное уравнение, дифференциал, второе, решение уравнения, метод выделения, общий интеграл, первое.

В этой статье изложен метод решения линейных интегральных уравнений сведением к дифференциальным уравнениям в частных производных первого порядка с запаздывающим аргументом.

— интегрированию составленного дифференциального уравнения и определению его общего решения

Далее рассмотрим ретроспективную идентификацию динамической системы, описываемой системой дифференциальных уравнений второго порядка.

Постановка задачи. Нелинейные уравнения в общем имеет вид.

Для приближенного решения уравнения (2) методом вариационных итераций сначала ее дифференцируем один раз по x, тогда.

Методы решения нелинейных уравнений | Задачи работы.

Основные термины (генерируются автоматически): решение уравнения, коэффициент уравнения, общее решение уравнения, решение

разностное уравнение третьего порядка, периодические решения, циклы, предельные циклы. Методы решения нелинейных уравнений.

Если выступает как исходный реагент, то , если – продукт, то .

Во-первых, построенный алгоритм интегрирования второго порядка с контролем точности вычислений и

Литература: 1. Хайрер Э., Ваннер Г. Решение обыкновенных дифференциальных уравнений.

В этой статье изложен метод решения линейных интегральных уравнений сведением к дифференциальным уравнениям в частных производных первого порядка с запаздывающим аргументом.

В равенстве интегрирующий множитель считаем а=1. Тогда имеем. . (16). Так как для уравнение (12) выполнятся, условия (13) то находим.

то для решения уравнения. (27). с начальным условием на отрезке имеет место оценка.

Методы решения нелинейных уравнений | Задачи работы.

. Далее уравнение решают устно описанным выше способом, затем возвращаются к исходной переменной и находят корни уравнений и . Применение метода «переброски» при решении квадратных уравнений или…

Метод построения двумерного интегрируемого уравнения, связанный с уравнением Лакса.

Уравнения во второй строке (3) являются следствиями уравнений первой строки, в результате находим.

Интегрирование высшего нелинейного уравнения Шредингера…

В статье представлены усовершенствованные варианты логарифмических методов решения некоторых видов дифференциальных уравнений. Здесь и далее: , … — известные интегрируемые функции, — неизвестная функция, , – вещественные постоянные…

Источник: https://moluch.ru/archive/215/52109/

Дифференциальные уравнения Понятие о частных производных Дифференциальные уравнения в полных дифференциалах Интегрирующий множ — презентация, доклад, проект скачать

Слайд 1Описание слайда:

Дифференциальные уравнения Понятие о частных производных Дифференциальные уравнения в полных дифференциалах Интегрирующий множитель

Слайд 2Описание слайда:

Понятие о частных производных

Слайд 3Описание слайда:

Понятие о частных производных

Слайд 4Описание слайда:

Дифференциальные уравнения в полных дифференциалах

Слайд 5Описание слайда:

Дифференциальные уравнения в полных дифференциалах

Слайд 6Описание слайда:

Дифференциальные уравнения в полных дифференциалах

Слайд 7Описание слайда:

Дифференциальные уравнения в полных дифференциалах

Слайд 8Описание слайда:

Дифференциальные уравнения в полных дифференциалах

Слайд 9Описание слайда:

Дифференциальные уравнения в полных дифференциалах

Слайд 10Описание слайда:

Интегрирующий множитель

Слайд 11Описание слайда:

Интегрирующий множитель

Слайд 12Описание слайда:

Интегрирующий множитель

Слайд 13Описание слайда:

Интегрирующий множитель

Слайд 14Описание слайда:

Интегрирующий множитель

Слайд 15Описание слайда:

Интегрирующий множитель

Источник: https://mypresentation.ru/presentation/differencialnye-uravneniya-ponyatie-o-chastnyx-proizvodnyx-differencialnye-uravneniya-v-polnyx-differencialax-integriruyushhij-mnozh

Дифференциальные уравнения в полных дифференциалах

• 1º. Основные понятия
• Рассмотрим ОДУ в дифференциальной форме
• M(x, y)dx + N(x, y)dy = 0,                                                 (1)
• Считаем, что функции M(x, y), N(x, y) — непрерывные по обеим переменным в некоторой односвязной области D плоскости XOY, причём
• M2(x, y) + N2(x, y) ¹ 0.

Определение 1. ОДУ (1) называется уравнением в полных дифференциалах, если его левая часть является полным дифференциалом некоторой функции двух переменных.

1. Таким образом, если (1) — уравнение в полных дифференциалах, то существует функция u(x, y), такая что
2. du(x, y) = M(x, y)dx + N(x, y)dy.
3. Тогда ОДУ (1) можно записать в виде
4. du(x, y) = 0.
5. Автоматически следует, что общий интеграл этого уравнения
6. u(x, y) = C.

Пример 1. ydx + xdy = 0.

• Левая часть уравнения есть полный дифференциал функции u(x, y) = xy.
• Действительно,
• 
• поэтому полный дифференциал имеет вид d(xy) = ydx + xdy Þ d(xy) = 0
• И общий интеграл этого уравнения xy = C.
• На практике, чтобы использовать этот метод интегрирования, нужно решить две задачи:

1). Каким образом можно отличить дифференциальное уравнение в полных дифференциалах от остальных.

2). Как найти функцию двух переменных, если известен её полный дифференциал.

Этим мы и будем заниматься.

2º. Признак уравнения в полных дифференциалах

Теорема 1. Пусть функции M(x, y), N(x, y) — непрерывно дифференцируемые в отмеченной области D. Уравнение (1) будет уравнением в полных дифференциалах, тогда и только тогда, когда для функций M(x, y), N(x, y) выполняется условие Эйлера

 » (x, y) Î D.                                            (2)

Доказательство. Необходимость. Считаем, что существует функция u(x, y), что

du(x, y) = M(x, y)dx + N(x, y)dy.

С другой стороны

поэтому имеем тождество

1. Дифференцируем (3) по y, (4) по x:
2. , .
3. Так как частные производные функций M(x, y), N(x, y) непрерывные по условию, поэтому будут непрерывными смешанные производные функции u(x, y). А это значит, они равны между собой, тогда выполняется условие Эйлера

Достаточность. Считаем, что выполняется условие Эйлера (2). Нужно показать, что существует функция u(x, y), для которой выполняются равенства (3), (4).

Доказательство конструктивное— функция u(x, y) строится.

Сначала рассмотрим формулу (3) как уравнение относительно неизвестной функции u(x, y)

• Фиксируем точку (x0, y0) Î D, которая принадлежит D вместе с некоторой окрестностью.
• В этой же окрестности рассмотрим подвижную точку (x, y).    
• Из (3¢) найдём выражение для функции u(x, y) интегрированием по x на прамежутке от x0 до x:

Интеграл имеет смысл, т.к. M(x, y) – непрерывная. Здесь j(y) — любая функция, дифференцируемая по y, т.к. производная  должна существовать.

Найдём выражение для производной по y

.

Поднесение знака дифференцирования под знак интеграла возможно, т.к. функция M(x, y) и её производная  непрерывные по обеим переменным.

1. С другой стороны, из равенства (4) имеем
2. ,                                                                     (4¢)
3. поэтому
4. N(x, y) = .       
5. Воспользовавшись формулой Эйлера (2)
6. ,
7. делаем замену функции под интегралом
8. N(x, y) = .                                                             (6)
9. Интегрируем
10.  = N(x, y) – N(x0, y).
11. Из (6) получаем
12. N(x, y) = N(x, y) – N(x0, y) + j¢(y).
13. Тогда j¢(y) = N(x0, y) и
14. j(y) = ,                                   (7)
15. где C — произвольная константа.
16. Из (5) и (7) получаем формулу для функции u(x, y)
17. .
18. Нам нужна одна функция, а мы получили семейство функций. Считаем C = 0 и
19. .
20. Теорема доказательствоана.

Замечание. Достаточность условия Эйлера в теореме можно доказательствоать, используя криволинейный интеграл. При таком подходе функция u(x, y) определяется криволинейным интегралом от дифференциальной формы

• Так как дифференциальная форма является полным дифференциалом, то значение интеграла не зависит от пути интегрирования, а только от начальной и конечнойточек.
• 3º. Метод нахождения общего интеграла
• Метод интегрирования уравнения в полных дифференциалах фактически определяется доказательствоательством достаточности в теореме. Формула общего интеграла имеет вид
• нужно отметить, что доказательство достаточности можно было бы начать с интегрирования формулы
• ,                                         (4¢)
• тогда бы получили формулу
• .
• Соответственно общий интеграл
• .
• Формулы равнозначные.

Пример 2. (y3 – 2xy) dx+ (3xy2 – x2) dy= 0.

1. Это не уравнение с разделяющимися переменными.
2. Проверяемем условие Эйлера
3.  = 3y2 – 2x,  = 3y2 – 2x.
4. Выполняется. Воспользуемся первой формулой
5. .
6. В качестве точки (x0, y0) возьмём начало координат (0, 0)
7. .
8. Получаем общий интеграл
9. y3x – x2y = C.
10. 4º. Интегрирующий множитель
11. Часто уравнение в дифференциальной форме
12. M(x, y)dx + N(x, y)dy = 0,                                                 (1)
13. уравнением в полных дифференциалах не является, но его можно свести к уравнению в полных дифференциалах с помощью умножения на некоторую функцию.
14. Определение 2. Интегрирующий множитель — это функция m(x, y), которая уравнение
15. M(x, y)dx + N(x, y)dy = 0
16. приводит к уравнению в полных дифференциалах
17. m(x, y)M(x, y)dx + m(x, y)N(x, y)dy = 0.                                       (8)
18. Поскольку (8) — уравнение в полных дифференциалах, то должно выполняться условие Эйлера. Тогда
19. ,
20. ,
21. ,
22. .

Последнее уравнение — уравнение в частных производных, и, вообще говоря, более сложное, чем исходное. Но есть частные случаи.

• Пример 3. Проверить, что для уравнения
• (3x + 2y + y2)dx + (x + 4xy + 5y2)dy = 0
• интегрирующий множитель имеет вид m(x, y) = x + y2.
• (x + y2)(3x + 2y + y2) = 2y(3x + 2y + y2) + (x + y2)(2 + 2y) = 2x + 8xy + 6y2 +4y3
• (x + y2)(x + 4xy + 5y2) = (x + 4xy + 5y2) + (x + y2)(1 + 4y) = 2x + 8xy + 6y2 + 4y3
• Формула Эйлера выполняется.
• Одним из частных случаев существованя интегрирующего множителя является уравнение с разделяющимися переменными (§ 6)
• M1(x)N1(y)dx + M2(x)N2(y)dy = 0.                                               (9)
• Делением на N1(y)M2(x) (умножением на ) мы приводили его к  уравнению с разделёнными переменными
• .
• Если проверить формулу Эйлера:
•  и ,
• то получается, что уравнение с разделёнными переменными, есть уравнение в полных дифференциалах, а для уравнения (9) интегрирующий множитель имеет вид
• m(x, y) = .

Дата добавления: 2018-08-06; просмотров: 127;

Источник: https://studopedia.net/7_28419_differentsialnie-uravneniya-v-polnih-differentsialah.html

УравнениЯ в полных дифференциалах

Сведения из теории

Будем рассматривать дифференциальное уравнение первого порядка, заданное в дифференциальной форме

В нормальной форме оно имеет вид

Уравнение называется уравнением в полных дифференциалах, если его левая часть является дифференциалом некоторой функции

• Если функции и непрерывны вместе со своими производными в некоторой односвязной области[1] D, то равенство
• 
• – необходимое и достаточное условие того, что является в области D уравнением в полных дифференциалах.
• Так как уравнение можно переписать в виде , то — его общий интеграл. Функцию u можно найти по формуле
• ,
• где – какая-нибудь точка из D.
• Примеры решения задач

7.2.1.Решить уравнение .

◄ Данное уравнение не принадлежит ни к одному из типов, которые мы умеем определять по их нормальной форме. Перепишем исходное уравнение в дифференциальной форме

.

Область определения этого уравнения – односвязна. Проверяем условие .

. .

Таким образом, мы имеем уравнение в полных дифференциалах. Находим по формуле при

Итак, общий интеграл уравнения имеет вид . ►

7.3. Задачи для самостоятельного решения

7.3.1. .	7.3.2. .
7.3.3. .	7.3.4. .
7.3.5. .	7.3.6. .

Смешанные задачи на дифференциальные уравнения первого порядка

Примеры решения задач

8.1.1.Для каждого из дифференциальных уравнений

1. ,
2. ,
3. ,
4. ,
5. ,
6. определить, является ли оно уравнением одного из следующих типов:
7. 1) уравнением с разделяющимися переменными,
8. 2) однородным уравнением,
9. 3) линейным уравнением,
10. 4) уравнением Бернулли (но не линейным уравнением),
11. 5) уравнением в полных дифференциалах,
12. 6) не является уравнением типов 1) – 5).

◄ Уравнение приведем нормальному виду . В его правую часть переменные входят только в виде отношения , следовательно, – однородное уравнение и его можно решать заменой , . С другой стороны, правая часть является линейной функцией переменной y и уравнение является линейным. Поэтому его можно решать, например, методом Бернулли.

Уравнение имеет нормальный вид. Правую часть можно представить в виде произведения функции от x на функцию от y: , поэтому это уравнение с разделяющими переменными.

Поскольку правую часть можно представить в виде , то уравнение является и линейным (линейным неоднородным).

Однако нет смысла решать его ни методом Бернулли, ни методом Лагранжа (то есть делать замену переменных, сводящую уравнение к уравнению с разделяющимися переменными) ибо переменные изначально разделяются.

Уравнение записано в дифференциальной форме. Однако уравнением в полных дифференциалах оно не является, так как

, и . Приведем уравнение (8.3) к нормальному виду . Правая часть является отношением однородных многочленов первой степени. Разделив числитель и знаменатель на x, запишем уравнение в виде , то есть уравнение имеет вид и, следовательно, является однородным.

• Уравнение равносильно уравнению , имеющему вид , то есть оно является уравнением Бернулли.
• Уравнение является уравнением в полных дифференциалах, так как совпадают производные
• и ,
• а область определения уравнения – односвязна.

Ясно, что уравнение не принадлежит ни одному из типов 1) – 4) (хотя строго доказать это совсем непросто). Записав уравнение в дифференциальной форме , нетрудно убедиться, что условие не выполняется, и потому это уравнение не является уравнением в полных дифференциалах. Итак, для уравнения имеет место случай 6), то есть мы не можем решить уравнение разобранными выше методами. ►

8.2. Задачи для самостоятельного решения

Решить следующие дифференциальные уравнения.

8.2.1. .	8.2.2. .
8.2.3. .	8.2.4. .
8.2.5. .	8.2.6. .
8.2.7. .	8.2.8. .
8.2.9. .	8.2.10. .

Источник: https://infopedia.su/14x16ed.html

Дифференциальные уравнения в полных дифференциалах

Показано как распознать дифференциальное уравнение в полных дифференциалах. Даны методы его решения. Приводится пример решения уравнения в полных дифференциалах двумя способами.

Дифференциальное уравнение первого порядка в полных дифференциалах – это уравнение вида: (1)   , где левая часть уравнения является полным дифференциалом некоторой функции U(x, y) от переменных x, y: . При этом   .

Если найдена такая функция U(x, y), то уравнение принимает вид: dU(x, y) = 0. Его общий интеграл:

U(x, y) = C,

где C – постоянная.

Если дифференциальное уравнение первого порядка записано через производную: , то его легко привести к форме (1). Для этого умножим уравнение на dx. Тогда   . В результате получаем уравнение, выраженное через дифференциалы: (1)   .

Свойство дифференциального уравнения в полных дифференциалах

Для того, чтобы уравнение (1) было уравнением в полных дифференциалах, необходимо и достаточно, чтобы выполнялось соотношение: (2)   .

Доказательство

Далее мы полагаем, что все функции, используемые в доказательстве, определены и имеют соответствующие производные в некоторой области значений переменных x и y. Точка x0, y0 также принадлежит этой области.

Докажем необходимость условия (2). Пусть левая часть уравнения (1) является дифференциалом некоторой функции U(x, y): . Тогда

;

. Поскольку вторая производная не зависит от порядка дифференцирования, то

;

. Отсюда следует, что   . Необходимость условия (2) доказана.

Докажем достаточность условия (2). Пусть выполняется условие (2): (2)   . Покажем, что можно найти такую функцию U(x, y), что ее дифференциал: . Это означает, что существует такая функция U(x, y), которая удовлетворяет уравнениям: (3)   ; (4)   . Найдем такую функцию.

Проинтегрируем уравнение (3) по x от x0 до x, считая что y – это постоянная: ; ; (5)   . Дифференцируем по y считая, что x – это постоянная и применим (2): . Уравнение (4) будет выполнено, если . Интегрируем по y от y0 до y: ; ; . Подставляем в (5): (6)   .

Итак, мы нашли функцию, дифференциал которой

.

Достаточность доказана.

В формуле (6), U(x0, y0) является постоянной – значением функции U(x, y) в точке x0, y0. Ей можно присвоить любое значение.

Как распознать дифференциальное уравнение в полных дифференциалах

Рассмотрим дифференциальное уравнение: (1)   . Чтобы определить, является ли это уравнение в полных дифференциалах, нужно проверить выполнение условия (2): (2)   . Если оно выполняется, то это уравнение в полных дифференциалах. Если нет – то это не уравнение в полных дифференциалах.

Пример

Проверить, является ли уравнение в полных дифференциалах: .

Решение

Здесь ,   . Дифференцируем по y, считая x постоянной: . Дифференцируем по x, считая y постоянной: . Поскольку:

,

то заданное уравнение – в полных дифференциалах.

Методы решения дифференциальных уравнений в полных дифференциалах

Метод последовательного выделения дифференциала

Наиболее простым методом решения уравнения в полных дифференциалах является метод последовательного выделения дифференциала. Для этого мы применяем формулы дифференцирования, записанные в дифференциальной форме: du ± dv = d(u ± v); v du + u dv = d(uv); ; . В этих формулах u и v – произвольные выражения, составленные из любых комбинаций переменных.

Пример 1

Решить уравнение: .

Решение

Ранее мы нашли, что это уравнение – в полных дифференциалах. Преобразуем его: (П1)   . Решаем уравнение, последовательно выделяя дифференциал.

;

; ; ; . Подставляем в (П1): ; .

• Ответ
• .

Метод последовательного интегрирования

В этом методе мы ищем функцию U(x, y), удовлетворяющую уравнениям: (3)   ; (4)   .

Проинтегрируем уравнение (3) по x, считая y постоянной: . Здесь φ(y) – произвольная функция от y, которую нужно определить. Она является постоянной интегрирования. Подставляем в уравнение (4): . Отсюда:

.

Интегрируя, находим φ(y) и, тем самым, U(x, y).

Пример 2

Решить уравнение в полных дифференциалах: .

Решение

Ранее мы нашли, что это уравнение – в полных дифференциалах. Введем обозначения: ,   . Ищем Функцию U(x, y), дифференциал которой является левой частью уравнения: . Тогда:

(3)   ;

(4)   . Проинтегрируем уравнение (3) по x, считая y постоянной: (П2)   . Дифференцируем по y: . Подставим в (4): ; . Интегрируем:

.

Подставим в (П2): . Общий интеграл уравнения:

1. U(x, y) = const.
2. Ответ
3. .

Объединяем две постоянные в одну.

Метод интегрирования вдоль кривой

Функцию U, определяемую соотношением: dU = p(x, y) dx + q(x, y) dy, можно найти, если проинтегрировать это уравнение вдоль кривой, соединяющей точки (x0, y0) и (x, y): (7)   . Поскольку

(8)   ,

то интеграл зависит только от координат начальной (x0, y0) и конечной (x, y) точек и не зависит от формы кривой. Из (7) и (8) находим: (9)   . Здесь x0 и y0 – постоянные. Поэтому U(x0, y0) – также постоянная.

Пример такого определения U был получен при доказательстве свойства уравнения в полных дифференциалах: (6)   . Здесь интегрирование производится сначала по отрезку, параллельному оси y, от точки (x0 , y0) до точки (x0 , y) . Затем интегрирование производится по отрезку, параллельному оси x, от точки (x0 , y) до точки (x, y) .

В более общем случае, нужно представить уравнение кривой, соединяющей точки (x0 , y0) и (x, y) в параметрическом виде: x1 = s(t1);   y1 = r(t1); x0 = s(t0);   y0 = r(t0); x = s(t);   y = r(t); и интегрировать по t1 от t0 до t.

Наиболее просто выполняется интегрирование по отрезку, соединяющим точки (x0 , y0) и (x, y). В этом случае: x1 = x0 + (x – x0) t1; y1 = y0 + (y – y0) t1; t0 = 0;   t = 1; dx1 = (x – x0) dt1; dy1 = (y – y0) dt1. После подстановки, получается интеграл по t от 0 до 1. Данный способ, однако, приводит к довольно громоздким вычислениям.

Использованная литература: В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.

Источник: https://1cov-edu.ru/differentsialnye-uravneniya/polnie_differentsiali/

Уравнение в полных дифференциалах

Уравнение в полных дифференциалах всегда можно переписать в виде $dFleft(x,y
ight)=0$, где $Fleft(x,y
ight)$ — такая функция, что $dFleft(x,y
ight)=Pleft(x,y
ight)cdot dx+Qleft(x,y
ight)cdot dy$.

Проинтегрируем обе части уравнения $dFleft(x,y
ight)=0$: $int dFleft(x,y
ight)=Fleft(x,y
ight) $; интеграл от нулевой правой части равен произвольной постоянной $C$. Таким образом, общее решение данного уравнения в неявной форме имеет вид $Fleft(x,y
ight)=C$.

Для того, чтобы данное дифференциальное уравнение представляло собой уравнение в полных дифференциалах, необходимо и достаточно, чтобы выполнялось условие $frac{partial P}{partial y} =frac{partial Q}{partial x} $.

Если указанное условие выполнено, то существует такая функция $Fleft(x,y
ight)$, для которой можно записать: $dF=frac{partial F}{partial x} cdot dx+frac{partial F}{partial y} cdot dy=Pleft(x,y
ight)cdot dx+Qleft(x,y
ight)cdot dy$, откуда получаем два соотношения: $frac{partial F}{partial x} =Pleft(x,y
ight)$ и $frac{partial F}{partial y} =Qleft(x,y
ight)$.

Интегрируем первое соотношение $frac{partial F}{partial x} =Pleft(x,y
ight)$ по $x$ и получаем $Fleft(x,y
ight)=int Pleft(x,y
ight)cdot dx +Uleft(y
ight)$, где $Uleft(y
ight)$ — произвольная функция от $y$.

Подберем её так, чтобы удовлетворялось второе соотношение $frac{partial F}{partial y} =Qleft(x,y
ight)$. Для этого продифференцируем полученное соотношение для $Fleft(x,y
ight)$ по $y$ и приравняем результат к $Qleft(x,y
ight)$. Получаем: $frac{partial }{partial y} left(int Pleft(x,y
ight)cdot dx
ight)+U’left(y
ight)=Qleft(x,y
ight)$.

Дальнейшее решение таково:

• из последнего равенства находим $U’left(y
  ight)$;
• интегрируем $U’left(y
  ight)$ и находим $Uleft(y
  ight)$;
• подставляем $Uleft(y
  ight)$ в равенство $Fleft(x,y
  ight)=int Pleft(x,y
  ight)cdot dx +Uleft(y
  ight)$ и окончательно получаем функцию $Fleft(x,y
  ight)$.

Чтобы получить частное решение уравнения в полных дифференциалах, начальное условие $y=y_{0} $ при $x=x_{0} $ нужно подставить в общее решение $Fleft(x,y
ight)=C$. Получаем $Fleft(x_{0} ,y_{0}
ight)=C$. Таким образом, частное решение имеет вид $Fleft(x,y
ight)=Fleft(x_{0} ,y_{0}
ight)$.

Интегрирующие множители

Если для дифференциального уравнения $Pleft(x,y
ight)cdot dx+Qleft(x,y
ight)cdot dy=0$ условие $frac{partial P}{partial y} =frac{partial Q}{partial x} $ не выполняется, то такое уравнение не является уравнением в полных дифференциалах. Но в некоторых случаях его можно преобразовать в уравнение в полных дифференциалах посредством умножения на некоторую функцию $mu left(x,y
ight)$, которая называется интегрирующим множителем.

Будем искать интегрирующий множитель в следующих двух простейших случаях:

• когда он зависит только от $x$, то есть $mu =mu left(x
  ight)$;
• когда он зависит только от $y$, то есть $mu =mu left(y
  ight)$.

Первый случай имеем тогда, когда отношение $frac{frac{partial P}{partial y} -frac{partial Q}{partial x} }{Q} =phi _{1} left(x
ight)$ зависит только от $x$. Тогда интегрирующий множитель можно найти по следующей формуле $mu =e^{int phi _{1} left(x
ight)cdot dx } $.

Второй случай имеем тогда, когда отношение $frac{frac{partial P}{partial y} -frac{partial Q}{partial x} }{P} =phi _{2} left(y
ight)$ зависит только от $y$. Тогда интегрирующий множитель можно найти по следующей формуле $mu =e^{-int phi _{2} left(y
ight)cdot dy } $.

В обоих формулах для интегрирующего множителя допустимо взять какое-то конкретное значение неопределенного интеграла.

Если интегрирующий множитель найти удалось, то на него следует умножить данное дифференциальное уравнение, представленное в стандартном виде.

После этого оно становится дифференциальным уравнением в полных дифференциалах, и к нему можно применить соответствующий метод решения.

Алгоритмы решения

Рассмотренный метод решения может быть представлен в виде следующего алгоритма:

1. Данное дифференциальное уравнение следует представить в стандартном виде $Pleft(x,y
   ight)cdot dx+Qleft(x,y
   ight)cdot dy=0$. Оно может быть уравнением в полных дифференциалах. Чтобы убедиться в этом, следует проверить условие $frac{partial P}{partial y} =frac{partial Q}{partial x} $. Если это условие не выполняется, нужно перейти к поиску интегрирующего множителя. Иначе выполнение алгоритма продолжаем.
2. Вычисляем интеграл $Vleft(x,y
   ight)=int Pleft(x,y
   ight)cdot dx $ и выбираем для него какое-то простое значение.
3. Находим частную производную $V’_{y} left(x,y
   ight)=frac{partial }{partial y} Vleft(x,y
   ight)$.
4. Находим разность $U’left(y
   ight)=Qleft(x,y
   ight)-V’_{y} left(x,y
   ight)$.
5. Интегрируем $U’left(y
   ight)$ по $y$, находим $Uleft(y
   ight)$ и выбираем для неё какое-то простое значение.
6. Записываем искомую функцию $Fleft(x,y
   ight)=Vleft(x,y
   ight)+Uleft(y
   ight)$.
7. Записываем общее решение $Fleft(x,y
   ight)=C$ и частное решение $Fleft(x,y
   ight)=Fleft(x_{0} ,y_{0}
   ight)$, где $y=y_{0} $ при $x=x_{0} $ — начальное условие.

Поиск интегрирующего множителя может быть представлен в виде следующего алгоритма:

1. Вычисляем вспомогательную функцию $R=frac{partial P}{partial y} -frac{partial Q}{partial x} $.
2. Находим функции $phi _{1} left(x
   ight)=frac{R}{Q} $ и $phi _{2} left(y
   ight)=frac{R}{P} $. Если функция $phi _{1} left(x
   ight)$действительно зависит только от $x$, то интегрирующий множитель находим по формуле $mu =e^{int phi _{1} left(x
   ight)cdot dx } $. Если функция $phi _{2} left(y
   ight)$ действительно зависит только от $y$, то интегрирующий множитель находим по формуле $mu =e^{-int phi _{2} left(y
   ight)cdot dy } $. В обоих случаях для интегрирующего множителя выбираем какое-то конкретное значение неопределенного интеграла.
3. Если интегрирующий множитель найти удалось, то умножаем на него данное дифференциальное уравнение, представленное в стандартном виде. После этого оно становится дифференциальным уравнением в полных дифференциалах и можно переходить на соответствующий алгоритм его решения. Если интегрирующий множитель найти не удалось, то дифференциальное уравнение должно решаться иным методом.

Решение типичной задачи

Дано дифференциальное уравнение, имеющее следующий вид:

[left(5cdot y^{3} +13cdot y^{2} +6cdot y
ight)cdot dx+left(10cdot xcdot y^{2} +23cdot xcdot y-2cdot y+6cdot x-4
ight)cdot dy=0.]

Найти его общее решение. Найти также его частное решение для начального условия $y=3$ при $x=2$.

Данное дифференциальное уравнение имеет вид $Pleft(x,y
ight)cdot dx+Qleft(x,y
ight)cdot dy=0$, где $Pleft(x,y
ight)=5cdot y^{3} +13cdot y^{2} +6cdot y$, $Qleft(x,y
ight)=10cdot xcdot y^{2} +23cdot xcdot y-2cdot y+6cdot x-4$. Оно может быть уравнением в полных дифференциалах. Поэтому проверяем условие $frac{partial P}{partial y} =frac{partial Q}{partial x} $.

Находим частные производные: $frac{partial P}{partial y} =15cdot y^{2} +26cdot y+6$, $frac{partial Q}{partial x} =10cdot y^{2} +23cdot y+6$. Условие $frac{partial P}{partial y} =frac{partial Q}{partial x} $ не выполняется. Следовательно, данное дифференциальное уравнение не является уравнением в полных дифференциалах. Поэтому переходим к поиску интегрирующего множителя.

Находим вспомогательную функцию $R=frac{partial P}{partial y} -frac{partial Q}{partial x} $. Получаем$R=15cdot y^{2} +26cdot y+6-10cdot y^{2} -23cdot y-6=5cdot y^{2} +3cdot y$.

Находим функции: $phi _{1} left(x
ight)=frac{R}{Q} =frac{5cdot y^{2} +3cdot y}{10cdot xcdot y^{2} +23cdot xcdot y-2cdot y+6cdot x-4} $ и $phi _{2} left(y
ight)=frac{R}{P} =frac{5cdot y^{2} +3cdot y}{5cdot y^{3} +13cdot y^{2} +6cdot y} $.

Выполняем упрощение найденных функций посредством сокращения дробей. Оказывается, что для функции $phi _{1} left(x
ight)$ сокращение невозможно. Функция $phi _{2} left(y
ight)$ в результате сокращения получает вид $phi _{2} left(y
ight)=frac{1}{y+2} $. При этом она зависит только от $y$ и поэтому подходит для определения интегрирующего множителя.

Интегрирующий множитель находим по формуле $mu =e^{-int phi _{2} left(y
ight)cdot dy } $. Получаем: $mu =e^{-int phi _{2} left(y
ight)cdot dy } =e^{-int frac{1}{y+2} cdot dy } =e^{-ln left|y+2
ight|} =frac{1}{e^{ln left|y+2
ight|} } =frac{1}{left|y+2
ight|} $. Выбираем конкретное значение $mu =frac{1}{y+2} $.

• Умножаем полученный интегрирующий множитель на данное дифференциальное уравнение:
• После деления многочленов имеем:
• Получили новое дифференциальное уравнение, в котором $Pleft(x,y
  ight)=5cdot y^{2} +3cdot y$, $Qleft(x,y
  ight)=10cdot xcdot y+3cdot x-2$.

[frac{5cdot y^{3} +13cdot y^{2} +6cdot y}{y+2} cdot dx+frac{10cdot xcdot y^{2} +23cdot xcdot y-2cdot y+6cdot x-4}{y+2} cdot dy=0.] [left(5cdot y^{2} +3cdot y
ight)cdot dx+left(10cdot xcdot y+3cdot x-2
ight)cdot dy=0. ]

Снова проверяем условие $frac{partial P}{partial y} =frac{partial Q}{partial x} $: получаем $frac{partial P}{partial y} =10cdot y+3$, $frac{partial Q}{partial x} =10cdot y+3$. Условие $frac{partial P}{partial y} =frac{partial Q}{partial x} $ выполняется. Следовательно, новое дифференциальное уравнение является уравнением в полных дифференциалах. Переходим к алгоритму его решения.

1. Вычисляем интеграл: $Vleft(x,y
   ight)=int Pleft(x,y
   ight)cdot dx =int left(5cdot y^{2} +3cdot y
   ight)cdot dx =$
2. Находим частную производную:
3. Находим разность:
4. Интегрируем $U’left(y
   ight)$ по $y$ и находим $Uleft(y
   ight)=int left(-2
   ight)cdot dy =-2cdot y$.
5. Находим результат: $Fleft(x,y
   ight)=Vleft(x,y
   ight)+Uleft(y
   ight)=5cdot xcdot y^{2} +3cdot xcdot y-2cdot y$.
6. Записываем общее решение в виде $Fleft(x,y
   ight)=C$, а именно:
7. Находим частное решение $Fleft(x,y
   ight)=Fleft(x_{0} ,y_{0}
   ight)$, где $y_{0} =3$, $x_{0} =2$:
8. Частное решение имеет вид: $5cdot xcdot y^{2} +3cdot xcdot y-2cdot y=102$.

[=left(5cdot y^{2} +3cdot y
ight)cdot int dx =left(5cdot y^{2} +3cdot y
ight)cdot x=5cdot xcdot y^{2} +3cdot xcdot y.] [V’_{y} left(x,y
ight)=frac{partial }{partial y} Vleft(x,y
ight)=frac{partial }{partial y} left(5cdot xcdot y^{2} +3cdot xcdot y
ight)=10cdot xcdot y+3cdot x.] [U’left(y
ight)=Qleft(x,y
ight)-V’_{y} left(x,y
ight)=10cdot xcdot y+3cdot x-2-10cdot xcdot y-3cdot x=-2.] [5cdot xcdot y^{2} +3cdot xcdot y-2cdot y=C.] [Fleft(2,3
ight)=5cdot 2cdot 3^{2} +3cdot 2cdot 3-2cdot 3=90+18-6=102.]

Источник: https://spravochnick.ru/matematika/differencialnye_uravneniya/uravnenie_v_polnyh_differencialah/

Имеющее стандартный вид $Pleft(x,yright)cdot dx+Qleft(x,yright)cdot dy=0$, в котором левая часть представляет собой полный дифференциал некоторой функции $Fleft(x,yright)$, называется уравнением в полных дифференциалах.

Уравнение в полных дифференциалах всегда можно переписать в виде $dFleft(x,yright)=0$, где $Fleft(x,yright)$ — такая функция, что $dFleft(x,yright)=Pleft(x,yright)cdot dx+Qleft(x,yright)cdot dy$.

Проинтегрируем обе части уравнения $dFleft(x,yright)=0$: $int dFleft(x,yright)=Fleft(x,yright) $; интеграл от нулевой правой части равен произвольной постоянной $C$. Таким образом, общее решение данного уравнения в неявной форме имеет вид $Fleft(x,yright)=C$.

Для того, чтобы данное дифференциальное уравнение представляло собой уравнение в полных дифференциалах, необходимо и достаточно, чтобы выполнялось условие $frac{partial P}{partial y} =frac{partial Q}{partial x} $. Если указанное условие выполнено, то существует такая функция $Fleft(x,yright)$, для которой можно записать: $dF=frac{partial F}{partial x} cdot dx+frac{partial F}{partial y} cdot dy=Pleft(x,yright)cdot dx+Qleft(x,yright)cdot dy$, откуда получаем два соотношения: $frac{partial F}{partial x} =Pleft(x,yright)$ и $frac{partial F}{partial y} =Qleft(x,yright)$.

Интегрируем первое соотношение $frac{partial F}{partial x} =Pleft(x,yright)$ по $x$ и получаем $Fleft(x,yright)=int Pleft(x,yright)cdot dx +Uleft(yright)$, где $Uleft(yright)$ — произвольная функция от $y$.

Подберем её так, чтобы удовлетворялось второе соотношение $frac{partial F}{partial y} =Qleft(x,yright)$. Для этого продифференцируем полученное соотношение для $Fleft(x,yright)$ по $y$ и приравняем результат к $Qleft(x,yright)$. Получаем: $frac{partial }{partial y} left(int Pleft(x,yright)cdot dx right)+U”left(yright)=Qleft(x,yright)$.

Дальнейшее решение таково:

• из последнего равенства находим $U”left(yright)$;
• интегрируем $U”left(yright)$ и находим $Uleft(yright)$;
• подставляем $Uleft(yright)$ в равенство $Fleft(x,yright)=int Pleft(x,yright)cdot dx +Uleft(yright)$ и окончательно получаем функцию $Fleft(x,yright)$.

Находим разность:

Интегрируем $U”left(yright)$ по $y$ и находим $Uleft(yright)=int left(-2right)cdot dy =-2cdot y$.

Находим результат: $Fleft(x,yright)=Vleft(x,yright)+Uleft(yright)=5cdot xcdot y^{2} +3cdot xcdot y-2cdot y$.

Записываем общее решение в виде $Fleft(x,yright)=C$, а именно:

Находим частное решение $Fleft(x,yright)=Fleft(x_{0} ,y_{0} right)$, где $y_{0} =3$, $x_{0} =2$:

Частное решение имеет вид: $5cdot xcdot y^{2} +3cdot xcdot y-2cdot y=102$.

В этой теме мы рассмотрим метод восстановления функции по ее полному дифференциалу, дадим примеры задач с полным разбором решения.

Бывает так, что дифференциальные уравнения (ДУ) вида P (x , y) d x + Q (x , y) d y = 0 могут содержать в левых частях полные дифференциалы некоторых функций. Тогда мы можем найти общий интеграл ДУ, если предварительно восстановим функцию по ее полному дифференциалу.

Пример 1

Рассмотрим уравнение P (x , y) d x + Q (x , y) d y = 0 . В записи левой его части содержится дифференциал некоторой функции U (x , y) = 0
. Для этого должно выполняться условие ∂ P ∂ y ≡ ∂ Q ∂ x .

Полный дифференциал функции U (x , y) = 0 имеет вид d U = ∂ U ∂ x d x + ∂ U ∂ y d y . С учетом условия ∂ P ∂ y ≡ ∂ Q ∂ x получаем:

P (x , y) d x + Q (x , y) d y = ∂ U ∂ x d x + ∂ U ∂ y d y

∂ U ∂ x = P (x , y) ∂ U ∂ y = Q (x , y)

Преобразовав первое уравнение из полученной системы уравнений, мы можем получить:

U (x , y) = ∫ P (x , y) d x + φ (y)

Функцию φ (y) мы можем найти из второго уравнения полученной ранее системы:
∂ U (x , y) ∂ y = ∂ ∫ P (x , y) d x ∂ y + φ y ” (y) = Q (x , y) ⇒ φ (y) = ∫ Q (x , y) – ∂ ∫ P (x , y) d x ∂ y d y

Так мы нашли искомую функцию U (x , y) = 0 .

Пример 2

Найдите для ДУ (x 2 – y 2) d x – 2 x y d y = 0 общее решение.

Решение

P (x , y) = x 2 – y 2 , Q (x , y) = – 2 x y

Проверим, выполняется ли условие ∂ P ∂ y ≡ ∂ Q ∂ x:

∂ P ∂ y = ∂ (x 2 – y 2) ∂ y = – 2 y ∂ Q ∂ x = ∂ (- 2 x y) ∂ x = – 2 y

Наше условие выполняется.

На основе вычислений мы можем сделать вывод, что левая часть исходного ДУ является полным дифференциалом некоторой функции U (x , y) = 0 . Нам нужно найти эту функцию.

Так как (x 2 – y 2) d x – 2 x y d y является полным дифференциалом функции U (x , y) = 0 , то

∂ U ∂ x = x 2 – y 2 ∂ U ∂ y = – 2 x y

Интегрируем по x первое уравнение системы:

U (x , y) = ∫ (x 2 – y 2) d x + φ (y) = x 3 3 – x y 2 + φ (y)

Теперь дифференцируем по y полученный результат:

∂ U ∂ y = ∂ x 3 3 – x y 2 + φ (y) ∂ y = – 2 x y + φ y ” (y)

Преобразовав второе уравнение системы, получаем: ∂ U ∂ y = – 2 x y . Это значит, что
– 2 x y + φ y ” (y) = – 2 x y φ y ” (y) = 0 ⇒ φ (y) = ∫ 0 d x = C

где С – произвольная постоянная.

Получаем: U (x , y) = x 3 3 – x y 2 + φ (y) = x 3 3 – x y 2 + C . Общим интегралом исходного уравнения является x 3 3 – x y 2 + C = 0 .

Разберем еще один метод нахождения функции по известному полному дифференциалу. Он предполагает применение криволинейного интеграла от фиксированной точки (x 0 , y 0) до точки с переменными координатами (x , y) :

U (x , y) = ∫ (x 0 , y 0) (x , y) P (x , y) d x + Q (x , y) d y + C

В таких случаях значение интеграла никак не зависит от пути интегрирования. Мы можем взять в качестве пути интегрировании ломаную, звенья которой располагаются параллельно осям координат.

Пример 3

Найдите общее решение дифференциального уравнения (y – y 2) d x + (x – 2 x y) d y = 0 .

Решение

Проведем проверку, выполняется ли условие ∂ P ∂ y ≡ ∂ Q ∂ x:

∂ P ∂ y = ∂ (y – y 2) ∂ y = 1 – 2 y ∂ Q ∂ x = ∂ (x – 2 x y) ∂ x = 1 – 2 y

Получается, что левая часть дифференциального уравнения представлена полным дифференциалом некоторой функции U (x , y) = 0 . Для того, чтобы найти эту функцию, необходимо вычислить криволинейный интеграл от точки (1 ; 1)
до (x , y)
. Возьмем в качестве пути интегрирования ломаную, участки которой пройдут по прямой y = 1
от точки (1 , 1) до (x , 1) , а затем от точки (x , 1) до (x , y) :

∫ (1 , 1) (x , y) y – y 2 d x + (x – 2 x y) d y = = ∫ (1 , 1) (x , 1) (y – y 2) d x + (x – 2 x y) d y + + ∫ (x , 1) (x , y) (y – y 2) d x + (x – 2 x y) d y = = ∫ 1 x (1 – 1 2) d x + ∫ 1 y (x – 2 x y) d y = (x y – x y 2) y 1 = = x y – x y 2 – (x · 1 – x · 1 2) = x y – x y 2

Мы получили общее решение дифференциального уравнения вида x y – x y 2 + C = 0 .

Пример 4

Определите общее решение дифференциального уравнения y · cos x d x + sin 2 x d y = 0 .

Решение

Проверим, выполняется ли условие ∂ P ∂ y ≡ ∂ Q ∂ x .

Так как ∂ (y · cos x) ∂ y = cos x , ∂ (sin 2 x) ∂ x = 2 sin x · cos x , то условие выполняться не будет. Это значит, что левая часть дифференциального уравнения не является полным дифференциалом функции. Это дифференциальное уравнение с разделяющимися переменными и для его решения подходят другие способы решения.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Показано как распознать дифференциальное уравнение в полных дифференциалах. Даны методы его решения. Приводится пример решения уравнения в полных дифференциалах двумя способами.

Содержание

Введение

Дифференциальное уравнение первого порядка в полных дифференциалах – это уравнение вида:
(1)
,

где левая часть уравнения является полным дифференциалом некоторой функции U(x, y)

от переменных x, y
:

.

При этом .

Если найдена такая функция U(x, y)

,
то уравнение принимает вид:
dU(x, y) = 0

.

Его общий интеграл:
U(x, y)
= C
,

где C
– постоянная.

Если дифференциальное уравнение первого порядка записано через производную:
,

то его легко привести к форме (1)
. Для этого умножим уравнение на dx
.
Тогда .
В результате получаем уравнение, выраженное через дифференциалы:
(1)
.

Свойство дифференциального уравнения в полных дифференциалах

Для того, чтобы уравнение (1)
было уравнением в полных дифференциалах, необходимо и достаточно, чтобы выполнялось соотношение:
(2)
.

Доказательство

Далее мы полагаем, что все функции, используемые в доказательстве, определены и имеют соответствующие производные в некоторой области значений переменных x
и y
.
Точка x 0
, y 0

также принадлежит этой области.

Докажем необходимость условия (2)
.
Пусть левая часть уравнения (1)
является дифференциалом некоторой функции U(x, y)

:

.

Тогда
;

.

Поскольку вторая производная не зависит от порядка дифференцирования, то
;

.

Отсюда следует, что .
Необходимость условия (2)
доказана.

В формуле (6)
, U(x 0
, y 0)

является постоянной – значением функции U(x, y)

в точке x 0
, y 0

.
Ей можно присвоить любое значение.

Как распознать дифференциальное уравнение в полных дифференциалах

Рассмотрим дифференциальное уравнение:
(1)
.

Чтобы определить, является ли это уравнение в полных дифференциалах, нужно проверить выполнение условия (2)
:
(2)
.

Если оно выполняется, то это уравнение в полных дифференциалах. Если нет – то это не уравнение в полных дифференциалах.

Пример

Проверить, является ли уравнение в полных дифференциалах:
.

Методы решения дифференциальных уравнений в полных дифференциалах

Метод последовательного выделения дифференциала

Наиболее простым методом решения уравнения в полных дифференциалах является метод последовательного выделения дифференциала. Для этого мы применяем формулы дифференцирования, записанные в дифференциальной форме:
du ± dv = d(u ± v)

;

v du + u dv = d(uv)

;

;

.

В этих формулах u
и v
– произвольные выражения, составленные из любых комбинаций переменных.

Пример 1

Решить уравнение:
.

Метод последовательного интегрирования

В этом методе мы ищем функцию U(x, y)

,
удовлетворяющую уравнениям:
(3)
;

(4)
.

Проинтегрируем уравнение (3)
по x
,
считая y
постоянной:
.

Здесь φ(y)

– произвольная функция от y
,
которую нужно определить. Она является постоянной интегрирования. Подставляем в уравнение (4)
:
.

Отсюда:
.

Интегрируя, находим φ(y)

и, тем самым, U(x, y)

.

Пример 2

Решить уравнение в полных дифференциалах:
.

Метод интегрирования вдоль кривой

Функцию U
,
определяемую соотношением:
dU = p(x, y)
dx + q(x, y)
dy
,

можно найти, если проинтегрировать это уравнение вдоль кривой, соединяющей точки (x 0
, y 0)

и (x, y)

:

(7)
.

Поскольку
(8)
,

то интеграл зависит только от координат начальной (x 0
, y 0)

и конечной (x, y)

точек и не зависит от формы кривой. Из (7)
и (8)
находим:
(9)
.

Здесь x 0

и y 0

– постоянные. Поэтому U(x 0
, y 0)

– также постоянная.

Пример такого определения U
был получен при доказательстве :
(6)
.

Здесь интегрирование производится сначала по отрезку, параллельному оси y
,
от точки (x 0
, y 0
)

до точки (x 0
, y)

.
Затем интегрирование производится по отрезку, параллельному оси x
,
от точки (x 0
, y)

до точки (x, y)

.

В более общем случае, нужно представить уравнение кривой, соединяющей точки (x 0
, y 0
)

и (x, y)

в параметрическом виде:
x 1
= s(t 1)

;
y 1
= r(t 1)

;

x 0
= s(t 0)

;
y 0
= r(t 0)

;

x = s(t)

;
y = r(t)

;

и интегрировать по t 1

от t 0

до t
.

Наиболее просто выполняется интегрирование по отрезку, соединяющим точки (x 0
, y 0
)

и (x, y)

.
В этом случае:
x 1
= x 0 + (x – x 0)
t 1

;
y 1
= y 0 + (y – y 0)
t 1

;

t 0 = 0

;
t = 1

;

dx 1
= (x – x 0)
dt 1

;
dy 1
= (y – y 0)
dt 1

.

После подстановки, получается интеграл по t
от 0

до 1

.

Данный способ, однако, приводит к довольно громоздким вычислениям.

Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.

Дифференциальным
называется уравнение вида

P
(x,y
)dx
+ Q
(x,y
)dy
= 0
,

где левая часть является полным дифференциалом какой-либо функции двух переменных.

Обозначим неизвестную функцию двух переменных (её-то и требуется найти при решении
уравнений в полных дифференциалах) через F

и скоро вернёмся к ней.

Первое, на что следует обратить внимание: в правой части уравнения обязательно должен
быть нуль, а знак, соединяющий два члена в левой части, должен быть плюсом.

Второе – должно соблюдаться некоторое равенство, которое является подтверждением
того, что данное дифференциальное уравнение является уравнением в полных дифференциалах. Эта проверка
является обязательной частью алгоритма решения уравнений в полных дифференциалах (он во втором параграфе
этого урока), так процесс поиска функции F

достаточно трудоёмкий
и важно на начальном этапе убедиться в том, что мы не потратим время зря.

Итак, неизвестную функцию, которую требуется найти, обозначили через F

.
Сумма частных дифференциалов по всем независимым переменным даёт полный дифференциал. Следовательно, если уравнение является уравнением
в полных дифференциалах, левая часть уравнения представляет собой сумму частных дифференциалов. Тогда по
определению

dF
= P
(x,y
)dx
+ Q
(x,y
)dy

.

Вспоминаем формулу вычисления полного дифференциала функции двух переменных:

Решая два последних равенства, можем записать

.

Первое равенство дифференцируем по переменной “игрек”, второе – по переменной “икс”:

.

что является условием того, что данное дифференциальное уравнение действительно представляет собой
уравнение в полных дифференциалах.

Алгоритм решения дифференциальных уравнений в полных дифференциалах

Шаг 1.
Убедиться, что уравнение является уравнением в полных дифференциалах. Для
того, чтобы выражение было
полным дифференциалом некоторой функции F
(x, y
)
, необходимо и достаточно, чтобы .
Иными словами, нужно взять частную производную по x
и частную
производную по y
другого слагаемого и, если эти производные равны, то уравнение является уравнением в полных дифференциалах.

Шаг 2.
Записать систему уравнений из частных производных, составляющих функцию F
:

Шаг 3.
Проинтегрировать первое уравнение системы –
по x
(y
F
:

,
y
.

Альтернативный вариант (если так интеграл найти проще) – проинтегрировать второе уравнение системы
– по y
(x
остаётся константой и выносится за знак интеграла).
Таким образом так же восстанавливается функция F
:

,
где – пока неизвестная функция от х
.

Шаг 4.
Результат шага 3 (найденный общий интеграл) продифференцировать по y

(в альтернативном варианте – по x
) и приравнять ко второму уравнению системы:

,

а в альтернативном варианте – к первому уравнению системы:

.

Из полученного уравнения определяем
(в альтернативном варианте )

Шаг 5.
Результат шага 4 интегрировать и найти
(в альтернативном варианте найти ).

Шаг 6.
Результат шага 5 подставить в результат шага 3 – в восстановленную частным интегрированием
функцию F
. Произвольную постоянную C
чаще записывают после знака равенства – в правой части уравнения.
Таким образом получаем общее решение дифференциального уравнения в полных дифференциалах. Оно, как уже говорилось, имеет
вид F
(x, y
) = C
.

Примеры решений дифференциальных уравнений в полных дифференциалах

Пример 1.

Шаг 2.
F
:

Шаг 3.

по x
(y
остаётся константой и выносится за знак интеграла). Таким образом восстанавливаем функцию F
:

где – пока неизвестная функция от y
.

Шаг 4.
y

.

.

Шаг 5.

Шаг 6.
F
. Произвольную постоянную C

:
.

Какая ошибка возможна здесь с наибольшей вероятностью? Самые распространённые ошибки – принять частный интеграл по одной из переменных за обычный интеграл
произведения функций и пытаться интегрировать по частям или заменной переменной а также принять частную производную
двух сомножителей за производную произведения функций и искать производную по соответствующей формуле.

Это надо запомнить: при вычислении частного интеграла по одной из переменной другая является константой и выносится
за знак интеграла, а при вычислении частной производной по одной из переменной другая также является константой и производная выражения
находится как производная “действующей” переменной, умноженной на константу.

Среди уравнений в полных дифференциалах

не редкость – примеры с экспонентой. Таков следующий пример.
Он же примечателен и тем, что в его решении используется альтернативный вариант.

Пример 2.
Решить дифференциальное уравнение

.

Шаг 1.
Убедимся, что уравнение является уравнением в полных дифференциалах

. Для
этого находим частную производную по x
одного слагаемого в левой части выражения

и частную
производную по y
другого слагаемого
.
Эти производные равны, значит, уравнение является уравнением в полных дифференциалах

.

Шаг 2.
Запишем систему уравнений из частных производных, составляющих функцию F
:

Шаг 3.
Проинтегрируем второе уравнение системы –
по y
(x
остаётся константой и выносится за знак интеграла). Таким образом восстанавливаем функцию F
:

где – пока неизвестная функция от х
.

Из полученного уравнения определяем :
.

Шаг 5.
Результат шага 4 интегрируем и находим :
.

Шаг 6.
Результат шага 5 подставляем в результат шага 3 – в восстановленную частным интегрированием
функцию F
. Произвольную постоянную C
записываем после знака равенства.
Таким образом получаем общее решение дифференциального уравнения в полных дифференциалах

:
.

В следующем примере возвращаемся от альтернативного варианта к основному.

Пример 3.
Решить дифференциальное уравнение

Шаг 2.
Запишем систему уравнений из частных производных, составляющих функцию F
:

Шаг 3.
Проинтегрируем первое уравнение системы –
по x
(y
остаётся константой и выносится за знак интеграла). Таким образом восстанавливаем функцию F
:

где – пока неизвестная функция от y
.

Шаг 4.
Результат шага 3 (найденный общий интеграл) продифференцируем по y


и приравняем ко второму уравнению системы:

Из полученного уравнения определяем :
.

Шаг 5.
Результат шага 4 интегрируем и находим :

Шаг 6.
Результат шага 5 подставляем в результат шага 3 – в восстановленную частным интегрированием
функцию F
. Произвольную постоянную C
записываем после знака равенства.
Таким образом получаем общее решение дифференциального уравнения в полных дифференциалах

:
.

Пример 4.
Решить дифференциальное уравнение

Шаг 2.
Запишем систему уравнений из частных производных, составляющих функцию F
:

Шаг 3.
Проинтегрируем первое уравнение системы –
по x
(y
остаётся константой и выносится за знак интеграла). Таким образом восстанавливаем функцию F
:

где – пока неизвестная функция от y
.

Шаг 4.
Результат шага 3 (найденный общий интеграл) продифференцируем по y


и приравняем ко второму уравнению системы:

Из полученного уравнения определяем :
.

Шаг 5.
Результат шага 4 интегрируем и находим :

Шаг 6.
Результат шага 5 подставляем в результат шага 3 – в восстановленную частным интегрированием
функцию F
. Произвольную постоянную C
записываем после знака равенства.
Таким образом получаем общее решение дифференциального уравнения в полных дифференциалах

:
.

Пример 5.
Решить дифференциальное уравнение

.

Шаг 1.
Убедимся, что уравнение является уравнением в полных дифференциалах

. Для
этого находим частную производную по y
одного слагаемого в левой части выражения

и частную
производную по x
другого слагаемого
.
Эти производные равны, значит, уравнение является уравнением в полных дифференциалах

.

Может случиться, что левая часть дифференциального уравнения

является полным дифференциалом некоторой функции :

и следовательно, уравнение (7) принимает вид .

Если функция является решением уравнения (7), то , и, следовательно,

где – постоянная, и наоборот, если некоторая функция обращает в тождество конечное уравнение (8), то, дифференцируя полученное тождество, получим , и следовательно, , где – произвольная постоянная, является общим интегралом исходного уравнения.

Если даны начальные значения , то постоянная определяется из (8) и

является искомым частным интегралом. Если в точке , то уравнение (9) определяет как неявную функцию от .

Для того, чтобы левая часть уравнения (7) являлась полным дифференциалом некоторой функции , необходимо и достаточно, чтобы

Если это условие, указанное Эйлером, выполнено, то уравнение (7) легко интегрируется. Действительно, . С другой стороны, . Следовательно,

При вычислении интеграла величина рассматривается как постоянная, поэтому является произвольной функцией от . Для определения функции дифференцируем найденную функцию по и, так как , получим

Из этого уравнения определяем и, интегрируя, находим .

Как известно из курса математического анализа, еще проще можно определить функцию по ее полному дифференциалу , взяв криволинейный интеграл от между некоторой фиксированной точкой и точкой с переменными координатами по любому пути:

Чаще всего в качестве пути интегрирования удобно брать ломаную, составленную из двух звеньев, параллельных осям координат; в этом случае

Пример.
.

Левая часть уравнения является полным дифференциалом некоторой функции , так как

Следовательно, общий интеграл имеет вид

Можно применить и другой метод определения функции :

За начальную точку выбираем, например, начало координат, в качестве пути интегрирования -ломаную. Тогда

и общий интеграл имеет вид

Что совпадает с предыдущим результатом, приводя к общему знаменателю.

В некоторых случаях, когда левая часть уравнения (7) не является полным дифференциалом, легко удается подобрать функцию , после умножения на которую левая часть уравнения (7) превращается в полный дифференциал . Такая функция называется интегрирующим множителем
. Заметим, что умножение на интегрирующий множитель может привести к появлению лишних частных решений, обращающих этот множитель в нуль.

Пример
. .

Очевидно, что после умножения на множитель левая часть превращается в полный дифференциал. Действительно, после умножения на получим

или, интегрируя, . Умножая на 2 и потенцируя, будем иметь .

Конечно, далеко не всегда интегрирующий множитель подбирается столь легко. В общем случае для нахождения интегрирующего множителя надо подобрать хотя бы одно не равное тождественно нулю частное решение уравнения в частных производных , или в развернутом виде

которое после деления на и переноса некоторых слагаемых в другую часть равенства приводится к виду

В общем случае интегрирование этого уравнения в частных производных является задачей отнюдь не более простой, чем интегрирование исходного уравнения, однако в некоторых случаях подбор частного решения уравнения (11) не представляет затруднений.

Кроме того, считая, что интегрирующий множитель является функцией только одного аргумента (например, является функцией только или только , или функцией только , или только и т.д.), можно уже без труда проинтегрировать уравнение (11) и указать условия, при которых интегрирующий множитель рассматриваемого вида существует. Тем самым выделяются классы уравнений, для которых интегрирующий множитель легко может быть найден.

Например, найдем условия, при которых уравнение имеет интегрирующий множитель, зависящий только от , т.е. . При этом уравнение (11) упрощается и приобретает вид , откуда, считая непрерывной функцией от , получим

Если является функцией только от , то интегрирующий множитель, зависящий лишь от , существует и равен (12), в противном случае интегрирующего множителя вида не существует.

Условие существования интегрирующего множителя, зависящего только от , выполнено, например, для линейного уравнения или . Действительно, и, следовательно, . Совершенно аналогично могут быть найдены условия существования интегрирующих множителей вида и т.д.

Пример.
Имеет ли уравнение интегрирующий множитель вида ?

Обозначим . Уравнение (11) при принимает вид , откуда или

Для существования интегрирующего множителя заданного вида необходимо и в предположении непрерывности достаточно, чтобы была функцией только . В данном случае , следовательно, интегрирующий множитель существует и равен (13). При получим . Умножая исходное уравнение на , приведем его к виду

Интегрируя, получим , а после потенцирования будем иметь , или в полярных координатах – семейство логарифмических спиралей.

Пример
. Найти форму зеркала, отражающего параллельно данному направлению все лучи, выходящие из заданной точки.

Поместим начало координат в заданную точку и направим ось абсцисс параллельно заданному в условиях задачи направлению. Пусть луч падает на зеркало в точке . Рассмотрим сечение зеркала плоскостью , проходящее через ось абсцисс и точку . Проведем касательную к рассматриваемому сечению поверхности зеркала в точке . Так как угол падения луча равен углу отражения, то треугольник – равнобедренный. Следовательно,

Полученное однородное уравнение легко интегрируется заменой переменных , но еще проще, освободившись от иррациональности в знаменателе, переписать его в виде . Это уравнение имеет очевидный интегрирующий множитель , , , (семейство парабол).

Эта задача еще проще решается в координатах и , где , при этом уравнение сечения искомых поверхностей приобретает вид .

Можно доказать существование интегрирующего множителя, или, что то же самое, существование ненулевого решения уравнения в частных производных (11) в некоторой области, если функции и имеют непрерывные производные и по крайней мере одна из этих функций не обращается в нуль. Следовательно, метод интегрирующего множителя можно рассматривать как общий метод интегрирования уравнений вида , однако ввиду трудности нахождения интегрирующего множителя этот метод чаще всего применяется в тех случаях, когда интегрирующий множитель очевиден.