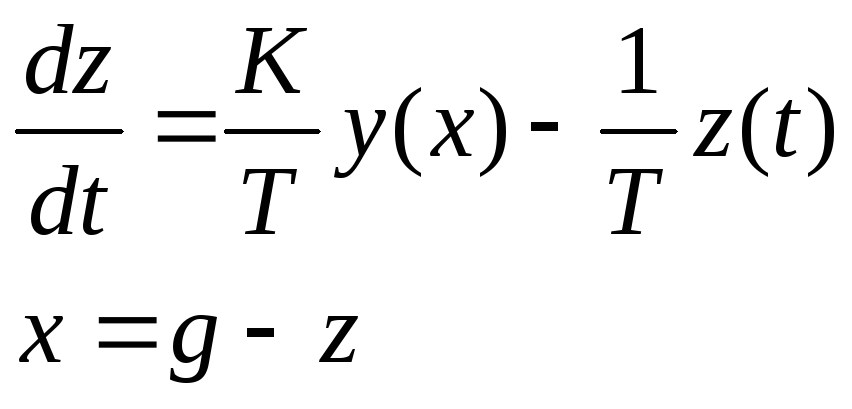Как найти функцию ляпунова

Метод функций Ляпунова

Метод функций Ляпунова состоит в непосредственном исследовании устойчивости положения равновесия системы

$frac{dx_i}{dt}=f_i(t,x_1,x_2,ldots,x_n),quad i=1,2,ldots,n,$

при помощи подходящим образом подобранной функции V(t,x_1,x_2,ldots,x_n) — функции Ляпунова, причем делается это без предварительного нахождения решений системы.

Ограничимся рассмотрением автономных систем

$frac{dx_i}{dt}=f_i(x_1,x_2,ldots,x_n),quad i=1,2,ldots,n,$

(1)

для которых x_iequiv0,~ i=1,2,ldots,n , есть точка покоя.

Функция V(x_1,x_2,ldots,x_n) , определенная в некоторой окрестности начала координат, называется знакоопределенной (определенно-положительной или определенно-отрицательной), если она в области

|x_i|leqslant h, quad i=1,2,ldots,n,

(2)

где — достаточно малое положительное число, может принимать значения только одного определенного знака и обращается в ноль лишь при x_1=ldots=x_n=0 . Так, в случае n=3 функции

V=x_1^2+x_2^2+x_3^2 и V=x_1^2+2x_1x_2+2x_2^2+x_3^2

будут определенно-положительными, причем здесь величина h>0 может быть взята сколько угодно большой.

Функция V(x_1,x_2,ldots,x_n) называется знакопостоянной (положительной или отрицательной), если она в области (2) может принимать значения только одного определенного знака, но может обращаться в ноль и при x_1^2+x_2^2+ldots+x_n^2ne0 . Например, функция

V(x_1,x_2,x_3)=x_1^2+x_2^2+2x_1x_2+x_3^2

будет знакопостоянной (положительной). В самом деле, функцию V(x_1,x_2,x_3) можно записать так: V(x_1,x_2,x_3)=(x_1+x_2)^2+x_3^2 откуда видно, что она обращается в ноль и при x_1^2+x_2^2+x_3^2ne0 , а именно при x_3=0 и любых x_1 и x_2 таких, что x_1=-x_2 .

Пусть V(x_1,x_2,ldots,x_n) есть дифференцируемая функция своих аргументов и пусть являются некоторыми функциями времени, удовлетворяющими системе дифференциальных уравнений (1). Тогда для полной производной функции по времени будем иметь:

$frac{dV}{dt}= sum_{i=1}^{n}frac{partial V}{partial x_i}cdotfrac{dx_i}{dt}= sum_{i=1}^{n}frac{partial V}{partial x_i}f_i(x_1,x_2,ldots,x_n).$

(6)

Величина $frac{dV}{dt}$ , определяемая формулой (3), называется полной производной функции по времени, составленной в силу системы уравнений (1).

Теорема (1) Ляпунова об устойчивости. Если для системы дифференциальных уравнений (1) существует знакоопределенная функция V(x_1,x_2,ldots,x_n) (функция Ляпунова), полная производная $frac{dV}{dt}$ которой по времени, составленная в силу системы (1), есть функция знакопостоянная, знака, противоположного с , или тождественно равная нулю, то точка покоя x_i=0, i=1,2,ldots,n , системы (1) устойчива.

Теорема (2) Ляпунова об асимптотической устойчивости. Если для системы дифференциальных уравнений (I) существует знакоопределенная функция V(x_1,x_2,ldots,x_n) , полная производная которой по времени, составленная в силу системы (1), есть также функция знакоопределенная, знака противоположного с , то тонка покоя x_i=0 системы (1) асимптотически устойчива.

Пример 1. Исследовать на устойчивость точку покоя системы

$begin{cases}x'(t)=y(t),\y'(t)=-x(t).end{cases}$

(4)

Решение. Выберем в качестве функции V(x,y) функцию V=x^2+y^2 . Эта функция определенно-положительная. Производная функции в силу системы (4) равна

$frac{dV}{dt}= 2x,frac{dx}{dt}+2y,frac{dy}{dt}= 2xy-2xyequiv0.$

Из теоремы 1 следует, что точка покоя O(0,0) системы (4) устойчива. Однако асимптотической устойчивости нет: траектории системы (4) — окружности и они не стремятся к точке O(0,0) при tto+infty .

Пример 2. Исследовать на устойчивость точку покоя системы

$begin{cases}x'(t)=y(t)-x^3(t),\y'(t)=-x(t)-3y^3(t).end{cases}$

(5)

Решение. Беря опять V(x,y)=x^2+y^2 , найдем

$frac{dV}{dt}= 2x(y-x^3)+2y(-x-3y^3)= -2(x^4+3y^4).$

Таким образом, $frac{dV}{dt}$ есть определенно-отрицательная функция. В силу теоремы 2 точка покоя O(0,0) системы (5) устойчива асимптотически.

Общего метода построения функции Ляпунова нет. В простейших случаях функцию Ляпунова можно искать в виде

V(x,y)=ax^2+by^2,quad V(x,y)=ax^4+by^4,quad V(x,y)=ax^4+by^2quad (a,b>0) и т.д.

Пример 3. С помощью функции Ляпунова исследовать на устойчивость тривиальное решение xequiv0, yequiv0 системы

$begin{cases}dfrac{dx}{dt}=-x-2y+x^2y^2,\[9pt] dfrac{dy}{dt}=x-dfrac{y}{2}-dfrac{x^3y}{2}.end{cases}$

Решение. Будем искать функцию Ляпунова в виде V=ax^2+by^2 , где a,b>0 — произвольные параметры. Имеем

$begin{aligned}frac{dV}{dt}&=frac{partial V}{partial x}cdotfrac{dx}{dt}+frac{partial V}{partial y}cdotfrac{dy}{dt}=\ &= 2ax(-x-2y+x^2y^2)+2by!left(x-frac{1}{2}y-frac{1}{2}x^3yright)=\ &=-(2ax^2+by^2)+(2xy-x^3y^2)(b-2a).end{aligned}$

Полагая b=2a , получим, что $frac{dV}{dt}=-2a(x^2+y^2)leqslant0$ . Таким образом, при всяком a>0 и b=2a функция V=ax^2+2ay^2 будет определенно-положительной, а ее производная $frac{dV}{dt}$ , составленная в силу данной системы, является определенно-отрицательной. Из теоремы 2 Ляпунова следует, что тривиальное решение xequiv0, yequiv0 данной системы устойчиво асимптотически.

Если бы в указанной выше форме функцию V(x,y) не удалось найти, то ее следовало бы поискать в форме

V(x,y)=ax^4+by^4 или V(x,y)=ax^4+by^2 и т.д.

Теорема (3) Ляпунова о неустойчивости. Пусть для системы дифференциальных уравнений (1) существует дифференцируемая в окрестности начала координат функция V(x_1,x_2,ldots,x_n) такая, что V(0,0,ldots,0)=0 . Если ее полная производная $frac{dV}{dt}$ , составленная в силу системы (1), есть определенно-положительная функция и сколь угодно близко от начала координат имеются точки, в которых функция V(x_1,x_2,ldots,x_n) принимает положи тельные значения, то точка покоя x_i=0, i=1,2,ldots,n , неустойчива.

Замкнутая окрестность точки покоя

Теорема (4) Четаева о не устойчивости. Пусть для системы дифференциальных уравнений (1) существует непрерывно дифференцируемая в некоторой окрестности точки покоя x_i=0, i=1,2,ldots,n , функция v(x_1,x_2,ldots,x_n) , удовлетворяющая в некоторой замкнутой окрестности точки покоя условиям:

1) в сколь угодно малой окрестности Omega точки покоя x_i=0, i=1,2,ldots,n существует область Omega_1 , в которой v(x_1,x_2,ldots,x_n)>0 , причем v=0 в тех граничных точках Omega_1 , которые являются внутренними для Omega (рис. 43);

2) точка покоя O(0,0,ldots,0) является граничной точкой области Omega_1 ;

3) в области Omega_1 производная $frac{dv}{dt}$ , составленная в силу системы (1), определенно-положительная.

Тогда точка покоя x_i=0, i=1,2,ldots,n , системы (1) неустойчива.

Пример 4. Исследовать на устойчивость точку покоя x=0,~y=0 системы

$begin{cases}x'(t)=x(t),\ y'(t)=-y(t).end{cases}$

Решение. Возьмем функцию v(x,y)=x^2-y^2 . Тогда

$frac{dv}{dt}= frac{partial v}{partial x}cdotfrac{dx}{dt}+ frac{partial v}{partial y}cdotfrac{dy}{dt}= 2x^2+2y^2$

есть функция определенно-положительная. Так как сколь угодно близко к началу координат найдутся точки, в которых v>0 (например, v=x^2>0 вдоль прямой y=0 ), то выполнены все условия теоремы 3 и точка покоя O(0,0) неустойчива (седло).

Пример 5. Исследовать на устойчивость точку покоя x=0,~y=0 системы

$begin{cases}dfrac{dx}{dt}=y^3+x^5,\[9pt] dfrac{dy}{dt}=x^3+y^5.end{cases}$

Решение. Функция v=x^4-y^4 удовлетворяет условиям теоремы Четаева:

1) v>0 при |x|>|y| ;

2) $frac{dv}{dt}=4(x^8-y^8)$ — определенно-положительная в области |x|>|y| .

Следовательно, точка покоя x=0,~y=0 неустойчива.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

В теории устойчивости решений дифференциальных уравнений функция Ляпунова — скалярная функция, используемая для исследования устойчивости решений обыкновенного дифференциального уравнения или системы обыкновенных дифференциальных уравнений с помощью второго (прямого) метода Ляпунова.

Названа в честь русского математика и механика Александра Михайловича Ляпунова (1857—1918), основоположника современной теории устойчивости^[1].

Описание[править | править код]

В общих теоремах об устойчивости существование функции Ляпунова с определёнными свойствами является достаточным условием устойчивости (неустойчивости) решения уравнения движения. Однако теоремы являются обратимыми и для многих классов обыкновенных дифференциальных уравнений существование функций Ляпунова является также необходимым условием.

Второй метод Ляпунова не требует нахождения самих решений дифференциальных уравнений, благодаря чему можно исследовать сложные нелинейные системы. Однако нахождение подходящей функции Ляпунова всегда являлось очень сложной задачей. Есть ряд исследованных случаев, для которых теоретически выводится критерий устойчивости с помощью общих теорем и функций Ляпунова. Например, устойчивость по первому приближению. Благодаря этому, второй метод Ляпунова является методом, имеющим, главным образом теоретический интерес, поскольку построение вспомогательных функций требует от исследователя неординарной математической интуиции. Однако, этот метод имеет и важное практическое значение^[2].

Тем не менее, всё же самым главным преимуществом метода функций Ляпунова перед всеми остальными подходами к решению разнообразных задач устойчивости является его универсальность. Сейчас он является единственным математическим методом, который может использоваться для исследования устойчивости динамических систем любого нелинейного вида и любой размерности.

Уравнения возмущённого движения^[3][править | править код]

Для исследования устойчивости исходные уравнения преобразуют к уравнениям возмущённого движения.

Пусть дана некая система дифференциальных уравнений

${displaystyle {frac {dy_{i}}{dt}}=Y_{i}(t,y_{1},y_{2},...,y_{n}),}$

$y_{i}=f_{i}(t)$ — частное решение этой системы. Будем считать его невозмущённым, остальные же движения будут возмущёнными.

Тогда, чтобы исследовать его на устойчивость, нужно составить уравнения возмущённого движения.

Обозначим $x_{i}=y_{i}-f_{i}(t)$ возмущение выбранного движения.

Тогда ${displaystyle {frac {dx_{i}}{dt}}={frac {dy_{i}}{dt}}-{frac {df_{i}}{dt}}=Y_{i}(t,x_{1}+f_{1},x_{2}+f_{2},...,x_{n}+f_{n})-Y_{i}(t,f_{1},f_{2},...,f_{n})=X_{i}(t,x_{1},x_{2},...,x_{n}).}$

Каждому движению исходной системы будет соответствовать решение новой системы. При этом невозмущённому решению будет соответствовать решение ${displaystyle x_{1}=x_{2}=...=x_{n}=0.}$ Это видно из уравнений ${displaystyle X_{i}(t,0,0,...,0)=0.}$

Определение функции Ляпунова (для автономных систем)^[3][править | править код]

Пусть дана система возмущённого движения состоящая из обыкновенных дифференциальных уравнений:

${frac {dx_{i}}{dt}}=X_{i}(x_{1},x_{2},...,x_{n})$

При этом $X_{i}$ пусть определены и непрерывны в области $|x_{i}|leq H$ (где некоторая положительная постоянная) и обращаются в ноль при нулевых значениях переменных.

Функцией Ляпунова называется некоторая функция переменных ${displaystyle V(x_{1},x_{2},...,x_{n}),}$ принимающая вещественные значения и удовлетворяющая свойствам:

Функция однозначная;
Непрерывная вместе со своими частными производными.

$V=V(x_{1},x_{2},...,x_{n})$ называется знакоопределенной (определенно-положительной или определённо-отрицательной) если в области $|x_{i}|leq hleq H$ она принимает значение только одного знака и обращается в ноль только в начале координат.

$V=V(x_{1},x_{2},...,x_{n})$ называется знакопостоянной (положительной или отрицательной) если в области $|x_{i}|leq hleq H$ она принимает значения только одного знака и обращается в ноль не только в начале координат.

$V=V(x_{1},x_{2},...,x_{n})$ называется знакопеременной если принимает различные значения.

Теоремы Ляпунова для автономных систем[править | править код]

Пусть

${displaystyle x^{*}=0}$

является точкой равновесия системы автономных дифференциальных уравнений

и пусть

${dot {V}}(x)={frac {partial V}{partial x}}cdot {frac {dx}{dt}}=nabla Vcdot {dot {x}}=nabla Vcdot f(x)$

будет производная по времени кандидата на функцию Ляпунова

Устойчивость точки равновесия[править | править код]

Если кандидат-функция Ляпунова является локально положительной и производная по времени является локально неположительной:

{dot {V}}(x)leq 0quad forall xin {mathcal {B}}setminus {0}

в некоторой окрестности точки тогда точка равновесия является устойчивой.

Локальная асимптотическая устойчивость[править | править код]

Если кандидат-функция Ляпунова является локально положительной и производная по времени локально является отрицательной:

{dot {V}}(x)<0quad forall xin {mathcal {B}}setminus {0}

в некоторой окрестности точки тогда точка равновесия является локально асимптотически устойчивой.

Глобальная асимптотическая устойчивость[править | править код]

Если кандидат-функция Ляпунова является глобально положительной, радиально неограниченной и производная по времени является глобально отрицательной:

${dot {V}}(x)<0quad forall xin {mathbb {R}}^{n}setminus {0},$

тогда точка равновесия глобально асимптотически устойчива.

Кандидат-функция Ляпунова V(x) является радиально неограниченной если

{displaystyle |x|to infty Rightarrow V(x)to infty .}

Пример[править | править код]

Рассмотрим следующее дифференциальное уравнение с решением x на

Принимая во внимание то, что функция $x^{2}$ положительна в любой окрестности начала координат без точки нуль, она будет естественным кандидатом функции Ляпунова для изучения поведения Итак, пусть ${displaystyle V(x)=x^{2}}$ на Тогда,

${displaystyle {dot {V}}(x)=V'(x)f(x)=2xcdot (-x)=-2x^{2}<0.}$

Это показывает, что точка равновесия дифференциального уравнения является асимптотически устойчивой, а так как функция ${displaystyle V(x)=x^{2}}$ является радиально неограниченной, то точка равновесия глобально асимптотически устойчива.

Примечания[править | править код]

↑ Ляпунов А. М. Общая задача об устойчивости. — Москва Ленинград: государственное издание технико-теоретической литературы, 1950.
↑ Руш Н., Абетс П., Лалуа М. Прямой метод Ляпунова в теории устойчивости. — Москва: Мир, 1980. — С. 7—8. — 300 с.
↑ ¹ ² Малкин И. Г. Теория устойчивости. — Москва: Наука, 1966. — 531 с.

Ссылки[править | править код]

Weisstein, Eric W. Lyapunov Function (англ.) на сайте Wolfram MathWorld.
Khalil, H.K. Nonlinear systems. — Prentice Hall Upper Saddle River, NJ, 1996.
La Salle, Joseph. Stability by Liapunov’s Direct Method: With Applications / Joseph La Salle, Solomon Lefschetz. — New York : Academic Press, 1961.

Источник

Метод функций Ляпунова в задаче об эффекте Джанибекова

Время на прочтение
8 мин

Количество просмотров 20K

Введение

Данная статья не имеет отношения к циклу «Магия тензорной алгебры», но вызвана к жизни публикациями из него. Небрежно щелкая по ссылкам в поисковике набрел на обсуждение одной из своих статей, посвященных эффекту Джанибекова, и обратил внимание на справедливое замечание о том, что исследование устойчивости гайки Джанибекова по первому приближению не дает однозначного ответа на вопрос о том при каких параметрах движение будет устойчивым. Это так, поскольку корни характеристического полинома, при вращении вокруг оси с наименьшим и наибольшим моментом инерции чисто мнимые, их действительная часть равна нулю. При таких условиях нельзя ответить на вопрос будет ли движение устойчивым, не проведя дополнительного исследования.

Интерпретация Мак-Куллага — наверно самое простое объяснение эффекта Джанибекова

Такое исследование можно выполнить используя метод функций Ляпунова (второй или прямой метод Ляпунова). И чтобы окончательно закрыть вопрос с гайкой Джанибекова, я решил написать эту заметку.

1.Дифференциальные уравнения возмущенного движения. Снова.

Пусть имеется система, в общем случае нелинейных дифференциальных уравнений движения некоторой механической системы

$frac{dmathbf y}{dt} = mathbf F(t, , mathbf y)$

где $mathbf y = begin{bmatrix} y_1 && y_2 && cdots && y_n end{bmatrix}^T$ — вектор-столбец переменных состояния системы; — нелинейная вектор функция.

Решение системы (1) дает так называемое невозмущенное движение. По сути это обычный, установившийся режим движения системы под действием приложенных к ней сил. Зададим некоторое возмущение, определяемое вектором отклонений от невозмущенного движения, то есть

Подставляя (3) в (1), получаем

$frac{dmathbf y_0}{dt} + frac{dmathbf x}{dt} = mathbf F(t, , mathbf y_0 + mathbf x)$

Вычтем (1) из (4)

$frac{dmathbf x}{dt} = mathbf F(t, , mathbf y_0 + mathbf x) - mathbf F(t, , mathbf y_0)$

или

$frac{dmathbf x}{dt} = mathbf G(t, , mathbf x)$

где , и полученное уравнение называется уравнением возмущенного движения, тривиальное решение которого соответствует невозмущенному движению системы.

В нашем случае ограничимся рассмотрением автономной системы, где правая часть явно не зависит от времени

$frac{dmathbf x}{dt} = mathbf G(mathbf x)$

2. Xитрая функция V(x) — кандидат в функции Ляпунова

Рассмотрим некоторую скалярную функцию

определенную в некоторой окрестности начала координат, такой что

$|x_i| < h, quad i = overline{1,n}$

где — некоторое, достаточно малое, положительное число.

Функция (6) называется знакоопределенной, если в области (7) она принимает значения только одного знака (только положительные либо только отрицательные), и равна нулю лишь в начале координат (при )

Функция (6) называется знакопостоянной, если в области (7) она принимает значения только одного определенного знака, но может обращаться в нуль и при .

Вычислим полную производную от функции (6) по времени. Так как $x_i = x_i(t), quad i = overline{1,n}$ , по определению полной производной получаем

$frac{dV}{dt} = sum_{i=1}^n frac{partial V}{partial x_i} , dot x_i$

что, принимая во внимание уравнение (5), эквивалентно соотношению

$frac{dV}{dt} = sum_{i=1}^n frac{partial V}{partial x_i} , G_i(x_1, , x_2, , ..., , x_n)$

Функцию (8) называют полной производной функции (6) по времени, составленной в силу уравнения (5).

3. Теоремы Ляпунова об устойчивости

Два параграфа, что выше, написаны сухим математическим языком определений, и иначе наверное нельзя. Добавим ещё немного формальной математики, сформулировав

Теорема Ляпунова об устойчивости

Если для системы уравнений (5) существует знакоопределённая функция (функция Ляпунова), полная производная по времени которой, составленная в силу системы (5) есть функция знакопостоянная, знака, противоположного V, либо тождественно равная нулю, то точка покоя системы (5) устойчива

Под точкой покоя системы (5) здесь понимается её тривиальное решение, соответствующее невозмущенному движению рассматриваемой механической системы. Грубо говоря, согласно сформулированной теореме, следует подобрать функцию , удовлетворяющую свойствам, указанным в условии теоремы. Если она удовлетворяет данным свойствам, то её называют функцией Ляпунова, и если таковая функция (хотя бы одна!) существует, то установившийся режим движения рассматриваемой механической системы будет устойчивым.

Однако, в данной теореме не идёт речь об асимптотической устойчивости, то есть таком характере движения системы, при котором возмущенное её движение будет стремится к исходному установившемуся режиму. Под устойчивым здесь понимается и такое движение, при котором система будет колебаться в окретсности исходного установившегося режима, но никогда к нему не вернется. Условие асимптотической устойчивости будет более строгим

Теорема Ляпунова об асимптотической устойчивости

Если для системы уравнений (5) существует знакоопределённая функция (функция Ляпунова), полная производная по времени которой, составленная в силу системы (5) есть функция знакоопределенная, знака, противоположного V, то точка покоя системы (5) асимптотически устойчива

Асимптотически устойчивая система, после возмущения, будет стремится вернуться к установившемуся режиму движения, то есть решение системы (5) будет сходится к началу координат $x_i = 0, quad i=overline{1,n}$ .

Эти теоремы дают путь к исследованию устойчивости линейных и нелинейных механических систем, более общий, чем исследование по первому приближению.

Другой вопрос, как найти функцию Ляпунова, удовлетворяющую уравнению (5) и требованиям теорем. Однозначного ответа на этот вопрос математика ещё не знает. Есть ряд работ, всецело посвященных этому вопросу, например книга Е. А. Барабашина «Функции Ляпунова». Для большинства линейных систем можно искать функции Ляпунова в виде квадратичных форм, например, для системы третьего порядка эта функция может быть такой

данная функция — определенно-положительная, причем в сколь угодно большой окрестности точки покоя системы. Или такая функция

будет знакопостоянной, положительной, ибо может быть равна нулю как в точке покоя системы , так и в точке, удовлетворяющей условию .

В случае консервативных механических систем функцией Ляпунова может служить полная механическая энергия системы, которая, при отсутствии диссипации, является константой (знакопостоянна) и ещё производная по времени равная нулю — она ведь константа. И вытекает эта функция из системы уравнений движения, ибо является одним из её интегралов.

В случае с гайкой Джанибекова, в качестве весьма элегантного решения мной взята идея из книги А. П. Маркеева «Теоретическая механика». Это решение несколько переработано и расширено мной, чтобы быть в контексте ранее написанных статей.

4. Интегралы движения гайки Джанибекова

Получим два первых интеграла движения, опираясь на систему уравнений, приведенную в тензорном цикле. Оперировать будем тензорными соотношениями, чтобы не терять хватки. Итак, уравнение вращения гайки вокруг центра масс имеет вид

$I_{,j}^{,i} , dotomega^{j} + varepsilon^{,ijk} , omega_{,j} , g_{,kl} , I_{,p}^{,l} , omega^{,p} = 0$

перейдем в данном уравнении к вектору МКД

$dot L^{,i} + varepsilon^{,ijk} , omega_{,j} , L_{,k} = 0$

Умножим уравнение (10) скалярно на удвоенный вектор МКД

$2, L_{,i} , frac{dL^{,i}}{dt} + 2, varepsilon^{,ijk} , L_{,i} , L_{,k} , omega_{,j} = 0$

Нетрудно заметить, что во втором слагаемом (11) свертка $varepsilon^{,ijk} , L_{,i} , L_{,k} = 0$ , а в первом — производная от квадрата модуля МКД. Преобразуем уравнение (11) и проинтегрируем его

$begin{align*} &frac{d}{dt} left( L^{,2} right) = 0 \ &L^{,2} = rm const end{align*}$

или

$I_x^{,2} , omega_x^2 + I_y^{,2} , omega_y^2 + I_z^{,2} , omega_z^2 = rm const$

Выражение (12) есть первый интеграл движения, выражающий постоянство модуля МКД рассматриваемой нами гайки. Чтобы получить ещё один первый интеграл движения, умножим (9) скалярно на вектор угловой скорости

$omega_{,i} , I_{,j}^{,i} , dotomega^{j} + varepsilon^{,ijk} , omega_{,i} , omega_{,j} , g_{,kl} , I_{,p}^{,l} , omega^{,p} = 0$

после чего, внезапно, обнаруживаем во втором слагаемом свертку $varepsilon^{,ijk} , omega_{,i} , omega_{,j}$ равную нулю, получая уравнение

$omega_{,i} , I_{,j}^{,i} , dotomega^{j} = 0$

Вспомним, ведь что-то похожее мы уже видели ранее. Ведь кинетическая энергия тела в его вращении относительно центра масс равна

$T = frac{1}{2} , omega_i , I_j^i , omega^{,j}$

и если мы продифференцируем её по времени, что получим

$frac{dT}{dt} = frac{1}{2} , dotomega_i , I_j^i , omega^{,j} + frac{1}{2} , omega_i , I_j^i , dotomega^{,j} = omega_i , I_j^i , dotomega^{,j}$

в соответствии с этим, мы можем переписать уравнение (13) и проинтегрировать его

$begin{align*} &frac{d}{dt} , left( frac{1}{2} , omega_i , I_j^i , omega^{,j} right) = 0 \ &frac{1}{2} , omega_i , I_j^i , omega^{,j} = rm const end{align*}$

Учитывая, что умножение константы на двойку не меняет её «константности», можно окончательно записать первый интеграл в компонентной форме (учитывая декартов базис!)

Выражение (14) выражает постоянство кинетической энергии вращения гайки вокруг центра масс. Осталось перейти в выражениях (12) и (14) к безразмерным моментам инерции $i_y = frac{I_y}{I_x}, quad i_z = frac{I_z}{I_x}$

$begin{align*} &omega_x^2 + i_y^{,2} , omega_y^2 + i_z^{,2} , omega_z^2 = rm const \ &omega_x^2 + i_y , omega_y^2 + i_z , omega_z^2 = rm const end{align*}$

Полученные уравнения и есть те первые интегралы движения, которые мы используем для построения функции Ляпунова

4. Построение функции Ляпунова из интегралов движения

Метод построения функции Ляпунова из уравнений вида (15) носит название метода интегральных связок Четаева и говорит о том, что означенную функцию можно искать в виде связки интегралов движения вида

где — первые интегралы уравнений возмущенного движения; и — неопределенные константы, подбором которых можно сделать функцию (16) определенно положительной, удовлетворяющей теореме Ляпунова об устойчивости.

Невозмущенное вращение гайки происходит вокруг оси с постоянной угловой скоростью omega . Возмутим это движение, дав угловой скорости малое приращение , и перепишем выражения (15)

$begin{align*} &(omega + Deltaomega_x)^2 + i_y^{,2} , Deltaomega_y^2 + i_z^{,2} , Deltaomega_z^2 = rm const \ &(omega + Deltaomega_x)^2 + i_y , Deltaomega_y^2 + i_z , Deltaomega_z^2 = rm const end{align*}$

или

$begin{align*} &omega^2 + 2omega , Deltaomega_x + Deltaomega_x^2 + i_y^{,2} , Deltaomega_y^2 + i_z^{,2} , Deltaomega_z^2 = rm const \ &omega^2 + 2omega , Deltaomega_x + Deltaomega_x^2 + i_y , Deltaomega_y^2 + i_z , Deltaomega_z^2 = rm const end{align*}$

При установившемся вращении гайки с постоянной угловой скоростью, константу omega^2 можно вычесть из обоих частей получившихся уравнений, получив в их левой части функции

$begin{align*} &U_1 = Deltaomega_x^2 + i_y^{,2} , Deltaomega_y^2 + i_z^{,2} , Deltaomega_z^2 + 2omega , Deltaomega_x \ &U_2 = Deltaomega_x^2 + i_y , Deltaomega_y^2 + i_z , Deltaomega_z^2 + 2omega , Deltaomega_x end{align*}$

Функция Ляпунова будет иметь вид

Исходя из уравнений (15) понятно, что $frac{dV}{dt} = 0$ , значит об асимптотической устойчивости речи не будет. Но, исходя из теоремы Ляпунова, необходимо убедится в том, что функция (18) определенно-положительна. Из выражений (18) и (17) понятно, что её значения положительны при любых , и . Теперь покажем, что (18) обращается в нуль только в точке покоя системы . Выражение (18) равно нулю исключительно в случае

Из первого уравнения системы (19) вычтем второе

Если i_y, , i_z < 1 (момент инерции, вокруг которого вращается гайка наибольший), или же i_y, , i_z > 1 (момент инерции, вокруг которого вращается гайка наименьший), то равенство (20) будет справедливо лишь в случае когда . Учтем данный факт и сложим уравнения (19)

Уравнение (21) справедливо при и при . Но, так как мы полагаем , функция (18) будет равна нулю исключительно в точке покоя системы .

Таким образом, вращение гайки вокруг оси с наименьшим и наибольшим моментом инерции будет устойчивым по Ляпунову.

Однако, спешу заметить, что при i_y > 1, quad i_z < 1 , или i_y < 1, quad i_z > 1 , то есть когда момент инерции относительно оси, вокруг которой происходит вращение имеет промежуточное между максимальным и минимальным значение, функцию (18) уже нельзя назвать определенной положительно, из-за того что слагаемые в (20) будут иметь разные знаки. Но совершенно нельзя сказать о том, что движение будет неустойчивым. Особенность теорем Ляпунова об устойчивости в том, что они декларируют условие устойчивости, но не декларируют обратного. Неустойчивость движения придется доказывать отдельно.

5. Неустойчивость вращения гайки Джанибекова

Сформулируем определение

Областью будем называть какую либо область окрестности $|x_i| < h, quad i = overline{1,n}$ , где для некоторой функции выполняется условие , причем на границе области и точка покоя системы принадлежит этой границе.

и теорему

Теорема Четаева о неустойчивости

Если дифференциальные уравнения возмущенного движения (5) таковы, что существует функция , такая, что в сколь угодно малой окрестности

$|x_i| < h, quad i = overline{1,n}$

существует область , и во всех точках этой области производная в силу уравнений (5) принимает положительные значения, то невозмущенное движение неустойчиво.

Функция о которой говорится в теореме называется функцией Четаева. Теперь рассмотрим снова нашу гайку, уравнения вращения которой выглядят так (с учетом работы в связанных с телом декартовых координатах и введенных нами безразмерных моментов инерции)

$begin{align*} &dotomega_x = left(i_y - i_z) , omega_y , omega_z \ &dotomega_y = frac{i_z - 1}{i_y} , omega_x , omega_z \ &dotomega_z = frac{1 - i_y}{i_z} , omega_x , omega_y end{align*}$

Учитывая, что изначально вращение происходит с постоянной угловой скоростью omega вокруг оси , построим уравнения возмущенного движения. Будем считать, что omega > 0 — этого всегда можно добиться выбором осей собственной системы координат.

$begin{align*} &Deltadotomega_x = left(i_y - i_z) , Deltaomega_y , Deltaomega_z \ &Deltadotomega_y = frac{i_z - 1}{i_y} , (omega + Deltaomega_x) , Deltaomega_z \ &Deltadotomega_z = frac{1 - i_y}{i_z} , (omega + Deltaomega_x) , Deltaomega_y end{align*}$

Построим функцию Четаева

Точка покоя системы лежит на границе v > 0 , а функция (23) положительна при Deltaomega_y, , Deltaomega_z > 0 . Производная по времени от (23) в силу (22) имеет вид

$dot v = Deltadotomega_y , Deltaomega_z + Deltaomega_y , Deltadotomega_z = (omega + Deltaomega_x) , left(frac{i_z - 1}{i_y} , Deltaomega_z^2 + frac{1 - i_y}{i_z} , Deltaomega_y^2 right)$

В силу того, что omega > 0, quad omega gg |Deltaomega_x| , а так же при условии вращения гайки вокруг среднего момента инерции, так что i_z > 1, quad i_y < 1 , то есть I_z > I_x > I_y , производная (24) положительна в области v > 0 , а значит движение будет неустойчивым.

Если же, как в рассматриваемом нами изначально случае, I_y > I_x > I_z , или i_z < 1, quad i_y > 1 , то в качестве функции Четаева выберем

Тогда область v > 0 соответствует условию Deltaomega_y, , Deltaomega_z < 0 , точка покоя системы так же лежит на её границе, а производная (25), равная

$dot v = -Deltadotomega_y , Deltaomega_z - Deltaomega_y , Deltadotomega_z = (omega + Deltaomega_x) , left(frac{1 - i_z}{i_y} , Deltaomega_z^2 + frac{i_y - 1}{i_z} , Deltaomega_y^2 right)$

так же будет положительна. Движение будет неустойчивым.

Заключение

Данная статья — дополнение к статье об устойчивости движения гайки Джанибекова. Основной материал взят из приведенных выше литературных источников, а так же сайта Math Help Planet. Авторский вклад в эту статью — поэтапное подробное рассмотрение второго метода Ляпунова на примере конкретной задачи. Кроме того, чуть более развернуто, чем в книге Маркеева, рассмотрен вопрос о неустойчивости движения применительно к различным вариантам соотношения между моментами инерции гайки.

Таким образом считаю, что я исправил недочет, связанный с неполнотой изложения вопроса о причинах эффекта Джанибекова. А заодно и сам подробнее изучил второй метод Ляпунова.

Благодарю читателей за проявленное внимание!

Источник

From Wikipedia, the free encyclopedia

In the theory of ordinary differential equations (ODEs), Lyapunov functions, named after Aleksandr Lyapunov, are scalar functions that may be used to prove the stability of an equilibrium of an ODE. Lyapunov functions (also called Lyapunov’s second method for stability) are important to stability theory of dynamical systems and control theory. A similar concept appears in the theory of general state space Markov chains, usually under the name Foster–Lyapunov functions.

For certain classes of ODEs, the existence of Lyapunov functions is a necessary and sufficient condition for stability. Whereas there is no general technique for constructing Lyapunov functions for ODEs, in many specific cases the construction of Lyapunov functions is known. For instance, quadratic functions suffice for systems with one state; the solution of a particular linear matrix inequality provides Lyapunov functions for linear systems, and conservation laws can often be used to construct Lyapunov functions for physical systems.

Definition[edit]

A Lyapunov function for an autonomous dynamical system

${displaystyle {begin{cases}g:mathbb {R} ^{n}to mathbb {R} ^{n}&\{dot {y}}=g(y)end{cases}}}$

with an equilibrium point at y=0 is a scalar function ${displaystyle V:mathbb {R} ^{n}to mathbb {R} }$ that is continuous, has continuous first derivatives, is strictly positive for , and for which the time derivative is non positive (these conditions are required on some region containing the origin). The (stronger) condition that is strictly positive for is sometimes stated as is locally positive definite, or is locally negative definite.

Further discussion of the terms arising in the definition[edit]

Lyapunov functions arise in the study of equilibrium points of dynamical systems. In ${displaystyle mathbb {R} ^{n},}$ an arbitrary autonomous dynamical system can be written as

for some smooth ${displaystyle g:mathbb {R} ^{n}to mathbb {R} ^{n}.}$

An equilibrium point is a point $y^{*}$ such that ${displaystyle gleft(y^{*}right)=0.}$ Given an equilibrium point, ${displaystyle y^{*},}$ there always exists a coordinate transformation ${displaystyle x=y-y^{*},}$ such that:

${displaystyle {begin{cases}{dot {x}}={dot {y}}=g(y)=gleft(x+y^{*}right)=f(x)\f(0)=0end{cases}}}$

Thus, in studying equilibrium points, it is sufficient to assume the equilibrium point occurs at .

By the chain rule, for any function, ${displaystyle H:mathbb {R} ^{n}to mathbb {R} ,}$ the time derivative of the function evaluated along a solution of the dynamical system is

${displaystyle {dot {H}}={frac {d}{dt}}H(x(t))={frac {partial H}{partial x}}cdot {frac {dx}{dt}}=nabla Hcdot {dot {x}}=nabla Hcdot f(x).}$

A function is defined to be locally positive-definite function (in the sense of dynamical systems) if both and there is a neighborhood of the origin, , such that:

{displaystyle H(x)>0quad forall xin {mathcal {B}}setminus {0}.}

Basic Lyapunov theorems for autonomous systems[edit]

Let ${displaystyle x^{*}=0}$ be an equilibrium of the autonomous system

and use the notation to denote the time derivative of the Lyapunov-candidate-function :

${displaystyle {dot {V}}(x)={frac {d}{dt}}V(x(t))={frac {partial V}{partial x}}cdot {frac {dx}{dt}}=nabla Vcdot {dot {x}}=nabla Vcdot f(x).}$

Locally asymptotically stable equilibrium[edit]

If the equilibrium is isolated, the Lyapunov-candidate-function is locally positive definite, and the time derivative of the Lyapunov-candidate-function is locally negative definite:

for some neighborhood of origin then the equilibrium is proven to be locally asymptotically stable.

Stable equilibrium[edit]

If is a Lyapunov function, then the equilibrium is Lyapunov stable. The converse is also true, and was proved by J. L. Massera.

Globally asymptotically stable equilibrium[edit]

If the Lyapunov-candidate-function is globally positive definite, radially unbounded, the equilibrium isolated and the time derivative of the Lyapunov-candidate-function is globally negative definite:

${displaystyle {dot {V}}(x)<0quad forall xin mathbb {R} ^{n}setminus {0},}$

then the equilibrium is proven to be globally asymptotically stable.

The Lyapunov-candidate function V(x) is radially unbounded if

(This is also referred to as norm-coercivity.)

Example[edit]

Consider the following differential equation on :

Considering that $x^{2}$ is always positive around the origin it is a natural candidate to be a Lyapunov function to help us study . So let ${displaystyle V(x)=x^{2}}$ on . Then,

${displaystyle {dot {V}}(x)=V'(x){dot {x}}=2xcdot (-x)=-2x^{2}<0.}$

This correctly shows that the above differential equation, is asymptotically stable about the origin. Note that using the same Lyapunov candidate one can show that the equilibrium is also globally asymptotically stable.

References[edit]

Weisstein, Eric W. “Lyapunov Function”. MathWorld.
Khalil, H.K. (1996). Nonlinear systems. Prentice Hall Upper Saddle River, NJ.
La Salle, Joseph; Lefschetz, Solomon (1961). Stability by Liapunov’s Direct Method: With Applications. New York: Academic Press.
This article incorporates material from Lyapunov function on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.

External links[edit]

Example of determining the stability of the equilibrium solution of a system of ODEs with a Lyapunov function

Источник

В общем случае для
всякой системы дифференциальных
уравнений относительно нетрудно
подобрать определенно положительную
функцию V(x₁,_,…,x_n),
которая может служить функцией Ляпунова.
Основной
проблемой данного метода является то,
что не всякая такая функция имеет
знакоопределенную или знакопостоянную
производную W.

А.М.Ляпунов
рекомендовал сначала выбирать отрицательно
определенную функцию ,
а затем определять соответствующую
положительную функцию .

Для
линейных системa
функцию
ищут в виде квадратичной формы :

(7.3.1)

Для
определения коэффициентов B_ij
задаются функцией в
виде отрицательной квадратичной формы:

(7.3.2)

Предположим,
что уравнения, описывающее динамику
системы, имеют вид:

(7.3.3)

Тогда
из выражения (7.31) с учетом (7.3.3) получим
выражение для производной:

(7.3.4)

Приравняв выражения
(7.3.4) и (7.3.2), получим:

Затем, сгруппировав
и приведя подобные члены, можно приравнять
коэффициенты в левой и правой части. В
итоге получим уравнения для определения
коэффициентов B_ij:

(7.3.5)

Полагая
величины
заданными, можно решить систему (7.3.5)
относительно коэффициентов
и, получив в результате функцию ,
производная которой
имеет заданный вид.

Коэффициенты

при этом назначаются так, чтобы функция
была заведомо
знакоопределенной. Это можно сделать
разными способами, например, принять

Тогда
производная
имеет определённо отрицательный вид.

В
этом случае коэффициенты
определяются из системы уравнений:

(7.3.6)

Пример:

выбор функции
Ляпунова для линейной системы второго
порядка (n=2).

(7.3.7)

(7.3.8)

Примем

Предположим,
что уравнения возмущённого движения
системы имеют вид:

(7.3.9)

Откуда
найдём значения коэффициентов

(7.3.10)

Используя
формулы соответствия:

(7.3.11)

получим

(7.3.12)

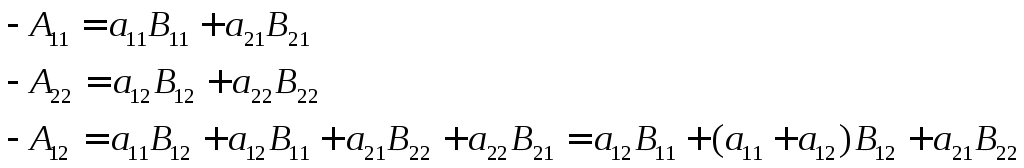
Учитывая
значения коэффициентов (7.3.10):

(7.3.13)

Примем

(7.3.15)

и
решим систему уравнений

(7.3.16)

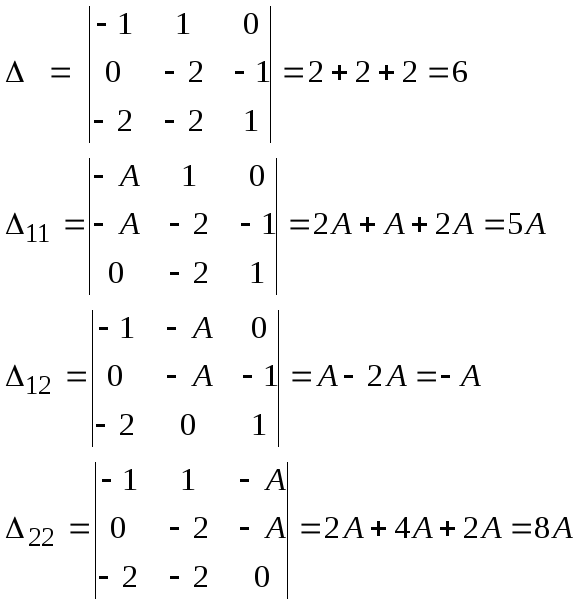
(7.3.17)

(7.3.18)

При

В случае нелинейных
систем единая методика выбора функции
Ляпунова отсутствует, однако для систем
отдельных типов имеются рекомендации
по выбору функции Ляпунова. Например,
для системы вида:

Рис. 7.3.1

с
характеристикой (рис.7.3.2) НЭ, удовлетворяющей
условиям

f(0)=0,

А.И.
Лурье и В.М. Постниковым был предложен
следующий подход: функция Ляпунова
находится как квадратичная форма от
координат системы плюс интеграл от
нелинейности

Рис. 7.3.2

β
– постоянные коэффициенты (7.3.19)

Можно показать,
что поверхности постоянных значений
V=const,
взятых в такой форме, содержат внутри
себя начало координат и имеют значения
d,
возрастающие по модулю по мере удаления
от начала координат. Эти поверхности
заполняют все фазовое пространство и
при соответствующем выборе значений
и

могут служить для определения устойчивости
равновесия системы в целом (и в «малом»,
и в «большом»).

Пример: проверить
устойчивость равновесия в системе

Линейная
часть описывается выражением

.(7.3.20)

(7.3.21)

(7.3.22)

(7.3.23)

(7.3.24)

айдем дифференциальное уравнение
системы

При определении
устойчивости положения равновесия
внешние воздействия должны отсутствовать,
следовательно входной сигнал g=0,
поэтому
.

Дифференциальное
уравнение нелинейной системы

. (7.3.25)

Функцию
Ляпунова V
выбираем в виде квадратичной формы
плюс интеграл от нелинейности

(7.3.26)

Если нелинейная характеристика
проходит через первый и третий квадранты
, то .
При определённо положительной функции
Ляпунова
из (7.3.26) следует, что
– функция определенно отрицательная
при, что и является условием
устойчивости.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Метод функций Ляпунова

Описание[править | править код]

Уравнения возмущённого движения^[3][править | править код]

Определение функции Ляпунова (для автономных систем)^[3][править | править код]

Теоремы Ляпунова для автономных систем[править | править код]

Устойчивость точки равновесия[править | править код]

Локальная асимптотическая устойчивость[править | править код]

Глобальная асимптотическая устойчивость[править | править код]

Пример[править | править код]

Примечания[править | править код]

Ссылки[править | править код]

Метод функций Ляпунова в задаче об эффекте Джанибекова

Введение

1.Дифференциальные уравнения возмущенного движения. Снова.

2. Xитрая функция V(x) — кандидат в функции Ляпунова

3. Теоремы Ляпунова об устойчивости

Теорема Ляпунова об устойчивости

Теорема Ляпунова об асимптотической устойчивости

4. Интегралы движения гайки Джанибекова

4. Построение функции Ляпунова из интегралов движения

5. Неустойчивость вращения гайки Джанибекова

Теорема Четаева о неустойчивости

Заключение

Definition[edit]

Further discussion of the terms arising in the definition[edit]

Basic Lyapunov theorems for autonomous systems[edit]

Locally asymptotically stable equilibrium[edit]

Stable equilibrium[edit]

Globally asymptotically stable equilibrium[edit]

Example[edit]

See also[edit]

References[edit]

External links[edit]

Добавить комментарий Отменить ответ

Метод функций Ляпунова

Описание[править | править код]

Уравнения возмущённого движения[3][править | править код]

Определение функции Ляпунова (для автономных систем)[3][править | править код]

Теоремы Ляпунова для автономных систем[править | править код]

Устойчивость точки равновесия[править | править код]

Локальная асимптотическая устойчивость[править | править код]

Глобальная асимптотическая устойчивость[править | править код]

Пример[править | править код]

Примечания[править | править код]

Ссылки[править | править код]

Метод функций Ляпунова в задаче об эффекте Джанибекова

Введение

1.Дифференциальные уравнения возмущенного движения. Снова.

2. Xитрая функция V(x) — кандидат в функции Ляпунова

3. Теоремы Ляпунова об устойчивости

Теорема Ляпунова об устойчивости

Теорема Ляпунова об асимптотической устойчивости

4. Интегралы движения гайки Джанибекова

4. Построение функции Ляпунова из интегралов движения

5. Неустойчивость вращения гайки Джанибекова

Теорема Четаева о неустойчивости

Заключение

Definition[edit]

Further discussion of the terms arising in the definition[edit]

Basic Lyapunov theorems for autonomous systems[edit]

Locally asymptotically stable equilibrium[edit]

Stable equilibrium[edit]

Globally asymptotically stable equilibrium[edit]

Example[edit]

See also[edit]

References[edit]

External links[edit]

Вам также может понравиться

Как исправить негативное мышление

Как найти ноль если нет напряжение

Как найти обороты в балансе

Добавить комментарий Отменить ответ

Уравнения возмущённого движения^[3][править | править код]

Определение функции Ляпунова (для автономных систем)^[3][править | править код]