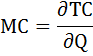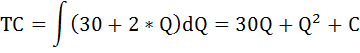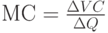Как найти функцию общих затрат фирмы

Общие затраты = постоянные затраты + (количество единиц продукции * переменные затраты на единицу продукции)

Функция затрат может быть простым инструментом для определения того, сколько стоит управление компанией, производство продукции или предоставление услуг. В самом простом виде это то же самое, что и формула общих затрат, но компания может адаптировать формулу общих затрат к своей ситуации, что приведет к уникальной функции затрат, зависящей от конкретных затрат, продуктов и расходов компании. Изучение функций затрат может помочь вам понять финансы вашего бизнеса и сделать прогнозы на будущее.

В этой статье мы объясним, что такое функция затрат, для чего она нужна, как рассчитать ее для вашего бизнеса и некоторые распространенные вариации базовой функции затрат.

Что такое функция затрат?

Предприятия могут использовать функцию затрат, чтобы определить, сколько будет стоить производство определенного количества единиц продукции. Каждая компания может настроить эту функцию для своего производства, поэтому функция затрат компании обычно сложнее, чем основная формула общих затрат. Она полезна, поскольку учитывает, что некоторые затраты являются фиксированными, например, арендная плата или зарплата административного персонала, некоторые затраты зависят от количества производимой продукции, например, материальные затраты, а другие затраты, такие как оплата труда или доставка, могут увеличиваться при увеличении количества единиц продукции.

Для чего используется функция затрат?

Функция затрат может быть полезна при прогнозировании будущих расходов, определении средней стоимости единицы продукции или при запуске моделей производственных сценариев. Разработка точной функции затрат может помочь компаниям построить график своих затрат и даже доходов для различных объемов производства, и это визуальное отображение может помочь объяснить прогнозы заинтересованным сторонам, сотрудникам и руководителям компании. Функции затрат также могут помочь вам спрогнозировать, сколько единиц данной продукции вам нужно продать, чтобы окупить производственные затраты или получить прибыль.

Как найти и использовать функцию затрат

Вот шаги, которые вы можете предпринять, чтобы найти функцию затрат:

1. Найти постоянные затраты

Сначала отследите свои постоянные расходы. Если у вас есть отчет о доходах или бухгалтерское программное обеспечение, вы можете найти свои постоянные расходы в виде бюджетной статьи. Если нет, вы можете рассчитать свои собственные постоянные затраты, добавив все статьи, которые не меняются в зависимости от количества продукции. Обычно сюда входят арендная плата и административные расходы.

Пример: Вымышленная компания, которая предоставляет макияж и другие косметические услуги своим клиентам на дому или на выезде. В следующем году они могут получить контракт с местным театром, поэтому они используют функцию затрат, чтобы определить, какими будут их затраты с этим контрактом или без него. Сначала они перечисляют свои постоянные затраты. После анализа постатейных расходов за прошлый год они определили, что их постоянные затраты составляют $10 000.

2. Найдите переменные затраты на единицу продукции

Затем найдите переменные затраты. Для производственных компаний они обычно включают такие расходы, как сырье, упаковочные материалы и часы работы. Для компаний, предоставляющих услуги, это может включать топливо для транспортных средств или расходы на снабжение, связанные с каждой услугой. Разделите общие переменные затраты на количество произведенных единиц продукции или оказанных услуг, чтобы найти переменные затраты на единицу продукции.

Пример: Переменные затраты вымышленной компании включают бензин для их автомобилей, расходные материалы для макияжа и затраты на чистку оборудования. За прошлый год, когда они делали макияж примерно для 1 000 человек, их переменные затраты составили $15 000. Они делятся на количество услуг, чтобы найти переменные затраты на единицу продукции:

$15 000 1 000 услуг = $15 за единицу

3. Умножьте средние переменные затраты на количество товаров, затем добавьте постоянные затраты

Наконец, умножьте средние переменные затраты на единицу продукции на количество потенциальных единиц, чтобы найти общие переменные затраты. Добавьте общие переменные затраты к постоянным затратам, чтобы получить общие затраты. Вы можете рассчитать это несколько раз с разным количеством единиц продукции, чтобы сравнить результаты.

Пример: Если компания Fictional получит контракт, то в течение следующего года она будет делать макияж 1 500 клиентам. Чтобы рассчитать затраты для этого сценария, они складывают числа в функции затрат:

Общие затраты = $10,000 + (1,500 * $15) = $32,500

Если Fictional не получит свой контракт, они прогнозируют 1 200 клиентов в течение следующего года:

Общие затраты = $10,000 + (1,200 * $15) = $28,000

Когда вам может понадобиться более сложная функция затрат

Если ваши затраты не все легко классифицируются как постоянные или переменные, или если вы продаете несколько продуктов, вам может потребоваться корректировка функции затрат. Вот как следует подходить к этим ситуациям:

Многочисленные продукты

Если вы продаете несколько продуктов по разным ценам, вы можете модифицировать уравнение общих затрат, чтобы включить в него информацию по дополнительным продуктам. Раздел уравнения затрат, который зависит от количества продукции, – это переменные затраты. Поскольку мы находим переменные затраты для одного продукта путем умножения количества единиц продукции на переменные затраты на единицу этого продукта, мы можем просто добавить новый раздел переменных затрат в функцию затрат. Если компания производит два продукта, A и B, ее функция затрат может выглядеть следующим образом:

Общие затраты = постоянные затраты + (количество единиц продукции A * переменные затраты на единицу продукции A) + (количество единиц продукции B * переменные затраты на единицу продукции B)

Затраты, которые иногда являются постоянными, а иногда переменными

Некоторые затраты могут быть постоянными или переменными в зависимости от масштаба. Компании может потребоваться нанять дополнительных сотрудников, если объем ее заказов увеличится, или купить новое помещение. В обстоятельствах, подобных этим, вы можете добавить раздел к вашей функции затрат. Например, если ваши переменные затраты на материалы составляют определенную сумму на единицу продукции, но ваши переменные затраты на труд изменяются в зависимости от количества единиц по-разному, ваша функция затрат может выглядеть следующим образом:

Общие затраты = постоянные затраты + (количество единиц * материальные переменные затраты) + затраты на оплату труда

Важно учитывать, как затраты связаны с объемом производства единицы продукции, поскольку некоторые затраты могут иметь определенную цену за единицу продукции, например, материалы, в то время как другие затраты, например, труд или доставка, могут быть связаны экспоненциально. Если вы добавляете в уравнение отдельный раздел для одного вида затрат, убедитесь, что вы убрали его из любого другого раздела, где он был ранее, чтобы не считать его дважды.

Способы использования функции затрат

Знание функции затрат может помочь вам рассчитать несколько других вещей, в том числе:

Функция прибыли

Прибыль = общая выручка – общие затраты

Чтобы получить функцию прибыли компании, вы можете объединить функцию общих затрат компании и общую выручку. Общая выручка – это количество проданных единиц товара, умноженное на цену покупки. Поскольку выручка и переменные затраты зависят от количества произведенных изделий, вы также можете выразить функцию прибыли на основе количества произведенных изделий:

Прибыль = (закупочная цена за единицу продукции * количество единиц продукции) – постоянные затраты – (переменные затраты на единицу продукции * количество единиц продукции)

Прибыль = [(закупочная цена за единицу – переменные затраты на единицу) * количество единиц] – постоянные затраты

Пример: Вымышленная компания продает свои услуги по макияжу по цене $40 за человека. Чтобы рассчитать свою прибыль за прошедший год, они вводят в уравнение прибыли закупочную цену, переменные затраты на одно изделие, количество изделий и постоянные затраты:

Прибыль = [($40 – $15) * 1000] – $10,000 = $25,000 – $10,000 = $15,000

Стоимость одного сеанса

Стоимость одного изделия = общие затраты количество изделий

Поскольку постоянные затраты остаются неизменными, а переменные затраты зависят от того, сколько изделий производит компания, стоимость одного изделия также зависит от количества произведенных изделий. После подсчета общих затрат на изготовление определенного количества изделий, вы можете разделить общие затраты на количество изделий, чтобы рассчитать, сколько потребуется для изготовления одной единицы продукции. Знание этого может помочь вам решить, как устанавливать цены и видеть, сколько прибыли вы получаете.

Пример: Вымышленная компания хотела бы узнать, сколько стоит каждый сеанс макияжа, чтобы установить цены на предстоящий год. Сначала они рассчитывают стоимость одного сеанса, если они получат контракт и больше клиентов:

Стоимость одной сессии = $42 500 1 500 = $28.34

Далее они рассчитывают стоимость одного сеанса при меньшем количестве клиентов:

Стоимость одного занятия = $38 000 1 200 = $31.67

Они видят, что стоимость одного сеанса снизится, если количество сеансов увеличится, поскольку постоянные расходы остаются неизменными.

Функция
затрат
(издержек)
производства
отражает зависимость между объемом
произведенной продукции и минимально
необходимыми затратами на данное
производство.

В
краткосрочном периоде общие
или
валовые
издержки
(TC) состоят из постоянных (FC) и переменных
(VC).

TC(Q)=
FC + VC,

где

FC
– постоянные издержки,
величина которых не зависит от объёма
производства. К ним относятся: заработная
плата повременных работников; банковский
процент за кредит; плата за коммунальные
услуги; арендные платежи; амортизационные
отчисления.

VC
– переменные издержки,
величина которых растёт по мере
увеличения объёма производства. К ним
относят расходы на: сырьё, материалы,
топливо, заработную плату сдельщиков.

Допустим,
что функция
общих издержек фирмы
на выпуск Q единиц продукции представлена
следующим образом:

TC
= Q² + 16Q + 400.

Выведим
уравнения функций всех видов издержек,
используемых в экономической теории
для описания поведения фирмы.

Отсюда,
согласно теории:

• FC
  = 400 – это постоянные издержки, т.к. они
  не зависят от выпуска продукции (Q);

• VC
  = Q² + 16Q – переменные издержки – зависят
  от выпуска продукции (Q).

Для
экономического анализа деятельности
фирм, предприятий особый интерес
представляют средние и предельные
издержки.

Средние
общие издержки (AC или ATC)
– это общие расходы на единицу выпуска
продукции:

AТC
= TC / Q = (FC / Q + VC / Q),

где

• FC
  / Q = AFC есть средние постоянные издержки;

• VC
  / Q = AVC – средние переменные издержки.

Средние
переменные издержки (AVC)
– это переменные издержки на единицу
выпуска продукции:

AVC
= VC / Q
= Q + 16.

Средние
постоянные издержки (AFC)
– это постоянные издержки на единицу
выпуска продукции:

AFC
= FC / Q
= 400 / Q.

Применительно
к анализируемой нами функции общих
издержек, уравнение функции средних
общих издержек примет вид:

AТC
= (Q + 16) + 400 / Q.

Предельные
(маржинальные) издержки (MC)
– это прирост издержек на выпуск
дополнительной единицы продукции:

MC
= ∆TC / ∆Q

или
MC
= dTC / dQ,
т.е. производная общих издержек.

Тогда
уравнение функции предельных издержек,
анализируемой нами функции общих
издержек, будет иметь следующий вид:

MC
= 2Q + 16.

Таким
образом функция затрат производства
отражает зависимость между объемом
произведенной продукции и минимально
необходимыми затратами на его
производство.

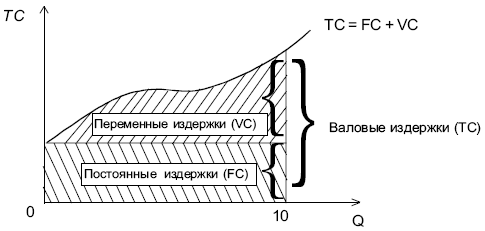
Характер
изменения краткосрочных издержек
производства можно
изобразить графически:

Рис.
8.14. Издержки производства в кратковременном
периоде.

Проведем
анализ данного графического изображения,
опираясь на общеизвестные теоретические
положения:

1
участок:
от 0 до Q1
характеризует снижение всех видов
издержек (предельных и средних);

2
участок:
от Q1
до
Q2
–
снижение средних переменных, постоянных
и общих средних издержек при повышении
предельных.

3
участок:
от Q2
до Q3
отражает повышение предельных и средних
переменных издержек при соответствующем
снижении

средних
общих издержек. При объёме выпуска
продукции Q3
достигается минимум средних общих
издержек, т.е. производственный
оптимум (AТC
= MC).

Производственный
оптимум
предполагает достижение такого объёма
выпуска, при котором все производственные
мощности, задействованы полностью,
работники работают без прогулов и
перенапряжения. Применительно к
анализируемой нами функции общих
издержек фирмы: TC
= Q² + 16Q + 400
можно заключить, что оптимальный выпуск
продукции достигнут при объеме выпуска
продукции Q3
= 20 (AТC = MC или Q + 16 + 400 / Q = 2Q + 16). Следовательно,
точка Q3
= 20 – точка производственного оптимума.

4
участок:
от Q3
и
выше – одновременное повышение всех
видов издержек. Значит, дальнейшее
увеличение выпуска продукции будет
невыгодным.

На
величину издержек производства в
кратковременном периоде влияют следующие
факторы:

• общий
  выпуск продукции;

• закон
  убывающей предельной производительности;

• эффект
  масштаба.

Эффект
масштаба
производства
– реакция объёма выпуска на изменение
масштаба производства.

Масштаб
производства определяется размером
используемых ресурсов (см. рис. 9.15).

Рис.
9.15. Реакция объёма выпуска продукции
на изменение масштаба производства.

1
участок
– если с ростом выпуска продукции
средние издержки снижаются, то говорят,
что наблюдается положительный эффект
масштаба (растущая отдача);

2
участок
– если издержки не зависят от масштаба
производства, то это нулевой эффект
(постоянная отдача);

3
участок
– если с ростом выпуска растут средние
издержки, то это отрицательный эффект
(убывающая отдача).

Определим
эффект масштаба производства на основе
анализа функции общих издержек
производства: TC = Q² + 16Q + 400.

Вычислим
значение выпуска Q, при котором средние
общие издержки минимальны. Для этого
необходимо найти первую производную
общих средних издержек и приравнять
её к нулю:

(ATC)’
= (Q + 16 + 400 / Q)’ = 1 – 400 / Q² = 0.

Отсюда
получим, что при Q = 20 средние общие
издержки будут минимальны. Значит, до
объёма выпуска Q = 20 наблюдается
положительный эффект масштаба
производства, а начиная с Q = 20, имеет
место отрицательный эффект масштаба.

Следовательно,
если:

• (ATC)’
  < 0 – положительный эффект масштаба
  производства;

• (ATC)’
  > 0 – отрицательный эффект масштаба
  производства;

• (ATC)’
  = 0 – постоянный эффект масштаба
  производства.

Функционирование
фирм в долгосрочном периоде
теоретически предполагает ряд допущений:

• все
  факторы производства и труд, и капитал
  и НТП, являются переменными;

• цены
  на факторы производства неизменны;

• средние
  постоянные издержки исчезают в силу
  большого объема выпуска продукции, а
  значит АFC
  = 0;

• средние
  переменные издержки равны средним
  общим AVC=
  AТC
  (в долговременном периоде используется
  только понятие кратковременные средние
  издержки – SRAC);

• между
  предприятиями, к примеру П_1–4,
  входящими в состав фирмы, возможен
  перелив капитала;

• А,
  В, С, D
  – точки минимума краткосрочных средних
  издержек, т.е. точки оптимального
  выпуска продукции;

• LRAC
  – долгосрочные средние издержки;

• принцип
  минимизации издержек определяется по
  предельному продукту труда в расчете
  на единицу стоимости данного фактора;

• на
  участке [OD]
  прослеживается растущая отдача или
  положительный эффект масштаба
  производства;

• выше
  этого участка идет повышение
  долговременных средних издержек.

Графическое
изображение долгосрочных средних
издержк (см. рис. 8.16).

Рис.
8.16. Долгосрочные средние издержки.

Контрольные
вопросы и задания по теме:

1.
Сформулируйте
понятие производственной функции?

1. Почему
   ее называют технологической функцией?

2. Что
   означает экономически эффективный и
   технологически эффективный способы
   производства?

3. Как
   рассчитывается производительность
   факторов производства. Приведите
   графическое изображение общей, средней
   и предельной производительности
   факторов производства.

4. Что
   отражает закон убывающей средней и
   предельной производительности факторов
   производства? Как он действует
   краткосрочном в долгосрочном периодах?

5. Зависят
   ли средний, предельный и общий продукты
   труда от величины используемого фирмой
   капитала? Если «да», то каким образом?

6. В
   чем проявляется проблема уровня и
   темпов физического и морального износа
   оборудования и других капитальных
   благ в России?

7. Сформулируйте
   амортизационную политику российских
   предприятий.

8. Как
   вы понимаете смысл следующих выражений:
   «Издержки производства не оказывали
   бы никакого влияния на конкурентную
   цену, если бы они не воздействовали бы
   на предложение» и «Множество бесплодных
   споров об «истинной стоимости» вещей
   возникает из-за неспособности понять,
   что только действиям присущи затраты
   и что одни и те же действия нередко
   означают различные затраты для разных
   людей»?

10.
Почему в России возможно резкое улучшение
положения предприятий при относительно
небольших издержках (эффект увеличивающей
отдачи).

11.
Покажите графически и объясните, как
внедрение прогрессивных форм организации
производства повлияет на карту изоквант.

12.
Какую программу нужно проводить
предприятию, чтобы минимизировать
издержи производства?

13.
На конкретном примере приведите
оптимальную комбинацию факторов
производства.

14.
Что предполагает многофакторный анализ
прибыли?

15.
Начертите и охарактеризуйте траекторию
развития производства.

Соседние файлы в папке Экономика

• #
• #
• #

Задача №1. Расчёт экономической прибыли конкурентной фирмы

Фирма, находясь в условиях совершенной конкуренции, имеет следующую функцию общих затрат:

ТС = 140 + 10 × Q + 40 × Q².

При каком выпуске прибыль фирмы достигнет максимума, если цена установилась на уровне 250 ден. ед.? Определить размер прибыли фирмы.

Будут ли в длительном периоде в эту отрасль стремиться войти новые фирмы?

Решение:

Наличие  в составе общих затрат фиксированных (постоянных) затрат (FC = 140) свидетельствует о том, что речь идёт о краткосрочном периоде.

Найдём объём производства, при котором прибыль будет максимальна. Условие максимизации прибыли на рынке совершенной конкуренции в краткосрочном периоде имеет вид:

Р = МС = МR = AR.

Определим функцию предельных издержек фирмы: найдём производную общих издержек.

МС = (ТС)’ = 10 + 80 × Q.

Приравняем эту функцию к цене равной 250.

10 + 80 × Q = 250

80 × Q = 240

Q = 3

Вычислим прибыль фирмы при объёме выпуска равном 3 по формуле:

П = TR — TC = P × Q — TC = 250 × 3 — (140 + 10 × 3 + 40 × 3²) = 220 ден. ед.

В долгосрочном периоде наличие неотрицательной экономической прибыли будет привлекать в отрасль новые фирмы.

Задача № 2. Определение рыночной цены и отраслевого выпуска продукции

В отрасли действуют 130 одинаковых фирм. Издержки производства каждой фирмы описываются функциями

ТС =Q³ — 36*Q² + 384*Q,

где

Q — объём производства в тысячах штук. Найти рыночную цену и отраслевой выпуск продукции, при которых на конкурентном рынке устанавливается долгосрочное равновесие.

Решение:

В долгосрочном периоде на рынке совершенной конкуренции соблюдается равенство:

P = MC = MR = AR = minAC.

Найдём функцию средних издержек каждой фирмы по следующей формуле:

АС = ТС / Q = Q² — 36*Q + 384

Далее необходимо найти минимум данной функции. Для этого определим производную функции АС и приравняем её к нулю.

2*Q — 36 = 0

Q = 18

AC(18) = 18² — 36*18 + 384 = 60

Так как Р = minAC в долгосрочном периоде, следовательно, рыночная цена равна Р = 60.

Найдём отраслевой выпуск. Так как каждая из фирм отрасли производит 18 тысяч штук продукции, значит 130 фирм произведут:

Q_отр. = 18*130 = 2340 тысяч штук

Задача № 3. Определение рыночной цены в долгосрочном периоде

Конкурентная фирма находится в состоянии равновесия в долгосрочном периоде и имеет следующие затраты: TC = Q³ — 38*Q² + 418*Q. Определите цену на этом рынке в долгосрочном периоде.

Решение:

В долгосрочном периоде цена в условиях соверешенной конкуренции устанавливается на уровне минимума средних затрат. При этом фирма совершенный конкурент получает нулевую экономическую прибыль.

Условие равновесия на рынке будет иметь вид:

Р = МС = МR = AR = min AC

Найдём средние затраты фирмы по формуле:

АС = ТС / Q = Q² — 38*Q + 418

Определим минимум функции средних затрат. Для нахождения экстремума функции  приравняем к нулю её производную:

АС’ = 2*Q — 38

2*Q — 38 = 0

Q = 19

При выпуске Q = 19 средние затраты будут равны:

АС = 19² — 38*19 + 418 = 57.

Таким образом, цена в долгосрочном периоде будет равна 57.

Задача № 4. Расчёт рыночной цены, при которой фирма уйдёт с рынка

Общие затраты фирмы, действующей на рынке совершенной конкуренции, составляют

0,5*Q³ — 15*Q² + 300*Q + 250 000.

При какой цене фирме становится невыгодным работать на этом рынке в краткосрочном периоде?

Решение:

В краткосрочном периоде фирма совершенный конкурент уйдёт с рынка, если цена окажется меньше  минимума её средних переменных издержек: Р < min AVC.

Найдём переменные издержки фирмы, а точнее запишем функцию переменных издержек:

VC = 0,5*Q³ — 15*Q² + 300*Q

Теперь определим функцию средних переменных издержек  по формуле:

АVC = VC / Q = 0,5*Q² — 15*Q + 300

Найдём экстремум этой функции, приравняв к нулю её производную.

Q — 15 = 0

Q = 15.

При объёме производства Q = 15 средние переменные издержки будут минимальными.

АVC(15) = 0,5*15² — 15*15 + 300 = 187,5

Это так называемая точка закрытия фирмы. Фирма совершенный конкурент уйдёт с рынка, если цена упадёт ниже этой точки в краткосрочном периоде.

При Р < 187,5 фирме становится невыгодным работать на этом рынке в краткосрочном периоде.

Задача № 5. Расчёт объёма выпуска, максимизирующего прибыль фирмы

Функция издержек фирмы ТС = Q² — Q + 3, где Q — объём производства. Рыночная цена на продукцию фирмы составляет 7 и не зависит от объёма продаж этой фирмы. Найти объём выпуска продукции, максимизирующий прибыль фирмы.

Решение:

По условию рыночная цена не зависит от объёма продаж этой фирмы, это говорит о том, что фирма функционирует в условиях совершенной конкуренции.

Максимум прибыли фирмы действующей в условиях совершенной конкуренции определяется тождеством: Р = МС.

Найдём предельные издержки фирмы по формуле:

МС =(TC)’= 2Q — 1

Найдём объём выпуска продукции, максимизирующий прибыль фирмы.

Цена по условию равна Р = 7.

Р = МС

7 = 2Q — 1

Q = 4

Задача №6. Расчёт объёма производства в краткосрочном периоде

В отрасли совершенной конкуренции установилась цена Р = 30. В эту отрасль входит фирма с общими издержками ТС = 1/2 * Q² + 10 * Q + 100. Найти её объём производства в краткосрочном периоде.

Решение:

Фирма выберет такой объём производства, при котором прибыль будет максимальна. Условие максимизации прибыли: МС = MR.

На рынке совершенной конкуренции предельный доход равен цене: MR = P.

Отсюда следует, что цена равна предельным издержкам: P = MC.

Найдём предельные издержки. Предельные издержки в непрерывном случае (т.е. когда общие издержки заданы функцией) равны производной от функции общих издержек:

Функция предельных издержек будет иметь вид:

МС = Q + 10
P = MC
30 = Q + 10
Q = 20 — оптимальный объём производства фирмы.

Задача № 7. Расчёт рыночной цены и объёма выпуска на конкурентном рынке

Конкурентная фирма имеет общие затраты

ТС = 800 + 40*Q + 2*Q²

Она получает в краткосрочном периоде максимально возможную прибыль, равную 1000.

Определить цену на рынке и объём выпуска данной фирмы.

Решение:

Формула прибыли фирмы имеет вид:

П = TR — TC = P*Q — TC

По условию максимально возможная прибыль равна 1000.

P*Q — (800 + 40*Q + 2*Q²) = 1000

Найдём цену.

Условие максимизации прибыли на рынке совершенной конкуренции имеет вид:

Р = МС = MR = AR

Так как Р = МС, а МС = ТС’ = 40 + 4*Q, следовательно, Р = 40 + 4*Q. Подставим это выражение в формулу прибыли и получим:

(40 + 4*Q)*Q — (800 + 40*Q + 2*Q²) = 1000

40*Q + 4*Q² — 800 — 40*Q — 2*Q² — 1000 = 0

2*Q² = 1800

Q² = 900

Q_1,2 = ±30

Так как отрицательный корень экономического содержания не имеет, берём Q = 30.

Тогда цена будет равна:

Р = 40 + 4*30 = 160

Задача № 8. Расчёт рыночной цены на конкурентном рынке в долгосрочном периоде

Допустим, общие затраты фирмы на выпуск Q единиц продукции составляют:

Q³ – 16*Q² + 400*Q.

а) При каком значении Q средние затраты достигают минимума?

б) При какой цене этой фирме становится выгодным участвовать в совершенной конкуренции в долгосрочном периоде?

Решение:

а) Найдём функцию средних затрат по формуле:

АС = ТС / Q = (Q³ – 16*Q² + 400*Q) / Q = Q² – 16*Q + 400

Определим минимум функции. Для нахождения экстремума функции необходимо найти её производную и приравнять её к нулю.

AC’ =(Q2 – 16*Q + 400)’ = 2*Q – 16
2*Q – 16 = 0
Q = 8

При Q = 8 средние затраты достигают минимума.

б) В долгосрочном периоде фирме становится выгодным участвовать в совершенной конкуренции, если Р ≥ АС. При этом фирма имеет нулевую прибыль. И выполняется условие:

Р = МС = MR = minАС

Рассчитаем minAC. Подставим Q = 8 в функцию средних затрат:

minAC(Q=8) = 82 – 16*8 + 400 = 336

Итак, при цене Р ≥ 336 фирме становится выгодным участвовать в совершенной конкуренции в долгосрочном периоде.

Задача № 9. Расчёт цены и объёма производства, максимизирующих прибыль

Спрос на продукцию конкурентной отрасли:

Q_d = 55 – P

Предложение:

Q_s = 2P – 5

Если у одной из фирм отрасли восходящий участок кривой предельных издержек:

МС = 3Q + 5

При каких цене и объёме производства фирма максимизирует прибыль?

Решение:

Найдём цену равновесия. Приравняем функцию спроса и предложения:

Qd = Qs
55 – P = 2P – 5
3 * Р = 60
Р = 20 – цена рыночного равновесия, то есть цена по которой фирмы будут продавать свою продукцию.

Фирма в условиях совершенной конкуренции получает максимум прибыли при условии равенства цены и предельных затрат.

МС = Р
3Q + 5 = 20
Q = 5 – объём производства, при котором прибыль фирмы будет максимальной.

Задача №10. Расчёт рыночной цены и объёма выпуска на конкурентном рынке

Конкурентная фирма имеет предельные затраты:

МС = 30 + 2 × Q

при фиксированных затратах, равных 500 денежным единицам.

Она получает в краткосрочном периоде максимально возможную прибыль, равную 1100 денежным единицам.

Определить цену на рынке и объём выпуска данной фирмы.

Решение:

Формула прибыли имеет вид:

П = TR – TC = P*Q – TC

Определим функцию общих затрат. Так как функция предельных затрат это производная функции общих затрат, следовательно, функцию общих затрат можно определить как первообразную от функции предельных затрат.

где

С – константа, равная величине фиксированных затрат, которые по условию равны 500.

Таким образом функция общих затрат имеет вид:

ТС = Q² +30*Q + 500

Теперь запишем условие максимизации прибыли на рынке совершенной конкуренции в краткосрочном периоде:
Р = МС = MR = AR

Воспользуемся тем, что:

Р = МС

По условию задачи:

МС = 30 + 2 × Q, то есть Р = 30 + 2 * Q

Подставим это выражение, а так же функцию общих затрат в формулу прибыли и получим уравнение с одной неизвестной.

(30 + 2 * Q) * Q – (Q² +30*Q + 500) = 1100
Q2 = 1600
Q = ± 40

Так как отрицательное значение Q экономического смысла не имеет, следовательно, объём выпуска данной фирмы Q = 40.

Тогда рыночная цена будет равна:

Р = 30 + 2 * 40 = 110.

Функции затрат: понятие, виды, примеры

На чтение 3 мин Просмотров 1к. Опубликовано 29.10.2020

Функция затрат отражает математическую зависимость между затратами и выпуском продукции. Она показывает, как изменяются затраты в ответ на изменения в объеме производства.

Связь между затратами фирмы и выпуском продукции может быть изучена с помощью таблиц затрат (которые показывают общие затраты, общие переменные затраты и предельные затраты для каждой единицы) или графиков, которые строят различные кривые затрат.

При этом функция затрат является наиболее компактным и прямым методом инкапсуляции информации о затратах фирмы.

Функции затрат обычно в качестве зависимой переменной имеют стоимость, а в качестве независимой переменной – выпуск (количество) продукции.

Такие функции затрат не учитывают каких-либо изменений в стоимости вводимых ресурсов, поскольку они предполагают фиксированные цены на них.

Виды функций стоимости

Типичные функции затрат бывают: (1) линейными, (2) квадратичными и (3) кубическими.

В линейной функции затрат показатель степени аргумента Q (количество) равен 1. Она подходит только для структур затрат, в которых предельные издержки постоянны.

Квадратичная функция затрат отражает структуру затрат, в которой средние переменные затраты имеют U-образную форму (в ней показатель степени независимой переменной равен 2).

Кубическая функция (в ней показатель степени независимой переменной равен 3) затрат позволяет построить U-образную кривую предельных издержек. Функция затрат в приведенном ниже примере является кубической функцией затрат.

Функция общих затрат является наиболее фундаментальной зависимостью между затратами на выпуск продукции, поскольку функции для других затрат, таких как переменные затраты, средние переменные затраты и предельные издержки и так далее, могут быть получены из функции общих затрат.

Пример

Представьте, что вы работаете в фирме, чья функция общих затрат (TC) выглядит следующим образом:

TC = 0.1Q³ – 2Q² + 60Q + 200

Средняя функция общих затрат может быть получена путем деления функции общих затрат на Q:

ATC = TC/Q = 0.1Q² – 2Q + 60 + 200/Q

Постоянное значение в функции общих затрат представляет собой общую фиксированную стоимость. Функция для общей переменной стоимости может быть получена путем вычитания постоянного значения из функции общей стоимости:

VC = TC – FC

VC = 0.1Q³ – 2Q² + 60Q

Функция средних переменных издержек составляет результат деления общих переменных затрат на Q:

AVC = VC/Q = 0.1Q² – 2Q + 60

Предельные издержки равны наклону кривой общих издержек, которая, в свою очередь, равна первой производной функции общих издержек.

MC_Q = dTC/dQ = 0.3Q² – 4Q + 60

Функции затрат можно использовать для создания таблиц затрат и кривых затрат. Подключив различные уровни количества в функции затрат, определенные выше, мы можем создать таблицу затрат, которая может быть использована для построения кривых затрат.

Кривые общей стоимости и общей переменной стоимости, представленные функциями, рассмотренными выше, дают следующий график:

Поскольку функция общих затрат является кубической функцией, кривая средних переменных затрат и кривая предельных затрат имеют U-образную форму, как показано ниже:

Основные понятия: авансированный капитал, издержки производства, краткосрочный и долговременный периоды

Чтобы начать любое производство, нужно первоначально авансировать капитал, а потом его расходовать.

Первоначально авансированный капитал – расходы на приобретение постоянных ресурсов (покупку зданий, сооружений, оборудования) и переменных ресурсов (сырья, материалов, рабочей силы, в том числе и менеджеров, и маркетологов, коммунальное обслуживание и т.д.) с целью организации какого-то дела и получения прибыли.

Таким образом, авансированный капитал равен сумме постоянного и переменного капиталов.

Если мы живем по понятиям, то ясно: если крупное производство, то и первоначально авансированный капитал должен быть крупным, если мелкое (табачная палатка) – то и капитал <с гулькин нос>, т.е. маленький. Следовательно, одно дело – организовать выпуск книг или пирожков, совсем другое – компьютеров. Но и в том, и другом случае требуется первоначально авансированный капитал. Предположим, что все приобрели, чтобы начать производство. Остается врубить рукоятку и сказать крылатую фразу первого космонавта Советского Союза (12 апреля 1961 г.) Юрия Гагарина: <Поехали!> Как только начинается производство, или, как говорится, закрутится машина, капитал превращается в издержки производства.

Издержки производства – это расходы фирм, связанные с производством и реализацией продукта, в определенный период времени (обычно за месяц, квартал, год).

Отсюда все очень просто: издержки – это расчетная величина, зависимая от первоначального капитала. Поэтому издержки производства отличаются от авансированного капитала.

Издержки производства всегда меньше, чем авансированный капитал.

В издержки производства включается не вся стоимость зданий, станков, оборудования и т.д., а только стоимость изношенной их части в виде амортизационных отчислений, которые в дальнейшем пойдут на их возмещение. В авансированный же капитал включается вся стоимость станков, оборудования зданий и т.д.

Авансированный капитал всегда больше, чем издержки производства.

Издержки производства подобно авансированному капиталу делятся на постоянные и переменные, а также общие, средние и предельные. Анализ издержек производства должен происходить с учетом фактора времени. Отсюда издержки производства анализируются в краткосрочных и долговременных периодах.

Краткосрочный период (short-run). Этот период времени – слишком короткий, чтобы фирма смогла изменить свои постоянные ресурсы или производственные мощности.

В этом периоде постоянные ресурсы остаются неизменными, а переменные ресурсы могут измениться за счет количества переменных ресурсов – сырья и дополнительной рабочей силы вследствие удлинения рабочего дня. Таким образом, в течение краткосрочного периода фирма может изменить объем производства путем соединения изменяющегося количества переменных ресурсов с фиксированными постоянными мощностями. Таким образом, краткосрочный период – это отрезок времени, в течение которого постоянные ресурсы, или факторы, остаются неизменными, а переменные могут изменяться не только за счет цен, но и за счет количества.

Долговременный период (long-run). Этот период времени достаточно продолжительный, чтобы фирма могла успеть изменить количество всех используемых ресурсов: и постоянных, и переменных, включая размеры предприятия.

В этом периоде все ресурсы являются переменными.

Таким образом, краткосрочный период представляет собой период фиксированных мощностей, а долговременный период – период изменяющихся мощностей.

Теперь перейдем к анализу издержек производства в краткосрочном периоде.

Издержки производства в краткосрочном периоде: постоянные, переменные, общие, средние

Издержки производства в краткосрочном периоде делятся на постоянные, переменные, общие, средние и предельные.

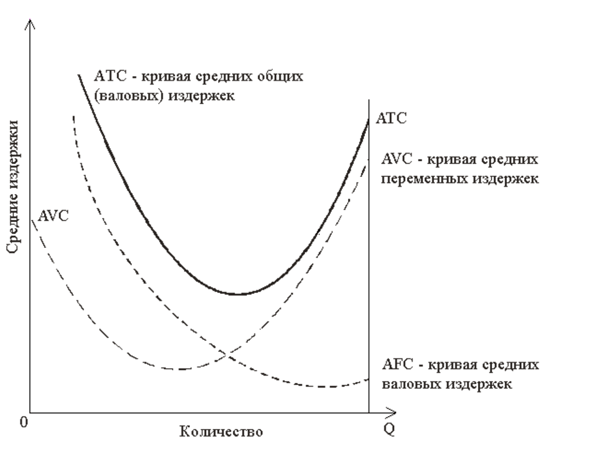
Постоянные издержки (fixed cost, FC) – издержки, которые не зависят от объема производства. Они всегда будут иметь место, даже если фирма ничего не производит. К ним относятся: аренда, отчисления на амортизацию зданий и оборудования, страховые взносы, расходы на капитальный ремонт, оплата обязательств по облигационным займам, а также жалованье высшему управленческому персоналу и т.д. Постоянные издержки остаются неизменными при всех уровнях производства, включая нулевой. Графически их можно представить в виде прямой параллельной оси абсцисс (см. рис. 15.1). Она обозначается линией FC.

Переменные (variable cost, VC) – издержки, которые зависят от объема производства. К ним относятся затраты на заработную плату, сырье, топливо, электроэнергию, транспортные услуги и тому подобные ресурсы. В отличие от постоянных переменные издержки изменяются в прямой зависимости от объема производства. Графически они изображаются в виде восходящей кривой (см. рис. 15.1), обозначаемой линией VC.

Кривая переменных издержек показывает, что с ростом выпуска продукта растут переменные издержки производства.

Различие между постоянными и переменными издержками имеет существенное значение для каждого бизнесмена. Переменными издержками предприниматель может управлять, так как их величина изменяется в течение краткосрочного периода в результате изменения объема производства. Постоянные же издержки находятся вне контроля администрации фирмы, так как они обязательны и должны быть оплачены независимо от объема производства.

Общие, или валовые, издержки (total cost, TC) – издержки в целом при данном объеме производства. Они равны сумме постоянных и переменных издержек: .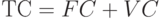

Если наложить друг на друга кривые постоянных и переменных издержек, то получим новую кривую, отражающую общие издержки (см. рис. 15.1). Она обозначается линией ТС.

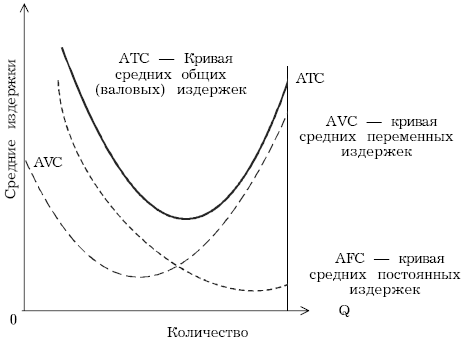
Средние общие (average total cost, АТС, иногда называют АС) – это издержки в расчете на единицу продукции, т. е. общие издержки (ТС), деленные на количество произведенной продукции .

Показатели средних общих издержек обычно используются для сравнения с ценой, которая всегда указывается в расчете на единицу продукции. Такое сравнение дает возможность определить величину прибыли, что позволяет определить тактику и стратегию фирмы в ближайшее время и на перспективу. Графически кривая средних общих (валовых) издержек изображается кривой АТС (см. рис. 15.2).

Кривая средних издержек имеет U-образную форму. Это говорит о том, что средние издержки могут быть равны рыночной цене, а могут отклоняться от нее. Фирма рентабельна или прибыльна в том случае, если рыночная цена выше средних издержек.

В экономическом анализе кроме средних общих издержек используются такие понятия, как средние постоянные и средние переменные издержки. Это подобно средним общим издержкам, постоянным и переменным издержкам в расчете на единицу продукции. Рассчитываются они следующим образом: средние постоянные издержки (AFC) равны отношению постоянных издержек (FC) к выпуску продукции . Средние переменные (AVC), по аналогии, равны отношению переменных издержек (VC) к выпуску продукции (СЗ):

Средние общие издержки – сумма средних постоянных и переменных издержек, т.е.:

, или

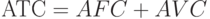
Величина средних постоянных издержек непрерывно уменьшается по мере роста объема производства, поскольку фиксированная сумма издержек распределяется на все большее и большее количество единиц продукции. Средние переменные издержки изменяются в соответствии с законом убывающей отдачи.

Важное значение для определения стратегии фирмы в экономическом анализе отводится предельным издержкам.

Предельные, или маржинальные, издержки (marginal cost, МС) – издержки, связанные с производством дополнительной единицы продукции.

МС можно определить для каждой добавочной единицы продукции путем деления изменения прироста суммы общих издержек на величину прироста выпуска продукции, т.е.:

Предельные издержки (МС) равны приросту переменных издержек (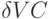) (сырья, рабочей силы), если предполагается, что постоянные издержки (FC) неизменны. Следовательно, предельные издержки есть функция от переменных издержек. В этом случае:

Таким образом, предельные издержки (иногда их называют приростными) представляют собой прирост издержек в результате производства одной дополнительной единицы продукции.

Предельные издержки показывают, во сколько обойдется фирме увеличение объема выпуска продукции на одну единицу. Графически кривая предельных издержек представляет собой восходящую линию МС, пересекающуюся в точке Б с кривой средних общих издержек АТС и точке В с кривой средних переменных издержек AVC (см. рис. 15.3). Сравнение средних переменных и предельных издержек производства – важная информация для управления фирмой, определения оптимальных размеров производства, в пределах которых фирма устойчиво получает доход.

Из рис. 15.3 видно, что кривая предельных издержек (МС) зависит от величины средних переменных издержек (AVC) и валовых средних издержек (АТС). В то же время она не зависит от средних постоянных издержек (AFC), потому что постоянные издержки FC существуют независимо от того, производится дополнительная продукция или нет.

Переменные и валовые издержки растут вместе с выпуском продукции. Скорость, с которой эти издержки увеличиваются, зависит от природы производственного процесса и, в частности, от степени, в которой производство подвержено действию закона убывающей отдачи по отношению к переменным факторам. Если труд является единственным переменным фактором, что происходит при увеличении объема выпуска продукции? Чтобы больше производить, фирма должна нанять больше рабочих. Тогда, если предельный продукт труда быстро снижается по мере увеличения трудозатрат (из-за действия закона убывающей отдачи), для ускорения выпуска продукции необходимы все большие и большие издержки. В итоге переменные и валовые издержки быстро растут одновременно с увеличением объема выпуска продукции. С другой стороны, если предельный продукт труда незначительно снижается при увеличении количества используемых трудовых ресурсов, издержки будут возрастать не столь быстро при увеличении объема выпуска продукции. Предельные и средние издержки представляют собой важные понятия. Как мы увидим в следующей главе, они решающим образом сказываются на выборе фирмой объема производства. Знание краткосрочных издержек особенно важно для фирм, действующих в условиях заметных колебаний спроса. Если фирма в настоящее время осуществляет выпуск продукции в объеме, при котором предельные издержки резко возрастают, неопределенность относительно увеличения спроса в будущем может заставить фирму внести изменения в производственный процесс и, вероятно, побудить к дополнительным затратам сегодня, чтобы избежать более высоких издержек завтра.