Как найти функцию плотности распределения онлайн – Сайт, где вы сможете решить свои вопросы

Нормальное распределение — занимает особую роль в теории вероятностей. Это наиболее общее непрерывное распределение вероятностей, часто использующееся для представления случайных величин, закон распределения которых не известен.

Функция плотности вероятности

Плотность нормального распределения выражается функцией Гаусса:
$f(x) = tfrac{1}{sigmasqrt{2pi}}; e^{ -frac{(x-mu)^2}{2sigma^2} }$

где μ — математическое ожидание,
σ — среднеквадратическое отклонение,
σ ² — дисперсия,
медиана и мода нормального распределения равны математическому ожиданию μ.

Калькулятор ниже вычисляет значения функции плотности вероятности и функции распределения в заданной точке при для нормального распределения, определяемого заданной дисперсией и математическим ожиданием:

Нормальное распределение

Точность вычисления

Знаков после запятой: 5

Значение функции распределения

График плотности вероятности

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Функция распределения

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Функция распределения

Функция распределения для нормального распределения задается формулой:
$frac12left[1 + operatorname{erf}left( frac{x-mu}{sigmasqrt{2}}right)right]$
где, erf(x) — функция ошибок (Лапласа) или интеграл вероятности, определяемый как:
$operatorname{erf}(x) = frac{2}{sqrt{pi}}intlimits_0^x e^{-t^2},mathrm dt$

Квантильная функция

Квантильная функция нормального распределения выражается через обратную функцию ошибок:

$F^{-1}(p) = mu + sigmasqrt2,operatorname{erf}^{-1}(2p - 1)$
p может принимать значения в диапазоне [0,1].

Квантильная функция стандартного нормального распределения (нормального распределения с σ =1, μ=0) упрощается до: $Phi^{-1}(p); =; sqrt2;operatorname{erf}^{-1}(2p - 1)$
Эту функцию называют пробит функцией, применяется она в различных областях, для анализа зависимости качественных переменных от множества факторов.
Калькулятор ниже вычисляет значение квантильной функции нормального распределения ( можно задать дисперсию = 1 и мат ожидание=0, чтобы получить значение пробит функции).

Квантильная функция нормального распределения

Точность вычисления

Знаков после запятой: 2

Источник

Probability Density Function – Calculator

Free Probability Density Function and Standard Normal Distribution calculation online. A random variable which has a normal distribution with a mean m=0 and a standard deviation σ=1
is referred to as Standard Normal Distribution. This calculator can be used for calculating
or creating new math problems.

Probability Density Function

Code to add this calci to your website Expand embed code Minimize embed code

Formula :
PDF of Normal Distribution = P(x) = (1/(σsqrt(2π)))e^{-(x-m)² / (2σ²)}
Standard Normal Distribution = P(x) = (1/sqrt(2π))e^{-(x² / 2)}

This tool will help you dynamically to calculate the statistical problems. Calculating Probability Density Function and Standard Normal Distribution is made easier.

Related Calculators:

Permutation And Combination Calculator
Negative Binomial Distribution
Poisson Distribution
Hypergeometric Distribution Calculator
Normal Distribution Calculator
Binomial Distribution Calculator

Источник

21:35

Найти функцию распределения, найти функцию плотности распределения, построить график

Тема занятия: на конкретном задании показать: как находить функцию плотности распределения случайной величины, если известна функция распределения, и наоборот, покажем как найти функцию распределения, если известна функция плотности распределения. А также рассмотрим вопрос: как находить математическое ожидание и дисперсию случайной величины. Найдем неизвестный параметр.

Задание № 2. Случайная величина X задана функцией распределения
$Fleft ( x right )=left{begin{matrix} 0, &xleq 1 \ frac{1}{2} left ( x^2-x right ),& 1< xleq 2\ 1, & x> 2 end{matrix}right.$
Найти плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины X. Построить графики функции и плотности распределения.

Задание №3. Дана плотность распределения

$fleft ( x right )=left{begin{matrix} frac{1}{2}, &xepsilon left [ 1,gamma right ] \ 0,& xbar{epsilon }left [ 1,gamma right ] end{matrix}right.$

Найти параметр у, математическое ожидание, дисперсию, функцию распределения случайной случайной величины X .

Задание №4. Известно, что функция распределения
$Fleft ( x right )=left{begin{matrix} 0, & x<0\ Asinlambda x,& 0leq x<1\ 1,&x>1 end{matrix}right.$
Определить в этих условиях коэффициенты, плотность вероятности математическое ожидание, дисперсию, среднеквадратическое отклонение: $A,lambda ,fleft ( x right ),Mleft ( x, right ),Dleft ( x right ),sigma$

Категория: Теория вероятности | Просмотров: 69416 | | Теги: построить график функции расп, найти параметр, найти математическое ожидание, дисперсию случайной величины, найти плотность распределения вероя | Рейтинг: 3.8/13

Источник

Плотность распределения вероятностей непрерывной случайной величины

Краткая теория
Примеры решения задач
Задачи контрольных и самостоятельных работ

Краткая теория

Ранее
непрерывная случайная величина задавалась с помощью функции распределения. Этот
способ задания не является единственным. Непрерывную случайную величину можно
также задать, используя другую функцию, которую называют плотностью
распределения или плотностью вероятности (иногда ее называют дифференциальной
функцией).

Плотностью распределения вероятностей непрерывной случайной величины

называют функцию

– первую производную от функции распределения

Из этого определения следует, что
функция распределения является первообразной для плотности распределения.

Заметим, что для описания
распределения вероятностей дискретной случайной величины плотность
распределения неприменима.

Зная плотность распределения, можно
вычислить вероятность того, что непрерывная случайная величина примет значение,
принадлежащее заданному интервалу.

Вероятность того, что непрерывная
случайная величина

примет
значение, принадлежащее интервалу

равна
определенному интегралу от плотности распределения, взятому в пределах от

до

Геометрически полученный результат
можно истолковать так: вероятность того, что непрерывная случайная величина
примет значение, принадлежащее интервалу

, равна площади криволинейной трапеции, ограниченной
осью

, кривой распределения

и прямыми

В частности, если

– четная
функция и концы интервала симметричны относительно начала координат, то:

Зная плотность распределения

можно найти
функцию распределения

по формуле:

Свойства плотности распределения

Свойство 1.

Плотность
распределения – неотрицательная функция:

Свойство 2.

Несобственный
интеграл от плотности распределения в пределах от

до

равен единице:

Смежные темы решебника:

Дискретная случайная величина
Непрерывная случайная величина
Интегральная функция распределения вероятностей

Примеры решения задач

Пример 1

Задана
плотность распределения вероятностей f(x) непрерывной случайной
величины X. Требуется:

1)
определить коэффициент A;

2) найти
функцию распределения F(x);

3)
схематично построить графики F(x) и f(x);

4) найти
математическое ожидание и дисперсию X;

5) найти
вероятность того, что X примет значение из
интервала (α,β):

α=1; β=1.7

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

1)
Постоянный параметр

найдем из
свойства плотности вероятности:

В
нашем случае эта формула имеет вид:

Получаем:

2)
Функцию распределения

найдем из
формулы:

Учитывая
свойства

, сразу можем
отметить, что:

Остается
найти выражение для

, когда

принадлежит
интервалу

Получаем:

3) Построим графики

График плотности распределения

График функции распределения

4)
Математическое ожидание находим по формуле:

Для
нашего примера:

Дисперсию
можно найти по формуле:

5)
Вероятность того, что случайная величина примет значение из интервала

Пример 2

Плотность
распределения вероятности непрерывной случайной величины равна

, x∈(0,∞). Найти нормировочный множитель C,
математическое ожидание M(X) и дисперсию D(X).

Решение

Нормировочный множитель

найдем из
свойства плотности вероятности:

В
нашем случае эта формула имеет вид:

Плотность
вероятности:

Математическое
ожидание находим по формуле:

Для
нашего примера:

Дисперсию
можно найти по формуле:

Пример 3

Непрерывная
случайная величина

имеет плотность распределения:

Найти
величину a, вероятность P(X<0) и математическое
ожидание X.

Решение

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Постоянный
параметр

найдем из
свойства плотности вероятности:

В
нашем случае эта формула имеет вид:

Плотность
вероятности имеет вид:

Вероятность:

Математическое
ожидание находим по формуле:

Для
нашего примера:

Задачи контрольных и самостоятельных работ

Задача 1

Плотность
распределения непрерывной случайной величины X имеет вид:

Найти:

а)
параметр a;

б)
функцию распределения F(x);

в)
вероятность попадания случайной величины X в интервал (6.5; 11);

г)
математическое ожидание M(X) и дисперсию D(X);

Построить
график функций f(x) и F(x).

Задача 2

Задана
функция распределения непрерывной случайной величины:

Найти и
построить график функции плотности распределения вероятностей.

Задача 3

Случайная
величина X задана функцией распределения F(x).
Найти плотность распределения вероятностей, математическое ожидание и дисперсию
случайной величины. Построить график функции
F(x).

Задача 4

Задана
плотность вероятности f(x) или функции распределения
непрерывной случайной величины X. Найти a, M[X], D[X], P(α<x<β).

α=1,β=2

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 5

Непрерывная
случайная величина

задана плотностью распределения вероятностей.

Требуется
найти:

– функцию
распределения вероятностей;

–
математическое ожидание;

–
дисперсию;

– среднее
квадратическое отклонение;

– вероятность
того, что случайная величина отклонится от своего математического ожидания не
более, чем на одну четвертую длины всего интервала возможных значений этой
величины;

–
построить графики функции распределения и плотности распределения вероятностей.

Задача 6

Случайная
величина X равномерно распределена на интервале (2;7).
Составить f(x),F(x), построить графики. Найти
M(X),D(X).

Задача 7

Случайная
величина X~N(a,σ)

a=25;
σ=4; α=13; β=30; δ=0.1.

Требуется:

–
составить функцию плотности распределения и построить ее график;

– найти
вероятность того, что случайная величина в результате испытания примет
значение, принадлежащее интервалу (α; β);

– найти
вероятность того, что абсолютная величина отклонения значений случайной
величины от ее математического ожидания не превысит δ.

Задача 8

Плотность
вероятности непрерывной случайной величины ξ задана следующим выражением:

Найти
постоянную C, функцию распределения Fξ (x), математическое
ожидание и дисперсию Dξ случайной величины ξ.

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 9

Случайная
величина X задана функцией распределения вероятностей F(x).

Требуется:

1. Найти
функцию плотности распределения f(x).

2. Найти M(X).

3. Найти
вероятность P(α<X<β)

4.
Построить графики f(x) и F(x).

α=2, β=4.5

Задача 10

Найти
функцию плотности нормально распределенной случайной величины X и
постройте ее график, зная M(X) и D(X).

M(X)=-1; D(X)=8

Задача 11

Случайная
величина X задана интегральной F(x) или дифференциальной f(x)
функцией. Требуется:

а) найти
параметр C;

б) при
заданной интегральной функции F(x) найти дифференциальную функцию f(x), а при
заданной дифференциальной функции f(x) найти интегральную функцию F(x);

в)
построить графики функций F(x) и f(x);

г) найти
математическое ожидание M(X), дисперсию D(X) и
среднее квадратическое отклонение σ(x);

д)
вычислить вероятность попадания в интервал P(a≤x≤b)

е)
определить, квантилем какого порядка является точка xp;

ж)
вычислить квантиль порядка p

a=π/4; b=π/3; xp=π/2; p=0.75

Краткая теория
Примеры решения задач
Задачи контрольных и самостоятельных работ

Источник

Нормальное распределение

Следующий калькулятор строит график плотности вероятности и функции плотности распределения для нормального распределения.

И так вспоминаем, что нормальное распределение это особенная часть теории вероятности, общее непрерывное распределение вероятностей, часто использующееся для представления случайных величин, закон распределения которых не известен.

Функция плотности вероятности

Плотность нормального распределения выражается

С помощью функции Гаусса узнаем плотность нормального распределения:

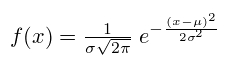
μ — математическое ожидание,

σ — среднеквадратическое отклонение,

σ ² — дисперсия,

Тут медиана и мода нормального распределения будут равны математическому ожиданию μ.

Калькулятор считает значения функции плотности вероятности и функции распределения в заданной вами точке для нормального распределения, определяемого заданной дисперсией и математическим ожиданием:

Функция распределения

Функция распределения для нормального распределения вычисляется:

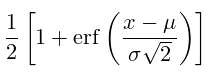
где, erf(x) – функция ошибок (Лапласа) или интеграл вероятности, определяемый как:

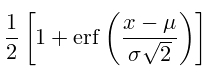
Квантильная функция

Квантильная функция нормального распределения вычисляется через обратную функцию ошибок:

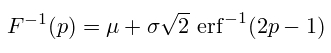
p может принимать значения в диапазоне [0,1]

Квантильная функция стандартного нормального распределения (нормального распределения с σ =1, μ=0) упрощается до: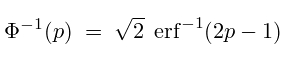

Нормальное распределение

Значение функции распределения:

График плотности вероятности:

14 декабря 2015
Статистика

Источник

Функция плотности вероятности

Нормальное распределение

Функция распределения

Квантильная функция

Квантильная функция нормального распределения

Probability Density Function – Calculator

Probability Density Function

Related Calculators:

Плотность распределения вероятностей непрерывной случайной величины

Краткая теория

Свойства плотности распределения

Примеры решения задач

Пример 1

Пример 2

Пример 3

Задачи контрольных и самостоятельных работ

Нормальное распределение

Вам также может понравиться

Как найти фм радио на андроид

Как the forest найти перья

Как найти залежи песка

Добавить комментарий Отменить ответ