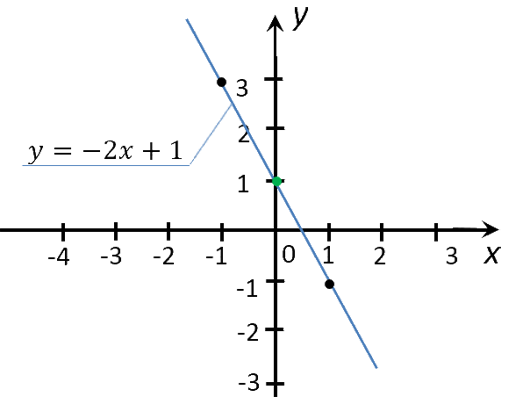
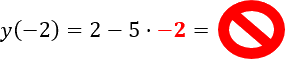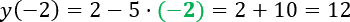Как определить a, b и c по графику параболы
Предположим, вам попался график функции (y=ax^2+bx+c) и нужно по этому графику определить коэффициенты (a), (b) и (c). В этой статье я расскажу 3 простых способа сделать это.
1 способ – ищем коэффициенты на графике
Данный способ хорош, когда координаты вершины и точка пересечения параболы с осью (y) – целые числа. Если это не так, советую использовать способ 2.
Коэффициент (a) можно найти с помощью следующих фактов:
– Если (a>0), то ветви параболы направленных вверх, если (a 1), то график вытянут вверх в (a) раз по сравнению с «базовым» графиком (у которого (a=1)). Вершина при этом остается на месте. Это наглядно видно по выделенным точкам.
Ищем 3 точки с целыми координатами, принадлежащие параболе.
Пример:
Выписываем координаты этих точек и подставляем в формулу квадратичной функции: (y=ax^2+bx+c). Получится система с тремя уравнениями.
Решаем систему.
Пример:
Вычтем из второго уравнения первое:
Подставим (9a) вместо (b):
Первое и второе уравнения совпали (это нормально для точек, симметричных относительно прямой проходящей через вершину – как точки (A) и (B) в нашем случае), но нас это не остановит – мы вычтем из второго уравнение третье:
Подставим в первое уравнение (a):
Получается квадратичная функция: (y=-x^2-9x-15).
Сразу заметим, что по графику можно сразу определить, что (c=4). Это сильно облегчит нашу систему – нам хватит 2 точек. Выберем их на параболе: (C(-1;8)), (D(1;2)) (на самом деле, если присмотреться, то можно заметить, что эти точки выделены жирно на изначальной картинке – это вам подсказка от авторов задачи).
Таким образом имеем систему:
Сложим 2 уравнения:
Подставим во второе уравнение:
Теперь найдем точки пересечения двух функций:
Теперь можно найти ординату второй точки пересечения:
3 способ – используем преобразование графиков функций
Этот способ быстрее первого и более универсальный, в частности он может пригодится и в задачах на другие функции.
Главный недостаток этого способа – вершина должна иметь целые координаты.
Сам способ базируется на следующих идеях:
График (y=-x^2) симметричен относительно оси (x) графику (y=x^2).
– Если (a>1) график (y=ax^2) получается растяжением графика (y=x^2) вдоль оси (y) в (a) раз.
– Если (a∈(0;1)) график (y=ax^2) получается сжатием графика (y=x^2) вдоль оси (y) в (a) раз.
– График (y=a(x+d)^2) получается сдвигом графика (y=ax^2) влево на (d) единиц.
– График (y=a(x-d)^2) получается сдвигом графика (y=ax^2) вправо на (d) единиц.
График (y=a(x+d)^2+e) получается переносом графика (y=a(x+d)^2) на (e) единиц вверх.
График (y=a(x+d)^2-e) получается переносом графика (y=a(x+d)^2) на (e) единиц вниз.
У вас наверно остался вопрос – как этим пользоваться? Предположим, мы видим такую параболу:
Сначала смотрим на её форму и направленность её ветвей. Видим, что форма стандартная, базовая и ветви направлены вверх, поэтому (a=1). То есть она получена перемещениями графика базовой параболы (y=x^2).
А как надо было перемещать зеленый график чтоб получить оранжевый? Надо сдвинуться вправо на пять единиц и вниз на (4).
То есть наша функция выглядит так: (y=(x-5)^2-4).
После раскрытия скобок и приведения подобных получаем искомую формулу:
Чтобы найти (f(6)), надо сначала узнать формулу функции (f(x)). Найдем её:
Парабола растянута на (2) и ветви направлены вниз, поэтому (a=-2). Иными словами, первоначальной, перемещаемой функцией является функция (y=-2x^2).
Парабола смещена на 2 клеточки вправо, поэтому (y=-2(x-2)^2).
Парабола поднята на 4 клеточки вверх, поэтому (y=-2(x-2)^2+4).
Уравнение с двумя переменными и его график. Уравнение окружности
п.1. Понятие уравнения с двумя переменными
Мы уже знакомы со многими функциями и умеем их записывать в виде формул:
y = 2x + 5 – прямая, y = 5x 2 + 2x – 1 – парабола, (mathrm) – гипербола.
Если записать такое выражение: x 2 (x + y) = 1 – y – в нём тоже есть две переменные x и y, и постоянная 1.
Для наших примеров:
F(x; y) = 2x – y + 5 = 0 – прямая
F(x; y) = 5x 2 + 2x – y – 1 = 0 – парабола
F(x; y) = (mathrm<frac1x>) – y = 0 – гипербола
F(x; y)=x 2 (x + y) + y – 1 = 0 – некоторая кривая (график – ниже).
п.2. Обобщенные правила преобразования графика уравнения
Пусть F(x; y) = 0 – исходный график некоторой функции
Симметричное отображение относительно оси OY
Симметричное отображение относительно оси OX
Центральная симметрия относительно начала координат
Параллельный перенос графика на a единиц вправо
Параллельный перенос графика на a единиц влево
Параллельный перенос графика на b единиц вниз
Параллельный перенос графика на b единиц вверх
Сжатие графика к оси OY в a раз
Сжатие графика к оси OX в b раз
F(x; by) = 0
0 Например:
Окружность с центром в точке O(2; 1) и радиусом R = 3 задаётся уравнением: $$ mathrm <(x-2)^2+(y-1)^2=9>$$
п.4. Примеры
Пример 1. Постройте график уравнения:
а) 2x + 7y – 14 = 0
Выразим y из уравнения: ( mathrm<7>=-frac<2> + 2 > ) – это прямая
б) xy + 4 = 0
Выразим y из уравнения: ( mathrm> ) – это гипербола
в) ( x+ 2) 2 + y 2 = 4
Это – уравнение окружности с центром O(–2; 0), радиусом ( mathrm=2> )
г) x 2 + 5y – 2 = 0
Выразим y из уравнения: ( mathrm<5>> ) – это парабола
Пример 2*. Постройте график уравнения:
а) 2|x| + 5y = 10
( mathrm<5>=-frac25|x|+2> )
Строим график для ( mathrm ), а затем отражаем его относительно оси OY в левую полуплоскость.
б) 3x + |y| = 6
|y| = –3x + 6
Строим график для y > 0: y = –3x + 6, а затем отражаем его относительно оси OX в нижнюю полуплоскость.
в) |x| + |y| = 2
|y| = –|x| + 2
Строим график для x > 0, y > 0: y = –x + 2, а затем отражаем его относительно осей OX и OY.
г) |x – 1| + |y – 2| = 4
Получим тот же ромб (квадрат), что и в (в), но его центр будет перенесен из начала координат в точку O(1; 2).
д) (mathrm<frac<|x-1|><2>+2|y-2|=4>)
Ромб по x растянется в 2 раза по диагонали, а по y – сожмётся в 2 раза по диагонали.
Пример 3. Постройте график уравнения:
а) x 2 + y 2 + 4x – 6y + 4 = 0
Выделим полные квадраты:
(x 2 + 4x + 4) + (y 2 – 6y + 9) – 9 = 0
(x + 2) 2 + (y – 3) 2 = 3 2 – уравнение окружности с центром (–2; 3), радиусом 3.
Касательная к графику функции в точке. Уравнение касательной. Геометрический смысл производной
Статья дает подробное разъяснение определений, геометрического смысла производной с графическими обозначениями. Будет рассмотрено уравнение касательной прямой с приведением примеров, найдено уравнения касательной к кривым 2 порядка.
Определения и понятия
Угол наклона прямой y = k x + b называется угол α , который отсчитывается от положительного направления оси о х к прямой y = k x + b в положительном направлении.
На рисунке направление о х обозначается при помощи зеленой стрелки и в виде зеленой дуги, а угол наклона при помощи красной дуги. Синяя линия относится к прямой.
Угловой коэффициент прямой y = k x + b называют числовым коэффициентом k .
Угловой коэффициент равняется тангенсу наклона прямой, иначе говоря k = t g α .
- Угол наклона прямой равняется 0 только при параллельности о х и угловом коэффициенте, равному нулю, потому как тангенс нуля равен 0 . Значит, вид уравнения будет y = b .
- Если угол наклона прямой y = k x + b острый, тогда выполняются условия 0 α π 2 или 0 ° α 90 ° . Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию t g α > 0 , причем имеется возрастание графика.
- Если α = π 2 , тогда расположение прямой перпендикулярно о х . Равенство задается при помощи равенства x = c со значением с , являющимся действительным числом.
- Если угол наклона прямой y = k x + b тупой, то соответствует условиям π 2 α π или 90 ° α 180 ° , значение углового коэффициента k принимает отрицательное значение, а график убывает.
Определение 3
Секущей называют прямую, которая проходит через 2 точки функции f ( x ) . Иначе говоря, секущая – это прямая, которая проводится через любые две точки графика заданной функции.
По рисунку видно, что А В является секущей, а f ( x ) – черная кривая, α – красная дуга, означающая угол наклона секущей.
Когда угловой коэффициент прямой равняется тангенсу угла наклона, то видно, что тангенс из прямоугольного треугольника А В С можно найти по отношению противолежащего катета к прилежащему.
Получаем формулу для нахождения секущей вида:
k = t g α = B C A C = f ( x B ) – f x A x B – x A , где абсциссами точек А и В являются значения x A , x B , а f ( x A ) , f ( x B ) – это значения функции в этих точках.
Очевидно, что угловой коэффициент секущей определен при помощи равенства k = f ( x B ) – f ( x A ) x B – x A или k = f ( x A ) – f ( x B ) x A – x B , причем уравнение необходимо записать как y = f ( x B ) – f ( x A ) x B – x A · x – x A + f ( x A ) или
y = f ( x A ) – f ( x B ) x A – x B · x – x B + f ( x B ) .
Секущая делит график визуально на 3 части: слева от точки А , от А до В , справа от В . На располагаемом ниже рисунке видно, что имеются три секущие, которые считаются совпадающими, то есть задаются при помощи аналогичного уравнения.
По определению видно, что прямая и ее секущая в данном случае совпадают.
Секущая может множественно раз пересекать график заданной функции. Если имеется уравнение вида у = 0 для секущей, тогда количество точек пересечения с синусоидой бесконечно.
Касательная к графику функции f ( x ) в точке x 0 ; f ( x 0 ) называется прямая, проходящая через заданную точку x 0 ; f ( x 0 ) , с наличием отрезка, который имеет множество значений х , близких к x 0 .
Рассмотрим подробно на ниже приведенном примере. Тогда видно, что прямая, заданная функцией y = x + 1 , считается касательной к y = 2 x в точке с координатами ( 1 ; 2 ) . Для наглядности, необходимо рассмотреть графики с приближенными к ( 1 ; 2 ) значениями. Функция y = 2 x обозначена черным цветом, синяя линия – касательная, красная точка – точка пересечения.
Очевидно, что y = 2 x сливается с прямой у = х + 1 .
Для определения касательной следует рассмотреть поведение касательной А В при бесконечном приближении точки В к точке А . Для наглядности приведем рисунок.
Секущая А В , обозначенная при помощи синей линии, стремится к положению самой касательной, а угол наклона секущей α начнет стремиться к углу наклона самой касательной α x .
Касательной к графику функции y = f ( x ) в точке А считается предельное положение секущей А В при В стремящейся к А , то есть B → A .
Теперь перейдем к рассмотрению геометрического смысла производной функции в точке.
Геометрический смысл производной функции в точке
Перейдем к рассмотрению секущей А В для функции f ( x ) , где А и В с координатами x 0 , f ( x 0 ) и x 0 + ∆ x , f ( x 0 + ∆ x ) , а ∆ x обозначаем как приращение аргумента. Теперь функция примет вид ∆ y = ∆ f ( x ) = f ( x 0 + ∆ x ) – f ( ∆ x ) . Для наглядности приведем в пример рисунок.
Рассмотрим полученный прямоугольный треугольник А В С . Используем определение тангенса для решения, то есть получим отношение ∆ y ∆ x = t g α . Из определения касательной следует, что lim ∆ x → 0 ∆ y ∆ x = t g α x . По правилу производной в точке имеем, что производную f ( x ) в точке x 0 называют пределом отношений приращения функции к приращению аргумента, где ∆ x → 0 , тогда обозначим как f ( x 0 ) = lim ∆ x → 0 ∆ y ∆ x .
Отсюда следует, что f ‘ ( x 0 ) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x , где k x обозначают в качестве углового коэффициента касательной.
То есть получаем, что f ’ ( x ) может существовать в точке x 0 причем как и касательная к заданному графику функции в точке касания равной x 0 , f 0 ( x 0 ) , где значение углового коэффициента касательной в точке равняется производной в точке x 0 . Тогда получаем, что k x = f ‘ ( x 0 ) .
Геометрический смысл производной функции в точке в том, что дается понятие существования касательной к графику в этой же точке.
Уравнение касательной прямой
Чтобы записать уравнение любой прямой на плоскости, необходимо иметь угловой коэффициент с точкой, через которую она проходит. Его обозначение принимается как x 0 при пересечении.
Уравнение касательной к графику функции y = f ( x ) в точке x 0 , f 0 ( x 0 ) принимает вид y = f ‘ ( x 0 ) · x – x 0 + f ( x 0 ) .
Имеется в виду, что конечным значением производной f ‘ ( x 0 ) можно определить положение касательной, то есть вертикально при условии lim x → x 0 + 0 f ‘ ( x ) = ∞ и lim x → x 0 – 0 f ‘ ( x ) = ∞ или отсутствие вовсе при условии lim x → x 0 + 0 f ‘ ( x ) ≠ lim x → x 0 – 0 f ‘ ( x ) .
Расположение касательной зависит от значения ее углового коэффициента k x = f ‘ ( x 0 ) . При параллельности к оси о х получаем, что k k = 0 , при параллельности к о у – k x = ∞ , причем вид уравнения касательной x = x 0 возрастает при k x > 0 , убывает при k x 0 .
Произвести составление уравнения касательной к графику функции y = e x + 1 + x 3 3 – 6 – 3 3 x – 17 – 3 3 в точке с координатами ( 1 ; 3 ) с определением угла наклона.
Решение
По условию имеем, что функция определяется для всех действительных чисел. Получаем, что точка с координатами, заданными по условию, ( 1 ; 3 ) является точкой касания, тогда x 0 = – 1 , f ( x 0 ) = – 3 .
Необходимо найти производную в точке со значением – 1 . Получаем, что
y ‘ = e x + 1 + x 3 3 – 6 – 3 3 x – 17 – 3 3 ‘ = = e x + 1 ‘ + x 3 3 ‘ – 6 – 3 3 x ‘ – 17 – 3 3 ‘ = e x + 1 + x 2 – 6 – 3 3 y ‘ ( x 0 ) = y ‘ ( – 1 ) = e – 1 + 1 + – 1 2 – 6 – 3 3 = 3 3
Значение f ’ ( x ) в точке касания является угловым коэффициентом касательной, который равняется тангенсу наклона.
Тогда k x = t g α x = y ‘ ( x 0 ) = 3 3
Отсюда следует, что α x = a r c t g 3 3 = π 6
Ответ: уравнение касательной приобретает вид
y = f ‘ ( x 0 ) · x – x 0 + f ( x 0 ) y = 3 3 ( x + 1 ) – 3 y = 3 3 x – 9 – 3 3
Для наглядности приведем пример в графической иллюстрации.
Черный цвет используется для графика исходной функции, синий цвет – изображение касательной, красная точка – точка касания. Рисунок, располагаемый справа, показывает в увеличенном виде.
Выяснить наличие существования касательной к графику заданной функции
y = 3 · x – 1 5 + 1 в точке с координатами ( 1 ; 1 ) . Составить уравнение и определить угол наклона.
Решение
По условию имеем, что областью определения заданной функции считается множество всех действительных чисел.
Перейдем к нахождению производной
y ‘ = 3 · x – 1 5 + 1 ‘ = 3 · 1 5 · ( x – 1 ) 1 5 – 1 = 3 5 · 1 ( x – 1 ) 4 5
Если x 0 = 1 , тогда f ’ ( x ) не определена, но пределы записываются как lim x → 1 + 0 3 5 · 1 ( x – 1 ) 4 5 = 3 5 · 1 ( + 0 ) 4 5 = 3 5 · 1 + 0 = + ∞ и lim x → 1 – 0 3 5 · 1 ( x – 1 ) 4 5 = 3 5 · 1 ( – 0 ) 4 5 = 3 5 · 1 + 0 = + ∞ , что означает существование вертикальной касательной в точке ( 1 ; 1 ) .
Ответ: уравнение примет вид х = 1 , где угол наклона будет равен π 2 .
Для наглядности изобразим графически.
Найти точки графика функции y = 1 15 x + 2 3 – 4 5 x 2 – 16 5 x – 26 5 + 3 x + 2 , где
- Касательная не существует;
- Касательная располагается параллельно о х ;
- Касательная параллельна прямой y = 8 5 x + 4 .
Решение
Необходимо обратить внимание на область определения. По условию имеем, что функция определена на множестве всех действительных чисел. Раскрываем модуль и решаем систему с промежутками x ∈ – ∞ ; 2 и [ – 2 ; + ∞ ) . Получаем, что
y = – 1 15 x 3 + 18 x 2 + 105 x + 176 , x ∈ – ∞ ; – 2 1 15 x 3 – 6 x 2 + 9 x + 12 , x ∈ [ – 2 ; + ∞ )
Необходимо продифференцировать функцию. Имеем, что
y ‘ = – 1 15 x 3 + 18 x 2 + 105 x + 176 ‘ , x ∈ – ∞ ; – 2 1 15 x 3 – 6 x 2 + 9 x + 12 ‘ , x ∈ [ – 2 ; + ∞ ) ⇔ y ‘ = – 1 5 ( x 2 + 12 x + 35 ) , x ∈ – ∞ ; – 2 1 5 x 2 – 4 x + 3 , x ∈ [ – 2 ; + ∞ )
Когда х = – 2 , тогда производная не существует, потому что односторонние пределы не равны в этой точке:
lim x → – 2 – 0 y ‘ ( x ) = lim x → – 2 – 0 – 1 5 ( x 2 + 12 x + 35 = – 1 5 ( – 2 ) 2 + 12 ( – 2 ) + 35 = – 3 lim x → – 2 + 0 y ‘ ( x ) = lim x → – 2 + 0 1 5 ( x 2 – 4 x + 3 ) = 1 5 – 2 2 – 4 – 2 + 3 = 3
Вычисляем значение функции в точке х = – 2 , где получаем, что
- y ( – 2 ) = 1 15 – 2 + 2 3 – 4 5 ( – 2 ) 2 – 16 5 ( – 2 ) – 26 5 + 3 – 2 + 2 = – 2 , то есть касательная в точке ( – 2 ; – 2 ) не будет существовать.
- Касательная параллельна о х , когда угловой коэффициент равняется нулю. Тогда k x = t g α x = f ‘ ( x 0 ) . То есть необходимо найти значения таких х , когда производная функции обращает ее в ноль. То есть значения f ’ ( x ) и будут являться точками касания, где касательная является параллельной о х .
Когда x ∈ – ∞ ; – 2 , тогда – 1 5 ( x 2 + 12 x + 35 ) = 0 , а при x ∈ ( – 2 ; + ∞ ) получаем 1 5 ( x 2 – 4 x + 3 ) = 0 .
– 1 5 ( x 2 + 12 x + 35 ) = 0 D = 12 2 – 4 · 35 = 144 – 140 = 4 x 1 = – 12 + 4 2 = – 5 ∈ – ∞ ; – 2 x 2 = – 12 – 4 2 = – 7 ∈ – ∞ ; – 2 1 5 ( x 2 – 4 x + 3 ) = 0 D = 4 2 – 4 · 3 = 4 x 3 = 4 – 4 2 = 1 ∈ – 2 ; + ∞ x 4 = 4 + 4 2 = 3 ∈ – 2 ; + ∞
Вычисляем соответствующие значения функции
y 1 = y – 5 = 1 15 – 5 + 2 3 – 4 5 – 5 2 – 16 5 – 5 – 26 5 + 3 – 5 + 2 = 8 5 y 2 = y ( – 7 ) = 1 15 – 7 + 2 3 – 4 5 ( – 7 ) 2 – 16 5 – 7 – 26 5 + 3 – 7 + 2 = 4 3 y 3 = y ( 1 ) = 1 15 1 + 2 3 – 4 5 · 1 2 – 16 5 · 1 – 26 5 + 3 1 + 2 = 8 5 y 4 = y ( 3 ) = 1 15 3 + 2 3 – 4 5 · 3 2 – 16 5 · 3 – 26 5 + 3 3 + 2 = 4 3
Отсюда – 5 ; 8 5 , – 4 ; 4 3 , 1 ; 8 5 , 3 ; 4 3 считаются искомыми точками графика функции.
Рассмотрим графическое изображение решения.
Черная линия – график функции, красные точки – точки касания.
- Когда прямые располагаются параллельно, то угловые коэффициенты равны. Тогда необходимо заняться поиском точек графика функции, где угловой коэффициент будет равняться значению 8 5 . Для этого нужно решить уравнение вида y ‘ ( x ) = 8 5 . Тогда, если x ∈ – ∞ ; – 2 , получаем, что – 1 5 ( x 2 + 12 x + 35 ) = 8 5 , а если x ∈ ( – 2 ; + ∞ ) , тогда 1 5 ( x 2 – 4 x + 3 ) = 8 5 .
Первое уравнение не имеет корней, так как дискриминант меньше нуля. Запишем, что
– 1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 – 4 · 43 = – 28 0
Другое уравнение имеет два действительных корня, тогда
1 5 ( x 2 – 4 x + 3 ) = 8 5 x 2 – 4 x – 5 = 0 D = 4 2 – 4 · ( – 5 ) = 36 x 1 = 4 – 36 2 = – 1 ∈ – 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ – 2 ; + ∞
Перейдем к нахождению значений функции. Получаем, что
y 1 = y ( – 1 ) = 1 15 – 1 + 2 3 – 4 5 ( – 1 ) 2 – 16 5 ( – 1 ) – 26 5 + 3 – 1 + 2 = 4 15 y 2 = y ( 5 ) = 1 15 5 + 2 3 – 4 5 · 5 2 – 16 5 · 5 – 26 5 + 3 5 + 2 = 8 3
Точки со значениями – 1 ; 4 15 , 5 ; 8 3 являются точками, в которых касательные параллельны прямой y = 8 5 x + 4 .
Ответ: черная линия – график функции, красная линия – график y = 8 5 x + 4 , синяя линия – касательные в точках – 1 ; 4 15 , 5 ; 8 3 .
Возможно существование бесконечного количества касательных для заданных функций.
Написать уравнения всех имеющихся касательных функции y = 3 cos 3 2 x – π 4 – 1 3 , которые располагаются перпендикулярно прямой y = – 2 x + 1 2 .
Решение
Для составления уравнения касательной необходимо найти коэффициент и координаты точки касания, исходя из условия перпендикулярности прямых. Определение звучит так: произведение угловых коэффициентов, которые перпендикулярны прямым, равняется – 1 , то есть записывается как k x · k ⊥ = – 1 . Из условия имеем, что угловой коэффициент располагается перпендикулярно прямой и равняется k ⊥ = – 2 , тогда k x = – 1 k ⊥ = – 1 – 2 = 1 2 .
Теперь необходимо найти координаты точек касания. Нужно найти х , после чего его значение для заданной функции. Отметим, что из геометрического смысла производной в точке
x 0 получаем, что k x = y ‘ ( x 0 ) . Из данного равенства найдем значения х для точек касания.
y ‘ ( x 0 ) = 3 cos 3 2 x 0 – π 4 – 1 3 ‘ = 3 · – sin 3 2 x 0 – π 4 · 3 2 x 0 – π 4 ‘ = = – 3 · sin 3 2 x 0 – π 4 · 3 2 = – 9 2 · sin 3 2 x 0 – π 4 ⇒ k x = y ‘ ( x 0 ) ⇔ – 9 2 · sin 3 2 x 0 – π 4 = 1 2 ⇒ sin 3 2 x 0 – π 4 = – 1 9
Это тригонометрическое уравнение будет использовано для вычисления ординат точек касания.
3 2 x 0 – π 4 = a r c sin – 1 9 + 2 πk или 3 2 x 0 – π 4 = π – a r c sin – 1 9 + 2 πk
3 2 x 0 – π 4 = – a r c sin 1 9 + 2 πk или 3 2 x 0 – π 4 = π + a r c sin 1 9 + 2 πk
x 0 = 2 3 π 4 – a r c sin 1 9 + 2 πk или x 0 = 2 3 5 π 4 + a r c sin 1 9 + 2 πk , k ∈ Z
Z – множество целых чисел.
Найдены х точек касания. Теперь необходимо перейти к поиску значений у :
y 0 = 3 cos 3 2 x 0 – π 4 – 1 3
y 0 = 3 · 1 – sin 2 3 2 x 0 – π 4 – 1 3 или y 0 = 3 · – 1 – sin 2 3 2 x 0 – π 4 – 1 3
y 0 = 3 · 1 – – 1 9 2 – 1 3 или y 0 = 3 · – 1 – – 1 9 2 – 1 3
y 0 = 4 5 – 1 3 или y 0 = – 4 5 + 1 3
Отсюда получаем, что 2 3 π 4 – a r c sin 1 9 + 2 πk ; 4 5 – 1 3 , 2 3 5 π 4 + a r c sin 1 9 + 2 πk ; – 4 5 + 1 3 являются точками касания.
Ответ: необходимы уравнения запишутся как
y = 1 2 x – 2 3 π 4 – a r c sin 1 9 + 2 πk + 4 5 – 1 3 , y = 1 2 x – 2 3 5 π 4 + a r c sin 1 9 + 2 πk – 4 5 + 1 3 , k ∈ Z
Для наглядного изображения рассмотрим функцию и касательную на координатной прямой.
Рисунок показывает, что расположение функции идет на промежутке [ – 10 ; 10 ] , где черная прямя – график функции, синие линии – касательные, которые располагаются перпендикулярно заданной прямой вида y = – 2 x + 1 2 . Красные точки – это точки касания.
Касательная к окружности, эллипсу, гиперболе, параболе
Канонические уравнения кривых 2 порядка не являются однозначными функциями. Уравнения касательных для них составляются по известным схемам.
Касательная к окружности
Для задания окружности с центром в точке x c e n t e r ; y c e n t e r и радиусом R применяется формула x – x c e n t e r 2 + y – y c e n t e r 2 = R 2 .
Данное равенство может быть записано как объединение двух функций:
y = R 2 – x – x c e n t e r 2 + y c e n t e r y = – R 2 – x – x c e n t e r 2 + y c e n t e r
Первая функция располагается вверху, а вторая внизу, как показано на рисунке.
Для составления уравнения окружности в точке x 0 ; y 0 , которая располагается в верхней или нижней полуокружности, следует найти уравнение графика функции вида y = R 2 – x – x c e n t e r 2 + y c e n t e r или y = – R 2 – x – x c e n t e r 2 + y c e n t e r в указанной точке.
Когда в точках x c e n t e r ; y c e n t e r + R и x c e n t e r ; y c e n t e r – R касательные могут быть заданы уравнениями y = y c e n t e r + R и y = y c e n t e r – R , а в точках x c e n t e r + R ; y c e n t e r и
x c e n t e r – R ; y c e n t e r будут являться параллельными о у , тогда получим уравнения вида x = x c e n t e r + R и x = x c e n t e r – R .
Касательная к эллипсу
Когда эллипс имеет центр в точке x c e n t e r ; y c e n t e r с полуосями a и b , тогда он может быть задан при помощи уравнения x – x c e n t e r 2 a 2 + y – y c e n t e r 2 b 2 = 1 .
Эллипс и окружность могут быть обозначаться при помощи объединения двух функций, а именно: верхнего и нижнего полуэллипса. Тогда получаем, что
y = b a · a 2 – ( x – x c e n t e r ) 2 + y c e n t e r y = – b a · a 2 – ( x – x c e n t e r ) 2 + y c e n t e r
Если касательные располагаются на вершинах эллипса, тогда они параллельны о х или о у . Ниже для наглядности рассмотрим рисунок.
Написать уравнение касательной к эллипсу x – 3 2 4 + y – 5 2 25 = 1 в точках со значениями x равного х = 2 .
Решение
Необходимо найти точки касания, которые соответствуют значению х = 2 . Производим подстановку в имеющееся уравнение эллипса и получаем, что
x – 3 2 4 x = 2 + y – 5 2 25 = 1 1 4 + y – 5 2 25 = 1 ⇒ y – 5 2 = 3 4 · 25 ⇒ y = ± 5 3 2 + 5
Тогда 2 ; 5 3 2 + 5 и 2 ; – 5 3 2 + 5 являются точками касания, которые принадлежат верхнему и нижнему полуэллипсу.
Перейдем к нахождению и разрешению уравнения эллипса относительно y . Получим, что
x – 3 2 4 + y – 5 2 25 = 1 y – 5 2 25 = 1 – x – 3 2 4 ( y – 5 ) 2 = 25 · 1 – x – 3 2 4 y – 5 = ± 5 · 1 – x – 3 2 4 y = 5 ± 5 2 4 – x – 3 2
Очевидно, что верхний полуэллипс задается с помощью функции вида y = 5 + 5 2 4 – x – 3 2 , а нижний y = 5 – 5 2 4 – x – 3 2 .
Применим стандартный алгоритм для того, чтобы составить уравнение касательной к графику функции в точке. Запишем, что уравнение для первой касательной в точке 2 ; 5 3 2 + 5 будет иметь вид
y ‘ = 5 + 5 2 4 – x – 3 2 ‘ = 5 2 · 1 2 4 – ( x – 3 ) 2 · 4 – ( x – 3 ) 2 ‘ = = – 5 2 · x – 3 4 – ( x – 3 ) 2 ⇒ y ‘ ( x 0 ) = y ‘ ( 2 ) = – 5 2 · 2 – 3 4 – ( 2 – 3 ) 2 = 5 2 3 ⇒ y = y ‘ ( x 0 ) · x – x 0 + y 0 ⇔ y = 5 2 3 ( x – 2 ) + 5 3 2 + 5
Получаем, что уравнение второй касательной со значением в точке
2 ; – 5 3 2 + 5 принимает вид
y ‘ = 5 – 5 2 4 – ( x – 3 ) 2 ‘ = – 5 2 · 1 2 4 – ( x – 3 ) 2 · 4 – ( x – 3 ) 2 ‘ = = 5 2 · x – 3 4 – ( x – 3 ) 2 ⇒ y ‘ ( x 0 ) = y ‘ ( 2 ) = 5 2 · 2 – 3 4 – ( 2 – 3 ) 2 = – 5 2 3 ⇒ y = y ‘ ( x 0 ) · x – x 0 + y 0 ⇔ y = – 5 2 3 ( x – 2 ) – 5 3 2 + 5
Графически касательные обозначаются так:
Касательная к гиперболе
Когда гипербола имеет центр в точке x c e n t e r ; y c e n t e r и вершины x c e n t e r + α ; y c e n t e r и x c e n t e r – α ; y c e n t e r , имеет место задание неравенства x – x c e n t e r 2 α 2 – y – y c e n t e r 2 b 2 = 1 , если с вершинами x c e n t e r ; y c e n t e r + b и x c e n t e r ; y c e n t e r – b , тогда задается при помощи неравенства x – x c e n t e r 2 α 2 – y – y c e n t e r 2 b 2 = – 1 .
Гипербола может быть представлена в виде двух объединенных функций вида
y = b a · ( x – x c e n t e r ) 2 – a 2 + y c e n t e r y = – b a · ( x – x c e n t e r ) 2 – a 2 + y c e n t e r или y = b a · ( x – x c e n t e r ) 2 + a 2 + y c e n t e r y = – b a · ( x – x c e n t e r ) 2 + a 2 + y c e n t e r
В первом случае имеем, что касательные параллельны о у , а во втором параллельны о х .
Отсюда следует, что для того, чтобы найти уравнение касательной к гиперболе, необходимо выяснить, какой функции принадлежит точка касания. Чтобы определить это, необходимо произвести подстановку в уравнения и проверить их на тождественность.
Составить уравнение касательной к гиперболе x – 3 2 4 – y + 3 2 9 = 1 в точке 7 ; – 3 3 – 3 .
Решение
Необходимо преобразовать запись решения нахождения гиперболы при помощи 2 функций. Получим, что
x – 3 2 4 – y + 3 2 9 = 1 ⇒ y + 3 2 9 = x – 3 2 4 – 1 ⇒ y + 3 2 = 9 · x – 3 2 4 – 1 ⇒ y + 3 = 3 2 · x – 3 2 – 4 и л и y + 3 = – 3 2 · x – 3 2 – 4 ⇒ y = 3 2 · x – 3 2 – 4 – 3 y = – 3 2 · x – 3 2 – 4 – 3
Необходимо выявить, к какой функции принадлежит заданная точка с координатами 7 ; – 3 3 – 3 .
Очевидно, что для проверки первой функции необходимо y ( 7 ) = 3 2 · ( 7 – 3 ) 2 – 4 – 3 = 3 3 – 3 ≠ – 3 3 – 3 , тогда точка графику не принадлежит, так как равенство не выполняется.
Для второй функции имеем, что y ( 7 ) = – 3 2 · ( 7 – 3 ) 2 – 4 – 3 = – 3 3 – 3 ≠ – 3 3 – 3 , значит, точка принадлежит заданному графику. Отсюда следует найти угловой коэффициент.
y ‘ = – 3 2 · ( x – 3 ) 2 – 4 – 3 ‘ = – 3 2 · x – 3 ( x – 3 ) 2 – 4 ⇒ k x = y ‘ ( x 0 ) = – 3 2 · x 0 – 3 x 0 – 3 2 – 4 x 0 = 7 = – 3 2 · 7 – 3 7 – 3 2 – 4 = – 3
Ответ: уравнение касательной можно представить как
y = – 3 · x – 7 – 3 3 – 3 = – 3 · x + 4 3 – 3
Наглядно изображается так:
Касательная к параболе
Чтобы составить уравнение касательной к параболе y = a x 2 + b x + c в точке x 0 , y ( x 0 ) , необходимо использовать стандартный алгоритм, тогда уравнение примет вид y = y ‘ ( x 0 ) · x – x 0 + y ( x 0 ) . Такая касательная в вершине параллельна о х .
Следует задать параболу x = a y 2 + b y + c как объединение двух функций. Поэтому нужно разрешить уравнение относительно у . Получаем, что
x = a y 2 + b y + c ⇔ a y 2 + b y + c – x = 0 D = b 2 – 4 a ( c – x ) y = – b + b 2 – 4 a ( c – x ) 2 a y = – b – b 2 – 4 a ( c – x ) 2 a
Графически изобразим как:
Для выяснения принадлежности точки x 0 , y ( x 0 ) функции, нежно действовать по стандартному алгоритму. Такая касательная будет параллельна о у относительно параболы.
Написать уравнение касательной к графику x – 2 y 2 – 5 y + 3 , когда имеем угол наклона касательной 150 ° .
Решение
Начинаем решение с представления параболы в качестве двух функций. Получим, что
– 2 y 2 – 5 y + 3 – x = 0 D = ( – 5 ) 2 – 4 · ( – 2 ) · ( 3 – x ) = 49 – 8 x y = 5 + 49 – 8 x – 4 y = 5 – 49 – 8 x – 4
Значение углового коэффициента равняется значению производной в точке x 0 этой функции и равняется тангенсу угла наклона.
k x = y ‘ ( x 0 ) = t g α x = t g 150 ° = – 1 3
Отсюда определим значение х для точек касания.
Первая функция запишется как
y ‘ = 5 + 49 – 8 x – 4 ‘ = 1 49 – 8 x ⇒ y ‘ ( x 0 ) = 1 49 – 8 x 0 = – 1 3 ⇔ 49 – 8 x 0 = – 3
Очевидно, что действительных корней нет, так как получили отрицательное значение. Делаем вывод, что касательной с углом 150 ° для такой функции не существует.
Вторая функция запишется как
y ‘ = 5 – 49 – 8 x – 4 ‘ = – 1 49 – 8 x ⇒ y ‘ ( x 0 ) = – 1 49 – 8 x 0 = – 1 3 ⇔ 49 – 8 x 0 = – 3 x 0 = 23 4 ⇒ y ( x 0 ) = 5 – 49 – 8 · 23 4 – 4 = – 5 + 3 4
Имеем, что точки касания – 23 4 ; – 5 + 3 4 .
Ответ: уравнение касательной принимает вид
[spoiler title=”источники:”]
http://reshator.com/sprav/algebra/9-klass/uravnenie-s-dvumya-peremennymi-i-ego-grafik-uravnenie-okruzhnosti/
http://zaochnik.com/spravochnik/matematika/proizvodnye/kasatelnaja-k-grafiku-funktsii-v-tochke/
[/spoiler]
Как найти функцию по ее графику
Еще в школе мы подробно изучаем функции и строим их графики. Однако читать график функции и находить ее вид по готовому чертежу, нас, к сожалению, практически не учат. На самом деле, это совсем не сложно, если помнить несколько основных видов функций.Задача описания свойств функции по ее графику часто возникает при экспериментальных исследованиях. По графику можно определить промежутки возрастания и убывания функции, разрывы и экстремумы, а также можно видеть асимптоты.

Инструкция
Если графиком является прямая линия, проходящая через начало координат и образующая с осью ОX угол α (угол наклона прямой к положительной полуоси ОХ). Функция, описывающая эту прямую, будет иметь вид y = kx. Коэффициент пропорциональности k равен tg α. Если прямая проходит через 2-ю и 4-ю координатные четверти, то k < 0, и функция является убывающей, если через 1-ю и 3-ю, то k > 0 и функция возрастает.Пусть график представляет собой прямую линию, располагающуюся различным образом относительно осей координат. Это линейная функция, и она имеет вид y = kx + b, где переменные x и y стоят в первой степени, а k и b могут принимать как положительные, так и отрицательные значения или равны нулю. Прямая параллельна прямой y = kx и отсекает на оси ординат |b| единиц. Если прямая параллельна оси абсцисс, то k = 0, если оси ординат, то уравнение имеет вид x = const.
Кривая, состоящая из двух ветвей, располагающихся в разных четвертях и симметричных относительно начала координат, называется гиперболой. Этот график выражает обратную зависимость переменной y от x и описывается уравнением y = k/x. Здесь k ≠ 0 – коэффициент обратной пропорциональности. При этом если k > 0, функция убывает; если же k < 0 – функция возрастает. Таким образом, областью определения функции является вся числовая прямая, кроме x = 0. Ветви гиперболы приближаются к осям координат как к своим асимптотам. С уменьшением |k| ветки гиперболы все больше «вдавливаются» в координатные углы.
Квадратичная функция имеет вид y = ax2 + bx + с, где a, b и c – величины постоянные и a 0. При выполнении условия b = с = 0, уравнение функции выглядит, как y = ax2 (простейший случай квадратичной функции), а ее график является параболой, проходящей через начало координат. График функции y = ax2 + bx + с имеет ту же форму, что и простейший случай функции, однако ее вершина (точка пересечения параболы с осью OY) лежит не в начале координат.
Параболой является также график степенной функции, выраженной уравнением y = xⁿ, если n – любое четное число. Если n – любое нечетное число, график такой степенной функции будет иметь вид кубической параболы.
В случае, если n – любое отрицательное число, уравнение функции приобретает вид. Графиком функции при нечетном n будет гипербола, а при четном n их ветви будут симметричны относительно оси ОУ.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Предположим, вам попался график функции (y=ax^2+bx+c) и нужно по этому графику определить коэффициенты (a), (b) и (c). В этой статье я расскажу 3 простых способа сделать это.
1 способ – ищем коэффициенты на графике
Данный способ хорош, когда координаты вершины и точка пересечения параболы с осью (y) – целые числа. Если это не так, советую использовать способ 2.
-
Коэффициент (a) можно найти с помощью следующих фактов:
– Если (a>0), то ветви параболы направленных вверх, если (a<0), то ветви параболы направлены вниз.
– Если (a>1), то график вытянут вверх в (a) раз по сравнению с «базовым» графиком (у которого (a=1)). Вершина при этом остается на месте. Это наглядно видно по выделенным точкам.
– Аналогично с (a<-1), только график вытянут вниз.
– Если (a∈(0;1)), то график сжат в (a) раз (по сравнению с «базовым» графиком с (a=1)). Вершина при этом остается на месте.
– Аналогично (a∈(-1;0)), только ветви направлены вниз.
-
Парабола пересекает ось y в точке (c).
-
(b) напрямую по графику не видно, но его можно посчитать с помощью (x_в) – абсциссы (икса) вершины параболы:
(x_в=-frac{b}{2a})
(b=-x_вcdot 2a)
Пример (ЕГЭ):

Решение:
Во-первых, надо разобраться, где тут (f(x)), а где (g(x)). По коэффициенту (c) видно, что (f(x)) это функция, которая лежит ниже – именно она пересекает ось игрек в точке (4).

Значит нужно найти коэффициенты у параболы, которая лежит повыше.
Коэффициент (c) у неё равен (1).
Ветви параболы направлены вниз – значит (a<0). При этом форма этой параболы стандартная, базовая, значит (a=-1).

Найдем (b). (x_в=-2), (a=-1).
(x_в=-frac{b}{2a})
(-2=-frac{b}{-2})
(b=-4)
Получается (g(x)=-x^2-4x+1). Теперь найдем в каких точках функции пересекаются:
(-x^2-4x+1=-2x^2-2x+4)
(-x^2-4x+1+2x^2+2x-4=0)
(x^2-2x-3=0)
(D=4+4cdot 3=16=4^2)
(x_1=frac{2-4}{2}=-1); (x_2=frac{2+4}{2}=3).
Ответ: (3).
2 способ – находим формулу по точкам
Это самый надежный способ, потому что его можно применить практически в любой ситуации, но и самый не интересный, потому что думать тут особо не надо, только уметь решать системы линейных уравнений. Алгоритм прост:
-
Ищем 3 точки с целыми координатами, принадлежащие параболе.
Пример: -
Выписываем координаты этих точек и подставляем в формулу квадратичной функции: (y=ax^2+bx+c). Получится система с тремя уравнениями.
Пример: (A(-4;5)), (B(-5;5)), (C(-6;3)).
(begin{cases}5=a(-4)^2+b(-4)+c\5=a(-5)^2+b(-5)+c\3=a(-6)^2+b(-6)+c end{cases})
-
Решаем систему.
Пример:(begin{cases}5=16a-4b+c\5=25a-5b+c\3=36a-6b+c end{cases})
Вычтем из второго уравнения первое:
(0=9a-b)
(b=9a)Подставим (9a) вместо (b):
(begin{cases}5=16a-36a+c\5=25a-45a+c\3=36a-54a+c end{cases})
(begin{cases}5=-20a+c\5=-20a+c\3=-18a+c end{cases})Первое и второе уравнения совпали (это нормально для точек, симметричных относительно прямой проходящей через вершину – как точки (A) и (B) в нашем случае), но нас это не остановит – мы вычтем из второго уравнение третье:
(2=-2a)
(a=-1)Найдем (b):
(b=-9)
Подставим в первое уравнение (a):
(5=20+c)
(c=-15).Получается квадратичная функция: (y=-x^2-9x-15).
Пример (ЕГЭ):

Решение:
Сразу заметим, что по графику можно сразу определить, что (c=4). Это сильно облегчит нашу систему – нам хватит 2 точек. Выберем их на параболе: (C(-1;8)), (D(1;2)) (на самом деле, если присмотреться, то можно заметить, что эти точки выделены жирно на изначальной картинке – это вам подсказка от авторов задачи).

Таким образом имеем систему:
(begin{cases}8=a(-1)^2+b(-1)+4\2=a+b+4 end{cases})
(begin{cases}8=a-b+4\2=a+b+4 end{cases})
(begin{cases}4=a-b\-2=a+b end{cases})
Сложим 2 уравнения:
(2=2a)
(a=1)
Подставим во второе уравнение:
(-2=1+b)
(b=-3)
Получается:
(g(x)=x^2-3x+4)
Теперь найдем точки пересечения двух функций:
(-3x+13=x^2-3x+4)
(x^2-9=0)
(x=±3)
Теперь можно найти ординату второй точки пересечения:
(f(-3)=-3cdot (-3)+13)
(f(-3)=9+13)
(f(-3)=22)
Ответ: (22).
3 способ – используем преобразование графиков функций
Этот способ быстрее первого и более универсальный, в частности он может пригодится и в задачах на другие функции.
Главный недостаток этого способа – вершина должна иметь целые координаты.
Сам способ базируется на следующих идеях:
-
График (y=-x^2) симметричен относительно оси (x) графику (y=x^2).
-
– Если (a>1) график (y=ax^2) получается растяжением графика (y=x^2) вдоль оси (y) в (a) раз.
– Если (a∈(0;1)) график (y=ax^2) получается сжатием графика (y=x^2) вдоль оси (y) в (a) раз. -
– График (y=a(x+d)^2) получается сдвигом графика (y=ax^2) влево на (d) единиц.
– График (y=a(x-d)^2) получается сдвигом графика (y=ax^2) вправо на (d) единиц. -
График (y=a(x+d)^2+e) получается переносом графика (y=a(x+d)^2) на (e) единиц вверх.
График (y=a(x+d)^2-e) получается переносом графика (y=a(x+d)^2) на (e) единиц вниз.
У вас наверно остался вопрос – как этим пользоваться? Предположим, мы видим такую параболу:

Сначала смотрим на её форму и направленность её ветвей. Видим, что форма стандартная, базовая и ветви направлены вверх, поэтому (a=1). То есть она получена перемещениями графика базовой параболы (y=x^2).

А как надо было перемещать зеленый график чтоб получить оранжевый? Надо сдвинуться вправо на пять единиц и вниз на (4).

То есть наша функция выглядит так: (y=(x-5)^2-4).
После раскрытия скобок и приведения подобных получаем искомую формулу:
(y=x^2-10x+25-4)
(y=x^2-10x+21)
Готово.
Пример (ЕГЭ):

Чтобы найти (f(6)), надо сначала узнать формулу функции (f(x)). Найдем её:
-
Парабола растянута на (2) и ветви направлены вниз, поэтому (a=-2). Иными словами, первоначальной, перемещаемой функцией является функция (y=-2x^2).
-
Парабола смещена на 2 клеточки вправо, поэтому (y=-2(x-2)^2).
-
Парабола поднята на 4 клеточки вверх, поэтому (y=-2(x-2)^2+4).
-
Получается (y=-2(x^2-4x+4)+4=)(-2x^2+8x-8+4=-2x^2+8x-4).
-
(f(6)=-2cdot 6^2+8cdot 6-4=-72+48-4=-28)
Смотрите также:
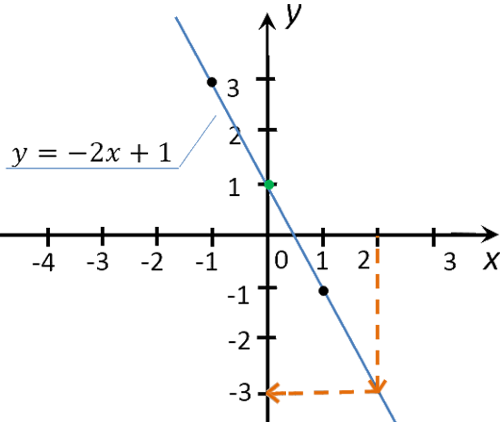
Как найти k и b по графику линейной функции?
Содержание
- как по графику определить ее функцию (нужно уравнение!), желательно проделать это в excel
- Как найти уравнение функции по графику эксель
- Графический способ решения уравнений в среде Microsoft Excel 2007
- Варианты построения графика функции в Microsoft Excel
- Вариант 1: График функции X^2
- Вариант 2: График функции y=sin(x)
- Как построить график в Excel по уравнению
- Что это такое
- А нужно ли это
- Как построить график уравнения регрессии в Excel
- Подготовительные работы
- Как пользоваться
- Анализ
- Как построить график квадратного уравнения в Excel
- Как построить график линейного уравнения
- Вывод
как по графику определить ее функцию (нужно уравнение!), желательно проделать это в excel
саша, так вопросы не решаются.
..
1 самый простой способ: налепить апроксимированных участков прямых и окружностей.
.
сложный муторный способ
2. изъебствовать с кривыми, порядка числа имеющихся точек.
дальше кривых пятого порядка влезать не советую, потому что могут быть неоднозначные решения.
(с порядком разнообразности всяких кривых тоже растут)
—
это не кХ — 100% ПОТОМУ ЧТО ПРИРАЩЕНИЕ НЕ не одинаковое.
шаги 4, 9, 16, 32, 64( скопейками — подъебашь препода)
то что ет не линейная фнкция — 100 % .. какая — ищи сам.
Ищем кривую в виде y=a*x^n + b.
61=a*1^n + b
65=a*2^n + b
90=a*3^n + b
122.8=a*4^n + b
187=a*5^n + b
285.3=a*6^n + b
418.8=a*7^n + b
Решив эту систему уравнений, найдём:
a = 0.91926948,
b = 60.080731,
n = 3.0662855,
x = 0.95522773,
при максимальной ошибке апроксимации 3.2240912,
потому что кривая в точке х=3 должна быть у=86.775909
Excel для таких вещей слабоват. Нужен какой нибудь специальный статпакет.
Для приведенных данных достаточно высоким коэффициентом детерминации 98,57% обладает уравнение вида Y=1/(A+B*X)
После него идет экспоненциальное уравнение Y=exp(A+B*X) c коэффициентом детерминации 94,35. Вот это можно сделать в Excell. Построив график и добавив в него линию тренда. Там есть большой выбор — выбирайте экспонециальную зависимость. Запросите показ уравнения. И будет Вам счастье.
Источник
Как найти уравнение функции по графику эксель
Графический способ решения уравнений в среде Microsoft Excel 2007
Тип урока: Обобщение, закрепление пройденного материала и объяснение нового.
Цели и задачи урока:
- повторение изученных графиков функций;
- повторение и закрепление графического способа решения уравнений;
- закрепление навыков записи и копирования формул, построения графиков функций в электронных таблицах Excel 2007;
- формирование и первичное закрепление знаний о решении уравнений с использованием возможностей электронных таблиц Excel 2007;
- формирование мышления, направленного на выбор оптимального решения;
- формирование информационной культуры школьников.
Оборудование: персональные компьютеры, мультимедиапроектор, проекционный экран.
Материалы к уроку: презентация Power Point на компьютере учителя (Приложение 1).
Слайд 1 из Приложения1 ( далее ссылки на слайды идут без указания Приложения1).
Объявление темы урока.
1. Устная работа (актуализация знаний).
Слайд 2 — Соотнесите перечисленные ниже функции с графиками на чертеже (Рис. 1):
у = 6 — х; у = 2х + 3; у = (х + 3) 2 ; у = -(х — 4) 2 ; 
Слайд 3 Графический способ решения уравнений вида f(x)=0.
Корнями уравнения f(x)=0 являются значения х1, х2, … точек пересечения графика функции y=f(x) с осью абсцисс (Рис. 2).
Найдите корни уравнения х 2 -2х-3=0, используя графический способ решения уравнений (Рис.3).
Слайд 5 Графический способ решения уравнений вида f (x)=g (x).
Корнями уравнения f(x)=g(x) являются значения х1, х2, … точек пересечения графиков функций y=f(x) и у=g(x). (Рис. 4):
Слайд 6 Найдите корни уравнения 
2. Объяснение нового материала. Практическая работа.
Решение уравнений графическим способом требует больших временных затрат на построение графиков функций и в большинстве случаев дает грубо приближенные решения. При использовании электронных таблиц, в данном случае – Microsoft Excel 2007, существенно экономится время на построение графиков функций, и появляются дополнительные возможности нахождения корней уравнения с заданной точностью (метод Подбор параметра).
I. Графический способ решения уравнений вида f(x)=0 в Excel.
Дальнейшая работа выполняется учителем в Excel одновременно с учениками с подробными (при необходимости) инструкциями и выводом результатов на проекционный экран. Слайды Приложения 1 используются для формулировки задач и подведения промежуточных итогов.
Пример1: Используя средства построения диаграмм в Excel, решить графическим способом уравнение —х 2 +5х-4=0.
Для этого: построить график функции у=-х 2 +5х-4 на промежутке [ 0; 5 ] с шагом 0,25; найти значения х точек пересечения графика функции с осью абсцисс.
Выполнение задания можно разбить на этапы:
1 этап: Представление функции в табличной форме (рис. 6):
- в ячейку А1 ввести текст Х, в ячейку A2 — Y;
- в ячейку В1 ввести число 0, в ячейку С1 – число 0,25;
- выделить ячейки В1:С1, подвести указатель мыши к маркеру выделения, и в тот момент, когда указатель мыши примет форму черного крестика, протянуть маркер выделения вправо до ячейки V1 (Рис. 7).
При вводе формулы можно вводить адрес ячейки с клавиатуры (не забыть переключиться на латиницу), а можно просто щелкнуть мышью на ячейке с нужным адресом.
После ввода формулы в ячейке окажется результат вычисления по формуле, а в поле ввода строки формул — сама формула (Рис. 8):
- скопировать содержимое ячейки B2 в ячейки C2:V2 за маркер выделения. Весь ряд выделенных ячеек заполнится содержимым первой ячейки. При этом ссылки на ячейки в формулах изменятся относительно смещения самой формулы.
2 этап: Построение диаграммы типа График.
- выделить диапазон ячеек B2:V2;
- на вкладке Вставка|Диаграммы|График выбрать вид График;
- на вкладке Конструктор|Выбрать данные (Рис. 9) в открывшемся окне «Выбор источника данных» щелкнуть по кнопке Изменить в поле Подписи горизонтальной оси — откроется окно «Подписи оси». Выделить в таблице диапазон ячеек B1:V1 (значения переменной х). В обоих окнах щелкнуть по кнопкам ОК;
- на вкладке Макет|Оси|Основная горизонтальная ось|Дополнительные параметры основной горизонтальной оси выбрать:
Интервал между делениями: 4;
Интервал между подписями: Единица измерения интервала: 4;
Положение оси: по делениям;
Выбрать ширину и цвет линии (Вкладки Тип линии и Цвет линии);
- самостоятельно изменить ширину и цвет линии для вертикальной оси;
- на вкладке Макет|Сетка|Вертикальные линии сетки по основной оси выбрать Основные линии сетки.
Примерный результат работы приведен на рис. 10:
3 этап: Определение корней уравнения.
График функции у=-х 2 +5х-4 пересекает ось абсцисс в двух точках и, следовательно, уравнение -х 2 +5х-4=0 имеет два корня: х1=1; х2=4.
II. Графический способ решения уравнений вида f(x)=g(x) в Excel.
Пример 2: Решить графическим способом уравнение 
Для этого: в одной системе координат построить графики функций у1= 
1 этап: Представление функций в табличной форме (рис. 1):
 воспользоваться встроенной функцией Корень (Рис. 11).
воспользоваться встроенной функцией Корень (Рис. 11).2 этап: Построение диаграммы типа График.
Примерный результат работы приведен на Рис. 12:
3 этап: Определение корней уравнения.
Графики функций у1= 

III. Метод Подбор параметра.
Графический способ решения уравнений красив, но далеко не всегда точки пересечения могут быть такими «хорошими», как в специально подобранных примерах 1 и 2.
Возможности электронных таблиц позволяют находить приближенные значения коней уравнения с заданной точностью. Для этого используется метод Подбор параметра.
Пример 3: Разберем метод Подбор параметра на примере решения уравнения —х 2 +5х-3=0.
1 этап: Построение диаграммы типа График для приближенного определения корней уравнения.
Построить график функции у=—х 2 +5х-3, отредактировав полученные в Примере 1 формулы.
- выполнить двойной щелчок по ячейке B2, внести необходимые изменения;
- с помощью маркера выделения скопировать формулу во все ячейки диапазона C2:V2.
Все изменения сразу отобразятся на графике.
Примерный результат работы приведен на Рис. 13:
2 этап: Определение приближенных значений корней уравнения.
График функции у=-х 2 +5х-3 пересекает ось абсцисс в двух точках и, следовательно, уравнение -х 2 +5х-4=0 имеет два корня.
По графику приближенно можно определить, что х1≈0,7; х2≈4,3.
3 этап: Поиск приближенного решения уравнения с заданной точностью методом Подбор параметра.
1) Начать с поиска более точного значения меньшего корня.
По графику видно, что ближайший аргумент к точке пересечения графика с осью абсцисс равен 0,75. В таблице значений функции этот аргумент размещается в ячейке E1.
- Выделить ячейку Е2;
- перейти на вкладку Данные|Анализ «что-если»|Подбор параметра…;
В открывшемся диалоговом окне Подбор параметра (Рис. 14) в поле Значение ввести требуемое значение функции: 0.
В поле Изменяя значение ячейки: ввести $E$1 (щелкнув по ячейке E1).
Щелкнуть по кнопке ОК.
- В окне Результат подбора (Рис. 15) выводится информация о величине подбираемого и подобранного значения функции:
- В ячейке E1 выводится подобранное значение аргумента 0,6972 с требуемой точностью (0,0001).
Установить точность можно путем установки в ячейках таблицы точности представления чисел – числа знаков после запятой (Формат ячеек|Число|Числовой).
Итак, первый корень уравнения определен с заданной точностью: х1≈0,6972.
2) Самостоятельно найти значение большего корня с той же точностью. (х2≈4,3029).
IV. Метод Подбор параметра для решения уравнений вида f(x)=g(x).
При использовании метода Подбор параметров для решения уравнений вида f(x)=g(x) вводят вспомогательную функцию y(x)=f(x)-g(x) и находят с требуемой точностью значения х точек пересечения графика функции y(x) с осью абсцисс.
3. Закрепление изученного материала. Самостоятельная работа.
Задание: Используя метода Подбор параметров, найти корни уравнения 
- ввести функцию у=
и построить ее график на промежутке [ -1; 4 ] с шагом 0,25 (Рис. 16):
- найти приближенное значение х точки пересечения графика функции с осью абсцисс (х≈1,4);
- найти приближенное решение уравнения с точностью до 0,001 методом Подбор параметра (х≈1,438).
Слайд 12 Проверка результатов самостоятельной работы.
Слайд 13 Повторение графического способа решения уравнения вида f(x)=0.
Слайд 14 Повторение графического способа решения уравнения вида f(x)=g(x).
5. Домашнее задание.
Используя средства построения диаграмм в Excel и метод Подбор параметра, определите корни уравнения х 2 -5х+2=0 с точностью до 0,01.
Варианты построения графика функции в Microsoft Excel
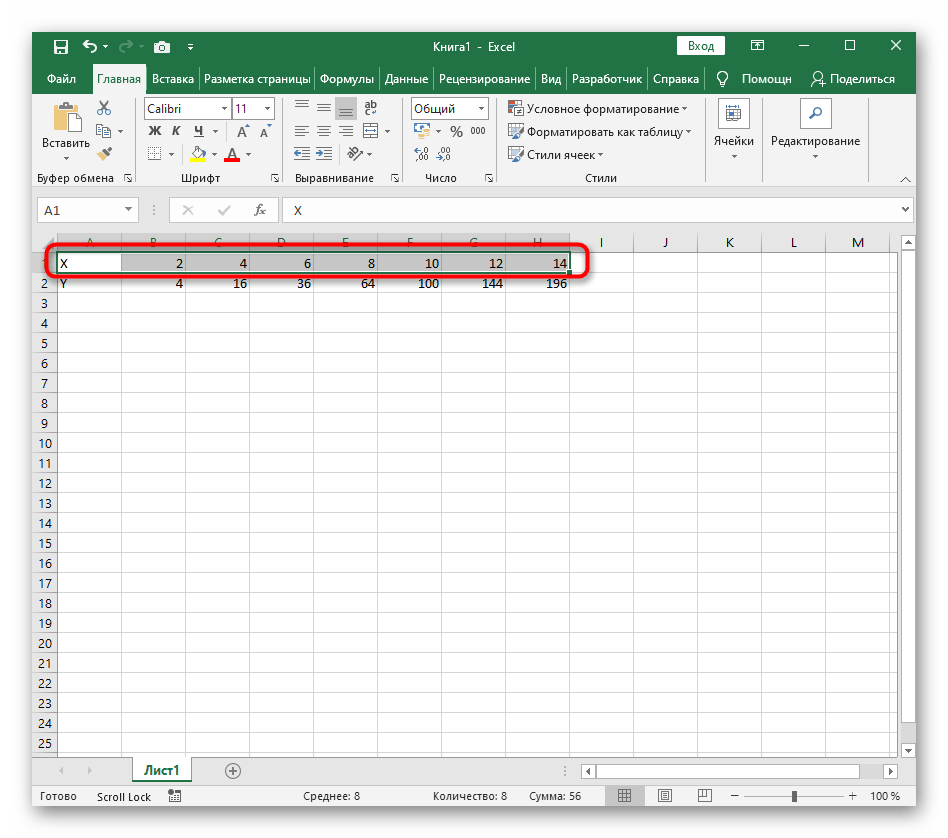
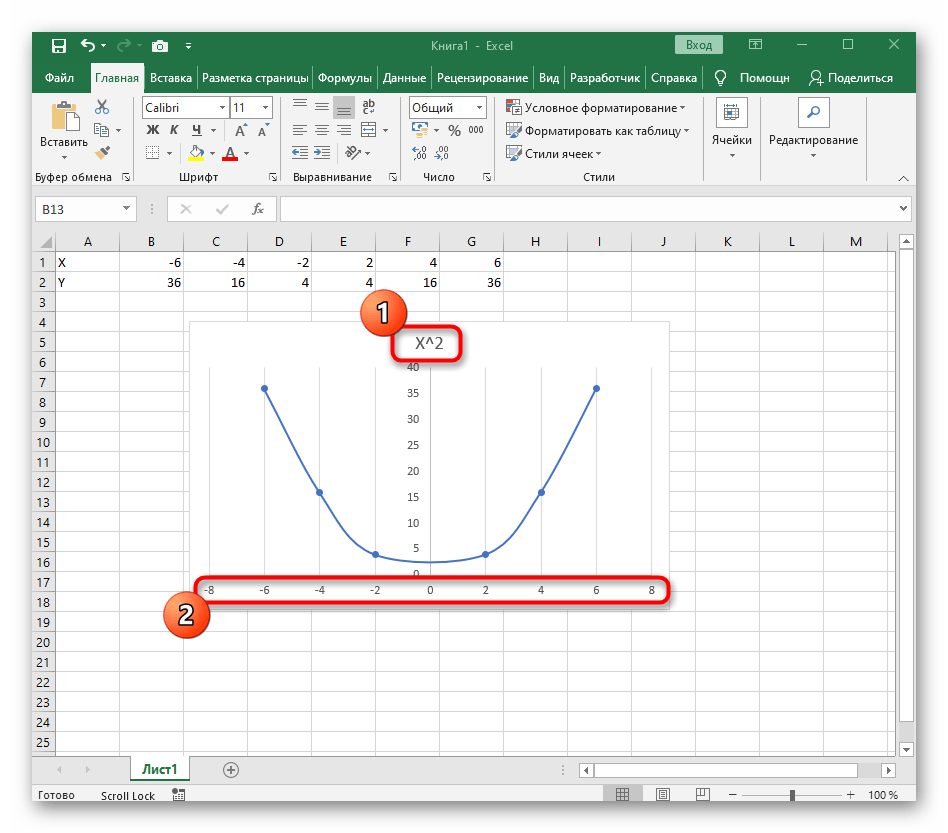
Вариант 1: График функции X^2
В качестве первого примера для Excel рассмотрим самую популярную функцию F(x)=X^2. График от этой функции в большинстве случаев должен содержать точки, что мы и реализуем при его составлении в будущем, а пока разберем основные составляющие.
- Создайте строку X, где укажите необходимый диапазон чисел для графика функции.
Ниже сделайте то же самое с Y, но можно обойтись и без ручного вычисления всех значений, к тому же это будет удобно, если они изначально не заданы и их нужно рассчитать.
Растяните функцию, зажав правый нижний угол ячейки, и приведя таблицу в тот вид, который продемонстрирован на следующем скриншоте.
Диапазон данных для построения графика функции указан, а это означает, что можно выделять его и переходить на вкладку «Вставка».
В новом окне перейдите на вкладку «Все диаграммы» и в списке найдите «Точечная».
Подойдет вариант «Точечная с гладкими кривыми и маркерами».
После ее вставки в таблицу обратите внимание, что мы добавили равнозначный диапазон отрицательных и плюсовых значений, чтобы получить примерно стандартное представление параболы.
Из дополнительных возможностей отметим копирование и перенос графика в любой текстовый редактор. Для этого щелкните в нем по пустому месту ПКМ и из контекстного меню выберите «Копировать».
Если график должен быть точечным, но функция не соответствует указанной, составляйте его точно в таком же порядке, формируя требуемые вычисления в таблице, чтобы оптимизировать их и упростить весь процесс работы с данными.
Вариант 2: График функции y=sin(x)
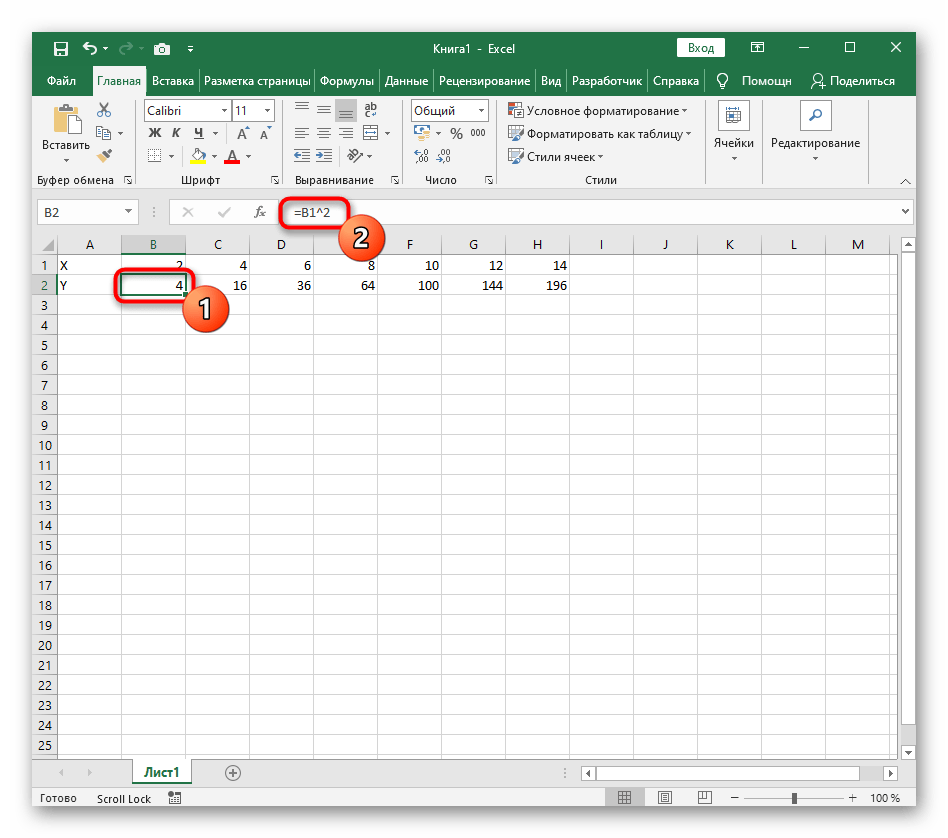
Функций очень много и разобрать их в рамках этой статьи просто невозможно, поэтому в качестве альтернативы предыдущему варианту предлагаем остановиться на еще одном популярном, но сложном — y=sin(x). То есть изначально есть диапазон значений X, затем нужно посчитать синус, чему и будет равняться Y. В этом тоже поможет созданная таблица, из которой потом и построим график функции.
- Для удобства укажем всю необходимую информацию на листе в Excel. Это будет сама функция sin(x), интервал значений от -1 до 5 и их шаг весом в 0.25.
Создайте сразу два столбца — X и Y, куда будете записывать данные.
Запишите самостоятельно первые два или три значения с указанным шагом.
Далее растяните столбец с X так же, как обычно растягиваете функции, чтобы автоматически не заполнять каждый шаг.
Перейдите к столбцу Y и объявите функцию =SIN( , а в качестве числа укажите первое значение X.
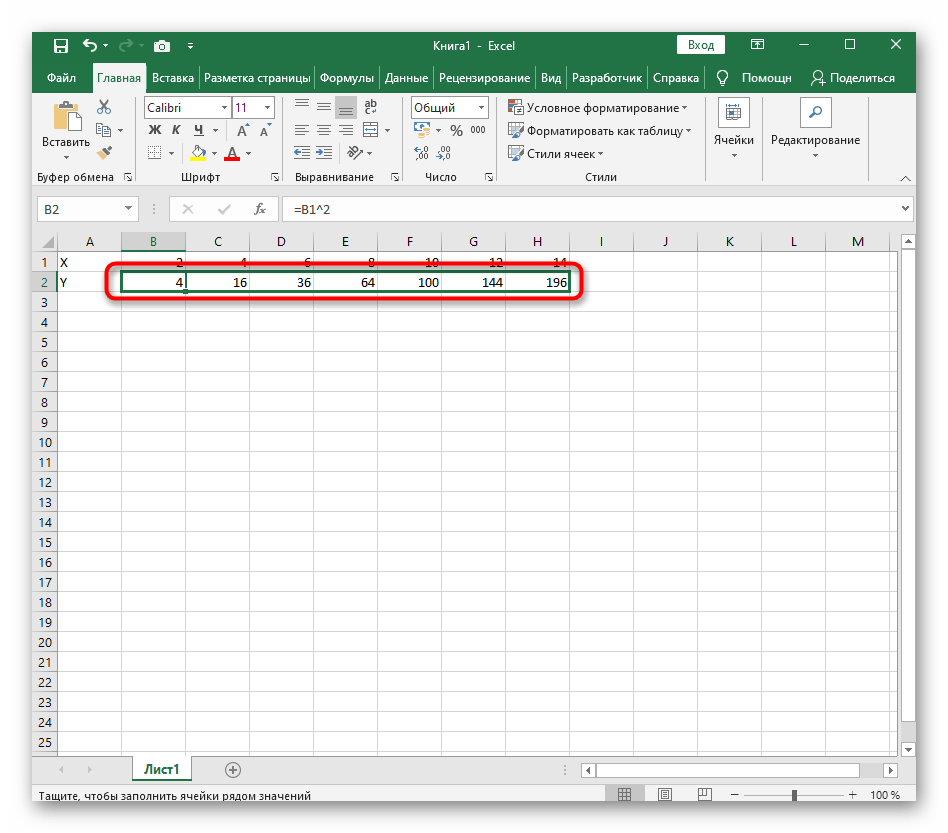
Сама функция автоматически высчитает синус заданного числа.
Растяните столбец точно так же, как это было показано ранее.
Если чисел после запятой слишком много, уменьшите разрядность, несколько раз нажав по соответствующей кнопке.
Выделите столбец с Y и перейдите на вкладку «Вставка».
Создайте стандартный график, развернув выпадающее меню.
График функции от y=sin(x) успешно построен и отображается правильно. Редактируйте его название и отображаемые шаги для простоты понимания.

Помимо этой статьи, на сайте еще 12698 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Как построить график в Excel по уравнению
Как предоставить информацию, чтобы она лучше воспринималась. Используйте графики. Это особенно актуально в аналитике. Рассмотрим, как построить график в Excel по уравнению.
Что это такое
График показывает, как одни величины зависят от других. Информация легче воспринимается. Посмотрите визуально, как отображается динамика изменения данных.
А нужно ли это
Графический способ отображения информации востребован в учебных или научных работах, исследованиях, при создании деловых планов, отчетов, презентаций, формул. Разработчики для построения графиков добавили способы визуального представления: диаграммы, пиктограммы.
Как построить график уравнения регрессии в Excel
Регрессионный анализ — статистический метод исследования. Устанавливает, как независимые величины влияют на зависимую переменную. Редактор предлагает инструменты для такого анализа.
Подготовительные работы
Перед использованием функции активируйте Пакет анализа. Перейдите:
Выберите раздел:
Далее:
Прокрутите окно вниз, выберите:
Отметьте пункт:
Открыв раздел «Данные», появится кнопка «Анализ».
Как пользоваться
Рассмотрим на примере. В таблице указана температура воздуха и число покупателей. Данные выводятся за рабочий день. Как температура влияет на посещаемость. Перейдите:
Выберите:
Отобразится окно настроек, где входной интервал:
- Y. Ячейки с данными влияние факторов на которые нужно установить. Это число покупателей. Адрес пропишите вручную или выделите соответствующий столбец;
- Х. Данные, влияние на которые нужно установить. В примере, нужно узнать, как температура влияет на количество покупателей. Поэтому выделяем ячейки в столбце «Температура».
Анализ
Нажав кнопку «ОК», отобразится результат.
Основной показатель — R-квадрат. Обозначает качество. Он равен 0,825 (82,5%). Что это означает? Зависимости, где показатель меньше 0,5 считается плохим. Поэтому в примере это хороший показатель. Y-пересечение. Число покупателей, если другие показатели равны нулю. 62,02 высокий показатель.
Как построить график квадратного уравнения в Excel
График функции имеет вид: y=ax2+bx+c. Рассмотрим диапазон значений: [-4:4].
- Составьте таблицу как на скриншоте;
- В третьей строке указываем коэффициенты и их значения;
- Пятая — диапазон значений;
- В ячейку B6 вписываем формулу =$B3*B5*B5+$D3*B5+$F3;

При вычислении формулы прописывается знак «$». Используется чтобы ссылка была постоянной. Подробнее смотрите в статье: «Как зафиксировать ячейку».
Выделите диапазон значений по ним будем строить график. Перейдите:
Поместите график в свободное место на листе.
Как построить график линейного уравнения
Функция имеет вид: y=kx+b. Построим в интервале [-4;4].
- В таблицу прописываем значение постоянных величин. Строка три;
- Строка 5. Вводим диапазон значений;
- Ячейка В6. Прописываем формулу.

График — прямая линия.
Вывод
Мы рассмотрели, как построить график в Экселе (Excel) по уравнению. Главное — правильно выбрать параметры и диаграмму. Тогда график точно отобразит данные.
Источник
Прежде чем перейти к разбору решения задач с функциями обязательно прочитайте урок
«Что такое функция в математике».
После того, как вы действительно поймете, что такое функция
(возможно, придется прочитать урок не один раз) вы с бóльшей уверенностью сможете решать задания с функциями.
В этом уроке мы разберем, как решать основные типы задач на функцию и графики функций.
Как получить значение функции
Рассмотрим задание.
Функция задана формулой «y = 2x − 1»
- Вычислить «y» при «x = 15»
- Найти значение «x», при котором
значение «y» равно «−19».
Для того, чтобы вычислить «y» при
«x = 15» достаточно подставить в функцию вместо «x»
необходимое числовое значение.
Запись решения выглядит следующим образом.
y(15) = 2 · 15 − 1 = 30 − 1 = 29
Для того, чтобы найти «x»
по известному «y», необходимо подставить вместо
«y» в формулу функции числовое значение.
То есть теперь наоборот, для поиска «x»
мы подставляем в функцию «y = 2x − 1» вместо
«y» число «−19» .
−19 = 2x − 1
Мы получили линейное уравнение с неизвестным «x»,
которое решается по правилам решения линейных уравнений.
Запомните!
Не забывайте про правило переноса в уравнениях.
При переносе из левой части уравнения в правую (и наоборот) буква или число меняет знак на
противоположный.
−19 = 2x − 1
0 = 2x − 1 + 19
−2x = −1 + 19
−2x = 18
Как и при решении линейного уравнения, чтобы найти неизвестное, сейчас
требуется умножить и левую, и правую часть на «−1» для смены знака.
−2x = 18 | · (−1)
2x = −18
Теперь разделим и левую, и правую часть на «2», чтобы найти «x» .
2x = −18 | (: 2)
x = −9
Как проверить верно ли равенство для функции
Рассмотрим задание.
Функция задана формулой «f(x) = 2 − 5x».
Верно ли равенство
«f(−2) = −18»?
Чтобы проверить верно ли равенство, нужно подставить в функцию «f(x) = 2 − 5x»
числовое значение «x = −2» и сопоставить с тем, что получится при расчетах.
Важно!
Когда подставляете отрицательное число вместо «x», обязательно заключайте его в скобки.
Не забывайте использовать
правило знаков.
Неправильно
Правильно
С помощью расчетов мы получили
«f(−2) = 12».
Это означает, что «f(−2) = −18»
для функции «f(x) = 2 − 5x» не является верным равенством.
Как проверить, что точка принадлежит графику функции
Рассмотрим функцию «y = x2 −5x + 6»
Требуется выяснить, принадлежит ли графику этой функции точка с координатами
(1; 2).
Для этой задачи нет необходимости, строить график заданной функции.
Запомните!
Чтобы определить, принадлежит ли точка функции,
достаточно подставить её координаты в функцию (координату по оси
«Ox» вместо
«x» и координату по оси «Oy»
вместо «y»).
Если получится верное равенство, значит, точка принадлежит функции.
Вернемся к нашему заданию. Подставим в функцию «y = x2 − 5x + 6»
координаты точки (1; 2).
Вместо «x» подставим «1».
Вместо «y» подставим «2».
2 = 12 − 5 · 1 + 6
2 = 1 − 5 + 6
2 = −4 + 6
2 = 2 (верно)
У нас получилось верное равенство, значит, точка с координатами
(1; 2) принадлежит заданной функции.
Теперь проверим точку с координатами (0; 1).
Принадлежит ли она
функции «y = x2 − 5x + 6»?
Вместо «x» подставим «0».
Вместо «y» подставим «1».
1 = 02 − 5 · 0 + 6
1 = 0 − 0 + 6
1 = 6 (неверно)
В этом случае мы не получили верное равенство.
Это означает, что точка с координатами (0; 1) не принадлежит функции
«y = x2 − 5x + 6»
Как получить координаты точки функции
С любого графика функции можно снять координаты точки. Затем необходимо убедиться, что при подстановке координат
в формулу функции получается верное равенство.
Рассмотрим функцию «y(x) = −2x + 1». Её график
мы уже
строили
в предыдущем уроке.
Найдем на графике функции «y(x) = −2x + 1», чему равен «y»
при x = 2.
Для этого из значения «2» на оси «Ox» проведем перпендикуляр к графику функции.
Из точки пересечения перпендикуляра и графика функции проведем еще один перпендикуляр к оси «Oy».
Полученное значение «−3» на оси «Oy» и будет искомым значением «y».
Убедимся, что мы правильно сняли координаты точки для x = 2
в функции «y(x) = −2x + 1».
Для этого мы подставим x = 2 в формулу функции
«y(x) = −2x + 1». Если мы правильно
провели перпендикуляр, мы также должны получить в итоге y = −3.
y(2) = −2 · 2 + 1 = −4 + 1 = −3
При расчетах мы также получили y = −3.
Значит, мы правильно получили координаты с графика функции.
Важно!
Все полученные координаты точки с графика функции обязательно проверяйте
подстановкой значений «x» в функцию.
При подстановке числового значения «x» в функцию в результате должно получиться
то же значение «y», которое вы получили на графике.
При получении координат точек с графика функции высока вероятность, что вы ошибетесь, т.к. проведение перпендикуляра к осям выполняется «на глазок».
Только подстановка значений в формулу функции дает точные результаты.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
11 ноября 2018 в 15:46
Веточка Сакуры
Профиль
Благодарили: 0
Сообщений: 1
Веточка Сакуры
Профиль
Благодарили: 0
Сообщений: 1
Функция y=f(x) является нечётной и при x ⩽0 задаётся формулой y= – x² — 8x.Найдите значение фун. в т. минимума (y min).
0
Спасибо
Ответить
12 ноября 2018 в 3:25
Ответ для Веточка Сакуры
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
ymin = y(4) = -16.
0
Спасибо
Ответить
17 сентября 2018 в 13:28
Alesger Mammedov
Профиль
Благодарили: 0
Сообщений: 1
Alesger Mammedov
Профиль
Благодарили: 0
Сообщений: 1
Добрый день помогите пожалуйста с задачкой
f(x2-3x)=3x2+5x-4
f(3)=?
0
Спасибо
Ответить
17 сентября 2018 в 23:01
Ответ для Alesger Mammedov
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
f(3) = 26 ± 7√21
0
Спасибо
Ответить
13 ноября 2016 в 6:43
Роман Безбородов
Профиль
Благодарили: 0
Сообщений: 1
Роман Безбородов
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
14 ноября 2016 в 17:30
Ответ для Роман Безбородов
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
y = ax; a > 1.
0
Спасибо
Ответить
7 сентября 2016 в 22:08
Иван Баранов
Профиль
Благодарили: 0
Сообщений: 3
Иван Баранов
Профиль
Благодарили: 0
Сообщений: 3
у=Х2+2Х-3 найдите значение функции, если значение аргумента равно -2
у=3х-5 при каком значении аргумента значение функции раво 10
0
Спасибо
Ответить
8 сентября 2016 в 15:26
Ответ для Иван Баранов
Юлия Анарметова
Профиль
Благодарили: 0
Сообщений: 11
Юлия Анарметова
Профиль
Благодарили: 0
Сообщений: 11
аргумент это х значит у=(-2)2+2 · (-2)-3=4-4-3=-3
у=3х-5 значит 10=3х-5
10+5=3х
15=3х
х=15:3=5
0
Спасибо
Ответить

























































 и построить ее график на промежутке [ -1; 4 ] с шагом 0,25 (Рис. 16):
и построить ее график на промежутке [ -1; 4 ] с шагом 0,25 (Рис. 16):