Содержание
- Простейший график изменений
- График с двумя и более кривыми
- Добавление второй оси
- Строим график функций в Excel
- Наложение и комбинирование графиков
- Графики зависимости
Информация воспринимается легче, если представлена наглядно. Один из способов презентации отчетов, планов, показателей и другого вида делового материала – графики и диаграммы. В аналитике это незаменимые инструменты.
Построить график в Excel по данным таблицы можно несколькими способами. Каждый из них обладает своими преимуществами и недостатками для конкретной ситуации. Рассмотрим все по порядку.
Простейший график изменений
График нужен тогда, когда необходимо показать изменения данных. Начнем с простейшей диаграммы для демонстрации событий в разные промежутки времени.
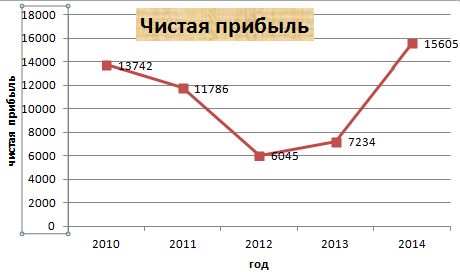
Допустим, у нас есть данные по чистой прибыли предприятия за 5 лет:
| Год | Чистая прибыль* |
| 2010 | 13742 |
| 2011 | 11786 |
| 2012 | 6045 |
| 2013 | 7234 |
| 2014 | 15605 |
* Цифры условные, для учебных целей.
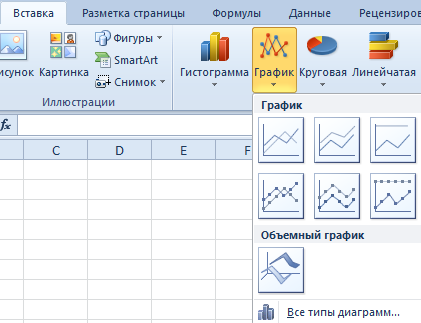
Заходим во вкладку «Вставка». Предлагается несколько типов диаграмм:
Выбираем «График». Во всплывающем окне – его вид. Когда наводишь курсор на тот или иной тип диаграммы, показывается подсказка: где лучше использовать этот график, для каких данных.
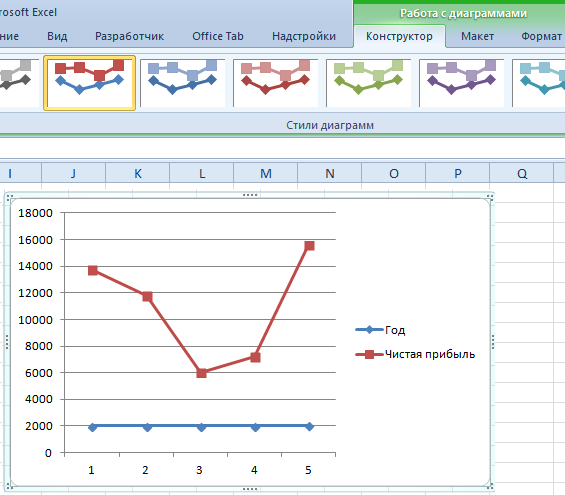
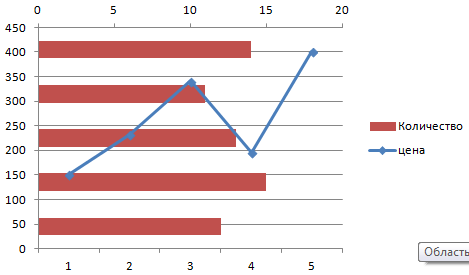
Выбрали – скопировали таблицу с данными – вставили в область диаграммы. Получается вот такой вариант:
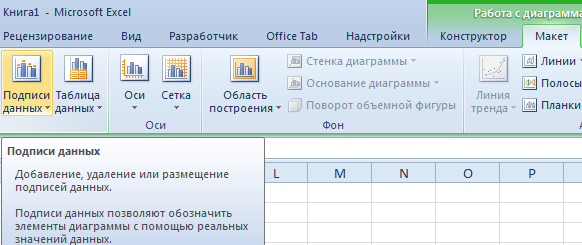
Прямая горизонтальная (синяя) не нужна. Просто выделяем ее и удаляем. Так как у нас одна кривая – легенду (справа от графика) тоже убираем. Чтобы уточнить информацию, подписываем маркеры. На вкладке «Подписи данных» определяем местоположение цифр. В примере – справа.
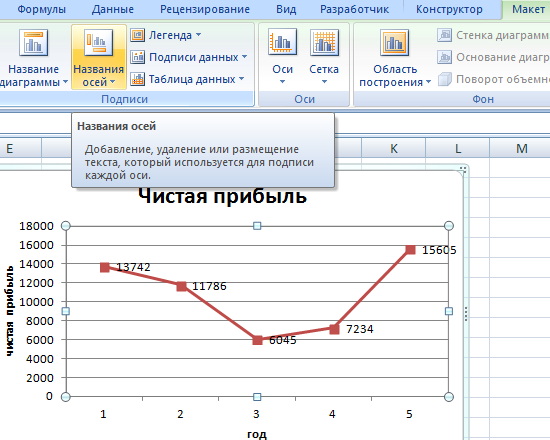
Улучшим изображение – подпишем оси. «Макет» – «Название осей» – «Название основной горизонтальной (вертикальной) оси»:
Заголовок можно убрать, переместить в область графика, над ним. Изменить стиль, сделать заливку и т.д. Все манипуляции – на вкладке «Название диаграммы».
Вместо порядкового номера отчетного года нам нужен именно год. Выделяем значения горизонтальной оси. Правой кнопкой мыши – «Выбрать данные» — «Изменить подписи горизонтальной оси». В открывшейся вкладке выбрать диапазон. В таблице с данными – первый столбец. Как показано ниже на рисунке:
Можем оставить график в таком виде. А можем сделать заливку, поменять шрифт, переместить диаграмму на другой лист («Конструктор» — «Переместить диаграмму»).
График с двумя и более кривыми
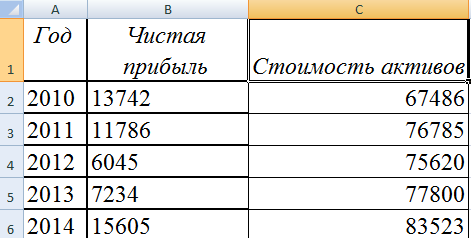
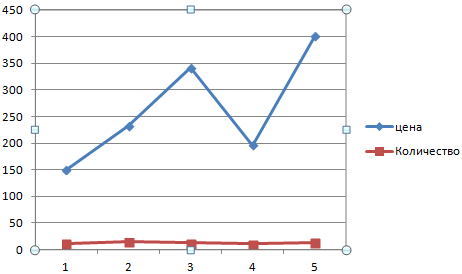
Допустим, нам нужно показать не только чистую прибыль, но и стоимость активов. Данных стало больше:
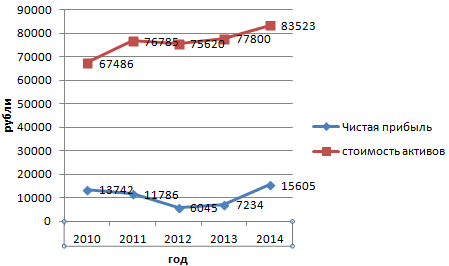
Но принцип построения остался прежним. Только теперь есть смысл оставить легенду. Так как у нас 2 кривые.
Добавление второй оси
Как добавить вторую (дополнительную) ось? Когда единицы измерения одинаковы, пользуемся предложенной выше инструкцией. Если же нужно показать данные разных типов, понадобится вспомогательная ось.
Сначала строим график так, будто у нас одинаковые единицы измерения.
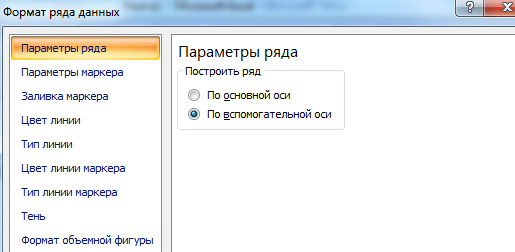
Выделяем ось, для которой хотим добавить вспомогательную. Правая кнопка мыши – «Формат ряда данных» – «Параметры ряда» — «По вспомогательной оси».
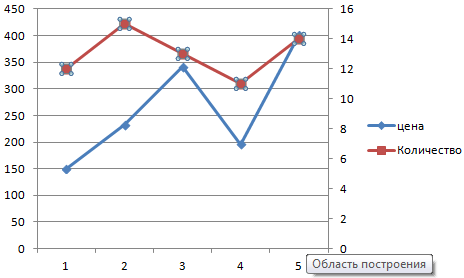
Нажимаем «Закрыть» — на графике появилась вторая ось, которая «подстроилась» под данные кривой.
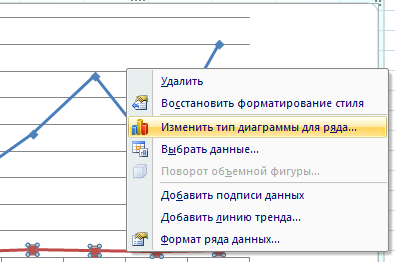
Это один из способов. Есть и другой – изменение типа диаграммы.
Щелкаем правой кнопкой мыши по линии, для которой нужна дополнительная ось. Выбираем «Изменить тип диаграммы для ряда».
Определяемся с видом для второго ряда данных. В примере – линейчатая диаграмма.
Всего несколько нажатий – дополнительная ось для другого типа измерений готова.
Строим график функций в Excel
Вся работа состоит из двух этапов:
- Создание таблицы с данными.
- Построение графика.
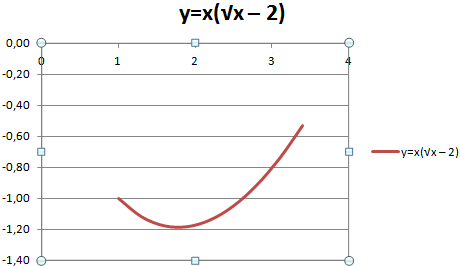
Пример: y=x(√x – 2). Шаг – 0,3.
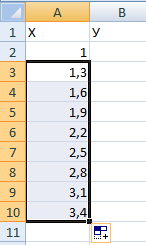
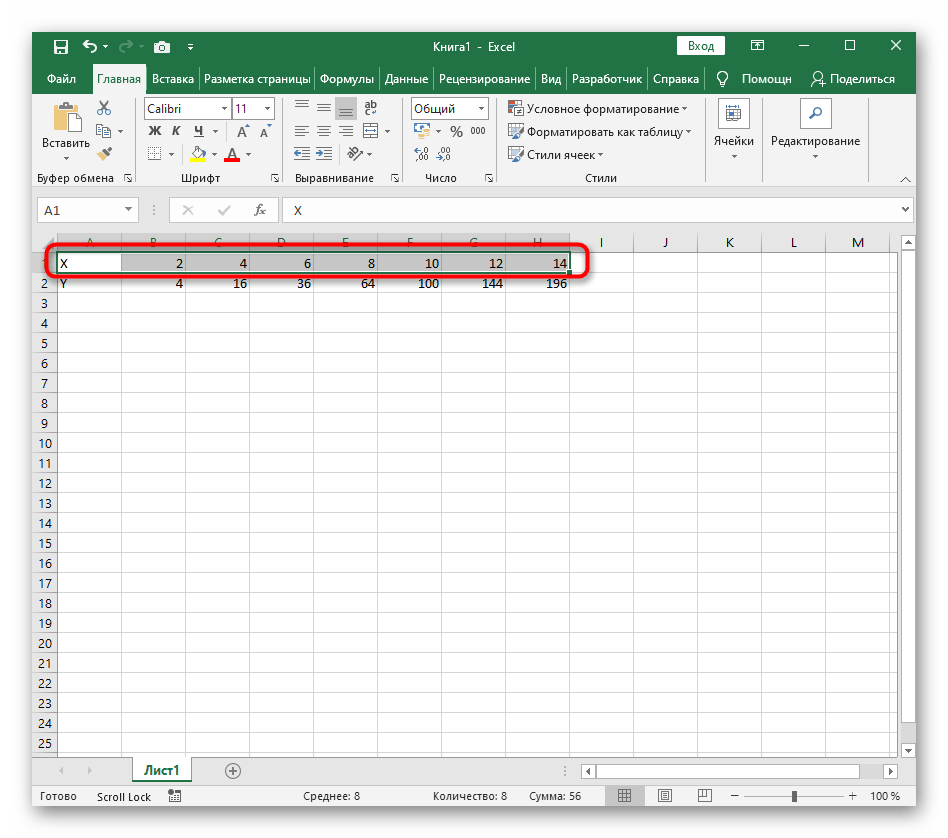
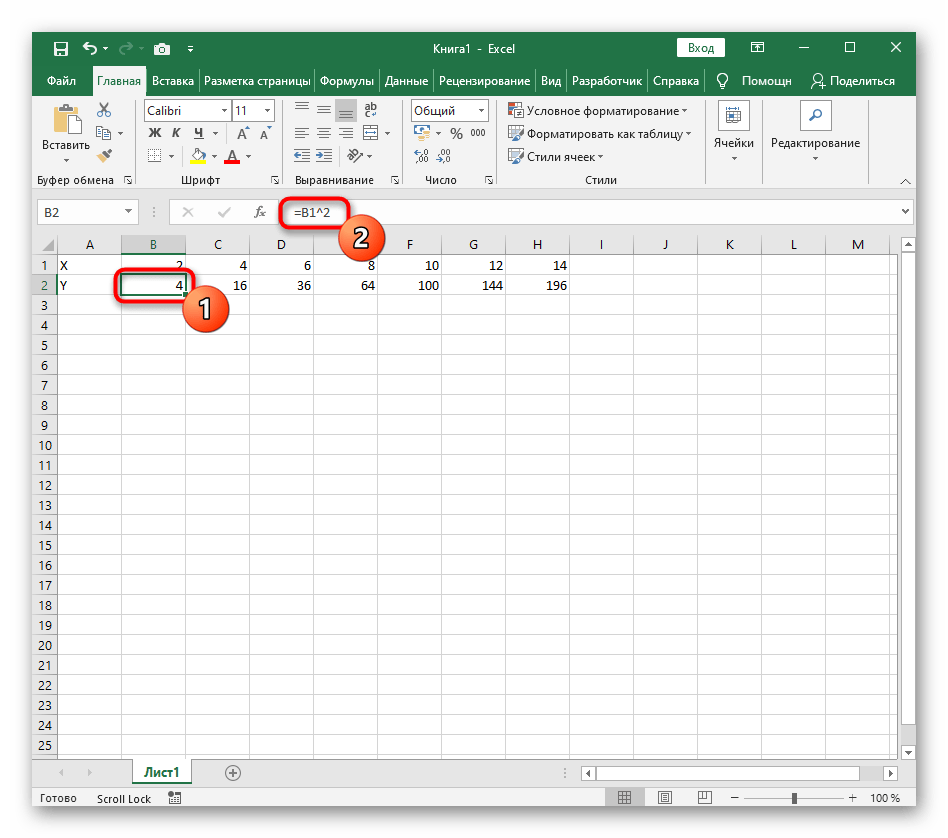
Составляем таблицу. Первый столбец – значения Х. Используем формулы. Значение первой ячейки – 1. Второй: = (имя первой ячейки) + 0,3. Выделяем правый нижний угол ячейки с формулой – тянем вниз столько, сколько нужно.
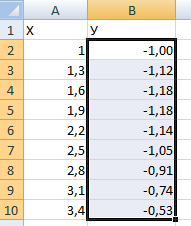
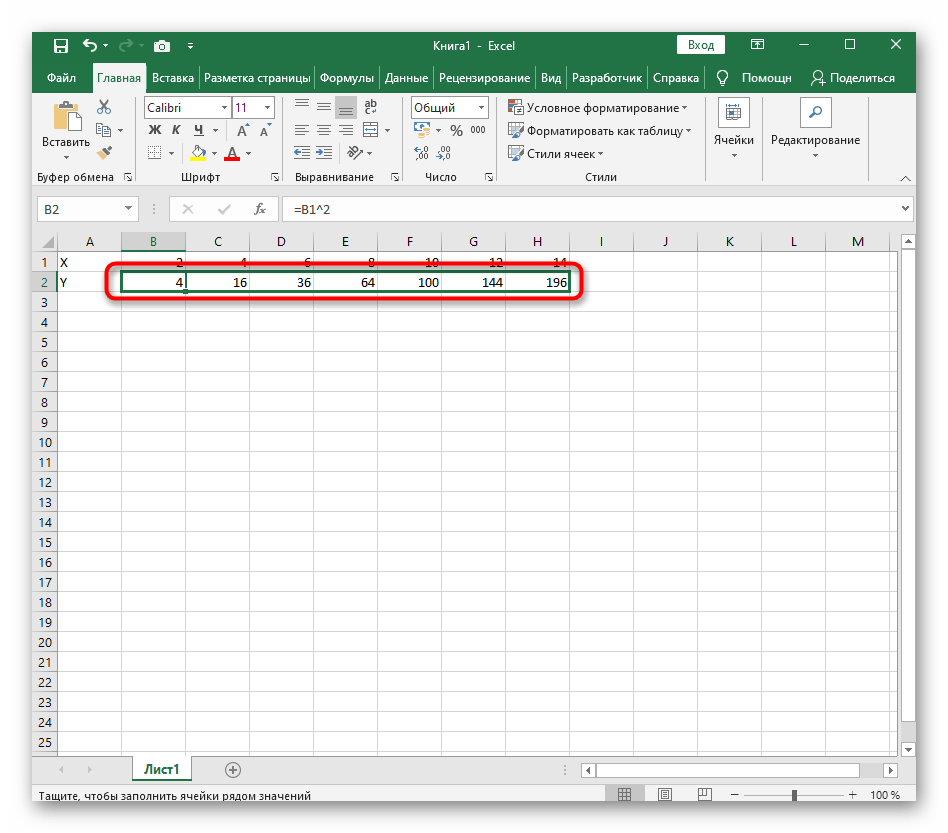
В столбце У прописываем формулу для расчета функции. В нашем примере: =A2*(КОРЕНЬ(A2)-2). Нажимаем «Ввод». Excel посчитал значение. «Размножаем» формулу по всему столбцу (потянув за правый нижний угол ячейки). Таблица с данными готова.
Переходим на новый лист (можно остаться и на этом – поставить курсор в свободную ячейку). «Вставка» — «Диаграмма» — «Точечная». Выбираем понравившийся тип. Щелкаем по области диаграммы правой кнопкой мыши – «Выбрать данные».
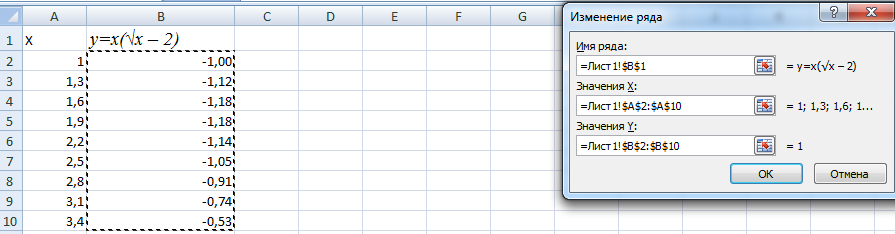
Выделяем значения Х (первый столбец). И нажимаем «Добавить». Открывается окно «Изменение ряда». Задаем имя ряда – функция. Значения Х – первый столбец таблицы с данными. Значения У – второй.
Жмем ОК и любуемся результатом.
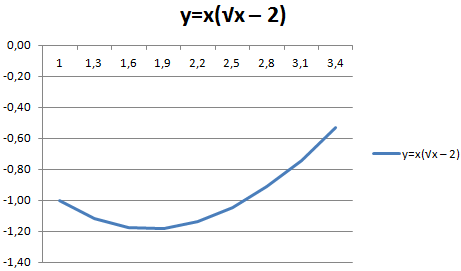
С осью У все в порядке. На оси Х нет значений. Проставлены только номера точек. Это нужно исправить. Необходимо подписать оси графика в excel. Правая кнопка мыши – «Выбрать данные» — «Изменить подписи горизонтальной оси». И выделяем диапазон с нужными значениями (в таблице с данными). График становится таким, каким должен быть.
Наложение и комбинирование графиков
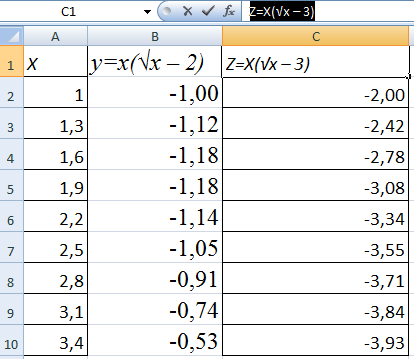
Построить два графика в Excel не представляет никакой сложности. Совместим на одном поле два графика функций в Excel. Добавим к предыдущей Z=X(√x – 3). Таблица с данными:
Выделяем данные и вставляем в поле диаграммы. Если что-то не так (не те названия рядов, неправильно отразились цифры на оси), редактируем через вкладку «Выбрать данные».
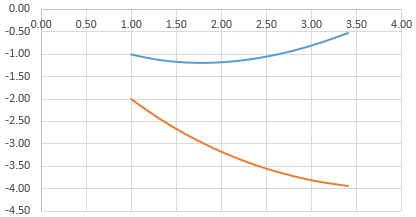
А вот наши 2 графика функций в одном поле.
Графики зависимости
Данные одного столбца (строки) зависят от данных другого столбца (строки).
Построить график зависимости одного столбца от другого в Excel можно так:
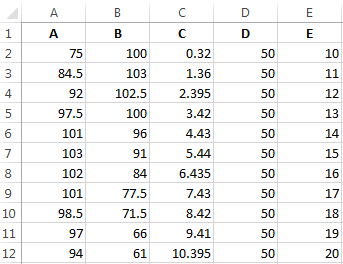
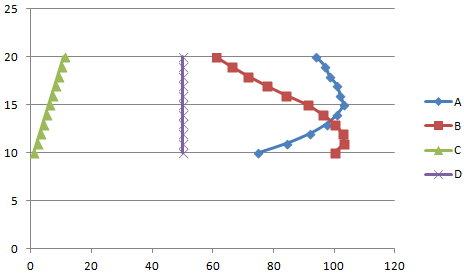
Условия: А = f (E); В = f (E); С = f (E); D = f (E).
Выбираем тип диаграммы. Точечная. С гладкими кривыми и маркерами.
Выбор данных – «Добавить». Имя ряда – А. Значения Х – значения А. Значения У – значения Е. Снова «Добавить». Имя ряда – В. Значения Х – данные в столбце В. Значения У – данные в столбце Е. И по такому принципу всю таблицу.
Готовые примеры графиков и диаграмм в Excel скачать:
Точно так же можно строить кольцевые и линейчатые диаграммы, гистограммы, пузырьковые, биржевые и т.д. Возможности Excel разнообразны. Вполне достаточно, чтобы наглядно изобразить разные типы данных.
Построение графиков функции в Excel – тема не сложная и Эксель с ней может справиться без проблем. Главное правильно задать параметры и выбрать подходящую диаграмму. В данном примере будем строить точечную диаграмму в Excel.
Учитывая, что функция – зависимость одного параметра от другого, зададим значения для оси абсцисс с шагом 0,5. Строить график будем на отрезке [-3;3]. Называем столбец «х» , пишем первое значение «-3» , второе – «-2,5» . Выделяем их и тянем вниз за черный крестик в правом нижнем углу ячейки.
Будем строить график функции вида y=х^3+2х^2+2. В ячейке В1 пишем «у» , для удобства можно вписать всю формулу. Выделяем ячейку В2 , ставим «=» и в «Строке формул» пишем формулу: вместо «х» ставим ссылку на нужную ячейку, чтобы возвести число в степень, нажмите «Shift+6» . Когда закончите, нажмите «Enter» и растяните формулу вниз.
У нас получилась таблица, в одном столбце которой записаны значения аргумента – «х» , в другом – рассчитаны значения для заданной функции.
Перейдем к построению графика функции в Excel. Выделяем значения для «х» и для «у» , переходим на вкладку «Вставка» и в группе «Диаграммы» нажимаем на кнопочку «Точечная» . Выберите одну из предложенных видов.
График функции выглядит следующим образом.
Теперь покажем, что по оси «х» установлен шаг 0,5. Выделите ее и кликните по ней правой кнопкой мши. Из контекстного меню выберите пункт «Формат оси» .
Откроется соответствующее диалоговое окно. На вкладке «Параметры оси» в поле «цена основных делений» , поставьте маркер в пункте «фиксированное» и впишите значение «0,5» .
Чтобы добавить название диаграммы и название для осей, отключить легенду, добавить сетку, залить ее или выбрать контур, поклацайте по вкладкам «Конструктор» , «Макет» , «Формат» .
Построить график функции в Эксель можно и с помощью «Графика» . О том, как построить график в Эксель, Вы можете прочесть, перейдя по ссылке.
Давайте добавим еще один график на данную диаграмму. На этот раз функция будет иметь вид: у1=2*х+5. Называем столбец и рассчитываем формулу для различных значений «х» .
Выделяем диаграмму, кликаем по ней правой кнопкой мыши и выбираем из контекстного меню «Выбрать данные» .
В поле «Элементы легенды» кликаем на кнопочку «Добавить» .
Появится окно «Изменение ряда» . Поставьте курсор в поле «Имя ряда» и выделите ячейку С1 . Для полей «Значения Х» и «Значения У» выделяем данные из соответствующих столбцов. Нажмите «ОК» .
Чтобы для первого графика в Легенде не было написано «Ряд 1» , выделите его и нажмите на кнопку «Изменить» .
Ставим курсор в поле «Имя ряда» и выделяем мышкой нужную ячейку. Нажмите «ОК» .
Ввести данные можно и с клавиатуры, но в этом случае, если Вы измените данные в ячейке В1 , подпись на диаграмме не поменяется.
В результате получилась следующая диаграмма, на которой построены два графика: для «у» и «у1» .
Думаю теперь, Вы сможете построить график функции в Excel, и при необходимости добавлять на диаграмму нужные графики.
Для рассмотренных выше задач удавалось построить уравнение или систему уравнений. Но во многих случаях при решении практических задач имеются лишь экспериментальные (результаты измерений, статистические, справочные, опытные) данные. По ним с определенной мерой близости пытаются восстановить эмпирическую формулу (уравнение), которая может быть использована для поиска решения, моделирования, оценки решений, прогнозов.
Процесс подбора эмпирической формулы P(x) для опытной зависимости F(x) называется аппроксимацией (сглаживанием). Для зависимостей с одним неизвестным в Excel используются графики, а для зависимостей со многими неизвестными – пары функций из группы Статистические ЛИНЕЙН и ТЕНДЕНЦИЯ, ЛГРФПРИБЛ и РОСТ .
В настоящем разделе рассматривается аппроксимация экспериментальных данных с помощью графиков Excel: на основе данных стоится график, к нему подбирается линия тренда, т.е. аппроксимирующая функция, которая с максимальной степенью близости приближается к опытной зависимости.
Степень близости подбираемой функции оценивается коэффициентом детерминации R 2 . Если нет других теоретических соображений, то выбирают функцию с коэффициентом R 2 , стремящимся к 1. Отметим, что подбор формул с использованием линии тренда позволяет установить как вид эмпирической формулы, так и определить численные значения неизвестных параметров.

1. Линейная – y=cx+b. Это простейшая функция, отражающая рост и убывание данных с постоянной скоростью.
2. Полиномиальная – y=c+c1x+c2x 2 +…+c6x 6 . Функция описывает попеременно возрастающие и убывающие данные. Полином 2-ой степени может иметь один экстремум (min или max), 3-ей степени – до 2-х экстремумов, 4-ой степени – до 3-х и т.д.
3. Логарифмическая – y=clnx+b. Эта функция описывает быстро возрастающие (убывающие) данные, которые затем стабилизируются.
4. Степенная – y=cx b , (х>0и y>0). Функция отражает данные с постоянно увеличивающейся (убывающей) скоростью роста.
5. Экспоненциальная – y=ce bx , (e – основание натурального логарифма). Функция описывает быстро растущие (убывающие) данные, которые затем стабилизируются.
Для всех 5-ти видов функций используется аппроксимация данных по методу наименьших квадратов (см. справку по F1 “линия тренда”).
В качестве примера рассмотрим зависимость продаж от рекламы, заданную следующими статистическими данными по некоторой фирме:
| Реклама (тыс. руб.) | 1,5 | 2,5 | 3,5 | 4,5 | 5,5 |
| Продажи (тыс. руб.) |
Необходимо построить функцию, наилучшим образом отражающую эту зависимость. Кроме того, необходимо оценить продажи для рекламных вложений в 6 тыс. руб.
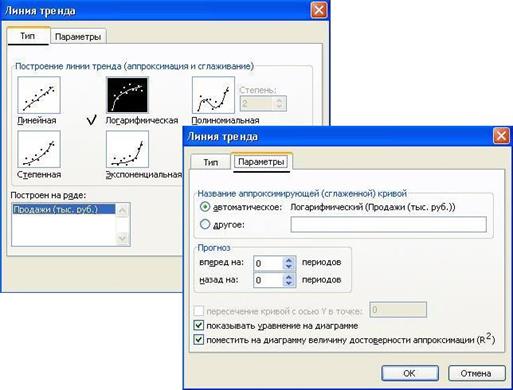
Приступим к решению. В первую очередь введите эти данные в Excel и постройте график, как на рис. 38. Как видно, график построен на основании диапазона B2:J2. Далее, щелкнув правой кнопкой мыши по графику, добавьте линию тренда, как показано на рис. 38.

В открывшемся окне настройки (рис. 39), на закладке Тип выберите для аппроксимации логарифмическую линию тренда (по виду графика). На закладке Параметры установите флажки, отображающие на графике уравнение и коэффициент детерминации.
После нажатия ОК Вы получите результат, как на рис. 40. Коэффициент детерминации R 2 =0.9846, что является неплохой степенью близости. Для подтверждения правильности выбранной функции (поскольку других теоретических соображений нет) спрогнозируйте развитие продаж на 10 периодов вперед. Для этого щелкните правой кнопкой по линии тренда – измените формат – после этого в поле Прогноз: вперед на: установите 10 (рис. 41).
После установки прогноза Вы увидите изменение кривой графика на 10 периодов наблюдения вперед, как на рис. 42. Он с большой долей вероятности отражает дальнейшее увеличение продаж с увеличением рекламных вложений.
Вычисление по полученной формуле =237,96*LN(6)+5,9606 в Excel дает значение 432 тыс. руб.

Часть11. Контрольные задания
Последнее изменение этой страницы: 2016-08-26; Нарушение авторского права страницы
Профи
(774),
закрыт
1 месяц назад
dmitry melkov
Мастер
(1189)
13 лет назад
в принципе можно попробывать.. .
правой кнопкой по графику, выбрать “добавить линию тренда”, выбрать наиболее подходящий по виду тренд и на вкладке “параметры” поставить галочку “показывать уравнение на диаграмме”
Варианты построения графика функции в Microsoft Excel
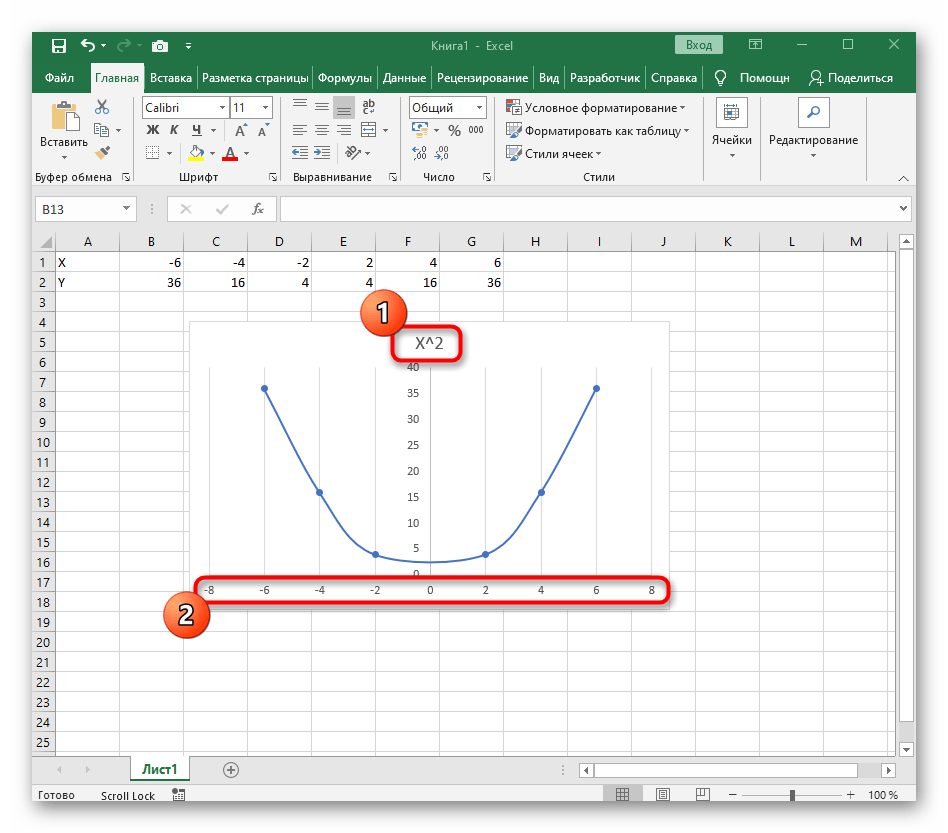
Вариант 1: График функции X^2
В качестве первого примера для Excel рассмотрим самую популярную функцию F(x)=X^2. График от этой функции в большинстве случаев должен содержать точки, что мы и реализуем при его составлении в будущем, а пока разберем основные составляющие.
-
Создайте строку X, где укажите необходимый диапазон чисел для графика функции.
Ниже сделайте то же самое с Y, но можно обойтись и без ручного вычисления всех значений, к тому же это будет удобно, если они изначально не заданы и их нужно рассчитать.
Растяните функцию, зажав правый нижний угол ячейки, и приведя таблицу в тот вид, который продемонстрирован на следующем скриншоте.
Диапазон данных для построения графика функции указан, а это означает, что можно выделять его и переходить на вкладку «Вставка».
В новом окне перейдите на вкладку «Все диаграммы» и в списке найдите «Точечная».
Подойдет вариант «Точечная с гладкими кривыми и маркерами».
После ее вставки в таблицу обратите внимание, что мы добавили равнозначный диапазон отрицательных и плюсовых значений, чтобы получить примерно стандартное представление параболы.
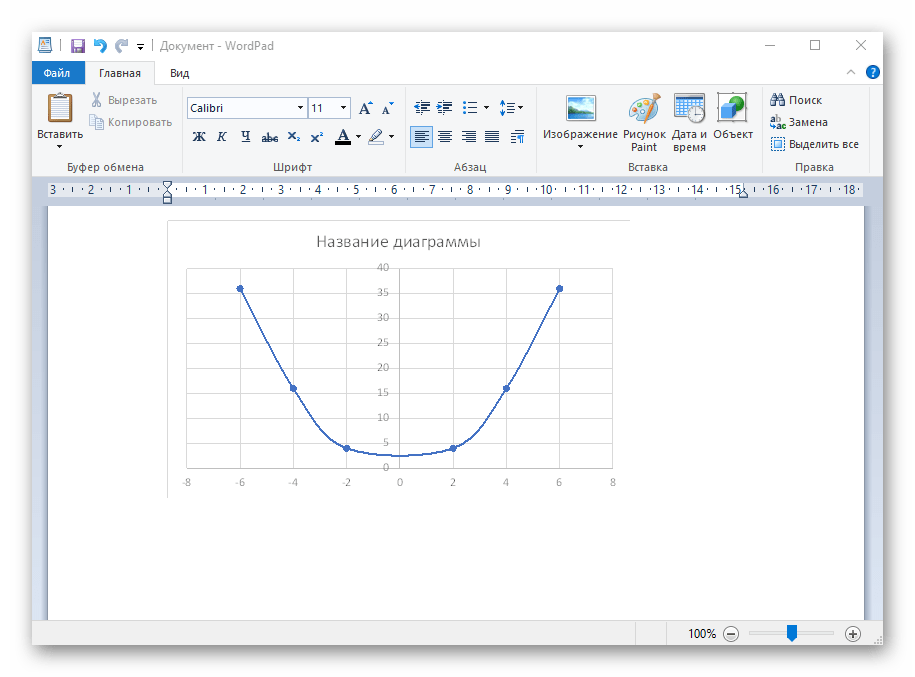
Из дополнительных возможностей отметим копирование и перенос графика в любой текстовый редактор. Для этого щелкните в нем по пустому месту ПКМ и из контекстного меню выберите «Копировать».
Если график должен быть точечным, но функция не соответствует указанной, составляйте его точно в таком же порядке, формируя требуемые вычисления в таблице, чтобы оптимизировать их и упростить весь процесс работы с данными.
Вариант 2: График функции y=sin(x)
Функций очень много и разобрать их в рамках этой статьи просто невозможно, поэтому в качестве альтернативы предыдущему варианту предлагаем остановиться на еще одном популярном, но сложном — y=sin(x). То есть изначально есть диапазон значений X, затем нужно посчитать синус, чему и будет равняться Y. В этом тоже поможет созданная таблица, из которой потом и построим график функции.
-
Для удобства укажем всю необходимую информацию на листе в Excel. Это будет сама функция sin(x), интервал значений от -1 до 5 и их шаг весом в 0.25.
Создайте сразу два столбца — X и Y, куда будете записывать данные.
Запишите самостоятельно первые два или три значения с указанным шагом.
Далее растяните столбец с X так же, как обычно растягиваете функции, чтобы автоматически не заполнять каждый шаг.
Перейдите к столбцу Y и объявите функцию =SIN( , а в качестве числа укажите первое значение X.
Сама функция автоматически высчитает синус заданного числа.
Растяните столбец точно так же, как это было показано ранее.
Если чисел после запятой слишком много, уменьшите разрядность, несколько раз нажав по соответствующей кнопке.
Выделите столбец с Y и перейдите на вкладку «Вставка».
Создайте стандартный график, развернув выпадающее меню.
График функции от y=sin(x) успешно построен и отображается правильно. Редактируйте его название и отображаемые шаги для простоты понимания.
Помимо этой статьи, на сайте еще 12704 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Как в экселе построить график по уравнению?
Рассмотрим на примере, как можно в программе эксель построить график по уравнению. В качестве уравнения будем использовать следующую функцию: y=x 2 /2+1.
Первый этап. Чтобы построить график, нужно найти несколько его точек. Поэтому сначала сделаем таблицу для значений «y» и «x». Сразу запишем значения «x» от -8 до 8 с шагом 2.
Второй этап. Посчитаем значения «y», начнем с ячейки «В2», в которой пропишем формулу: =(A2^2)/2+1. Данную формулу копируем на все остальные ячейки с «В3» по «В10».
Третий этап. Выделим область, содержащую значения «y» и «x», после на верхней панели выберем вкладку «Вставка» и найдем иконку в блоке «Диаграммы» с названием «Точечная».
Четвертый этап. При нажатии на иконку «Точечная», нам будет доступен вид графика, выберем третий по счету.
В итоге мы построили в программе эксель график по уравнению.
Видео
Как построить график в Excel по уравнению
Как предоставить информацию, чтобы она лучше воспринималась. Используйте графики. Это особенно актуально в аналитике. Рассмотрим, как построить график в Excel по уравнению.
Что это такое
График показывает, как одни величины зависят от других. Информация легче воспринимается. Посмотрите визуально, как отображается динамика изменения данных.
А нужно ли это
Графический способ отображения информации востребован в учебных или научных работах, исследованиях, при создании деловых планов, отчетов, презентаций, формул. Разработчики для построения графиков добавили способы визуального представления: диаграммы, пиктограммы.
Как построить график уравнения регрессии в Excel
Регрессионный анализ — статистический метод исследования. Устанавливает, как независимые величины влияют на зависимую переменную. Редактор предлагает инструменты для такого анализа.
Подготовительные работы
Перед использованием функции активируйте Пакет анализа. Перейдите: 
Выберите раздел: 
Далее: 
Прокрутите окно вниз, выберите: 
Отметьте пункт: 
Открыв раздел «Данные», появится кнопка «Анализ».
Как пользоваться
Рассмотрим на примере. В таблице указана температура воздуха и число покупателей. Данные выводятся за рабочий день. Как температура влияет на посещаемость. Перейдите: 
Выберите: 
Отобразится окно настроек, где входной интервал:
- Y. Ячейки с данными влияние факторов на которые нужно установить. Это число покупателей. Адрес пропишите вручную или выделите соответствующий столбец;
- Х. Данные, влияние на которые нужно установить. В примере, нужно узнать, как температура влияет на количество покупателей. Поэтому выделяем ячейки в столбце «Температура».
Анализ
Нажав кнопку «ОК», отобразится результат. 
Основной показатель — R-квадрат. Обозначает качество. Он равен 0,825 (82,5%). Что это означает? Зависимости, где показатель меньше 0,5 считается плохим. Поэтому в примере это хороший показатель. Y-пересечение. Число покупателей, если другие показатели равны нулю. 62,02 высокий показатель.
Как построить график квадратного уравнения в Excel
График функции имеет вид: y=ax2+bx+c. Рассмотрим диапазон значений: [-4:4].
- Составьте таблицу как на скриншоте;
- В третьей строке указываем коэффициенты и их значения;
- Пятая — диапазон значений;
- В ячейку B6 вписываем формулу =$B3*B5*B5+$D3*B5+$F3;


При вычислении формулы прописывается знак «$». Используется чтобы ссылка была постоянной. Подробнее смотрите в статье: «Как зафиксировать ячейку».
Выделите диапазон значений по ним будем строить график. Перейдите: 
Поместите график в свободное место на листе.
Как построить график линейного уравнения
Функция имеет вид: y=kx+b. Построим в интервале [-4;4].
- В таблицу прописываем значение постоянных величин. Строка три;
- Строка 5. Вводим диапазон значений;
- Ячейка В6. Прописываем формулу.


График — прямая линия.
Вывод
Мы рассмотрели, как построить график в Экселе (Excel) по уравнению. Главное — правильно выбрать параметры и диаграмму. Тогда график точно отобразит данные.
[spoiler title=”источники:”]
http://portalonline.ru/kompyutery-i-programmy/1536-kak-v-eksele-postroit-grafik-po-uravneniyu.html
http://public-pc.com/kak-postroit-grafik-v-excel-po-uravneniyu/
[/spoiler]
Содержание
Подбор
формул по графику. Линия тренда
Подбор
формул со многими неизвестными
Расчет
стоимости недвижимости
Оценка
эффективности рекламы
Подбор
формул по графику. Линия тренда
Для
всех рассмотренных выше задач удавалось
построить уравнение или систему
уравнений. Но во многих случаях при
решении практических задач имеются
лишь экспериментальные (результаты
измерений, статистические, справочные,
опытные) данные. По ним с определенной
мерой близости пытаются восстановить
эмпирическую формулу (уравнение), которая
может быть использована для поиска
решения, моделирования, оценки решений,
прогнозов.
Процесс
подбора эмпирической формулы P(x)
для опытной зависимости F(x)
называется аппроксимацией
(сглаживанием).
Для зависимостей с одним неизвестным
в Excel
используются графики, а для зависимостей
со многими неизвестными – пары функций
из группы Статистические
ЛИНЕЙН и ТЕНДЕНЦИЯ, ЛГРФПРИБЛ и РОСТ.
В
настоящем разделе рассматривается
аппроксимация экспериментальных данных
с помощью графиков Excel:
на основе данных стоится график, к нему
подбирается линия
тренда, т.е.
аппроксимирующая функция, которая с
максимальной степенью близости
приближается к опытной зависимости.
Excel
предоставляет 5 видов аппроксимирующих
функций:
-
Линейная
– y=cx+b.
Это простейшая функция, отражающая
рост и убывание данных с постоянной
скоростью. -
Полиномиальная
– y=c0+c1x+c2x2+…+c6x6.
Функция описывает попеременно
возрастающие и убывающие данные. Полином
2-ой степени может иметь один экстремум
(min
или max),
3-ей степени – до 2-х экстремумов, 4-ой
степени – до 3-х и т.д. -
Логарифмическая
– y=clnx+b.
Эта функция описывает быстро возрастающие
(убывающие) данные, которые затем
стабилизируются. -
Степенная
– y=cxb,
(х>0
и
y>0).
Функция отражает данные с постоянно
увеличивающейся (убывающей) скоростью
роста. -
Экспоненциальная
– y=cebx,
(e
– основание натурального логарифма).
Функция описывает быстро растущие
(убывающие) данные, которые затем
стабилизируются.
Степень
близости подбираемой функции оценивается
коэффициентом
детерминации
R2.
Если нет других теоретических соображений,
то выбирают функцию с коэффициентом
R2,
стремящимся к 1. Отметим, что подбор
формул с использованием линии тренда
позволяет установить как вид эмпирической
формулы, так и определить численные
значения неизвестных параметров.
Для
всех 5 видов функций используется
аппроксимация данных по методу наименьших
квадратов. Подробнее о формулах расчета
линии тренда и коэффициента детерминации
смотрите в справке по F1,
введя поиск слов «линия тренда».
В
качестве примера рассмотрим зависимость
продаж от рекламы, заданную следующими
статистическими данными по некоторой
фирме:
|
Реклама |
1,5 |
2 |
2,5 |
3 |
3,5 |
4 |
4,5 |
5 |
5,5 |
6 |
|
Продажи |
3 |
13 |
25 |
35 |
40 |
45 |
48 |
50 |
51 |
Необходимо
построить функцию, наилучшим образом
отражающую эту зависимость. Кроме того,
необходимо оценить продажи для рекламных
вложений в 6 тыс. руб.
Приступим
к решению: в первую очередь введите эти
данные в Excel
и постройте график, как на рис. 2.48. Как
видно, график построен на основании
диапазона B2:J2.
Далее, щелкнув правой кнопкой мыши по
графику, добавьте линию тренда, как
показано на рис. 2.48.
В
открывшемся окне настройки (рис. 2.49), в
закладке Тип
выберите для аппроксимации логарифмическую
линию тренда (по виду графика). В закладке
Параметры
установите флажки, отображающие на
графике уравнение и коэффициент
детерминации.
После
нажатия ОК
Вы получите результат, как на рис. 2.50.
Коэффициент детерминации R2=0.9846,
что является неплохой степенью близости.
Для подтверждения правильности выбранной
функции (поскольку других теоретических
соображений нет) спрогнозируйте развитие
продаж на 10 периодов вперед. Для этого
щелкните правой кнопкой по линии тренда
– измените формат – после этого в поле
Прогноз: вперед
на: (рис. 2.49)
установите значение 10.
Рис.
2.48
Рис.
2.49
Рис.
2.50
После
установки прогноза Вы увидите изменение
кривой графика на 10 периодов наблюдения
вперед, как на рис. 2.51. Он с большой долей
вероятности отражает дальнейшее
увеличение продаж с увеличением рекламных
вложений.
Рис.
2.51
Теперь
вернитесь к состоянию рис. 2.50, нажав
кнопку
Отменить
на Панели инструментов. Попробуйте
изменить формат линии тренда – установите
полиномиальную
линию тренда полиномом 2-ой степени –
получите рис. 2.52.
Рис.
2.52
Как
видно, полученная формула аппроксимирует
исходную зависимость (на отрезке B2:J2)
с большей степенью близости, т.к.
R2=0.9973.
В то же время, если сделать прогноз на
10 периодов вперед, то он будет не совсем
верно отражать реальность: продажи не
могут уменьшаться с увеличением рекламных
вложений. Убедитесь в этом: сделайте
прогноз на 10 периодов наблюдения вперед
и получите график.
Опять
вернитесь к состоянию рис. 2.50, нажав
кнопку
Отменить.
Для вычисления продаж при рекламе в 6
тыс. руб. запишите в ячейку К2 формулу
=23,796*LN(K1)+0,5961: должно получиться 43,2 тыс.
штук.
В
Excel
имеется функция ПРЕДСКАЗ, которая
вычисляет будущее значение Y
по существующим парам значений X и Y
значениям с использованием линейной
регрессии. Функция Y
по возможности должна быть линейной,
т.е. описываться уравнением типа c+bx.
Функция предсказания для нашего примера
запишется так: =ПРЕДСКАЗ(K1;B2:J2;B1:J1).
Запишите – должно получится значение
64.4.
Обратите
внимание, что
на
рис. 2.50 ось Х подписана номерами периодов
наблюдения, а на рис. 2.52 – значениями в
точках наблюдения. Для нанесения значений
на ось Х щелкните правой кнопкой мыши
по графику и в выпавшем меню выберите
пункт Исходные
данные:
В
открывшемся одноименном окне, в закладке
Ряд,
в поле Подписи
оси Х,
укажите диапазон ячеек, где записаны
значения Х (здесь $B$1:$K$1).
Задачи
для самостоятельного выполнения:
-
Постройте
функцию, наилучшим образом отражающую
зависимость и спрогнозируйте значения
для следующего периода наблюдения со
значением 5, основываясь на следующих
данных:
|
Цена |
1 |
1,5 |
2 |
2,5 |
3 |
3,5 |
4 |
4,5 |
5 |
|
Спрос |
1300 |
700 |
500 |
200 |
100 |
70 |
50 |
40 |
-
Концентрация
ядовитого вещества в водоеме изменялась
во времени согласно таблице:
|
Время после |
1 |
3 |
5 |
8 |
|
Концентрация |
8 |
2.8 |
1 |
0.3 |
Определите
вид зависимости концентрации от времени
и расчетную концентрацию в момент
выброса.
Подбор
формул со многими неизвестными
Использование
линии тренда графиков Excel
– наиболее наглядный и информативный
способ восстановления зависимости и
исследования связи между двумя
переменными. Для зависимостей со многими
неизвестными подбор формул выполняют
с помощью специальных функций из группы
Статистические
– ЛИНЕЙН и ЛГРФПРИБЛ. Кроме того, функции
ТЕНДЕНЦИЯ и РОСТ позволяют вычислить
значения аппроксимирующей функции в
диапазоне наблюдения. Еще один инструмент
для подбора формул со многими неизвестными
Регрессия,
входящий в Пакет
анализа (СервисАнализ
данных…),
будет рассмотрен в следующем разделе.
В
настоящем разделе рассматривается
аппроксимация экспериментальных данных
с помощью функций ЛИНЕЙН, ТЕНДЕНЦИЯ,
ЛГРФПРИБЛ и РОСТ. Функции ЛИНЕЙН и
ТЕНДЕНЦИЯ применяют для восстановления
линейных зависимостей вида
y=b+a1x1+a2x2+…+anxn,
а функции ЛГРФПРИБЛ и РОСТ – для нелинейных
(показательных) зависимостей вида
y=ba1X1a2X2…anXn.
Функции
ЛИНЕЙН и ЛГРФПРИБЛ возвращают массив
с т.н. регрессионной статистикой, в
котором содержатся вычисленные значения
параметров (b,a1,a2,…an),
коэффициент детерминации
R2
и другие данные, характеризующие
аппроксимирующую функцию. Формат функций
ЛИНЕЙН, ЛГРФПРИБЛ и их применение
поясним на примере.
Расчет
стоимости недвижимости
Агентство
недвижимости оценивает однокомнатные
квартиры по трем переменным: х1 – общая
площадь, х2 – площадь кухни, х3 – этаж
квартиры, предполагая, что между каждой
переменной х1, х2, х3 и зависимой переменной
y
(стоимость) существует линейная
зависимость. Подобрать формулу для
вычисления стоимости однокомнатных
квартир и вычислить стоимость квартиры
с данными: х1=42кв.м, х2=11кв.м, х3=5эт. Собранные
рекламные данные занесены в приведенную
ниже таблицу.
Последовательность
действий для решения задачи следующая:
-
Заведите
приведенную таблицу в Excel,
в ячейки A1:D14. -
Выделите
диапазон ячеек B17:E21
(рис. 2.54) для сохранения результатов
вычислений функции ЛИНЕЙН – массива
регрессионной статистики. -
Вызовите
мастер функций, выберите статистическую
функцию ЛИНЕЙН и заполните параметры
функции как на рис. 2.53. Параметр Изв_знач_y
содержит диапазон D2:D14,
т.е. известные значения y.
Параметр Изв_знач_х
содержит диапазон A2:C14,
т.е. известные значения х. Параметр
Стат=1,
поскольку мы хотим получить дополнительную
статистику.
Рис.
2.53
-
После
нажатия ОК встаньте на строку формул
и нажмите Ctrl+Shift+Enter.
В результате должен получиться массив
значений, показанный на рис. 2.54.
Интересующие нас коэффициенты выделены
на рисунке (подробнее см. справку F1).
Коэффициент детерминации
R2=0.9725
вполне удовлетворителен. Таким образом,
искомая формула имеет вид:
Y
= 1,36*х1 + 0,1*х2 – 0,21*х3 – 19,27
Рис.
2.54
-
После
подбора формулы осталось вычислить
стоимость при х1=42, х2=11, х3=5. В любую
ячейку запишите выражение
=1,36*42+0,1*11–0,21*5–19,27. В результате получится
y=37.9
тыс. $.
Использование
функции ТЕНДЕНЦИЯ покажем на этом же
примере для расчета стоимостей различных
вариантов квартир, как показано на рис.
2.55.
Рис.
2.55
Новые
значения Х, для которых надо рассчитать
стоимость, следует ввести в ячейки
F2:H14.
Диапазон I2:I14
используйте для записи рассчитанных
значений y,
Вызовите мастер функций и функцию
ТЕНДЕНЦИЯ. Параметры функции заполните
как на рис. 2.56. Как видно параметр
Нов_знач_х
содержит диапазон F2:H14,
т.е. новые значения х. После нажатия ОК
встаньте на строку формул и нажмите
Ctrl+Shift+Enter
– результат, заполненный диапазон
I2:I14
на рис. 2.55.
Рис.
2.56
Оценка
эффективности рекламы
Следующий
пример. Подобрать формулу для вычисления
процента увеличения оборота при различных
затратах на рекламу. Экспериментально
известны проценты увеличения оборота
при затратах в 5, 10, 15, 20 тыс.$ в 3-х масс-медиа
– на телевидении, радио и в прессе:
|
5 тыс. |
10 тыс. |
15 |
20 тыс. |
|
|
1. |
28% |
43% |
61% |
95% |
|
2. |
15% |
24% |
34% |
50% |
|
3. |
6% |
9% |
13% |
20% |
Кроме
этого, надо вычислить процент увеличения
оборота в прессе при затратах 2 тыс.$ и
на телевидении при затратах в 22 тыс.$.
Дополнительно вычислите проценты для
всех масс-медиа при затратах 2, 17 и 25
тыс.$.
Для
решения задачи в первую очередь следует
правильно разместить данные – рис.
2.57.
Рис.
2.57
Затем
вычислите массив с регрессионной
статистикой функцией ЛИНЕЙН: выделите
диапазон ячеек F2:H6
и проделайте известные из предыдущего
примера действия. В итоге должен
получиться массив:
Как
видно, коэффициент детерминации
R2=0.8757
не удовлетворителен. Поэтому выполните
подбор формулы с помощью функции для
нелинейных зависимостей ЛГРФПРИБЛ:
выделите диапазон ячеек F2:H6
и проделайте известные из предыдущего
примера действия. В итоге должен
получиться массив:
В
этом случае коэффициент детерминации
R2=0.989
вполне удовлетворителен и можно записать
искомую аппроксимирующую формулу
показательного типа (т.к. использована
функция ЛГРФПРИБЛ):
Y
= 0,44 * 0,46х1
* 1,08х2
Теперь
вычислите проценты увеличения оборота
из условия задачи: введите формулы и не
забудьте установить процентный формат
отображения значений в ячейках. Результаты
приведены в таблице:
|
Пресса, |
5,0% |
=0,44*0,46^3*1,08^2 |
|
TV, |
110,0% |
=0,44*0,46^1*1,08^22 |
В
заключении, вычислите проценты для всех
масс-медиа при затратах 2, 17 и 25 тыс.$.
Подготовьте данные, колонки J
и K,
как на рис. 2.58.
Для
вычисления значений Y
используем функцию РОСТ, поскольку уже
известно, что зависимость нелинейная,
показательная. Выделите диапазон ячеек
L2:L10
и введите функцию РОСТ; заполнение
параметров функции показано на рис.
2.59.
Рис.
2.58
Рис.
2.59
После
нажатия ОК и Ctrl+Shift+Enter
на строке формул, колонка L
будет заполнена как на рис. 2.58. Сравните
результаты с результатами вычисления
по подобранной формуле.
Задачи
для самостоятельного выполнения:
-
Источник
радиоактивного излучения помещен в
жидкость. Датчик расположен на расстоянии
(х1) 20, 50 и 100 см от источника. Измерения
интенсивности излучения (y,
мРн) проводились через 1, 5 и 10 суток (х2)
после установки источника. Необходимо
подобрать аппроксимирующее уравнение.
Результаты измерений приведены в
таблице:
|
х1 |
1 |
5 |
10 |
|
20 |
61.2 |
43.6 |
28.3 |
|
50 |
33.6 |
24.0 |
15.6 |
|
100 |
12.3 |
8.8 |
5.7 |
-
В
бассейне проводится ежедневная частичная
смена воды. Необходимо подобрать формулу
для вычисления уровня воды в бассейне,
которая зависит от двух переменных: х1
– длительность впуска воды, х2 –
длительность выпуска воды. Кроме этого,
необходимо вычислить значения уровня
воды для х1[90;140]
с шагом 10 и х2[10;30]
с шагом 5. Исходные данные – результаты
наблюдений за неделю приведены в
таблице:
|
х1 |
х2 |
y |
|
120 |
20 |
3.2 |
|
100 |
25 |
2.8 |
|
130 |
20 |
3.3 |
|
100 |
15 |
3.3 |
|
110 |
23 |
3.0 |
|
105 |
26 |
2.8 |
|
112 |
13 |
3.3 |
9
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
|
0 / 0 / 0 Регистрация: 04.05.2018 Сообщений: 3 |
|
|
1 |
|
Найти функцию по ее графику (аппроксимация)05.05.2018, 14:35. Показов 7882. Ответов 3
Добрый день. Дано: Задача: найти функцию, отражающую (приблизительно) зависимость между параметрами. Я эту задачу пытаюсь решить с помощью инструмента в экселе (построение тренда; полиноминальная линия тренда 6й степени). Файл приложен. В чем косяк?
0 |
|
0 / 0 / 0 Регистрация: 04.05.2018 Сообщений: 3 |
|
|
05.05.2018, 14:53 [ТС] |
2 |
|
правильный файл-вложение
0 |
|
1062 / 506 / 137 Регистрация: 27.02.2013 Сообщений: 1,451 |
|
|
05.05.2018, 17:16 |
3 |
|
Решениеp1111, замените график на точечную диаграмму.
1 |
|
0 / 0 / 0 Регистрация: 04.05.2018 Сообщений: 3 |
|
|
05.05.2018, 18:04 [ТС] |
4 |
|
Как, оказывается, было просто. Спасибо огромное, очень выручили.
0 |

















































 Сообщение было отмечено p1111 как решение
Сообщение было отмечено p1111 как решение
