Помогаю со студенческими работами здесь
Составить уравнение касательной к графику
Составить уравнение касательной к графику функции y=x^3+2*x в точке M(1,3). Построить график
Нужно написать функцию по заданному графику
Нужно написать функцию которая отображена на графике
 Как определить функцию по имеющемуся графику
Как определить функцию по имеющемуся графику
Доброго времени суток, как найти формулу функции если есть график, далее имея данные на этом…
 Помогите написать функцию по заданному графику
Помогите написать функцию по заданному графику
Помогите написать функцию которая есть в архиве в файле маткад
Согласно Правилам Форума, пишем…
Подскажите как можно описать функцию по графику
Господа, подскажите пожалуйста как будет выглядеть функция графика, который находиться во…
 Задать функцию по графику и разложить в ряд Фурье
Задать функцию по графику и разложить в ряд Фурье
Всем доброго времени суток. Прошу, выручайте! Благодаря форуму я уже более менее понял, как в…
Искать еще темы с ответами
Или воспользуйтесь поиском по форуму:
For example, if I define the following in Matlab,
f(x) = x^2 + 3x - 2
How do I find what value the function evaluates to when x = 3?
tvanfosson
522k99 gold badges697 silver badges794 bronze badges
asked Mar 4, 2011 at 0:12
![]()
Eng.FouadEng.Fouad
114k70 gold badges312 silver badges415 bronze badges
Create a file called f.m that contains:
function y = f(x)
y = x^2 + 3x - 2
then in the command window, type f(3) and you should get back ans=16
See documentation on creating functions in MATLAB: http://www.mathworks.com/help/techdoc/ref/function.html
You can also use polyval(p,x) where p = [1 3 -2] in your example (the coeffients of your polynomial in descending order) and you will get the value of the polynomial at that point x (in your case, you would pass in 3).
answered Mar 4, 2011 at 0:27
1
Plot expression or function
Syntax
Description
example
fplot( plots thef)
curve defined by the function y = f(x) over the
default interval [-5 5] for x.
example
fplot( plotsf,xinterval)
over the specified interval. Specify the interval as a two-element
vector of the form [xmin xmax].
example
fplot( plotsfunx,funy)
the curve defined by x = funx(t) and y over the default interval
= funy(t)[-5 5] for t.
fplot( plotsfunx,funy,tinterval)
over the specified interval. Specify the interval as a two-element
vector of the form [tmin tmax].
fplot(___, specifiesLineSpec)
the line style, marker symbol, and line color. For example, '-r' plots
a red line. Use this option after any of the input argument combinations
in the previous syntaxes.
example
fplot(___, specifiesName,Value)
line properties using one or more name-value pair arguments. For example, 'LineWidth',2 specifies
a line width of 2 points.
fplot( plotsax,___)
into the axes specified byax instead of the current
axes (gca). Specify the axes as the first input
argument.
[x,y] = returns the abscissas and ordinates for
fplot(___)
the function without creating a plot. This syntax will be removed in a future
release. Use the XData and YData
properties of the line object, fp, instead.
Note
fplot no longer supports input arguments for
specifying the error tolerance or the number of evaluation points. To
specify the number of evaluation points, use the MeshDensity property.
Examples
collapse all
Plot Expression
Plot sin(x) over the default x interval [-5 5].
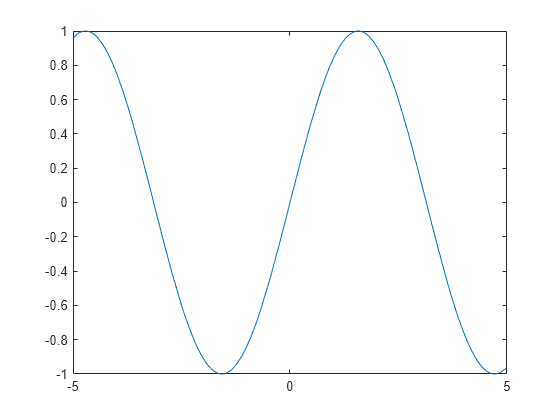
Plot Parametric Curve
Plot the parametric curve x=cos(3t) and y=sin(2t).
xt = @(t) cos(3*t); yt = @(t) sin(2*t); fplot(xt,yt)

Specify Plotting Interval and Plot Piecewise Functions
Plot the piecewise function
ex-3<x<0cos(x)0<x<3.
Plot multiple lines using hold on. Specify the plotting intervals using the second input argument of fplot. Specify the color of the plotted lines as blue using 'b'. When you plot multiple lines in the same axes, the axis limits adjust to incorporate all the data.
fplot(@(x) exp(x),[-3 0],'b') hold on fplot(@(x) cos(x),[0 3],'b') hold off grid on
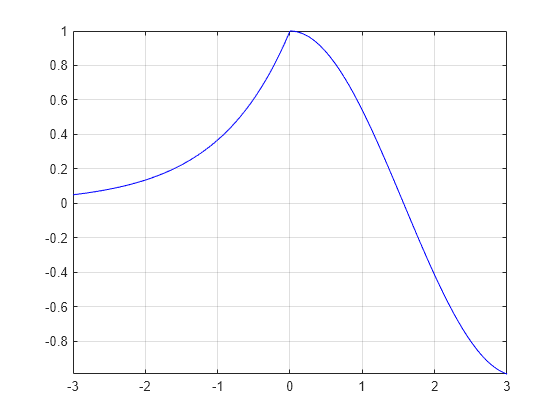
Specify Line Properties and Display Markers
Plot three sine waves with different phases. For the first, use a line width of 2 points. For the second, specify a dashed red line style with circle markers. For the third, specify a cyan, dash-dotted line style with asterisk markers.
fplot(@(x) sin(x+pi/5),'Linewidth',2); hold on fplot(@(x) sin(x-pi/5),'--or'); fplot(@(x) sin(x),'-.*c') hold off
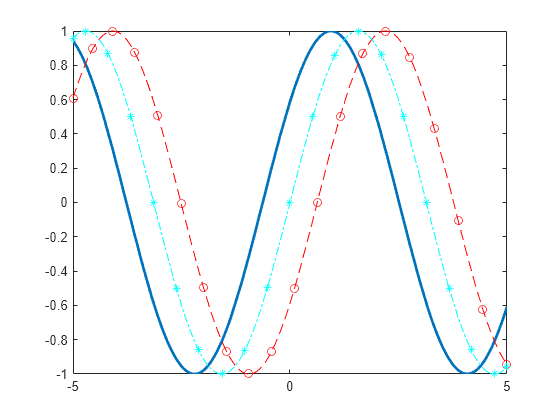
Modify Line Properties After Creation
Plot sin(x) and assign the function line object to a variable.

fp =
FunctionLine with properties:
Function: @(x)sin(x)
Color: [0 0.4470 0.7410]
LineStyle: '-'
LineWidth: 0.5000
Show all properties
Change the line to a dotted red line by using dot notation to set properties. Add cross markers and set the marker color to blue.
fp.LineStyle = ':'; fp.Color = 'r'; fp.Marker = 'x'; fp.MarkerEdgeColor = 'b';
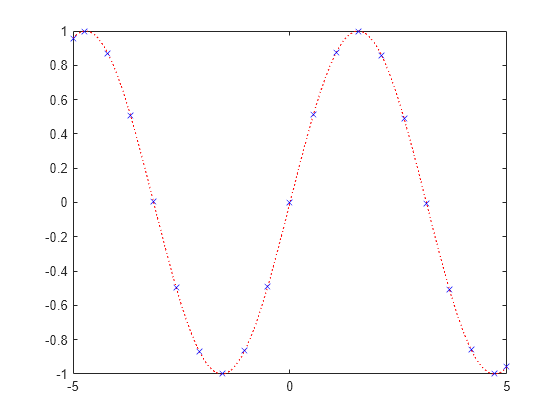
Plot Multiple Lines in Same Axes
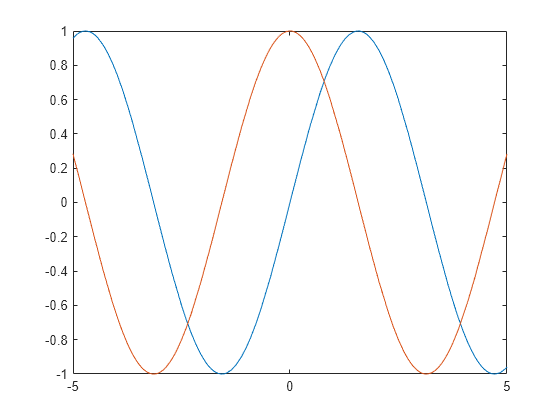
Plot two lines using hold on.
fplot(@(x) sin(x)) hold on fplot(@(x) cos(x)) hold off
Add Title and Axis Labels and Format Ticks
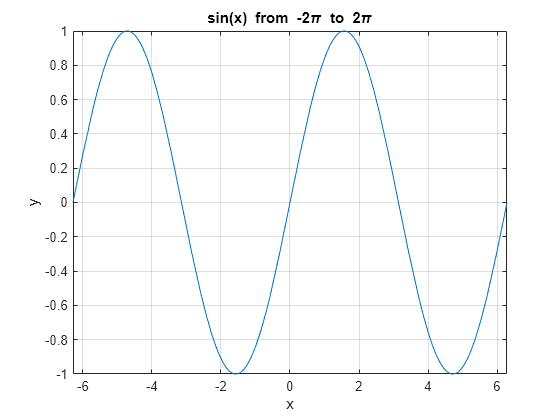
Plot sin(x) from -2π to 2π using a function handle. Display the grid lines. Then, add a title and label the x-axis and y-axis.
fplot(@sin,[-2*pi 2*pi]) grid on title('sin(x) from -2pi to 2pi') xlabel('x'); ylabel('y');
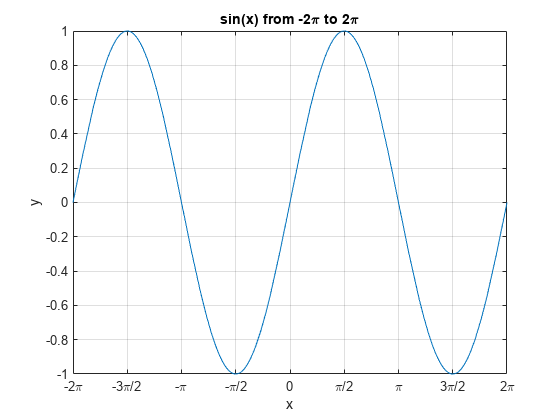
Use gca to access the current axes object. Display tick marks along the x-axis at intervals of π/2. Format the x-axis tick values by setting the XTick and XTickLabel properties of the axes object. Similar properties exist for the y-axis.
ax = gca;
ax.XTick = -2*pi:pi/2:2*pi;
ax.XTickLabel = {'-2pi','-3pi/2','-pi','-pi/2','0',...
'pi/2','pi','3pi/2','2pi'};
Input Arguments
collapse all
f — Function to plot
function handle
Function to plot, specified as a function handle to a named
or anonymous function.
Specify a function of the form y = f(x).
The function must accept a vector input argument and return a vector
output argument of the same size. Use array operators instead of matrix
operators for the best performance. For example, use .* (times)
instead of * (mtimes).
Note
Support for character vector inputs will be removed in a future
release. Use function handles instead.
Example: fplot(@(x) sin(x)) plots sin(x) over the default
interval, [-5, 5].
xinterval — Interval for x
[–5 5] (default) | two-element vector of form [xmin xmax]
Interval for x, specified as a two-element
vector of the form [xmin xmax].
funx — Parametric function for x coordinates
function handle
Parametric function for x coordinates, specified
as a function handle to a named or anonymous function.
Specify a function of the form x = funx(t).
The function must accept a vector input argument and return a vector
output argument of the same size. Use array operators instead of matrix
operators for the best performance. For example, use .* (times)
instead of * (mtimes).
Example: funx = @(t) sin(2*t);
funy — Parametric function for y coordinates
anonymous function | function handle
Parametric function for y coordinates, specified
as a function handle to a named or anonymous function.
Specify a function of the form y = funy(t).
The function must accept a vector input argument and return a vector
output argument of the same size. Use array operators instead of matrix
operators for the best performance. For example, use .* (times)
instead of * (mtimes).
Example: funy = @(t) cos(3*t);
tinterval — Interval for t
[-5 5] (default) | two-element vector of form [tmin tmax]
Interval for t, specified as a two-element
vector of the form [tmin tmax].
ax — Axes object
axes object
Axes object. If you do not specify an axes object, then fplot uses
the current axes (gca).
LineSpec — Line style, marker, and color
string scalar | character vector
Line style, marker, and color, specified as a string scalar or character vector containing
symbols. The symbols can appear in any order. You do not need to specify all
three characteristics (line style, marker, and color). For example, if you
omit the line style and specify the marker, then the plot shows only the
marker and no line.
Example: "--or" is a red dashed line with circle markers.
| Line Style | Description | Resulting Line |
|---|---|---|
"-" |
Solid line |
|
"--" |
Dashed line |
|
":" |
Dotted line |
|
"-." |
Dash-dotted line |
|
| Marker | Description | Resulting Marker |
|---|---|---|
"o" |
Circle |
|
"+" |
Plus sign |
|
"*" |
Asterisk |
|
"." |
Point |
|
"x" |
Cross |
|
"_" |
Horizontal line |
|
"|" |
Vertical line |
|
"square" |
Square |
|
"diamond" |
Diamond |
|
"^" |
Upward-pointing triangle |
|
"v" |
Downward-pointing triangle |
|
">" |
Right-pointing triangle |
|
"<" |
Left-pointing triangle |
|
"pentagram" |
Pentagram |
|
"hexagram" |
Hexagram |
|
| Color Name | Short Name | RGB Triplet | Appearance |
|---|---|---|---|
"red" |
"r" |
[1 0 0] |
|
"green" |
"g" |
[0 1 0] |
|
"blue" |
"b" |
[0 0 1] |
|
"cyan"
|
"c" |
[0 1 1] |
|
"magenta" |
"m" |
[1 0 1] |
|
"yellow" |
"y" |
[1 1 0] |
|
"black" |
"k" |
[0 0 0] |
|
"white" |
"w" |
[1 1 1] |
|
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: 'Marker','o','MarkerFaceColor','red'
The properties listed here are only a subset. For a complete
list, see FunctionLine Properties or ParameterizedFunctionLine Properties.
Number of evaluation points, specified as a number. The default
is 23. Because fplot uses
adaptive evaluation, the actual number of evaluation points is greater.
Line color, specified as an RGB triplet, a hexadecimal color code, a color name, or a short
name.
For a custom color, specify an RGB triplet or a hexadecimal color code.
-
An RGB triplet is a three-element row vector whose elements
specify the intensities of the red, green, and blue
components of the color. The intensities must be in the
range[0,1], for example,[0.4.
0.6 0.7] -
A hexadecimal color code is a string scalar or character
vector that starts with a hash symbol (#)
followed by three or six hexadecimal digits, which can range
from0toF. The
values are not case sensitive. Therefore, the color codes
"#FF8800",
"#ff8800",
"#F80", and
"#f80"are equivalent.
Alternatively, you can specify some common colors by name. This table lists the named color
options, the equivalent RGB triplets, and hexadecimal color codes.
| Color Name | Short Name | RGB Triplet | Hexadecimal Color Code | Appearance |
|---|---|---|---|---|
"red" |
"r" |
[1 0 0] |
"#FF0000" |
|
"green" |
"g" |
[0 1 0] |
"#00FF00" |
|
"blue" |
"b" |
[0 0 1] |
"#0000FF" |
|
"cyan"
|
"c" |
[0 1 1] |
"#00FFFF" |
|
"magenta" |
"m" |
[1 0 1] |
"#FF00FF" |
|
"yellow" |
"y" |
[1 1 0] |
"#FFFF00" |
|
"black" |
"k" |
[0 0 0] |
"#000000" |
|
"white" |
"w" |
[1 1 1] |
"#FFFFFF" |
|
Here are the RGB triplets and hexadecimal color codes for the default colors MATLAB® uses in many types of plots.
| RGB Triplet | Hexadecimal Color Code | Appearance |
|---|---|---|
[0 0.4470 0.7410] |
"#0072BD" |
|
[0.8500 0.3250 0.0980] |
"#D95319" |
|
[0.9290 0.6940 0.1250] |
"#EDB120" |
|
[0.4940 0.1840 0.5560] |
"#7E2F8E" |
|
[0.4660 0.6740 0.1880] |
"#77AC30" |
|
[0.3010 0.7450 0.9330] |
"#4DBEEE" |
|
[0.6350 0.0780 0.1840] |
"#A2142F" |
|
Example: 'blue'
Example: [0
0 1]
Example: '#0000FF'
Line style, specified as one of the options listed in this table.
| Line Style | Description | Resulting Line |
|---|---|---|
"-" |
Solid line |
|
"--" |
Dashed line |
|
":" |
Dotted line |
|
"-." |
Dash-dotted line |
|
"none" |
No line | No line |
Line width, specified as a positive value in points, where 1 point = 1/72 of an inch. If the
line has markers, then the line width also affects the marker
edges.
The line width cannot be thinner than the width of a pixel. If you set the line width
to a value that is less than the width of a pixel on your system, the line displays as
one pixel wide.
Marker symbol, specified as one of the values listed in this table. By default, the object
does not display markers. Specifying a marker symbol adds markers at each data point or
vertex.
| Marker | Description | Resulting Marker |
|---|---|---|
"o" |
Circle |
|
"+" |
Plus sign |
|
"*" |
Asterisk |
|
"." |
Point |
|
"x" |
Cross |
|
"_" |
Horizontal line |
|
"|" |
Vertical line |
|
"square" |
Square |
|
"diamond" |
Diamond |
|
"^" |
Upward-pointing triangle |
|
"v" |
Downward-pointing triangle |
|
">" |
Right-pointing triangle |
|
"<" |
Left-pointing triangle |
|
"pentagram" |
Pentagram |
|
"hexagram" |
Hexagram |
|
"none" |
No markers | Not applicable |
Marker outline color, specified as "auto", an RGB triplet, a
hexadecimal color code, a color name, or a short name. The default value of
"auto" uses the same color as the Color
property.
For a custom color, specify an RGB triplet or a hexadecimal color code.
-
An RGB triplet is a three-element row vector whose elements
specify the intensities of the red, green, and blue
components of the color. The intensities must be in the
range[0,1], for example,[0.4.
0.6 0.7] -
A hexadecimal color code is a string scalar or character
vector that starts with a hash symbol (#)
followed by three or six hexadecimal digits, which can range
from0toF. The
values are not case sensitive. Therefore, the color codes
"#FF8800",
"#ff8800",
"#F80", and
"#f80"are equivalent.
Alternatively, you can specify some common colors by name. This table lists the named color
options, the equivalent RGB triplets, and hexadecimal color codes.
| Color Name | Short Name | RGB Triplet | Hexadecimal Color Code | Appearance |
|---|---|---|---|---|
"red" |
"r" |
[1 0 0] |
"#FF0000" |
|
"green" |
"g" |
[0 1 0] |
"#00FF00" |
|
"blue" |
"b" |
[0 0 1] |
"#0000FF" |
|
"cyan"
|
"c" |
[0 1 1] |
"#00FFFF" |
|
"magenta" |
"m" |
[1 0 1] |
"#FF00FF" |
|
"yellow" |
"y" |
[1 1 0] |
"#FFFF00" |
|
"black" |
"k" |
[0 0 0] |
"#000000" |
|
"white" |
"w" |
[1 1 1] |
"#FFFFFF" |
|
"none" |
Not applicable | Not applicable | Not applicable | No color |
Here are the RGB triplets and hexadecimal color codes for the default colors MATLAB uses in many types of plots.
| RGB Triplet | Hexadecimal Color Code | Appearance |
|---|---|---|
[0 0.4470 0.7410] |
"#0072BD" |
|
[0.8500 0.3250 0.0980] |
"#D95319" |
|
[0.9290 0.6940 0.1250] |
"#EDB120" |
|
[0.4940 0.1840 0.5560] |
"#7E2F8E" |
|
[0.4660 0.6740 0.1880] |
"#77AC30" |
|
[0.3010 0.7450 0.9330] |
"#4DBEEE" |
|
[0.6350 0.0780 0.1840] |
"#A2142F" |
|
Marker fill color, specified as 'auto', an RGB triplet, a hexadecimal color
code, a color name, or a short name. The 'auto' value uses the same
color as the MarkerEdgeColor property.
For a custom color, specify an RGB triplet or a hexadecimal color code.
-
An RGB triplet is a three-element row vector whose elements
specify the intensities of the red, green, and blue
components of the color. The intensities must be in the
range[0,1], for example,[0.4.
0.6 0.7] -
A hexadecimal color code is a string scalar or character
vector that starts with a hash symbol (#)
followed by three or six hexadecimal digits, which can range
from0toF. The
values are not case sensitive. Therefore, the color codes
"#FF8800",
"#ff8800",
"#F80", and
"#f80"are equivalent.
Alternatively, you can specify some common colors by name. This table lists the named color
options, the equivalent RGB triplets, and hexadecimal color codes.
| Color Name | Short Name | RGB Triplet | Hexadecimal Color Code | Appearance |
|---|---|---|---|---|
"red" |
"r" |
[1 0 0] |
"#FF0000" |
|
"green" |
"g" |
[0 1 0] |
"#00FF00" |
|
"blue" |
"b" |
[0 0 1] |
"#0000FF" |
|
"cyan"
|
"c" |
[0 1 1] |
"#00FFFF" |
|
"magenta" |
"m" |
[1 0 1] |
"#FF00FF" |
|
"yellow" |
"y" |
[1 1 0] |
"#FFFF00" |
|
"black" |
"k" |
[0 0 0] |
"#000000" |
|
"white" |
"w" |
[1 1 1] |
"#FFFFFF" |
|
"none" |
Not applicable | Not applicable | Not applicable | No color |
Here are the RGB triplets and hexadecimal color codes for the default colors MATLAB uses in many types of plots.
| RGB Triplet | Hexadecimal Color Code | Appearance |
|---|---|---|
[0 0.4470 0.7410] |
"#0072BD" |
|
[0.8500 0.3250 0.0980] |
"#D95319" |
|
[0.9290 0.6940 0.1250] |
"#EDB120" |
|
[0.4940 0.1840 0.5560] |
"#7E2F8E" |
|
[0.4660 0.6740 0.1880] |
"#77AC30" |
|
[0.3010 0.7450 0.9330] |
"#4DBEEE" |
|
[0.6350 0.0780 0.1840] |
"#A2142F" |
|
Example: [0.3 0.2 0.1]
Example: 'green'
Example: '#D2F9A7'
Marker size, specified as a positive value in points, where 1 point = 1/72 of an inch.
Output Arguments
collapse all
fp — One or more FunctionLine or ParameterizedFunctionLine objects
scalar | vector
One or more FunctionLine or ParameterizedFunctionLine objects,
returned as a scalar or a vector.
-
If you use the
fplot(f)syntax
or a variation of this syntax, thenfplotreturnsFunctionLineobjects. -
If you use the
fplot(funx,funy)syntax
or a variation of this syntax, thenfplotreturnsParameterizedFunctionLineobjects.
You can use these objects to query and modify properties of
a specific line. For a list of properties, see FunctionLine Properties and ParameterizedFunctionLine Properties.
Tips
-
Use element-wise operators for the best performance
and to avoid a warning message. For example, usex.*yinstead
ofx*y. For more information, see Array vs. Matrix Operations. -
When you zoom in on the chart,
fplotreplots
the data, which can reveal hidden details.
Extended Capabilities
GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.
Usage notes and limitations:
-
This function accepts GPU arrays, but does not run on a GPU.
For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Distributed Arrays
Partition large arrays across the combined memory of your cluster using Parallel Computing Toolbox™.
Usage notes and limitations:
-
This function operates on distributed arrays, but executes in the client MATLAB.
For more information, see Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox).
Version History
Introduced before R2006a
Аппроксимация в Matlab
Приветствую! Сегодня продолжаем говорить об обработке экспериментальных данных. Сегодняшняя статья — продолжение предыдущей темы: Интерполяция в Matlab. Настоятельно советую с ней ознакомиться перед чтением данной статьи. По сути аппроксимация в Matlab очень похожа на интерполяцию, однако, для её реализации используются другие правила и функции.
Аппроксимация

Относительно интерполяции, аппроксимация получила более широкое распространение. Сущность этого метода состоит в том, что табличные данные аппроксимируют кривой, которая не обязательно должна пройти через все узловые точки, а должна как бы сгладить все случайные помехи табличной функции.
МНК (Метод Наименьших Квадратов)
Одним из самых популярных методов аппроксимации в Matlab и в других средах, это Метод Наименьших Квадратов ( МНК ). В этом методе при сглаживании опытных данных аппроксимирующую кривую стремятся провести так, чтобы её отклонения от табличных данных по всем узловым точкам были минимальными.
Суть МНК заключается в следующем: для табличных данных, полученных в результате эксперимента, отыскать аналитическую зависимость, сумма квадратов уклонений которой от табличных данных во всех узловых точках была бы минимальной.
Аппроксимация в Matlab по МНК осуществляется с помощью функции polyfit. Функция p = polyfit(x, y, n) находит коэффициенты полинома p(x) степени n, который аппроксимирует функцию y(x) в смысле метода наименьших квадратов. Выходом является строка p длины n+1, содержащая коэффициенты аппроксимирующего полинома.
Примеры задач
Разберём задачу, в которой разрешается использование встроенных матлабовских функций.
Осуществить аппроксимацию в Matlab табличных данных x = [0, 0.1 , 0.2, 0.3, 0.5] и y = [3, 4.5, 1.7, 0.7, -1] . Применяя метод наименьших квадратов, приблизить ее многочленами 1-ой и 2-ой степени. Для каждого определить величину среднеквадратической ошибки. Построить (на одном листе) графики и заданной таблично функции (ломанная линия) и приближающих ее многочленов 1-ой и 2-ой степени.

Вывод:
ans = 0.9253
ans = 0.8973
Однако, встречаются задачи, где требуется реализовать аппроксимацию в Matlab без использования специальных функций.
Найти у(0.25) путём построения аппроксимирующего полинома методом наименьших квадратов согласно данным:
x: 0, 0.1, 0.2, 0.3, 0.5
y: 3, 4.5, 1.7, 0.7, -1
p: 0.5, 0.8, 1.6, 0.8, 0.1
Построить этот полином без учёта весовых коэффициентов с использованием определителя Вандермонда и стандартных операторов.

Вывод:
a =
228.1447
-176.0984
22.7745
3.1590
qq = 228.1447 -176.0984 22.7745 3.1590
y2 = 1.4113
Как видите встроенные функции для аппроксимации в Matlab укорачивают алгоритм почти вдвое.
Существует также возможность реализации всего алгоритма через одну функцию, но для преподавателей студентов она скорее всего будет не приемлема. С помощью функции lsqcurvefit(fun,x0,xdata,ydata), где:
xdata,ydata– табличные значения аппроксимируемой функции;
x0 –стартовое значение параметров функции;
fun – функция аппроксимации, задаваемая пользователем
С аналитически-теоретической стороны, существуют такие виды аппроксимации:
- Аппроксимация ортогональными классическими полиномами.
- Аппроксимация каноническим полиномом
Но на практике их реализацию требуют редко.
Вот и вся основная информация по аппроксимации в Matlab, если остались вопросы, задавайте их в комментариях.
Документация
Два MATLAB ® функции могут смоделировать ваши данные полиномом.
Функции аппроксимации полиномом
polyfit(x,y,n) находит коэффициенты полиномиального p(x) из степени n это соответствует y данные путем минимизации суммы квадратов отклонений данных из модели (метод наименьших квадратов).
polyval(p,x) возвращает значение полинома степени n это было определено polyfit , оцененный в x .
В этом примере показано, как моделировать данные с помощью полинома.
Измерьте количество y в нескольких значениях времени t .

Можно попытаться моделировать эти данные с помощью полиномиальной функции второй степени,
y = a 2 t 2 + a 1 t + a 0 .
Неизвестные коэффициенты, a 0 , a 1 , и a 2 , вычисляются путем минимизации суммы квадратов отклонений данных из модели (метод наименьших квадратов).
Используйте polyfit найти полиномиальные коэффициенты.
MATLAB вычисляет полиномиальные коэффициенты в убывающих степенях.
Полиномиальная модель второй степени данных дана уравнением
y = — 0 . 2 9 4 2 t 2 + 1 . 0 2 3 1 t + 0 . 4 9 8 1 .
Оцените полином в однородно расположенные с интервалами времена, t2 . Затем отобразите на графике исходные данные и модель на том же графике.

Оцените модель во временном векторе данных
Вычислите остаточные значения.
Постройте остаточные значения.

Заметьте, что подгонка второй степени примерно следует за основной формой данных, но не получает плавную кривую, на которой данные, кажется, лежат. В остаточных значениях, кажется, существует шаблон, который указывает, что различная сила модели необходима. Полином пятой степени (показанный затем) делает лучшее задание следующих колебания данных.
Повторите осуществление, на этот раз с помощью полинома пятой степени от polyfit .
Оцените полином в t2 и постройте подгонку сверху данных в новом окне рисунка.

Примечание
При попытке смоделировать физическую ситуацию, всегда важно рассмотреть, значима ли модель определенного порядка в вашей ситуации.
Линейная модель с неполиномиальными условиями
В этом примере показано, как соответствовать данным линейной моделью, содержащей неполиномиальные термины.
Когда полиномиальная функция не производит удовлетворительную модель ваших данных, можно попытаться использовать линейную модель с неполиномиальными терминами. Например, рассмотрите следующую функцию, которая линейна в параметрах a 0 , a 1 , и a 2 , но нелинейный в t данные:
y = a 0 + a 1 e — t + a 2 t e — t .
Можно вычислить неизвестные коэффициенты a 0 , a 1 , и a 2 путем построения и решения набора одновременных уравнений и решения для параметров. Следующий синтаксис выполняет это путем формирования матрицы проекта , где каждый столбец представляет переменную, используемую, чтобы предсказать ответ (член в модели), и каждая строка соответствует одному наблюдению за теми переменными.
Введите t и y как вектор-столбцы.
Сформируйте матрицу проекта.
Вычислите коэффициенты модели.
Поэтому моделью данных дают
y = 1 . 3 9 8 3 — 0 . 8 8 6 0 e — t + 0 . 3 0 8 5 t e — t .
Теперь оцените модель в расположенных с равными интервалами точках и постройте модель с исходными данными.

Множественная регрессия
В этом примере показано, как использовать множественную регрессию для данных модели, которые являются функцией больше чем одного переменного предиктора.
Когда y является функцией больше чем одного переменного предиктора, матричные уравнения, которые описывают отношения среди переменных, должны быть расширены, чтобы хранить дополнительные данные. Это называется множественной регрессией .
Измерьте количество y для нескольких значений x 1 и x 2 . Сохраните эти значения в векторах x1 x2 , и y , соответственно.
Модель этих данных имеет вид
y = a 0 + a 1 x 1 + a 2 x 2 .
Множественная регрессия определяет неизвестные коэффициенты a 0 , a 1 , и a 2 путем минимизации суммы квадратов отклонений данных из модели (метод наименьших квадратов).
Создайте и решите набор одновременных уравнений путем формирования матрицы проекта, X .
Решите для параметров при помощи оператора обратной косой черты.
Модель метода наименьших квадратов данных
y = 0 . 1 0 1 8 + 0 . 4 8 4 4 x 1 — 0 . 2 8 4 7 x 2 .
Чтобы подтвердить модель, найдите максимум абсолютного значения отклонения данных из модели.
Это значение намного меньше, чем любое из значений данных, указывая, что эта модель точно следует за данными.
Программная аппроксимация
В этом примере показано, как использовать функции MATLAB для:
Загрузите демонстрационные данные о переписи из census.mat , который содержит американские данные о населении с лет 1790 — 1990.
Это добавляет следующие две переменные в рабочее пространство MATLAB.
cdate вектор-столбец, содержащий годы 1790 — 1990 с шагом 10.
pop вектор-столбец с американской численностью населения, соответствующей каждый год в cdate .
Отобразите данные на графике.

График показывает сильный шаблон, который указывает на высокую корреляцию между переменными.
Вычисление коэффициентов корреляции
В этом фрагменте примера вы определяете статистическую корреляцию между переменными cdate и pop выровнять по ширине моделирование данных. Для получения дополнительной информации о коэффициентах корреляции, смотрите Линейную корреляцию.
Вычислите матрицу коэффициента корреляции.
Диагональные элементы матрицы представляют совершенную корреляцию каждой переменной с собой и равны 1. Недиагональные элементы очень близко к 1, указывая, что существует сильная статистическая корреляция между переменными cdate и pop .
Подбор кривой многочлену к данным
Этот фрагмент примера применяется polyfit и polyval Функции MATLAB, чтобы смоделировать данные.
Вычислите подходящие параметры.
Отобразите на графике данные и подгонку.

График показывает, что квадратичная аппроксимация полиномом предоставляет хорошее приближение данным.
Вычислите остаточные значения для этой подгонки.

Заметьте, что график остаточных значений показывает шаблон, который указывает, что полиномиальная сила второй степени не подходит для моделирования этих данных.
Графическое изображение и вычисление доверительных границ
Доверительные границы являются доверительными интервалами для предсказанного ответа. Ширина интервала указывает на степень уверенности в соответствии.
Этот фрагмент примера применяется polyfit и polyval к census выборочные данные, чтобы произвести доверительные границы для полиномиальной модели второго порядка.
Следующий код использует интервал ± 2 Δ , который соответствует 95%-му доверительному интервалу для больших выборок.
Оцените подгонку и ошибочную оценку предсказания (дельта).
Отобразите на графике данные, подгонку и доверительные границы.

95%-й интервал указывает, что у вас есть 95%-й шанс, что новое наблюдение будет находиться в пределах границ.
Открытый пример
У вас есть модифицированная версия этого примера. Вы хотите открыть этот пример со своими редактированиями?
Документация MATLAB
Поддержка
© 1994-2021 The MathWorks, Inc.
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста — например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.
Аппроксимация и интерполяция функций
Пусть имеется набор узловых точек xk (где k=1,2,…,n) и значения функции y(xk)в этих точках, а также некоторая функция f(x,a1, a2, …,am), которая кроме аргумента х зависит еще и от параметров as(где s=1, 2, …m). Задача аппроксимации состоит в том, чтобы подобрать такие значения параметров as, что функция f(x, a1, a2, …am)наилучшим образом описывала бы исходную функцию. Как правило, m<<n, поэтому добиться, чтобы функция f(x, a1, a2, …am) давала точные результаты даже в узловых точках не удастся. Нужен критерий, который оценивает точность аппроксимации таблично заданной функции. Например, в методе наименьших квадратов в качестве такого критерия используется среднеквадратическое отклонение
 .
.
Частным случаем задачи аппроксимации является задача интерполяции функции. В этом случае также имеем набор узловых точек xk (где k=1,2,…,n) и значения функции yk в этих точках. Однако, в соответствии с критерием интерполяции, требуется построить такую функцию f(x),которая в узловых точках x1, x2,…,xnпринимала бы значения y1, y2, …,yn, то есть f(xk) = ykдля всех kот 1до n.Чаще всего функцию f(x) ищут в виде полинома, степень которого n-1. Поэтому задача сводится к определению коэффициентов интерполяционного полинома на основании значений функции в базовых точках.
На практике для решения задачи интерполяции (вычисления значений функции в точках, несовпадающих с узлами интерполяции) используются интерполяционные формулы Ньютона и формула Лагранжа [1].
Для выполнения полиномиальной аппроксимации в MatLab используется функция polyfit(). Эта функция предназначена для выполнения аппроксимации методом наименьших квадратов. Функция polyfit(x,y,n)возвращает вектор коэффициентов полинома степени n, который с наименьшей среднеквадратичной погрешностью аппроксимирует функцию, заданную таблично. Результатом является вектор строка длиной n+1, содержащий коэффициенты полинома в порядке уменьшения степеней. Аргументами функции являются список узловых точек, список значений интерполируемой функции в этих точках и степень интерполяционного полинома. Как правило, степень полинома много меньше количества узлов (m<<n). В качестве результата возвращается список коэффициентов аппроксимирующего полинома.
Ниже приведены пример линейной и кубической аппроксимации функции, заданной таблицей (рис. 2.2.1-1), и графики аппроксимирующих функций (рис. 2.2.1-2).

Рис. 2.2.1-1. Пример линейной и кубической аппроксимации функции
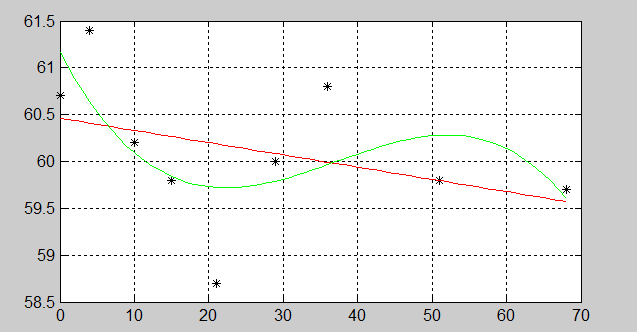
Рис. 2.2.1-2. Графики исходной и аппроксимирующих функций
Чтобы результатом выполнения функции Matlab polyfit() был именно интерполяционный полином, необходимо, чтобы степень этого полинома была на единицу меньше количества узловых точек.
Пример 2.2.1-1. Используя в качестве узлов интерполяции
x=-5,-4…5, построить полином, интерполирующий функцию  .
.
Выполняя команды Matlab в окне Command Window, получим таблицу значений функции и проведем ее интерполяцию с использованием функции Matlab polyfit() (рис. 2.2.1-3). Графики интерполяционных узлов и интерполяционного полинома приведены на рис. 2.2.1-4.Здесь для вычисления значений полинома в точках используется функция polival(p,z), где вектор z покрывает интервал интерполяции и даже выходит за его пределы.
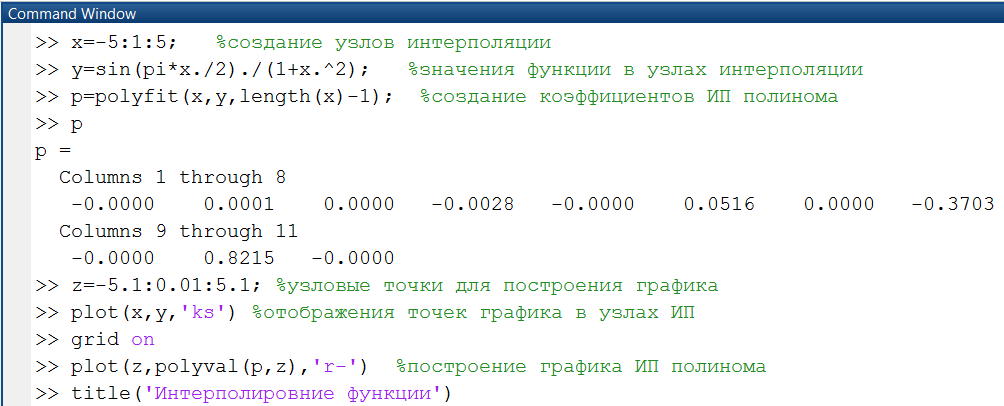
Рис. 2.2.1-3. Интерполяция таблично заданной функции
с использованием функции Matlab polyfit()

Рис. 2.2.1-4. Графики интерполируемой и интерполирующей функций
При большом количестве базовых точек интерполяция полиномом может оказаться малопродуктивной, поэтому нередко используют интерполяцию сплайнами. Идея сплайн-интерполяции состоит в разбиении диапазона интерполирования на отрезки, в пределах которых используются разные функции одного вида (чаще всего алгебраические многочлены). Эта функция и ее несколько производных на всем диапазоне интерполяции непрерывны. В результате имеем кусочно-гладкую интерполяционную зависимость.
Сплайн-интерполяцию можно реализовать с помощью функции Matlabinterp1(). В качестве аргументов функции передают: набор узловых точек аргумента, значения функции в этих точках, список значений точек, для которых вычисляется значения интерполяционной зависимости и, наконец (в апострофах), тип базового полинома (табл. 2.2.1-1).
| Имя функции | Описание |
| nearest() | Интерполяция полиномами нулевой степени – график имеет ступенчатый вид |
| linear() | Интерполяция полиномами первой степени – базовые точки соединяются отрезками прямой |
| spline() | Интерполяция полиномами третьей степени |
Рассмотрим пример использования функцииMatlab interp1().
Пример 2.2.1-2. Используя значения интерполирующей функции, заданной таблично,
выполнить сплайн-интерполяцию с использованием полиномов нулевой, первой и третьей степени, и получить значения функции в точке х=0.58.
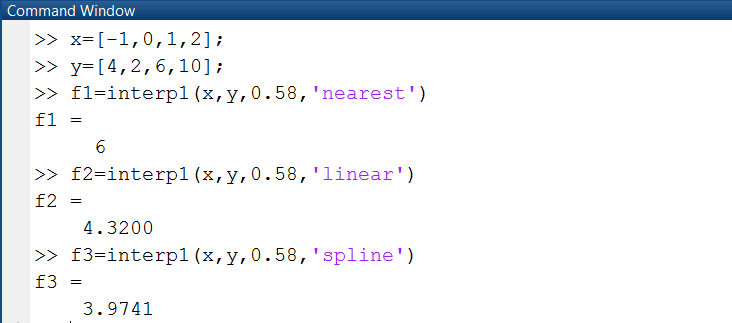
Рис. 2.2.1-5. Вычисление функции в точке х=0.58
На рис. 2.2.1-6 и 2.2.1-7 приведены команды, необходимые для проведения интерполяции таблично заданной функции и построения графиков интерполируемой функции и интерполирующих ее интерполяционных многочленов различных степеней.

Рис. 2.2.2-6. Команды построения графиков интерполяционных функций

Рис. 2.2.2-7. Графики интерполирующих функций
Лабораторная работа по теме
«Технология аппроксимации интерполяции функций»
Вопросы, подлежащие изучению
1) Задание векторов и матриц в пакете Matlab.
2) Технология аппроксимации функции, заданной таблично, с использованием функций polyfit().
3) Технология линейной, кубической и сплайн-интерполяции таблично заданной функции с использованием функций interp1().
4) Получение интерполяционных многочленов в явном виде.
5) Построение графиков аппроксимирующих и интерполирующих функций.
2. Общее задание
1) Изучите материал Темы 2.2. (п. 2.2.1).
2) Выберите индивидуальное задание: номера узлов и номер аппроксимируемой функции из табл. 2.2.2-1; узлы аппроксимации и значения функции в узлах из табл. 2.2.2-2.
3) Задайте в виде векторов значения узлов и значения функции в выбранных узлах.
4) Вычислите коэффициенты аппроксимирующих функций для линейной, квадратичной и кубической аппроксимации с использованием функции polyfit() и получите три аппроксимирующие функции в явном виде.
5) Получите с использованием этих функций значение аппроксимирующей функции в произвольной точке, принадлежащей отрезку, но не совпадающей с узлами аппроксимации, и сравните полученные результаты.
6) Постройте графики табличной и трех аппроксимирующих функций в одном шаблоне, снабдив их легендой.
7) Проведите линейную и кубическую интерполяцию функции с использованием функции interp1(), заданной таблично. Получив значения интерполирующей функции в точке, не совпадающей с узлами интерполяции, сравните полученные результаты.
8) Постройте графики табличной и двух интерполирующих функций в одном шаблоне, снабдив их легендой.
9) Представьте результаты работы преподавателю, ответьте на поставленные вопросы.
10) Выполните команду clear all.
11) Оформите отчет по выполненной работе.
3. Варианты заданий
Таблица 2.2.2-1
| Вариант № | Номера узлов xi | Номер функции |
| 1 3 5 7 9 10 13 |  |
|
| 1 2 4 5 7 10 12 |  |
|
| 1 3 6 7 10 11 13 |  |
|
| 1 2 4 7 9 11 13 |  |
|
| 3 6 7 9 10 11 12 |  |
|
| 2 3 6 8 9 10 13 |  |
|
| 1 4 5 7 9 11 12 |  |
|
| 1 2 4 7 9 12 13 |  |
|
| 2 3 5 7 8 11 12 |  |
|
| 1 3 6 7 9 10 13 |  |
|
| 1 3 7 8 10 11 13 |  |
|
| 1 2 5 6 7 10 12 | 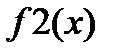 |
|
| 1 4 5 8 10 12 13 |  |
|
| 1 3 5 7 9 10 13 | 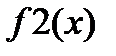 |
|
| 1 3 6 7 8 10 13 |  |
|
| 1 4 5 7 9 11 12 |  |
|
| 2 4 5 6 8 12 13 | 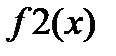 |
|
| 1 4 5 7 9 11 12 |  |
|
| 1 4 5 8 10 11 12 |  |
|
| 2 4 5 6 8 12 13 | 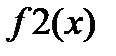 |
|
| 1 4 5 8 10 12 13 | 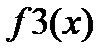 |
|
| 2 3 6 8 9 10 13 |  |
|
| 1 3 5 8 10 12 13 | 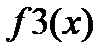 |
|
| 1 4 5 7 9 11 12 | 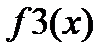 |
|
| 2 4 5 6 8 12 13 | 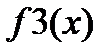 |
|
| 3 4 5 7 8 9 12 | 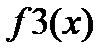 |
|
| 3 5 8 10 11 12 13 | 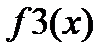 |
|
| 2 4 7 9 10 11 13 | 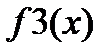 |
|
| 2 4 5 7 8 10 12 | 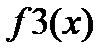 |
|
| 1 4 5 7 9 11 13 | 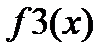 |
| i | xi | 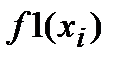 |
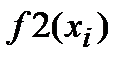 |
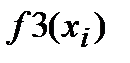 |
| -5 | 1.38 | 2.44 | 1.676 | |
| -4.5 | 1.221 | 2.359 | 2.025 | |
| -4 | 1.511 | 1.751 | 1.736 | |
| -3.5 | 1.501 | 2.13 | 1.203 | |
| -3 | 1.455 | 1.511 | ||
| -2.5 | 0.728 | 1.482 | 1.362 | |
| -2 | 0.976 | 1.437 | 0.75 | |
| -1.5 | 1.065 | 0.803 | 0.976 | |
| -1 | 0.599 | 1.175 | 0.957 | |
| -0.5 | 0.192 | 0.49 | 0.272 | |
| 0.3 | 0.375 | 0.3 | ||
| 0.5 | 0.319 | -6.51*10 -3 | 0.165 | |
| -0.405 | -1.965 | -1.185 |
Содержание отчета
1) В форме комментариев:
· Название лабораторной работы
· ФИО студента, номер группы
2) Протокол вычислений (сессии) в окне Command Window, снабженный необходимыми комментариями.
2.2.3. Контрольные вопросы по теме
1) Что такое аппроксимация функции и в каких случаях она используется?
2) В чем отличие аппроксимации от интерполяции?
3) Какой метод аппроксимации реализован в функции polyfit()?
4) Что служит результатом выполнения функции polyfit()?
5) Для чего предназначена функция polyval()?
6) Назначение и формат функции interp1()?
7) Каким параметром определяется тип интерполяции в функции interp1()?
Тема 2.3. Технология интегрирования
в среде MatLab
2.3.1. Вычисление неопределенных и определенных интегралов
2.3.2. Лабораторная работа по теме «Технология интегрирования
2.3.3. Контрольные вопросы по теме
2.3.1. Вычисление неопределенных и
определенных интегралов
При вычислении определенных интегралов первообразную функцию F(x)не всегда удается выразить аналитически, а кроме того иногда подынтегральная функция f(x) задана в виде таблицы (xi и yi, где i = 1, 2, …, n). Это приводит к необходимости использования численных методов интегрирования.
Существует ряд методов численного интегрирования. Во всех этих методах вычисление осуществляется по приближенным формулам, называемым квадратурами.
Суть получения формул численного интегрирования состоит в том, что на элементарных отрезках интегрирования подынтегральную функцию заменяют простейшим интерполяционным полиномом, который легко может быть проинтегрирован в аналитическом виде. Так, например, для получения формул прямоугольников, трапецийиСимпсонаиспользуют полиномы соответственно нулевой, первой и второй степени.
Формулы прямоугольников:

h– шаг интегрирования;
yi – значение подынтегральной функции от аргумента xi, k=0, 1, …,n;
n– число разбиений интервала интегрирования a, b.
Формула трапеций:
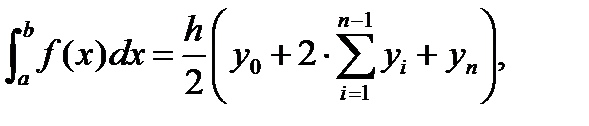
h– шаг интегрирования;
y0 – значение подынтегральной функции при х = a;
yn – значение подынтегральной функции при х = b;
Формула Симпсона:
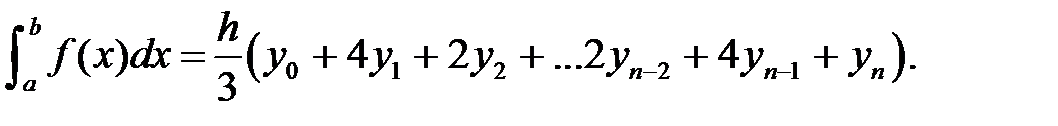
Для символьного вычисления неопределенных и определенных интегралов используется функция Matlab int(), которая может иметь один из следующих форматов:
· int(S)– возвращает символьное значение неопределенного интеграла от символьного выражения или массива символьных выражений S по переменной, которая автоматически определяется функцией findsym(). Если S– скаляр или матрица, то вычисляется интеграл по переменной ‘х’.
· int(S, v)– возвращает неопределенный интеграл от S по символьной переменной v.
· int(S, a, b)– возвращает определенный интеграл от S с пределами интегрирования от а до b, причем пределы интегрирования могут быть как символьными, так и числовыми.
· int(S, v, a, b)– возвращает определенный интеграл от S по переменной v с пределами от а до b.
Ниже приведены примеры использования функции Matlabint()
(рис. 2.3.1-1).

Рис. 2.3.1-1. Примеры вычисления интегралов
В системе MatLab функции вычисления интегралов используют численные методы трапеции, Симпсонаи некоторые другие. Рассмотрим технологию интегрирования с использованием некоторых функций.
Для вычисления интеграла по формуле трапеции в MatLab используется функция trapz(x,y). Эта функция возвращает значение интеграла  от функции y(x), которая может быть представлена вектором или матрицей. Если y(x) – матрица, то функция возвращает вектор значений интеграла каждого столбца матрицы. Если вектор узлов не задан — trapz(y), то в качестве ординат xиспользуются индексы вектора y(x=1:length(y)), где функция определяет длину вектора y. Важно, что узлы по оси x могут быть как равноотстоящими, так и неравноотстоящими.
от функции y(x), которая может быть представлена вектором или матрицей. Если y(x) – матрица, то функция возвращает вектор значений интеграла каждого столбца матрицы. Если вектор узлов не задан — trapz(y), то в качестве ординат xиспользуются индексы вектора y(x=1:length(y)), где функция определяет длину вектора y. Важно, что узлы по оси x могут быть как равноотстоящими, так и неравноотстоящими.
Рассмотрим несколько примеров вычисления значений определенных интегралов методом трапеций при различных способах задания узлов подынтегральной функции (рис. 2.3.1-2).

Рис. 2.3.1-2. Вычисление определенных интегралов с использованием
ФункцииMatlab trapz()
Для вычисления интеграла по формуле Симпсона в MatLab применяется функция quad(). При обращении к этой функции шаг интегрирования не задается, а используется параметр – требуемая точность вычисления интеграла.
Минимальная форма обращения к функции – q=quad(‘f’,a,b), где f– имя функции, взятое в одинарные кавычки, второй и третий аргументы – пределы интегрирования.

Рис. 2.3.1-3. Вычисление определенных интегралов
с использованием функции quad()
Допускается задание четвертого входного параметра eps– абсолютной погрешности: q=quad(‘f’, a, b, eps). По умолчанию eps =10 -6 .
Рассмотрим примеры вычисления определенного интеграла 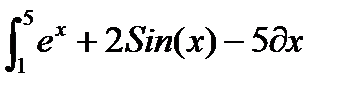 с использованием функции Matlab quad()(рис. 2.3.1-3).
с использованием функции Matlab quad()(рис. 2.3.1-3).
Лабораторная работа по теме
«Технология интегрирования в среде Matlab»
Вопросы, подлежащие изучению
1) Получение символьного выражения неопределенного интеграла средствами пакета Matlab.
2) Вычисление значения определенного интеграла с использованием функций.
3) Вычисление значения определенного интеграла с использованием функций Matlab int(), trapz(), quad().
4) Формулы численного интегрирования: средних прямоугольников, трапеций и Симпсона.
2. Общее задание
1) Изучите материал Темы 2.3 (п. 2.3.1).
2) Выберите из табл. 2.3.2-1 вариант индивидуального задания.
3) Получить символьное выражение неопределенного интеграла с использованием функций int(S) и int(S, x), где S – символьное выражение, а х — переменная.
4) Вычислите значение определенного интеграла с использованием функции int() формата int(S,a,b), где a, b – пределы интегрирования.
5) Вычислите определенный интеграл с использованием функции Matlab, реализующей формулу трапеций, — trapz(x, y), предварительно получив таблицу значений подынтегральной функции с шагом h и задав значения аргумента и функции в виде векторов.
6) Вычислите значение определенного интеграла с использованием функции Matlab, реализующей формулу Симпсона, – quad(‘f’,a,b),где f – имя функции, взятое в одинарные кавычки.
7) Представьте результаты работы преподавателю, ответьте на поставленные вопросы.
8) Выполните команду clear all.
9) Оформите отчет по выполненной работе.
Варианты индивидуальных заданий
| № | Интеграл 1 | Интеграл 2 |
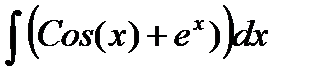 |
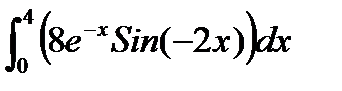 |
|
 |
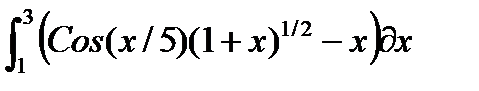 |
|
 |
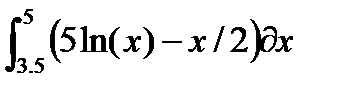 |
|
 |
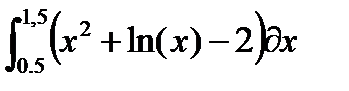 |
|
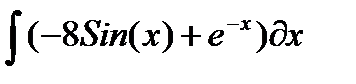 |
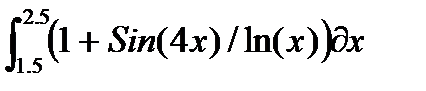 |
|
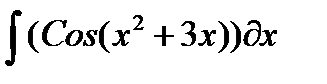 |
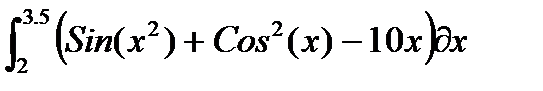 |
|
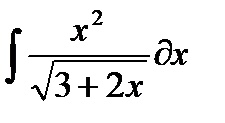 |
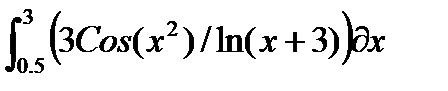 |
|
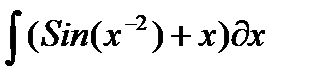 |
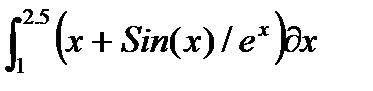 |
|
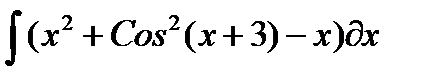 |
 |
|
 |
 |
|
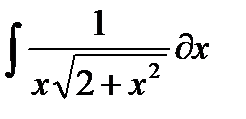 |
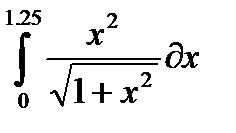 |
|
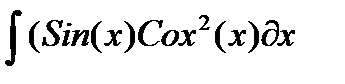 |
 |
|
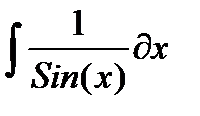 |
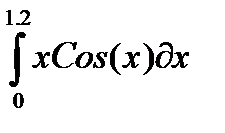 |
|
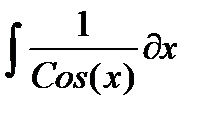 |
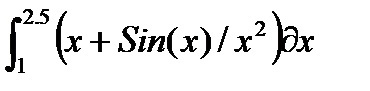 |
|
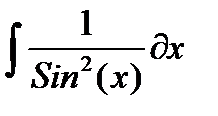 |
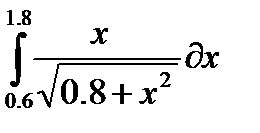 |
|
 |
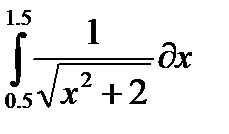 |
|
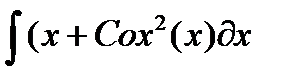 |
 |
|
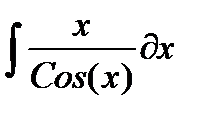 |
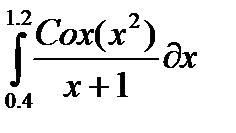 |
|
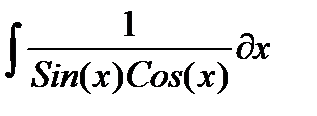 |
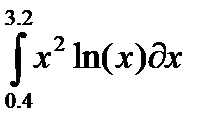 |
|
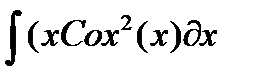 |
 |
|
 |
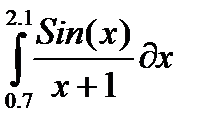 |
|
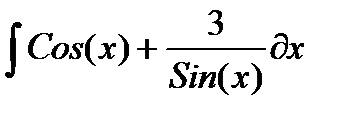 |
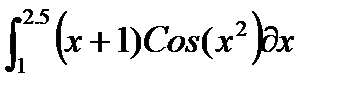 |
|
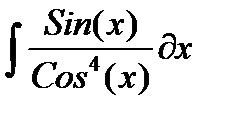 |
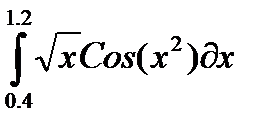 |
|
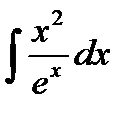 |
 |
|
 |
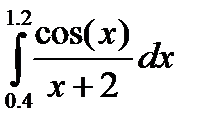 |
|
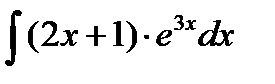 |
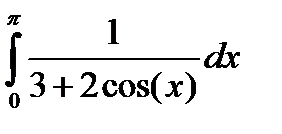 |
|
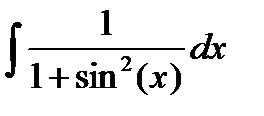 |
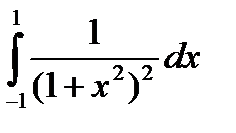 |
|
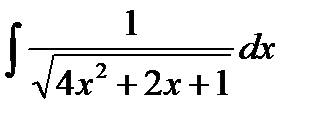 |
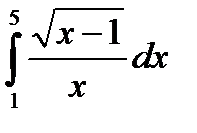 |
|
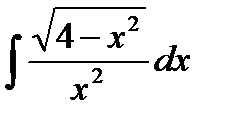 |
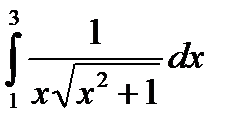 |
|
 |
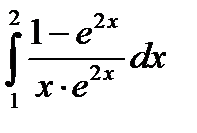 |
Содержание отчета
1) В форме комментариев:
· Название лабораторной работы
· ФИО студента, номер группы
2) Протокол вычислений (сессии) в окне Command Window, снабженный необходимыми комментариями.
2.3.3. Контрольные вопросы по теме
1) Какой функцией в Matlab определяется символьное значение определенного интеграла?
2) Назначение функции trap(x,y).
3) Что возвращает функция trap(x,y), если y(x) – матрица?
4) Можно ли использовать функцию trap(x,y), если узлы по оси х — не равноотстоящие?
5) Какая функция Matlab позволяет вычислить определенный интеграл с заданной точностью?
6) Способы задания подынтегральной функции при вычислении определенного интеграла с использованием функции quad().
7) Какова точность вычисления определенного интеграла по умолчанию?
Тема 2.4. Технология решения обыкновенных
дифференциальных уравнений
2.4.1. Численное решение обыкновенных дифференциальных уравнений
2.4.2. Лабораторная работа по теме
2.4.3. Контрольные вопросы по теме
2.4.1. Численное решение обыкновенных
дифференциальных уравнений
Представим обыкновенное дифференциальное уравнение (ОДУ) первого порядка в виде, разрешенном относительно производной 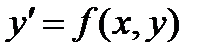 , и пусть
, и пусть  – начальные условия его решения.
– начальные условия его решения.
Тогда решением ОДУ является функция 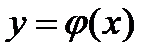 , которая, будучи подставленной в исходное уравнение, обратит его в тождество, и одновременно будут выполняться начальные условия. Эта задача в математике называется задачей Коши.
, которая, будучи подставленной в исходное уравнение, обратит его в тождество, и одновременно будут выполняться начальные условия. Эта задача в математике называется задачей Коши.
Задача Коши при решении ОДУ n-го порядка 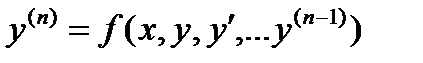 формулируется аналогично, при этом начальными условиями должны быть:
формулируется аналогично, при этом начальными условиями должны быть: 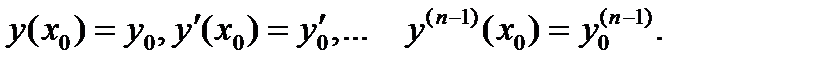 При решении ОДУ n-го порядка уравнение путем выполнения ряда обозначений
При решении ОДУ n-го порядка уравнение путем выполнения ряда обозначений  представляется в виде системы дифференциальных уравнений:
представляется в виде системы дифференциальных уравнений:

Результатом решения ОДУ численными методами является таблица значений y = j(x) на некотором множестве значений аргументов. Поэтому при постановке задачи численного решения ОДУ наряду с начальными условиями x0, y0необходимо задать область решения – отрезок [a;b] и шаг изменения аргумента h (шаг интегрирования).
Для получения численного решения ОДУ используются методы Рунге-Кутты[1]. Методы различаются порядком. Чем выше порядок метода, тем точнее решение, полученное при равном шаге интегрирования.
В Matlab имеется несколько функций для решения задачи Коши. Рассмотрим две функции, используемые для решения обыкновенных дифференциальных уравнений (ОДУ): ode23()– использует метод Рунге-Кутты второго и третьего порядка; ode45()– использует метод Рунге-Кутты четвёртого и пятого порядка точности с автоматическим выбором шага.
В MatLab обращением к функциям, предназначенным для решения ОДУ, является:
[x, y] = ode23(‘fun’,t0,tf,x0)
[x, y] = ode45(‘fun’,t0,tf,x0)
Входными параметрамифункций являются:
· ‘fun’– имя функции (в виде строчной переменной) или ссылка на функцию, задающую правую часть дифференциального уравнения (уравнение должно быть записано в нормальной форме
y’ = fun(x,y));
· t0– начальное значение аргумента;
· tf– конечное значение аргумента;
· х0 – вектор начальных условий.
Выходными параметрамифункций являются:
· x– вектор, содержащий отсчёты аргумента в точках решения;
· y– вектор, содержащий вычисленные значения результата решения ОДУ в точках, соответствующих отсчетам независимой перемен-ной x.
Требования к точности и другие параметры численного решения задаются в Matlab по умолчанию. Изменить эти настройки позволяет дополнительный аргумент OPTIONS.

Рис. 2.4.1-1. Решение ОДУ методом Рунге-Кутты второго порядка
Рассмотрим примеры использования функций ode23() и ode45()для решения ОДУ вида:  на отрезке [1;10] с шагом интегрирования 1 при начальных условиях y(1)=1. Решение ОДУ с использованием функции ode23()приведено на рис. 2.4.1-1.
на отрезке [1;10] с шагом интегрирования 1 при начальных условиях y(1)=1. Решение ОДУ с использованием функции ode23()приведено на рис. 2.4.1-1.
На рис. 2.4.1-2 приведено решение того же ОДУ, но с использованием функции ode45(). Вывод таблицы решения дополнен графиком функции y(x) (рис. 2.4.1-3).
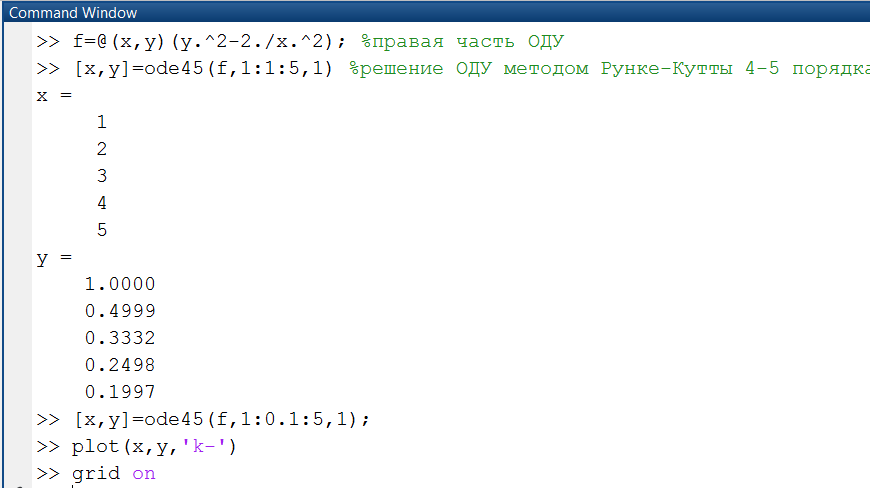
Рис. 2.4.1-2. Решение ОДУ методом Рунге-Кутты четвертого порядка
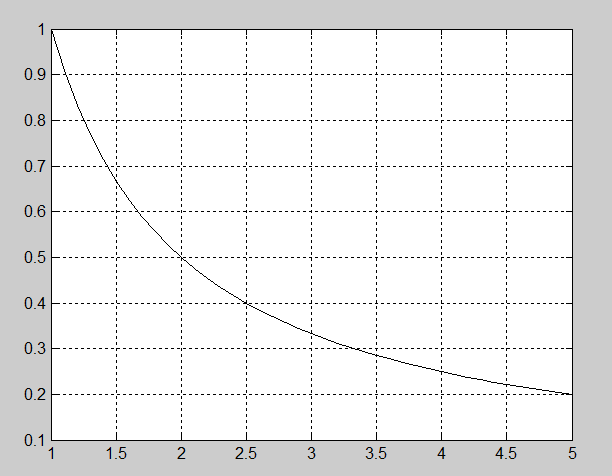
Рис. 2.4.1-3. Графическое решение ОДУ
При решении ОДУ высокого порядка вводят обозначения (новые функции) для всех производных, кроме самой старшей. В этих обозначениях самая старшая производная становится записанной, как первая. Исходное уравнение дополняется тождествами, определяющими правила введения новых функций. Проиллюстрируем описанный подход при решении ОДУ второго порядка.
Требуется решить 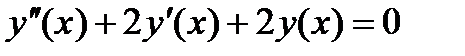 с начальными условиями: и
с начальными условиями: и 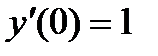 . Сведем заданное ОДУ к равноценной системе ОДУ первого порядка. Для этого переобозначим функцию
. Сведем заданное ОДУ к равноценной системе ОДУ первого порядка. Для этого переобозначим функцию 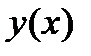 , как
, как  , и введем функцию
, и введем функцию  . Запишем исходное уравнение в новых обозначениях:
. Запишем исходное уравнение в новых обозначениях: 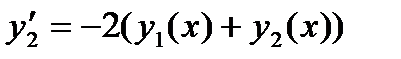 (здесь учтено, что
(здесь учтено, что  ). Дополним это уравнение тождеством
). Дополним это уравнение тождеством 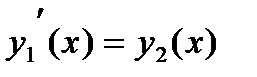 и получим нужную систему ОДУ. Эту систему следует дополнить начальными условиями:
и получим нужную систему ОДУ. Эту систему следует дополнить начальными условиями: 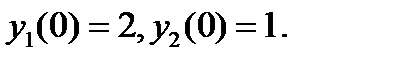
Решение системы ОДУ в Matlab начинается с определения векторной функции (рис. 2.4.1-4).
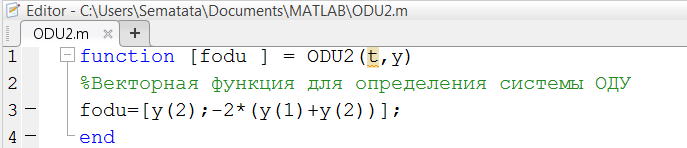
Рис. 2.4.1-4. Определение векторной функции
Для решения дифференциального уравнения (системы уравнений) используем команды, где решение системы ОДУ записывается в переменную y. При этом элемент y(1) содержит значение функции y(x), а y(2) значение производной y'(x). Команда plot(x, y) строит график функции решения ОДУ и ее производной (рис. 2.4.1-6).
Приветствую! Сегодня продолжаем говорить об обработке экспериментальных данных. Сегодняшняя статья — продолжение предыдущей темы: Интерполяция в Matlab. Настоятельно советую с ней ознакомиться перед чтением данной статьи. По сути аппроксимация в Matlab очень похожа на интерполяцию, однако, для её реализации используются другие правила и функции.
Аппроксимация
Относительно интерполяции, аппроксимация получила более широкое распространение. Сущность этого метода состоит в том, что табличные данные аппроксимируют кривой, которая не обязательно должна пройти через все узловые точки, а должна как бы сгладить все случайные помехи табличной функции. 
МНК (Метод Наименьших Квадратов)
Одним из самых популярных методов аппроксимации в Matlab и в других средах, это Метод Наименьших Квадратов ( МНК ). В этом методе при сглаживании опытных данных аппроксимирующую кривую стремятся провести так, чтобы её отклонения от табличных данных по всем узловым точкам были минимальными.
Суть МНК заключается в следующем: для табличных данных, полученных в результате эксперимента, отыскать аналитическую зависимость, сумма квадратов уклонений которой от табличных данных во всех узловых точках была бы минимальной.
Аппроксимация в Matlab по МНК осуществляется с помощью функции polyfit. Функция p = polyfit(x, y, n) находит коэффициенты полинома p(x) степени n, который аппроксимирует функцию y(x) в смысле метода наименьших квадратов. Выходом является строка p длины n+1, содержащая коэффициенты аппроксимирующего полинома.
Примеры задач
Разберём задачу, в которой разрешается использование встроенных матлабовских функций.
Осуществить аппроксимацию в Matlab табличных данных x = [0, 0.1 , 0.2, 0.3, 0.5] и y = [3, 4.5, 1.7, 0.7, -1] . Применяя метод наименьших квадратов, приблизить ее многочленами 1-ой и 2-ой степени. Для каждого определить величину среднеквадратической ошибки. Построить (на одном листе) графики и заданной таблично функции (ломанная линия) и приближающих ее многочленов 1-ой и 2-ой степени.
x = [0, 0.1 , 0.2, 0.3, 0.5]; y = [3, 4.5, 1.7, 0.7, -1]; grid on plot(x, y, '*r'); xi = min(x):0.1:max(x); N = 1; % степень coeff1 = polyfit(x, y, N); y2 = 0; for k=0:N y2 = y2 + coeff1(N-k+1) * xi.^k; end hold on; plot(xi, y2, 'r'); N = 2; coeff2 = polyfit(x, y, N); y3 = 0; for k=0:N y3 = y3 + coeff2(N-k+1) * xi.^k; end hold on; plot(xi, y3, 'g'); std(y-(coeff1(1)*x+coeff1(2))) std(y-(coeff2(1)*x.^2+coeff2(2)*x+coeff2(3)))

Вывод:
ans = 0.9253
ans = 0.8973
Однако, встречаются задачи, где требуется реализовать аппроксимацию в Matlab без использования специальных функций.
Найти у(0.25) путём построения аппроксимирующего полинома методом наименьших квадратов согласно данным:
x: 0, 0.1, 0.2, 0.3, 0.5
y: 3, 4.5, 1.7, 0.7, -1
p: 0.5, 0.8, 1.6, 0.8, 0.1
Построить этот полином без учёта весовых коэффициентов с использованием определителя Вандермонда и стандартных операторов.
%Задаем массивы данных: x = [0; 0.1; 0.2; 0.3; 0.5]; y = [3;4.5;1.7;0.7;-1]; %Строим матрицу W – матрицу Вандермонда с вырезанным первым столбцом: W = vander(x); W = W(1:5,2:5); %Вычисляем элементы матрицы А как произведение транспонированной матрицы W и просто матрицы W A = W'*W; %Вычисляем элементы вектора b b = W'*y; %Решая систему уравнений Aa = b, находим значения вектор-столбца a: a = inv(A)*b %Это будут коэффициенты аппроксимирующего полинома. %Проверяем, используя методы MATLAB = функцию polyfit: qq = polyfit(x,y,3) %Получаем аппроксимированные значения y: x1 = [-0.2:0.001:0.7]; y1 = a(1)*x1.^3 + a(2)*x1.^2 + a(3)*x1 + a(4); %Строим график функции plot(x,y,'*'); hold on; grid on; plot(x1,y1,'Color','r'); %Находим значение в точке x = 0.25 x2 = 0.25; y2 = a(1)*x2^3 + a(2)*x2^2 + a(3)*x2 + a(4)

Вывод:
a =
228.1447
-176.0984
22.7745
3.1590
qq = 228.1447 -176.0984 22.7745 3.1590
y2 = 1.4113
Как видите встроенные функции для аппроксимации в Matlab укорачивают алгоритм почти вдвое.
Существует также возможность реализации всего алгоритма через одну функцию, но для преподавателей студентов она скорее всего будет не приемлема. С помощью функции lsqcurvefit(fun,x0,xdata,ydata), где:
xdata,ydata– табличные значения аппроксимируемой функции;
x0 –стартовое значение параметров функции;
fun – функция аппроксимации, задаваемая пользователем
С аналитически-теоретической стороны, существуют такие виды аппроксимации:
- Аппроксимация ортогональными классическими полиномами.
- Аппроксимация каноническим полиномом
Но на практике их реализацию требуют редко.
Вот и вся основная информация по аппроксимации в Matlab, если остались вопросы, задавайте их в комментариях.
Скачать исходник первой задачи
Скачать исходник второй задачи
