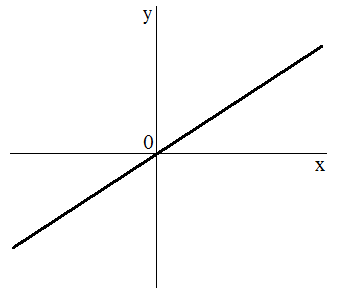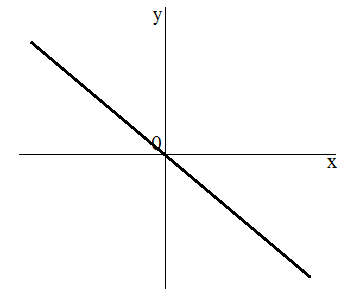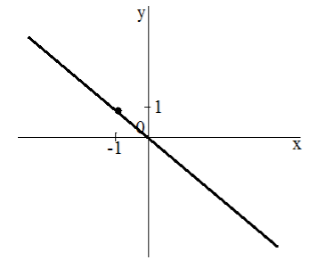Как найти функцию по графику прямой пропорциональности

Прямая пропорциональность и её график

Александр Мельник

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Определение прямой пропорциональности

Для начала напомним следующее определение:

Определение

Две величины называются прямо пропорциональными, если их отношение равно конкретному, отличному от нуля числу, то есть:

[frac{y}{x}=k]

Отсюда мы видим, что $y=kx$.

Определение

Функция вида $y=kx$ называется прямой пропорциональностью.

Прямая пропорциональность является частным случаем линейной функции $y=kx+b$ при $b=0$. Число $k$ называется коэффициентом пропорциональности.

Примером прямой пропорциональности может служить второй закон Ньютона: Ускорение тела прямо пропорционально приложенной к нему силе:

[F=ma]

Здесь масса — коэффициент пропорциональности.

Исследование функции прямой пропорциональности $f(x)=kx$ и её график

Вначале рассмотрим функцию $fleft(xright)=kx$, где $k > 0$.

1. Область определения — все числа.
2. Область значения — все числа.
3. $fleft(-xright)=-kx=-f(x)$. Функция прямой пропорциональности нечетна.
4. Функция проходит через начало координат.
5. $f’left(xright)={left(kxright)}’=k>0$. Следовательно, данная функция возрастает на всей области определения. Точек экстремума нет.
6. $f^{”}left(xright)=k’=0$. Следовательно, функция не имеет точек перегиба.
7. ${mathop{lim}_{xto -infty } kx }=-infty $, ${mathop{lim}_{xto +infty } kx }=+infty $
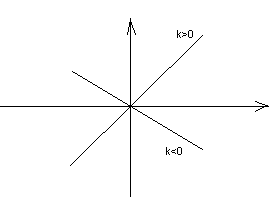
8. График (рис. 1).

Рис. 1. График функции $y=kx$, при $k>0$

Теперь рассмотрим функцию $fleft(xright)=kx$, где $k

1. Область определения — все числа.
2. Область значения — все числа.
3. $fleft(-xright)=-kx=-f(x)$. Функция прямой пропорциональности нечетна.
4. Функция проходит через начало координат.
5. $f’left(xright)={left(kxright)}’=k
6. $f^{”}left(xright)=k’=0$. Следовательно, функция не имеет точек перегиба.
7. ${mathop{lim}_{xto -infty } kx }=+infty $, ${mathop{lim}_{xto +infty } kx }=-infty $
8. График (рис. 2).

Рис. 2. График функции $y=kx$, при $k

Важно: для построения графика функции $y=kx$ достаточно найти одну, отличную от начала координат точку $left(x_0, y_0right)$ и провести прямую через эту точку и начало координат.

Задачи на построение графиков функции прямой пропорциональности

Сдай на права пока
учишься в ВУЗе

Вся теория в удобном приложении. Выбери инструктора и начни заниматься!

Получить скидку 3 000 ₽

Задача 1

Построить график функции $y=-x$

Найдем точку, принадлежащую данной функции. Пусть $x=1$, тогда $y=-1$. Проведем прямую через точки $left(1,-1right) и (0, 0)$. Получим

Задача 2

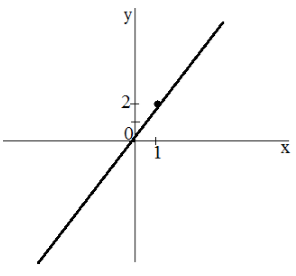
Построить график функции $y=2x$

Найдем точку, принадлежащую данной функции. Пусть $x=1$, тогда $y=2$. Проведем прямую через точки $left(1,2right) и (0, 0)$. Получим

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Дата последнего обновления статьи: 02.02.2023

Понятие о прямой пропорциональности

Представьте, что вы задумали купить своих любимых конфет (или чего угодно, что вам очень нравится). У конфет в магазине своя цена. Предположим, 300 рублей за килограмм. Чем больше конфет вы купите, тем больше денег заплатите. То есть если захотите 2 килограмма – заплатите 600 р., а захотите 3 кило – отдадите 900 рублей. С этим вроде бы все ясно, верно?

Если да, то тогда вам сейчас ясно и что такоепрямая пропорциональность– это понятие, которое описывает отношение двух зависящих друг от друга величин. И отношение этих величин остается неизменным и постоянным: на сколько частей увеличивается или уменьшается одна из них, на столько же частей пропорционально увеличивается или уменьшается вторая.

Описать прямую пропорциональность можно такой вот формулой:f(x) = a*x, и a в этой формуле – постоянная величина (a = const). В нашем примере про конфеты цена – это постоянная величина, константа. Она не возрастает и не уменьшается, сколько бы конфет вы не задумали купить. Независимая переменная (аргумент)x– это то, сколько килограммов конфет купить вы собираетесь. А зависимая переменнаяf(x) (функция) – то, сколько денег вы в итоге заплатите за свою покупку. Так что можем подставить в формулу цифры и получить: 600 р. = 300 р. * 2 кг.

Промежуточный вывод такой: если возрастает аргумент, возрастает и функция, если аргумент убывает, функция тоже убывает

Функция и ее свойства

Функцией прямой пропорциональности является частный случай линейной функции. Если линейная функция это y = k*x + b, то для прямой пропорциональности это выглядит так: y = k*x, гдеk называется коэффициентом пропорциональности, и это всегда не равно нулю число. Вычислитьk легко – он находится как частное функции и аргумента: k = у/х.

Чтобы было нагляднее, возьмем еще один пример. Представьте, что из пункта А в пункт Б движется автомобиль. Его скорость – 60 км/ч. Если предположить, что скорость движения остается постоянной, то ее можно принять за константу. И тогда запишем условия в виде: S = 60*t, и эта формула аналогична функции прямой пропорциональности y = k*x. Проведем параллель дальше: если k = у/х, то и скорость автомобиля можно вычислить, зная расстояние между А и Б и затраченное на дорогу время: V = S/t.

А теперь от прикладного применения знаний о прямой пропорциональности вернемся обратно к ее функции. К свойствам которой относится:

• областью ее определения является множество всех действительных чисел (а также его подмножества);

• функция нечетная;

• изменение переменных прямо пропорционально осуществляется по всей длине числовой прямой.

Прямая пропорциональность и ее график

График функции прямой пропорциональности – это прямая, которая пересекает точку начала координат. Чтобы его построить, достаточно отметить только еще одну точку. И соединить ее и начало координат прямой.

В случае с графикомk– это угловой коэффициент. Если угловой коэффициент меньше нуля (k < 0), то угол между графиком функции прямой пропорциональности и осью абсцисс тупой, а функция убывающая. Если угловой коэффициент больше нуля (k > 0), график и ось абсцисс образуют острый угол, а функция – возрастающая.

И еще одно свойство графика функции прямой пропорциональности напрямую связано с угловым коэффициентомk. Предположим, у нас две не идентичных функции и, соответственно, два графика. Так вот, если коэффициентыkэтих функций равны, их графики расположены на оси координат параллельно. А если коэффициентыkне равны друг другу, графики пересекаются.

Примеры задач

А теперь решим пару задач на прямую пропорциональность

Начнем с простого.

Задача 1: Представьте, что 5 куриц за 5 дней снесли 5 яиц. А если будет 20 куриц, сколько яиц они снесут за 20 дней?

Решение: Обозначим неизвестное какх. И рассуждать будем следующим образом: во сколько раз больше куриц стало? Разделим 20 на 5 и узнаем, что в 4 раза. А во сколько раз больше яиц снесут 20 куриц за те же 5 дней? Тоже в 4 раза больше. Значит, находим нашх так: 5*4*4 = 80 яиц снесут 20 куриц за 20 дней.

Теперь пример чуть сложнее, перефразируем задачу из «Всеобщей арифметики» Ньютона. Задача 2: Писатель за 8 дней может сочинить 14 страниц новой книги. Если бы у него были помощники, сколько бы человек понадобилось, чтобы написать 420 страниц за 12 дней?

Решение: Рассуждаем, что количество человек (писатель + помощники) увеличивается с увеличением объема работы, если бы ее пришлось сделать за то же количество времени. Но во сколько раз? Разделив 420 на 14, узнаем, что увеличивается в 30 раз. Но так как по условию задачи на работу дается больше времени, то количество помощников увеличивается не в 30 раз, а таким образом: х = 1 (писатель) * 30 (раз) : 12/8 (дней). Преобразуем и выясним, что х = 20 человек напишут 420 страниц за 12 дней.

Решим еще задачу, похожую на те, что были у нас в примерах.

Задача 3: В одно и то же путешествие отправилось два автомобиля. Один двигался со скоростью 70 км/ч и за 2 часа проделал тот же путь, что другой за 7 часов. Найдите скорость второго автомобиля.

Решение: Как вы помните, путь определяется через скорость и время – S = V *t. Поскольку путь оба автомобиля проделали одинаковый, мы можем приравнять два выражения: 70*2 = V*7. Откуда найдем, что скорость второго автомобиля, это V = 70*2/7 = 20 км/ч.

И еще пару примеров заданий с функциями прямой пропорциональности. Иногда в задачах требуется найти коэффициент k.

Задача 4: Даны функции у = – х/16 и у = 5х/2, определите их коэффициенты пропорциональности.

Решение: Как вы помните, k = у/х. Значит, для первой функции коэффициент равен -1/16, а для второй k = 5/2.

А еще вам может встретиться задание, как Задача 5: Запишите формулой прямую пропорциональность. Ее график и график функции у = -5х + 3 расположены параллельно.

Решение: Функция, которая дана нам в условии, – линейная. Нам известно, что прямая пропорциональность – частный случай линейной функции. А также мы знаем, что если коэффициенты k функций равны, их графики параллельны. Значит, все, что требуется – это вычислить коэффициент известной функции и задать прямую пропорциональность по знакомой нам формуле: y = k*x. Коэффициент k = -5, прямая пропорциональность: у = -5*х.

Вывод

Теперь вы узнали (или вспомнили, если уже проходили эту тему раньше), что называется прямой пропорциональностью, и рассмотрели ее примеры. Мы также поговорили о функции прямой пропорциональности и ее графике, решили несколько задач для примера.

Если эта статья оказалась полезной и помогла разобраться в теме, расскажите нам об этом в комментариях. Чтобы мы знали, смогли ли принести вам пользу.

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Прямая пропорциональность — базовые понятия

Пропорциональность бывает двух видов:

• прямая;
• обратная.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Если автомобиль движется в течение еще одного часа с такой же скоростью 50 км/ч, то он преодолеет расстояние в 100 км.

Согласно примеру, увеличение времени в 2 раза сопровождается увеличением пройденного расстояния во столько же раз, то есть в 2 раза. Величины времени и расстояния будут прямо пропорциональными. Они обладают взаимосвязью, которую называют прямой пропорциональностью.

Предположим, что вначале водитель планировал проехать 100 км за 2 часа, но после того, как он преодолел 50 км, произошла остановка. В таком случае, уменьшая расстояние в 2 раза, получим, что время уменьшится тоже в 2 раза.

Особенностью прямо пропорциональных величин является стабильность их отношений. Таким образом, во время изменения значений прямо пропорциональных величин, их отношение остается постоянным. Рассмотренная ситуация характеризуется изменением расстояния с 50 км при значении времени в 1 час. Отношение расстояния ко времени равно 50 и определяется формулой:

(frac{50}{1}=50)

После увеличения времени движения автомобиля в 2 раза, оно составит 2 часа. Таким образом, расстояние также увеличилось в 2 раза до 100 км. Отношение 100 км к 2 часам равно числу 50:

(frac{100}{2}=50)

Число 50 представляет собой коэффициент прямой пропорциональности. Эта величина демонстрирует, какое расстояние соответствует одному часу движения. В условиях рассматриваемого примера данный коэффициент является скоростью движения автомобиля, исходя из ее определения.

С помощью прямо пропорциональных характеристик можно составлять пропорции. Например, записанные ранее отношения составляют пропорционально:

(frac{50}{1}=frac{100}{2})

Представленное выражение читают таким образом: 50 км так относятся к 1 часу, как 100 км относятся к 2 часам.

Линейное уравнение относительно двух переменных x и y имеет такой вид:

ax + by + c = 0

(aneq 0)

(bneq 0)

Известно, что график записанного равенства является прямая линия, любая точка на которой имеет два числа в виде координат x и y, то есть абсциссы и ординаты. Каждая точка этой прямой соответствует заданному уравнению. Если выразить y через x, получим:

by = -ax – c

Принимая во внимание, что (bneq 0), можно поделить на него две части выражения:

(y=-frac{a}{b}x-frac{c}{b})

Сделать уравнение более удобным можно с помощью следующих обозначений:

(-frac{a}{b}=k)

(-frac{c}{b}=m)

Таким образом:

y = kx + m

Данным способом была выведена линейная функция y от x в общем виде. В этом случае были применены новые обозначения:

• x — в виде независимой переменной или аргумента;
• y — представляет собой зависимую переменную или функцию;
• k и m — являются параметрами, полностью и однозначно определяющими конкретную линейную функцию.

В том случае, когда m = 0, уравнение примет вид:

y = kx

Данная функция представляет собой прямую пропорциональность. Она определяется с помощью единственного параметра k.

Исследование функции прямой пропорциональности и ее график

Число k представляет собой коэффициент пропорциональности. Переменная y пропорциональна переменной x. Прямая пропорциональность является частным случаем линейной функции

 y = kx + m, если m=0

График прямой пропорциональности изображают в виде прямой, которая пересекает начало координат или точку O (0;0). Для того чтобы построить график прямой пропорциональности, требуется взять одну точку, вторая – будет точкой O.

Прямая пропорциональность характеризуется следующими свойствами:

• областью определения является множество действительных чисел: D(y): x∈(-∞;+∞) (или x∈R);
• областью значений является множество действительных чисел: D(y): y∈(-∞;+∞) (или y∈R);
• нуль функции (y=0) при x=0;
• если k>0, функция y = kx возрастает, а при k<0 — убывает;

Если k>0, график функции пересекает первую и третью координатные четверти. Функция будет обладать положительными значениями, если значения аргумента положительные:

y > 0 при x > 0.

Функция будет обладать отрицательными значениями, если значения аргумента отрицательные:

y < 0 при x < 0.

Если k < 0, то функция будет иметь график, проходящий через вторую и четвертую координатную четверть. Функция будет характеризоваться положительными значениями, если значения аргумента отрицательные:

y > 0 при x < 0.

Функция будет характеризоваться отрицательными значениями, если значения аргумента положительные:

y < 0 при x > 0.

Величина k представляет собой угловой коэффициент прямой y = kx. С другой стороны, k является тангенсом угла α, образованного прямой и положительным направлением оси Ох.

В качестве примера можно рассмотреть такие функции:

• y = 2x в виде прямой пропорциональности;
• y = 2x + 1 в виде линейной функции;
• y = 2x – 1 в виде линейной функции.

Можно построить график рассматриваемых функций. Каждая из них обладает коэффициентом k = 2. Для первой функции m = 0, для второй: m = 1, для третьей: m = -1. Данные величины вытекают из стандартной записи линейного уравнения:

y = kx + m

Необходимо представить данные в виде таблицы:

График примет такой вид:

Прямые, которые были построены, параллельны. Это объясняется равенством их угловых коэффициентов. Согласно теореме, если y = kx является графиком прямой пропорциональности, тогда график y = kx + m будет ему параллелен, так как коэффициентом k определяется угол наклона к оси x, и данный коэффициент y функций будет обладать равными значениями.

Примеры задач на прямую пропорциональность

Задача 1

Требуется определить соотношение между угловыми коэффициентами, согласно графику:

Решение:

(k_{1}=frac{y_{1}}{x})

(k_{2}=frac{y_{2}}{x})

x = x;

(y_{1}> y_{2})

Таким образом:

(k_{1}>k_{2})

Ответ: (k_{1}>k_{2})

Задача 2

Требуется построить график прямой пропорциональности при том, что на данном графике есть точка с координатами (2;8).

Решение:

Построить прямую можно через пару точек. Первая будет обладать координатами (0;0), исходя из того, что любой график прямой пропорциональности пересекает точку (0;0). Вторая точка дана в условии задачи (2;8).

Задачу можно решить другим способом. Согласно координатам точки (2;8), получим:

x=2 и y=8

Данные выражения подходят для уравнения вида:

y = kx

Можно подставить известные значения и определить k:

8 = 2k

k = 4

Таким образом, уравнение примет вид:

y = 4x

С помощью данного уравнения можно построить график: 

В этой статье мы рассмотрим линейную функцию, график линейной функции и его свойства. И, как обычно, решим несколько задач на эту тему.

Линейной функцией называется функция вида

В уравнении функции число , которое мы умножаем на называется коэффициентом наклона.

Например, в уравнении функции ;

в уравнении функции    ;

в уравнении функции   ;

в уравнении функции   .

Графиком линейной функции является прямая линия.

1. Чтобы построить график функции, нам нужны координаты двух точек, принадлежащих графику функции. Чтобы их найти, нужно взять два значения х, подставить их в уравнение функции, и по ним вычислить соответствующие значения y.

Например, чтобы построить график функции , удобно взять   и , тогда ординаты эти точек будут равны  и .

Получим точки А(0;2) и В(3;3). Соединим их и получим график  функции :

2. В уравнении функции  коэффициент  отвечает за наклон графика функции:

Коэффициент  отвечает за сдвиг графика вдоль оси :

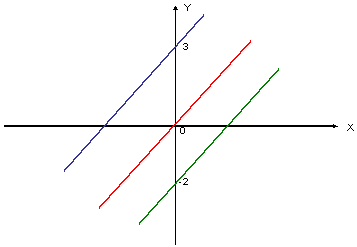
На рисунке ниже изображены графики функций ; ; 

Заметим, что во всех этих функциях коэффициент больше нуля, и все графики функций наклонены вправо. Причем, чем больше значение , тем круче идет прямая.

Во всех функциях – и мы видим, что все графики пересекают ось OY в точке (0;3)

Теперь рассмотрим графики функций ; ; 

На этот раз  во всех  функциях коэффициент меньше нуля, и все графики функций наклонены влево.

Заметим, что чем больше |k|, тем круче идет прямая. Коэффициент b тот же, b=3, и графики также как в предыдущем случае пересекают ось OY в точке (0;3)

Рассмотрим графики функций  ; ;

Теперь  во всех уравнениях функций коэффициенты равны. И мы получили три параллельные прямые.

Но коэффициенты b различны, и эти графики пересекают ось OY  в различных точках:

График функции (b=3) пересекает ось OY  в точке (0;3)

График функции (b=0) пересекает ось OY  в точке (0;0) –  начале координат.

График функции (b=-2) пересекает ось OY  в точке (0;-2)

Итак, если мы знаем знаки коэффициентов k и b, то можем сразу представить, как выглядит график функции .

Если  k<0 и b>0, то график функции  имеет вид:

Если  k>0 и b>0, то график функции  имеет вид:

Если  k>0 и b<0, то график функции  имеет вид:

Если  k<0 и b<0, то график функции  имеет вид:

Если  k=0 , то  функция превращается в функцию    и ее график имеет вид:

Ординаты всех точек графика функции  равны 

Если b=0, то график функции  проходит через начало координат:

 Это график прямой пропорциональности.

3. Отдельно отмечу график уравнения . График этого уравнения представляет собой прямую линию, параллельую оси  все точки которой имеют абсциссу .

Например, график уравнения  выглядит так:

Внимание! Уравнение  не является функцией, так  как различным значениям функции соответствует одно и то же значение аргумента, что не соответствует определению функции.

4. Условие параллельности двух прямых:

График функции  параллелен графику функции , если 

5. Условие перпендикулярности двух прямых:

График функции  перпендикулярен графику функции , если  или 

6. Точки пересечения графика функции  с осями координат.

С осью ОY. Абсцисса любой точки, принадлежащей оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY нужно в уравнение функции вместо х подставить ноль. Получим y=b. То есть точка пересечения с осью OY имеет координаты (0;b).

С осью ОХ: Ордината любой точки, принадлежащей оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ нужно в уравнение функции вместо y подставить ноль. Получим 0=kx+b. Отсюда . То есть точка пересечения с осью OX имеет координаты (;0):

Рассмотрим решение задач.

1. Постройте график функции , если известно, что он проходит через точку А(-3;2) и параллелен прямой y=-4x.

В уравнении функции   два неизвестных параметра: k и b. Поэтому в тексте задачи должны быть два условия, характеризующих график функции.

а) Из того, что график функции  параллелен прямой y=-4x, следует, что k=-4. То есть уравнение функции имеет вид 

б) Нам осталось найти b. Известно, что график функции  проходит через точку А(-3;2). Если точка принадлежит графику функции, то при подстановке ее координат в уравнение функции, мы получим верное равенство:

  отсюда b=-10

Таким образом, нам надо построить график функции 

Точка А(-3;2) нам известна, возьмем точку B(0;-10)

Поставим эти точки в координатной плоскости и соединим их прямой:

2. Написать уравнение прямой, проходящей через точки A(1;1); B(2;4).

Если прямая проходит через точки с заданными координатами, следовательно, координаты точек удовлетворяют уравнению прямой  . То есть если мы координаты точек подставим в уравнение прямой, то получим верное равенство.

Подставим координаты каждой точки в уравнение   и получим систему линейных уравнений.

Вычтем из второго уравнения системы первое, и получим . Подставим значение k в первое уравнение системы, и получим b=-2.

Итак, уравнение прямой .

3. Постройте график уравнения

Чтобы найти,  при каких значениях неизвестного произведение нескольких множителей равно нулю, нужно каждый множитель приравнять к нулю и учесть ОДЗ каждого множителя. 

Это уравнение не имеет ограничений на ОДЗ. Разложим на множители вторую скобку и приравняем каждый множитель к нулю. Получим совокупность уравнений:

Построим графики всех  уравнений совокупности в одной коорднатной плоскости. Это и есть график уравнения  :

4. Постройте график функции , если он перпендикулярен прямой  и проходит через точку М(-1;2)

Мы не будем строить график, только найдем уравнение прямой.

а) Так как график функции , если он перпендикулярен прямой , следовательно , отсюда . То есть уравнение функции имеет вид 

б) Мы знаем, что  график функции  проходит через точку М(-1;2). Подставим ее координаты в уравнение функции. Получим:

, отсюда .

Следовательно, наша функция имеет вид: .

5. Постройте график функции 

Упростим выражение, стоящее в правой части уравнения функции.

Важно! Прежде чем упрощать выражение, найдем его ОДЗ.

Знаменатель дроби не может быть равен нулю, поэтому , .

Тогда наша функция принимает вид:

То есть нам надо построить график функции  и выколоть на нем две точки: с абсциссами x=1 и x=-1:

И.В. Фельдман, репетитор по математике.