Matlab построить график по точкам
Построение графика по узловым точкам
Графики в Matlab, так же как в табличном процессоре, могут быть построены по узловым точкам. Поскольку Matlab — матричная система, совокупность узловых точек у(х) для построения графика задается векторами X и Y одинакового размера.
Графики Matlab строит в отдельных окнах, называемых графическими окнами. С первого взгляда видны отличия графического окна, показанного на рис. 4.5, от командного окна Matlab. В главном меню окна появилась позиция Tools (Инструменты), которая позволяет вывести или скрыть инструментальную панель, видимую в верхней части окна графики на рис. 4.5. Средства этой панели позволяют легко управлять параметрами графиков и наносить на них текстовые комментарии в любом месте.
Рис. 4.5. График, построенный с помощью функции plot
В Matlab для построения графиков функций по узловым точкам в декартовой системе координат служит функция plot. Функция plot имеет несколько синтаксических конструкций:
— plot (X, Y) — строит график функции у(х), координаты точек (х, у) которой берутся из векторов одинакового размера Y и X. Если X или Yматрица, то строится семейство графиков по данным, содержащимся в колонках матрицы;
- — plot( Y) — строит график y(i), где значения у берутся из вектора Y, a i представляет собой индекс соответствующего элемента. Если Yсодержит комплексные элементы, то выполняется команда plot (real (Y), imag( Y)). Во всех других случаях мнимая часть данных игнорируется;
- — plot(X,Y,S) — аналогична команде plot(X,Y), но тип линии графика можно задавать с помощью строковой константы S.
Значениями константы S могут быть символы, приведенные в табл. 4.5.
Построение графиков в matlab командой plot. Она работает с векторами числовых данных. Синтаксис команды представляет собой: plot (X, Y), где X и Y являются векторами одинаковой длины.
Например вот такой график по точкам matlab:
X = [1 2 3]; Y = [4 6 5]; plot (X, Y)
Рис. 2.5. Построение линейных сегментов
• В этом случае мы отделили несколько команд в одной строке с помощью точки
с запятой, вместо запятой. Обратите внимание, что вывод команд,
предшествующих знаку точка с запятой, запрещается.
Команда plot рассматривает вектора X и Y, как перечни координат
последовательных точек на графике, и соединяет точки в виде линейных
сегментов. Таким образом, на Рис. 2.5 показано, как программа MATLAB
соединяет точки с координатами (1, 4), (2, 6) и (3, 5).
Чтобы начертить графики функций matlab например х 2 в интервале от -1 до 2, сначала требуется создать перечень X из значений х, а затем ввести plot (X, Х.^2). (Точка в
данном выражении обязательна, так как Х.^2 представляет собой
поэлементное возведение в квадрат вектора X, но не матричный квадрат.) Нам
необходимо использовать достаточное количество значений х для уверенности в
том, что результирующий график, нарисованный путем соединения точек,
будет выглядеть нормально (плавная, а не ломаная линия). Мы используем
приращение в размере 0.01. Таким образом, чтобы отобразить график
параболы, введите:
X = -1:0.01:2; plot(X, X.^2)
Результат отображен на Рис. 2.6. Обратите внимание, что мы использовали точку
с запятой, чтобы запретить вывод вектора X из 301 элемента.
Рис. 2.6. Построенная парабола
Более подробно графические команды программы MA TLAB рассматриваются в уроке 5.
А пока удовлетворимся демонстрацией построения пары выражений на одном и
том же графике. Надеюсь теперь вы получили подробный ответ на свой вопрос: как строить графики в matlab.
Поэтому из выше всего сказанного можно сделать вывод, что вам необходимо просмотреть много дополнительной информации и альтернатив!
MATLABимеет исключительно мощную систему для построения различных двухмерных и трехмерных графиков, а также их настройки, редактирования и форматирования. Типы и подтипы графиковMATLABочень разнообразны. Список функций двумерной графики можно получить командойhelp graph2d, трехмерной –help graph3d.
Графики выводятся в отдельных графических окнах с помощью команды вида figure(n), гдеn – номер графического окна. На одном графике можно построить несколько кривых, отличающихся цветом и типами линий и точек. Графики могут быть скопированы и вставлены в другие приложения:Word,Excel,PowerPointи др. Для этого используется командаEdit/ Copy Figureокна графики.
Часто используемые команды при построении графиков
plot(t,y) % График непрерывной функции y(t)
plot(x1, y1, x2, y2) % Графики зависимостей y1 от x1 и y2 от x1
stem(x,y) %График дискретной функции (сигнала)y(x)
stairs(x,y) % График в виде ступенчатой линии
loglog(f,Y) %График с логарифмическими масштабами по x и y
semilogx(f,Y) %Логарифмический масштаб поxи линейный поy
polar(phi,r) % График в полярных координатах
title(‘ название’) % Вывод заголовка графика
xlabel(‘время’) % Метка по осиx
ylabel(‘Напряжение’) % Метка по осиy
legend(‘АЧХ системы‘) % Вывод поясняющей надписи
axis([xmin, xmax, ymin, ymax]) % Установка масштабов по осямxи y
xlim([xmin,xmax]) % Установка масштаба по осиx
ylim([ymin,ymax]) % Установка масштаба по осиy
figure(n) % Устанавливает фигуру (окно)nактивной
subplot(r,c,n) % Разбивает графическое окно наr * cподокон иsubplot(rcn) % устанавливает подокноn в качестве активного.
gridon% к графику добавляется сетка
holdon% позволяет построить несколько графиков в окне
holdoff% отменяетholdonдля текущего графика
text% позволяет разместить текст на графике
zoomon/off% включение / выключение возможности увеличения % фрагментов графика с использованием
% левой и правой кнопок мыши
Построение графика зависимости функции yот индекса массива (номера элемента)x
Построение графика зависимости y(x)
Несколько пар аргументов в функции plot()позволяют построить несколько графиков в одном графическом окне. При этомMATLABдля каждого графика использует отдельный цвет линии.
Цвет, тип линии и обозначение (тип) точек являются аргументами функции plot, соответствующие справочные сведения можно получить с помощью команды вызова справкиhelp plot .
Для разбиения графического окна на подокна служит команда plot(m,n,p)илиplot(mnp),в которойm– число строк,n— число столбцов,p— номер подокна. Пример построения графика функциив двух подокнах с помощью функцииplot()в одном случае и функцииstem()в другом с разными пределами по оси аргумента (рис. 7):
t=linspace(0, 8, 401); % вычисление 402 точек в интервале [0,8]
axis([0 1 min(x) max(x)] )
Fs=1024; % Частота отсчетов
f1=50; % частота гармоники
N=512; % число отсчетов сигнала
t=0:1/Fs:(N-1)/Fs; % вектор времени
plot(t,x), grid % график сигнала
Для добавления графиков к уже существующим применяют команду hold on
Для отмены действия hold on (освобождения окна графики) используют hold off.
Пример построения графика в полярной системе координат
В окне графики MATLABпозволяют выполнять разнообразную настройку графического окна и его объектов с помощью меню или панели инструментов (рис.9).
В окне редактора или с помощью контекстного меню по правой кнопке мыши производятся необходимые установки (цвет, размер, тип, толщина линии и др.) объекта окна графики.
Возможности для подобной интерактивной настройки графики — очень широкие. В первую очередь они обеспечиваются кнопкой Edit Plot инструментальной панели окна.
Трехмерная графика MATLAB– очень развитая и многообразная, сама по себе очень важная часть программы, но в курсе «Сигналы и системы» она используется редко.
Некоторые из команд построения 3D– графиков
>> plot3(…) % строит аксонометрическое изображение 3D-поверхности
>> mesh(…) % строит трехмерные поверхности со специфицированной
Пример построения графика передаточной функции системы второго порядка с передаточной функцией .
Нули и полюса системы :
Как найти уравнение графика, соединяющего точки данных в Matlab?
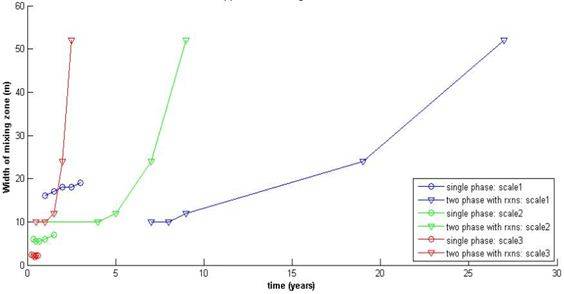
У меня есть различные сюжеты (с hold on ), как показано на следующем рисунке:
Я хотел бы знать, как найти уравнения этих шести кривых в Matlab. Спасибо.
5 ответов
нашел интерактивный инструмент установки в Matlab простой и полезный, хотя несколько ограниченный по объему:
график выше кажется линейной интерполяцией. Учитывая векторы X и Y данных, где X содержит аргументы, а Y-точки функции, вы можете сделать
чтобы получить линейно интерполированное значение f (x). Например, если данные
должно дать вам очень грубое приближение к 1.5^2 . interp1 будет точно соответствовать графику, но вас могут заинтересовать более причудливые операции подгонки кривых, такие как сплайн приближений и т. д.
тут rxns подставка для реакции? В этом случае, ваши кривые, скорее всего, экспоненциальный. Экспоненциальная функция имеет вид: y = a*exp(b * x) . В твоем случае, y – ширина зоны смешивания и x – это время в годах. Теперь, все, что вам нужно сделать, это запустить экспоненциальная регрессия в Matlab найти оптимальные значения параметров a и b , и у вас будут свои уравнения.
совет, хотя может быть лучший ответ, от меня: попробуйте увидеть скорость увеличения кривой. Например, кубический является более репрезентативным, чем квадратичный, если скорость увеличения кажется быстрой и найти полином и вычислить ошибку отклонения. Для нерегулярных кривых, вы можете попробовать сплайн сторона. Я думаю, что в matlab также есть набор инструментов для сплайн-фитинга.
существует способ извлечения информации с помощью текущего дескриптора фигуры (gcf) из вашего графика.
например, вы можете получить ряд, который был нанесен на график:
должна быть другая информация, которую вы можете получить от ” findall(gcf. )” методы.
Аппроксимация в Matlab
Приветствую! Сегодня продолжаем говорить об обработке экспериментальных данных. Сегодняшняя статья — продолжение предыдущей темы: Интерполяция в Matlab. Настоятельно советую с ней ознакомиться перед чтением данной статьи. По сути аппроксимация в Matlab очень похожа на интерполяцию, однако, для её реализации используются другие правила и функции.
Аппроксимация
Относительно интерполяции, аппроксимация получила более широкое распространение. Сущность этого метода состоит в том, что табличные данные аппроксимируют кривой, которая не обязательно должна пройти через все узловые точки, а должна как бы сгладить все случайные помехи табличной функции.
МНК (Метод Наименьших Квадратов)
Одним из самых популярных методов аппроксимации в Matlab и в других средах, это Метод Наименьших Квадратов ( МНК ). В этом методе при сглаживании опытных данных аппроксимирующую кривую стремятся провести так, чтобы её отклонения от табличных данных по всем узловым точкам были минимальными.
Суть МНК заключается в следующем: для табличных данных, полученных в результате эксперимента, отыскать аналитическую зависимость, сумма квадратов уклонений которой от табличных данных во всех узловых точках была бы минимальной.
Аппроксимация в Matlab по МНК осуществляется с помощью функции polyfit. Функция p = polyfit(x, y, n) находит коэффициенты полинома p(x) степени n, который аппроксимирует функцию y(x) в смысле метода наименьших квадратов. Выходом является строка p длины n+1, содержащая коэффициенты аппроксимирующего полинома.
Примеры задач
Разберём задачу, в которой разрешается использование встроенных матлабовских функций.
Осуществить аппроксимацию в Matlab табличных данных x = [0, 0.1 , 0.2, 0.3, 0.5] и y = [3, 4.5, 1.7, 0.7, -1] . Применяя метод наименьших квадратов, приблизить ее многочленами 1-ой и 2-ой степени. Для каждого определить величину среднеквадратической ошибки. Построить (на одном листе) графики и заданной таблично функции (ломанная линия) и приближающих ее многочленов 1-ой и 2-ой степени.
Вывод:
ans = 0.9253
ans = 0.8973
Однако, встречаются задачи, где требуется реализовать аппроксимацию в Matlab без использования специальных функций.
Найти у(0.25) путём построения аппроксимирующего полинома методом наименьших квадратов согласно данным:
x: 0, 0.1, 0.2, 0.3, 0.5
y: 3, 4.5, 1.7, 0.7, -1
p: 0.5, 0.8, 1.6, 0.8, 0.1
Построить этот полином без учёта весовых коэффициентов с использованием определителя Вандермонда и стандартных операторов.
Вывод:
a =
228.1447
-176.0984
22.7745
3.1590
qq = 228.1447 -176.0984 22.7745 3.1590
y2 = 1.4113
Как видите встроенные функции для аппроксимации в Matlab укорачивают алгоритм почти вдвое.
Существует также возможность реализации всего алгоритма через одну функцию, но для преподавателей студентов она скорее всего будет не приемлема. С помощью функции lsqcurvefit(fun,x0,xdata,ydata), где:
xdata,ydata– табличные значения аппроксимируемой функции;
x0 –стартовое значение параметров функции;
fun – функция аппроксимации, задаваемая пользователем
С аналитически-теоретической стороны, существуют такие виды аппроксимации:
- Аппроксимация ортогональными классическими полиномами.
- Аппроксимация каноническим полиномом
Но на практике их реализацию требуют редко.
Вот и вся основная информация по аппроксимации в Matlab, если остались вопросы, задавайте их в комментариях.
[spoiler title=”источники:”]
http://askdev.ru/q/kak-nayti-uravnenie-grafika-soedinyayuschego-tochki-dannyh-v-matlab-420467/
http://codetown.ru/matlab/approksimaciya/
[/spoiler]
|
ZondArt 7 / 4 / 0 Регистрация: 22.01.2012 Сообщений: 63 |
||||
|
1 |
||||
График функции задан по точкам. Найти производную этой функции13.01.2014, 17:19. Показов 8284. Ответов 1 Метки нет (Все метки)
Дана функция, заданная точками (X, Y). Необходимо найти её производную. Собственно что я и сделал в матлабе. Вот код программы:
В результате получился вот такой график: Красным обозначена моя функция, а синим это её найденная производная. Не понятно откуда в производной взялся участок, выделенный зелёным. Так вот хотелось бы узнать, правильно ли я нашёл производную и откуда такой “отросток” там появился?
0 |
|
Зосима 5221 / 3552 / 372 Регистрация: 02.04.2012 Сообщений: 6,458 Записей в блоге: 17 |
||||
|
14.01.2014, 12:59 |
2 |
|||
|
РешениеZondArt, если команде diff скормить массив, то она вернет поэлементные разности , а это не производные!
*если график убывает, то производная должна быть меньше нуля!
1 |
Доброго времени суток! Сегодня поговорим о работе с данными полученными «экспериментально». Подразумевается, что даны значения по двум или более координатам (точки), с которыми в задаче нас просят выполнить то или иное действие. В этой статье мы с вами узнаем, что такое интерполяция в Matlab, и какие действия она позволяет выполнять.
Интерполяция
Задав такой вопрос поисковику, вы получите весьма развёрнутый ответ от Wikipedia. Но в двух словах, интерполяция (интерполирование) — процесс нахождения промежуточных значений по ряду данных, для восполнения пробелов между точными значениями приближенными. Точные значения так же называют узловыми точками.
Линейная интерполяция Matlab
Не будем вдаваться в математические определения и термины, перейдём сразу к сути:
Алгоритм интерполяции определяется способом вычисления приближенных значений между точными. Наиболее простым и очевидным вариантом является построение прямой между двумя узловыми точками. Этот метод называется методом линейной интерполяции.
В Matlab такой способ реализован с помощью команды
interp1(x,y, xi, 'linear') или просто interp1(x,y, xi), где x и y массивы из табличных данных (координаты точек), xi — массив промежуточных точек, координаты которых требуется найти.
Интерполяционные полиномы
Есть разные интерполяционные полиномы — функции, определяющие как будут изменяться приближенные значения между узловыми точками:
- Канонический полином
- Полином Лагранжа
- Полином Ньютона
Разберём для самого часто встречающегося полинома реализацию в Matlab. Вот пример использования:
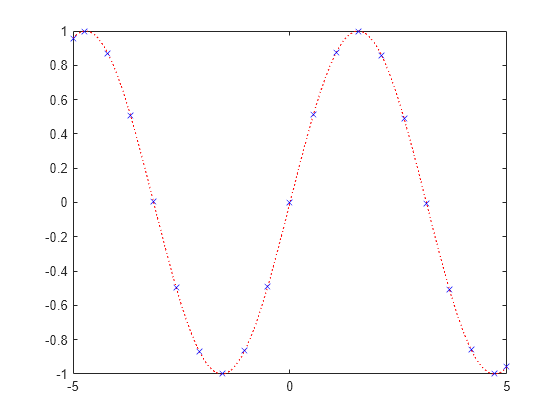
Проинтерполировать функцию sin x на отрезке [1, 9] с шагом 2 и построим графики sin x и полученного интерполяционного полинома.
Для начала необходимо создать функцию, по которой Matlab будет считать. Создайте файл с именем «lagrange» и скопируйте в него:
function yy=lagrange(x,y,xx) % вычисление интерполяционного полинома в форме Лагранжа % x - массив координат узлов % y - массив значений интерполируемой функции % xx - массив значений аргумента, для которых надо вычислить значения полинома % yy - массив значений полинома в точках xx % узнаем число узлов интерполяции (N=n+1) N=length(x); % создаем нулевой массив значений интерполяционного полинома yy=zeros(size(xx)); % в цикле считаем сумму по узлам for k=1:N % вычисляем произведения, т.е. функции Psi_k t=ones(size(xx)); for j=[1:k-1, k+1:N] t=t.*(xx-x(j))/(x(k)-x(j)); end % накапливаем сумму yy = yy + y(k)*t; end
Теперь создайте ещё один файл и запишем в него само решение поставленной задачи:
% задание узлов интерполяции x=1:2:9; y=sin(x); % задание точек, в которых требуется найти значения интерполяционного полинома xx=linspace(1,9,1000); % нахождение значений интерполяционного полинома yy=lagrange(x,y,xx); % построение графиков figure('Color','w') % вывод графика sin(x) fplot(@sin,[1 9]) hold on % вывод графика полинома plot(xx,yy,'r') % вывод узлов интерполяции plot(x,y,'bo') % размещение легенды legend('sinitx','{itL_n (интерполяция)}','узлы',-1)
Ссылки на файлы — исходники сможете найти в конце статьи. Более подробную информацию о полиноме Лагранжа вы сможете найти на официальном сайте Matlab.
Интерполяция сплайнами
Ещё один часто встречающийся метод интерполяции. Происхождение термина “сплайны” связано с гибкой чертежной линейкой, которой пользовались для рисования гладких кривых, проходящих через заданные точки. Сплайн — это группа кубических многочленов, которые также называют кубическими сплайнами.
Вычисление сплайн интерполяции в Matlab осуществляется с помощью команды spline(x, y, xx), где х и у — массивы табличных данных, а хх — промежуточные значения по оси абцисс (Х). Вот небольшой пример:
Построить интерполяцию сплайнами функции Рунге.
% Введём функцию Рунге f = inline('1./(1+25*x.^2)'); % Вычислим таблицу значений x = linspace(-1, 1, 10); y = f(x); % Вычислим сплайн-интерполяцию xx = linspace(-1, 1, 100); yy = spline(x, y, xx); % Начертим графики axes('NextPlot','Add'); plot(x, y,'LineWidth', 2); % Красным на графике - аппроксимация, жирным - исходная функция plot(xx, yy,'Color','r');
Вывод:
interp1
Большинство задач в Matlab реализуются с помощью этой команды. yi = interp1 (x,y,xi, metod), где х – массив абсцисс экспериментальных точек, у – массив ординат экспериментальных точек, xi — точки, в которых необходимо вычислить значения с помощью сплайна, metod – определяет метод построения сплайна. Этот параметр может принимать следующие значения:
- ‘nearest’ – интерполяция по соседним точкам – этот метод построения кусочной функции, при котором значение в любой точке равно значению в ближайшей узловой точке – интерполяция полиномами 0-ой степени;
- ‘linear’ – линейная сплайн-интерполяция — интерполяция полиномами 1-ой степени (применяется по умолчанию, если способ интерполирования не задан);
- ‘cubic’ – интерполяция кубическим полиномом;
- ‘spline’ – интерполяция кубическим сплайном;
- ‘pchip’ — интерполяция кубическим эрмитовым сплайном.
Вот и вся основная информация по интерполяции в Matlab, если остались вопросы, задавайте их в комментариях.
Скачать исходник — lagrange
Скачать исходник — Полином Лагранжа
Скачать исходник — Сплайном функцию Рунге
У меня есть различные сюжеты (с hold on), как показано на следующем рисунке:
Я хотел бы знать, как найти уравнения этих шести кривых в Matlab. Спасибо.
5 ответов
график выше кажется линейной интерполяцией. Учитывая векторы X и Y данных, где X содержит аргументы, а Y-точки функции, вы можете сделать
f = interp1(X, Y, x)
чтобы получить линейно интерполированное значение f (x). Например, если данные
X = [0 1 2 3 4 5];
Y = [0 1 4 9 16 25];
затем
y = interp1(X, Y, 1.5)
должно дать вам очень грубое приближение к 1.5^2. interp1 будет точно соответствовать графику, но вас могут заинтересовать более причудливые операции подгонки кривых, такие как сплайн приближений и т. д.
тут rxns подставка для реакции? В этом случае, ваши кривые, скорее всего, экспоненциальный. Экспоненциальная функция имеет вид: y = a*exp(b * x) . В твоем случае, y – ширина зоны смешивания и x – это время в годах. Теперь, все, что вам нужно сделать, это запустить экспоненциальная регрессия в Matlab найти оптимальные значения параметров a и b, и у вас будут свои уравнения.
совет, хотя может быть лучший ответ, от меня: попробуйте увидеть скорость увеличения кривой. Например, кубический является более репрезентативным, чем квадратичный, если скорость увеличения кажется быстрой и найти полином и вычислить ошибку отклонения. Для нерегулярных кривых, вы можете попробовать сплайн сторона. Я думаю, что в matlab также есть набор инструментов для сплайн-фитинга.
0
автор: Jack_of_All_Trades
существует способ извлечения информации с помощью текущего дескриптора фигуры (gcf) из вашего графика.
например, вы можете получить ряд, который был нанесен на график:
% Some figure is created and data are plotted on it
figure;
hold on;
A = [ 1 2 3 4 5 7] % Dummy data
B = A.*A % Some other dummy data
plot(A,B);
plot(A.*3,B-1);
% Those three lines of code will get you series that were plotted on your graph
lh=findall(gcf,'type','line'); % Extract the plotted line from the figure handle
xp=get(lh,'xdata'); % Extract the Xs
yp=get(lh,'ydata'); % Extract the Ys
должна быть другая информация, которую вы можете получить от ” findall(gcf,…)” методы.
Plot expression or function
Syntax
Description
example
fplot( plots thef)
curve defined by the function y = f(x) over the
default interval [-5 5] for x.
example
fplot( plotsf,xinterval)
over the specified interval. Specify the interval as a two-element
vector of the form [xmin xmax].
example
fplot( plotsfunx,funy)
the curve defined by x = funx(t) and y over the default interval
= funy(t)[-5 5] for t.
fplot( plotsfunx,funy,tinterval)
over the specified interval. Specify the interval as a two-element
vector of the form [tmin tmax].
fplot(___, specifiesLineSpec)
the line style, marker symbol, and line color. For example, '-r' plots
a red line. Use this option after any of the input argument combinations
in the previous syntaxes.
example
fplot(___, specifiesName,Value)
line properties using one or more name-value pair arguments. For example, 'LineWidth',2 specifies
a line width of 2 points.
fplot( plotsax,___)
into the axes specified byax instead of the current
axes (gca). Specify the axes as the first input
argument.
[x,y] = returns the abscissas and ordinates for
fplot(___)
the function without creating a plot. This syntax will be removed in a future
release. Use the XData and YData
properties of the line object, fp, instead.
Note
fplot no longer supports input arguments for
specifying the error tolerance or the number of evaluation points. To
specify the number of evaluation points, use the MeshDensity property.
Examples
collapse all
Plot Expression
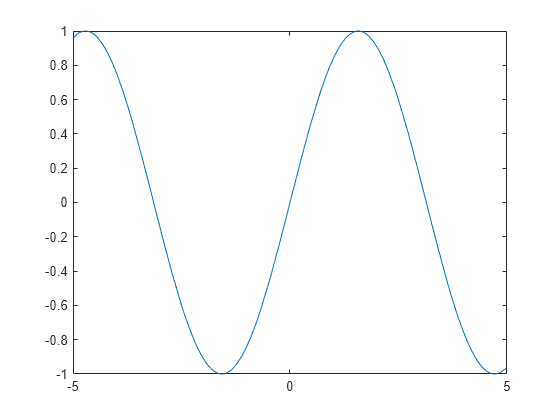
Plot sin(x) over the default x interval [-5 5].
Plot Parametric Curve
Plot the parametric curve x=cos(3t) and y=sin(2t).
xt = @(t) cos(3*t); yt = @(t) sin(2*t); fplot(xt,yt)
Specify Plotting Interval and Plot Piecewise Functions
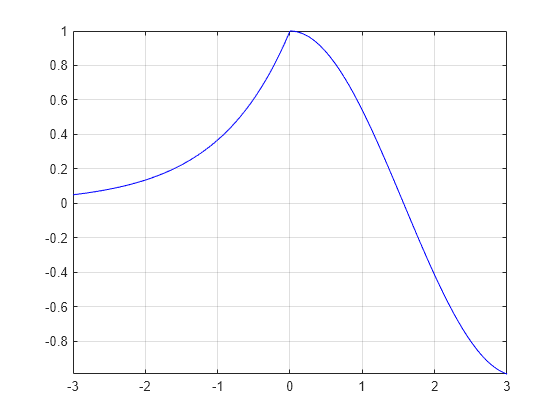
Plot the piecewise function
ex-3<x<0cos(x)0<x<3.
Plot multiple lines using hold on. Specify the plotting intervals using the second input argument of fplot. Specify the color of the plotted lines as blue using 'b'. When you plot multiple lines in the same axes, the axis limits adjust to incorporate all the data.
fplot(@(x) exp(x),[-3 0],'b') hold on fplot(@(x) cos(x),[0 3],'b') hold off grid on
Specify Line Properties and Display Markers
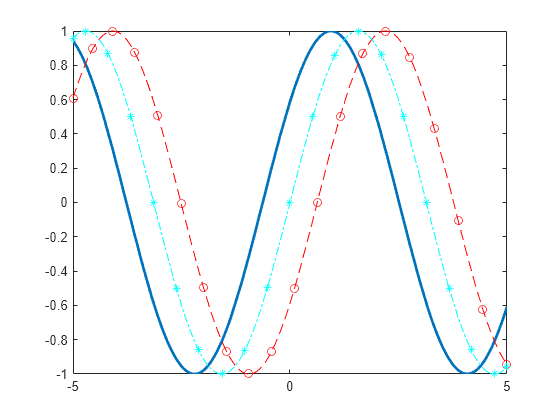
Plot three sine waves with different phases. For the first, use a line width of 2 points. For the second, specify a dashed red line style with circle markers. For the third, specify a cyan, dash-dotted line style with asterisk markers.
fplot(@(x) sin(x+pi/5),'Linewidth',2); hold on fplot(@(x) sin(x-pi/5),'--or'); fplot(@(x) sin(x),'-.*c') hold off
Modify Line Properties After Creation
Plot sin(x) and assign the function line object to a variable.
fp =
FunctionLine with properties:
Function: @(x)sin(x)
Color: [0 0.4470 0.7410]
LineStyle: '-'
LineWidth: 0.5000
Show all properties
Change the line to a dotted red line by using dot notation to set properties. Add cross markers and set the marker color to blue.
fp.LineStyle = ':'; fp.Color = 'r'; fp.Marker = 'x'; fp.MarkerEdgeColor = 'b';
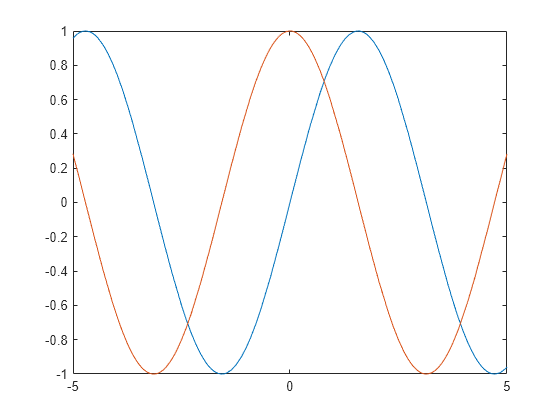
Plot Multiple Lines in Same Axes
Plot two lines using hold on.
fplot(@(x) sin(x)) hold on fplot(@(x) cos(x)) hold off
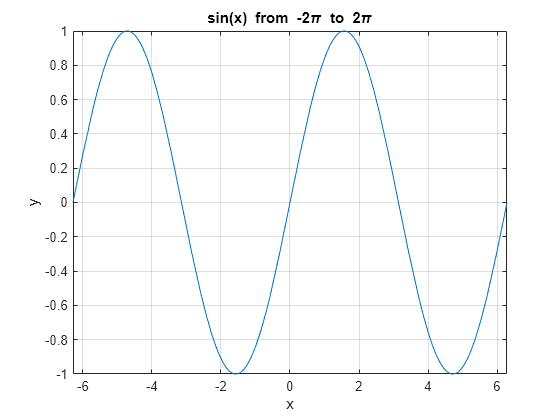
Add Title and Axis Labels and Format Ticks
Plot sin(x) from -2π to 2π using a function handle. Display the grid lines. Then, add a title and label the x-axis and y-axis.
fplot(@sin,[-2*pi 2*pi]) grid on title('sin(x) from -2pi to 2pi') xlabel('x'); ylabel('y');
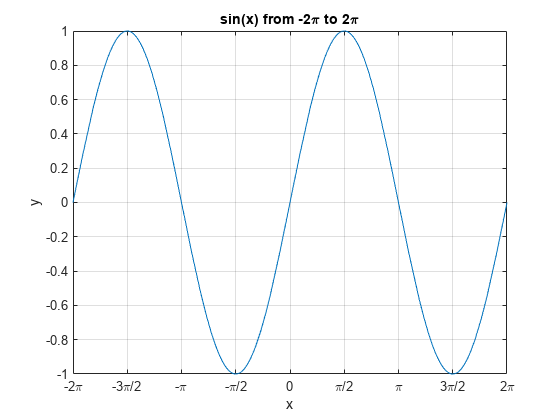
Use gca to access the current axes object. Display tick marks along the x-axis at intervals of π/2. Format the x-axis tick values by setting the XTick and XTickLabel properties of the axes object. Similar properties exist for the y-axis.
ax = gca;
ax.XTick = -2*pi:pi/2:2*pi;
ax.XTickLabel = {'-2pi','-3pi/2','-pi','-pi/2','0',...
'pi/2','pi','3pi/2','2pi'};
Input Arguments
collapse all
f — Function to plot
function handle
Function to plot, specified as a function handle to a named
or anonymous function.
Specify a function of the form y = f(x).
The function must accept a vector input argument and return a vector
output argument of the same size. Use array operators instead of matrix
operators for the best performance. For example, use .* (times)
instead of * (mtimes).
Note
Support for character vector inputs will be removed in a future
release. Use function handles instead.
Example: fplot(@(x) sin(x)) plots sin(x) over the default
interval, [-5, 5].
xinterval — Interval for x
[–5 5] (default) | two-element vector of form [xmin xmax]
Interval for x, specified as a two-element
vector of the form [xmin xmax].
funx — Parametric function for x coordinates
function handle
Parametric function for x coordinates, specified
as a function handle to a named or anonymous function.
Specify a function of the form x = funx(t).
The function must accept a vector input argument and return a vector
output argument of the same size. Use array operators instead of matrix
operators for the best performance. For example, use .* (times)
instead of * (mtimes).
Example: funx = @(t) sin(2*t);
funy — Parametric function for y coordinates
anonymous function | function handle
Parametric function for y coordinates, specified
as a function handle to a named or anonymous function.
Specify a function of the form y = funy(t).
The function must accept a vector input argument and return a vector
output argument of the same size. Use array operators instead of matrix
operators for the best performance. For example, use .* (times)
instead of * (mtimes).
Example: funy = @(t) cos(3*t);
tinterval — Interval for t
[-5 5] (default) | two-element vector of form [tmin tmax]
Interval for t, specified as a two-element
vector of the form [tmin tmax].
ax — Axes object
axes object
Axes object. If you do not specify an axes object, then fplot uses
the current axes (gca).
LineSpec — Line style, marker, and color
string scalar | character vector
Line style, marker, and color, specified as a string scalar or character vector containing
symbols. The symbols can appear in any order. You do not need to specify all
three characteristics (line style, marker, and color). For example, if you
omit the line style and specify the marker, then the plot shows only the
marker and no line.
Example: "--or" is a red dashed line with circle markers.
| Line Style | Description | Resulting Line |
|---|---|---|
"-" |
Solid line |
|
"--" |
Dashed line |
|
":" |
Dotted line |
|
"-." |
Dash-dotted line |
|
| Marker | Description | Resulting Marker |
|---|---|---|
"o" |
Circle |
|
"+" |
Plus sign |
|
"*" |
Asterisk |
|
"." |
Point |
|
"x" |
Cross |
|
"_" |
Horizontal line |
|
"|" |
Vertical line |
|
"square" |
Square |
|
"diamond" |
Diamond |
|
"^" |
Upward-pointing triangle |
|
"v" |
Downward-pointing triangle |
|
">" |
Right-pointing triangle |
|
"<" |
Left-pointing triangle |
|
"pentagram" |
Pentagram |
|
"hexagram" |
Hexagram |
|
| Color Name | Short Name | RGB Triplet | Appearance |
|---|---|---|---|
"red" |
"r" |
[1 0 0] |
|
"green" |
"g" |
[0 1 0] |
|
"blue" |
"b" |
[0 0 1] |
|
"cyan"
|
"c" |
[0 1 1] |
|
"magenta" |
"m" |
[1 0 1] |
|
"yellow" |
"y" |
[1 1 0] |
|
"black" |
"k" |
[0 0 0] |
|
"white" |
"w" |
[1 1 1] |
|
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: 'Marker','o','MarkerFaceColor','red'
The properties listed here are only a subset. For a complete
list, see FunctionLine Properties or ParameterizedFunctionLine Properties.
Number of evaluation points, specified as a number. The default
is 23. Because fplot uses
adaptive evaluation, the actual number of evaluation points is greater.
Line color, specified as an RGB triplet, a hexadecimal color code, a color name, or a short
name.
For a custom color, specify an RGB triplet or a hexadecimal color code.
-
An RGB triplet is a three-element row vector whose elements
specify the intensities of the red, green, and blue
components of the color. The intensities must be in the
range[0,1], for example,[0.4.
0.6 0.7] -
A hexadecimal color code is a string scalar or character
vector that starts with a hash symbol (#)
followed by three or six hexadecimal digits, which can range
from0toF. The
values are not case sensitive. Therefore, the color codes
"#FF8800",
"#ff8800",
"#F80", and
"#f80"are equivalent.
Alternatively, you can specify some common colors by name. This table lists the named color
options, the equivalent RGB triplets, and hexadecimal color codes.
| Color Name | Short Name | RGB Triplet | Hexadecimal Color Code | Appearance |
|---|---|---|---|---|
"red" |
"r" |
[1 0 0] |
"#FF0000" |
|
"green" |
"g" |
[0 1 0] |
"#00FF00" |
|
"blue" |
"b" |
[0 0 1] |
"#0000FF" |
|
"cyan"
|
"c" |
[0 1 1] |
"#00FFFF" |
|
"magenta" |
"m" |
[1 0 1] |
"#FF00FF" |
|
"yellow" |
"y" |
[1 1 0] |
"#FFFF00" |
|
"black" |
"k" |
[0 0 0] |
"#000000" |
|
"white" |
"w" |
[1 1 1] |
"#FFFFFF" |
|
Here are the RGB triplets and hexadecimal color codes for the default colors MATLAB® uses in many types of plots.
| RGB Triplet | Hexadecimal Color Code | Appearance |
|---|---|---|
[0 0.4470 0.7410] |
"#0072BD" |
|
[0.8500 0.3250 0.0980] |
"#D95319" |
|
[0.9290 0.6940 0.1250] |
"#EDB120" |
|
[0.4940 0.1840 0.5560] |
"#7E2F8E" |
|
[0.4660 0.6740 0.1880] |
"#77AC30" |
|
[0.3010 0.7450 0.9330] |
"#4DBEEE" |
|
[0.6350 0.0780 0.1840] |
"#A2142F" |
|
Example: 'blue'
Example: [0
0 1]
Example: '#0000FF'
Line style, specified as one of the options listed in this table.
| Line Style | Description | Resulting Line |
|---|---|---|
"-" |
Solid line |
|
"--" |
Dashed line |
|
":" |
Dotted line |
|
"-." |
Dash-dotted line |
|
"none" |
No line | No line |
Line width, specified as a positive value in points, where 1 point = 1/72 of an inch. If the
line has markers, then the line width also affects the marker
edges.
The line width cannot be thinner than the width of a pixel. If you set the line width
to a value that is less than the width of a pixel on your system, the line displays as
one pixel wide.
Marker symbol, specified as one of the values listed in this table. By default, the object
does not display markers. Specifying a marker symbol adds markers at each data point or
vertex.
| Marker | Description | Resulting Marker |
|---|---|---|
"o" |
Circle |
|
"+" |
Plus sign |
|
"*" |
Asterisk |
|
"." |
Point |
|
"x" |
Cross |
|
"_" |
Horizontal line |
|
"|" |
Vertical line |
|
"square" |
Square |
|
"diamond" |
Diamond |
|
"^" |
Upward-pointing triangle |
|
"v" |
Downward-pointing triangle |
|
">" |
Right-pointing triangle |
|
"<" |
Left-pointing triangle |
|
"pentagram" |
Pentagram |
|
"hexagram" |
Hexagram |
|
"none" |
No markers | Not applicable |
Marker outline color, specified as "auto", an RGB triplet, a
hexadecimal color code, a color name, or a short name. The default value of
"auto" uses the same color as the Color
property.
For a custom color, specify an RGB triplet or a hexadecimal color code.
-
An RGB triplet is a three-element row vector whose elements
specify the intensities of the red, green, and blue
components of the color. The intensities must be in the
range[0,1], for example,[0.4.
0.6 0.7] -
A hexadecimal color code is a string scalar or character
vector that starts with a hash symbol (#)
followed by three or six hexadecimal digits, which can range
from0toF. The
values are not case sensitive. Therefore, the color codes
"#FF8800",
"#ff8800",
"#F80", and
"#f80"are equivalent.
Alternatively, you can specify some common colors by name. This table lists the named color
options, the equivalent RGB triplets, and hexadecimal color codes.
| Color Name | Short Name | RGB Triplet | Hexadecimal Color Code | Appearance |
|---|---|---|---|---|
"red" |
"r" |
[1 0 0] |
"#FF0000" |
|
"green" |
"g" |
[0 1 0] |
"#00FF00" |
|
"blue" |
"b" |
[0 0 1] |
"#0000FF" |
|
"cyan"
|
"c" |
[0 1 1] |
"#00FFFF" |
|
"magenta" |
"m" |
[1 0 1] |
"#FF00FF" |
|
"yellow" |
"y" |
[1 1 0] |
"#FFFF00" |
|
"black" |
"k" |
[0 0 0] |
"#000000" |
|
"white" |
"w" |
[1 1 1] |
"#FFFFFF" |
|
"none" |
Not applicable | Not applicable | Not applicable | No color |
Here are the RGB triplets and hexadecimal color codes for the default colors MATLAB uses in many types of plots.
| RGB Triplet | Hexadecimal Color Code | Appearance |
|---|---|---|
[0 0.4470 0.7410] |
"#0072BD" |
|
[0.8500 0.3250 0.0980] |
"#D95319" |
|
[0.9290 0.6940 0.1250] |
"#EDB120" |
|
[0.4940 0.1840 0.5560] |
"#7E2F8E" |
|
[0.4660 0.6740 0.1880] |
"#77AC30" |
|
[0.3010 0.7450 0.9330] |
"#4DBEEE" |
|
[0.6350 0.0780 0.1840] |
"#A2142F" |
|
Marker fill color, specified as 'auto', an RGB triplet, a hexadecimal color
code, a color name, or a short name. The 'auto' value uses the same
color as the MarkerEdgeColor property.
For a custom color, specify an RGB triplet or a hexadecimal color code.
-
An RGB triplet is a three-element row vector whose elements
specify the intensities of the red, green, and blue
components of the color. The intensities must be in the
range[0,1], for example,[0.4.
0.6 0.7] -
A hexadecimal color code is a string scalar or character
vector that starts with a hash symbol (#)
followed by three or six hexadecimal digits, which can range
from0toF. The
values are not case sensitive. Therefore, the color codes
"#FF8800",
"#ff8800",
"#F80", and
"#f80"are equivalent.
Alternatively, you can specify some common colors by name. This table lists the named color
options, the equivalent RGB triplets, and hexadecimal color codes.
| Color Name | Short Name | RGB Triplet | Hexadecimal Color Code | Appearance |
|---|---|---|---|---|
"red" |
"r" |
[1 0 0] |
"#FF0000" |
|
"green" |
"g" |
[0 1 0] |
"#00FF00" |
|
"blue" |
"b" |
[0 0 1] |
"#0000FF" |
|
"cyan"
|
"c" |
[0 1 1] |
"#00FFFF" |
|
"magenta" |
"m" |
[1 0 1] |
"#FF00FF" |
|
"yellow" |
"y" |
[1 1 0] |
"#FFFF00" |
|
"black" |
"k" |
[0 0 0] |
"#000000" |
|
"white" |
"w" |
[1 1 1] |
"#FFFFFF" |
|
"none" |
Not applicable | Not applicable | Not applicable | No color |
Here are the RGB triplets and hexadecimal color codes for the default colors MATLAB uses in many types of plots.
| RGB Triplet | Hexadecimal Color Code | Appearance |
|---|---|---|
[0 0.4470 0.7410] |
"#0072BD" |
|
[0.8500 0.3250 0.0980] |
"#D95319" |
|
[0.9290 0.6940 0.1250] |
"#EDB120" |
|
[0.4940 0.1840 0.5560] |
"#7E2F8E" |
|
[0.4660 0.6740 0.1880] |
"#77AC30" |
|
[0.3010 0.7450 0.9330] |
"#4DBEEE" |
|
[0.6350 0.0780 0.1840] |
"#A2142F" |
|
Example: [0.3 0.2 0.1]
Example: 'green'
Example: '#D2F9A7'
Marker size, specified as a positive value in points, where 1 point = 1/72 of an inch.
Output Arguments
collapse all
fp — One or more FunctionLine or ParameterizedFunctionLine objects
scalar | vector
One or more FunctionLine or ParameterizedFunctionLine objects,
returned as a scalar or a vector.
-
If you use the
fplot(f)syntax
or a variation of this syntax, thenfplotreturnsFunctionLineobjects. -
If you use the
fplot(funx,funy)syntax
or a variation of this syntax, thenfplotreturnsParameterizedFunctionLineobjects.
You can use these objects to query and modify properties of
a specific line. For a list of properties, see FunctionLine Properties and ParameterizedFunctionLine Properties.
Tips
-
Use element-wise operators for the best performance
and to avoid a warning message. For example, usex.*yinstead
ofx*y. For more information, see Array vs. Matrix Operations. -
When you zoom in on the chart,
fplotreplots
the data, which can reveal hidden details.
Extended Capabilities
GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.
Usage notes and limitations:
-
This function accepts GPU arrays, but does not run on a GPU.
For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Distributed Arrays
Partition large arrays across the combined memory of your cluster using Parallel Computing Toolbox™.
Usage notes and limitations:
-
This function operates on distributed arrays, but executes in the client MATLAB.
For more information, see Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox).
Version History
Introduced before R2006a

 Сообщение было отмечено ZondArt как решение
Сообщение было отмечено ZondArt как решение