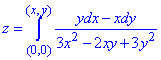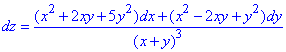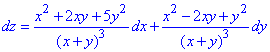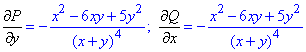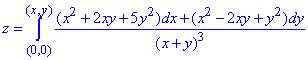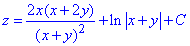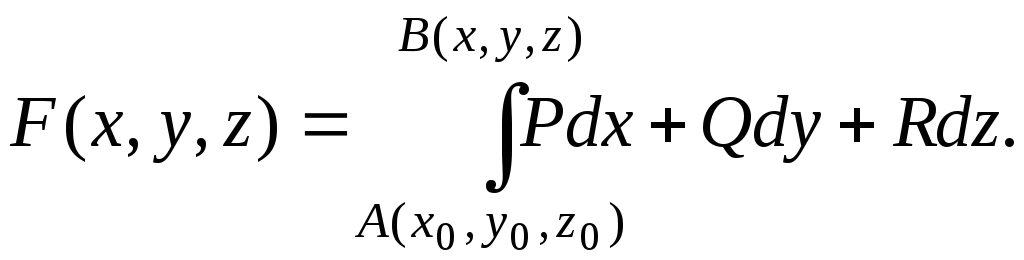Сегодня научим Вас возобновлять функцию через интеграл от ее полного дифференциала.
Алгоритм который описывает что за чем нужно делать детально расписан в приведенной дальше статье.
Формула Ньютона-Лейбница для криволинейного интеграла от полного дифференциала имеет вид
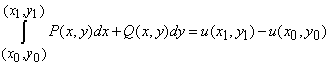
где P(x, y) частичная производная функции u по переменной y,
Q(x, y) частичная производная функции u по переменной x.
Для ее использования необходимо лишь убедиться, что частичные производные P(x, y), Q(x, y) равны между собой
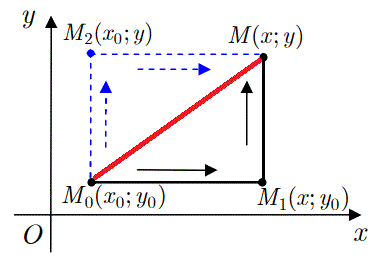
Криволинейный интеграл 2 рода (1) упрощается, если контур интегрирования от точки M0(x0,y0) к M(x, y) по прямой заменить ломаной, что состоит из прямых параллельных к осям координат M0M1 но M1M или M0M2 но M2M.
С одной стороны это позволяют свойства криволинейных интегралов.
Из другой такой способ имеет практическую выгоду.
На практике можем превратить в нуль один из дифференциалов под интегралом, если интегрировать вдоль прямых параллельных осям, в замен придется интегрировать вдоль двух отрезков прямых, тоесть вычислять сумму двух интегралов. Детальнее об этом можете почитать в статье об интегрировании полных дифференциалов.
Пример 1 Найти функцию z, если известен полный дифференциал функции
dz=(ydx-xdy)/(3x2-2xy+3y2)
Решение: Разделяем слагаемые при dx, dy, но выписываем для функции z дифференциалы P, Q:

Найдем частичные производные первого порядка функций P(x, y), Q(x, y):
Из равенства частичных производных 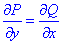
Функцию z найдем с помощью криволинейного интегралу 2-го рода:
Приведенный криволинейный интеграл от точки (0,0) к точке (x, y) будем вычислять вдоль прямых x=0 и y=y0.
Так как криволинейный интеграл не зависит от контура интегрирования, то кривую интегрирования будем строить в виде ломанной из двух прямых, которые параллельны осям и соединяют крайние точки.
Это делается с целью избавиться от одного из дифференциалов на каждом из промежутков интегрирования.
В этом случае ломаную можно выбрать из следующих прямых
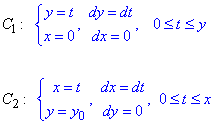
Здесь также записано почему ровные соответствующие дифференциалы.
Вычислим криволинейный интеграл 2 рода для возобновления функции z через полный дифференциал:
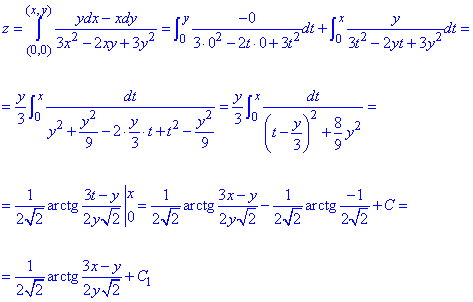
Внимательно разберите интегрирование.
Пример 2 Найти функцию z, если
Решение: Имеем дифференциал:
Здесь обозначено
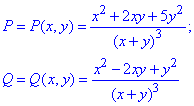
Найдем частичные производные первого порядка функций P(x, y) но Q(x, y):
Как видим условие равенства частных производных выполняется 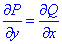
Функцию z найдем с помощью криволинейного интеграла 2-го рода:
Полученный криволинейный интеграл от точки (1,0) к точке (x,y) будем вычислять вдоль прямых y=1 и x=x0.
То есть
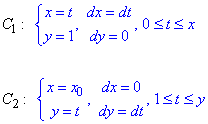
Возобновим функцию z за ее полным дифференциалом с помощью криволинейного интегралу второго рода
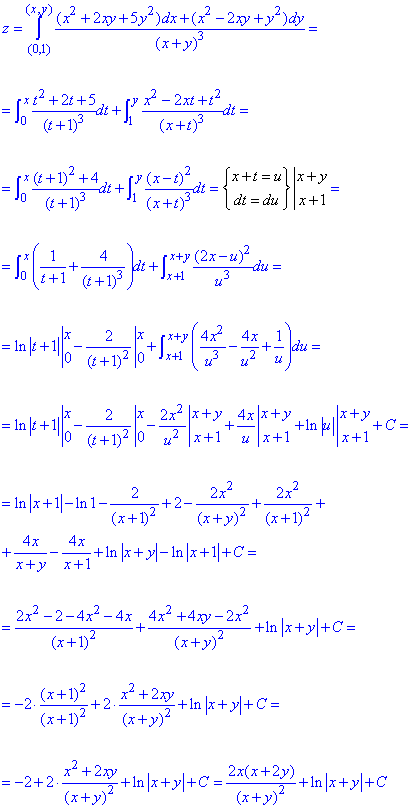
При интегрировании выполнили замену переменных
Выписываем конечное значение интеграла
Впереди Вас ожидают новые решения на криволинейные, поверхностные, тройные и другие интегралы.
Теорема
1.
Пусть функции
непрерывны
в ограниченной правильной области
.
Для того, чтобы выражение
было полным дифференциалом некоторой
функции
необходимо
и достаточно, чтобы в области
выполнялось условие
(1)
При
этом сама функция восстанавливается
по полному дифференциалу с помощью
криволинейного интеграла 2го
рода:

Доказательство.
Необходимость.
Если
,
то (по определению)
и
.
Теорема о равенстве смешанных производных
доказывает равенство (1).
Достаточность.
Равенство (1)
обеспечивает независимость
от
пути (теорема из §7). В доказательстве
леммы 2, §7, мы уже построили функцию
такую, что
.
Эта функция имеет вид (2);
криволинейный интеграл можно свести к
определённому, например, таким образом:
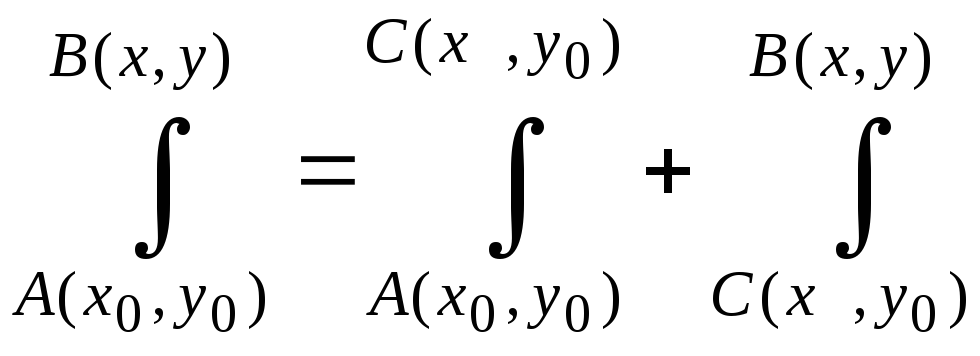
Тогда
получим выражение функции двух переменных
через её частные производные первого
порядка:
Замечание
1.
Условие правильности области было
введено лишь для упрощения доказательства
формулы Грина. На самом же деле всё
доказанное в этом и предыдущем параграфах
имеет место для т.н. односвязной области:
плоская
область
называется односвязной, если каков бы
не был замкнутый контур
,
ограниченная этим контуром часть
плоскости целиком принадлежит
(другими словами, область не содержит
“дыр”).
Всё
доказанное можно свести в такую теорему.
Теорема
2.
Пусть функции
непрерывны
в ограниченной замкнутой односвязной
области
.
Тогда следующие четыре утверждения
равносильны:
1)
2)
по любому контуру
.
3)
интеграл
не зависит от пути в
;
4)
выражение
является полным дифференциалом некоторой
функции.
Действительно,
из 1) следует 2) в силу формулы Грина.
Далее из 2) следует 3) (лемма 1), а из 3)
следует 4) в силу леммы 2. И, наконец, из
4) следует 1) в силу теоремы о равенстве
смешанных производных.
Замечание
2.
Примем без доказательства, что выражение
является полным дифферен-циалом некоторой
функции
,
если выполняются равенства:
(3)
Как
и в двумерном случае, эта функция
восстанавливается криволинейным
интегралом 2го
рода:
Если
в качестве пути
выбрать ломанную, звенья которой
параллельны осям координат, то получим
выражение
через определённые интегралы:
Пример2.
Убедиться, что выражение
является
полным дифференциалом некоторой функции
и найти эту функцию.
Решение.
Выпишем
и
и найдём их производные:
Равенства
(3)
выполняются,
значит, данное выражение – это полный
дифференциал некоторой функции. Эта
функция имеет вид (в качестве пути
интегрирования выберем начало координат):
Соседние файлы в папке Лекции по мат.анализу
- #
- #
- #
- #
- #
- #
- #
Уравнения в полных дифференциалах
В этой теме мы рассмотрим метод восстановления функции по ее полному дифференциалу, дадим примеры задач с полным разбором решения.
Бывает так, что дифференциальные уравнения (ДУ) вида P(x,y)dx+Q(x,y)dy=0 могут содержать в левых частях полные дифференциалы некоторых функций. Тогда мы можем найти общий интеграл ДУ, если предварительно восстановим функцию по ее полному дифференциалу.
Рассмотрим уравнение P(x,y)dx+Q(x,y)dy=0. В записи левой его части содержится дифференциал некоторой функции U(x, y) = 0. Для этого должно выполняться условие ∂P∂y≡∂Q∂x.
Полный дифференциал функции U(x, y) = 0 имеет вид dU=∂U∂xdx+∂U∂ydy. С учетом условия ∂P∂y≡∂Q∂x получаем:
P(x,y)dx+Q(x,y)dy=∂U∂xdx+∂U∂ydy
Откуда:
∂U∂x=P(x,y)∂U∂y=Q(x,y)
Преобразовав первое уравнение из полученной системы уравнений, мы можем получить:
U(x,y)=∫P(x,y)dx+φ(y)
Функцию φ(y) мы можем найти из второго уравнения полученной ранее системы:
∂U(x,y)∂y=∂∫P(x,y)dx∂y+φy'(y)=Q(x,y)⇒φ(y)=∫Q(x,y)-∂∫P(x,y)dx∂ydy
Так мы нашли искомую функцию U(x, y) = 0.
Найдите для ДУ (x2-y2)dx-2xydy=0 общее решение.
Решение
P(x,y)=x2-y2, Q(x,y)=-2xy
Проверим, выполняется ли условие ∂P∂y≡∂Q∂x:
∂P∂y=∂(x2-y2)∂y=-2y∂Q∂x=∂(-2xy)∂x=-2y
Наше условие выполняется.
На основе вычислений мы можем сделать вывод, что левая часть исходного ДУ является полным дифференциалом некоторой функции U(x, y) = 0. Нам нужно найти эту функцию.
Так как (x2-y2)dx-2xydy является полным дифференциалом функции U(x, y) = 0, то
∂U∂x=x2-y2∂U∂y=-2xy
Интегрируем по x первое уравнение системы:
U(x,y)=∫(x2-y2)dx+φ(y)=x33-xy2+φ(y)
Теперь дифференцируем по y полученный результат:
∂U∂y=∂x33-xy2+φ(y)∂y=-2xy+φy'(y)
Преобразовав второе уравнение системы, получаем: ∂U∂y=-2xy. Это значит, что
-2xy+φy'(y)=-2xyφy'(y)=0⇒φ(y)=∫0dx=C
где С – произвольная постоянная.
Получаем: U(x,y)=x33-xy2+φ(y)=x33-xy2+C. Общим интегралом исходного уравнения является x33-xy2+C=0.
Разберем еще один метод нахождения функции по известному полному дифференциалу. Он предполагает применение криволинейного интеграла от фиксированной точки (x0 , y0) до точки с переменными координатами (x, y):
U(x,y)=∫(x0,y0)(x,y)P(x,y)dx+Q(x,y)dy+C
В таких случаях значение интеграла никак не зависит от пути интегрирования. Мы можем взять в качестве пути интегрировании ломаную, звенья которой располагаются параллельно осям координат.
Найдите общее решение дифференциального уравнения (y-y2)dx+(x-2xy)dy=0.
Решение
Проведем проверку, выполняется ли условие ∂P∂y≡∂Q∂x:
∂P∂y=∂(y-y2)∂y=1-2y∂Q∂x=∂(x-2xy)∂x=1-2y
Получается, что левая часть дифференциального уравнения представлена полным дифференциалом некоторой функции U(x, y)=0. Для того, чтобы найти эту функцию, необходимо вычислить криволинейный интеграл от точки (1; 1) до (x, y). Возьмем в качестве пути интегрирования ломаную, участки которой пройдут по прямой y = 1 от точки (1, 1) до (x, 1), а затем от точки (x, 1) до (x, y):
∫(1,1)(x,y)y-y2dx+(x-2xy)dy==∫(1,1)(x,1)(y-y2)dx+(x-2xy)dy++∫(x,1)(x,y)(y-y2)dx+(x-2xy)dy==∫1x(1-12)dx+∫1y(x-2xy)dy=(xy-xy2)y1==xy-xy2-(x·1-x·12)=xy-xy2
Мы получили общее решение дифференциального уравнения вида xy-xy2+C=0.
Определите общее решение дифференциального уравнения y·cosxdx+sin2xdy=0.
Решение
Проверим, выполняется ли условие ∂P∂y≡∂Q∂x.
Так как ∂(y·cosx)∂y=cosx, ∂(sin2x)∂x=2sinx·cosx, то условие выполняться не будет. Это значит, что левая часть дифференциального уравнения не является полным дифференциалом функции. Это дифференциальное уравнение с разделяющимися переменными и для его решения подходят другие способы решения.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Обычно вопрос нахождения функции по полному дифференциалу рассматривают в разделе функций нескольких переменных. Поскольку эта операция играет важную роль в приложениях, то, не прибегая к строгости построения такой функции, покажем на примерах этот процесс.
Пример 1
Вычислить:
Решение. Здесь Х = y2, Y = 2xy, поэтому проверяем условие (1.30) (которое называют часто условием интегрируемости по формуле Ньютона-Лейбница (1.28)).
Видно, что условие интегрируемости выполняется. Найдем неопределенный интеграл:
.
Имеем:
Подберем функцию так, чтобы
, т.е. чтобы
, откуда
, тогда
.
Итак,
,
то есть
.
Берем из этого неопределенного интеграла первообразную (частную при с = 0) .
По формуле Ньютона-Лейбница (1.28) находим:
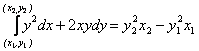
Например, при и
получим
Пример 2
Вычислить: .
Решение. Условие интегрируемости (1.30) выполняется (проверьте).
Найдем:
.
Имеем:
.
Подберем так, чтобы
, т.е. чтобы
, откуда
, тогда
,
то есть
.
Тогда (с = 0)
.
Задачи для упражнений
1) Вычислить следующие криволинейные интегралы, независящие от пути интегрирования:
а) , Ответ: -2.
б) , (у >0) Ответ: 0.
в) , Ответ:
.
г) , Ответ:
.
2) Вычислить работу, производимую вдоль окружности переменной силой
. Почему здесь работа равна нулю?