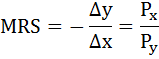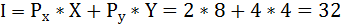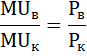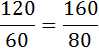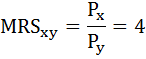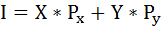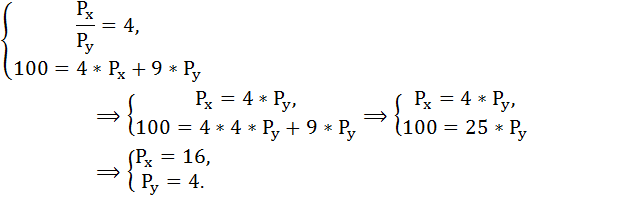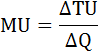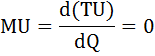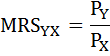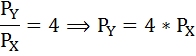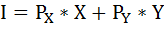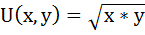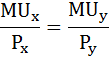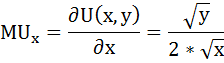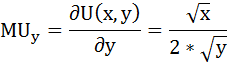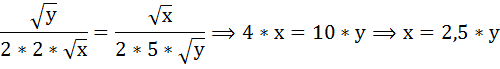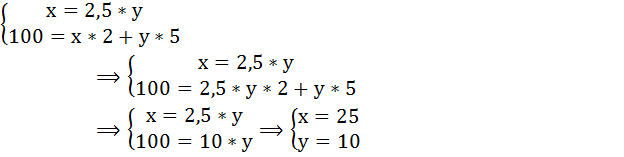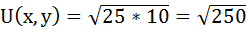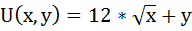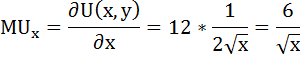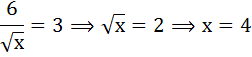Фу́нкция поле́зности — функция, с помощью которой можно представить предпочтения потребителя на множестве допустимых альтернатив[1]. Числовые значения функции помогают упорядочить альтернативы по степени предпочтительности для потребителя. Большее значение соответствует большей предпочтительности. В современной ординалистской теории полезности сами числа значения не имеют — важны только отношения «больше», «меньше» и «равно».
Не каждое отношение предпочтения можно представить с помощью функции полезности. Однако для используемых в экономических моделях предпочтений такая функция существует. Существование функции позволяет использовать математический анализ при решении оптимизационных задач в экономике. Например, при решении задачи потребителя[2]. Без использования функции полезности решение такой задачи становится затруднительным.
Формальное определение[править | править код]
Пусть дано множество допустимых альтернатив 


Большее значение функции полезности означает большую желательность альтернативы в смысле предпочтения, которое эта функция представляет. С математической точки зрения, функция полезности является способом скалярного ранжирования.
Кардинализм и ординализм[править | править код]
Современная микроэкономика опирается на ординалистский подход к моделированию потребительского поведения и выбора. В соответствии с ним, числовые значения функции полезности не играют роли, важны лишь порядок «больше-меньше». Если значение функции полезности для одной из альтернатив выше, то эта альтернатива является более предпочтительной для потребителя. При этом разность значений или частное от их деления не несёт никакой информации[4]. Противоположным является кардиналистский подход, при использовании которого числовые значения, наоборот, несут информацию о полезности. Кардиналистcкий подход неявно предполагает существование эталона полезности, то есть универсальной единицы, с которой можно производить сравнения. Именно такое понимание полезности использовал создатель философии утилитаризма Иеремия Бентам[5].
Современные экономисты исходят из того, что представления о полезности субъективны, поэтому непосредственное их сравнение невозможно. Поэтому для оценки совместного благосостояния потребителей используется концепция эффективности по Парето. Исключением являются квазилинейные предпочтения. Они предполагают существование счетного товара (англ. numeraire), который является аналогом денег. Тогда суммирование и другие операции над полезностью становятся возможными.
Условия существования функции полезности[править | править код]
Для того чтобы предпочтения можно было представить в виде функции полезности, необходимо, чтобы само предпочтение было рациональным, то есть отвечало аксиомам полноты и транзитивности.
Достаточные условия зависят от самого множества допустимых альтернатив 

Если множество 

Часто на предпочтения накладываются дополнительные условия, чтобы получить функции с теми или иными свойствами. Так, можно требовать монотонности, локальной ненасыщаемости и выпуклости. Эти свойства предпочтений отражаются в свойствах функции полезности. Например, монотонность предпочтений ведет в монотонности функции, а выпуклость предпочтений делает функцию квазивогнутной.
Теорема Дебре[править | править код]
Для любых рациональных и непрерывных предпочтений на 
Свойства функции полезности[править | править код]
Пусть задана строго возрастающая функция 




Если множество 
Если предпочтения отвечают свойству монотонности (строгой монотонности), то функция будет монотонной (строго монотонной).
Свойство убывающей предельной полезности является следствием вогнутости функции полезности. Если функция дважды дифференцируема, то свойство означает, что вторая частная производная такой функции отрицательна.

Кривая безразличия — это линия (поверхность, гиперповерхность) уровня функции полезности.
Важнейшие примеры функций полезности[править | править код]
Постоянная эластичность замещения[править | править код]
Одной из важнейших функций полезности является CES-функция. Аббревиатура CES (англ. constant elasticity of substitution) означает постоянную эластичность замещения альтернатив. Функция имеет следующий вид для двумерного случая.

При разных значениях параметра 
Если 


Если 

При 


Отношение к риску[править | править код]
Важными примерами функций полезности являются функции с постоянным абсолютным и относительным показателем отношения к риску. Функция с постоянным абсолютным показателем отношения к риску (англ. CARA — constant absolute risk aversion):
Абсолютная мера Эрроу-Пратта для такой функции равна: 
Функция с постоянным относительным показателем отношения к риску (англ. CRRA — constant relative risk aversion):
Относительная мера Эрроу-Пратта для такой функции равна: 
Функция полезности Стоуна-Гири[править | править код]
Функция полезности Стоуна-Гири определяется следующим образом.
Для 
См. также[править | править код]
- Полезность
- Предельная полезность
- Отношение предпочтения
- Множество допустимых альтернатив
- Предельная норма замещения
- Эластичность замещения
- Моральное ожидание
- Линейная система расходов
Примечания[править | править код]
- ↑ Бусыгин и др., 2008, с. 39.
- ↑ 1 2 Джейли, Рени, 2011, с. 27.
- ↑ Джейли, Рени, 2011, с. 26.
- ↑ Вариан, 1997, с. 74-75.
- ↑ Джейли, Рени, 2011, с. 15.
- ↑ Вариан, 1997, с. 74.
Литература[править | править код]
- Бусыгин В. П., Желободько Е. В., Цыплаков А. А. Микроэкономика: третий уровень: в 2 томах. — Новосибирск: Издательство СО РАН, 2008. — Т. 1. — 525 с. — ISBN 978-5-7692-0976-5.
- Вариан Хэл Р. Микроэкономика. Промежуточный уровень. Современный подход. Учебник для вузов. — ЮНИТИ, 1997. — 768 с. — ISBN 5-85173-072-2.
- Джеффри А. Джейли, Филип Дж. Рени. Микроэкономика: продвинутый уровень. — НИУ ВШЭ, 2011. — 384 с. — ISBN 978-5-7598-0362-1.
- Mas-Colell A., Whinston M., Green J. Microeconomic theory (англ.). — Oxford University Press, 1995. — 1008 p. — ISBN 978-0195073409.
Задача № 1 Расчёт дохода потребителя
Индивид покупает 8 единиц товара Х и 4 единицы товара Y. Найти его доход, если известно, что цена товара Х равна 2 ден. ед., а предельная норма замены равна 0,5.
Решение:
В точке оптимума выполняется равенство:
По условию MRS = 0,5 и Рх = 2. Следовательно, Ру = Рх / MRS = 2/0,5=4.
Найдём доход индивида, используя бюджетное ограничение:
где I – доход,
Рх и Ру – цены двух рассматриваемых благ,
Х и Y – их количества.
Задача № 2. Расчёт общей и предельной полезности
Общая TU и предельная MU полезности товаров А, В, С представлены в таблице. Заполнить пропуски в таблице.
Решение:
Найдём общую полезность товара А.
Общая полезность N-й единицы товара = Предельная полезность N-й единицы товара + Общая полезность N-1-й единицы товара
TU(1)=MU(1)=20
TU(2)=MU(2) + TU(1)=15 + 20=35
TU(3)=MU(3) + TU(2)=12 + 35=47
TU(4)=MU(4) + TU(3)=8 + 47=55
TU(5)=MU(5) + TU(4)=6 + 55=61
Найдём предельную полезность товара В.
Предельная полезность N-й единицы товара=Общая полезность N-й единицы товара — Общая полезность N-1-й единицы товара
MU(1)=TU(1)=19
MU(2)= TU(2) — TU(1)=30 – 19 = 11
MU(3)= TU(3) — TU(2)=38 – 30 = 8
MU(4)= TU(4) — TU(3)=43 – 38=5
MU(5)= TU(5) — TU(4)=45 – 43=2
Найдём общую и предельную полезности товара С.
MU(1)=TU(1)=22
TU(2)=MU(2) + TU(1)=10 + 22=32
MU(3)= TU(3) — TU(2)=39 – 32=7
MU(4)= TU(4) — TU(3)=44 – 39=5
TU(5)=MU(5) + TU(4)=3 + 44=47
Заполним пропуски в таблице:
Задача № 3. Расчёт общей полезности
Предельная полезность первой единицы блага равна 420. При потреблении первых трёх единиц блага предельная полезность каждой последующей единицы уменьшается в 2 раза; предельная полезность каждой последующей единицы блага при дальнейшем потреблении падает в 4 раза. Найти общую полезность блага при условии, что его потребление составляет 8 единиц.
Решение:
Распишем условие задачи следующим образом:
MU(1) = 420,
MU(2) = 420/2=210,
MU(3) = 210/2=105,
MU(4) = 105/4=26,25,
MU(5) = 26,25/4=6,5625,
MU(6) = 6,5625/4=1,640625,
MU(7) = 1,640625/4=0,410156,
MU(8) = 0,410156/4=0,102539.
Найдём общую полезность блага при условии, что его потребление составляет 8 единиц.
TU(8) = MU(8) + TU(7) = MU(8) + MU(7) + TU(6) =…=
= MU(8) + MU(7) + MU(6) + MU(5) + MU(4) + MU(3) + MU(2) + MU(1) =
= 420 + 210 + 105 + 26,25 + 6,5625 + 1,640625 + 0,410156 + 0,102539 = 769,96582
Задача № 4. Расчёт оптимального объёма потребления двух благ
В таблице представлены следующие данные о предельной полезности двух благ.
| Количество, кг | Конфеты | Виноград |
|---|---|---|
| 1 | 60 | 150 |
| 2 | 40 | 120 |
| 3 | 20 | 90 |
Цена 1 кг конфет 80 ден. ед., а цена 1 кг винограда 160 ден. ед.
Бюджет потребителя составляет 400 ден. ед.
Определить оптимальный объём потребления конфет и винограда.
Решение:
Оптимальный объём потребления конфет и винограда достигается тогда, когда отношение предельных полезностей равно отношению цен этих благ.
Среди перечисленных вариантов таким свойством обладает комбинация 2 кг винограда (MUв=120) и 1 кг конфет (MUк=60).
Предельная полезность винограда, разделённая на предельную полезность конфет равна отношению их цен:
Проверим соответствие этой комбинации бюджетному ограничению:
80*1 + 160*2 = 400
Бюджет полностью израсходован.
Задача № 5. Расчёт цен товаров Х и Y
Потребитель покупает 4 единицы блага Х и 9 единиц блага Y, имея доход 100 ден. ед. Найти цены товаров X и Y, если известно, что предельная норма замены товара Y товаром X (MRSxy) равна 4.
Решение:
Предельную норму замены товара Y товаром X(MRSxy) можно определить как отношение цены товара Х к цене товара Y:
Запишем бюджетное ограничение:
100 = 4*Px + 9*Py,
где
Px, Py – цены благ Х и Y соответственно.
Составим и решим систему уравнений:
Задача № 6. Расчёт оптимального объёма потребления
У студента Иванова в холодильнике сыр и колбаса нарезаны для удобства кусочками по 100 г. Общая полезность их потребления представлена в таблице. Определите количество съеденного им в день, если известно, что он в целом употребляет 700 г названных продуктов и при этом добивается максимума полезности.
| Количество, г | Колбаса (общая польза) | Сыр (общая польза) |
| 100 | 2000 | 1900 |
| 200 | 3900 | 3750 |
| 300 | 5700 | 5550 |
| 400 | 7400 | 7300 |
| 500 | 8000 | 9000 |
| 600 | 9500 | 10650 |
Решение:
Рассчитаем предельную полезность от потребления этих двух продуктов.
Предельная полезность в дискретном случае определяется по формуле:
где
ΔTU – приращение общей полезности (TU1 – TU0),
ΔQ – приращение количества потребляемого блага (Q1 – Q0).
Вычисления занесём в таблицу.
| Количество, г | Колбаса (общая польза) | Сыр (общая польза) | Предельная полезность колбасы | Предельная полезность сыра |
| 100 | 2000 | 1900 | 2000 | 1900 |
| 200 | 3900 | 3750 | 1900 | 1850 |
| 300 | 5700 | 5550 | 1800 | 1800 |
| 400 | 7400 | 7300 | 1700 | 1750 |
| 500 | 9000 | 9000 | 1600 | 1700 |
| 600 | 10500 | 10650 | 1500 | 1650 |
Известно, что в целом студент употребляет 700 г колбасы и сыра, то есть всего 7 кусочков, и при этом добивается максимума полезности.
Решение об оптимальном объёме потребления можно представить в виде таблицы, где на каждом шаге будем сравнивать предельную полезность каждого кусочка колбасы и сыра и выбирать наибольшую величину предельной полезности, что в сумме даст их максимум.
Итак, на первом шаге наибольшая предельная полезность, равная 2000 будет получена от потребления 1 кусочка/100 грамм колбасы. Дальше студенту без разницы, что употребить, так как первый кусочек сыра и второй кусочек колбасы приносят одинаковую полезность – 1900. Пусть, например, это будет сначала сыр, а затем колбаса. Но вот на четвёртом шаге наибольшую полезность принесёт второй кусочек сыра. Предельная полезность, полученная от его потребления 1850 больше, чем 1800 – предельная полезность третьего куска колбасы или третьего кусочка сыра. На пятом шаге студенту опять всё равно, что съесть первым, третий кусочек сыра или третий кусочек колбасы, так как полезность от дополнительного потребления этих продуктов одинакова. И наконец, седьмым кусочком должен стать сыр, поскольку предельная полезность четвёртого кусочка сыра (1750), больше чем предельная полезность четвёртого кусочка колбасы (1700).
Общая полезность от потребления 3 кусочков колбасы и 4 кусочков сыра будет максимальной и составит:
TU = 2000 + 1900 + 1900 + 1850 + 1800 + 1800 + 1750 = 13 000
Таким образом, студент Иванов получит максимум полезности при употреблении 3 кусочков (300 грамм) колбасы и 4 кусочков (400 грамм) сыра.
Задача № 7. Расчёт отимального объёма потребления
Определите оптимальный для потребителя объем блага Q, если известно, что функция полезности индивида от обладания этим благом имеет вид:
1) U(Q)= 1 – 5 × Q2
2) U(Q)= 5 + Q – Q2
3) U(Q) = Q2 – 5 × Q3
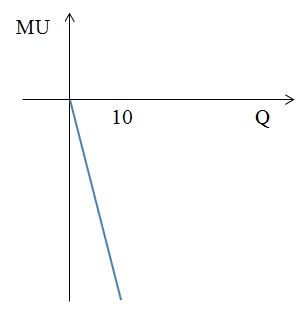
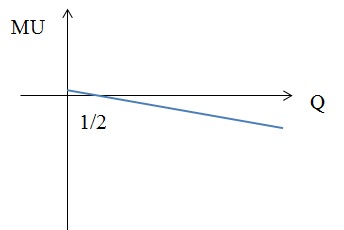
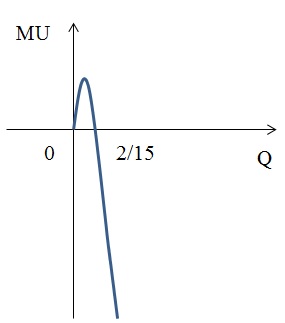
Как будут выглядеть функции предельной полезности? Проиллюстрируйте ответ.
Решение:
Оптимальный для потребителя объем блага Q будет определяться в точке, где потребитель получит максимум удовлетворения полезности. Задача сводится к нахождению экстремума функции полезности. Найдём производную функции полезности (предельную полезность MU) и приравняем её к нулю.
1) MU = –10 × Q = 0, следовательно, Q = 0;
2) MU = 1 – 2 × Q = 0, следовательно, Q = 1/2;
3) MU = 2 × Q – 15 × Q2 = 0, следовательно, Q = 0; Q = 2/15.
Задача № 8. Расчёт цен товаров X и Y
Индивид покупает 4 единицы блага X и 9 единиц блага Y, имея доход равный 100 денежным единицам. Найти цены товаров X и Y, если известно, что предельная норма замены X на Y равна 4.
Решение:
По условию задачи предельная норма замены благом Y блага X () равно 4. Это значит, что количество блага Х должно быть сокращено на 4 единицы в обмен на увеличение количества блага Y на единицу, при неизменном уровне удовлетворения потребителя.
Равновесие потребителя может быть представлено математически как:
— это предельная норма замещения, равная отношению цен благ Y и X. Данное условие оптимума потребителя следует понимать так. Соотношение, в котором потребитель при данных ценах способен замещать один товар другим, равно соотношению, в котором потребитель согласен замещать один товар другим, не изменяя уровень своего удовлетворения.
Отсюда
Далее воспользуемся формулой бюджетного ограничения:
где I – доход или бюджет потребителя.
100 = 4 × PX + 9 × PY
100 = 4 × PX + 9 × 4 × PX
100 = 40 × PX
PX = 2,5
PY = 4 × 2,5 = 10.
Ответ: PX = 2,5; PY = 10.
Задача № 9. Определение рационального выбора потребителя
Потребитель имеет функцию полезности:
и может на свой доход равный 100 единицам приобретать только эти два товара по ценам:
Px = 2
Py = 5
Определить рациональный выбор потребителя. Какой максимальный уровень полезности достижим?
Решение:
Рациональный выбор потребителя осуществляется в соответствии со вторым законом Госсена:
Предельная полезность товара х будет равна производной функции общей полезности по аргументу х:
Аналогично находим предельную полезность товара y:
Далее воспользуемся бюджетным ограничением:
Из условия задачи известно, что:
I = 100
Px = 2
Py = 5
Составим и решим систему уравнений:
При х = 25 и у = 10 общая полезность достигнет максимума:
Задача № 10. Расчёт оптимального объёма потребления
У Оксаны есть 30 рублей. Она хочет купить шоколадки «Шок» ценой 3 р. Полезность от этой покупки она оценивает функцией:
х – приобретённое количество шоколадок,
y – оставшаяся часть дохода.
Сколько купит шоколадок «Шок» рациональная Оксана?
Решение:
Рациональное поведение потребителя можно определить, как стремление максимизировать излишек потребителя. Потребитель будет покупать дополнительные единицы до тех пор, пока они приносят дополнительный избыток, т.е. пока цена, которую потребитель готов уплатить за единицу блага, превосходит реальную цену:
MU > P
Однако каждая последующая единица потребления обычно приносит уменьшающийся прирост полезности, т.е. при покупке благ «одно за другим» рано или поздно предельная полезность какого-то блага сравняется с его ценой:
MU = P
После того как предельная полезность сравняется с ценой, потребитель прекратит дальнейшие покупки: оптимальный объём потребления достигнут.
Найдём предельную полезность MU, как производную функции общей полезности по аргументу х:
Оптимальный объём потребления будет достигнут при МU = P:
Таким образом, рациональная Оксана купит 4 шоколадки, потратив на эту покупку 12 рублей.
What Is Utility Function?
In economics, utility represents the satisfaction or pleasure that consumers receive for consuming a good or service. Utility function measures consumers’ preferences for a set of goods and services.
Utility is measured in units called utils—the Spanish word for useful— but calculating the benefit or satisfaction that consumers receive is abstract and difficult to pinpoint. As a result, economists measure utility in terms of revealed preferences by observing consumers’ choices. From there, economists create an ordering of consumption baskets from least desired to the most preferred.
Key Takeaways
- In economics, utility function is an important concept that measures preferences over a set of goods and services.
- Utility represents the satisfaction that consumers receive for choosing and consuming a product or service.
- Economists track consumer choices to ascertain one product’s utility versus another and assign a numerical value to that utility.
- Company executives research consumers’ utility to guide the company’s sales and marketing plans, advertising, and new product offerings.
- Ordinal utility ranks choices by preference, whereas cardinal utility measures the utility received from a choice.
Understanding Utility Function
In economics, the utility function measures the welfare or satisfaction of a consumer as a function of the consumption of real goods, such as food or clothing. Utility function is widely used in rational choice theory to analyze human behavior.
When economists measure or rank the preferences of consumers, it is referred to as ordinal utility. In other words, the order in which consumers choose one product over another can establish that consumers assign a higher value to the chosen product. Ordinal utility measures how consumers rank products, but it does not measure how much more one ranks above the other.
To better understand ordinal utility, consider the following example. Three contestants vie for first place in a dance competition. Contestant A is declared the winner. Contestant B is the runner-up, and contestant B ranked third. Ordinal utility reveals that the judges preferred contestant A over contestants B and C and contestant B over C. What ordinal function does not tell us is to what degree one was preferred over the other.
Mainly used in microeconomics, cardinal utility assigns a numeric value to the consumer’s preference, indicating the degree to which one choice ranks above another. Cardinal utility will define how much more contestant A was preferred over contestants B and C, and so on.
When considering utility, it is important to understand the concepts of total utility and marginal utility. Marginal utility measures the satisfaction or benefits a person gets from consuming an additional unit of a product or service. Total utility measures the satisfaction or benefits a person gets from the total consumption—including marginal utility—of a product or service.
If consuming 10 units of a product yields 20 utils, and consuming one additional unit yields 1 util, the total utility is 21 utils. If consuming another unit yields .5 utils, the total utility would then become 21.5 utils.
Economists believe that the amount of satisfaction one receives from each additional unit of consumption diminishes with each unit consumed. This concept is called the law of diminishing marginal utility. Diminishing marginal utility doesn’t state that consuming additional units will fail to satisfy the consumer; it states that the satisfaction from consuming more and more units is less than the first additional units consumed.
How to Calculate a Utility Function
Utility functions are expressed as a function of the quantities of a bundle of goods or services. It is often denoted as U(X1, X2, X3, Xn).
A utility function that describes a preference for one bundle of goods (Xa) vs another bundle of goods (Xb) is expressed as U(Xa, Xb).
Where there are perfect complements, the utility function is written as U(Xa, Xb) = MIN[Xa, Xb], where the smaller of the two is assigned the function’s value.
In certain situations, the goods may be considered perfect substitutes for each other, and the appropriate utility function must reflect such preferences with a utility form of U(Xa, Xb) = Xa+ Xb.
Example of Utility Function
Let’s say a consumer is shopping for a new car and has narrowed the choice down to two cars. The cars are nearly identical, except the second car has enhanced safety features. As a result, the second car costs $2,000 more than the first car.
The incremental or marginal utility or satisfaction derived from car two could be represented numerically as the $2,000 price difference between the two cars. In other words, the consumer is receiving $2,000 in incremental or marginal utility from car two.
Furthermore, let’s say that 100,000 consumers throughout the economy preferred car two to car one. Economists might infer that consumers, overall, received $200 million (100,000 x $2,000) worth of incremental utility from the safety features of car two. Utility is derived from the consumer’s belief that they are likely to have fewer accidents due to the added safety features of car two.
Advantages and Disadvantages of Utility Function
Economists can’t assign a true numerical value to a consumer’s level of satisfaction from a preference or choice. Also, pinpointing the reason for purchase can be difficult; there are usually many variables to consider.
In the previous example, the two cars were nearly identical. In reality, there might be several features or differences between the two cars. As a result, assigning a value to a consumer’s preference can be challenging since one consumer might prefer the safety features while another might prefer something else.
Tracking and assigning values to utility can still be useful to economists. Over time, choices and preferences may indicate changes in spending patterns and in utility.
Understanding the logic behind consumer choices and their level of satisfaction is not only important to economists but to companies, as well. Company executives can use utility to track how consumers view their products.
Important
Utility function is essentially a “model” used to represent consumer preferences, so companies often implement them to gain an edge on the competition. For example, studying consumers’ utility can help guide management on anything from marketing and sales to product upgrades and new offerings.
Utility Function FAQs
What Is Utility Function?
Utility describes the benefits gained or satisfaction experienced with the consumption of goods or services. Utility function measures the preferences consumers apply to their consumption of goods and services. For instance, if a customer prefers apples to oranges no matter the amount consumed, the utility function could be expressed as U(apples) > U(oranges).
What Is the Difference Between Utility Function and Marginal Utility?
Utility function ranks consumers’ consumption of goods or services by preference. Marginal utility measures the change in utility when the rate of consumption changes (i.e., how much more satisfaction is gained by consuming another unit of a good or service).
Why Is Utility Function Important?
Economists use utility function to better understand consumer behaviors, as well as determine how well goods and services provide satisfaction to consumers.
Utility function can also help analysts determine how to distribute goods and services to consumers in a way that total utility is realized.
Companies can use utility function to determine which product(s) within their product line (or that of a competitor) consumers prefer. Knowing these preferences can help management teams enhance product development to assume a competitive advantage.
The Bottom Line
Utility describes the benefit or satisfaction received from consuming a good or service. The unit of measurement economists use to gauge satisfaction is called util. Utility function measures consumers’ preferences for bundles of goods or services. Ordinal utility ranks a customer’s choice by preference, and cardinal utility assigns a numeric value to each preference to determine how much more one good is preferred over another.
Как
известно, на рынке потребитель сталкивается
с бесконечно большим количеством
товаров и услуг, однако для упрощения
нашего анализа мы предположим существование
всего двух товаров.
Пусть
потребитель выбирает первый товар в
количестве
q1,
а
второй – в количестве
q2.
Тогда
набор (q1,
q2)
определит
потребительский
набор
(потребительскую
корзину),
включающую то или иное количество
обоих товаров и обладающую для потребителя
некоторым качеством, которое можно
измерить.
Так,
если наборы пищевые, то таким качеством
будет калорийность данных благ, либо
содержание в них витамина С, либо
содержание сахара и т.д. Если рассматриваемые
товары — металлы, то таким качеством
будет прочность сплава, либо температура
его плавления, либо другая аналогичная
характеристика.
Естественно,
что не
всякое качество товара может быть
охарактеризовано числом.
Например, качество одежды оценивается
и продолжительностью носки (ее можно
охарактеризовать числом), и ее
соответствием современной моде или
красотой (а это числом охарактеризовать
невозможно). В дальнейшем будем
считать, что каждой потребительской
корзине
(q1,
q2)
соответствует
некоторое число
TU(total
utility),
называемое
совокупной полезностью.
Совокупная
полезность (TU)
есть
совокупное удовлетворение, получаемое
человеком в результате потребления
данного количества товаров или услуг
за данное время.
На
совокупную полезность блага влияют не
только его физические характеристики,
но и психология потребителя, его личный
опыт, социальная и культурная среда. И
хотя экономисты проявляют интерес
к этим факторам, однако на практике
обычно уделяют внимание только
количественным показателям (таким,
как объем продаж, количество единиц
товара, приобретенных покупателями, и
т.д.), предполагая постоянными все
прочие факторы, влияющие на поведение
человека. Допущение «при прочих равных
условиях» позволяет упростить анализ
условий максимизации полезности без
особого ущерба для модели.
Математически
это означает, что задается общая функция
полезности от потребления за определенный
период времени n-го
количества товаров:
TU=
U(q1,
q2,
…, qn).
где
q
–
количество товаров, включенных в
потребительский набор.
Функция
полезности
показывает количественную зависимость
между объемом потребления каждого из
n-благ
за данный промежуток времени и совокупной
полезностью блага, отражающей
индивидуальные предпочтения потребителя.
Как
и любая другая функция, функция полезности
может быть представлена в виде таблицы,
графика или уравнения.
Если
мы отвлечемся от отдельных случаев
функции полезности, то для большинства
товаров и услуг действует следующая
закономерность: чем
больше объем потребления, какого- либо
товара, тем больше значение совокупной
полезности, получаемой потребителем.
Изменение
(или приращение) совокупной полезности
отражается в показателе предельной
полезности.
Предельная
полезность
MU
(marginal
utility)
–
это дополнительная полезность,
получаемая человеком от потребления
одной дополнительной единицы данного
блага за единицу времени.
Математически
предельная полезность является первой
производной функции совокупной
полезности по количеству данного
блага и рассчитывается по формуле2:
MU
=
TU(q)
=
d(TU)/dq,
где
d(TU)
–
приращение совокупной полезности,
dq
–
приращение количества потребляемого
блага.
Существует
множество уравнений, которые могут
описывать функцию совокупной
полезности, однако наиболее простым
и наиболее часто применяемым является
общее уравнение
кубической функции:
TU
= а
+ bq
+
cq2–
dq3,
где
q
–
количество потребленного товара;
а,
d,
с, d
–
положительные константы.
Если
последовательное потребление какого-либо
блага постепенно приводит человека
к состоянию насыщенности, то дополнительная
полезность от использования одной
дополнительной единицы данного блага
начинает сокращаться. Эта закономерность
имеет универсальный характер и называется
законом
убывания предельной полезности или
первым законом Госсена.
Закон назван так в честь немецкого
экономиста Германа Госсена (1810-1858),
впервые сформулировавшего данный
принцип.
Начиная
с некоторого момента, дополнительная
полезность от потребления одного
дополнительного блага уменьшается по
мере того, как возрастает объем потребления
данного блага.
Математически
это означает, что вторая производная
общей полезности по количеству
данного блага является отрицательной
величиной.
Принцип
убывания предельной полезности был
использован английским экономистом
А. Маршаллом (1890) для объяснения
знаменитого
парадокса
воды и алмазов.
Суть
парадокса заключалась в том, что на
рынке алмазы ценятся неизмеримо
дороже, чем вода, и в то же время все
понимают, что если без алмазов человек
может обойтись, то без воды выжить
невозможно.
Объяснение
Маршалла состояло в следующем. Цена
товара определяется не его совокупной
полезностью для человека, а той предельной
полезностью, которую человек извлекает
из последнего глотка воды. Другими
словами, стоимость воды определяется
той суммой денег, которую индивидуум
захочет заплатить, чтобы получить
дополнительную меру воды. В силу того,
что предельная ценность убывает по мере
возрастания количества потребленной
воды, а запасов воды на земле существенно
больше, чем запасов алмазов, вода имеет
более низкую стоимость при обмене, чем
алмазы.
Рассмотрим
конкретные задачи 4.1 и 4.2.
Задача
4.1.
Определение точки насыщения
Пусть
дана функция полезности отдельного
потребителя:
TU
=
130q
–
2,5q2.
Определить
точку, при которой совокупная полезность
(TU)
является
максимальной и человек достигает
насыщения.
Решение:
Функция
совокупной полезности достигает своего
максимума при условии MU
=
0:
MU
=
dTU/dq
=
130 – 5q.
Приняв
функцию предельной полезности равной
нулю, получаем:
130 – 5q
= 0; q
= 26.
Это
и есть искомая точка насыщения.
Задача
4.2.
Закон убывания предельной полезности
Пусть
функция полезности задана уравнением:
TU=
18q
+7q2
– (l/3)
q3
Найти
объем потребления (q),
при
котором начинает действовать закон
убывания предельной полезности, т.е.
предельная полезность (MU)
начинает
уменьшаться.
Решение:
Очевидно,
что MU
начнет
уменьшаться в точке, в которой функция
предельной полезности имеет максимальное
значение:
MU
=
dTU/dq
=
18 + 14q
– q2.
Приравняв
dMU/dq
к
нулю и решая это уравнение относительно
q,
получим
q=7
это
степень потребления, при которой
начинается уменьшение MU.
Если
известны или могут быть оценены функции
потребительской полезности, то можно
судить о том, какие товары и услуги
потребители будут или не будут покупать
на рынке.
Для
дальнейшего анализа дополним наше
предположение о рациональности
потребителя допущениями о независимости
рассматриваемых нами функций полезности
(функция полезности одного товара
или услуги не зависит от степени
потребления других благ) и о полной
информированности потребителей.
Каждый потребитель обладает всей
необходимой для принятия решений
информацией, вполне определенными
вкусами и предпочтениями; знает,
какие товары и услуги доступны для
приобретения, качественные характеристики
этих товаров и их способность
удовлетворять его желания, цены, по
которым они продаются.
С
учетом представленных допущений
проанализируем поведение отдельного
потребителя, выбирающего комбинацию
из двух товаров
(q1,
q2)
и
располагающего доходом
(R),
равным
40 у.е. Эксперимент позволил выявить
следующие потребительские предпочтения
(табл. 4.1) для двух товаров (q1,
q2)
(в
баллах). Рыночные цены товаров
соответственно: p1
= 3 у.е., p2
=
5 у.е.
Таблица
4.1
Потребительские
предпочтения индивидуума
|
q1 |
TU1 |
MU1 |
MU1/P1 |
q2 |
TU2 |
MU2 |
MU2/P2 |
|
0 |
0 |
– |
– |
0 |
0 |
– |
– |
|
1 |
54 |
54 |
18 |
1 |
75 |
75 |
15 |
|
2 |
99 |
45 |
15 |
2 |
135 |
60 |
12 |
|
3 |
129 |
30 |
10 |
3 |
175 |
40 |
8 |
|
4 |
138 |
9 |
3 |
4 |
200 |
25 |
5 |
|
5 |
141 |
3 |
1 |
5 |
215 |
15 |
3 |
|
6 |
138 |
-3 |
-1 |
6 |
220 |
5 |
1 |
Как
видно из табл. 4.1, наибольшее удовольствие
потребителю принесло бы потребление
5 ед. товара
q1,
6 ед.
товара
q2.
Однако
на эти покупки пришлось бы потратить
45
у.е.
(5×3+5×6),
которых у человека нет.
Критерием
правильности
потребительского выбора является не
совокупная и даже не предельная
полезность, а предельная полезность на
1 у.е. затрат (MU/P).
Прибавочное
удовлетворение, получаемое на 1 у.е.
затрат, является наилучшим критерием,
поскольку объединяет и фактор
удовлетворения, и фактор затрат,
необходимые для обоснованного сравнения
товаров между собой.
В
нашем примере потребитель получит
наибольшее удовлетворение, распределяя
свой доход (40 у.е.) следующим образом:
4 ед. товара
q1
(4
х 3 у.е. = 12 у.е.), 5 ед. товара
q2
(5×6
у.е. = 30 у.е.).
3
у.е. (45 у.е. – (12 + 30 у.е.) = 3 у.е. останутся на
сбережениях.
С
учетом полученных результатов сформулируем
основное условие
потребительского оптимума, или второй
закон Госсена, для
двух и более товаров.
Для
максимизации полезности потребитель
должен таким образом распределить свой
ограниченный бюджет, чтобы предельные
полезности на один рубль, затраченный
на последнюю единицу каждого товара,
равнялись бы между собой
MU1/P1
=
MU2/P2
=
… = MUn
/Pn
а
сумма всех затрат потребителя на товары
и услуги плюс сбережения (S)
соответствовала
его денежному доходу (R),
т.е.
P1Q1
+P2
Q2 +…
+ PnQn
+S
= R
Если
эти предельные полезности не равны, то
совокупное удовлетворение может быть
увеличено путем уменьшения расходов
на товары с меньшей степенью полезности
и увеличения затрат на товары с большей
степенью полезности.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Поведение потребителя
Задача №59. Расчёт общей и предельной полезности
Общая TU и предельная MU полезности товаров А, В, С представлены в таблице. Заполнить пропуски в таблице.
| Количество товара | А | В | С | |||
|---|---|---|---|---|---|---|
| TU | MU | TU | MU | TU | MU | |
| 1 | … | 20 | 19 | … | 22 | … |
| 2 | … | 15 | 30 | … | … | 10 |
| 3 | … | 12 | 38 | … | 39 | … |
| 4 | … | 8 | 43 | … | 44 | … |
| 5 | … | 6 | 45 | … | … | 3 |
Решение
Задача №60. Расчёт общей полезности
Предельная полезность первой единицы блага равна 420. При потреблении первых трёх единиц блага предельная полезность каждой последующей единицы уменьшается в 2 раза; предельная полезность каждой последующей единицы блага при дальнейшем потреблении падает в 4 раза. Найти общую полезность блага при условии, что его потребление составляет 8 единиц.
Решение
Задача №61. Расчёт оптимального объёма потребления двух благ
В таблице представлены следующие данные о предельной полезности двух благ.
| Количество, кг | Конфеты | Виноград |
|---|---|---|
| 1 | 60 | 150 |
| 2 | 40 | 120 |
| 3 | 20 | 90 |
Цена 1 кг конфет 80 ден. ед., а цена 1 кг винограда 160 ден. ед.
Бюджет потребителя составляет 400 ден. ед.
Определить оптимальный объём потребления конфет и винограда.
Решение
Задача №62. Расчёт цен товаров Х и Y
Потребитель покупает 4 единицы блага Х и 9 единиц блага Y, имея доход 100 ден. ед.
Найти цены товаров X и Y, если известно, что предельная норма замены товара Y товаром X (MRSxy) равна 4.
Решение
Рыночное рановесие
Рыночное равновесие
Рыночное равновесие
Эластичность
ВВП
Задача №63. Расчёт цен товаров Х и Y
Функция общей полезности индивида от потребления блага X имеет вид:
TUx = 40X – X2
а от потребления блага Y:
TUy = 18Y – 4Y2
Он потребляет 10 единиц блага X и 2 единицы блага Y. Предельная полезность денег составляет 1/2.
Определите цены товаров X и Y.
Решение
Задача №64. Расчёт оптимального объёма потребления
У Оксаны есть 30 рублей. Она хочет купить шоколадки «Шок» ценой 3 р. Полезность от этой покупки она оценивает функцией:
х – приобретённое количество шоколадок,
y – оставшаяся часть дохода.
Сколько купит шоколадок «Шок» рациональная Оксана?
Решение
Задача №66. Расчёт оптимального объёма потребления
Определите оптимальный для потребителя объем блага Q, если известно, что функция полезности индивида от обладания этим благом имеет вид:
1) U(Q) = 1 – 2Q2;
2) U(Q) = 5 + Q – Q2;
3) U(Q) = Q2 – Q3.
Как будут выглядеть функции предельной полезности?
Решение