Как
известно, на рынке потребитель сталкивается
с бесконечно большим количеством
товаров и услуг, однако для упрощения
нашего анализа мы предположим существование
всего двух товаров.
Пусть
потребитель выбирает первый товар в
количестве
q1,
а
второй – в количестве
q2.
Тогда
набор (q1,
q2)
определит
потребительский
набор
(потребительскую
корзину),
включающую то или иное количество
обоих товаров и обладающую для потребителя
некоторым качеством, которое можно
измерить.
Так,
если наборы пищевые, то таким качеством
будет калорийность данных благ, либо
содержание в них витамина С, либо
содержание сахара и т.д. Если рассматриваемые
товары — металлы, то таким качеством
будет прочность сплава, либо температура
его плавления, либо другая аналогичная
характеристика.
Естественно,
что не
всякое качество товара может быть
охарактеризовано числом.
Например, качество одежды оценивается
и продолжительностью носки (ее можно
охарактеризовать числом), и ее
соответствием современной моде или
красотой (а это числом охарактеризовать
невозможно). В дальнейшем будем
считать, что каждой потребительской
корзине
(q1,
q2)
соответствует
некоторое число
TU(total
utility),
называемое
совокупной полезностью.
Совокупная
полезность (TU)
есть
совокупное удовлетворение, получаемое
человеком в результате потребления
данного количества товаров или услуг
за данное время.
На
совокупную полезность блага влияют не
только его физические характеристики,
но и психология потребителя, его личный
опыт, социальная и культурная среда. И
хотя экономисты проявляют интерес
к этим факторам, однако на практике
обычно уделяют внимание только
количественным показателям (таким,
как объем продаж, количество единиц
товара, приобретенных покупателями, и
т.д.), предполагая постоянными все
прочие факторы, влияющие на поведение
человека. Допущение «при прочих равных
условиях» позволяет упростить анализ
условий максимизации полезности без
особого ущерба для модели.
Математически
это означает, что задается общая функция
полезности от потребления за определенный
период времени n-го
количества товаров:
TU=
U(q1,
q2,
…, qn).
где
q
–
количество товаров, включенных в
потребительский набор.
Функция
полезности
показывает количественную зависимость
между объемом потребления каждого из
n-благ
за данный промежуток времени и совокупной
полезностью блага, отражающей
индивидуальные предпочтения потребителя.
Как
и любая другая функция, функция полезности
может быть представлена в виде таблицы,
графика или уравнения.
Если
мы отвлечемся от отдельных случаев
функции полезности, то для большинства
товаров и услуг действует следующая
закономерность: чем
больше объем потребления, какого- либо
товара, тем больше значение совокупной
полезности, получаемой потребителем.
Изменение
(или приращение) совокупной полезности
отражается в показателе предельной
полезности.
Предельная
полезность
MU
(marginal
utility)
–
это дополнительная полезность,
получаемая человеком от потребления
одной дополнительной единицы данного
блага за единицу времени.
Математически
предельная полезность является первой
производной функции совокупной
полезности по количеству данного
блага и рассчитывается по формуле2:
MU
=
TU(q)
=
d(TU)/dq,
где
d(TU)
–
приращение совокупной полезности,
dq
–
приращение количества потребляемого
блага.
Существует
множество уравнений, которые могут
описывать функцию совокупной
полезности, однако наиболее простым
и наиболее часто применяемым является
общее уравнение
кубической функции:
TU
= а
+ bq
+
cq2–
dq3,
где
q
–
количество потребленного товара;
а,
d,
с, d
–
положительные константы.
Если
последовательное потребление какого-либо
блага постепенно приводит человека
к состоянию насыщенности, то дополнительная
полезность от использования одной
дополнительной единицы данного блага
начинает сокращаться. Эта закономерность
имеет универсальный характер и называется
законом
убывания предельной полезности или
первым законом Госсена.
Закон назван так в честь немецкого
экономиста Германа Госсена (1810-1858),
впервые сформулировавшего данный
принцип.
Начиная
с некоторого момента, дополнительная
полезность от потребления одного
дополнительного блага уменьшается по
мере того, как возрастает объем потребления
данного блага.
Математически
это означает, что вторая производная
общей полезности по количеству
данного блага является отрицательной
величиной.
Принцип
убывания предельной полезности был
использован английским экономистом
А. Маршаллом (1890) для объяснения
знаменитого
парадокса
воды и алмазов.
Суть
парадокса заключалась в том, что на
рынке алмазы ценятся неизмеримо
дороже, чем вода, и в то же время все
понимают, что если без алмазов человек
может обойтись, то без воды выжить
невозможно.
Объяснение
Маршалла состояло в следующем. Цена
товара определяется не его совокупной
полезностью для человека, а той предельной
полезностью, которую человек извлекает
из последнего глотка воды. Другими
словами, стоимость воды определяется
той суммой денег, которую индивидуум
захочет заплатить, чтобы получить
дополнительную меру воды. В силу того,
что предельная ценность убывает по мере
возрастания количества потребленной
воды, а запасов воды на земле существенно
больше, чем запасов алмазов, вода имеет
более низкую стоимость при обмене, чем
алмазы.
Рассмотрим
конкретные задачи 4.1 и 4.2.
Задача
4.1.
Определение точки насыщения
Пусть
дана функция полезности отдельного
потребителя:
TU
=
130q
–
2,5q2.
Определить
точку, при которой совокупная полезность
(TU)
является
максимальной и человек достигает
насыщения.
Решение:
Функция
совокупной полезности достигает своего
максимума при условии MU
=
0:
MU
=
dTU/dq
=
130 – 5q.
Приняв
функцию предельной полезности равной
нулю, получаем:
130 – 5q
= 0; q
= 26.
Это
и есть искомая точка насыщения.
Задача
4.2.
Закон убывания предельной полезности
Пусть
функция полезности задана уравнением:
TU=
18q
+7q2
– (l/3)
q3
Найти
объем потребления (q),
при
котором начинает действовать закон
убывания предельной полезности, т.е.
предельная полезность (MU)
начинает
уменьшаться.
Решение:
Очевидно,
что MU
начнет
уменьшаться в точке, в которой функция
предельной полезности имеет максимальное
значение:
MU
=
dTU/dq
=
18 + 14q
– q2.
Приравняв
dMU/dq
к
нулю и решая это уравнение относительно
q,
получим
q=7
это
степень потребления, при которой
начинается уменьшение MU.
Если
известны или могут быть оценены функции
потребительской полезности, то можно
судить о том, какие товары и услуги
потребители будут или не будут покупать
на рынке.
Для
дальнейшего анализа дополним наше
предположение о рациональности
потребителя допущениями о независимости
рассматриваемых нами функций полезности
(функция полезности одного товара
или услуги не зависит от степени
потребления других благ) и о полной
информированности потребителей.
Каждый потребитель обладает всей
необходимой для принятия решений
информацией, вполне определенными
вкусами и предпочтениями; знает,
какие товары и услуги доступны для
приобретения, качественные характеристики
этих товаров и их способность
удовлетворять его желания, цены, по
которым они продаются.
С
учетом представленных допущений
проанализируем поведение отдельного
потребителя, выбирающего комбинацию
из двух товаров
(q1,
q2)
и
располагающего доходом
(R),
равным
40 у.е. Эксперимент позволил выявить
следующие потребительские предпочтения
(табл. 4.1) для двух товаров (q1,
q2)
(в
баллах). Рыночные цены товаров
соответственно: p1
= 3 у.е., p2
=
5 у.е.
Таблица
4.1
Потребительские
предпочтения индивидуума
|
q1 |
TU1 |
MU1 |
MU1/P1 |
q2 |
TU2 |
MU2 |
MU2/P2 |
|
0 |
0 |
– |
– |
0 |
0 |
– |
– |
|
1 |
54 |
54 |
18 |
1 |
75 |
75 |
15 |
|
2 |
99 |
45 |
15 |
2 |
135 |
60 |
12 |
|
3 |
129 |
30 |
10 |
3 |
175 |
40 |
8 |
|
4 |
138 |
9 |
3 |
4 |
200 |
25 |
5 |
|
5 |
141 |
3 |
1 |
5 |
215 |
15 |
3 |
|
6 |
138 |
-3 |
-1 |
6 |
220 |
5 |
1 |
Как
видно из табл. 4.1, наибольшее удовольствие
потребителю принесло бы потребление
5 ед. товара
q1,
6 ед.
товара
q2.
Однако
на эти покупки пришлось бы потратить
45
у.е.
(5×3+5×6),
которых у человека нет.
Критерием
правильности
потребительского выбора является не
совокупная и даже не предельная
полезность, а предельная полезность на
1 у.е. затрат (MU/P).
Прибавочное
удовлетворение, получаемое на 1 у.е.
затрат, является наилучшим критерием,
поскольку объединяет и фактор
удовлетворения, и фактор затрат,
необходимые для обоснованного сравнения
товаров между собой.
В
нашем примере потребитель получит
наибольшее удовлетворение, распределяя
свой доход (40 у.е.) следующим образом:
4 ед. товара
q1
(4
х 3 у.е. = 12 у.е.), 5 ед. товара
q2
(5×6
у.е. = 30 у.е.).
3
у.е. (45 у.е. – (12 + 30 у.е.) = 3 у.е. останутся на
сбережениях.
С
учетом полученных результатов сформулируем
основное условие
потребительского оптимума, или второй
закон Госсена, для
двух и более товаров.
Для
максимизации полезности потребитель
должен таким образом распределить свой
ограниченный бюджет, чтобы предельные
полезности на один рубль, затраченный
на последнюю единицу каждого товара,
равнялись бы между собой
MU1/P1
=
MU2/P2
=
… = MUn
/Pn
а
сумма всех затрат потребителя на товары
и услуги плюс сбережения (S)
соответствовала
его денежному доходу (R),
т.е.
P1Q1
+P2
Q2 +…
+ PnQn
+S
= R
Если
эти предельные полезности не равны, то
совокупное удовлетворение может быть
увеличено путем уменьшения расходов
на товары с меньшей степенью полезности
и увеличения затрат на товары с большей
степенью полезности.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
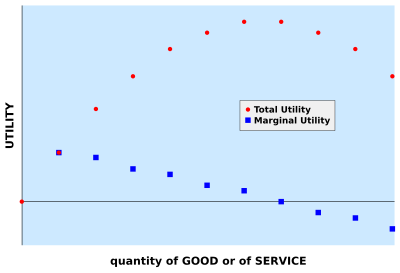
Сравнение общей и предельной полезности
Предельная полезность — это полезность, которую потребитель получает от использования ещё одной дополнительной единицы блага.
Другими словами, предельная полезность — это увеличение общей полезности при потреблении одной дополнительной единицы блага (производная):
где 

Принцип предельной полезности сводится к следующему: ценность блага данного рода определяется полезностью предельного экземпляра, удовлетворяющего наименее настоятельную потребность[1]. Предельная полезность определяет спрос на товар.
История[править | править код]
Теория предельной полезности возникла как альтернатива трудовой теории стоимости для пояснения наблюдаемых закономерностей в ценах на товары. Основные положения теории предельной полезности были сформулированы Германом Генрихом Госсеном в надолго всеми забытой работе 1854 года. Массированное проникновение маржиналистских идей в экономическую литературу, получившее название «маржиналистская революция», началось в середине 1880-х годов. Принцип предельной полезности был изложен почти одновременно тремя учёными-экономистами Стенли Джевонсом, Карлом Менгером и Леоном Вальрасом. Хотя Джевонс изложил свои идеи в лекции, опубликованной в 1866, Менгер в «Основаниях политической экономии» в 1871, а Леон Вальрас в 1874, все трое писали независимо друг от друга. Термин «предельная полезность» (нем. Grenznutzen) был введён в экономическую науку Фридрихом фон Визером[2].
Согласно данной концепции, ценность товаров определяется их предельной полезностью на базе субъективных оценок. Даже в отношении одной и той же потребности благо может иметь различную предельную полезность (например, полезность хлеба для сытого и для голодного). Предельная полезность какого-либо блага обозначает ту пользу, которую приносит последняя единица этого блага, причём последнее благо обычно удовлетворяет самые маловажные нужды. При этом фактором ценности считается и редкость товара. Предельная полезность повышается при недостатке блага и понижается при его избытке.
Субъективная ценность — это личная оценка товара как потребителем, так и продавцом; объективная же ценность — это меновые пропорции, цены, которые формируются в ходе конкуренции на рынке. По мере постепенного насыщения потребностей субъекта, полезность вещи для него падает. Теория предельной полезности пытается дать совет, как наилучшим образом распределить средства для удовлетворения потребностей при ограниченности ресурсов.
В 1890 году английский экономист Альфред Маршалл опубликовал монографию «Принципы экономической науки», ставшую основным учебником по микроэкономике. Он предложил компромиссный вариант определения рыночной стоимости предельной полезностью, определяющей спрос на товар, и затратами производства, сформулировал закон спроса и предложения.
Современные экономисты продолжают использовать теорию предельной полезности, акцентируя внимание на изучении закономерностей потребительского спроса, анализе предложения, исследовании рынков и ценообразования на микроэкономическом уровне.
Закон убывающей предельной полезности[править | править код]
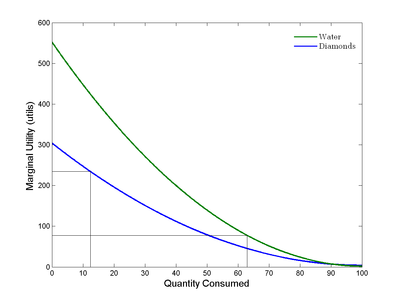
График показывает предельную полезность (измеряется в единицах полезности) алмазов и воды как функцию объёма потребления
Закон убывающей предельной полезности заключается в том, что с ростом потребления блага (при неизменном объёме потребления всех остальных благ) общая полезность, получаемая потребителем, возрастает, но скорость роста замедляется.
Математически это означает, что первая производная функции общей полезности в зависимости от потребления данного блага положительна, но уменьшается, а вторая — отрицательна. Иначе говоря, закон убывающей предельной полезности гласит, что функция общей полезности возрастает и выпукла вверх.
Предельная полезность (производная) убывает с ростом потребления, обращается в ноль при максимальной общей полезности и затем становится отрицательной, а общая полезность, достигнув максимального значения, начинает уменьшаться.
Например, для голодного человека предельная полезность первой тарелки супа выше, чем второй, второй — выше, чем третьей. Так и с другим благом.
Из этого закона следует необходимость понижения цены для того, чтобы побудить потребителя к увеличению покупок конкретного продукта.
Однако закон убывающей предельной полезности не всегда действует при малых количествах товара. Например, если человек принимает одну таблетку — он излечивается не полностью. Если две — то он излечивается полностью, и предельная полезность возрастает по сравнению с одной таблеткой. Однако дальнейшее потребление таблеток может только вредить организму, и предельная полезность станет отрицательной.
Ограниченность применимости закона[править | править код]
- Однородные единицы. Сравнивать можно товар с однородными единицами и потребляемые одним потребителем. Например, нельзя рассматривать яблоки и бананы. Точно так же нельзя рассматривать зелёные и красные яблоки вместе. Все единицы товара должны быть одного веса и качества. Например, если первое яблоко кислое, а второе — сладкое, то второе яблоко даст больше удовлетворения потребителю, чем первое.
- Рассматривается потребитель с неизменными вкусами. Не должно быть никаких изменений во вкусах, привычках, обычаях, предпочтениях и доходах потребителя. Изменение в одном из перечисленных факторов изменит полезность продукта и закон становится неприменимым.
- Непрерывность потребления. Формулировка закона исходит из того, что процесс потребления какого-либо продукта потребителем непрерывен. В противном случае его предельная полезность не обязательно пойдёт на спад. Если после потребления одной единицы продукта есть пауза, то вполне возможно, что потребность в нём возобновится и потребление последующей единицы продукта даст такое же удовлетворение, как от предыдущей .
- Постоянные цены. Цены на продукт или на его заместителей предполагаются неизменными. Потребитель может отказаться от покупки товара или увеличить покупки лишь в силу изменения цены, а не потому, что произошло изменение оценки полезности товара.
На практике одновременное выполнение всех этих условий встречается крайне редко.
Ограниченность законов предельной полезности обсуждалась многократно, однако показать их в микроэкономической модели пока удается только в виртуализированной экономике[источник не указан 1242 дня].
Предельная полезность и спрос[править | править код]
Теория субъективной полезности выводит закон убывания объёма спроса с ростом цены из аксиомы снижения предельной полезности[3].
См. также[править | править код]
- Ординалистская теория полезности
- Функция полезности
- Законы Госсена
- Предельная норма замещения
- Предельные издержки
- Маржинализм
Примечания[править | править код]
- ↑ Курс экономической теории: учебник — 6-е исправленное, дополненное и переработанное издание. — Киров: «АСА», 2009. — 848 с.
- ↑ Хайек Ф. А. Глава 2. Карл Менгер (1840-1921) // Судьбы либерализма в XX веке. — М.: ИРИСЭН, 2009. — С. 79—118. — 337 с. — 1000 экз. — ISBN 978-5-91066-028-5.
- ↑ Лекция 2. Спрос Архивная копия от 12 июня 2020 на Wayback Machine // 50 лекций по микроэкономике. — СПб.: Экономическая школа. 2004. Т. 1.
Литература[править | править код]
- Блюмин, И. Г. Эволюция теории «предельной полезности» // Критика буржуазной политической экономии: В 3 томах. — М.: Изд-во АН СССР, 1962. — Т. III. Кризис современной буржуазной политической экономии. — С. 97-113. — 379 с. — 3200 экз.
- Веблен, Торстейн. Ограниченность теории предельной полезности Архивная копия от 20 января 2022 на Wayback Machine.
Общая TU и предельная MU полезности товаров А, В, С представлены в таблице. Заполнить пропуски в таблице.
| Количество товара | А | В | С | |||
|---|---|---|---|---|---|---|
| TU | MU | TU | MU | TU | MU | |
| 1 | … | 20 | 19 | … | 22 | … |
| 2 | … | 15 | 30 | … | … | 10 |
| 3 | … | 12 | 38 | … | 39 | … |
| 4 | … | 8 | 43 | … | 44 | … |
| 5 | … | 6 | 45 | … | … | 3 |
Решение:
Найдём общую полезность товара А.
Общая полезность N-й единицы товара = Предельная полезность N-й единицы товара + Общая полезность N-1-й единицы товара
TU(1)=MU(1)=20
TU(2)=MU(2) + TU(1)=15 + 20=35
TU(3)=MU(3) + TU(2)=12 + 35=47
TU(4)=MU(4) + TU(3)=8 + 47=55
TU(5)=MU(5) + TU(4)=6 + 55=61
Найдём предельную полезность товара В.
Предельная полезность N-й единицы товара=Общая полезность N-й единицы товара – Общая полезность N-1-й единицы товара
MU(1)=TU(1)=19
MU(2)= TU(2) – TU(1)=30 – 19 = 11
MU(3)= TU(3) – TU(2)=38 – 30 = 8
MU(4)= TU(4) – TU(3)=43 – 38=5
MU(5)= TU(5) – TU(4)=45 – 43=2
Найдём общую и предельную полезности товара С.
MU(1)=TU(1)=22
TU(2)=MU(2) + TU(1)=10 + 22=32
MU(3)= TU(3) – TU(2)=39 – 32=7
MU(4)= TU(4) – TU(3)=44 – 39=5
TU(5)=MU(5) + TU(4)=3 + 44=47
Заполним пропуски в таблице:
| Количество товара | А | В | С | |||
|---|---|---|---|---|---|---|
| TU | MU | TU | MU | TU | MU | |
| 1 | 20 | 20 | 19 | 19 | 22 | 22 |
| 2 | 35 | 15 | 30 | 11 | 32 | 10 |
| 3 | 47 | 12 | 38 | 8 | 39 | 7 |
| 4 | 55 | 8 | 43 | 5 | 44 | 5 |
| 5 | 61 | 6 | 45 | 2 | 47 | 3 |
Download Article
Download Article
In economics, marginal utility (MU) is a way to measure how much value or satisfaction a consumer gets out of consuming something. As a general rule, MU is equal to the change in total utility divided by the change in the quantity of goods consumed.[1]
A common way of thinking of this is that MU is the utility someone gets from each additional unit of goods consumed.
-
1
Understand the economic concept of utility. Utility is the “value” or “satisfaction” that a consumer gets from consuming a certain number of goods. A good way of thinking of it is that utility is how much money a consumer would hypothetically pay for the satisfaction provided by a good.[2]
- For example, let’s say that you are hungry and are buying fish to eat for supper. Let’s also say that one fish costs $2. If you’re so hungry that you would pay $8 for the fish, the fish is said to provide $8 worth of utility. In other words, you’re willing to pay $8 to get the satisfaction from the fish no matter what it actually costs.
-
2
Find the total utility from consuming a certain number of goods. Total utility is just the concept of utility applied to more than one good. If consuming one good gives you a certain amount of utility, consuming more than one of the same good will give you an amount that is higher, lower, or the same.[3]
- For example, let’s say that you plan to eat two fish. However, after eating the first fish, you’re not quite as hungry as before. Now, you’d only pay $6 for the extra satisfaction of the second fish. It’s not worth as much to you now that you’re somewhat full. This means the two fish provide $6 + $8 (first fish) = $14 of “total utility” together.
- Note that it doesn’t matter whether or not you actually buy the second fish. MU is only concerned with what you would pay for it. In real life, economists use complex mathematical models to predict what consumers hypothetically would pay for something.
Advertisement
-
3
Find the total utility from consuming a different number of goods. To find MU, you need two different total utility measurements. You’ll use the difference between them to make your MU calculation.[4]
- Let’s say that, in the example situation in Step 2, you decide that you’re hungry enough to eat four whole fish. After the second fish, you’re feeling a little full, so you would only pay about $3 for the next fish. After the third fish, you’re almost completely full, so you would only pay $1 for the final fish.
- The satisfaction you would get from it is almost cancelled out by the feeling of being uncomfortably full. You can say that the four fish provide a total utility of $8 + $6 + $3 + $1 = $18.
-
4
Calculate MU. Divide the difference in total utility over the difference in units. The answer you get will be the marginal utility, or the utility given by each additional unit consumed.[5]
In the example situation, you would calculate your MU as follows:- $18 – $14 (example from Step 2) = $4
- 4 (fish) – 2 (fish) = 2
- $4/2 = $2
- This means that, between the second and the fourth fish, each extra fish is only worth $2 of utility to you. This is an average value; the third fish is actually worth $3 and the fourth is actually worth $1, of course.
Advertisement
-
1
Use the equation to find the MU for each additional unit. In the example above, we found the average MU for several goods being consumed. This is one valid way to use MU. However, it’s actually more often applied to individual units of goods consumed. This gives us the precise MU for each additional good (not an average value).[6]
- Finding this is easier than it sounds. Just use the normal equation to find the MU when the change in quantity of goods consumed is one.
- In the example situation, you already know the MUs for each individual unit. When you haven’t had any fish, the MU of the first fish is $8 ($8 of total utility – the $0 you had before/change of 1 unit), the MU of the second fish is $6 ($14 of total utility – the $8 you had before/change of 1 unit), and so on.
-
2
Use the equation to maximize your utility. In economic theory, consumers make decisions about how to spend their money in an effort to maximize their utility. In other words, consumers want to get as much satisfaction as possible for their money. This means that consumers will tend to buy products or goods until the marginal utility of buying one more good is smaller than the marginal cost (the price of one more unit).[7]
-
3
Determine lost utility. Let’s look at the example situation one more time. First we said that each fish costs $2. Then we determined that the first fish has an MU of $8, the second has an MU of $6, the third has an MU of $3, and the fourth has an MU of $1.[8]
- Given this information, you wouldn’t actually end up buying the fourth fish. Its marginal utility ($1) is less than its marginal cost ($2). Basically, you’re losing utility on this transaction, so it’s not in your favor.)
Advertisement
| Tickets Bought | Total utility | Marginal utility |
|---|---|---|
| 1 | 10 | 10 |
| 2 | 18 | 8 |
| 3 | 24 | 6 |
| 4 | 28 | 4 |
| 5 | 30 | 2 |
| 6 | 30 | 0 |
| 7 | 28 | -2 |
| 8 | 18 | -10 |
-
1
Assign columns for quantity, total utility, and marginal utility. Most MU charts have at least these three columns. There may sometimes be more, but these display the most crucial information. Typically, these are arranged from left to right.[9]
- Note that the column headers will not always match these exactly. For example, the “Quantity” column may be labeled “Items bought,” “Units purchased,” or something similar. The important thing is the information in the column.
-
2
Look for a trend of diminishing returns. A “classic” MU chart is often used to demonstrate that, as a consumer buys more of a certain good, the desire to purchase even more goods will drop. In other words, after a point, the marginal utility of each additional good purchased will start to decrease. Eventually, the consumer will start to be less satisfied overall than before buying the additional goods.[10]
- In the example chart above, this trend of diminishing returns starts almost immediately. The first ticket to the film festival provides lots of marginal utility, but each ticket after the first gives a little less. After six tickets, each extra ticket actually has a negative MU, which decreases the total satisfaction. An explanation for this might be that, after six visits, the consumer starts to get tired of seeing the same movies again and again.
-
3
Determine Maximum Utility. This is the point where marginal price exceeds MU. A marginal utility chart makes it easy to predict how many units of goods a consumer will buy. As a reminder, consumers tend to buy goods until the marginal price (the cost of one more unit of the goods) is greater than the MU. If you know how much the goods being analyzed in the chart cost, the point where utility is maximized is the last row where MU is higher than the marginal cost.[11]
- Let’s say that the tickets in the example chart cost $3 each. In this case, utility is maximized when the consumer buys 4 tickets. The next ticket after this has an MU of $2, which is less than the marginal cost of $3.
- Note that utility isn’t necessarily maximized when the MU starts to become negative. It’s possible for goods to give some benefit to the consumer without being “worth it.” For instance, the fifth ticket in the chart above still gives $2 worth of MU. This isn’t a negative MU but it still decreases the total utility because it’s not worth the cost.
-
4
Use the chart data to find additional information. Once you have the three “core” columns above, it becomes easy to get more numerical data about the model situation the chart is analyzing. This is especially true if you’re using a spreadsheet program such as Microsoft Excel that can do the math for you. Here are two types of data you may want to put in extra columns to the right of the three used above:[12]
- Average Utility: The total utility in each row divided by the quantity of goods purchased.[13]
- Consumer Surplus: The marginal utility in each row minus the product’s marginal cost. It represents the “profit” in terms of utility the consumer gets from buying each product. It is also called “economic surplus.”[14]
- Average Utility: The total utility in each row divided by the quantity of goods purchased.[13]
Advertisement
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
It’s important to understand that the situations in the examples are model situations. That is, they represent hypothetical consumers (rather than real ones). In real life, consumers aren’t perfectly rational; they may, for instance, not buy exactly as many goods as are needed to maximize utility. Good economic models are great tools for predicting consumer behavior on a broad scale, but they often don’t “match” real life exactly.[15]
-
If you add a consumer surplus column to your chart (as discussed above), the point at which utility is maximized will be the last row before consumer surplus becomes negative.
Advertisement
References
About This Article
Article SummaryX
Marginal utility is used to measure how satisfying or valuable something is to a consumer. To calculate the marginal utility of something, just divide the change in total utility by the change in the number of goods consumed. In other words, divide the difference in total utility by the difference in units to find marginal utility. To learn more from our Entrepreneur co-author, like how to use a marginal utility chart, keep reading the article!
Did this summary help you?
Thanks to all authors for creating a page that has been read 659,385 times.
Reader Success Stories
-
Mujammil Islam
Apr 19, 2017
“Thank you for this article. At first I could not understand the total and marginal utility. Then I found this…” more