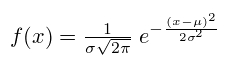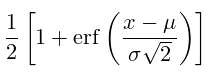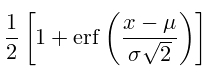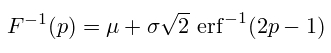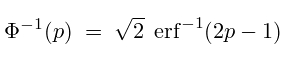Функция распределения дискретной случайной величины
Этот онлайн калькулятор строит график функции распределения по набору значений дискретной случайной величины либо по таблице распределения.
Статьи, описывающие этот калькулятор
- Функция распределения дискретной случайной величины
Функция распределения дискретной случайной величины
Дискретная случайная величина задана
Таблица распределения
| Значение | Вероятность | ||
|---|---|---|---|
Точность вычисления
Знаков после запятой: 4
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
График распределения
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Функция распределения
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Ссылка скопирована в буфер обмена
Похожие калькуляторы
- • Вероятность возникновения некоторого числа событий при проведении нескольких испытаний. Испытания Бернулли.
- • Таблица независимых испытаний по формуле Бернулли
- • Биномиальное распределение. Функция плотности вероятности, кумулятивная функция распределения, математическое ожидание и дисперсия
- • Наивероятнейшее число появления события в независимых испытаниях
- • Логнормальное распределение
- • Раздел: Математика ( 269 калькуляторов )
PLANETCALC, Функция распределения дискретной случайной величины
Probability Density Function – Calculator
Free Probability Density Function and Standard Normal Distribution calculation online. A random variable which has a normal distribution with a mean m=0 and a standard deviation σ=1
is referred to as Standard Normal Distribution. This calculator can be used for calculating
or creating new math problems.
Probability Density Function
Free Probability Density Function and Standard Normal Distribution calculation online. A random variable which has a normal distribution with a mean m=0 and a standard deviation σ=1
is referred to as Standard Normal Distribution. This calculator can be used for calculating
or creating new math problems.
Code to add this calci to your website 
Formula :
PDF of Normal Distribution = P(x) = (1/(σsqrt(2π)))e-(x-m)2 / (2σ2)
Standard Normal Distribution = P(x) = (1/sqrt(2π))e-(x2 / 2)
This tool will help you dynamically to calculate the statistical problems. Calculating Probability Density Function and Standard Normal Distribution is made easier.
Related Calculators:
- Permutation And Combination Calculator
- Negative Binomial Distribution
- Poisson Distribution
- Hypergeometric Distribution Calculator
- Normal Distribution Calculator
- Binomial Distribution Calculator
Нормальное распределение
Следующий калькулятор строит график плотности вероятности и функции плотности распределения для нормального распределения.
И так вспоминаем, что нормальное распределение это особенная часть теории вероятности, общее непрерывное распределение вероятностей, часто использующееся для представления случайных величин, закон распределения которых не известен.
Функция плотности вероятности
Плотность нормального распределения выражается
С помощью функции Гаусса узнаем плотность нормального распределения:
μ — математическое ожидание,
σ — среднеквадратическое отклонение,
σ ² — дисперсия,
Тут медиана и мода нормального распределения будут равны математическому ожиданию μ.
Калькулятор считает значения функции плотности вероятности и функции распределения в заданной вами точке для нормального распределения, определяемого заданной дисперсией и математическим ожиданием:
Функция распределения
Функция распределения для нормального распределения вычисляется:
где, erf(x) – функция ошибок (Лапласа) или интеграл вероятности, определяемый как:
Квантильная функция
Квантильная функция нормального распределения вычисляется через обратную функцию ошибок:
p может принимать значения в диапазоне [0,1]
Квантильная функция стандартного нормального распределения (нормального распределения с σ =1, μ=0) упрощается до:
Значение функции распределения:
График плотности вероятности:
- 14 декабря 2015
- Статистика
Инструкции:
Калькулятор нормальной вероятности позволяет рассчитать вероятность нормального распределения, используя приведенную ниже форму, а также может быть использован в качестве генератора графиков нормального распределения. Пожалуйста, введите среднее значение популяции и стандартное отклонение популяции, а также предоставьте подробную информацию о событии, для которого вы хотите рассчитать вероятность (для стандартного нормального распределения среднее значение равно 0, а стандартное отклонение равно 1):
Подробнее об этом инструменте калькулятор вероятности нормального распределения
Вот некоторые факты о
вероятность нормального распределения
чтобы вы могли лучше понять этот генератор графиков нормального распределения. Прежде всего, нормальная вероятность – это тип непрерывного распределения вероятности, которое может принимать случайные значения на всей вещественной прямой. Основными свойствами нормального распределения являются:
- Она непрерывна (и, как следствие, вероятность получения любого отдельного, конкретного результата равна нулю)
- Он имеет “колоколообразное” распределение (отсюда и название “колоколообразная кривая”)
- Нормальное распределение определяется двумя параметрами: средним значением популяции и стандартным отклонением популяции
- Он симметричен относительно своего среднего значения
Используя вышеизложенное
калькулятор кривой нормального распределения
мы можем вычислить вероятности вида (Pr(a le X le b)), вместе с соответствующими им
графики нормального распределения
. Это не совсем
калькулятор нормальной плотности вероятности
но это калькулятор нормального распределения (кумулятивный). Измените параметры для a и b для построения графика нормального распределения в зависимости от ваших потребностей в вычислениях. Если вам нужно вычислить (Pr(3 le X le 4)), введите “3” и “4” в соответствующие поля скрипта.
Одним из очень важных особых случаев является случай
Стандартное нормальное распределение
что соответствует случаю нормального распределения со средним значением, равным (mu = 0), и стандартным отклонением, равным (sigma = 1). Все случаи обычного нормального распределения или стандартного нормального распределения могут быть рассмотрены с помощью приведенного выше калькулятора вероятностей.
Параметры нормального распределения
Поэтому не забывайте, что нормальное распределение в общем случае определяется его средним значением и стандартным отклонением. Среднее значение может быть любым действительным числом, а стандартное отклонение – любым неотрицательным числом.
Но в частности, стандартное нормальное распределение – это нормальное распределение, которое обладает тем свойством, что среднее значение стандартного нормального распределения равно нулю, а стандартное отклонение стандартного нормального распределения равно 1.
Пожалуйста, не стесняйтесь обращаться к нам, если у вас возникли вопросы по поводу этого генератора графиков нормального распределения.
Связь с нормальным распределением и нормальным cdf
Нормальная cdf – это сокращение от нормальной кумулятивной функции распределения, которая для заданного значения (z) дает общую вероятность до значения данного значения (z).
Вы можете использовать это
нормальный калькулятор
для вычисления желаемой кумулятивной вероятности, и это то же самое, что использовать этот калькулятор нормального распределения с нижним пределом (-infty) и верхним пределом (z).
Нормальное распределение и z-коэффициенты
Во многих аспектах калькулятор нормального распределения можно рассматривать как
калькулятор вероятности z score
из-за того, как мы вычисляем нормальные вероятности в целом.
Действительно, когда у вас есть общее нормальное распределение со средним (mu) и (sigma) в качестве распределения X, и вы хотите вычислить (P(a le Xle b)), то вы фактически используете z-коэффициенты:
[P(a le Xle b) = Prleft(frac{a-mu}{sigma} le frac{X-mu}{sigma} le frac{b-mu}{sigma} right)]
[ = Prleft(z_a le Z le z_b right)]
Другими словами, вместо вычисления вероятности того, что X находится между a и b, вы вычисляете соответствующие z-коэффициенты a и b, называете их (z_a) и (z_b) и вычисляете вероятность того, что Z (переменная со стандартным нормальным распределением) находится между (z_a) и (z_b).
Другой калькулятор нормального распределения
Нормальное распределение является важнейшим непрерывным распределением. Помимо этого калькулятора распределения вероятностей для нормальных распределений, вы можете использовать
калькулятор правил 68-95-99
в котором показано, как использовать эмпирическое правило.
Кроме того, часто вас интересует поведение размеров выборки, для чего вы можете использовать наши
калькулятор выборочного распределения
где вы берете среднее значение выборок размером (n)
Другие непрерывные распределения
Для других типов непрерывных распределений вы можете попробовать, например, наш сайт предоставляет множество других калькуляторов непрерывных распределений, таких как
калькулятор экспоненциального распределения
. F
калькулятор равномерного распределения
.
Кумулятивная функция распределения Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Средняя продолжительность затухания: 3.5 Второй –> 3.5 Второй Конверсия не требуется
Нормализованный LCR: 10 –> Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
35 –> Конверсия не требуется
12 Основные параметры Калькуляторы
Кумулятивная функция распределения формула
Кумулятивная функция распределения = Средняя продолжительность затухания*Нормализованный LCR
CDF = tavg*nR
Всегда ли CDF непрерывен?
Кумулятивная функция распределения (CDF) всегда непрерывна (хотя может и не быть дифференцируемой) для непрерывной случайной величины. Для дискретных случайных величин функция CDF разрывна.