Как найти функцию распределения по функции плотности - Сайт, где вы сможете решить свои вопросы

Зная плотность распределения F(X), можно найти функцию распределения F(X) по формуле

Действительно, F(X) = P(X < X) = P(-∞ < X < X).

Следовательно,

Или

Таким образом, Зная плотность распределения, можно найти функцию распределения. Разумеется, по известной функции распределения можно найти плотность распределения, а именно:

F(X) = F'(X).

Пример. Найти функцию распределения по данной плотности распределения:

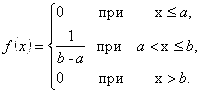
Решение: Воспользуемся формулой

Если X ≤ A, то F(X) = 0, следовательно, F(X) = 0. Если A < x ≤ b, то F(x) = 1/(b-a),

Следовательно,

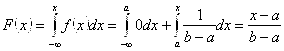Если X > B, то

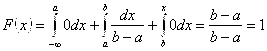Итак, искомая функция распределения

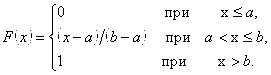
Замечание: Получили функцию распределения равномерно распределенной случайной величины (см. равномерное распределение).

< Предыдущая		Следующая >

Источник

Плотность распределения вероятностей непрерывной случайной величины

Краткая теория
Примеры решения задач
Задачи контрольных и самостоятельных работ

Краткая теория

Ранее
непрерывная случайная величина задавалась с помощью функции распределения. Этот
способ задания не является единственным. Непрерывную случайную величину можно
также задать, используя другую функцию, которую называют плотностью
распределения или плотностью вероятности (иногда ее называют дифференциальной
функцией).

Плотностью распределения вероятностей непрерывной случайной величины

называют функцию

– первую производную от функции распределения

Из этого определения следует, что
функция распределения является первообразной для плотности распределения.

Заметим, что для описания
распределения вероятностей дискретной случайной величины плотность
распределения неприменима.

Зная плотность распределения, можно
вычислить вероятность того, что непрерывная случайная величина примет значение,
принадлежащее заданному интервалу.

Вероятность того, что непрерывная
случайная величина

примет
значение, принадлежащее интервалу

равна
определенному интегралу от плотности распределения, взятому в пределах от

до

Геометрически полученный результат
можно истолковать так: вероятность того, что непрерывная случайная величина
примет значение, принадлежащее интервалу

, равна площади криволинейной трапеции, ограниченной
осью

, кривой распределения

и прямыми

В частности, если

– четная
функция и концы интервала симметричны относительно начала координат, то:

Зная плотность распределения

можно найти
функцию распределения

по формуле:

Свойства плотности распределения

Свойство 1.

Плотность
распределения – неотрицательная функция:

Свойство 2.

Несобственный
интеграл от плотности распределения в пределах от

до

равен единице:

Смежные темы решебника:

Дискретная случайная величина
Непрерывная случайная величина
Интегральная функция распределения вероятностей

Примеры решения задач

Пример 1

Задана
плотность распределения вероятностей f(x) непрерывной случайной
величины X. Требуется:

1)
определить коэффициент A;

2) найти
функцию распределения F(x);

3)
схематично построить графики F(x) и f(x);

4) найти
математическое ожидание и дисперсию X;

5) найти
вероятность того, что X примет значение из
интервала (α,β):

α=1; β=1.7

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

1)
Постоянный параметр

найдем из
свойства плотности вероятности:

В
нашем случае эта формула имеет вид:

Получаем:

2)
Функцию распределения

найдем из
формулы:

Учитывая
свойства

, сразу можем
отметить, что:

Остается
найти выражение для

, когда

принадлежит
интервалу

Получаем:

3) Построим графики

График плотности распределения

График функции распределения

4)
Математическое ожидание находим по формуле:

Для
нашего примера:

Дисперсию
можно найти по формуле:

5)
Вероятность того, что случайная величина примет значение из интервала

Пример 2

Плотность
распределения вероятности непрерывной случайной величины равна

, x∈(0,∞). Найти нормировочный множитель C,
математическое ожидание M(X) и дисперсию D(X).

Решение

Нормировочный множитель

найдем из
свойства плотности вероятности:

В
нашем случае эта формула имеет вид:

Плотность
вероятности:

Математическое
ожидание находим по формуле:

Для
нашего примера:

Дисперсию
можно найти по формуле:

Пример 3

Непрерывная
случайная величина

имеет плотность распределения:

Найти
величину a, вероятность P(X<0) и математическое
ожидание X.

Решение

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Постоянный
параметр

найдем из
свойства плотности вероятности:

В
нашем случае эта формула имеет вид:

Плотность
вероятности имеет вид:

Вероятность:

Математическое
ожидание находим по формуле:

Для
нашего примера:

Задачи контрольных и самостоятельных работ

Задача 1

Плотность
распределения непрерывной случайной величины X имеет вид:

Найти:

а)
параметр a;

б)
функцию распределения F(x);

в)
вероятность попадания случайной величины X в интервал (6.5; 11);

г)
математическое ожидание M(X) и дисперсию D(X);

Построить
график функций f(x) и F(x).

Задача 2

Задана
функция распределения непрерывной случайной величины:

Найти и
построить график функции плотности распределения вероятностей.

Задача 3

Случайная
величина X задана функцией распределения F(x).
Найти плотность распределения вероятностей, математическое ожидание и дисперсию
случайной величины. Построить график функции
F(x).

Задача 4

Задана
плотность вероятности f(x) или функции распределения
непрерывной случайной величины X. Найти a, M[X], D[X], P(α<x<β).

α=1,β=2

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 5

Непрерывная
случайная величина

задана плотностью распределения вероятностей.

Требуется
найти:

– функцию
распределения вероятностей;

–
математическое ожидание;

–
дисперсию;

– среднее
квадратическое отклонение;

– вероятность
того, что случайная величина отклонится от своего математического ожидания не
более, чем на одну четвертую длины всего интервала возможных значений этой
величины;

–
построить графики функции распределения и плотности распределения вероятностей.

Задача 6

Случайная
величина X равномерно распределена на интервале (2;7).
Составить f(x),F(x), построить графики. Найти
M(X),D(X).

Задача 7

Случайная
величина X~N(a,σ)

a=25;
σ=4; α=13; β=30; δ=0.1.

Требуется:

–
составить функцию плотности распределения и построить ее график;

– найти
вероятность того, что случайная величина в результате испытания примет
значение, принадлежащее интервалу (α; β);

– найти
вероятность того, что абсолютная величина отклонения значений случайной
величины от ее математического ожидания не превысит δ.

Задача 8

Плотность
вероятности непрерывной случайной величины ξ задана следующим выражением:

Найти
постоянную C, функцию распределения Fξ (x), математическое
ожидание и дисперсию Dξ случайной величины ξ.

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 9

Случайная
величина X задана функцией распределения вероятностей F(x).

Требуется:

1. Найти
функцию плотности распределения f(x).

2. Найти M(X).

3. Найти
вероятность P(α<X<β)

4.
Построить графики f(x) и F(x).

α=2, β=4.5

Задача 10

Найти
функцию плотности нормально распределенной случайной величины X и
постройте ее график, зная M(X) и D(X).

M(X)=-1; D(X)=8

Задача 11

Случайная
величина X задана интегральной F(x) или дифференциальной f(x)
функцией. Требуется:

а) найти
параметр C;

б) при
заданной интегральной функции F(x) найти дифференциальную функцию f(x), а при
заданной дифференциальной функции f(x) найти интегральную функцию F(x);

в)
построить графики функций F(x) и f(x);

г) найти
математическое ожидание M(X), дисперсию D(X) и
среднее квадратическое отклонение σ(x);

д)
вычислить вероятность попадания в интервал P(a≤x≤b)

е)
определить, квантилем какого порядка является точка xp;

ж)
вычислить квантиль порядка p

a=π/4; b=π/3; xp=π/2; p=0.75

Краткая теория
Примеры решения задач
Задачи контрольных и самостоятельных работ

Источник

Зная плотность совместного
распределения f(x,у),
можно найти функцию
распределения F(x,у)
по формуле:

что непосредственно следует
из определения плотности распределения
двумерной непрерывной случайной величины
(X,
У).

Пример.
Найти
функцию распределения двумерной
случайной величины по данной плотности
совместного распределения

Решение.
Воспользуемся
формулой:

Положив

,
получим

§ 9. Вероятностный смысл двумерной плотности вероятности.

Вероятность попадания
случайной точки (X;Y)
в прямоугольник АВСD
(рис. 16) равна (см. § 6)

Р
(х₁
< X
< х₂,
у₁
< Y
< у₂)=
[F(x₂,
у₂)
– F(x₁,
у₂)]
– [F(x₂,
у₁)
– F(x₁,
у₁)].

Обозначив для краткости
левую часть равенства через P_abcd
и применив к правой
части теорему Лагранжа, получим

P_abcd=,

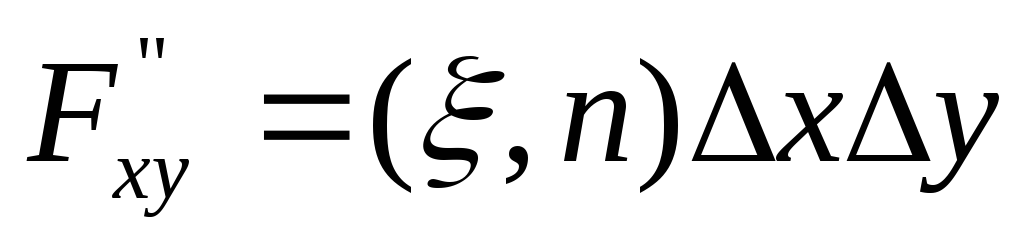где

Отсюда

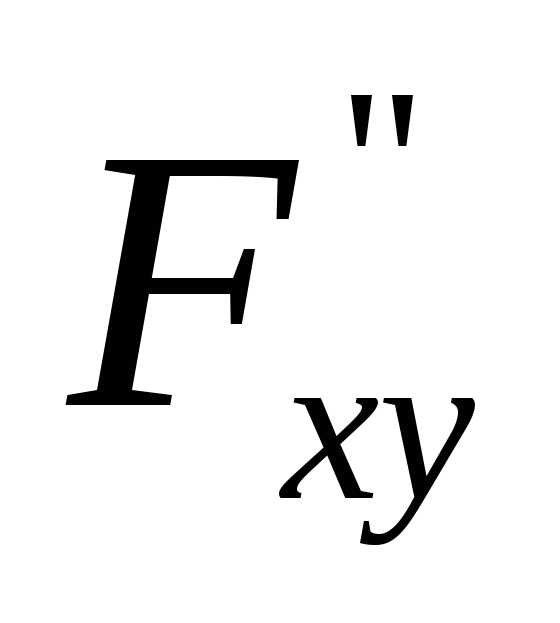
или

f=.
(**)

Приняв во внимание, что произведение
равно
площади прямоугольникаABCD,
заключаем:fесть отношение вероятности попадания
случайной точки в прямоугольникABCDк площади этого прямоугольника.

П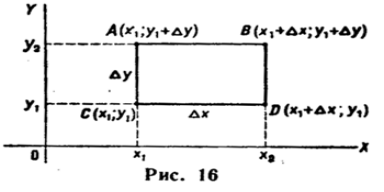ерейдем
теперь в равенство (**) к пределу при.
Тогдаи, следовательно,

Итак, функцию
можно рассматривать как предел отношения
вероятности попадания случайной точки
в прямоугольник (со сторонамии)
к площади этого прямоугольника, когда
обе стороны прямоугольник стремятся к
нулю.

§ 10. Вероятность попадания случайной точки в произвольную область

Перепишем соотношение (**)
§9 так: f=.

О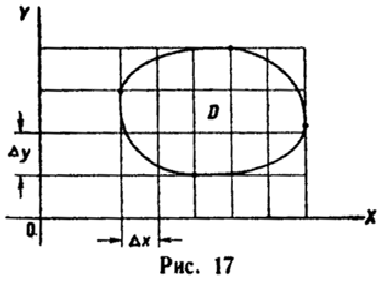тсюда
заключаем: произведение

fесть вероятность попадания
случайной точки в прямоугольник со
сторонами .

Пусть в плоскости xОy
задана произвольная
область D.
Обозначим событие,
состоящее в попадании случайной точки
в эту область, так: (X,
У).

Разобьем область D
на п
элементарных областей
прямыми, параллельными оси Оy,
находящимися на
расстоянии
x
одна от другой, и прямыми, параллельными
оси Ох,
находящимися на расстоянии
одна от другой (рис. 17) (для простоты
предполагается, что эти прямые пересекают
контур области не более чем в двух
точках). Так как события, состоящие в
попадании случайной точки в элементарные
области, несовместны, то вероятность
попадания в областьD
приближенно (сумма
элементарных областей приближенно
равна области D)
равна сумме вероятностей
попаданий точки в элементарные области:

Переходя к пределу при
и,
получим

=.
(*)

Итак, для того чтобы вычислить попадание
случайной точки (X,Y)
в областьD, достаточнонайти двойной интеграл по
области D
от функции f(x,y).

Геометрически равенство
(*) можно истолковать так: вероятность
попадания случайной точки (X,Y)в область D
равна объему тела,
ограниченного сверху поверхностью
z
= f(x,у),
основанием которого
служит проекция этой поверхности на
плоскость xOy.

Замечание.
Подынтегральное выражение f
(x,у)dxdу
называют
элементом
вероятности. Как
следует из предыдущего, элемент
вероятности определяет вероятность
попадания случайной точки в элементарный
прямоугольник со сторонами dx
и
dу.

Пример.
Плотность
распределения двумерной случайной
величины

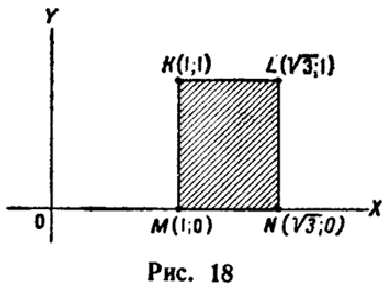
Найти вероятность
попадания случайной точки в прямоугольник
(рис. 18) с вершинами K(1,1),
L(,1),
M(1,0),
N(,0).

Решение.
Искомая вероятность

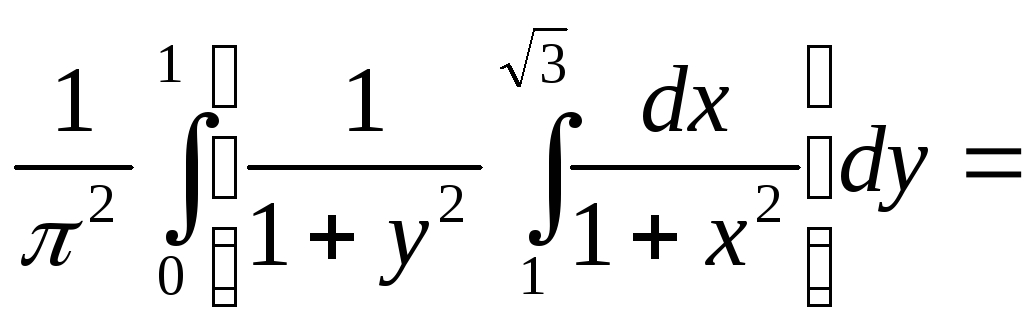
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Плотность распределения

Плотность распределения вероятностей непрерывной случайной величины

Опр Плотностью распределения вероятностей непрерывной случайной величины $X$ называют функцию $f( x )-$ первую производную от функции распределения $F( x )$ begin{equation} label { eq2 } { F } ‘( x )=f( x ) end{equation}

Следовательно, функция распределения $F( x )$ является первообразной для функции плотности распределения вероятностей $f( x )$.

Теорема Вероятность того, что непрерывная случайная величина X примет значение принадлежащее интервалу $( { a,b } )$ равна определенному интегралу от плотности. begin{equation} label { eq3 } P( { aleqslant X<b } )=intlimits_a^b { f( x )dx } end{equation}

Геометрически этот результат можно трактовать так: вероятность того, что случайная величина $X$ примет значение принадлежащее интервалу $( { a,b } )$ равна площади криволинейной трапеции.

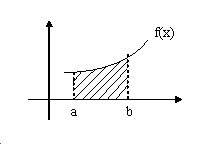
Нахождение функции распределения по известной плотности распределения

Зная плотность распределения вероятностей $f( x )$ можно найти функцию распределения $F( x )$ по формуле: begin{equation} label { eq4 } F( x )=intlimits_ { -infty } ^x { f( x )dx } end{equation}

Пример. Найти функцию распределения по данной плотности и построить график. $ f( x )=left{ { { begin{array} { c } { 0,при,x=1 } \ { frac { 1 } { 2 } ,при,1<xleqslant 3 } \ { 0,при,x>3 } \ end{array} } }right. $

Решение. Построим график функции плотности распределения вероятностей.

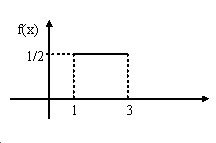
$F( x )=intlimits_ { -infty } ^x { f( x )dx } $

Воспользуемся формулой

при $xleqslant 1$ из условия $f( x )=0,Rightarrow F( x )=0 $
при $,1<xleqslant 2,, f( x )=frac { 1 } { 2 } $, тогда

$F( x )=intlimits_ { -infty } ^x { f( x )dx } =intlimits_ { -infty } ^1 { 0dx } +intlimits_1^x { frac { 1 } { 2 } dx } =frac { 1 } { 2 } xleft| { _ { _1 } ^ { ^x } }right.=frac { x-1 } { 2 } $

если $x>3$, тогда $ F( x )=intlimits_ { -infty } ^x { f( x )dx } =intlimits_ { -infty } ^1 { 0dx } +intlimits_1^3 { frac { 1 } { 2 } dx } +intlimits_3^x { 0dx } =frac { x } { 2 } left| { _ { _1 } ^ { ^3 } }right.=1. $

Итак $ F( x )=left{ { { begin{array} { c } { 0,если,xleqslant 1 } \ { frac { x-1 } { 2 } ,если,1<xleqslant 3 } \ { 1,если,x>3 } \ end{array} } }right. $

Построим график функции распределения

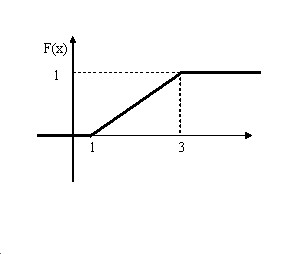
Свойства плотности распределения

1). Плотность распределения неотрицательная функция $f( x )geqslant 0$.

Доказательство Известно, что функция распределения $F( x )-$ неубывающая, следовательно, ее производная $ { F } ‘( x )=f( x )$ неотрицательная функция.

Геометрически это означает, что график $f( x )$ расположен выше оси OX или на оси OX.

График $f( x )$плотности распределения называется кривой распределения.

2). Несобственный интеграл от плотности распределения в пределах от $( { -infty ,infty } )$ равен 1. begin{equation} label { eq5 } intlimits_ { -infty } ^infty { f( x ) } dx=1 end{equation}

Если $X$ задана на $( { a,b } )$, то $intlimits_a^b { f( x )dx=1 } $

Геометрически это означает, что площадь под кривой распределения равна 1.

Источник

Функция распределения вероятностей случайной величины. Плотность
распределения вероятности непрерывной случайной величины

8.1. Функция распределения вероятностей случайной величины

8.1.1. Определение функции распределения

Вспомним, что дискретная случайная величина может быть
задана перечнем всех ее возможных значений и их вероятностей. Такой способ
задания не является общим: он неприменим, например, для непрерывных случайных
величин.

Действительно, рассмотрим случайную величину ,
возможные значения которой сплошь заполняют интервал .
Можно ли составить перечень всех возможных значений ?
Очевидно, что этого сделать нельзя. Этот пример указывает на целесообразность
дать общий способ задания любых типов случайных величин. С этой целью и вводят
функции распределения вероятностей случайной величины.

Пусть —
действительное число. Вероятность события, состоящего в том, что примет
значение, меньшее ,
т.е. вероятность события ,
обозначим через .
Разумеется, если изменяется,
то, вообще говоря, изменяется и ,
т.е. —
функция от .

Функцией распределения называют функцию ,
определяющую вероятность того, что случайная величина в
результате испытания примет значение, меньшее ,
т.е.

Геометрически это равенство можно истолковать так: есть
вероятность того, что случайная величина примет значение, которое изображается
на числовой оси точкой, лежащей левее точки .

Иногда вместо термина «функция распределения» используют
термин «интегральная функция».

Теперь можно дать более точное определение непрерывной
случайной величины: случайную величину называют непрерывной, если ее
функция распределения есть непрерывная, кусочно-дифференцируемая функция с
непрерывной производной.

8.1.2. Свойства функции распределения

Свойство 1.
Значения функции распределения принадлежат отрезку :

Доказательство.
Свойство вытекает из определения функции распределения как вероятности:
вероятность всегда есть неотрицательное число, не превышающее единицы.

Свойство 2. —неубывающая
функция, т.е.

,
если

Доказательство.
Пусть .
Событие, состоящее в том, что примет
значение, меньшее ,
можно подразделить на следующие два несовместных события: 1) примет
значение, меньшее ,
с вероятностью ;
2) примет
значение, удовлетворяющее неравенству ,
с вероятностью .

По теореме сложения имеем

Отсюда

или

(8.1)

Так как любая вероятность есть число неотрицательное, то ,
или ,
что и требовалось доказать.

Следствие 1.
Вероятность того, что случайная величина примет значение, заключенное в
интервале ,
равна приращению функции распределения на этом интервале:

(8.2)

Это важное следствие вытекает из формулы (8.1), если
положить и
.

Пример 8.1.
Случайная величина задана
функцией распределения

Найти вероятность того, что в результате испытания примет
значение, принадлежащее интервалу

Решение. Так как
на интервале ,
по условию,

то

Итак,

Следствие 2.
Вероятность того, что непрерывная случайная величина примет
одно определенное значение, равна нулю.

Действительно, положив в формуле (8.2) ,
имеем

Устремим к
нулю. Так как —
непрерывная случайная величина, то функция непрерывна.
В силу непрерывности в
точке разность
также
стремится к нулю; следовательно, Используя
это положение, легко убедиться в справедливости равенств

(8.3)

Например, равенство доказывается
так:

Таким образом, не представляет интереса говорить о
вероятности того, что непрерывная случайная величина примет одно определенное
значение, но имеет смысл рассматривать вероятность попадания ее в интервал,
пусть даже сколь угодно малый. Этот факт полностью соответствует требованиям
практических задач. Например, интересуются вероятностью того, что размеры
деталей не выходят за дозволенные границы, но не ставят вопроса о вероятности их
совпадения с проектным размером.

Заметим, что было бы неправильным думать, что равенство
нулю вероятности означает,
что событие невозможно
(если, конечно, не ограничиваться классическим определением вероятности).
Действительно, в результате испытания случайная величина обязательно примет одно
из возможных значений; в частности, это значение может оказаться равным .

Свойство 3.
Если возможные значения случайной величины принадлежат интервалу ,
то: 1) при
;
2) при
.

Доказательство.

1) Пусть .
Тогда событие невозможно
(так как значений, меньших величина
по
условию не принимает) и, следовательно, вероятность его равна нулю.

2) Пусть .
Тогда событие достоверно
(так как все возможные значения меньше
)
и, следовательно, вероятность его равна единице.

Следствие.
Если возможные значения непрерывной случайной величины расположены на всей оси
,
то справедливы следующие предельные соотношения:

8.1.3. График функции распределения

Доказанные свойства позволяют представить, как выглядит
график функции распределения непрерывной случайной величины.

График расположен в полосе, ограниченной прямыми ,
(первое
свойство).

При возрастании в
интервале ,
в котором заключены все возможные значения случайной величины, график
«подымается вверх» (второе свойство).

При ординаты
графика равны нулю; при ординаты
графика равны единице (третье свойство).

График функции распределения непрерывной случайной величины
изображен на рис. 2.

Рис. 8.1

Замечание.
График функции распределения дискретной случайной величины имеет ступенчатый
вид. Убедимся в этом на примере.

Пример 8.1.
Дискретная случайная величина задана
таблицей распределения

	1	4	8
	0,3	0,1	0,6

Найти функцию распределения и вычертить ее график.

Решение. Если ,
то (третье
свойство).

Если ,
то .
Действительно, может
принять значение 1 с вероятностью 0,3.

Если ,
то .
Действительно, если удовлетворяет
неравенству ,
то равно
вероятности события которое
может быть осуществлено, когда примет
значение 1 (вероятность этого события равна 0,3) или значение 4 (вероятность
этого события равна 0,1). Поскольку эти два события несовместны, то по теореме
сложения вероятность события равна
сумме вероятностей .

Если ,
то .
Действительно, событие достоверно,
следовательно, его вероятность равна единице.

Итак, функция распределения аналитически может быть
записана так:

График этой функции приведен на рис. 8.2.

Рис. 8.2.

8.2. Плотность распределения вероятностей
непрерывной случайной величины

8.2.1. Определение плотности распределения

Выше непрерывная случайная величина задавалась с помощью
функции распределения. Этот способ задания не является единственным. Непрерывную
случайную величину можно также задать, используя другую функцию, которую
называют плотностью распределения или плотностью вероятности (иногда ее называют
дифференциальной функцией).

Плотностью распределения вероятностей непрерывной
случайной величины называют
функцию —
первую производную от функции распределения :

Из этого определения следует, что функция распределения
является первообразной для плотности распределения.

Заметим, что для описания распределения вероятностей
дискретной случайной величины плотность распределения неприменима.

8.2.2. Вероятность попадания непрерывной случайной величины в заданный
интервал

Зная плотность распределения, можно вычислить вероятность
того, что непрерывная случайная величина примет значение, принадлежащее
заданному интервалу. Вычисление основано на следующей теореме.

Теорема 8.1.
Вероятность того, что непрерывная случайная величина примет
значение, принадлежащее интервалу ,
равна определенному интегралу от плотности распределения, взятому в пределах от
до
:

Доказательство.
Используем соотношение (8.2)

По формуле Ньютона–Лейбница,

Таким образом,

Так как ,
то окончательно получим

(8.4)

Геометрически полученный результат можно истолковать так:
вероятность того, что непрерывная случайная величина примет значение,
принадлежащее интервалу ,
равна площади криволинейной трапеции, ограниченной осью ,
кривой распределения и
прямыми и
.

Замечание. В
частности, если —
четная функция и концы интервала симметричны относительно начала координат, то

Пример 8.2.
Задана плотность вероятности случайной величины

Найти вероятность того, что в результате испытания примет
значение, принадлежащее интервалу .

Решение. Искомая
вероятность

8.2.3. Нахождение функции распределения по известной плотности распределения

Зная плотность распределения ,
можно найти функцию распределения по
формуле

Действительно, мы обозначили через вероятность
того, что случайная величина примет значение, меньшее ,
т.е.

Очевидно, неравенство можно
записать в виде двойного неравенства ,
следовательно,

(8.5)

Полагая в формуле (8.1) ,
,
имеем

Наконец, заменив на
,
в силу (8.5), окончательно получим

Таким образом, зная плотность распределения, можно найти
функцию распределения. Разумеется, по известной функции распределения может быть
найдена плотность распределения, а именно:

Пример 8.3.
Найти функцию распределения по данной плотности распределения:

Построить график найденной функции.

Решение.
Воспользуемся формулой

Если ,
то ,
следовательно, .
Если ,
то ,
следовательно,

Если то

Итак, искомая функция распределения

График этой функции изображен на рис. 8.3.

Рис. 8.3.

8.2.4. Свойства плотности распределения

Свойство 1.
Плотность распределения — неотрицательная функция:

Доказательство.
Функция распределения — неубывающая функция, следовательно, ее производная —
функция неотрицательная.

Геометрически это свойство означает, что точки,
принадлежащие графику плотности распределения, расположены либо над осью ,
либо на этой оси.

График плотности распределения называют кривой
распределения.

Свойство 2.
Несобственный интеграл от плотности распределения в пределах от -∞ до равен
единице:

Доказательство.
Несобственный интеграл

выражает вероятность события,
состоящего в том, что случайная величина примет значение, принадлежащее
интервалу .
Очевидно, такое событие достоверно, следовательно, вероятность его равна
единице.

Геометрически это означает, что вся площадь криволинейной
трапеции, ограниченной осью и
кривой распределения, равна единице.

В частности, если все возможные значения случайной величины
принадлежат интервалу ,
то

Пример 8.4.
Плотность распределения случайной величины задана:

Найти постоянный параметр .

Решение.
Плотность распределения должна удовлетворять условию

поэтому потребуем, чтобы
выполнялось равенство

Отсюда

Найдем неопределенный интеграл:

Вычислим несобственный интеграл:

Таким образом, искомый параметр

8.2.5. Вероятностный смысл плотности распределения

Пусть —
функция распределения непрерывной случайной величины .
По определению плотности распределения, ,
или в иной форме

Как уже известно, разность определяет
вероятность того, что примет
значение, принадлежащее интервалу .
Таким образом, предел отношения вероятности того, что непрерывная случайная
величина примет значение, принадлежащее интервалу .,
к длине этого интервала (при )
равен значению плотности распределения в точке .

По аналогии с определением плотности массы в точке[1]
целесообразно рассматривать значение функции в
точке как
плотность вероятности в этой точке.

Итак, функция определяет
плотность распределения вероятности для каждой точки .

Из дифференциального исчисления известно, что приращение
функции приближенно равно дифференциалу функции, т.е.

или

Так как и
,
то

Вероятностный смысл этого равенства таков: вероятность
того, что случайная величина примет значение, принадлежащее интервалу ,
приближенно равна (с точностью до бесконечно малых высшего порядка относительно )
произведению плотности вероятности в точке на
длину интервала .

Геометрически этот результат можно истолковать так:
вероятность того, что случайная величина примет значение, принадлежащее
интервалу ,
приближенно равна площади прямоугольника с основанием и
высотой .

На рис. 8.4 видно, что площадь заштрихованного
прямоугольника, равная произведению ,
лишь приближенно равна площади криволинейной трапеции (истинной вероятности,
определяемой определенным интегралом ).
Допущенная при этом погрешность равна площади криволинейного треугольника .

Рис. 8.4.

8.2.6. Закон равномерного распределения вероятностей

При решении задач, которые выдвигает практика, приходится
сталкиваться с различными распределениями непрерывных случайных величин.
Плотности распределений непрерывных случайных величин называют также законами
распределений. Часто встречаются, например, законы равномерного, нормального
и показательного распределений. В настоящем параграфе рассматривается закон
равномерного распределения вероятностей.

Нормальному и показательному законам посвящены следующие
две главы.

Распределение вероятностей называют равномерным, если на
интервале, которому принадлежат все возможные значения случайной величины,
плотность распределения сохраняет постоянное значение.

Приведем пример равномерно распределенной непрерывной
случайной величины.

Пример 8.5.
Шкала измерительного прибора проградуирована в некоторых единицах. Ошибку при
округлении отсчета до ближайшего целого деления можно рассматривать как
случайную величину ,
которая может принимать с постоянной плотностью вероятности любое значение между
двумя соседними целыми делениями. Таким образом, имеет
равномерное распределение.

Найдем плотность равномерного распределения ,
считая, что все возможные значения случайной величины заключены в интервале ,
на котором функция сохраняет
постоянные значения:

По условию, не
принимает значений вне интервала ,
поэтому при
и
.

Найдем постоянную .
Так как все возможные значения случайной величины принадлежат интервалу ,
то должно выполняться соотношение

или

Отсюда

Итак, искомая плотность вероятности равномерного
распределения

График плотности равномерного распределения изображен на
рис. 8.5, а график функции распределения — на рис. 8.3.

Рис. 8.5.

Замечание.
Обозначим через непрерывную
случайную величину, распределенную равномерно в интервале ,
а через —
ее возможные значения. Вероятность попадания величины (в
результате испытания) в интервал ,
принадлежащий интервалу ,
равна его длине: