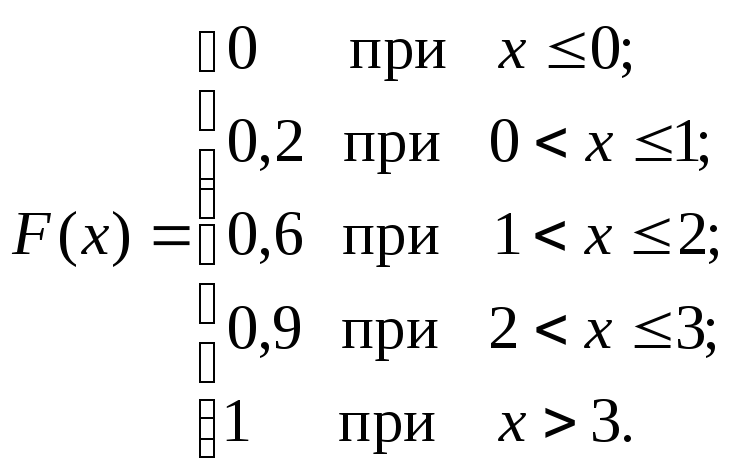Функция распределения случайной величины
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Краткая теория
Пусть
– действительное число. Вероятность события,
состоящего в том, что
примет значение, меньшее
, то есть вероятность
события
обозначим через
. Разумеется, если
изменяется, то, вообще говоря, изменяется и
, то есть
– функция от
.
Функцией распределения называют функцию
, определяющую вероятность
того, что случайная величина
в результате испытания примет значение,
меньшее
, то есть:
Геометрически
это равенство можно истолковать так:
есть вероятность того, что случайная величина примет
значение, которое изображается на числовой оси точкой, лежащей левее точки
.
Иногда
вместо термина «функция распределения» используют термин «интегральная
функция».
Функцию
распределения дискретной случайной величины
можно представить следующим соотношением:
Это
соотношение можно переписать в развернутом виде:
Функция
распределения дискретной случайной величины есть разрывная ступенчатая функция,
скачки которой происходят в точках, соответствующих возможным значениям
случайной величины и равны вероятностям этих значений. Сумма всех скачков
функции
равна 1.
Свойства функции распределения
Свойство 1.
Значения
функции распределения принадлежат отрезку
:
Свойство 2.
– неубывающая функция, то есть:
,
если
Свойство 3.
Если возможные значения случайной величины
принадлежат интервалу
,
то:
1)
при
;
2)
при
Свойство 4.
Справедливо равенство:
Свойство 5.
Вероятность того, что непрерывная случайная
величина
примет одно определенное значение, равна нулю.
Таким образом, не представляет интереса говорить о
вероятности того, что непрерывная случайная величина примет одно определенное
значение, но имеет смысл рассматривать вероятность попадания ее в интервал,
пусть даже сколь угодно малый.
Заметим, что было бы неправильным думать, что
равенство нулю вероятности
означает, что событие
невозможно (если, конечно, не ограничиваться
классическим определением вероятности). Действительно, в результате испытания
случайная величина обязательно примет одно из возможных значений; в частности,
это значение может оказаться равным
.
Свойство 6.
Если возможные значения непрерывной случайной величины
расположены на всей оси
,
то справедливы следующие предельные соотношения:
Свойство 7.
Функция распределения непрерывная слева, то есть:
Смежные темы решебника:
- Дискретная случайная величина
- Непрерывная случайная величина
- Математическое ожидание
- Дисперсия и среднее квадратическое отклонение
Примеры решения задач
Пример 1
Дан ряд
распределения случайной величины
:
|
|
1 | 2 | 6 | 8 |
|
|
0,2 | 0,3 | 0,1 | 0,4 |
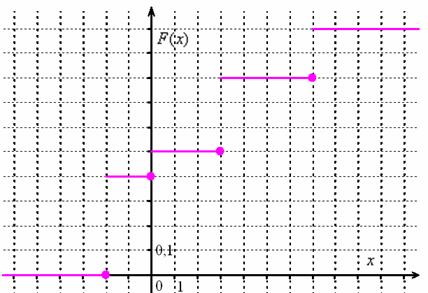
Найти и изобразить ее функцию распределения.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Будем задавать различные значения
и находить для них
1. Если
,
то, очевидно,
в том числе и при
2. Пусть
(например
)
Очевидно, что и
3. Пусть
(например
);
Очевидно, что и
4. Пусть
Очевидно, что и
5. Пусть
Итак:
График функции распределения
Пример 2
Случайная
величина
задана функцией распределения:
Найти
вероятность того, что в результате испытания
примет значение:
а) меньше
0,2;
б) меньше
трех;
в) не
меньше трех;
г) не
меньше пяти.
Решение
а) Так
как при
функция
, то
то есть
при
б)
в)
События
и
противоположны, поэтому
Отсюда:
г) сумма
вероятностей противоположных событий равна единице, поэтому
Отсюда, в
силу того что при
функция
, получим:
Пример 3
Задана
непрерывная случайная величина X своей плотностью
распределения вероятностей f(x). Требуется:
1)
определить коэффициент A;
2) найти
функцию распределения F(x);
3)
схематично построить графики функций f(x) и F(x);
4)
вычислить математическое ожидание и дисперсию X;
5)
определить вероятность того, что X примет значение из
интервала (a,b).
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
1)
Постоянный параметр
найдем из
свойства плотности вероятности:
В
нашем случае эта формула имеет вид:
Получаем:
2)
Функцию распределения
найдем из
формулы:
Учитывая
свойства
, сразу можем отметить,
что:
и
Остается
найти выражение для
, когда х принадлежит интервалу
:
Получаем:
3) Построим графики функций:
График плотности распределения
График функции распределения
4) Вычислим
математическое ожидание:
В нашем случае:
Вычислим дисперсию:
Искомая дисперсия:
5) Вероятность того, что
примет значение из интервала
:
Задачи контрольных и самостоятельных работ
Задача 1
Закон
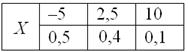
распределения случайной величины X задан таблицей.
Найти ее
математическое ожидание, дисперсию и значение функции распределения в заданной
точке.
F(1)=
M[X]=
D[X]=
Задача 2
Случайная
величины X задана функцией распределения
Найти
плотность распределения вероятностей, математическое ожидание и дисперсию
случайной величины. Построить графики дифференциальной и интегральной функций.
Найти вероятность попадания случайной величины X в интервалы (1,2; 1,8),
(1,8; 2,3)
Задача 3
Дискретная
случайная величина X задана рядом распределения. Найти:
1)
функцию распределения F(x) и ее график;
2)
математическое ожидание M(X);
3)
дисперсию D(X).
|
|
-5 | 5 | 25 | 45 | 65 |
|
|
0.2 | 0.15 | 0.3 | 0.25 | 0.1 |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 4
В задаче
дискретная случайная величина задана рядом распределения.
Найти
; M(X), D(X), P(0≤X≤2); F(x).
Начертить график F(x)
Задача 5
В задаче
непрерывная случайная величина X задана функцией
распределения F(x).
Найти a; f(x); M(X); D(X); P(X<0.2)
Начертить
графики функций f(x);F(x).
Задача 6
Функция
распределения непрерывной случайной величины X (времени безотказной работы
некоторого устройства) равна
(
). Найти вероятность безотказной
работы устройства за время x больше либо равно T.
Задача 7
Функция
распределения непрерывной случайной величины задана выражением:
Найдите:
1)
параметр a;
2)
плотность вероятностей;
4) P(0<x<1)
Постройте
графики интегральной и дифференциальной функции распределения.
Задача 8
Дана
интегральная функция распределения. Найти: дифференциальную функцию f(x),M(X),σ(X),D(X).
Задача 9
Дана
функция распределения F(х) случайной величины Х.
Найти плотность
распределения вероятностей f(x), математическое ожидание M(X),
дисперсию D(X) и вероятность попадания X на
отрезок [a,b]. Построить графики
функций F(x) и f(x).
Задача 10
НСВ X имеет
плотность вероятности (закон Коши)
Найти:
а)
постоянную C=const;
б)
функцию распределения F(x);
в)
вероятность попадания в интервал -1<x<1
г)
построить графики f(x), F(x).
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Наиболее общей
формой задания случайной величины
является функция распределения.
Функцей
распределения (интегральной
функцией)
случайной величины X
называется функция действительной
переменной х,
определяемая равенством
F(x) =P(X<x), (40)
где P(X
< x) –
вероятность того, что случайная величина
X примет
значение, меньшее x.
Основные свойства функции распределения
1.
Функция
распределения является неубывающей,
т. е. если x1
< x2,
то
.
2.
.
3.
Если возможные значения случайной
величины
,
то
при
,
,
.
4.
Вероятность того, что значение случайной
величины X
окажется на заданном интервале (a;b)
определяется формулой
.
(41)
Функция
распределения F(x)
для дискретной случайной величины X,
которая может принимать значения x1,
x2,
…, xn
с соответствующими вероятностями, имеет
следующий вид:
,
(42)
где
символ означает,
что суммируются вероятности тех значений,
которые меньше x.
Пример
2.4. Найти
функцию распределения случайной
величины, если закон распределения
дискретной случайной величины задан
следующей таблицей:
|
Х |
0 |
1 |
2 |
3 |
|
Р |
0,2 |
0,4 |
0,3 |
0,1 |
Решение.
1.
При
.
,
так как величина X
не принимает значений меньше 0.
2.
При
.
.
3.
При
.
.
4.
При
.
F(x)
==
P(X
= 0) + P(X
= 1) + P(X
= 2) = 0,2 + 0,4 + 0,3 =
= 0,9.
5.
При x >
3.
F(x)
= P(X
= 0) + P(X
= 1) + P(X
= 2) + P(X
= 3) = 0,2 + 0,4 + 0,3 +
+ 0,1 = 1.
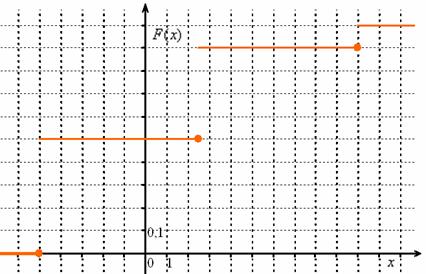
График
функции F(x)
отражен на рис. 2.2.
Рис. 2.2
Вероятность
попадания случайной величины X
в интервал (2;5) равна P(2
< X <
5) = F(5)
– F(2) =
1 – 0,6 = 0,4.
Пример
2.5. Охотник
имеет 4 патрона и стреляет до первого
попадания в цель (или пока не израсходуются
патроны). Найти функцию распределения
числа израсходованных патронов, если
вероятность попадания при каждом
выстреле равна 0,25.
Решение.
Вероятность попадания
р = 0,25,
следовательно q = 0,75.
Случайная
величина X
(число израсходованных патронов) имеет
следующие значения: x1
= 1 (одно попадание), x2
= 2 (один промах и одно попадание), x3
= 3 (два промаха и одно попадание), x4
= 4 (три промаха и одно попадание или
четыре промаха).
Найдем
вероятность того, что стрельба закончится
при четвертом выстреле, т. е. первые три
выстрела дали промахи, а четвертый
выстрел – попадание. Так как события
независимы, то искомая вероятность p
= q · q · q · p
= q3 · p.
Тогда искомый закон распределения
запишем в виде следующей таблицы:
|
X |
1 |
2 |
3 |
4 |
|
P |
0,25 |
0,75 · 0,25 |
0,752 · 0,25 |
0,753 · 0,25 |
.
Функция
распределения имеет вид:
Задачи для самостоятельного решения
1.
Игральную кость подбрасывают 3 раза.
Найти закон распределения случайной
величины X
(число невыпадений единицы).
-
X
0
1
2
3
P
2.
В партии 6 деталей, из которых 4 стандартных.
Наудачу отобраны 3 детали. Найти функцию
распределения случайной величины X
(число стандартных деталей среди
отобранных).
-
X
0
1
2
3
P
3.
Две игральные кости бросают 2 раза.
Написать закон распределения случайной
величины X
(число выпадений четного числа очков
на двух игральных костях).
|
X |
0 |
1 |
2 |
|
P |
4.
Подбрасываются две монеты. Найти функцию
распределения случайной величины X
(число выпадений герба
на верхних сторонах монеты). Построить
график этой функции.
5.
Из 25 контрольных работ, среди которых
5 оценены на “отлично”, наугад извлекают
3 работы. Найти функцию распределения
случайной величины X
(число оцененных на “отлично” работ
среди извлеченных). Используя функцию
распределения, найти вероятность события
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Функция распределения дискретной случайной величины
Этот онлайн калькулятор строит график функции распределения по набору значений дискретной случайной величины либо по таблице распределения.
Статьи, описывающие этот калькулятор
- Функция распределения дискретной случайной величины
Функция распределения дискретной случайной величины
Дискретная случайная величина задана
Таблица распределения
| Значение | Вероятность | ||
|---|---|---|---|
Точность вычисления
Знаков после запятой: 4
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
График распределения
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Функция распределения
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Ссылка скопирована в буфер обмена
Похожие калькуляторы
- • Вероятность возникновения некоторого числа событий при проведении нескольких испытаний. Испытания Бернулли.
- • Таблица независимых испытаний по формуле Бернулли
- • Биномиальное распределение. Функция плотности вероятности, кумулятивная функция распределения, математическое ожидание и дисперсия
- • Наивероятнейшее число появления события в независимых испытаниях
- • Логнормальное распределение
- • Раздел: Математика ( 269 калькуляторов )
PLANETCALC, Функция распределения дискретной случайной величины
2.2.7. Функция распределения случайной величины
Стандартное обозначение:
И для дискретной, и для непрерывной случайной величины она определяется одинаково:
, где
– вероятность того, что случайная величина
примет значение,
МЕНЬШЕЕ, чем переменная , которая«пробегает» все действительные значения от «минус» до
«плюс» бесконечности.
Построим функцию распределения для нашей подопытной игры:
Начинаем разбираться. Чему, например, равно значение ? Это вероятность того, что выигрыш будет меньше, чем –20. И это невозможное событие:
. Совершенно понятно, что
и для всех «икс» из интервала
, а также для
. Почему? По определению функции распределения:
– вы согласны? Функция
возвращает вероятность того,
что в точке выигрыш
будет СТРОГО МЕНЬШЕ «минус» пяти.
Таким образом: , если
.
На интервале функция
, поскольку левее
любой точки этого интервала есть только одно значение случайной величины, которое появляется с вероятностью 0,5. Кроме того,
сюда же следует отнести точку ,
так как:
– очень хорошо осознайте этот
момент!
Таким образом, если , то
Далее рассматриваем промежуток . СТРОГО ЛЕВЕЕ любой точки этого промежутка находятся два выигрыша
, поэтому:
И, наконец, если , то
, ибо все значения
случайной величины
лежат СТРОГО левее
любой точки интервала
Заметим, кстати, важную особенность: коль скоро функция характеризует вероятность, то
она может принимать значения лишь из промежутка – и никакие другие!
Итак, функция распределения вероятностей ДСВ является кусочной и, как многие знают, в таких случаях принято использовать
фигурные скобки:
График данной функции имеет разрывный «ступенчатый» вид:
Причём, функция или её
график однозначно определяют сам закон распределения: в точке высота «ступеньки» (разрыв) составляет
(следим по графику), в точке
«скачок» разрыва равен
и, наконец, в точке
он равен в точности
.
Таким образом, функция распределения вероятностей – это ещё один способ ЗАДАТЬ случайную величину. И этот способ
особо важен для непрерывной случайной величины – по той причине, что её невозможно описать таблицей (ввиду бесконечного и
несчётного количества принимаемых значений). Однако, всему своё время, и НСВ – тоже.
Освоим технические моменты решения типовой задачи:
Задача 93
Построить функцию распределения случайной величины
Найти вероятности того, что случайная величина примет значение из следующих промежутков:
…, пожалуй, достаточно.
Решение: На практике удобно использовать формальный алгоритм построения функции распределения:
Сначала берём первое значение и составляем нестрогое неравенство
. На этом промежутке
.
На промежутке (между
и
):
На промежутке (между
и
):
На промежутке (между
и
):
И, наконец, если строго
больше самого последнего значения , то:
Легко заметить, что с увеличением «икс» идёт накопление (суммирование) вероятностей, и поэтому функцию иногда называют интегральной функцией распределения. В
практических задачах проведённые выше действия обычно выполняют устно, а результат сразу записывают под единую скобку:
Выполним чертёж:
и проконтролируем правильность решения с помощью «скачков» графика: в точке «скачок» равен
, в точке
составляет
, в точке
равен
, и, наконец, в точке
–
.
При выполнении чертежа от руки оптимален следующий масштаб:
горизонтальная ось: 1 ед. = 2 или 1 тетрадная клетка;
вертикальная ось: 0,1 = 1 тетрадная клетка.
На левых концах ступенек (кроме нижнего луча) можно ставить выколотые точки – дело вкуса. Левый нижний луч следует прочертить жирно
(чтобы он не сливался с координатной осью) и до конца оси! Правая верхняя линия не должна заканчиваться раньше
острия оси! Такие оплошности могут говорить о непонимании функции распределения, а это, как вы понимаете, скверно. То было ручное
построение. Ну а о том, как строить такие красивые графики в Экселе можно узнать в этом ролике на Ютубе, к слову, полигон (многоугольник) распределения строится ещё проще.
Переходим ко второй части задания, её коротко можно сформулировать так:


Полную и свежую версию этой книги в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
Функция распределения вероятностей случайной величины
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Определение 1
Случайная величина — величина, которая в испытании может принимать то или иное неизвестное заранее значение.
Пример 1
Пусть в мешке находятся 10 пронумерованных шариков. Вытаскивается 1 шарик. Тогда случайная величина может принимать значения от 1 до 10.
Пример 2
Пусть в классе 30 учеников. Тогда значение случайной величины количества учеников на первом уроке принимает значения от 1 до 30.
Определение 2
Случайная величина называется дискретной, если множество его значений не более чем счётно.
Определение 3
Случайная величина называется непрерывной, если она полностью заполняет какой-либо числовой промежуток.
Определение 4
Случайная величина называется смешанной, если она не является ни дискретной, ни непрерывной.
Определение 5
Закон распределения случайной величины — соответствие между значениями дискретных случайных величин и их вероятностями.
Чаще всего закон распределения записывается в виде таблицы, которая называется рядом распределения.
Таблица 1. Ряд распределения случайной величины
Еще один способ задания закона распределения случайной величины — построение графика функции распределения вероятностей.
Функция распределения вероятностей.
Определение 6
Функция распределения вероятностей (или накопленная частота) $F_{xi }(x)$ случайной величины $xi $ — это функция, ставящая в соответствие любому значению $x$ величину вероятности события, то есть
[F_{xi }left(xright)=P{xi
Далее индекс $xi $ будем опускать.
Рассмотрим ряд задач по этой теме.
Задача 1
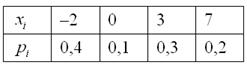
Найти функцию распределения случайной величины $X,$ заданную следующим рядом распределения и построить ее график.
Решение: Пусть $xle 1$, тогда $Fleft(xright)=0$, так как выполнение неравенства $x 3$, тогда $Fleft(xright)=p_1+p_2+p_3=1$.
Получаем следующую функцию распределения вероятностей:
[Fleft(xright)=left{ begin{array}{c}
0, если xle 1, \
0,2, если 1 3. end{array}
right.]
Изобразим график полученной функции
Задача 2
Найти коэффициент $alpha $ в функции распределения случайной величины, заданной выражением
[Fleft(xright)=left{ begin{array}{c}
0, если xfrac{11pi }{6}. end{array}
right.]
Решение.
При $x=frac{7pi }{6}$ функция распределения равна единице, следовательно, имеем
[alpha cosleft(frac{7pi }{6}-frac{pi }{6}right)+2=1,]
[alpha cospi =-1,]
[alpha =1.]
Функция имеет вид:
[Fleft(xright)=left{ begin{array}{c}
0, если xfrac{11pi }{6}. end{array}
right.]
Ответ. 1.
Плотность вероятности
Рассмотрим еще одно понятие, которое связано с понятием функции распределения вероятностей.
Определение 7
Пусть функция распределения вероятностей имеет непрерывную производную $F’left(xright)=varphi (x)$. Функция $varphi (x)$ называется плотностью вероятности.
Задача 3
Продолжительность срока реализации продукции имеет следующую плотность распределения:
[Fleft(xright)=left{ begin{array}{c}
frac{40000}{x^3},если x>200, \
0, если xle 200. end{array}
right.]
- Найти вероятность того, что продукция будет реализована позже 250 часов.
- Найти вероятность того, что продукция будет реализована позже 300, но не позже 500 часов.
Решение.
- Обозначим срок реализации товара через $X$.Так как $F’left(xright)=varphi (x)$ и $Pleft(x>250right)=1-Pleft(x
[Fleft(xright)=intlimits^x_{-infty }{varphi (t)dt}=intlimits^x_{200}{frac{40000}{t^3}}dt=1-frac{20000}{x^2}]
[Pleft(x>250right)=1-1+frac{20000}{62500}=0,24]
- $Pleft(300
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 12.02.2023