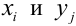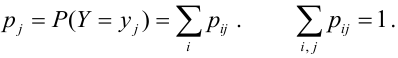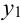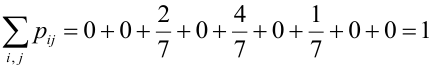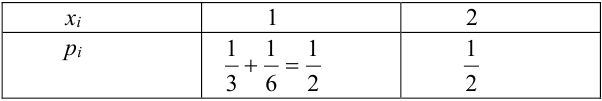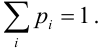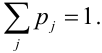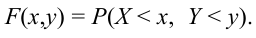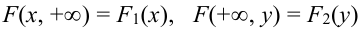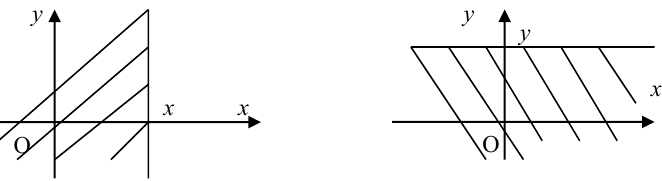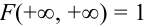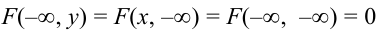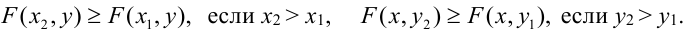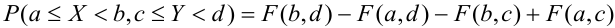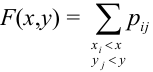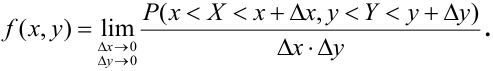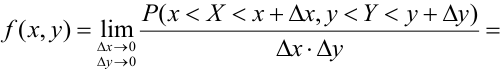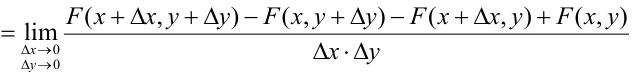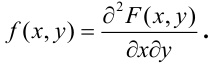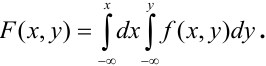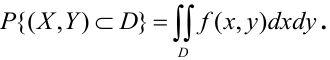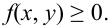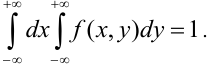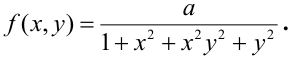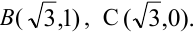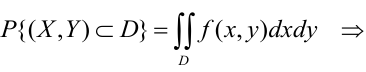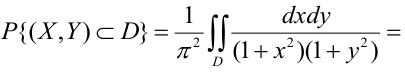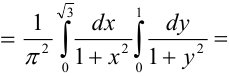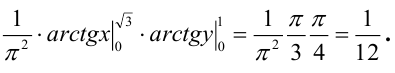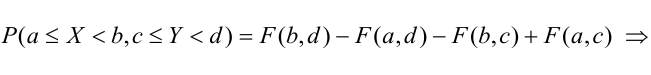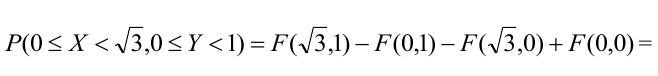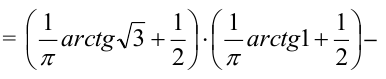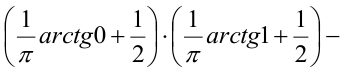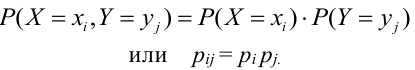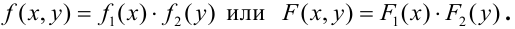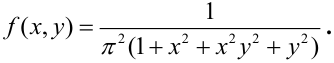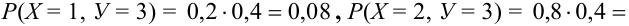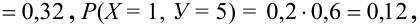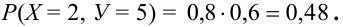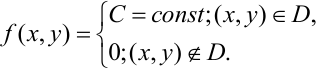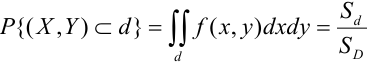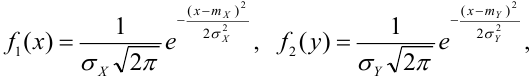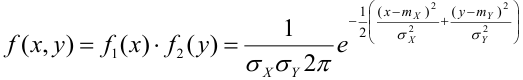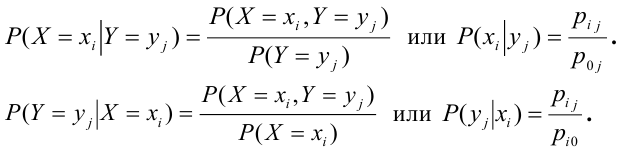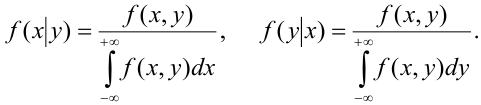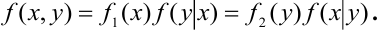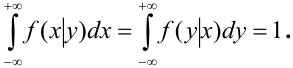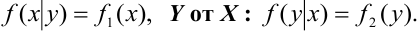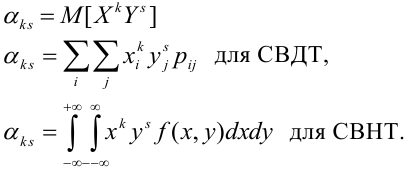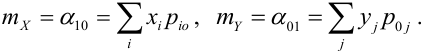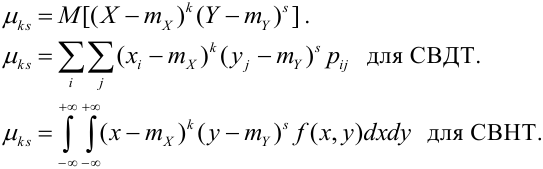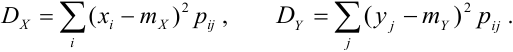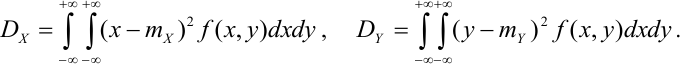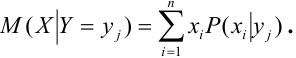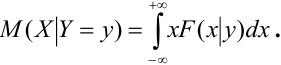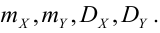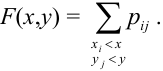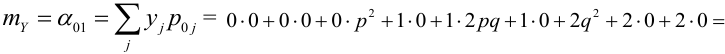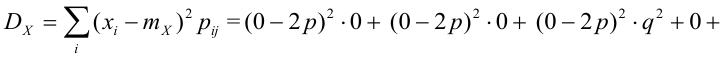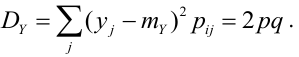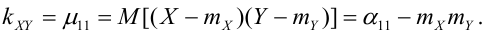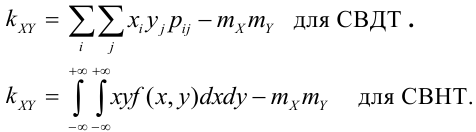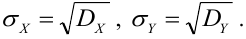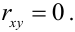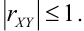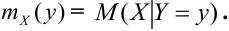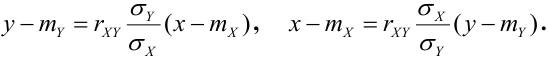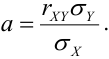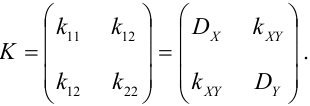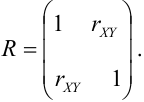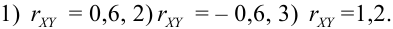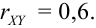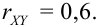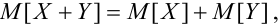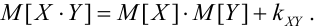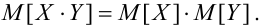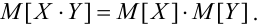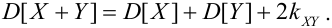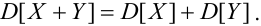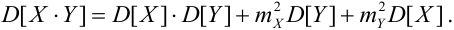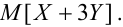Содержание:
- Случайные векторы
- Свойства функции распределения случайного вектора
- Двумерные дискретные случайные векторы
- Двумерные абсолютно непрерывные случайные векторы
- Сходимость случайных величин
Случайные векторы
Рассматриваем случайное явление и вероятностное пространство, которое отвечает этому случайному явлению. Пусть 
Определение. Функцией распределения случайного вектора 
Свойства функции распределения случайного вектора
1. Функция распределения непрерывна слева и монотонно неубывающая по всем аргументам.
2.
3.
4.
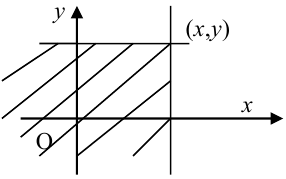
5. Функция распределения компоненты 
Определение. Случайный вектор 
Очевидно, что каждая компонента этого случайного вектора является дискретной случайной величиной.
Дискретный случайный вектор определяется значениями, которые он приобретает, и вероятностями, с которыми приобретаются эти значения.
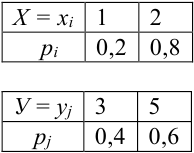
Далее будем считать, что компонента ξ1 приобретает значения 


Определение. Случайный вектор 


Определение. Компоненты случайного вектора 

Если случайный вектор является дискретным, то условие независимости конкретизируется так:
Для абсолютно непрерывного случайного вектора условие независимости является таким:
Пусть 

Если случайный вектор является дискретным и
если вектор ξ – абсолютно непрерывный.
Определение. Ковариантной матрицей случайного вектора 

где
и если 

Понятно, что на диагоналях стоят дисперсии соответствующих компонент.
Легко видеть, что
Доказательство.
Коэффициентом корреляции компонент 
корреляционной матрицей является матрица
Детальнее свойства случайных векторов рассмотрим для двумерного случая.
Двумерные дискретные случайные векторы
Рассматриваем двумерный случайный вектор 



Очевидно, что
где
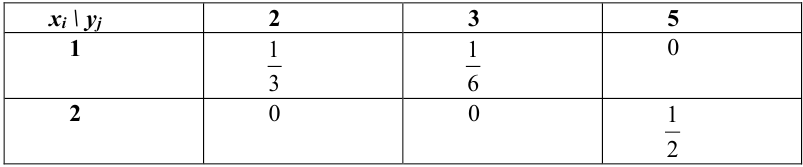
Пример. Дано распределение двумерного случайного вектора
Найти
Решение. Поскольку
то
Пример. Дано распределение двумерного случайного вектора
Найти
Решение. Очевидно, что
Распределение компонент находится так:
Далее определяем 
Пример. Дано распределение двумерного случайного вектора
Найти распределение компонент.
Решение.
Для контроля целесообразно сделать проверку. Известно, что 
Следовательно, распределение компоненты ξ является таким:
Переходим к компоненте η:
Проверка:
Следовательно, распределение компоненты η является таким:
Заметим, что распределение компонент можно находить значительно проще.
Запишем еще раз распределение вектора, добавив одну строку снизу и один столбец справа. Далее находим суммы элементов по строкам и записываем эти суммы в последний столбец, а также находим суммы элементов по столбцах и значения найденных сумм записываем в нижнюю строку. Полученные суммы являются значениями вероятностей. Например, сумма верхней строки является вероятностью 



Определение. Условным распределением компоненты ξ при условии, что 
Аналогично, условным распределением компоненты η при условии, что 
Условным математическим ожиданием компоненты ξ при условии, что 
Аналогично, условным математическим ожиданием компоненты η при условии, что 
Пример. Дано распределение дискретного случайного вектора
Найти условное распределение компоненты ξ при условии, что 


Решение.
Значение вероятности 
Далее
Следовательно, условное распределение компоненты ξ при условии, что 
Сразу находим условное математическое ожидание компоненты ξ при условии, что
Переходим к нахождения условного распределения компоненты η при условии, что
Запишем это условное распределение в виде таблицы
Далее найдем условное математическое ожидание.
Условие независимости для двумерного дискретного случайного вектора является такой:
для произвольных
Пример. Дано распределение двумерного случайного вектора
Проверить, являются ли независимыми компоненты этого вектора.
Решение. 

Очевидно, условие 
Функция распределения для двумерного случайного вектора 
Очевидно, что функция распределения является кусочно-постоянной на отрезках 
Поскольку случайный вектор 




Пример. Дано распределение двумерного случайного вектора 
Найти функцию распределения.
Решение. Поскольку наименьшим значением среди 

Осталось заполнить 4 строки и 3 столбца. Обозначим значения незаполненных клеточек через 
Пусть 

В частности ковариация находится по формуле
де
Коэффициент корреляции
Пример. Найти ковариацию и коэффициент корреляции случайного вектора
Решение. Сначала найдем распределение компонент.
Далее находим 

И, наконец, находим
Переходим к коэффициенту корреляции.
Запишем ковариационную и корреляционную матрицы
Заметим, что если компоненты случайного вектора является независимыми, то ковариация, а следовательно, и коэффициент корреляции равняются нулю. Наоборот не всегда правильно.
Пример случайного вектора, у которого ковариация равна нулю и коэффициенты зависимы.
Сначала покажем, что ковариация равно нулю.
Далее проверяем компоненты на независимость
Следовательно, 
Заметим, что если ковариация является ненулевой, то компоненты зависимы.
Двумерные абсолютно непрерывные случайные векторы
Рассматриваем двумерный абсолютно непрерывный вектор 


Пример. Плотность двумерного случайного вектора 
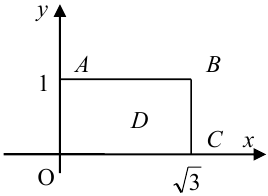
где область D ограничена линиями 


Решение. Сначала изобразим область D.
Вероятность попадания в область 
Очевидно, что
Пример. Дана плотность абсолютно непрерывного случайного вектора
Найти 






Решение. Сначала найдем неизвестную константу 
Сначала найдем 
Далее находим вероятность 
Переходим к нахождению вероятности 
И, наконец находим вероятность 
Как видно из рисунка, сначала нужно найти точку пересечения прямых 
Условие независимости компонент проверяется так:
Пример. Дана плотность случайного вектора
где область D ограничена линиями 




Решение. Прежде всего изобразим область D.
Следовательно,
Проверяем независимость компонент. Для этого находим их плотности
Следовательно,
Переходим к нахождению плотности η
Находим произведение 
В области D имеем
Следовательно, условие независимости не выполняется. ■
Пример. Известно, что компоненты случайного вектора 

Найти совместную плотность случайного вектора 
Решение. Из условия независимости
Поэтому
где область D ограничена линиями 


Функция распределения находится по определению
Пример. Дана плотность абсолютно непрерывного случайного вектора
Найти 



Решение. Прежде всего находим неизвестную константу.
По определению имеем
Аналитический вид функции распределения зависит от того, где находится точка
В частности:
1. Пусть 

Тогда, как видно из рисунка
2.
Тогда
3. Далее рассмотрим точки 

Очевидно аналитический вид функции распределения в этом случае будет таким:
4. Далее рассматриваем множество точек 

5. Наконец, если 

Условная плотность 
соответственно, условная плотность
Пример. Дана плотность абсолютно непрерывного случайного вектора
Найти неизвестную константу 




Решение. Сначала изображаем область D и находим неизвестную постоянную.
Далее находим распределение составляющих
Следовательно, условия плотности будут такими:
Математическое ожидание от функции компонент вектора 
Пример. Дана плотность абсолютно непрерывного случайного вектора
Найти ковариацию, коэффициент корреляции, ковариационную матрицу, корреляционную матрицу, если область D ограничена линиями 


Решение. Сначала находим неизвестную константу
Переходим к ковариации
Следовательно,
Далее находим дисперсии
Ковариационная матрица является такой:
Корреляционная матрица имеет вид
Сходимость случайных величин
Определение. Рассматриваем последовательность случайных величин 
или
и это обозначают
Определение. Последовательность случайных величин 


Это обозначают
Теорема. Если 

Закон больших чисел
Рассматриваем последовательность случайных величин 
Сходимость по вероятности всегда проверять нет смысла, потому что есть теоремы, которые являются достаточными условиями для выполнения закона больших чисел.
Теорема Чебышева. Пусть дана последовательность независимых случайных величин 



Теорема Хинчина. Пусть дана последовательность независимых одинаково распределенных случайных величин 

Теорема Маркова. Пусть дана последовательность произвольных случайных величин 

Тогда для этой последовательности выполняется закон больших чисел.
Теорема Бернулли. В схеме независимых испытаний 
Пример. Дана последовательность независимых случайных величин
Проверить, выполняется ли для этой последовательности закон больших чисел.
Решение. Для проверки используем теорему Чебышева. Независимость дана в условии.
Очевидно, что
Поэтому для данной последовательности выполняются условия теоремы Чебышева, а следовательно, выполняется закон больших чисел. ■
Пример. Дана последовательность независимых случайных величин, которые имеют распределение Коши. Проверить, выполняется ли для этой последовательности закон больших чисел 
Решение. Поскольку для распределения Коши не существует математического ожидания, то речь не идет о выполнении закона больших чисел. ■
Лекции:
- Биномиальный закон
- Равномерный закон
- Закон Пуассона
- Показательный закон
- Нормальный закон
- Теория вероятности: формулы, примеры
- Схема Бернулли теория вероятности
- Формула Пуассона теория вероятности
- Формула лапласа
- Статистическая вероятность
Совокупность
двух случайных величин (X,Y), заданных на
вероятностном пространстве
,
называют двумерной случайной величиной
или двумерным случайным вектором,
X,Y называют координатами случайного
вектора.
Это определение
можно обобщить и на совокупность n
случайных величин.
Функцией
распределения случайного вектора
(X,Y) или совместной функцией распределения
случайных величин X,Y называется
.
Свойства функции распределения.
-
(Это – свойство вероятности, а
– вероятность). -
– неубывающая функция по каждому из
своих аргументов. (В самом деле, если
,
то событие
включено в событие
,
следовательно, его вероятность меньше) -
(события
– невозможные, поэтому их вероятность
равна нулю). -
(событие
достоверно). -
=
–
–
+
Геометрически,
–
площадь
полосы левее
и ниже точки
,
Вычитая из нее
и
,
мы два раза
вычтем площадь
полосы левее и ниже точки
.
Для того, чтобы
получить
площадь
прямоугольника –
левую часть
равенства, надо
вычитать эту
площадь один раз,
п
надо добавить ее, т.е.
в правую часть равенства.
6.
непрерывна
слева по каждому из аргументов
7.
.
Так как событие
достоверно, то пересечение событий
и
есть событие
.
Поэтому первое равенство справедливо.
Аналогично доказывается справедливость
второго равенства.
Двумерная
случайная величина (X,Y) дискретна,
если X, Y –
дискретные случайные величины. Для нее
составляется таблица распределения –
аналог ряда распределения для одномерной
случайной величины.
-
X
Y
y1
y2
…..
ym
PX
x1
p11
p12
…
p1m
pX1
x2
p21
p22
…
p2m
pX2
…….
…
…
…
…
…
xn
pn1
pn2
…
pnm
pXn
PY
pY1
pY2
…
pYm
Здесь pnm
=
,
pYm
=
=
p1m+
p2m
+…+pnm,
pXn
= pn1
+ pn2
+ … +pnm.
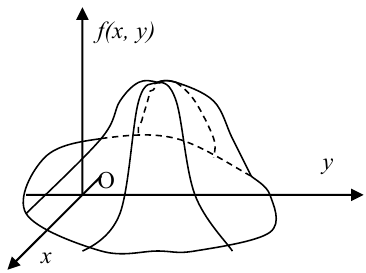
График функции
распределения для двумерной случайной
величины напоминает «лестницу», уровень
ступеней которой изменяется скачком
на pij
при переходе через точку (xi
, yj)
в положительном направлении по оси
OX и по оси OY.
Если зафиксировать x = xi,
то при увеличении y эти
скачки будут на pi1,
pi2, …
pim (от
нуля до pXi
). Если зафиксировать y
= yj,
то при увеличении x
скачки будут на p1j,
p2j, …
pnj
(от нуля до pYj).
Нижние ступени (при xx1
и yy1)
находятся на нулевом уровне, самая
верхняя ступень (при x>xn,
y>ym)
находится на уровне 1. Если зафиксировать
x > xn
то при увеличении y эти
скачки будут на pY1,
pY2, …
pYm (от
нуля до 1). Если зафиксировать
y > ym,
то при увеличении x
скачки будут на pX1,
pX2, …
pXn
(от нуля до 1).
Пример.
Проводятся два выстрела в мишень. При
каждом выстреле вероятность попадания
p, вероятность промаха q
= 1- p. Случайная величина
Xi
– число попаданий при i
– том выстреле. Найдем закон распределения
случайного вектора (X1,
X2)=.
-
X
Y
y1=0
y2=1
PX
x1=0
q2
qp
pX1=q
x2=1
pq
p2
pX2=p
PY
pY1=q
pY2=p
Построим функцию
распределения

В самом деле, при
– событие{X<x,Y<y} –
невозможное, при (x>1, y>1)
событие {X<x,Y<y} –
достоверное.
При
событие {X<x,Y<y} представляет
собой событие {X=0,Y=0}. Поэтому
при
F(x) = P{X=0,Y=0}= q2.
При
событие {X<x,Y<y} представляет
собой объединение несовместных событий
{X=0,Y=0} и {X=0,Y=1}. Поэтому при
F(x) =. P{X=0,Y=0}+ P{X=0,Y=1}= q2
+ pq = q(p+q)=q.Аналогично, в случае
F(x) = P{X=0,Y=0}+ P{X=1,Y=0}= q2
+ pq = q(p+q)=q
Двумерная
случайная величина непрерывна, если
X, Y, непрерывные случайные
величины и ее функцию распределения
можно представить в виде сходящегося
несобственного интеграла от плотности
распределения.
.
Двойной интеграл
можно записать в виде повторных (внешний
по x, внутренний по y
и наоборот). Если предполагать непрерывность
плотности по x и
y, то, дифференцируя по переменным
верхним пределам, получим
.
Свойства
плотности.
-
(функция распределения – неубывающая
функция). -
(по свойству 5 функции распределения)
Справедливо обобщение
.
-
-
(по свойству 4 функции распределения) -
-
,
(Свойство 7 функции распределения)
Независимость
случайных величин.
Случайные
величины X, Y называются
независимыми, если
,
где
– функции распределения случайных
величин X, Y.
Если
случайные величины непрерывны, то,
дифференцируя это соотношение по x,
y, получим
.
Соотношение
поэтому можно считать определением
независимости непрерывных случайных
величин.
Для
дискретных случайных величин
определение независимости можно
записать в виде
.
Математическое
ожидание.
Математическим
ожиданием функции двумерной случайной
величины называется
в дискретном случае,
в непрерывном случае.
Свойства
математического ожидания
-
(
по условию нормировки) -
=
-
для независимых случайных величин.
=
.
Ковариация
(корреляционный момент).
Ковариацией
случайных величин называют
.
Свойства
ковариации.
По свойству 1
-
Если X, Y
независимы, то
,
(обратное неверно).
Если случайные
величины независимы, то
,
тогда по свойству 1
.
Случайные
величины называются некоррелированными,
если
,
из некоррелированности не следует
независимость, из независимости
следует некоррелированность.
По свойству 1
=
=
=
Рассмотрим
случайную величину
.
.
Заметим, что
отсюда следует свойство дисперсии
(при a =1)
.
Так как
,
то
.
Это возможно только, если дискриминант
этого квадратного трехчлена относительно
a меньше или равен нулю. Выпишем это
требование к дискриминанту:
.
Отсюда следует свойство 5.
-
Для того, чтобы случайные
величины были линейно зависимы (Y
= aX +b), необходимо и достаточно,
чтобы
Необходимость.
Пусть Y=aX+b.
Тогда
=
Достаточность.
Пусть
.
Тогда (доказательство свойства 5)
следовательно, z
–детерминированная
величина, т.е.
,
поэтому величины X, Y –
линейно зависимы.
Коэффициентом
корреляции называется
.
Свойства
коэффициента корреляции.
-
-
Если X, Y –
независимы, то
-
-
-
тогда и только тогда, когда X,Y
линейно зависимы.
Двумерное
равномерное распределение
Случайный вектор
(X, Y) равномерно распределен
в области D (площадь D
равна S), если его плотность
распределения задана так: p(x,y)
= 0, если x
D, p(x,y) = 1/S, если xD.
Пример.
Случайный вектор (X,Y)
равномерно распределен в прямоугольнике
0xa,
0xb.
,
аналогично
.
,
аналогично
.
,
аналогично
.
Следовательно,
случайные величины X, Y не
коррелированны.
Двумерное
нормальное распределение
Двумерная
случайная величина (X,Y)
распределена нормально со средними
значениями m,
m2,
дисперсиями
и коэффициентом корреляции
,
если ее плотность задана:

Задача линейного
прогноза.
Заданы
характеристики
случайного вектора
.
Вводится случайная величина – оценка
– линейный прогноз. Вычислить
,
чтобы линейный прогноз был наилучшим
среднеквадратическим (в смысле минимума
погрешности оценки:).
.
За счет выбора
можно лишь минимизировать последнее
слагаемое, сделав его нулем:
.Теперь
остается обеспечить минимум квадратного
трехчлена от
(найти
вершину параболы):
.
Подставляя это значение, найдем
.
Вычислим погрешность оценки при этих
значениях параметров
.
При линейной
зависимости
оценка точна, погрешность равна нулю.
Чем меньше
коэффициент корреляции, тем грубее
оценка. В крайнем случае, при отсутствии
корреляции ()
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Системы случайных величин или случайные векторы:
При изучении случайных явлений в зависимости от их сложности приходится использовать два, три и большее число случайных величин.
Например, 1) попадание снаряда в цель определяется не одной, а двумя случайными величинами: абсциссой и ординатой точки попадания, 2) случайное отклонение точки разрыва снаряда при дистанционной стрельбе определяется комплексом трех случайных величин: тремя координатами этой точки.
Определение 57. Совместное рассмотрение двух или нескольких случайных величин приводит к системе случайных величин или к случайному вектору.
(X, Y) – двумерный случайный вектор или система двух СВ.
Изучать систему – значит изучать сами случайные величины, ее составляющие; связи и зависимости между ними.
Геометрическая интерпретация системы: 1) систему двух случайных величин (X, У) рассматривают как случайную точку на плоскости (Охх) или как случайный вектор с составляющими X, У; 2) систему трех случайных величин (X, У, Z) рассматривают как случайную точку на плоскости (Оxyz) или как случайный вектор с составляющими X, У; Z и т.д.
В зависимости от типа случайных величин, образующих систему, могут быть дискретные, непрерывные и смешанные системы.
Определение 58. Двумерный случайный вектор (X, У) называется вектором дискретного типа (СВДТ), если множество его возможных значений не более, чем счетно.
Определение 59. (первое определение) Двумерный случайный вектор (X, У) называется вектором непрерывного типа (СВНТ), если множество его возможных значений непрерывно заполняет некоторую область плоскости (Оху)-
Определение 60. Законом распределения системы случайных величин называется соотношение, устанавливающее связь между областями возможных значений системы случайных величин и вероятностями появления системы в этих областях.
Законы распределения СВДТ и СВНТ
Таблица распределения – закон распределения СВДТ:
Рассмотрим двумерный случайный вектор (X, У), где X и У – дискретные случайные величины с возможными значениями
Пример:
Из цифр 1, 2, 3, 4, 6, 8, 9 наудачу отбирают две цифры. Х – число четных цифр в выборке, Y – число нечетных. Описать закон распределения.
Решение.
X (четные) – 2, 4, 6, 8; Y ( нечетные) – 1, 3, 9. Следовательно, возможные значения X 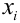
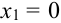
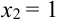
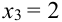
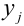
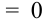
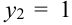
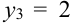
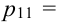
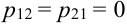
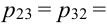
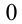
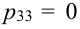
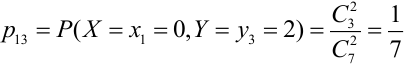
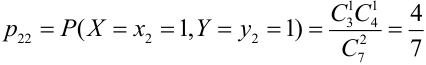
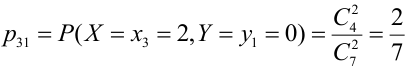
Таблица распределения имеет вид:
Проверка:
Пример:
Дана таблица распределения случайного вектора (X, Y). Получить ряды распределения для Х и Y отдельно.
Решение.
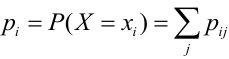
Проверка:
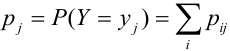
Проверка:
Функция распределения – закон распределения СВДТ и СВНТ
Функция распределения – универсальный закон распределения случайных векторов как дискретного, так и непрерывного типа.
Определение 61. Функцией распределения системы двух случайных величин называется функция двух аргументов F(x,y), равная вероятности совместного выполнения двух неравенств: X < х, Y < у, т.е.
Геометрически F(x,y) представляет вероятность попадания случайной точки (X,Y) в левый нижний бесконечный квадрант плоскости с вершиной в точке (х,у).
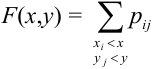
Свойства F(x;y).
1. Условие согласованности:
Пояснение. Отодвигая одну из границ квадранта в бесконечность, получаем полуплоскость, вероятность попадания в которую есть функция распределения одной случайной величины.
2.
Пояснение. Квадрант обращается во всю координатную плоскость, попадание случайной точки в которую есть достоверное событие.
3.
Пояснение. Отодвигая ту или иную границу квадранта в (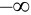
4. F(x, у) – неубывающая функция по каждому аргументу.
5. Вероятность попадания случайной точки (X, У) в произвольный прямоугольник со сторонами, параллельными координатным осям, вычисляется по формуле:
Определение 62. (второе определение) Двумерный случайный вектор называется случайным вектором непрерывного типа (СВНТ), если его функция распределения непрерывна на всей плоскости и существует неотрицательная и интегрируемая по Риману в бесконечных пределах по х, у функция 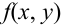
Пример №1
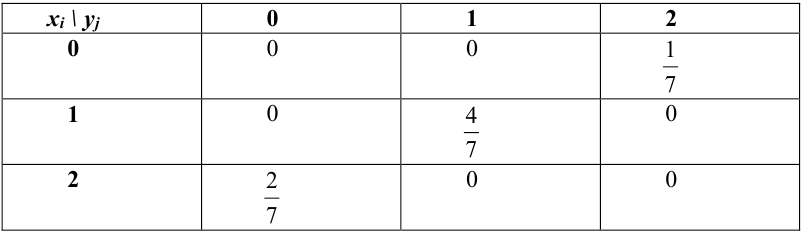
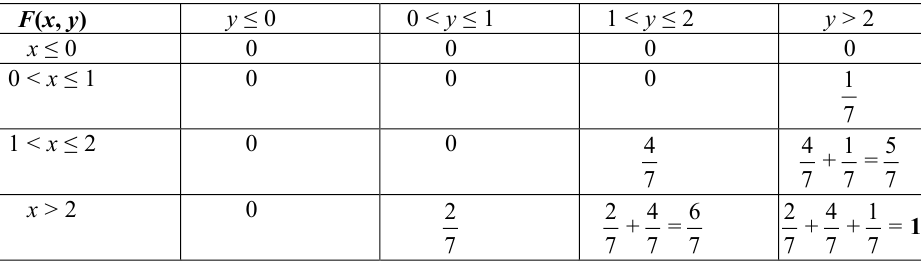
Найти функцию распределения, если случайный вектор задан таблицей распределения:
Решение.
Случайный вектор дискретного типа, следовательно,
Плотность распределения (Для СВНТ)
Определение 63. (первое определение) Плотностью распределения системы двух непрерывных случайных величин называется предел отношения вероятности попадания случайной точки (X, Y) в элементарный прямоугольник к площади прямоугольника, когда оба его размера стремятся к нулю:
Распишем интервальную вероятность с помощью функции распределения:
Правая часть равенства – определение смешанной производной функции двух переменных F(x, у), отсюда следует
Определение 64. (второе определение) Плотностью распределения системы двух непрерывных случайных величин называется смешанная частная производная от функции распределения системы:
Отсюда,
Геометрически 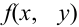
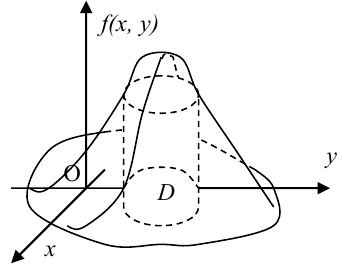
Вероятность попадания случайной точки в некоторую область D плоскости (Oxy) находится по формуле:
Геометрически вероятность попадания случайной точки в область D плоскости (Oxy) изображается объемом цилиндрического тела, ограниченного поверхностью распределения и опирающегося на эту область.
Свойства плотности
1. 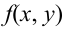
2. Условие нормировки:
Пример №2
Дана плотность распределения непрерывного вектора
Найти: 1) коэффициент а, 2) функцию распределения F(x, у), 3) вероятность попадания случайной точки в прямоугольник с вершинами в точках O(0,0), A(0,1),
Решение.
1) Для вычисления коэффициента а применим условие нормировки:
2) По определению
3) Вероятность попадания в прямоугольник.
1 способ:
2 способ (по 5 свойству):
Пример №3
Дана плотность распределения непрерывного вектора 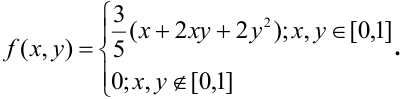
Решение.
Плотность распределения задана в квадрате. Область пересечения квадрата с заданным треугольником заштрихованный треугольник, ограниченный снизу прямой 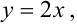
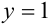
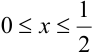
Плотности распределения отдельных величин, входящих в систему
Пусть известна плотность распределения 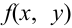
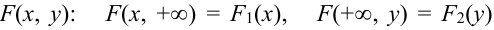
Отсюда, дифференцированием первого равенства по х, а второго по у, получим, что плотности распределения одной из величин равны интегралу от плотности распределения системы в бесконечных пределах по аргументу, соответствующему другой случайной величине:
Ставится вопрос, как по известным законам распределения отдельных величин, входящих в систему, найти закон распределения системы. В общем случае эта задача не разрешима, но, с другой стороны, закон распределения системы должен содержать все сведения о величинах, входящих в систему, в том числе и сведения о том, как они связаны между собой.
Определение 65. Случайные величины X и Y, входящие в систему, называются независимыми, если закон распределения каждой из них не зависит от того, какое значение приняла другая. В противном случае, они называются зависимыми.
Теорема. Для того, чтобы дискретные случайные величины X и Y , входящие в систему, были независимыми, необходимо и достаточно, чтобы выполнялось равенство:
Для того, чтобы непрерывные случайные величины X и Y , входящие в систему, были независимыми, необходимо и достаточно, чтобы выполнялось равенство:
Пример №4
Дана плотность распределения непрерывного вектора:
Зависимы или независимы случайные величины, входящие в систему?
Решение.
Представим плотность в виде произведения:
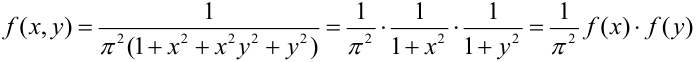
Пример №5
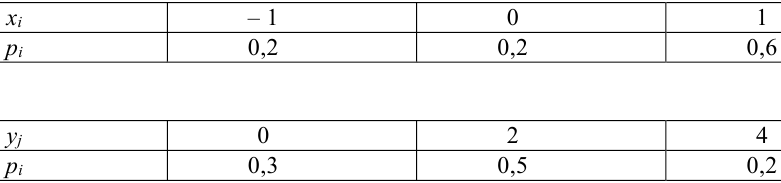
Дано распределение дискретных независимых случайных величин Х и Y:
Записать закон распределения случайного вектора (Х + Y).
Решение.
Найдем возможные значения случайного вектора (Х+ Y): 1 + 3 = 4, 2 + 3 =5, 1+5 = 6, 2 + 5 = 7.
Найдем их вероятности, пользуясь условием независимости:
Следовательно, ряд распределения случайного вектора (Х + Y) имеет вид:
Замечание. Одним из наиболее простых распределений системы двух непрерывных величин является равномерное распределение.
Определение 66. Система двух непрерывных случайных величин имеет равномерное распределение в области D плоскости (Оху), если плотность распределения в точках области D постоянна и равна нулю в остальных точках плоскости:
В силу свойства 2 плотности имеем, что 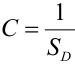
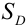
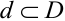
Определение 67. Пусть Х и Y независимые величины, распределенные по нормальному закону, их плотности распределения имеет вид:
Следовательно, плотность распределения системы (Х,Y) на основании теоремы умножения плотностей распределения для случая независимых величин получим в виде
Если X и Y зависимы между собой, то закон распределения системы не может быть выражен через законы распределения отдельных случайных величин, входящих в систему, что привело к введению условных законов распределения.
Определение 68. Распределение одной случайной величины, входящей в систему, найденное при условии, что другая случайная величина, входящая в систему, приняла определенное значение, называется условным законом распределения.
Обозначим G (х,у) – множество возможных значений случайного вектора (X, Y).
Рассмотрим СВДТ.
Условный закон распределения случайной компоненты X при условии, что Y приняла определенное значение у называется совокупность возможных значений 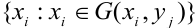
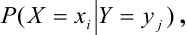
Рассмотрим CBHT.
Условный закон распределения случайной компоненты X при условии, что Y приняла определенное значение у :
Теорема (умножения законов распределения):
Условие нормировки:
Условие независимости Х от Y:
Числовые характеристики системы
Определение 69. Начальным моментом 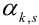
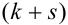
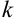
Математическое ожидание дискретных случайных величин Х и Y, входящих в систему:
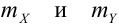
Определение 70. Центральным моментом 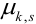
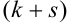
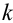
Дисперсия случайных величин X и Y, входящих в систему – характеристика рассеивания случайной точки в направлении осей (ох) и (оу):
Дисперсия дискретных случайных величин Х и Y, входящих в систему:
Дисперсия непрерывных случайных величин Х и Y, входящих в систему:
Замечание. Для краткого описания условных законов распределения используются различные характеристики, наиболее важной из которых является математическое ожидание:
Определение 71. Условным математическим ожиданием дискретной случайной величины X при условии, что Y принимает одно из своих возможных значений 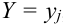
Для непрерывной случайной величины X:
Аналогично, вводится понятие условного мат. ожидания для СВ Y.
Пример №6
По некоторой цели производится два выстрела. Вероятность попадания при одном выстреле равна р. Рассмотрим две случайные величины: X – число попаданий в цель, Y – число промахов. Составить таблицу распределения, записать функцию распределения системы F(x,y) и найти числовые характеристики
Решение.
Случайный вектор дискретного типа, следовательно,
Пояснение:
Ковариация, корреляция и линии регрессии
Особую роль при исследовании системы играет второй смешанный центральный момент.
Определение 72. Второй смешанный центральный момент 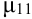
Теория корреляции решает две задачи: 1) установление формы связи между случайными величинами, 2) определение тесноты и силы этой связи.
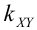
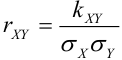
(Иногда его обозначают как 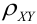
Средние квадратические отклонения случайных величин X и Y равны
Определение 17. X и Y называются некоррелированными случайными величинами, если их коэффициент корреляции 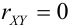
Свойства коэффициента корреляции
Свойства коэффициента корреляции 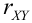
1. Если X и Y – независимые СВ, то 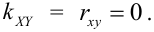
2.
3. В случае 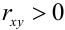
4. В случае 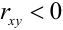
Взаимная связь двух случайных величин, помимо 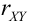
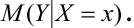
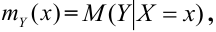
Аналогично, зависимость Х от Y описывает функция
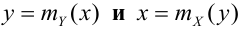
Линии, определенные этими уравнениями, называются кривыми или линиями регрессии. (Вводятся лишь для непрерывных СВ, для ДСВ линии будут состоять из точек.)
Если обе линии регрессии – прямые, то корреляционную зависимость называют линейной (линейная корреляция). Для нормально распределенного случайного вектора (X,Y) уравнения регрессии линейные:
Связь коэффициента корреляции и линий регрессии
1) Если 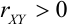
2) Если 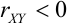
3) Если 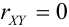
4) Если, 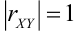
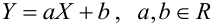
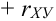
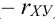
Часто пишут уравнение в виде: 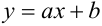
Определение 73. Ковариационной матрицей случайного вектора называется симметрическая действительная матрица, элемент которой представляет собой ковариации соответствующих пар компонент:
Определение 74. Корреляционной матрицей случайного вектора называется нормированная ковариационная матрица
Пример №7
Дано уравнение парной регрессии 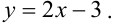
Решение.
Из рассмотрения исключаем 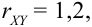
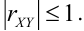
Замечание. Можно было знак 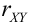
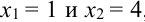
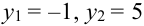
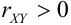
Пример №8
Дано уравнение парной регрессии 
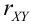
Решение.
Из формулы 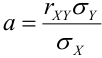
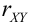
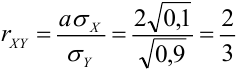
Свойства математического ожидания и дисперсии
1. X, Y как зависимые, так и независимые случайные величины, тогда
2.
Если X, Y – некоррелированные, то
Если X, Y- независимые, то
3.
Если X, Y- некоррелированные, то
4. Если X, Y-независимые, то
Пример №9
Даны законы распределения случайных величин X, Y:
Найти
Решение.
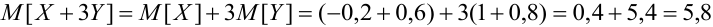
- Вероятность и риск
- Определения вероятности событий
- Предельные теоремы теории вероятностей
- Точечные оценки, свойства оценок
- Алгебра событий – определение и вычисление
- Свойства вероятности
- Многомерные случайные величины
- Случайные события – определение и вычисление
Распределение случайного вектора
Во многих реальных задачах мы имеем не одну, а несколько случайных величин в одном и том же эксперименте. Иногда их удобно рассматривать как единый объект. Это приводит нас к следующему определению.
Определение 1. 

Фактически случайный вектор






Определение 2 . Распределением случайного вектора 



Распределение является объективной характеристикой случайного вектора, которую можно однозначно восстановить из эксперимента. Но распределение, будучи удобной характеристикой в теоретических исследованиях, является довольно сложным для реальных задач. Как и в одномерном случае, используют понятие функции распределения.
Определение 3. Функцией распределения случайного вектора 


Основные свойства функции распределения случайного вектора собраны в следующем предложении.
Предложение 1 . Функция распределения 

1.
2. 


3. 
4. 



5-
Где
6. 
Задача 1 . Доказать предложение 1.
Замечание. В силу свойства 5 по функции распределения 


Классификация распределений
Как и в одномерном случае, мы выделим два важных частных случая распределений, которые наиболее часто используются на практике. Конечно, бывают и более общие примеры, но мы не будем их подробно рассматривать в нашем курсе.
Определение 4 . Случайный вектор 

Если 


появления значения 
Обычно используют следующую стандартную форму описания распределения дискретного случайного вектора. Ясно, что каждая координата 




Задача. Доказать, что 


Для произвольного вектора 

вероятность появления значения 


Пример. Случайный вектор 



Пару 


обычно задают в виде следующей таблицы, называемой таблицей распределения:
Здесь 


Предложение 2. Распределение 

1)
2)
3)

4)
Все эти свойства легко следуют из приведенных выше определений и свойств вероятностей. Поэтому доказательство этого предложения предлагается в виде задачи.
Пример. Пусть мы приводим 











Такое распределение называется полиномиальным распределением с параметрами
Определение 5 . Случайный вектор 


Функция 

Нетрудно доказать следующее утверждение, доказательство которого предлагается в качестве задачи.
Предложение 3 . Случайный вектор 

Тогда справедливы следующие свойства:
1)
2)
3)
4)

5)Если 

То 
6) плотность случайного вектора можно вычислить по формуле
Замечание. Если мы имеем некоторый случайный вектор 





Как и в одномерном случае, можно ввести понятие смеси распределений, но мы не будем его рассматривать подробно так как здесь не возникает ничего нового.
Примеры. 1. Случайный вектор 
где 
2. Случайный вектор 
Числа 
Независимые случайные величины
При изучении свойств вероятностей случайных событий мы видели, что понятие независимости событий играет важную роль при вычислении вероятностей сложных событий. Аналогично понятие независимости является центральным понятием в теории случайных величин, их функциональных преобразований и других вопросах.
Определение 6 . Случайные величины 

Дадим эквивалентные формулировки понятия независимости случайных величин в терминах функций распределения, а также для случаев дискретных и непрерывных распределений.
Предложение 4 . Пусть мы имеем случайный вектор 

В случае дискретных распределений условие независимости эквивалентно условию

а в случае непрерывных – условию
Доказательство. Рассмотрим множества
Для них из (3) следует (4). Обратно, из (4) легко получить (3) для параллелепипедов, а затем аппроксимировать произвольные 1ѕ с помощью сумм отрезков. Свойство (6) получается из (4) дифференцированием. Свойство(5) следует непосредственно из определения независимости.
Пример 1. Пусть мы имеем схему Бернулли с параметрами 




Кстати, число успехов 

Пример 2. Пусть 


Нетрудно доказать следующий полезный результат (задача!).
Предложение 5 . Пусть случайные величины 





Пример 3. Пусть мы имеем схему Бернулли с 




Функциональные преобразования случайных векторов
Как и в одномерном случае, важной с практической точки зрения является задача о вычислении распределения функционального преобразования случайного вектора.
Определение 7 . Отображение


Если 






Рассмотрим теперь отдельно случаи дискретного и непрерывного распределений.
Если 







Пример. Пусть 







Если 


Это формула свертки для дискретных распределений.
Пусть теперь 



Предложение 6 . Пусть 






Доказательство этого предложения дословно повторяет доказательство в одномерном случае, но теперь мы должны сделать замену переменных в
Пример. Пусть 




В тех случаях, когда 



Пример. Пусть случайный вектор 









В предыдущем примере мы получили, что
Чтобы найти плотность распределения для 

Если 




Это формула свертки для непрерывных распределений.
В более сложных ситуациях, когда не удается свести задачу к предложению б, необходимо провести прямые расчеты, вычисляя распределение 


Чтобы продемонстрировать, как работает этот метод, рассмотрим тот же самый пример: 

Фактически нам нужно найти вероятность попадания случайного вектора
Тогда мы имеем
Таким образом, мы имеем тот же результат, что и ранее.
Дифференцируя по 
Далее, расписывая двойной интеграл в виде повторного, получаем
Макеты страниц
ГЛАВА 3. ВЕКТОРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
§ 14. Функция распределения случайного вектора
При совместном изучении двух или трех случайных величин их можно рассматривать как коррдинаты случайной точки на плоскости или в трехмерном пространстве независимо от их конкретной природы. Можно также трактовать две или три случайные величины как составляющие случайного вектора на плоскости или в трехмерном пространстве. Такая трактовка совокупности двух или трех случайных величин дает возможность пользоваться наглядными геометрическими представлениями. Точно так же 



Функцией распределения двумерного случайного вектора с составляющими 




Функция распределения двумерного случайного вектора 
Совершенно так же, как в § 7 была выведена формула (7.5) для вероятности попадания значения случайной величины на данный отрезок числовой оси, можно вывести формулу для вероятности попадания случайной точки на плоскости в бесконечную полуполосу, изображенную на рис. 10:

Обозначая для краткости разность значений любой функции 



Аналогичный вид имеет формула для вероятности попадания случайной точки в бесконечную полуполосу, параллельную оси х.

Рис. 9.

Рис. 10.
Полагая в формуле 



или в развернутом виде


Рис. 11.
Переходя в формуле (14.2) к пределу при получим:

Аналогичную формулу получим для вероятности совместного выполнения неравенства 

Переходя в формуле (14.5) к пределу при 



Эта формула показывает, что вероятность попадания в данную точку 


Из формулы (14.2) следует, что функция распределения двумерного случайного вектора является неубывающей функцией каждой переменной при любом фиксированном значении другой переменной. Далее, так же, как были доказаны равенства (7.8), доказываются следующие свойства функции распределения 

Эти равенства ясны также непосредственно из геометрической интерпретации функции распределения двумерного вектора как вероятности попадания в четверть плоскости, изображенную на рис. 9.
Данное определение и изученные свойства функции распределения легко обобщаются на 







Эта функция является неубывающей функцией каждой переменной при фиксированных значениях других переменных. Если хотя бы одна из составляющих 






распределения 


Если все переменные 



Наконец, совершенно так же, как были выведены формулы (14.3) и (14.4), выводится формула для вероятностей попадания случайной точки с координатами 

Функции распределения являются достаточно общей характеристикой случайных векторов. Любой случайный вектор имеет функцию распределения.
Случайные векторы можно также характеризовать вероятностной мерой, которая определяется так же, как для скалярных величин. А именно, вероятностной мерой случайного вектора X называется такая функция множества 

Приведенное определение вероятностной меры применимо не только к скалярным и векторным случайным величинам, но и вообще к любым случайным объектам (в частности, к случайным функциям). При этом в приведенном определении и в формуле (7.10) X следует понимать как соответствующий случайный объект, 
Понятие вероятностной меры было введено А. Н. Колмогоровым, который впервые дал строгое математическое обоснование основных понятий теории вероятностей с точки зрения современной теории меры [27].