Уравнением
Лапласа называется уравнение
,
где–
Лапласиан.
В
Декартовых координатах
Уравнение
Лапласа самое простое из эллиптических
уравнений. Если-уравнение
Пуассона, это неоднородное уравнение
Лапласа, которое получается при наличии
источников тепла.
Дважды
непрерывно дифференцируемая функция,
удовлетворяющая уравнению Лапласа,
называется гармонической. Уравнение
Лапласа имеет бесконечное множество
решений. Для уравнения Лапласа ставятся
следующие краевые задачи.
Найти
функцию
,
гармоническую внутри области, ограниченной
замкнутой поверхностью,
и удовлетворяющую граничным условиям,
гдеи
– функции, заданные на границе
.
При постановке краевых задач начльные
условия отсутствуют в уравнениях
эллиптического типа.Задача
Дирихле.
Найти
функцию
,
удовлетворяющую уравнению Лапласа
внутри области, ограниченной замкнутой
поверхностью,
и принимающую на границезаданные значения
.Задача
Неймана.
Требуется
найти решение уравнения в некоторой
области пространства, на границе которой
задана внешняя нормальная производная
.
-
как внешняя, так и
внутренняя задачи Дирихле для уравнения
Лапласа имеет не более одного решения. -
Решение внутренней
задачи Неймана в пространстве, внешней
и внутренней задачи Неймана на плоскости
не единственно, определяется с точностью
до постоянного слагаемого. Решение
внешней задачи Неймана в пространстве
единственно.
Решение
уравнения Лапласа
(в сферических координатах) будет
определятся из д.у..
Интегрируя это уравнение, находим.
Полагая, например,=1,
,
получим– фундаментальное решение уравнения
Лапласа в пространстве.
В
цилиндрических координатах уравнение
Лапласа имеет вид
.
Полагая,
получаем.
Или,
которое называется фундаментальным
решением уравнения Лапласа на плоскости.
1-ая
формула Грина. ,
где
,
2-ая
формула Грина
2. Движение точки в поле центральных сил. Формулы Бине
Точка
под действием центральной силы движется
по плоской траектории с постоянной
секторной скоростью, т.е. так, что
радиус-вектор точки за равные промежутки
времени заметает равные площади.
Из
теор. об изменении момента количества
движения

площадей
Введём
полярные координаты

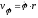
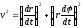




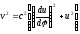
Бине. Вторая формула Бине

энергии:

где
проекцияF
на r.
“+”
– сила отталкивания, “–“ – сила
притяжения.




Бине +

закон движения.
3. Интегрирование дифференциального уравнения изогнутой оси балки
При
изгибе ось балки искривляется, а
поперечные сеч-я перемещ-ся поступательно
и поворачиваются вокруг нейтральных
осей, оставаясь при этом нормальными к
изогнутой продольной оси.
Между
прогибами y(x)
и углами поворота сечений θ(x)
существует определенная зависимость.
Из рис. видно, что угол поворота сечения
θ
равен углу φ
наклона касательной к упругой линии (θ
и φ
– углы с взаимноперпендикулярными
сторонами). Но согласно геометрическому
смыслу первой производной y/=tgθ.
Следовательно, tgθ=tgφ=y/.
Определим
теперь форму упругой линии. Влияние
перерезывающих силQна прогибы
балок, как правило, незначительно.
Поэтому с достаточной точностью можно
принять, что при поперечном изгибе
кривизна упругой линии зависит только
от величины изгибающего моментаMzи жесткостиEIz:
|
|
В
то же время в неподвижной системе
координат кривизна упругой линии, как
и всякой плоской кривой,
|
|
Приравнивая
правые части (1) и (2) и учитывая, что
правила знаков для Mz
и y//
были приняты независимо друг от друга,
получаем
|
|
Это
равенство называется дифференциальным
уравнением упругой линии. При малых
деформациях второе слагаемое в знаменателе
мало по сравнению с единицей (при θ=0.1
рад (y/)2=0.01)
и им можно пренебречь. В результате
получим приближенное дифференциальное
уравнение упругой линии балки
|
|
Выбор знака в правой
части (8.29) определяется направлением
координатной оси y, так как от этого
направления зависит знак второй
производнойy//. Если ось
направлена вверх, то, как видно из рис.
8.23, знакиy//иMzсовпадают, и в правой части надо оставить
знак плюс. Если же ось направлена вниз,
то знакиy//иMzпротивоположны, и это заставляет выбрать
в правой части знак минус.
Заметим, что уравнение
(4) справедливо только в пределах
применимости закона Гука и лишь в тех
случаях, когда плоскость действия
изгибающего момента Mzсодержит одну из главных осей инерции
сечения.
Интегрируя
(4), находим сначала углы поворота сечений
|
|
(5) |
а
после второго интегрирования – прогибы
балки
|
|
(6) |
Постоянные
интегрирования определяются из граничных
условий. На участках с различными
аналитическими выражениями для изгибающих
моментов дифференциальные уравнения
упругой линии также различны. Интегрирование
этих уравнений при n
участках дает 2n
произвольных
постоянных. Для их определения к граничным
условиям на опорах добавляются условия
равенства прогибов и углов поворота на
стыке двух смежных участков балки.
Билет
42
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Лекция 4. Краевые задачи для дифференциальных уравнений. Задача Штурма-Лиувилля.
Будем рассматривать однородное линейное уравнение второго порядка
Ly ≡ a2(x)y” + a1(x)y’ + a0(x)y = 0. Его можно записать по-другому:
Однородное уравнение Ly = 0 и неоднородное Ly = f, как известно, имеют бесконечное множество решений. На практике часто бывает нужно из множества решений выделить только одно. Для этого задают некоторые дополнительные условия. Если это начальные условия у(х0) = уo, y'(xo) = y1, то получают задачу Коши. Если задают дополнительные условия на концах некоторого отрезка, то получают задачу, которая называется краевой задачей. Условия, которые задаются на концах отрезка, называются краевыми условиями. Краевые условия иногда именуют также граничными условиями и тогда говорят о граничной задаче.
Мы будем задавать линейные краевые условия вида
где α1, α2, β1, β2, A, B – заданные числа, причем по крайней мере одно из чисел α1, α2, и одно из чисел β1, β2, отличны от нуля. Если в (16) хотя бы одно из чисел А и В не равно нулю, то краевые условия называют неоднородными. Если А = В = 0, то условия (16) называются однородными. Краевая задача называется однородной, если рассматривается однородное уравнение (15) Ly = 0 и однородные краевые условия (16). Решением краевой задачи называется такое решение дифференциального уравнения, которое удовлетворяет заданным краевым условиям. Заметим сразу, что однородная краевая задача всегда имеет решение у ≡ 0 (тривиальное решение).
Наряду с уравнением (15) рассмотрим уравнение
содержащее некоторый числовой параметр λ. Здесь функции р(х), q(x), r(x) действительные, а число λ может быть, вообще говоря, и комплексным. Краевая задача (17), (16) при А = В = 0 является однородной. Поэтому при любых λ она имеет тривиальное решение. Нас будут интересовать такие значения λ, при которых эта задача обладает не только тривиальными решениями.
Задача Штурма-Лиувилля. Найти те значения параметра λ, при которых уравнение (17) имеет нетривиальное решение, удовлетворяюшее однородным краевым условиям (16). В дальнейшем будем ее записывать в виде
λy = 0, l1y = 0, l2y = 0>.
Те значения параметра λ, при которых задача Штурма-Лиувилля имеет ненулевое решение, называются собственными значениями (собственными числами) задачи, а сами эти решения – собственными функциями. Задачу Штурма-Лиувилля называют также задачей на собственные значения. В силу однородности уравнения и краевых условий собственные функции задачи Штурма-Лиувилля определены с точностью до постоянного множителя. Это означает, что если y(х) -собственная функция при некотором значении λ, то произведение Cy(x), где С – произвольная постоянная, также является собственной функцией при том же значении параметра λ. В связи с этим часто в качестве собственной функции рассматривают нормированную функцию у <х), у которой ||у(х)|| = 1. Такая собственная функция определена, по существу, однозначно (с точностью до знака ±). Далее мы подробно изучим наиболее простой случай задачи Штурма-Лиувилля, когда уравнение имеет вид
Из множества краевых условий вида (16) ограничимся тремя частными случаями:
1) краевые условия первого рода
2) краевые условия второго рода
3) краевые условия третьего рода
Общая задача Штурма-Лиувилля будет обладать свойствами, очень похожими на свойства в этих простых случаях, если на коэффициенты уравнения (17) наложить дополнительные условия: р(х), q(x), f(x) -непрерывные функции, причем р(х) имеет, кроме того, непрерывную производную на [а, b], р(х) > 0, q(x) ≥ 0.
Основные свойства собственных значений и собственных функций задачи Штурма-Лиувилля.
Лемма. Определитель Вронского двух собственных функций задачи Штурма-Лиувилля на концах отрезка [а, b] равен нулю.
Доказательство. Напомним, что определителем Вронского функций у = y1(x) и у = у2(x) называется определитель вида
Рассмотрим однородные краевые условия общего вида (16). Пусть у1(x) и у2(x) – две любые собственные функции. Это означает, что в точке x = а выполняются равенства
Числа α1, и α2 не могут одновременно равняться нулю. Значит, алгебраическая система двух однородных уравнений с двумя неизвестными имеет ненулевое решение. Это возможно только в том случае, когда определитель этой системы равен нулю:
Этот определитель совпадает с определителем Вронского в точке x = а, то есть W(a) = 0.
Аналогичные рассуждения, проведенные для точки x = b, показывают, что W(b) = 0.
Свойство 1. Две собственные функции задачи Штурма-Лиувилля, соответствующие одному и тому же собственному значению λ, линейно зависимые.
Доказательство. Так как собственные функции являются решениями одного и того же однородного уравнения (17) (по условию число λ одно), то в случае их линейной независимости определитель Вронского не равен нулю ни в одной точке отрезка [а, b]. Это противоречит только что доказанной лемме. Следовательно, y1(x) и у2(x) – линейно зависимые функции.
Свойство 2. Две собственные функции у1(x) и у2(x), соответствующие различным собственным значениям λ1 и λ2 (λ1 ≠ λ2), на отрезке [а, b] ортогональны.
Доказательство этого свойства проведем для собственных функций такой задачи, в которой уравнение имеет вид (18). Составим определитель Вронского функций у1 и у2 и продифференцируем его:
Так как у1 и у2 – решения уравнения (18) при λ = λ1 и λ = λ2, соответственно, то получим
Проинтегрируем по отрезку [а, b] левую и правую части полученного равенства. С учетом леммы будем иметь
По условию λ1 – λ2 ≠0, следовательно
Функции y1(x) 0 и у2(х) 0, поэтому
Значит, y1(x) и у2(х) на отрезке [а, b] ортогональны.
Если уравнение, входящее в задачу Штурма-Лиувилля, имеет вид (17), где r(х) > 0 и r(x) 1, то под ортогональностью функций в этом случае подразумевают ортогональность с весом r(х): две функции y1(x) и у2(х) ортогональны на отрезке [а, b] с весом r(x), если
Под нормой функции ||у(x)|| в этом случае также подразумевают весовую норму:
Свойство 3. Собственные функции, соответствующие различным собственным значениям, образуют линейно независимую систему функций.
Это утверждение вытекает из попарной ортогональности собственных функций, соответствующих различным собственным значениям (см. свойство 2).
Свойство 4. Собственные значения задачи Штурма-Лиувилля действительные.
Доказательство. Предположим, что задача Штурма-Лиувилля λy = 0, l1y = 0, l2y = 0> имеет комплексное собственное значение λ = α + βi,β ≠ 0. Пусть ему соответствует собственная функция у(х) (вообще говоря, тоже комплекснозначная). Так как все коэффициенты уравнения и краевых условий имеют действительные значения, то
Здесь черта означает переход к комплексно сопряженному выражению. В нашем случае
Значит число также является собственным значением той же задачи Штурма-Лиувилля и ему соответствует собственная функция . Так как в силу свойства 2 функции y(x) и ортогональны на [а, b], то
Отсюда следует, что у(x) ≡ 0 на [а, b]. Значит ни одно комплексное число λ не может быть собственным значением.
Свойство 5. Пусть коэффициенты уравнения (17) удовлетворяют условиям: р(х), q(x), r(x) – непрерывные функции и, кроме того, р(х) имеет непрерывную производную на [а, b], р(х) > 0, q(x) > 0, r(х) > 0. Тогда задача Штурма-Лиувилля λ y = 0, l1 y = 0, l2 y = 0> имеет бесконечное число собственных значений λ 1, λ2, . λn, . Если краевые условия имеют вид (19) или (20), или (21), то собственные значения соответствующей задачи Штурма-Лиувилля удовлетворяют неравенствам
Теорема Стеклова.Всякая непрерывная функция f(x), удовлетворяющая однородным краевым условиям : l1f = 0 и l2f = 0 , и имеющая непрерывные производные до второго порядка на отрезке [а, b], разлагается на этом отрезке в сходящийся ряд Фурье по собственным функциям yn(х) задачи Штурма-Лиувилля λ y = 0, l1 y = 0, l2 y = 0> :
где коэффициенты Фурье Сn вычисляются по формулам:
Эта теорема применяется при решении уравнений математической физики методом Фурье.
Решение задач Штурма-Лиувилля
Вначале рассмотрим уравнение (18) y” + λy = 0. и краевые условия первого рода (19) y(a) = y(b) = 0. Для удобства будем считать, что a = 0 и b = l > 0. К такой задаче можно всегда свести данную задачу, если сделать замену переменной x’ = x – a, при этом вид уравнения не изменится.
Вид общего решения уравнения (18) зависит от значений параметра λ. Разберем три случая: 1) λ 0. В первом случае обозначим λ = – k 2 . Тогда характеристическое уравнение r 2 – k 2 = 0 будет иметь действительные различные корни r1 = k, r2 = – k: Поэтому, общее решение дифференциального уравнения запишется в виде y = C1e kx + C2e -kx . Подставим краевые условия в общее решение и получим
Определитель этой системы равен
Следовательно, система имеет только нулевое (тривиальное) решение C1 = C2 = 0. Значит, при λ 2 и получим характеристическое уравнение r 2 + k 2 = 0. Оно имеет комплексные корни r1 = ki и r2 = -ki и общее решение дифференциального уравнения в этом случае запишется в виде y = C1cos kx + C2sin kx. Подставим краевые условия в общее решение:
Для того, чтобы эта система имела нетривиальные решения, необходимо и достаточно, чтобы sin kl = 0. Следовательно kl = πn, то есть Так как то можно ограничиться только положительными значениями n = 1, 2, . . Таким образом, собственные значения данной задачи имеют вид При этих значениях алгебраическая система (22) имеет решения:C1 = 0, C2 – любое действительное число. Подставим эти значения в общее решение дифференциального уравнения и получим собственные функции задачи
Обычно постоянный множитель выбирают либо равным единице, либо из условия нормировки:
По тому же алгоритму решаются задачи Штурма-Лиувилля следующего вида:
и
Эти задачи так же, как и предыдущая, при λ 0 не имеют собственных значений. В случае λ > 0 общее решение уравнения записывается в виде y = C1cos kx +C2sin kx, где После подстановки у в краевые условия, получим:
а) для задачи (23)
Для того, чтобы эти системы уравнений имели нетривиальные решения, необходимо и достаточно, чтобы coskl = 0. Следовательно, то есть Отрицательные значения n можно не рассматривать, так как Таким образом, собственные значения у этих задач одинаковые
Собственные функции задачи (23) имеют вид А у задачи (24) они другие:
Некоторые отличия возникают при решении задачи Штурма-Лиувилля в случае краевых условий второго рода
| y” + λy = 0, y'(0) = y'(l) = 0. | (25) |
Рассуждениями, аналогичными тем, которые проводились для краевых условий первого рода, можно показать, что задача (25) при λ 0. В этом случае, общее решение уравнения имеет вид y = C1cos kx + C2sin kx, Найдем производную этой функции и подставим в нее краевые условия (25):
Эта алгебраическая система имеет нетривиальные решения тогда и только тогда, когда, sinkl = 0 то есть kl = πn или Таким образом, числа также являются собственными значениями задачи. Собственные функции при этих значениях имеют вид . Окончательно, задача (25) имеет собственные значения и собственные функции
Для задачи Штурма-Лиувилля с краевыми условиями третьего рода (21) уже не удается получить собственные значения в явном виде. В качестве примера рассмотрим одну такую задачу, когда
| y” + λy = 0, y'(0) = y(0), y'(l) = 0. | (26) |
При задача (26) не имеет собственных значений и собственных функций. Доказательство этого проводится так же, как и для краевых условий первого рода. При λ > 0 общее решение уравнения записывается в виде y = C1coskx + C2sinkx, где . После дифференцирования этой функции и подстановки её производной и самой функции в краевые условия (26) будем иметь:
или
Получившаяся алгебраическая система будет иметь нетривиальные решения только в том случае, когда
coskl – ksinkl = 0 или
Уравнение (28) является трансцендентным уравнением относительно k. Оно не решается в явном виде. Однако, построив графики левой и правой частей уравнения (28), видно, что оно имеет бесконечно много решений (см. рис.13). Обозначим корни уравнения (28) через rn, n = 1,2, . . Тогда при
Рис.13
Численными методами можно найти приближенные значения rn. Из системы (27) при k = rn получим C1n = rnC2n , где C2n -произвольные постоянные. При этих значениях постоянных решения дифференциального уравнения будут иметь вид
Они являются собственными функциями краевой задачи (26) с собственными значениями
Понятие о краевых задачах для дифференциальных уравнений
Помимо задачи с начальными условиями или задачи Коши в приложениях встречается и другая постановка задачи – значение искомой функции задается не в одной, а в двух точках, ограничивающих отрезок, на котором требуется определить решение. Такая задача называется краевой или граничной.
Например, в задаче о движении материальной точки массы m под действием заданной силы часто требуется найти закон движения, если в начальный момент t = t0 точка находилась в положении, характеризуемом радиус-вектором , а в момент t = t1 должна попасть в точку . Задача сводится к интегрированию дифференциального уравнения движения
с краевыми условиями .
Заметим, что эта задача имеет, вообще говоря, не единственное решение. Если речь идет о баллистической задаче и о точках земной поверхности, то в одну и ту же точку тело может попасть по разным траекториям.
Рассмотрим краевые задачи для линейных уравнений второго порядка
краевые условия сводятся к нулевым условиям z(x0)=z(x1)=0, причем линейность дифференциального уравнения не нарушается. Умножим это уравнение на exp(∫p1(x)dx), получим
где p(x)=exp(∫p1(x)dx). Без ограничения общности изучение исходной краевой задачи можем заменить изучением следующей краевой задачи:
(1)
с граничными условиями
(2)
Пусть функция f(x) равна нулю на всем отрезке [x0, x1], за исключением ε-окрестности точки x=s, s – ε < x < s + ε, причем
Обозначим эту функцию f(x)=fε(x, s).
Определение. Функцией Грина G(x, s) краевой задачи (1), (2) называется функция, удовлетворяющая следующим условиям:
- 1) G(x, s) непрерывна по x при фиксированном s при x0 ≤ x ≤ x1, x0 ≤ s ≤ x1;
- 2) G(x, s) является решением соответствующего однородного уравнения
на всем отрезке [x0, x1], за исключением точки x = s;
3) G(x, s) удовлетворяет граничным условиям:
является решением уравнения (1). Краевые условия (2) удовлетворяются по 2 свойству. Метод построения функции Грина. Рассмотрим решение y1(x) уравнения
определяемое начальными условиями
Это решение, вообще говоря, не удовлетворяет второму граничному условию y(x1)=0. Предполагаем, что не существует нетривиального решения y(x) этого однородного уравнения, удовлетворяющего нулевым граничным условиям y(x0)=y(x1)=0.
Очевидно, что решения C1y1(x), где C1 — произвольная постоянная, также удовлетворяет граничному условию y(x0)=0. Аналогично находим нетривиальное решение y2(x) однородного уравнения, удовлетворяющее второму граничному условию y2(x1)=0. Этому же условию удовлетворяют все решения C2y2(x), где C2 — произвольная постоянная.
Функцию Грина ищем в виде
причем постоянные C1, C2 выберем так, чтобы были выполнены свойства 1) и 4), то есть, чтобы функция G(x, s) была непрерывна по x при фиксированном s, и, в частности, непрерывна в точке x=s:
и чтобы G′x(x, s) в точке x=s имела скачок l/p(s):
В силу предположения, что y1(x1) ≤ 0, решения y1(x) и y2(x) линейно независимы, так как все линейно зависимые от y1(x) решения имеют вид C1y1(x) и, следовательно, при C1 ≠ 0 не обращаются в нуль в точке x1, в которой обращается в нуль решение y2(x). Следовательно, определитель системы
являющийся определителем Вронского: W(y1(x), y2(x))=W(x) в точке x=s, отличен от нуля и постоянные C1 и C2, удовлетворяющие этой системе, легко определяются:
Начальные и граничные условия
Здравствуйте, продолжаем нашу рубрику по дифференциальным уравнениям, это уже 2 статья, если вы хотите начать сначала и ознакомиться с видами дифференциальных уравнений, то вам в первую статью.
Введение
Итак, для использования численных методов при решении дифференциального уравнения необходимо дополнительные условия. Если искомая функция(концентрация, температура и т.д) является функцией времени u=u(t), то требуются начальные условия, которые являются значением этой функции в момент времени, принятый за начальный:
Если начальная функция также зависит и от пространственных координат u=u(t,x), то начальное условие характеризуют ее распределение в пространстве в начальный момент времени:
В последнем случае помимо начальных условий требуются еще и граничные условия, которые имеют значения функции u(t,x) на границе изучаемой системы для любого момента времени. Причем, если искомая функция зависит от нескольких пространственных координат, то необходимо задавать граничные условия по каждой из них.
Небольшой пример
Например для следующего уравнения:
- начальное условие
- 2 граничных условия по координате
- 1 граничное условие по координате
- 2 граничных условия по координате
Сразу же возникает вопрос, почему именно так? Так вот, порядок производной определяет количество граничных условий для переменной. Как вы заметили, по y присутствует только первая производная, поэтому и одно граничное условие.
Классификация граничных условий
Для лучшего понимания рассмотрим классификацию на примере уравнения:
будет изменятся от до , соответственно при , будет левая граница, а при , будет правая.
-
Граничные условия 1-ого рода
Записываются следующим образом:
— функции, зависящие от , как пример:
Граничные условия 2-ого рода
Здесь вместо самих функций используются их первые производные.
Граничные условия 3-ого рода
Смешанные граничные условия
В этом случае левое и правое граничные условия могут быть разных родов:
Заключение
На этом мы подходим к концу нашей статьи. Сегодня мы с вами изучили начальные и граничные условия в дифференциальных уравнениях. Если вам что то осталось непонятным, то это нормально, не пугайтесь. В будущих статьях мы будем еще подробнее разбираться с этими и другими тонкостями, ну а на сегодня это все.
Спасибо, что прочитали статью, если у вас остались вопросы, то задавайте их в комментариях.
И, буду вам очень признателен, если вы вступите в нашу группу вконтакте, ссылка на которую размещена слева вверху под названием сайта.
[spoiler title=”источники:”]
http://physmat.ru/diff_eqns/boundary_value_problem.html
http://codetown.ru/differencialnye-uravneniya/conditions/
[/spoiler]
Содержание:
- Метод Фурье
- Первое из граничных условий
По этой ссылке вы найдёте полный курс лекций по математике:
Метод Фурье, или метод разделения переменных, является одним из наиболее распространенных методов решения уравнений с частными производными. Рассмотрим этот метод, обратившись к простейшей задаче о свободных колебаниях однородной струны длины i, закрепленной на концах. §4. Свободные колебания однородной струны, закрепленной на концах Задача о свободных колебаниях однородной струны с закрепленными концами сводится к решению уравнения при граничных условиях и начальных условиях.
Метод Фурье Задачу (1 )-(3) называют смешанной: она содержит и начальные и граничные условия. Решение задачи начнем с поиска частных решений уравнения (1) вида При этом будем предполагать, что каждое из них удовлетворяет граничным условиям (2), но не равно нулю тождественно. Подставляя функцию и{х, t) в форме (4) в уравнение (1), получаем ИЛИ Последнее равенство (его левая часть зависит только от а правая — только от х) возможнолишь втом случае, если обе его части не зависят ни от ty ни от х,т.е. равны одной и той же постоянной.
Обозначим эту постоянную (разделения) через (-А), Из равенства (5) получаем два обыкновенных дифференциальных уравнения Граничные условия (2) дают откуда (T(t) £ 0) следует, что функция Х(х) должна удовлетворять граничным условиям Чтобы получить нетривиальные решения tt(x, t) вида (4), удовлетворяющие граничным условиям (2), необходимо найти нетривиальные решения уравнения удовлетворяющие граничным условиям.
Таким образом, мы приходим к следующей задаче: найти значения параметра А, при которых существуют нетривиальные решения задачи (7)-(8), а также сами эти решения. Такие значения параметра А называются собственными значениями, а соответствующие им нетривиальные решения — собственными функциями задачи (7)-(8). Сформулированную таким образом задачу называют задачей Штурма—Лиувилля. Найдем собственные значения и собственные функции задачи (7)-(8).
Рассмотрим отдельно три случая, когда 1.
При общее решение уравнения (7) имеет вид Потребовав выполнения граничных условий (8), получим (6) (7) Так как определитель системы (9) отличен от нуля, то . Следовательно, Х(х) = 0, т. е. при нетривиальных решений задачи не существует. (9) 2. При А = 0 общее решение уравнения (7) имеет вид Граничные условия (8) дают откуда С, = С2 = 0, и следовательно, при А = 0 нетривиальных решений задачи (7)-(8) также не существует. 3.
При Л > 0 общее решение уравнения (7) имеет вид Потребовав выполнение граничных условий (8), получим Система (10) имеет нетривиальные решениятогда и толькотогда, когда определитель системы равен нулю, Метод Фурье будут собственными функциями задачи. Собственные функции определены с точностью до постоянного множителя, который мы выбрали равным единице. При А = А* общее решение у равнения (6) имеетвид ктга кчга где Аки Bk — произвольные постоянные. Таким образом, функции удовлетворяют уравнению (1) и граничным условиям (2) при любых Ак и Вку В силу линейности и однородности уравнения (1) всякая коневая сумма решений будет также решением уравнения (1).
То же справедливо и для ряда если он сходится равномерно и его можно дважды почленно дифференцировать по х и по t. Поскольку каждое слагаемое в ряде (11) удовлетворяет граничным условиям (2), то этим условиям будет удовлетворять и сумма u(s, t) этого ряда. Остается определить в формуле (11) постоянные .4* и Вк так, чтобы выполнялись и начальные условия (3). Продифференцируем формально ряд (11) по t.
Имеем Полагая в соотношениях (l 1) и (12) t = 0, в силу начальных условий (3) получим Формулы (13) представляют собой разложения заданных функций вряд Фурье по синусам в интервале Коэффициенты разложений (13) вычисляются по известным формулам / I Теорема 2. Если и удоъчетворяет условиям и удовлетворяет условию то сумма tx(x, £) ряда (11), где -А* и В* опредыяются формулами (14), имеет в области непрерывные частные производные до второго порядка включительно по каждому из аргументов, удовлетворяет уравнению (1), граничным условиям (2) и начальным условиям (3), т. е. является решением задачи (1 )-(3).
Пример. Найти закон свободных колебаний однородной струны длины I, закрепленной на концах, если в начальный момент t = 0 струна имеет форму параболы — const), а начальная скорость отсутствует. 4 Задача сводится к решению уравнения при граничных условиях и начальных условиях.
Возможно вам будут полезны данные страницы:
Метод Фурье
Применяя метод Фурье, ищем нетривиальные решения уравнения (1), удовлетворяющие граничным условиям (2), в виде Подставляя «(*,*) в форме (4) в уравнение (1) и разделяя переменные, получим откуда причем в силу (2) Как было установлю но выше, собственные значения задачи (7)-(8) а соответствующие собственные функции Для А = Ащ общее решение уравнения (6) имеет вид пяа ижа Будем иска тъ решение исходной задачи в виде ряда Для определен ия коэффициентов -4Я и Z?„ воспользуемся начальными условия ми (3).
Имеем Из формулы (II) срезу
получаем, что 2?„ = 0 для любог о п, а из (10) Метод Фурье откуда, интегрируя по частям дважды . находи м . Подставляя наеденные значения А, и в ряд (9), получим решение поставленной задачи , Замечание. Если начальные фукхдда не удовлетворяют условиям теоремы 2, то дважды непрерывно дифференцируемого решения смешанной задачи (1)-(3) может и не существовать.
Однако если , то ряд (II) сходетс* равномерно при и любом t и определяет непрерывную функюао u(xtt). В этом случае можно говорить лишь об обобщенная решении задачи. Каждая из функций определяет так называемые собств енные колебания струны, закрепленной на концах. При собственных колебаниях, отвечающих к = 1, струна издает основной, самый низкий тон.
При колебаниях, соответствующих ббльшим Л.она издает более высокие тоны, обертоны. Записав *) в виде заключаем, что собственные колебания струны — стоячие волны, при которых точки струны совершают гармонические колебания с амплитудой Нк sin частотой Метод Фурье Мы рассмотрели случай свободных колебаний однородной струны, закрепленной на концах. Рассмотрим теперьслуч ай других граничных условий.
Пусть, например, левый конец струны закреплен, u(0, t) = 0, а правый конец х — 1 упругосвязан со своим положением равновесия, что соответствует условию . Нетривиальное решение u(x, t) уравнения (1), удовлетворяющее поставленным граничным условиям, будем опять искать в виде В результате подстановки в уравнение (1) приходим к следующей задаче о собственных значениям: найти такие значения параметра Л, для которых дифференциальное уравнение при граничных условиях имеет нетривиальные решения Х(х). Общее решение уравнения (15) имеет вид (А > 0)
Первое из граничных условий
Первое из граничных условий (16) дает С = 0, так что функциями Х(х) с точностью до постоянного множителя являются sin у/Хх. Из второго граничного условия Положим А = ir. Тогда Для отыскания и получаем трансцендентное уравнение. Корни этого уравнения можно найти графически, взяв в плоскости (f, z) сечения последовательных ветвей кривой z = tg(i//) прямой линией z = (рис. 7).
Обе части уравнения (18) — нечетные функции относительно р, поэтому каждому положительному корню i/fc соответствует равный ему по абсолютной величине отрицательный корень. Поскольку изменение знака Uk не влечет за собой появления новых собственных функций (они только изменят знак, что несущественно), достаточно ограничиться положительными корнями уравнения (18).
В результате опять получается последовательность собственных значений и отвечающие им последовательности собственных функций и собственных колебаний Кстати, для n-ой собственной частоты ип получается асимптотическое соотношение в частности, для I = т имеем Если правый конец струны х = I свободен, получаем cos vl = 0. Отсюда ul = § + тиг, так что в случае свободного конца собственные значения и собственные функции соответственно равны
Лекции:
- Треугольники
- Производная примеры решения
- Гиперболические функции
- Однородные дифференциальные уравнения первого порядка
- Натуральные числа
- Связь между графиком функции и графиком ее производной
- Предел последовательности. Свойства сходящихся последовательностей
- Задача двойной интеграл. Определение. Основные свойства двойного интеграла
- Метод вариации постоянных произвольных
- Производная частного
Выше мы рассмотрели ряд физических задач. Каждая из них приводила к следующей математической задаче: найти функцию и, которая во всех внутренних точках заданной области V удовлетворяет уравнению Лапласа 

Граничные задачи могут ставиться не только для уравнения Лапласа, но и для любых уравнений эллиптического типа.
В зависимости от вида граничного условия различают три основных вида граничной задачи:

Здесь 


К этим видам граничной задачи приводит изучение широкого круга стационарных физических процессов и явлений. В частности, примеры, рассмотренные в предыдущем параграфе, привели нас к задачам Дирихле и Неймана. Однако встречаются задачи и с другими граничными условиями. К их числу принадлежат, например, задачи гидродинамики, в которых рассматриваются свободные поверхности жидких сред, и др. Если рассматриваемая физическая среда неоднородна, но состоит из нескольких однородных частей, то на их границах должны выполняться некоторые условия сопряжения и т. п.
Если область, в которой ищется решение уравнения, ограничена, то граничная задача называется внутренней. Если же эта область является частью пространства, лежащей вне некоторой ограниченной области, то граничная задача называется внешней. Если границей области является плоскость, то говорят, что граничная задача ставится для полупространства. Задача о тепловом состоянии однородного тела, сформулированная в предыдущем параграфе, представляет пример внутренней задачи Дирихле, а электростатическая задача — внешней.
Уточним теперь математическую формулировку граничной задачи. Как упоминалось во введении, задачу математической физики называют поставленной корректно, если ее решение существует, единственно и непрерывно зависит от данных задачи.
Требования, содержащиеся в формулировке понятия корректности, отражают наше общее представление о широком круге физических явлений, как непременно происходящих, если созданы необходимые условия (решение существует), полностью определенных условиями их протекания (решение единственно) и протекающих почти одинаково, если условия их протекания достаточно
близки (непрерывная зависимость решения от данных задачи. Корректная постановка задачи обычно обеспечивает физическую содержательность решения.
Условия, обеспечивающие корректность постановки той или иной граничной задачи, несколько различаются для разного типа задач. Но существует основная группа условий, входящих во все эти формулировки. Она сводится к следующему. Функция, дающая решение граничной задачи (поставленной для уравнения в частных производных второго порядка) должна:
1) быть непрерывна в области, в которой ставится задача, вплоть до границы области;
2) внутри области иметь непрерывные вторые производные и удовлетворять заданному уравнению (например, уравнению Лапласа, Пуассона и т. д.);
3) на границе области удовлетворять заданному граничному условию;
4) если область трехмерна и бесконечна, то при перемещении к бесконечно удаленной точке вдоль любого луча, принадлежащего области, стремиться к нулю.
Решения граничных задач, поставленных в трехмерных областях, удовлетворяющие перечисленным условиям, будем называть регулярными.
Как мы покажем, регулярные решения основных граничных задач единственны (иногда при некоторых дополнительных условиях) и непрерывно зависят от граничных условий. Проблемы же существования решений, требующей применения специального математического аппарата, мы касаться не будем. Отметим лишь, что регулярные решения существуют только тогда, когда заданное граничное условие достаточно гладко. Это обстоятельство, практически, не является важным, так как любое граничное условие, имеющее физический смысл, может быть сколь угодно точно приближено достаточно гладкими функциями. В рамках идеализированного рассмотрения физических объектов как непрерывных, это приближение будет иметь тот же физический смысл, что и исходное условие. Другое решение вопроса о существовании решений дается теорией обобщенных решений.
В заключение отметим, что решения корректно поставленных граничных задач для любого уравнения эллиптического типа всегда оказываются не менее гладкими (в смысле существования у них определенного числа непрерывных производных), чем
определяющие их функции (коэффициенты уравнения и данные задачи). Обычно во всех внутренних точках изучаемой области они даже дифференцируемы неограниченное число раз. Это свойство решений граничных задач тесно связано с тем, что к граничным задачам приводит изучение установившихся (стационарных) физических процессов — равновесий, являющихся конечным результатом предшествующего процесса выравнивания. Из физических соображений очевидно, что при этом не только решения задачи, но и граничные условия, достаточно точно передающие природу явления, будут весьма гладкими.



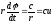



 .
.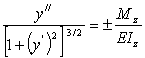 .
. .
.






