Как найти гамильтониан системы

Эта статья — об операторе Гамильтона в квантовой механике. О функции Гамильтона в классической механике см. Функция Гамильтона.

Квантовая механика
Введение[en] История[en] Математические основы
Основа Классическая механика Постоянная Планка Интерференция Бра и кет Гамильтониан Старая квантовая теория
Фундаментальные понятия Квантовое состояние Квантовая наблюдаемая Волновая функция Квантовая суперпозиция Квантовая запутанность Смешанное состояние Измерение Неопределённость Принцип Паули Дуализм Декогеренция Симметрия Теорема Эренфеста Туннельный эффект
Эксперименты Опыт Дэвиссона — Джермера Опыт Франка — Герца Опыт Штерна — Герлаха Опыт Юнга Квантовый ластик Квантовый ластик с отложенным выбором Проверка неравенств Белла Фотоэффект Эффект Комптона
Формулировки Представление Шрёдингера Представление Гейзенберга Представление взаимодействия Представление фазового пространства Матричная квантовая механика Интегралы по траекториям Диаграммы Фейнмана
Уравнения Шрёдингера Паули Клейна — Гордона Дирака Швингера — Томонаги фон Неймана Блоха Линдблада Гейзенберга
Интерпретации Копенгагенская Теория скрытых параметров Локальная[en] Многомировая Теория де Бройля — Бома
Развитие теории Квантовая теория поля Квантовая электродинамика Теория Глэшоу — Вайнберга — Салама Квантовая хромодинамика Стандартная модель Квантовая гравитация
Сложные темы Релятивистская квантовая механика Квантовая теория поля Квантовая гравитация Теория всего
Известные учёные Планк Эйнштейн Шрёдингер Гейзенберг Йордан Бор Паули Дирак Фок Борн де Бройль Ландау Фейнман Бом Эверетт
См. также История возникновения Глоссарий[en] ЭПР-парадокс
См. также: Портал:Физика

Гамильтониа́н ( или H) в квантовой теории — оператор полной энергии системы (ср. функция Гамильтона). Название «гамильтониан», как и название «функция Гамильтона», происходит от фамилии ирландского математика Уильяма Роуэна Гамильтона.

Его спектр — это множество возможных значений при измерении полной энергии системы. Спектр гамильтониана может быть дискретным или непрерывным. Также может быть ситуация (например, для кулоновского потенциала), когда спектр состоит из дискретной и непрерывной части.

Так как энергия — вещественная величина, гамильтониан является самосопряжённым оператором.

Уравнение Шрёдингера[править | править код]

Гамильтониан генерирует временную эволюцию квантовых состояний. Если  — состояние системы в момент времени t, то

Это уравнение называется уравнением Шрёдингера (оно выглядит так же, как и уравнение Гамильтона — Якоби в классической механике). Зная состояние в начальный момент времени (t = 0), мы можем решить уравнение Шрёдингера и получить вектор состояния в любой последующий момент времени. В частности, если H не зависит от времени, то

Оператор экспоненты в правой части уравнения Шрёдингера определяется через степенной ряд по H.

По свойству *-гомоморфизма, оператор

унитарен. Это оператор временной эволюции, или пропагатор замкнутой квантовой системы.

Если гамильтониан не зависит от времени, {U(t)} образует однопараметрическую группу; отсюда следует принцип детального равновесия.

Выражения для гамильтониана в координатном представлении[править | править код]

Свободная частица[править | править код]

Если у частицы нет потенциальной энергии, то гамильтониан самый простой. Для одного измерения:

и для трёх измерений:

Потенциальная яма[править | править код]

Для частицы в постоянном потенциале V = V₀ (нет зависимости от координаты и времени) в одном измерении гамильтониан такой:

В трёх измерениях:

Простой гармонический осциллятор[править | править код]

Для простого гармонического осциллятора в одном измерении потенциал зависит от координаты (но не от времени) как

где угловая частота коэффициент упругости k и масса m осциллятора удовлетворяют соотношению

поэтому гамильтониан имеет вид

Для трёх измерений гамильтониан принимает вид

где трёхмерный радиус-вектор r, его модуль определяется так:

Полный гамильтониан — это сумма одномерных гамильтонианов:

В квантовой теории поля[править | править код]

В классической теории поля роль обобщённых координат играют функции поля в каждой точке пространства-времени, в квантовой теории поля они становятся операторами. Для системы взаимодействующих полей гамильтониан представляет собой сумму операторов энергии свободных полей и энергии их взаимодействия. В отличие от лагранжиана, гамильтониан не даёт явно релятивистски-инвариантного описания системы — энергия в разных инерциальных системах отсчёта различна, хотя для релятивистских систем эта инвариантность может быть доказана.

Ссылки[править | править код]

• Блохинцев Д. И. Основы квантовой механики. 5-е изд. Наука, 1976. — 664 с.
• Боум А. Квантовая механика: основы и приложения. М.: Мир, 1990. — 720 c.
• Дирак П. Принципы квантовой механики. 2-е изд. М.: Наука, 1979. — 480 с.
• Ландау, Л. Д., Лифшиц, Е. М. Квантовая механика (нерелятивистская теория). — Физматлит, 2008. — 800 с. — («Теоретическая физика», том III). — 3000 экз. — ISBN 978-5-9221-0530-9.

Напомним основные постулаты квантовой механики, связанные с эрмитовыми операторами:

1. Все величины, которые можно экспериментально измерить, в квантовой механике выражаются эрмитовыми операторами (матрицами).
2. Результатом измерения величины, описываемой оператором, может являться только одно из собственных значений данного оператора.
3. Собственные векторы эрмитовых операторов формируют базис по которому можно разложить исходный вектор состояния.
4. Вектор состояния, описывающий систему, после измерения коллапсирует в один из собственных векторов оператора измеряемой величины, причем в тот, который соответствует измеренному собственному значению.
5. Коэффициенты в разложении по базисным векторам исходного вектора состояния есть амплитуды вероятности при измерении обнаружить собственное значение, связанное с данным собственным вектором.

Оператор, связанный с измерением энергии, в квантовой механике называется оператором Гамильтона или Гамильтонианом. Конкретный вид матрицы Гамильтониана зависит от деталей рассматриваемой системы. Если это система с двумя состояниями типа кубита с двумя базисными векторами, то Гамильтониан имеет вид квадратной матрицы 2х2. В общем случае он может быть и бесконечномерной матрицей.

В классической механике энергия частицы складывается из кинетической ( displaystyle T) и потенциальной ( displaystyle V). Кинетическая энергия  равна:

( displaystyle T = frac{mv^2}{2}= frac{p^2}{2m}) где ( displaystyle p = mv) — импульс.

Квантовомеханический аналог получается простой заменой числового значения импульса на оператор:

( displaystyle hat{T} = frac{hat{p}^{2}}{2m} )

Сам оператор импульса в квантовомеханическом случае выражается через оператор взятия производной:

( displaystyle hat{p}=-i frac{d}{dx})

Мы получили оператор Гамильтона в координатном базисе:

( displaystyle hat{H} = -frac{1}{2m}frac{d^{2}}{dx^2}+V(x) )

Его собственные векторы также бесконечномерные — это функции от координаты x. Аппроксимируя вторую производную квадратной матрицей и прибавляя дискретизированную функцию потенциала ( displaystyle V) получим конечномерную матрицу, аппроксимирующую Гамильтониан:

( displaystyle hat{H}=-frac{1}{2m(Delta x)^2}begin{pmatrix}
-2+V(x_1)&1 &0 &…  \
1&-2+V(x_2) &1 &…  \
0&1 &-2+V(x_3) &… \
…&… &… &… &\
end{pmatrix})

Все что остается — это выбрать конкретный вид функции потенциала и найти на компьютере собственные векторы и собственные значения данной матрицы.

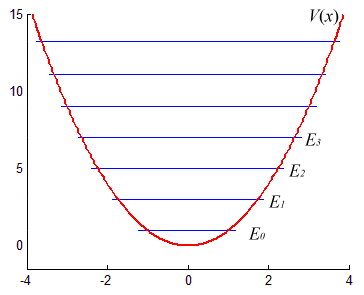
Давайте возьмем квадратичный потенциал ( displaystyle V = kx^2), отвечающий линейной силе в классическом случае (пружина, маятник). Система известна как гармонический осциллятор. Найдя собственные значения мы получим, что они отстоят друг от друга на одинаковом расстоянии, причем первый энергетический уровень не нулевой. Квантовый гармонический осциллятор, в отличие от классического, оказывается не может не совершать колебания (иметь нулевую энергию).

Мы наблюдаем эффект квантования. Измеренная энергия не может принимать любое значение, а только одно из разрешенных, дискретных.

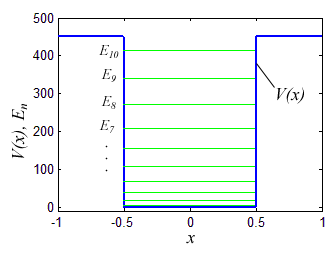
Численные величины собственных значений оператора Гамильтона зависят от вида функции потенциальной энергии. Возьмем, например, второй популярный пример — потенциал в виде прямоугольной ямы.

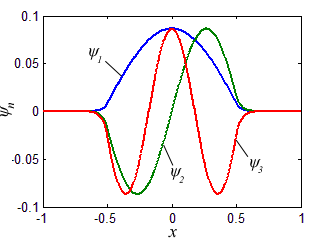
Каждому собственному значению (энергетическому уровню) соответствует собственный вектор — волновая функция в которую перейдет вектор состояния после измерения данного собственного значения (энергии). Несколько собственных функций, соответствующих нескольким первым собственным значениям Гамильтониана с прямоугольным потенциалом приведены на рисунке.

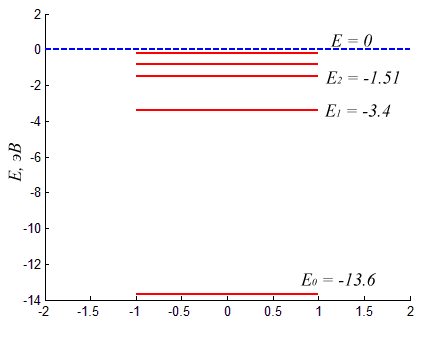
Из рисунка понятно почему квантовомеханический вектор состояния исторически получил название волновой функции. Аналогично можно найти и спектр атома водорода взяв за ( displaystyle V(x) ) кулоновский потенциал притяжения электрона и протона:

( displaystyle V(x) = -frac{e^2}{4 pi epsilon_0 |x|})

Оператор Гамильтона выделяется среди других эрмитовых операторов тем, что он является генератором эволюции во времени вектора состояния (поэтому он входит в уравнение Шредингера). В связи с этим ряд высказываний касательно времени можно сформулировать используя Гамильтониан. Так утверждение, что величина сохраняется означает ее неизменность с течением времени. На языке оператора Гамильтона данный факт преобразуется в:

Если данный эрмитов оператор коммутирует с Гамильтонианом, то физическая величина, представляемая данным оператором, сохраняется.

То есть, если ( displaystyle [A,H]=AH-HA=0), то ( displaystyle A) сохраняется.

Тривиальный случай — это закон сохранения энергии, поскольку любой оператор коммутирует сам с собой:

( displaystyle [H,H]=0 Rightarrow) энергия сохраняется.

Гамильтониан

В классической физике функцией Гамильтона ($Hleft(overrightarrow{r},overrightarrow{p}right)$) называют полную энергию, которая выражена через импульсы и координаты частицы. Для одной частицы полная энергия равна:

где $p$ — импульс частицы, $m$ — масса частицы, $U$ — потенциальная энергия частицы.

В квантовой механике функции Гамильтона соответствует оператор. Он получится, если в выражение (1) вместо вектора импульса подставить оператор $hat{p}$, равный:

То есть имеем:

где $-frac{{hbar }^2}{2m}triangle =-frac{{hbar }^2}{2m}(frac{{partial }^2}{partial x^2}+frac{{partial }^2}{partial y^2}+frac{{partial }^2}{partial z^2})$- оператор кинетической энергии.

Введенный гамильтониан дает возможность представиться уравнение Шредингера в компактном виде:

Определение энергетического спектра системы как задача на собственные значения оператора Гамильтона

Для стационарных процессов уравнение Шредингера можно записать в виде:

где $E_n$ — собственные значения энергии, $Psi_n$ — собственные функции, являющиеся решениями уравнения (5). Каждому собственному значению энергии соответствует одно или несколько состояний системы, которые описываются одной или несколькими собственными волновыми функциями. В том случае, если одному уровню энергии соответствует несколько собственных функций или состояний, то такие уровни именуются вырожденными. Количество состояний, соответствующих одной энергии называют кратностью вырождения (статистическим весом $g(E)).$

Задача поиска собственных значений и собственных функций оператора Гамильтона самая важная среди задач на собственные значения и собственные функции операторов физических величин. Данная задача имеет название: стационарное уравнение Шредингера.

Существенный вклад в разнообразие в эту задачу вносит вид потенциальной энергии, которая входит в гамильтониан. Энергетический спектр может быть дискретным, непрерывным, а может представлять собой часть дискретных уровней, а часть иметь непрерывного спектра.

«Гамильтониан» 👇

Известный набор собственных состояний Гамильтона полезен для решения уравнения (4). Допустим, что в начальный момент времени система пребывает в состоянии $varphi left(overrightarrow{r}right):$

Представим решение уравнения (5) в виде разложения в ряд по собственным функциям ($Psi_n(overrightarrow{r})$) оператора Гамильтона (данное разложение является всегда возможным и единственным):

где $C_n$ — постоянные коэффициенты разложения. Подставим выражение (7) в уравнение (5) получаем:

Примем во внимание то, что $Psi_n$ — собственное состояние оператора Гамильтона с собственным значением $E_n$ преобразуем выражение (8) к виду:

Равенство (9) выполняется, если:

Решением дифференциального уравнения (10) служит:

Коэффициенты $C_n$ определяют по волновой функции при $t=0 (6)$:

Из выражения (12) найдем:

Учтем, что при $T_nleft(t=0right)=1. $Следовательно, решением нестационарного уравнения Шредингера с начальным условием (6) является выражение:

Формула (14) описывает эволюцию собственного состояния оператора Гамильтона с течением времени. В нашем случае плотность вероятности не зависит от времени и ${left|Psi(overrightarrow{r},t)right|}^2={left|Psi_n(overrightarrow{r})right|}^2$. В связи с этим собственные состояния оператора Гамильтона именуют стационарными. Постоянными во времени являются средние значения физических величин.

И так, если Гамильтониан не зависит в явном виде от времени, то полную волновую функцию ($Psileft(overrightarrow{r,} tright)$), которая характеризует состояние системы можно представить как произведение координатной части $Psileft(overrightarrow{r} right)$ и экспоненты $e^{-frac{i}{hbar }E_nt}.$

From Wikipedia, the free encyclopedia

The Hamiltonian is a function used to solve a problem of optimal control for a dynamical system. It can be understood as an instantaneous increment of the Lagrangian expression of the problem that is to be optimized over a certain time period.^[1] Inspired by, but distinct from, the Hamiltonian of classical mechanics, the Hamiltonian of optimal control theory was developed by Lev Pontryagin as part of his maximum principle.^[2] Pontryagin proved that a necessary condition for solving the optimal control problem is that the control should be chosen so as to optimize the Hamiltonian.^[3]

Problem statement and definition of the Hamiltonian[edit]

Consider a dynamical system of first-order differential equations

where denotes a vector of state variables, and a vector of control variables. Once initial conditions and controls are specified, a solution to the differential equations, called a trajectory , can be found. The problem of optimal control is to choose (from some set ) so that maximizes or minimizes a certain objective function between an initial time and a terminal time (where may be infinity). Specifically, the goal is to optimize a performance index at each point in time,

subject to the above equations of motion of the state variables. The solution method involves defining an ancillary function known as the control Hamiltonian

which combines the objective function and the state equations much like a Lagrangian in a static optimization problem, only that the multipliers , referred to as costate variables, are functions of time rather than constants.

The goal is to find an optimal control policy function and, with it, an optimal trajectory of the state variable , which by Pontryagin’s maximum principle are the arguments that maximize the Hamiltonian,

for all

The first-order necessary conditions for a maximum are given by

which is the maximum principle,

which generates the state transition function ,

which generates

the latter of which are referred to as the costate equations. Together, the state and costate equations describe the Hamiltonian dynamical system (again analogous to but distinct from the Hamiltonian system in physics), the solution of which involves a two-point boundary value problem, given that there are boundary conditions involving two different points in time, the initial time (the differential equations for the state variables), and the terminal time (the differential equations for the costate variables; unless a final function is specified, the boundary conditions are , or for infinite time horizons).^[4]

A sufficient condition for a maximum is the concavity of the Hamiltonian evaluated at the solution, i.e.

where is the optimal control, and is resulting optimal trajectory for the state variable.^[5] Alternatively, by a result due to Olvi L. Mangasarian, the necessary conditions are sufficient if the functions and are both concave in and .^[6]

Derivation from the Lagrangian[edit]

A constrained optimization problem as the one stated above usually suggests a Lagrangian expression, specifically

where compares to the Lagrange multiplier in a static optimization problem but is now, as noted above, a function of time. In order to eliminate , the last term on the right-hand side can be rewritten using integration by parts, such that

which can be substituted back into the Lagrangian expression to give

To derive the first-order conditions for an optimum, assume that the solution has been found and the Lagrangian is maximized. Then any perturbation to or must cause the value of the Lagrangian to decline. Specifically, the total derivative of obeys

For this expression to equal zero necessitates the following optimality conditions:

If both the initial value and terminal value are fixed, i.e. , no conditions on and are needed. If the terminal value is free, as is often the case, the additional condition is necessary for optimality. The latter is called a transversality condition for a fixed horizon problem.^[7]

It can be seen that the necessary conditions are identical to the ones stated above for the Hamiltonian. Thus the Hamiltonian can be understood as a device to generate the first-order necessary conditions.^[8]

The Hamiltonian in discrete time[edit]

When the problem is formulated in discrete time, the Hamiltonian is defined as:

and the costate equations are

(Note that the discrete time Hamiltonian at time involves the costate variable at time ^[9] This small detail is essential so that when we differentiate with respect to we get a term involving on the right hand side of the costate equations. Using a wrong convention here can lead to incorrect results, i.e. a costate equation which is not a backwards difference equation).

Behavior of the Hamiltonian over time[edit]

From Pontryagin’s maximum principle, special conditions for the Hamiltonian can be derived.^[10] When the final time is fixed and the Hamiltonian does not depend explicitly on time , then:^[11]

or if the terminal time is free, then:

Further, if the terminal time tends to infinity, a transversality condition on the Hamiltonian applies.^[12]

The Hamiltonian of control compared to the Hamiltonian of mechanics[edit]

William Rowan Hamilton defined the Hamiltonian for describing the mechanics of a system. It is a function of three variables:

where is the Lagrangian, the extremizing of which determines the dynamics (not the Lagrangian defined above), is the state variable and is its time derivative.

is the so-called “conjugate momentum”, defined by

Hamilton then formulated his equations to describe the dynamics of the system as

The Hamiltonian of control theory describes not the dynamics of a system but conditions for extremizing some scalar function thereof (the Lagrangian) with respect to a control variable . As normally defined, it is a function of 4 variables

where is the state variable and is the control variable with respect to that which we are extremizing.

The associated conditions for a maximum are

This definition agrees with that given by the article by Sussmann and Willems.^[13] (see p. 39, equation 14). Sussmann and Willems show how the control Hamiltonian can be used in dynamics e.g. for the brachistochrone problem, but do not mention the prior work of Carathéodory on this approach.^[14]

Current value and present value Hamiltonian[edit]

In economics, the objective function in dynamic optimization problems often depends directly on time only through exponential discounting, such that it takes the form

where is referred to as the instantaneous utility function, or felicity function.^[15] This allows a redefinition of the Hamiltonian as where

which is referred to as the current value Hamiltonian, in contrast to the present value Hamiltonian defined in the first section. Most notably the costate variables are redefined as , which leads to modified first-order conditions.

,

which follows immediately from the product rule. Economically, represent current-valued shadow prices for the capital goods .

Example: Ramsey–Cass–Koopmans model[edit]

In economics, the Ramsey–Cass–Koopmans model is used to determine an optimal savings behavior for an economy. The objective function is the social welfare function,

to be maximized by choice of an optimal consumption path . The function indicates the utility the representative agent of consuming at any given point in time. The factor represents discounting. The maximization problem is subject to the following differential equation for capital intensity, describing the time evolution of capital per effective worker:

where is period t consumption, is period t capital per worker (with ), is period t production, is the population growth rate, is the capital depreciation rate, the agent discounts future utility at rate , with and .

Here, is the state variable which evolves according to the above equation, and is the control variable. The Hamiltonian becomes

The optimality conditions are

in addition to the transversality condition . If we let , then log-differentiating the first optimality condition with respect to yields

Inserting this equation into the second optimality condition yields

which is known as the Keynes–Ramsey rule, which gives a condition for consumption in every period which, if followed, ensures maximum lifetime utility.

References[edit]

Further reading[edit]

• Léonard, Daniel; Long, Ngo Van (1992). “The Maximum Principle”. Optimal Control Theory and Static Optimization in Economics. New York: Cambridge University Press. pp. 127–168. ISBN 0-521-33158-7.
• Takayama, Akira (1985). “Developments of Optimal Control Theory and Its Applications”. Mathematical Economics (2nd ed.). New York: Cambridge University Press. pp. 600–719. ISBN 0-521-31498-4.
• Wulwick, Nancy (1995). “The Hamiltonian Formalism and Optimal Growth Theory”. In Rima, I. H. (ed.). Measurement, Quantification, and Economic Analysis. London: Routledge. ISBN 978-0-415-08915-9.