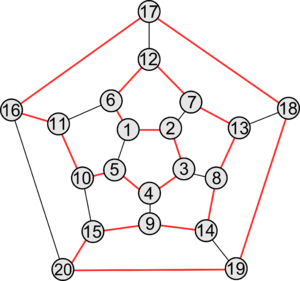
Граф додекаэдра с выделенным циклом Гамильтона
Содержание
- 1 Основные определения
- 2 Достаточные условия гамильтоновости графа
- 2.1 Теорема Дирака
- 2.2 Теорема Оре
- 2.3 Теорема Поша
- 2.4 Теорема Редеи-Камиона
- 2.5 Теорема Гуйя-Ури
- 2.6 Теорема Хватала
- 3 Задача о коммивояжере
- 3.1 Описание задачи
- 3.2 Варианты решения
- 3.2.1 Перебор перестановок
- 3.2.2 Динамическое программирование по подмножествам (по маскам)
- 3.2.3 Поиск любого гамильтонова пути методом динамического программирования
- 3.3 Псевдокод
- 3.4 Алгоритм нахождения гамильтонова цикла
- 3.5 Алгоритм нахождения гамильтонова пути
- 4 См. также
- 5 Источники информации
Основные определения
| Определение: |
| Гамильтоновым путём (англ. Hamiltonian path) называется простой путь, проходящий через каждую вершину графа ровно один раз. |
| Определение: |
| Гамильтоновым циклом (англ. Hamiltonian cycle) называют замкнутый гамильтонов путь. |
| Определение: |
| Граф называется полугамильтоновым (англ. Semihamiltonian graph), если он содержит гамильтонов путь. |
| Определение: |
| Граф называется гамильтоновым (англ. Hamiltonian graph), если он содержит гамильтонов цикл. |
Очевидно, что любой гамильтонов граф также и полугамильтонов.
Достаточные условия гамильтоновости графа
Теорема Дирака
| Теорема: |
|
Если и для любой вершины неориентированного графа , то — гамильтонов граф. |
Теорема Оре
| Теорема: |
|
Если и для любых двух различных несмежных вершин и неориентированного графа , то — гамильтонов граф. |
Теорема Поша
| Теорема (Поша): |
|
Пусть граф имеет вершин и выполнены следующие два условия:
тогда — гамильтонов граф. |
Теорема Редеи-Камиона
| Теорема: |
|
Любой сильносвязный турнир — гамильтонов. |
Теорема Гуйя-Ури
| Теорема (Ghouila-Houri): |
|
Пусть — сильносвязный ориентированный граф. |
Теорема Хватала
| Теорема (Хватал): |
|
Пусть:
Тогда если верна импликация: то граф гамильтонов. |
Задача о коммивояжере
Рассмотрим алгоритм нахождения гамильтонова цикла на примере задачи о коммивояжёре.
Описание задачи
| Задача: |
| Задача о коммивояжере (англ. Travelling salesman problem, TSP) — задача, в которой коммивояжер должен посетить городов, побывав в каждом из них ровно по одному разу и завершив путешествие в том городе, с которого он начал. В какой последовательности ему нужно обходить города, чтобы общая длина его пути была наименьшей? |
Варианты решения
Задача о коммивояжере относится к классу NP-полных задач. Рассмотрим два варианта решения с экспоненциальным временем работы.
Перебор перестановок
Можно решить задачу перебором всевозможных перестановок. Для этого нужно сгенерировать все всевозможных перестановок вершин исходного графа, подсчитать для каждой перестановки длину маршрута и выбрать минимальный из них. Но тогда задача оказывается неосуществимой даже для достаточно небольших . Сложность алгоритма .
Динамическое программирование по подмножествам (по маскам)
Задача о коммивояжере представляет собой поиск кратчайшего гамильтонова цикла в графе.
Зафиксируем начальную вершину и будем искать гамильтонов цикл наименьшей стоимости — путь от до , проходящий по всем вершинам (кроме первоначальной) один раз. Т.к. искомый цикл проходит через каждую вершину, то выбор не имеет значения. Поэтому будем считать .
Подмножества вершин будем кодировать битовыми векторами, обозначим значение -ого бита в векторе .
Обозначим как наименьшую стоимость пути из вершины в вершину , проходящую (не считая вершины ) единожды по всем тем и только тем вершинам , для которых (т.е. уже найденный оптимальный путь от -ой вершины до -ой, проходящий через те вершины, где . Если ,то эти вершины еще не посещены).
Алгоритм поиска цикла будет выглядеть следующим образом:
- Начальное состояние — когда находимся в -й вершине, ни одна вершина не посещена, а пройденный путь равен (т.е. и ).
- Для остальных состояний ( или ) перебираем все возможные переходы в -ую вершину из любой посещенной ранее и выбираем минимальный результат.
- Если возможные переходы отсутствуют, решения для данной подзадачи не существует (обозначим ответ для такой подзадачи как ).
Стоимостью минимального гамильтонова цикла в исходном графе будет значение — стоимость пути из -й вершины в -ю, при необходимости посетить все вершины. Данное решение требует памяти и времени.
Для того, чтобы восстановить сам путь, воспользуемся соотношением , которое выполняется для всех ребер, входящих в минимальный цикл . Начнем с состояния , , найдем вершину , для которой выполняется указанное соотношение, добавим в ответ, пересчитаем текущее состояние как , . Процесс заканчивается в состоянии , .
Поиск любого гамильтонова пути методом динамического программирования
Пусть содержит булево значение — существует ли в подмножестве гамильтонов путь, заканчивающийся в вершине .
Сама динамика будет такая:
Это решение требует памяти и времени. Эту оценку можно улучшить, если изменить динамику следующим образом.
Пусть теперь хранит маску подмножества всех вершин, для которых существует гамильтонов путь в подмножестве , заканчивающихся в этой вершине. Другими словами, сожмем предыдущую динамику: будет равно . Для графа выпишем масок , для каждой вершины задающие множество вершин, которые связаны ребром с данной вершиной. То есть .
Тогда динамика перепишется следующим образом:
Особое внимание следует уделить выражению . Первая часть выражения содержит подмножество вершин, для которых существует гамильтонов путь, заканчивающихся в соответствующих вершинах в подмножестве без вершины , а вторая — подмножество вершин, связанных с ребром. Если эти множества пересекаются хотя бы по одной вершине (их не равен ), то, как нетрудно понять, в существует гамильтонов путь, заканчивающийся в вершине .
Окончательная проверка состоит в сравнении c .
Это решение использует памяти и имеет асимптотику .
Псевдокод
Прежде чем писать код, скажем пару слов о порядке обхода состояний. Обозначим за количество единиц в маске (иначе говоря количество пройденных вершин не считая текущей). Тогда, поскольку при рассмотрении состояния мы смотрим на состояния
, и , то состояния с большим должны быть посещены позже, чтобы к моменту вычисления текущего состояния были вычислены все те, которые используются для его подсчёта.
Однако если использовать рекурсию, об этом можно не беспокоиться (и сэкономить немало кода, времени и памяти).
// все переменные используются из описания алгоритма, = бесконечность
function findCheapest(i, mask):
if d[i][mask] !=
return d[i][mask]
for j = 0 .. n - 1
if w(i, j) существует and j-ый бит mask == 1
d[i][mask] = min(d[i][mask], findCheapest(j, mask - ) + w(i, j))
return d[i][mask]
function start():
for i = 0 .. n - 1
for mask = 0 .. - 1
d[i][mask] =
d[0][0] = 0
ans = findCheapest(0, - 1)
return ans
Дальше ищем сам цикл:
function findWay():
i = 0
mask = - 1
path.push(0)
while mask != 0
for j = 0 .. n - 1
if w(i, j) существует and j-ый бит mask == 1 and d[i][mask] == d[j][mask - ] + w(i, j)
path.push(j)
i = j
mask = mask -
continue
Алгоритм нахождения гамильтонова цикла
Алгоритм нахождения гамильтонова цикла легко получить слегка изменив алгоритм нахождения минимального гамильтонова цикла.
В массиве мы хранили расстояния, но сейчас нас не интересует какой длины будет это расстояние, так как главной задачей является нахождение цикла. В этом массиве мы теперь просто храним посещение вершин. И каждый раз, когда при запуске находим непосещенную вершину, то запускаем функцию рекурсивно от нее. Если она возвращает , то есть до вершины можно добраться, то записываем, что мы можем посетить вершину. Проходы так же осуществляются по рёбрам.
Алгоритм нахождения гамильтонова пути
Алгоритм нахождения гамильтонова пути легко получить, используя алгоритм нахождения гамильтонова цикла. Нужно добавить в граф еще одну вершину и ребра от нее до всех остальных вершин и из всех остальных вершин до неё. И далее запустить алгоритм поиска цикла от новой вершины. В восстановлении пути учтем, что эта вершина лишняя, и не будем записывать её в путь.
См. также
- Кратчайший путь в ациклическом графе
- Задача о наибольшей общей подпоследовательности
- Задача о наибольшей возрастающей подпоследовательности
- Задача о рюкзаке
- Алгоритм нахождения Гамильтонова цикла в условиях теорем Дирака и Оре
Источники информации
- Харари Ф. Теория графов: Пер. с англ. / Предисл. В. П. Козырева; Под ред. Г.П.Гаврилова. Изд. 4-е. — М.: Книжный дом “ЛИБРОКОМ”, 2009. — 60 с.
- Седжвик Р. Фундаментальные алгоритмы на C++. Алгоритмы на графах. — СПб: ООО «ДиаСофтЮП», 2002.
- Гамильтонов граф
- Задача коммивояжера в русской википедии
- Задача коммивояжера в немецкой википедии
- Романовский И. В. Дискретный анализ. СПб.: Невский Диалект; БХВ-Петербург, 2003. ISBN 5-7940-0114-3
- Кормен Т., Лейзерсон Ч., Ривест Р., Штайн К. Алгоритмы: построение и анализ, 2-е издание. М.: Издательский дом “Вильямс”, 2005. ISBN 5-8459-0857-4
Задача о гамильтоновом пути и задача о гамильтоновом цикле — это задачи определения, существует ли гамильтонов путь или гамильтонов цикл в заданном графе (ориентированном или неориентированном). Обе задачи NP-полны[1].
Связь задач о гамильтоновом пути и гамильтоновом цикле[править | править код]
Существует простое отношение между задачами нахождения гамильтонова пути и нахождения гамильтонова цикла. В одном направлении задача о гамильтоновом пути для графа эквивалентна задаче о гамильтоновом цикле в графе H, полученного из графа G путём добавления новой вершины и соединения её со всеми вершинами графа G. Таким образом, поиск гамильтонова пути не может быть существенно медленнее (в худшем случае, как функция числа вершин), чем поиск гамильтонова цикла.
В обратном направлении задача о гамильтоновом цикле для графа G эквивалентна задаче о гамильтоновом пути в графе H, полученном копированием одной вершины v графа G (в v’), то есть вершина v’ будет иметь ту же окрестность, что и v, и добавлением двух вспомогательных вершин степени один, одна из которых соединена с v, а другая с v’[2].
Задача о гамильтоновом цикле является также частным случаем задачи коммивояжёра, полученной установкой всех расстояний между двумя пунктами в единицу, если они смежны, и двум в противном случае. После решения задачи коммивояжёра следует проверить, что полное расстояние равно n (если так, маршрут является гамильтоновым циклом, если же гамильтонова цикла нет, кратчайший путь будет длиннее этой величины).
Алгоритмы[править | править код]
Есть n! различных последовательностей вершин, которые могут быть гамильтоновыми путями в заданном графе с n вершинами (и их столько в полном графе), так что алгоритм полного перебора, который перебирает все возможные последовательности, был бы очень медленным.
Ранний точный алгоритм нахождения гамильтонова цикла в ориентированном графе был алгоритмом перебора (алгоритм Мартелло)[3].
Процедура поиска Франка Рубина[4] разбивает рёбра графа на три класса — те, которые должны быть на пути, те, которые пути принадлежать не могут, и рёбра, для которых решение не принято. В процессе поиска набор правил принятия решений классифицирует рёбра, для которых решение не принято, и определяет, остановиться или продолжить поиск. Алгоритм разбивает граф на компоненты, которые могут быть обработаны отдельно.
Для решения задачи за время 

Андреас Бьёрклунд даёт альтернативный подход, использующий принцип включения/исключения для сокращения числа перебираемых гамильтоновых циклов и задача подсчёта циклов может быть решена путём вычисления определителя некоторой матрицы.
Используя этот метод, он показал, как решить задачу о гамильтоновом цикле для произвольных графов с n вершинами с помощью алгоритма Монте-Карло за время 

Для графов с максимальной степенью три аккуратный поиск с возвратом может найти гамильтонов цикл (если таковой существует) за время 
Гамильтоновы пути и циклы можно найти с помощью SAT решателя.
Ввиду сложности решения задач о гамильтоновом пути и цикле на обычных компьютерах, они изучались для нестандартных моделей вычислений. Например, Леонард Адлеман показал, что задачи о гамильтоновом пути могут быть решены с помощью ДНК-компьютера. Используя параллелелизм, свойственный химическим реакциям, задача может быть решена с помощью нескольких шагов химических реакций, линейно зависящих от числа вершин графа. Однако это требует факториальное число молекул ДНК, участвующих в реакции[9].
Оптическое решение гамильтоновой задачи предложил Ольтеан[10]. Идея заключается в создании подобной графу структуры из оптических кабелей и расщепителей луча, через которую прогоняется луч в порядке решения задачи. Слабым моментом этого подхода является экспоненциальный рост требуемой энергии от числа узлов.
Сложность[править | править код]
Задача нахождения гамильтонова цикла или пути имеет сложность FNP[en]. Аналогичная задача разрешимости — проверить, существует ли гамильтонов цикл или путь. Ориентированные и неориентированные задачи о гамильтоновом цикле являлись двумя из 21 NP-полных задач Карпа. Они остаются NP-полными даже для неориентированных планарных графов максимальной степени три[11], для ориентированных планарных графов с полустепенью входа и выхода, не превосходящими двух[12], для неориентированных планарных 3-регулярных двудольных графов без мостов, для 3-связных 3-регулярных двудольных графов[13], подграфов квадратной решётки[14] и для кубических подграфов квадратной решётки[15].
Однако 4-связные планарные графы всегда гамильтоновы, согласно результату Татта, а задача нахождения гамильтонова цикла в этих графах может быть выполнена за линейное время[16] путём вычисления так называемого пути Татта. Татт доказал этот результат, показав, что любой 2-связный планарный граф содержит путь Татта. Пути Татта, в свою очередь, можно вычислить за квадратичное время даже для 2-связных планарных графов[17], что может быть использовано для поиска гамильтоновых циклов и длинных циклов в обобщённых планарных графах.
Складывая всё вместе, остаётся открытой задача, всегда ли 3-связные 3-регулярные двудольные планарные графы должны содержать гамильтонов цикл и если должны, задача, ограниченная этими графами, не будет NP-полной (см. статью «Гипотеза Барнетта»).
В графах в которых все вершины имеют нечётную степень, довод, связанный с леммой о рукопожатиях, показывает, что число гамильтоновых циклов через фиксированное ребро всегда чётно, так что если дан один гамильтонов цикл, то и другой должен существовать[18]. Однако поиск этого второго цикла не выглядит как простая вычислительная задача. Пападимитриу определил класс сложности PPA[en], чтобы собрать вместе задачи, подобные этой[19].
Примечания[править | править код]
- ↑ Garey, Johnson, 1979, с. 199—200, A1.3: GT37 – 39.
- ↑ graph theory – Reduction from Hamiltonian cycle to Hamiltonian path – Mathematics Stack Exchange. Дата обращения: 18 февраля 2019. Архивировано 23 апреля 2019 года.
- ↑ Martello, 1983, с. 131–138.
- ↑ Rubin, 1974, с. 576–80.
- ↑ Bellman, 1962, с. 61–63.
- ↑ Held, Karp, 1962, с. 196–210.
- ↑ Björklund, 2010, с. 173–182.
- ↑ Iwama, Nakashima, 2007, с. 108–117.
- ↑ Adleman, 1994, с. 1021–1024.
- ↑ Oltean, 2006, с. 217–227.
- ↑ Garey, Johnson, Stockmeyer, 1974, с. 47–63.
- ↑ Plesńik, 1979, с. 199–201.
- ↑ Akiyama, Nishizeki, Saito, 1980–1981, с. 73–76.
- ↑ Itai, Papadimitriou, Szwarcfiter, 1982, с. 676–686.
- ↑ Buro, 2000, с. 250–261.
- ↑ Chiba, Nishizeki, 1989, с. 187–211.
- ↑ Schmid, Schmidt, 2018.
- ↑ Thomason, 1978, с. 259–268.
- ↑ Papadimitriou, 1994, с. 498–532.
Литература[править | править код]
- Michael R. Garey, David S. Johnson. [Computers and Intractability: A Guide to the Theory of NP-Completeness Computers and Intractability: A Guide to the Theory of NP-Completeness]. — W.H. Freeman, 1979. — ISBN 978-0-7167-1045-5.
- Silvano Martello. An Enumerative Algorithm for Finding Hamiltonian Circuits in a Directed Graph // ACM Transactions on Mathematical Software. — 1983. — Т. 9, вып. 1. — С. 131–138. — doi:10.1145/356022.356030.
- Frank Rubin. A Search Procedure for Hamilton Paths and Circuits // Journal of the ACM. — 1974. — Т. 21, вып. 4. — С. 576–80. — doi:10.1145/321850.321854.
- Richard Bellman. Dynamic programming treatment of the travelling salesman problem // Journal of the ACM. — 1962. — Т. 9. — С. 61–63. — doi:10.1145/321105.321111.
- Held, Karp. A dynamic programming approach to sequencing problems // J. SIAM. — 1962. — Т. 10, вып. 1. — С. 196–210. — doi:10.1137/0110015.
- Andreas Björklund. Determinant sums for undirected Hamiltonicity // Proc. 51st IEEE Symposium on Foundations of Computer Science (FOCS ’10). — 2010. — С. 173–182. — ISBN 978-1-4244-8525-3. — doi:10.1109/FOCS.2010.24.
- Kazuo Iwama, Takuya Nakashima. An improved exact algorithm for cubic graph TSP // Proc. 13th Annual International Conference on Computing and Combinatorics (COCOON 2007). — 2007. — Т. 4598. — С. 108–117. — (Lecture Notes in Computer Science). — ISBN 978-3-540-73544-1. — doi:10.1007/978-3-540-73545-8_13.
- Leonard Adleman. Molecular computation of solutions to combinatorial problems // Science. — 1994. — Ноябрь (т. 266, вып. 5187). — С. 1021–1024. — doi:10.1126/science.7973651. — Bibcode: 1994Sci…266.1021A. — PMID 7973651. — JSTOR 2885489.
- Mihai Oltean. A light-based device for solving the Hamiltonian path problem // Unconventional Computing. — Springer LNCS 4135, 2006. — doi:10.1007/11839132_18.
- Michael Garey, David S. Johnson, Larry Stockmeyer. Some simplified NP-complete problems // Proc. 6th ACM Symposium on Theory of Computing (STOC ’74). — 1974. — С. 47–63. — doi:10.1145/800119.803884.
- Plesńik J. The NP-completeness of the Hamiltonian cycle problem in planar digraphs with degree bound two // Information Processing Letters. — 1979. — Т. 8, вып. 4. — С. 199–201. — doi:10.1016/0020-0190(79)90023-1.
- Takanori Akiyama, Takao Nishizeki, Nobuji Saito. NP-completeness of the Hamiltonian cycle problem for bipartite graphs // Journal of Information Processing. — 1980–1981. — Т. 3, вып. 2. — С. 73–76.
- Alon Itai, Christos Papadimitriou, Jayme Szwarcfiter. Hamilton Paths in Grid Graphs // SIAM Journal on Computing. — 1982. — Т. 4, вып. 11. — С. 676–686. — doi:10.1137/0211056.
- Michael Buro. Simple Amazons endgames and their connection to Hamilton circuits in cubic subgrid graphs // Conference on Computers and Games. — 2000. — Т. 2063. — С. 250–261. — (Lecture Notes in Computer Science). — ISBN 978-3-540-43080-3. — doi:10.1007/3-540-45579-5_17.
- Norishige Chiba, Takao Nishizeki. The Hamiltonian cycle problem is linear-time solvable for 4-connected planar graphs // Journal of Algorithms. — 1989. — Т. 10, вып. 2. — С. 187–211. — doi:10.1016/0196-6774(89)90012-6.
- Andreas Schmid, Jens M. Schmidt. Computing Tutte Paths // Proceedings of the 45th International Colloquium on Automata, Languages and Programming (ICALP’18), to appear.. — 2018.
- Thomason A. G. Hamiltonian cycles and uniquely edge colourable graphs // Advances in Graph Theory (Cambridge Combinatorial Conf., Trinity College, Cambridge, 1977). — 1978. — Т. 3. — С. 259–268. — (Annals of Discrete Mathematics). — ISBN 9780720408430. — doi:10.1016/S0167-5060(08)70511-9.
- Christos H. Papadimitriou. On the complexity of the parity argument and other inefficient proofs of existence // Journal of Computer and System Sciences. — 1994. — Т. 48, вып. 3. — С. 498–532. — doi:10.1016/S0022-0000(05)80063-7.
Время на прочтение
4 мин
Количество просмотров 76K
1. Постановка задачи
Полный взвешенный граф из 500 вершин задан матрицей смежности.
Необходимо найти гамильтонов цикл в этом графе как можно меньшей суммарной стоимости.
2. Решение
1. Жадный алгоритм
Тут все просто, запускаемся из любой вершины, выбираем минимальную стоимость ребра из тех, по которым можно идти, переходим в вершину x, нашу вершину вычеркиваем, в вершине х делаем тоже самое и т.д.
Просто и быстро.
Однако ответ может быть очень и очень далеким от правды.
Жадина хорошо работает на случайном графе, однако тут мы ничего про граф не знаем.
Поэтому идем дальше.
2. Честный перебор
Задача коммивояжера, она же поиск гамильтонова цикла минимальной суммарной стоимости — NP-тяжелая, так что полный перебор для такого графа может продлиться вечность, поэтому данная идея не подходит.
3. Метод ветвей и границ
Вторая идея, пришедшая в голову — использовать улучшенный перебор, откидывая на каждом шаге алгоритма явно неоптимальные решения.
Один из наиболее эффективных алгоритмов такого рода является метод ветвей и границ («поиск с возвратом», «backtracking»), разработанный Литтлом, Мерти, Суини, Кэрелом в 1963 г.
Пусть S(0) — множество всех допустимых замкнутых маршрутов задачи о коммивояжере с n городами и матрицей затрат c.
Метод Литтла основан на разбиении множества на два непересекающихся подмножества и на вычислении оценок каждого из них. Далее подмножество с минимальной оценкой (стоимостью) разбивается на два подмножества и вычисляются их оценки. На каждом шаге выбирается подмножество с наименьшей из всех полученных на этом шаге оценок и производится его разбиение на два подмножества. В конце концов получаем подмножество, содержащее один цикл (замкнутый маршрут, удовлетворяющий наложенным ограничениям), стоимость которого минимальна.
Алгоритм состоит из двух этапов:
Первый этап
Приведение матрицы затрат и вычисление нижней оценки стоимости маршрута r.
1. Вычисляем наименьший элемент в каждой строке(константа приведения для строки)
2. Переходим к новой матрице затрат, вычитая из каждой строки ее константу приведения
3. Вычисляем наименьший элемент в каждом столбце(константа приведения для столбца)
4. Переходим к новой матрице затрат, вычитая из каждого столбца его константу приведения.
Как результат имеем матрицу затрат, в которой в каждой строчке и в каждом столбце имеется хотя бы один нулевой элемент.
5. Вычисляем r как сумму констант приведения для столбцов и строк.
Второй (основной) этап
1.Вычисление штрафа за неиспользование для каждого нулевого элемента приведенной матрицы затрат.
Штраф за неиспользование означает элемента с индексом (h,k) в матрице, означает, что это ребро не включается в наш маршрут, а значит минимальная стоимость «неиспользования» этого ребра равна сумме минимальных элементов в строке h и столбце k.
а) Ищем все нулевые элементы в приведенной матрице
б) Для каждого из них считаем его штраф за неиспользование.
в) Выбираем элемент, которому соответствует максимальный штраф
Почему максимальный? Потому что это означает, что исключение из маршрута этого ребра приведет к максимальному увеличению стоимости оптимального маршрута, который мы как раз и ищем.
2. Теперь наше множество S(0) разбиваем на два — Sw(содержащие ребро h,k) и Sw/o(не содержащие ребро h,k)
3. Вычисление оценок затрат для маршрутов, входящих в каждое из этих множеств.
а) Для множества Sw/o все просто: раз мы не берем ребро (h,k), то для него оценка затрат равна оценки затрат множества S(0) + штраф за неиспользование ребра (h,k)
б) При вычислении затрат для множества Sw примем во внимание, что раз ребро (h,k) входит в маршрут, то значит ребро (k,h) в маршрут входить не может, поэтому в матрице затрат пишем c(k,h)=infinity, а так как из пункта h мы «уже ушли», а в пункт k мы «уже пришли», то ни одно ребро, выходящее из h, и ни одно ребро, приходящее в k, уже использоваться не могут, поэтому вычеркиваем из матрицы затрат строку h и столбец k. После этого приводим матрицу, и тогда оценка затрат для Sw равна сумме оценки затрат для S(0) и r(h,k), где r(h,k) — сумма констант приведения для измененной матрицы затрат.
4. Из множеств Sw и Sw/o выбирается то, которое имеет наибольшую оценку.
Так продолжаем, пока в матрице затрат не останется одна невычеркнутая строка и один невычеркнутый столбец.
Теперь результаты.
Если на каждом шаге выбирать только из двух множеств(Sw и Swo) то алгоритм работает вполне вменяемое время, однако точность просто ужасна ( проигрывает ОЧЕНЬ много жадине из п.1)
Если же на каждом шаге выбирать лучшее множество из всех, полученных к этому шагу и не использовавшихся до этого,
то для маленьких графов(порядка 40-50) вершин, получается хорошая точность, но 500 вершин дождаться не удалось.
Поэтому в голову приходит следующая идея:
4. Метод ветвей и границ с эвристикой
Да, правда, почему бы нам не ввести эвристику? Ведь в алгоритме ветвей и границ мы фактически строим дерево, в узлах которого решаем брать ребро (x,y) или нет, и вешаем двух детей — Sw(x,y) и Sw/o(x,y). Но лучший вариант для следующей итерации выбираем только по оценке. Так давайте выбирать лучший не только по оценке, но и по глубине в дереве, т.к. чем глубже выбранный элемент, тем ближе он к концу подсчета. Тем самым мы сможем наконец дождаться ответа.
Первый и самый простой вариант эвристики cost=mark — k*depth. k подбираем в зависимости от среднего веса ребра так, чтобы все-таки глубина не играла определяющей роли. Так же добавим, например, что depth равно минимум b, т.е. если наша вершина находится на расстоянии q от корня, и q<b, то depth=b, иначе depth=q. В качестве b выбираем такое число, что до такой глубины честный алгоритм ветвей и границ ( без эвристики ) доходит за адекватное время. В моем случае было b=30.
Запускаем, ждем.
За ночь работы получаем ответ, который выигрывает у жадного алгоритма ~2%.
Мало, очень мало, учитывая, что жадный алгоритм работает пару секунд и пишется за 5 минут.
И теперь победитель:
Жадный алгоритм с локальным методом границ и ветвей
Алгоритм такой:
1.Запускаем жадный алгоритм, получаем некоторый маршрут.
2. Делим маршрут на несколько частей.
3.В каждой части делаем фиктивное ребро — из последней вершины маршрута в первую, которое трогать запрещается
4. На каждой из этих частей запускаем метод ветвей и границ, без эвристики.
5. Объединяем части, оптимизированные методом ветвей и границ, размыкая фиктивные ребра и соединяя последнюю вершину n-1 части с первой n части.
Как легко понять, этот алгоритм имеет несколько плюсов.
— честный метод ветвей и границ, без использования эвристики;
— легко параллелится, выигрываем во времени работы;
— жадный алгоритм говорит нам лишь части разбиений, после объединения мы используем только NUMBER_OF_PARTS-1 ребер, данных нам жадным алгоритмом, и не оптимизированных методом ветвей и границ.
Результат.
Время работы на 25 частях — 3 минуты, выигрываем у жадины ~7%
10 частей — 4 часа, выигрыш ~15%
продолжение
Если граф содержит срезанную вершину или срезанное ребро, то у него нет гамильтонова цикла. Когда срезанные вершины или ребра пересекаются, пропадает возможность вернуться, чтобы завершить цикл. Например:

На графике видно, что нет способа вернуться на другую сторону графа, когда мы пересекаем вершину
или ребро
.
Рассмотрим следующую теорему:
Если существует некоторое подмножество
вершин
такое, что у
больше компонент, чем у
вершин, то у
нет гамильтонова цикла
Например, мы можем попытаться удалить одну вершину, которая разбивает граф на два или более компонентов. Это будет вершина разреза. Или мы можем попытаться удалить две вершины, чтобы разбить граф на три или более компонентов. И так дальше по возрастанию.
Например, возьмем
. Три компоненты графа
показаны справа:

Число компонентов
больше, чем
, поэтому гамильтонова цикла не существует.
и
действуют как узкое место. Каждый раз, когда мы хотим покинуть одну из компонент
, мы должны использовать либо
, либо
. Таким образом, мы расходуем
и
и не можем завершить наше круговое путешествие.
Эта теорема дает необходимое, но не достаточное условие для гамильтонова цикла. Существует множество графов, которые удовлетворяют этому условию, но не имеют гамильтоновых циклов. Одним из таких примеров является граф Петерсена.
Существует противоположная теорема:
Если у
есть гамильтонов цикл, то для каждого подмножества
вершин число компонент
больше или равно
Такую теорему доказать немного проще. Основная идея состоит в том, что когда мы проходим через гамильтонов цикл в
и достигаем компоненты
, единственный способ достичь других вершин, не входящих в эту компоненту — это вернуться через
. Получается, у
должно быть столько же вершин, сколько и компонент
:

Другой пример приведен ниже. Четыре вершины удалены, и полученный граф имеет пять компонент, поэтому в нем нет гамильтонова цикла:

From Wikipedia, the free encyclopedia
This article is about the specific problem of determining whether a Hamiltonian path or cycle exists in a given graph. For the general graph theory concepts, see Hamiltonian path.
In the mathematical field of graph theory the Hamiltonian path problem and the Hamiltonian cycle problem are problems of determining whether a Hamiltonian path (a path in an undirected or directed graph that visits each vertex exactly once) or a Hamiltonian cycle exists in a given graph (whether directed or undirected). Both problems are NP-complete.[1]
The Hamiltonian cycle problem is a special case of the travelling salesman problem, obtained by setting the distance between two cities to one if they are adjacent and two otherwise, and verifying that the total distance travelled is equal to n (if so, the route is a Hamiltonian circuit; if there is no Hamiltonian circuit then the shortest route will be longer).
Reduction between the path problem and the cycle problem[edit]
The problems of finding a Hamiltonian path and a Hamiltonian cycle can be related as follows:
Algorithms[edit]
There are n! different sequences of vertices that might be Hamiltonian paths in a given n-vertex graph (and are, in a complete graph), so a brute force search algorithm that tests all possible sequences would be very slow.
An early exact algorithm for finding a Hamiltonian cycle on a directed graph was the enumerative algorithm of Martello.[3] A search procedure by Frank Rubin[4] divides the edges of the graph into three classes: those that must be in the path, those that cannot be in the path, and undecided. As the search proceeds, a set of decision rules classifies the undecided edges, and determines whether to halt or continue the search. The algorithm divides the graph into components that can be solved separately. Also, a dynamic programming algorithm of Bellman, Held, and Karp can be used to solve the problem in time O(n2 2n). In this method, one determines, for each set S of vertices and each vertex v in S, whether there is a path that covers exactly the vertices in S and ends at v. For each choice of S and v, a path exists for (S,v) if and only if v has a neighbor w such that a path exists for (S − v,w), which can be looked up from already-computed information in the dynamic program.[5][6]
Andreas Björklund provided an alternative approach using the inclusion–exclusion principle to reduce the problem of counting the number of Hamiltonian cycles to a simpler counting problem, of counting cycle covers, which can be solved by computing certain matrix determinants. Using this method, he showed how to solve the Hamiltonian cycle problem in arbitrary n-vertex graphs by a Monte Carlo algorithm in time O(1.657n); for bipartite graphs this algorithm can be further improved to time o(1.415n).[7]
For graphs of maximum degree three, a careful backtracking search can find a Hamiltonian cycle (if one exists) in time O(1.251n).[8]
Hamiltonian paths and cycles can be found using a SAT solver.
Because of the difficulty of solving the Hamiltonian path and cycle problems on conventional computers, they have also been studied in unconventional models of computing. For instance, Leonard Adleman showed that the Hamiltonian path problem may be solved using a DNA computer. Exploiting the parallelism inherent in chemical reactions, the problem may be solved using a number of chemical reaction steps linear in the number of vertices of the graph; however, it requires a factorial number of DNA molecules to participate in the reaction.[9]
An optical solution to the Hamiltonian problem has been proposed as well.[10] The idea is to create a graph-like structure made from optical cables and beam splitters which are traversed by light in order to construct a solution for the problem. The weak point of this approach is the required amount of energy which is exponential in the number of nodes.
Complexity[edit]
The problem of finding a Hamiltonian cycle or path is in FNP; the analogous decision problem is to test whether a Hamiltonian cycle or path exists. The directed and undirected Hamiltonian cycle problems were two of Karp’s 21 NP-complete problems. They remain NP-complete even for special kinds of graphs, such as:
- bipartite graphs,[11]
- undirected planar graphs of maximum degree three,[12]
- directed planar graphs with indegree and outdegree at most two,[13]
- bridgeless undirected planar 3-regular bipartite graphs,
- 3-connected 3-regular bipartite graphs,[14]
- subgraphs of the square grid graph,[15]
- cubic subgraphs of the square grid graph.[16]
However, for some special classes of graphs, the problem can be solved in polynomial time:
- 4-connected planar graphs are always Hamiltonian by a result due to Tutte, and the computational task of finding a Hamiltonian cycle in these graphs can be carried out in linear time[17] by computing a so-called Tutte path.
- Tutte proved this result by showing that every 2-connected planar graph contains a Tutte path. Tutte paths in turn can be computed in quadratic time even for 2-connected planar graphs,[18] which may be used to find Hamiltonian cycles and long cycles in generalizations of planar graphs.
Putting all of these conditions together, it remains open whether 3-connected 3-regular bipartite planar graphs must always contain a Hamiltonian cycle, in which case the problem restricted to those graphs could not be NP-complete; see Barnette’s conjecture.
In graphs in which all vertices have odd degree, an argument related to the handshaking lemma shows that the number of Hamiltonian cycles through any fixed edge is always even, so if one Hamiltonian cycle is given, then a second one must also exist.[19] However, finding this second cycle does not seem to be an easy computational task. Papadimitriou defined the complexity class PPA to encapsulate problems such as this one.[20]
References[edit]
![]() Media related to Hamiltonian path problem at Wikimedia Commons
Media related to Hamiltonian path problem at Wikimedia Commons
- ^ Michael R. Garey and David S. Johnson (1979), Computers and Intractability: A Guide to the Theory of NP-Completeness, W.H. Freeman, ISBN 978-0-7167-1045-5 A1.3: GT37–39, pp. 199–200.
- ^ Reduction from Hamiltonian cycle to Hamiltonian path
- ^ Martello, Silvano (1983), “An Enumerative Algorithm for Finding Hamiltonian Circuits in a Directed Graph”, ACM Transactions on Mathematical Software, 9 (1): 131–138, doi:10.1145/356022.356030, S2CID 11879800
- ^ Rubin, Frank (1974), “A Search Procedure for Hamilton Paths and Circuits”, Journal of the ACM, 21 (4): 576–80, doi:10.1145/321850.321854, S2CID 7132716
- ^ Bellman, R. (1962), “Dynamic programming treatment of the travelling salesman problem”, Journal of the ACM, 9: 61–63, doi:10.1145/321105.321111.
- ^ Held, M.; Karp, R. M. (1962), “A dynamic programming approach to sequencing problems” (PDF), J. SIAM, 10 (1): 196–210, doi:10.1137/0110015, hdl:10338.dmlcz/103900.
- ^ Björklund, Andreas (2010), “Determinant sums for undirected Hamiltonicity”, Proc. 51st IEEE Symposium on Foundations of Computer Science (FOCS ’10), pp. 173–182, arXiv:1008.0541, doi:10.1109/FOCS.2010.24, ISBN 978-1-4244-8525-3.
- ^ Iwama, Kazuo; Nakashima, Takuya (2007), “An improved exact algorithm for cubic graph TSP”, Proc. 13th Annual International Conference on Computing and Combinatorics (COCOON 2007), Lecture Notes in Computer Science, vol. 4598, pp. 108–117, CiteSeerX 10.1.1.219.1672, doi:10.1007/978-3-540-73545-8_13, ISBN 978-3-540-73544-1.
- ^ Adleman, Leonard (November 1994), “Molecular computation of solutions to combinatorial problems”, Science, 266 (5187): 1021–1024, Bibcode:1994Sci…266.1021A, CiteSeerX 10.1.1.54.2565, doi:10.1126/science.7973651, JSTOR 2885489, PMID 7973651.
- ^ Mihai Oltean (2006). A light-based device for solving the Hamiltonian path problem. Unconventional Computing. Springer LNCS 4135. pp. 217–227. arXiv:0708.1496. doi:10.1007/11839132_18.
- ^ “Proof that the existence of a Hamilton Path in a bipartite graph is NP-complete”. Computer Science Stack Exchange. Retrieved 2019-03-18.
- ^ Garey, M. R.; Johnson, D. S.; Stockmeyer, L. (1974), “Some simplified NP-complete problems”, Proc. 6th ACM Symposium on Theory of Computing (STOC ’74), pp. 47–63, doi:10.1145/800119.803884, S2CID 207693360.
- ^ Plesńik, J. (1979), “The NP-completeness of the Hamiltonian cycle problem in planar digraphs with degree bound two” (PDF), Information Processing Letters, 8 (4): 199–201, doi:10.1016/0020-0190(79)90023-1.
- ^ Akiyama, Takanori; Nishizeki, Takao; Saito, Nobuji (1980–1981), “NP-completeness of the Hamiltonian cycle problem for bipartite graphs”, Journal of Information Processing, 3 (2): 73–76, MR 0596313.
- ^ Itai, Alon; Papadimitriou, Christos; Szwarcfiter, Jayme (1982), “Hamilton Paths in Grid Graphs”, SIAM Journal on Computing, 4 (11): 676–686, CiteSeerX 10.1.1.383.1078, doi:10.1137/0211056.
- ^ Buro, Michael (2000), “Simple Amazons endgames and their connection to Hamilton circuits in cubic subgrid graphs” (PDF), Conference on Computers and Games, Lecture Notes in Computer Science, vol. 2063, pp. 250–261, CiteSeerX 10.1.1.40.9731, doi:10.1007/3-540-45579-5_17, ISBN 978-3-540-43080-3.
- ^ Chiba, Norishige; Nishizeki, Takao (1989), “The Hamiltonian cycle problem is linear-time solvable for 4-connected planar graphs”, Journal of Algorithms, 10 (2): 187–211, doi:10.1016/0196-6774(89)90012-6
- ^ Schmid, Andreas; Schmidt, Jens M. (2018), “Computing Tutte Paths”, Proceedings of the 45th International Colloquium on Automata, Languages and Programming (ICALP’18), to appear.
- ^ Thomason, A. G. (1978), “Hamiltonian cycles and uniquely edge colourable graphs”, Advances in Graph Theory (Cambridge Combinatorial Conf., Trinity College, Cambridge, 1977), Annals of Discrete Mathematics, vol. 3, pp. 259–268, doi:10.1016/S0167-5060(08)70511-9, ISBN 9780720408430, MR 0499124.
- ^ Papadimitriou, Christos H. (1994), “On the complexity of the parity argument and other inefficient proofs of existence”, Journal of Computer and System Sciences, 48 (3): 498–532, CiteSeerX 10.1.1.321.7008, doi:10.1016/S0022-0000(05)80063-7, MR 1279412.
