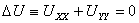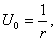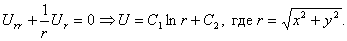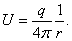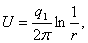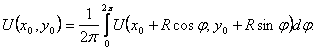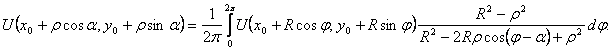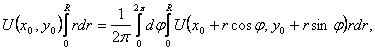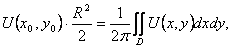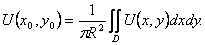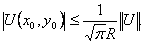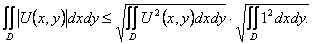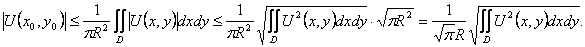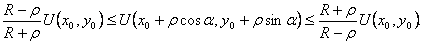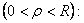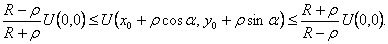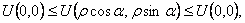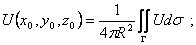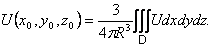Задача ставится так: найти функцию tx(r,у?), удовлетворяющую внутри ируга Kr0 радиуса с центром в начале координат уравнению Лапласа непрерывную в замжутой области KtQ и принимающую задан ные значения награнице круга, Решение задачи Дирихле для круга методом Фурье где f(tp) — достаточно гладкая функция, периодическая с периодом 2т.
В силу однозначности искомого решения оно должно быть периодическим по с периодом Из непрерывности решения в Кго следует его ограниченность в КГо. Уравнение (1) в полярных координатах имеет вид (3) Будем искать частные решения уравнения (3) в виде . Подставляя «(г, (р) в форме (4) в уравнение (3),умноженное на г2, получим откуда Из условия получаем находим , так что В частности, = Ао = const. Полагая в уравнении (6) (уравнении Эйлера) Л(г) = г*, при А = п2 получаем Отсюда) и, следовательно.
При п = 0 из (6) находам Так как ооприг 0+0,тодля решения внутренней задачи Дирихле нужно положить Решение внутренней задачи Дирихле будем искать в виде ряда (5) (6) где коэффициенты Ап, Вп определяются из граничного условия (2) При т — tq имеем Запишем разложение /(у) в ряд Фурье где Решение задачи Дирихле для круга методом Фурье Сравнивая ряды (8) и (9), получаем (9) * г0 г0.
Таким образом, формальное решение внутренней задачи Дирихле для круга предста-вимо в виде ряда оо где коэффициенты определяются по формулам (10).
Возможно вам будут полезны данные страницы:
При г го ряд (11) можно дифференцировать по г и любое число раз, и, значит, функция u(r, у) из (11) удовлетворяет уравнению Если предположить, что функция непрерывна и дифференцируема, то ряд (11) при г ^ г0 сходится равномерно, и, следовательно, функция и(г, непрерывна на границе круга и удовлетворяет всем условиям поставл енной задачи.
Решение внешней задачи Дирихле следует
искать в виде ряда где коэффициенты Ап, В„ определяются из граничного условия Для кольцевой области образованной двумя концентрическими окружностями с центром в точке 0 радиусов Г] и г2 (рис.8), решение задачи ищется в виде ряда коэффициенты которого Л0, определяются из граничных условий Пример.
Найти функцию, гармоническую внутри круга радиуса го с центром в начале координат и такую. что Решение задачи Дирихле для круга методом Фурье -4 Задача сводится к решению внутренней задачи Дирихле для уравнения при граничном условии Будем искать решение задачи в вида ряда ПО Из граничного условия (15) имеем Отсюда в силу ортогональности системы функций Искомое решение
Аналитическая функция бесконечно
дифференцируема (Б9). Из Коши-Римана
u’’xx = v’’xy
= v’’yx =
-u’’yy.
Оператор c = d^2/dx^2
+ d^2/dy^2 –
оператор Лапласа. Функция дважды
непрерывно дифференцируемая и
удоволетворяющая cu = 0
называется гармонической. Если функция
аналитическая, то Ref(z)
Imf(z)
гармонические. Построение аналитической
функции: v(x,y)
= $<x0, y0 x,
y> -u’ydx
+ u’xdy.
Интегрирование не зависит от пути. По
любому замкнутому контуру будет 0 ($<Г>
= $$<DГ>cudxdy
= 0). Дифференциал функции – выражение
под интегралом. cv = 0.
Функция f(z)
= u(x,y)
+ iv(x,y)
– аналитична в области, функции
определяются с точностью до константы.
Раз мы можем построить аналитическую
функцию, а она бесконечно дифференцируема,
в силу аддитивности получаем, что
гармоническая функция бесконечно
дифференцируема.
Т Если функция гармонична в области и
не постоянна, то она не достигает своих
точных верхних и нижних граней (принцип
максима гармонической функции). Док-во:
применяем формулу среднего значения,
повторяем принцип максиму аналитической
функции.
Билет 8. Разложение гармонических функций в ряды. Ряд Фурье для гармонической функции.
Рассмотрим гармоническую функцию u(x,
y) в круге радиуса R.
Существует аналитическая функция f(z)
такая, что её вещественная часть равна
u, так как круг односвязная
область. f(z)
= Add(n = 0, inf)
kn(z-z0)^n,
|z – z0| <
R. Пусть z =
z0 + pe^ih,
0 < p < R,
kn = an + ibn.
Подставим. Введем обозначение f(z0
+ pe^ih) = u(p,
h) + iv(p,
h). Тогда u(p,
h) = Add(n=0,
inf)(an(p^n)cos(nh)
– bn(p^n)sin(nh)),
v(p, h)
= Add(n=0,
inf)(bnp^ncosnh
+ anp^nsinnh).
Два тригонометрических ряда
Add(n=0,inf)(ancosnh
+ bnsinnh) и Add(n=0,
inf)(cncosnh +
dnsinnh) называются сопряженными,
если an = dn,
bn = -cn. ТЕ
комплексно сопряженным функциям
соответствуют сопряженные гармонические
ряды. Рассмотрим коэффициенты в разложении
f(z). kn
= (1/(2пi))$<|w –
z0|=r>f(w)dw/(w-z0)^(n+1),
заменяем w = z0
+ re^(ih). h
(~[0, 2п]. Получим, что kn =
(1/r^n)(1/2п)$<0,
2п>f(z0 +
re^ih)e^(-inh)dh.
Используя св-во аналитичной функции
(интеграл по контуру 0) получаем, что
(1/r^n)(1/2п)$<0,
2п>f(z0 +
re^(ih))e^(ih)dh
= 0. Записываем kn + 0, kn
– 0. выделяем действительную и мнимую
части и выражаем u(p,
h) = (1/2п)$<0, 2п>u(r,
h)dh + Add(n=1,
inf)((p/r)^n
* (1/п) $<0, 2п>[u(r,
h)cos(nh)dhcos(nh)]
+ (p/r)^n(1/п)$<0,
2п>[u(r,
h)sin(nh)dhsin(nh)]
и полная аналогия для v.
Получили, что соответствующие коэффициенты
– коэффициенты ряда Фурье.
Билет 9. Бесконечная дифференцируемость аналитических функций. Теорема Лиувилля.
Г – жорданова, кусочно гладкая кривая,
не обязательно гладкая, функция
непрерывна. F(z)
= (1/(2пi))$<Г>f(w)dw/(w
– z), z !(~ Г
– интеграл типа Коши. Т Интеграл типа
коши – аналитическая функция везде,
кроме самой кривой. При этом функция
F(z) имеет
производную любого порядка, равную
F(n)(z)
= (n!/2пi)
$<Г>f(w)dw/(w
– z)^(n+1).
Док-во методом индукции. Для 1: выберем
произвольную точку не из кривой. Тогда
у неё есть дельта окрестность не
пересекающаяся с кривой. p
– расстояние от этой окрестности до
кривой. Будем рассматривать приращения
аргумента меньше дельта по модулю.
Распишем разность [F(z
+ дz) – F(z)]/дz
– 1/(2пi)$<Г>f(w)dw/(w-z)^2
и получим (1/(2пi))$<Г>f(w)дzdw/[(w
– z)^2(w – (z
+ дz))]. Получим ограничение
на эту разность через максимум M
= max|f(z)|,
|w – z| >=
p, и длину кривой l.
Ограничение: (1/2п)Ml/p^3*|дz|
– получаем производную. Предполагаем
при n, доказываем для n+1.
Расписываем разность: F(n)(z
+ дz) – F(n)(z)/дz
– [(n+1)!/2пi]$<Г>f(w)dw/(w
– z)^(n+2).
Используем выражение из предположения
индукции. Путем преобразований получаем,
что разность равна (n!/2пi)$<Г>f(w)A(z,
w, дz)dw/[(w
– z)^(n+2)дz[w
– (z + дz)]^(n+1)].
Где A(z, w,
дz) = (w-z)[(w-z)^(n+1)
– [(w – z) –
дz]^(n+1)] –
(n+1)дz[(w
– z) – дz]^(n+1).
Он преобразуется к виду (дz^2)B(z,
w, дz), где
B(z, w,
дz) – многочлен фиксированной
степени по каждой из переменных, причем
при ограничении дz на
кривой Г он ограничен по модулю. Получаем.
Рассматриваем произвольную аналитическую
функцию. Выбираем произвольную точку
точку z0 из области и
произвольную её окрестность. По
интегральной формуле коши получаем
n-ую производную в точке
z0. Те функция, аналитическая
в области, бесконечно-дифференцируема
в этой области. Т Лиувилля. Пусть функция
f(z) аналитична
на всей комплексной плоскости и существует
a > 0, M >
0 такие, что для любого z
(~C |f(z)|
<=M|z|^a.
Тогда f(z) –
многочлен, степень которого не превышает
[a] – целой части a.
Док-во: a = m
+ r, m = [a].
Выбираем произвольную точку z0
и R > 0. Расписываем [a]+1
производную в z0 через
интегральную формулу Коши. f([a]
+1) = {([a]+1)!/2пi}$<|w-z0|=R>f(w)dw/(w-z0)^([a]+2).
Оцениваем сверху, используя условие
теоремы, получаем ([a]+1)!(1
+ |z0|/R)^a/R^([a]+1-a).
Так как функция целая, то можем устремить
радиус к бесконечности, получим, что
производная равна 0. В силу произвольности
точки получаем, что она везде равна 0,
те условие теоремы доказано. Следствие:
Если функция аналитическая на всей
плоскости и существует M
> |f(z)|, то
функция констнатна.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В предыдущем параграфе мы видели, что задача Дирихле может иметь только одно решение, но мы еще не знаем, имеет ли она вообще решение. Не рассматривая этого вопроса в общем случае, мы ограничимся лишь частными случаями. При этом мы применим к решению задачи различные методы. Начнем с плоского случая.
Пусть требуется найти функцию, гармоническую внутри круга и принимающую на окружности этого круга наперед заданные значения. Пусть 



или

Применим в данном случае метод Фурье и будем искать решение уравнения (17) в виде произведения функции только от 0 на функцию только от 

Подставляем это выражение в уравнение (17):

или

Левая часть написанного уравнения содержит одну независимую переменную 



Первое из них при 

Второе — есть уравнение Эйлера [42]. Ищем его решение в виде 

откуда, сокращая на 


если только постоянная k отлична от нуля. Подставив в формулу (18), получим для U выражение

При k = 0 будем иметь уравнения

и, как нетрудно показать, получим

В формулах (19) и 






Но если подставить в формулу 


Периодичность решения 

причем постоянные могут быть различными при различных значениях целого числа 







В силу линейности и однородности уравнения Лапласа сумма этих решений будет также решением, т. е. мы получаем решение
вида

Определим теперь произвольные постоянные 

где 



Отсюда видно, что 




и подставляя найденные отсюда значения в формулу (20), получим искомое решение задачи Дирихле.
Сравнивая ряд Фурье (22) с формулой (20), дающей решение задачи, можем формулировать полученный результат следующим образом: чтобы получить решение задачи Дирихле для круга, надо написать ряд Фурье для предельных значений 


Вместо бесконечного ряда (20) решение можно представить в виде определенного интеграла. Подставляем в формулу (20) выражения коэффициентов (23):

или

Формула (14) из [I, 174] дает непосредственно

Заменяя 



Заметим, что если бы обозначали обе части уравнения (18,) не через 



При выводе формулы (25) мы предполагали, что решение задачи Дирихле, т. е. искомая функция 




Решение задачи Дирихле для круга методом Фурье
По этой ссылке вы найдёте полный курс лекций по математике:
Задача ставится так: найти функцию tx(r,у?), удовлетворяющую внутри ируга Kr0 радиуса с центром в начале координат уравнению Лапласа непрерывную в замжутой области KtQ и принимающую задан ные значения награнице круга, Решение задачи Дирихле для круга методом Фурье где f(tp) — достаточно гладкая функция, периодическая с периодом 2т.
В силу однозначности искомого решения оно должно быть периодическим по с периодом Из непрерывности решения в Кго следует его ограниченность в КГо. Уравнение (1) в полярных координатах имеет вид (3) Будем искать частные решения уравнения (3) в виде . Подставляя «(г, (р) в форме (4) в уравнение (3),умноженное на г2, получим откуда Из условия получаем находим , так что В частности, = Ао = const. Полагая в уравнении (6) (уравнении Эйлера) Л(г) = г*, при А = п2 получаем Отсюда) и, следовательно.
При п = 0 из (6) находам Так как ооприг 0+0,тодля решения внутренней задачи Дирихле нужно положить Решение внутренней задачи Дирихле будем искать в виде ряда (5) (6) где коэффициенты Ап, Вп определяются из граничного условия (2) При т — tq имеем Запишем разложение /(у) в ряд Фурье где Решение задачи Дирихле для круга методом Фурье Сравнивая ряды (8) и (9), получаем (9) * г0 г0.
Таким образом, формальное решение внутренней задачи Дирихле для круга предста-вимо в виде ряда оо где коэффициенты определяются по формулам (10).
Возможно вам будут полезны данные страницы:
При г го ряд (11) можно дифференцировать по г и любое число раз, и, значит, функция u(r, у) из (11) удовлетворяет уравнению Если предположить, что функция непрерывна и дифференцируема, то ряд (11) при г ^ г0 сходится равномерно, и, следовательно, функция и(г, непрерывна на границе круга и удовлетворяет всем условиям поставл енной задачи.
Решение внешней задачи Дирихле следует
искать в виде ряда где коэффициенты Ап, В„ определяются из граничного условия Для кольцевой области образованной двумя концентрическими окружностями с центром в точке 0 радиусов Г] и г2 (рис.8), решение задачи ищется в виде ряда коэффициенты которого Л0, определяются из граничных условий Пример.
Найти функцию, гармоническую внутри круга радиуса го с центром в начале координат и такую. что Решение задачи Дирихле для круга методом Фурье -4 Задача сводится к решению внутренней задачи Дирихле для уравнения при граничном условии Будем искать решение задачи в вида ряда ПО Из граничного условия (15) имеем Отсюда в силу ортогональности системы функций Искомое решение
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Решение внутренней задачи Дирихле для круга методом Фурье. Формула Пуассона
Рассмотрим задачу Дирихле для уравнения Лапласа в круге радиуса r0. С учетом характера области D перейдем к полярной системе координат (г, (р) с началом в центре круга. Тогда с учетом (7.2) формулировка задачи примет вид: найти функцию и = и(г, ф), удовлетворяющую в круге D = <(г, ф) | 0 2 ,п =0, 1, 2, . Тогда
где Л„, Вп — произвольные постоянные.
Общее решение уравнения (7.25) при X = п 2 имеет вид
Функция и(г, ф) = /?(г)Ф(ф) должна быть непрерывной в круге Z), поэтому Dn = 0. Кроме того, полагаем Сп = 1, п = 0, 1, 2, . Тогда из (7.23) и (7.26) находим:
Функции (7.27) являются частными решениями уравнения Лапласа (7.21) в круге D. В соответствии с методом Фурье решение задачи Дирихле (7.21)—(7.22) будем искать в виде линейной комбинации частных решений ип(г, ф)
которая удовлетворяет граничному условию (7.22). Из этого условия следует:
Напомним, что функция р(ф) считается непрерывной и кусочногладкой на отрезке [0; 2л], причем р(0) = р(2л). Поэтому разложение Фурье функции р(ф) сходится к ней равномерно на [0; 2л]:
Из сравнения (7.28) и (7.29) следует, что
Таким образом, формально полученное решение задачи Дирихле для уравнения Лапласа в круге имеет вид
где коэффициенты ап и Ьп определяются равенствами (7.30).
Убедимся теперь, что функция и(г, ср) из (7.31) действительно является решением задачи Дирихле (7.21)—(7.22).
1. Покажем, что ряд (7.31) внутри круга D можно дифференцировать по р и по (р любое число к раз. Выберем произвольное положительное число гх + составленного из модулей ее коэффициентов
Фурье, см. [4]. Этот ряд является мажорирующим в области D для ряда из правой части (7.31). Следовательно, по признаку Вейер- штрасса ряд из (7.31) сходится равномерно в D, а значит, его сумма и(г, (р) является непрерывной функцией в замкнутой области D, см. там же.
5. В п. 7.1 доказана единственность решения задачи Дирихле для уравнения Лапласа.
Доказанные утверждения можно сформулировать следующим образом.
Теорема 7.1. Пусть функция р(ф) является непрерывной и кусочно-гладкой на отрезке [0; 2л], причем р(0) = р(2л).
Тогда внутренняя задача Дирихле (7.21)—(7.22) для круга радиуса г0 имеет единственное решение
Пример 7.3. Найти решение внутренней задачи Дирихле для уравнения Лапласа в круге радиуса r0 = 1, если граничное условие имеет види|г = и <1, ф) = р(ф) = 8С08 4 ф.
2 – 4у 2 + х 4 + у 4 – 6х 2 у 2 . >
Упростим формулу (7.31) преобразовав ее правую часть с учетом равенств (7.30):
[spoiler title=”источники:”]
http://studref.com/694570/matematika_himiya_fizik/reshenie_vnutrenney_zadachi_dirihle_kruga_metodom_fure_formula_puassona
[/spoiler]
Лекция 7. Гармонические функции и их свойства
Рассмотрим уравнение Лапласа на плоскости
(33)
и в пространстве
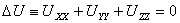
(34)
Уравнение (33) при переходе к полярным координатам преобразуется к виду
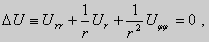
(33*)
Рис 14 Рис 14.1
Если в пространстве перейти к сферическим координатам
то уравнение (34) примет вид
(34*)
Функции U=U(x,y) на плоскости и U=U(x,y,z) в пространстве, имеющие непрерывные частные производные второго порядка и удовлетворяющие, соответственно, уравнению Лапласа (33) или (34) в некоторой области D, называются гармоническими в этой области. Простейшими примерами гармонических функций являются линейные функции: U = ах + by + с на плоскости и U = ax + by + cz + d в пространстве. Особый интерес представляют решения уравнения Лапласа, обладающие сферической или цилиндрической (в случае двух независимых переменных – круговой) симметрией.
Решение U=U(r), обладающее сферической симметрией, будет определяться из обыкновенного дифференциального уравнения
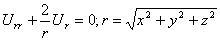
Это уравнение получится, если подставить искомую функцию в уравнение Лапласа (34*), записанное в сферических координатах. Интегрируя это уравнение, находим
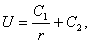
где C1 и C2 – произвольные постоянные. Полагая C1=1, C2=0, получим функцию
которую часто называют фундаментальным решением уравнения Лапласа в пространстве. Функция U0 является гармонической всюду в пространстве, кроме начала координат 0.
Аналогично, полагая U=U(r) и пользуясь уравнением Лапласа в цилиндрических или полярных координатах, найдем решения, обладающие цилиндрической или круговой симметрией:
Выбирая С1=-1 и С2=0, будем иметь функцию
которую называют фундаментальным решением уравнения Лапласа на плоскости (в случае двух независимых переменных). Функция U0 удовлетворяет уравнению Лапласа (33) всюду на плоскости, кроме начала координат 0, где она обращается в бесконечность. Фундаментальные решения уравнения Лапласа имеют, помимо большого значения в теории гармонических функций, важный физический смысл.
Рассмотрим в пространстве электрическое поле, образованное точечным зарядом величины q , помещенным в начало координат. Тогда потенциал этого поля равен
Аналогично, если рассмотреть поле, создаваемое заряженной прямой, то потенциал такого поля будет равен
где q1 – линейная плотность заряда (то есть заряд, рассчитанный на единицу длины).
Более сложные примеры будут рассмотрены далее, а сейчас изучим свойства гармонических функций.
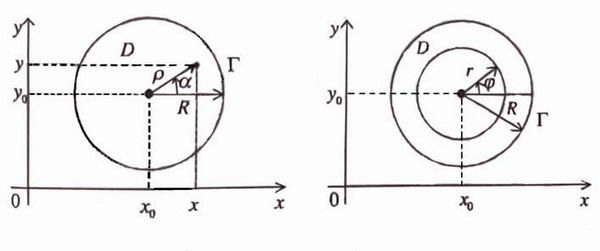
Теорема о среднем. Пусть функция U=U(x,y) гармоническая в некотором круге D радиуса R с центром (хo,уo) и непрерывная в соответствующем замкнутом круге 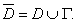
(35)
При доказательстве этой теоремы применим интегральную формулу Пуассона для круга, которая будет доказана позже в лекции 10. Она имеет вид (см. рис. 15)
Если в этой формуле положить ρ=0, то получится формула (35).
Теорему о среднем можно представить и в другой форме. Для этого запишем формулу (35) для произвольного круга радиуса r, где 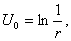
Рис. 15 Рис. 15.1
(36)
Умножив обе части равенства (36) на rdr и проинтегрировав по r в пределах от 0 до R, получим:
или
где D – круг радиуса R. Разделив обе части полученного равенства на R2/2 , будем иметь
(37)
В правой части формулы (37) записано среднее значение гармонической функции U(x,y) в круге радиуса R.
Имеет место и обратная теорема: если в некоторой области D функция U=U(x,y) непрерывная и для каждой точки 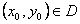
Следствие. Если функция U=U(x,y) гармоническая в некотором круге D радиуса R и непрерывная в соответствующем замкнутом круге 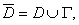
(38)
Число 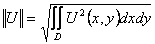
Неравенство (38) доказывается совсем просто, если воспользоваться известным неравенством Коши-Буняковского:
Применим это неравенство к формуле (37):
Что и требовалось доказать.
Гармонические функции, помимио вышеуказанных свойств, обладают и многими другими свойствами. Приведем еще два из них.
Неравенство Харнака. Пусть функция 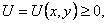
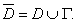
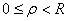
Из неравенства Харнака следует теорема Лиувилля.
Теорема Лиувилля. Гармоническая на всей плоскости функция U=U(x, у) не может быть ограниченной сверху или снизу, если она не постоянная.
Доказательство. Если функция U=U(x, у) ограничена сверху, то U1=-U(x, y) – ограничена снизу и тоже гармоническая. Поэтому достаточно рассмотреть случай, когда функция ограничена снизу: 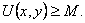
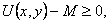
Воспользуемся неравенством Харнака
Если функция U(x, у) гармоническая во всей плоскости 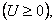
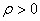
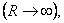
то есть 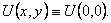
Замечание. Гармонические функции в пространстве обладают аналогичными свойсвами. Приведем формулировку одного из них.
Терема о среднем. Пусть функция U=U(x, у) гармоническая в некотором шаре D радиуса R c центром
(xo , уo , zo ) и непрерывная в соответствующем замкнутом шаре 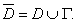
а) ее среднему значению на сфере Г, ограничивающей данный шар, то есть
б) ее среднему значению в шаре D, то есть