Как найти гармоники частоты

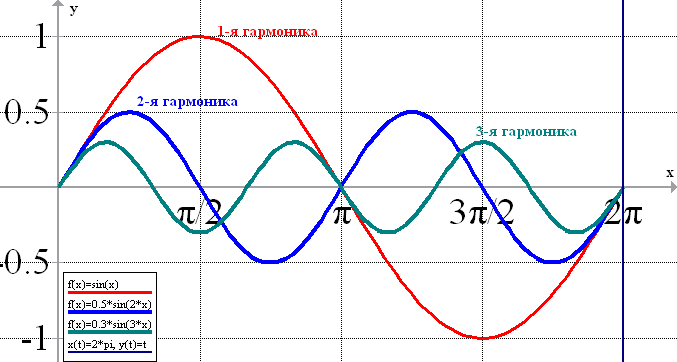
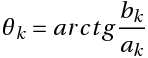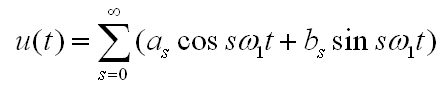Ранее
отмечалось, что любой электрический
сигнал может быть представлен в виде
суммы синусоид, каждая синусоида имеет
свою амплитуду, частоту и фазу.

где
А_к
– амплитуда f_к
– частота _к
– фаза.

Если
построить график, показывающий, как
зависит амплитуда синусоиды от частоты,
то это будет частотный спектр данного
сигнала.

U(t)
– сигнал, имеющий периодический
характер.

Частотный
спектр – зависимость А_к
от f_к.

Можно
вместо синусоиды брать косинусоиду,
частотный спектр от этого не изменится.
Выбор разложения по синусоиде или
косинусоиде зависит от выбора начала
отсчета (симметричный).

Каждая
синусоида носит название гармоника.
Поэтому представление в виде суммы
гармоник называется
гармоническим рядом.

Пусть импульсы
прямоугольной формы периодически
повторяются, амплитуда, период и
длительность – постоянны.

Выберем
начало отсчета времениt
= 0 так, чтобы картина была симметричной
относительно начала отсчета.

Тогда

– т.е. будут одни косинусоиды,

где
k
2 
f
_k
= 
_k
– частота
гармоники.

Отсутствует

_к
, т.е. все гармоники имеют нулевой фазовый
сдвиг.

Существует
косинусоида, у которой к = 0, f₀
= 0, нулевая гармоника, ей соответствует
постоянная составляющая U(t).

Частоты гармоник:

К
= 0, f
₀
= 0 – нулевая гармоника

К
= 1, f
₁
= 1/T
– первая гармоника

К
= 2, f
₂
= 2/T
– вторая гармоника и т.д.

Если Т постоянно,
т.е. сигнал периодический

Частоты
гармоник:

Амплитуды гармоник.

Определяются
из теории рядов Фурье.

Для прямоугольных
импульсов:

где
U₀
– амплитуда импульса,

К
– номер гармоники (чем больше к, тем
меньше U₀).

.

Как
следует из формулы для A_k
амплитуды гармоник идеальных прямоугольных
импульсов имеют тенденцию с ростом k
(частоты) убывать асимптотически, т.е.
формально ширина частотного спектра
идеальных прямоугольных импульсов
неограниченна.

Реальные
импульсы имеют отклонения от прямоугольной
формы и ширина их спектра не бесконечна.

Отдельно вычисляется
амплитуда нулевой гармоники.

Если к = 0 , знаком
синуса можно пренебречь и тогда:

-это
не что иное, как постоянная составляющая
напряжения U(t).

Изобразим
график частотного спектра.

Для
упрощения далее будет изображаться
только первая полуволна графика
частотного спектра – основной частотный
спектр.

Амплитуды
гармоник уменьшаются с увеличением
частоты, при этом наблюдается колебательный
характер.

Участок до первого
нуля (первая полуволна) – это основной
спектр.

Частотная
граница основного спектра определяет
ширину частотного спектра из условия:

откуда
k=k_осн=илиk_осн=q

k_осн
– количество линий в основном спектре.

Величина
F_осн=– ширина основного спектра

Часто
требуется количественная оценка ширины
частотного спектра F_c
. Для идеальных прямоугольных импульсов,
её условно принимают равной

F_c=(1..3)F_осн
или
.

Свойства
частотного спектра.

1. Чем
   больше период повторения импульсов,
   тем больше линий в основном частотном
   спектре – чаще расположены линии в
   частотном спектре.

2. Чем
   короче импульс, тем больше ширина
   частотного спектра.

3. Ширина
   ЧС определяется для прямоугольного
   импульса соотношением:

Это
соотношение справедливо для идеальных
прямоугольных импульсов.

Реальный
импульс отличается от идеального более
пологими фронтами.

Общая
формула вычисления амплитуды гармоник
для любого случая:

По
сравнению с идеальным прямоугольным
импульсом для реального импульса ЧС
имеет более определенную частотную
границу. Убывание амплитуд гармоник с
частотой может иметь монотонный характер.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #

  19.03.201580.9 Кб9Б.doc

• #
• #
• #
• #

Анонс: Что такое гармонические искажения, гармоники и как они влияют на стабильность электроснабжения и качество электроэнергии в сети. Эмиссия гармонических искажений силовым оборудованием, проблемы технических средств компенсации реактивной мощности и фильтров гармоник.

В идеале любой источник питания, в том числе ТП распределительной сети, должен стабильно давать ток идеально синусоидального напряжения в каждом месте силовой сети абонента-потребителя, однако по ряду причин электросетевым компаниям часто бывает трудно обеспечить такие условия из-за эмиссии и трансмиссии гармонических искажений. Гармонические искажения тока, напряжения далеко не новость, но в настоящее время они представляют собой одну из основных проблем, вызывающих нарушения стабильности электроснабжения и качества электроэнергии в электроэнергетике.

В первых электроэнергетических системах гармонические искажения в основном вызывались насыщением трансформаторов, промышленных дуговых печей, мощных электросварочных аппаратов и т. п., а сами гармоники представляли сравнительно небольшую проблему из-за консервативной конструкции силового оборудования. Сегодня все более широкое использование нелинейных нагрузок в силовых сетях промышленных и непромышленных объектов обуславливает увеличение объемов гармонических искажений в распределительных сетях, причем именно через распределительные сети из-за «перегенерации» искажений трансформаторами ТП электросетевой компании силовые сети абонентов обмениваются гармониками между собой, (трансмиссия).

Наиболее часто используемой нелинейной нагрузкой является, пожалуй, ШИМ-преобразователь, широко используемый в сталелитейной, бумажной и текстильной промышленности, в приводах управление скоростью электродвигателя.

Наряду с этим, свой вклад в засорение сетей гармониками вносят системы энергосберегающего освещения, электроника центров обработки данных, программно-технических комплексов АСУ, электрические транспортные системы, бытовые электроприборы и т. д. К 2000 году было зафиксировано, что на электронные нагрузки приходилось около половины спроса на электроэнергию в США и развитых странах мира, а за два десятка лет нового века эта доля возросла до 70-80 %, и это вывело проблему гармонических искажений в перечень приоритетных и критических.

Для справки
Упрощенно, нелинейные нагрузки — это нагрузки, в которых форма волны тока не похожа на форму волны приложенного напряжения по ряду причин, например, из-за использования электронных переключателей, которые проводят ток только в течение части периода промышленной частоты и, следовательно, здесь закон Ома не может описать связь между напряжением и током. Среди наиболее распространенных нелинейных нагрузок — все типы выпрямительных устройств, в том числе источники бесперебойного питания, преобразователи напряжения компьютеров, частотно-регулируемые приводы, электрические печи, люминесцентные лампы и т. д. Нелинейные нагрузки вызывают искажение формы сигнала напряжения, перегрев трансформаторов и других силовых устройств, перегрузку по току проводов и клемм соединения оборудования, телефонные помехи, сбои в управлении микропроцессорами и пр.

Сам термин «гармоники» заимствован из области акустики, где он был связан с вибрацией струны или молекул воздуха с частотой, кратной базовой частоте, а гармоническая составляющая в системе питания переменного тока определяется как синусоидальная составляющая периодической формы волны, частота которой равна целому кратному основной частоте системы. Тогда гармоники в формах волны напряжения или тока можно представить, как идеально синусоидальные составляющие частот, кратных основной частоте: fn=(n)·f1, где n — порядок гармоники. Т. е. для наших сетей с f1=50 Гц частота третьей (n = 3) гармоники будет f3=3·50=150 Гц, пятой (n=5) f5=5·50=250 Гц, седьмой (n=7) f7=7·50=350 Гц и т. д. Хотя кривые зависимости тока на фундаментальной частоте и токов гармоник имеют форму синусоиды, результирующая кривая искажена из-за взаимного влияния токов разных частот (см. на рис. ниже).

Ситуация стала более сложной с применением конденсаторных батарей, используемых на промышленных предприятиях для коррекции коэффициента мощности, и энергокомпаниями для стабилизации напряжения вдоль распределительных линий. Результирующее реактивное сопротивление емкости образует колебательный контур с индуктивным реактивным сопротивлением системы на определенной (резонансной) частоте, которая может совпадать с одной из характеристических гармоник нагрузки, что обуславливает значительный наброс токов гармоник, перенапряжения, способные повредить изоляцию. По факту далеко не решает проблему в полном объеме использование активных фильтров гармоник (АФГ), по сути, тех же ШИМ-преобразователей (инвертеров), которые демпфируют гармоники противофазными токами «ниже» места присоединения, а для силовой сети «выше» остаются источниками эмиссии гармонических искажений.

Такая ситуация ставит перед инженерами сложную задачу по выявлению и исправлению чрезмерных уровней гармонических искажений формы сигналов тока и напряжения от стадии планирования до стадии проектирования энергетических и промышленных установок, что позволит не только поддерживать сети и оборудование в оптимальных условиях эксплуатации, но и предвидеть потенциальные проблемы с интеграцией, модернизацией нелинейных нагрузок, а также технических средств для нивелирования перетоков реактивной мощности и/или фильтров гармоник.

Практическое применение преобразования Фурье для анализа сигналов. Введение для начинающих

1. Преобразование Фурье и спектр сигнала

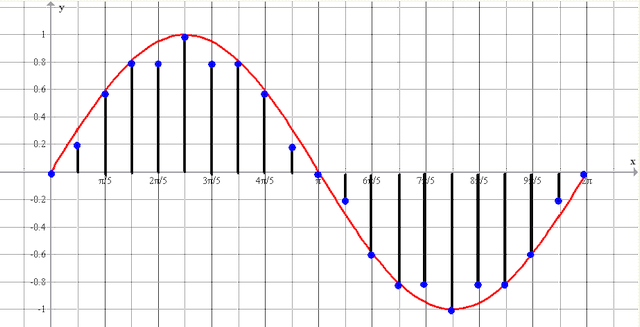
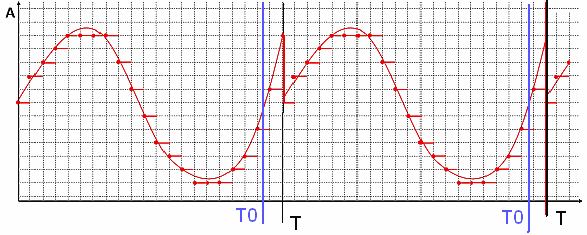
Во многих случаях задача получения (вычисления) спектра сигнала выглядит следующим образом. Имеется АЦП, который с частотой дискретизации Fd преобразует непрерывный сигнал, поступающий на его вход в течение времени Т, в цифровые отсчеты — N штук. Далее массив отсчетов подается в некую программку, которая выдает N/2 каких-то числовых значений (программист, который утянул из инета написал программку, уверяет, что она делает преобразование Фурье).

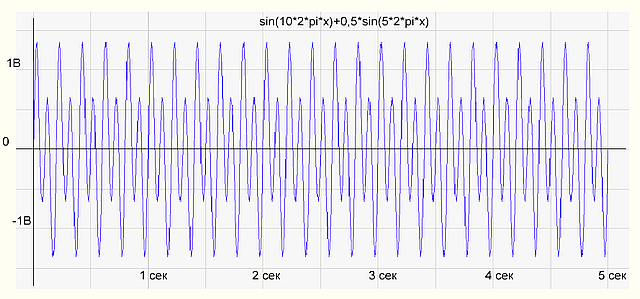
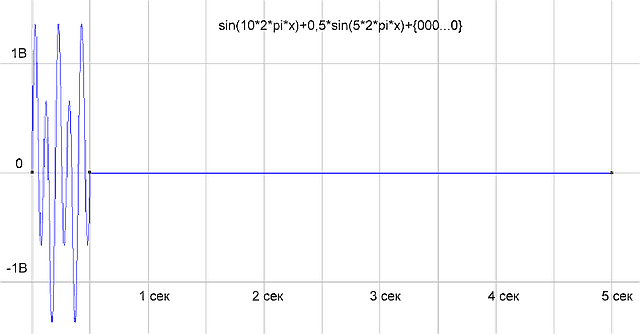
Чтобы проверить, правильно ли работает программа, сформируем массив отсчетов как сумму двух синусоид sin(10*2*pi*x)+0,5*sin(5*2*pi*x) и подсунем программке. Программа нарисовала следующее:

рис.1 График временной функции сигнала

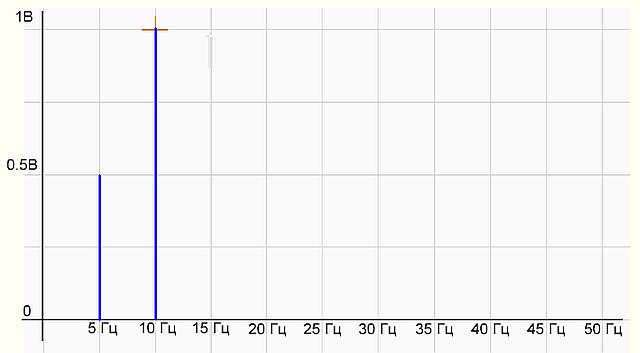
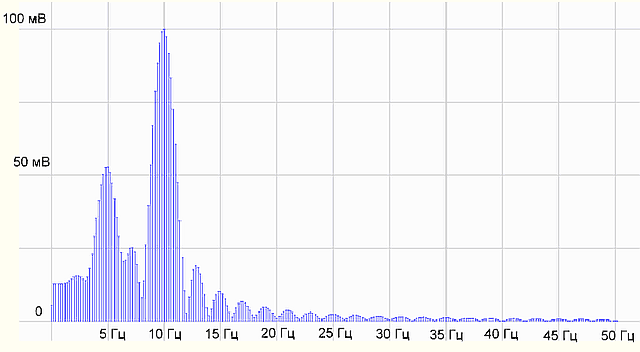
рис.2 График спектра сигнала

На графике спектра имеется две палки (гармоники) 5 Гц с амплитудой 0.5 В и 10 Гц — с амплитудой 1 В, все как в формуле исходного сигнала. Все отлично, программист молодец! Программа работает правильно.

Это значит, что если мы подадим на вход АЦП реальный сигнал из смеси двух синусоид, то мы получим аналогичный спектр, состоящий из двух гармоник.

Итого, наш реальный измеренный сигнал, длительностью 5 сек, оцифрованный АЦП, то есть представленный дискретными отсчетами, имеет дискретный непериодический спектр.

С математической точки зрения — сколько ошибок в этой фразе?

Теперь

начальство решило

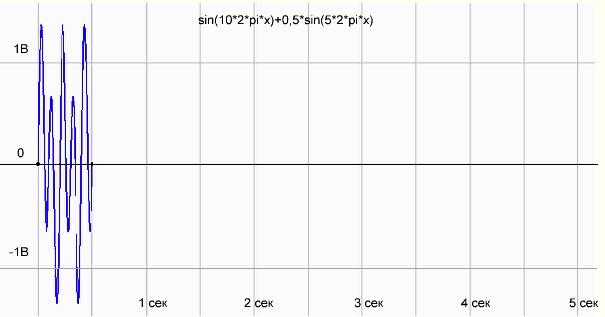
мы решили, что 5 секунд — это слишком долго, давай измерять сигнал за 0.5 сек.

рис.3 График функции sin(10*2*pi*x)+0,5*sin(5*2*pi*x) на периоде измерения 0.5 сек

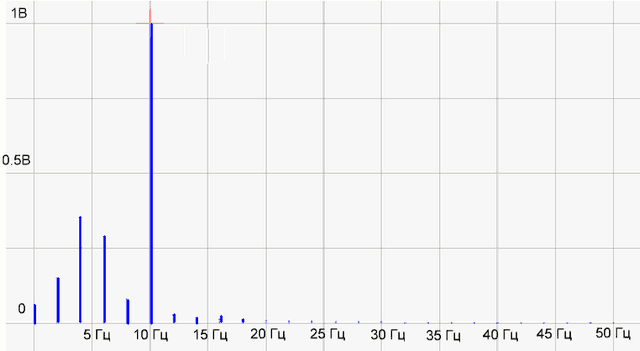
рис.4 Спектр функции

Что-то как бы не то! Гармоника 10 Гц рисуется нормально, а вместо палки на 5 Гц появилось несколько каких-то непонятных гармоник. Смотрим в интернетах, что да как…

Во, говорят, что в конец выборки надо добавить нули и спектр будет рисоваться нормальный.

рис.5 Добили нулей до 5 сек

рис.6 Получили спектр

Все равно не то, что было на 5 секундах. Придется разбираться с теорией. Идем в Википедию — источник знаний.

2. Непрерывная функция и представление её рядом Фурье

Математически наш сигнал длительностью T секунд является некоторой функцией f(x), заданной на отрезке {0, T} (X в данном случае — время). Такую функцию всегда можно представить в виде суммы гармонических функций (синусоид или косинусоид) вида:

(1), где:

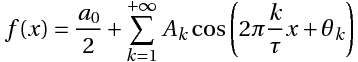
k — номер тригонометрической функции ( номер гармонической составляющей, номер гармоники)
T — отрезок, где функция определена (длительность сигнала)
Ak — амплитуда k-ой гармонической составляющей,
θk- начальная фаза k-ой гармонической составляющей

Что значит «представить функцию в виде суммы ряда»? Это значит, что, сложив в каждой точке значения гармонических составляющих ряда Фурье, мы получим значение нашей функции в этой точке.

(Более строго, среднеквадратичное отклонение ряда от функции f(x) будет стремиться к нулю, но несмотря на среднеквадратичную сходимость, ряд Фурье функции, вообще говоря, не обязан сходиться к ней поточечно. См. https://ru.wikipedia.org/wiki/Ряд_Фурье.)

Этот ряд может быть также записан в виде:

(2),
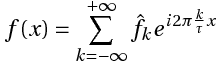
где 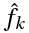, k-я комплексная амплитуда.

или

(3)

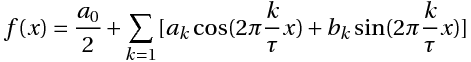
Связь между коэффициентами (1) и (3) выражается следующими формулами:

и

Отметим, что все эти три представления ряда Фурье совершенно равнозначны. Иногда при работе с рядами Фурье бывает удобнее использовать вместо синусов и косинусов экспоненты мнимого аргумента, то есть использовать преобразование Фурье в комплексной форме. Но нам удобно использовать формулу (1), где ряд Фурье представлен в виде суммы косинусоид с соответствующими амплитудами и фазами. В любом случае неправильно говорить, что результатом преобразования Фурье действительного сигнала будут комплексные амплитуды гармоник. Как правильно говорится в Вики «Преобразование Фурье (ℱ) — операция, сопоставляющая одной функции вещественной переменной другую функцию, также вещественной переменной.»

Итого:
Математической основой спектрального анализа сигналов является преобразование Фурье.

Отметим еще некоторые моменты, понимание которых требуется для правильного применения преобразования Фурье к анализу сигналов. Если рассмотреть ряд Фурье (сумму синусоид) на всей оси Х, то можно увидеть, что вне отрезка {0, T} функция представленная рядом Фурье будет будет периодически повторять нашу функцию.

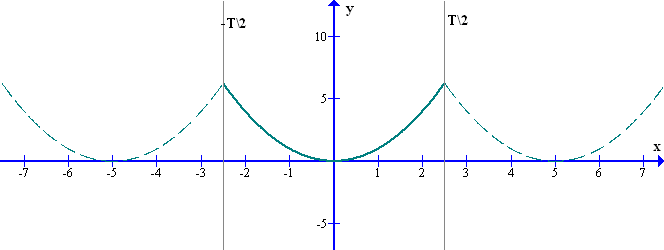
Например, на графике рис.7 исходная функция определена на отрезке {-T2, +T2}, а ряд Фурье представляет периодическую функцию, определенную на всей оси х.

Это происходит потому, что синусоиды сами являются периодическими функциями, соответственно и их сумма будет периодической функцией.

рис.7 Представление непериодической исходной функции рядом Фурье

Таким образом:

Наша исходная функция — непрерывная, непериодическая, определена на некотором отрезке длиной T.
Спектр этой функции — дискретный, то есть представлен в виде бесконечного ряда гармонических составляющих — ряда Фурье.
По факту, рядом Фурье определяется некоторая периодическая функция, совпадающая с нашей на отрезке {0, T}, но для нас эта периодичность не существенна.

Далее.

Периоды гармонических составляющих кратны величине отрезка {0, T}, на котором определена исходная функция f(x). Другими словами, периоды гармоник кратны длительности измерения сигнала. Например, период первой гармоники ряда Фурье равен интервалу Т, на котором определена функция f(x). Период второй гармоники ряда Фурье равен интервалу Т/2. И так далее (см. рис. 8).

рис.8 Периоды (частоты) гармонических составляющих ряда Фурье (здесь Т=2π)

Соответственно, частоты гармонических составляющих кратны величине 1/Т. То есть частоты гармонических составляющих Fk равны Fk= кТ, где к пробегает значения от 0 до ∞, например к=0 F0=0; к=1 F1=1T; к=2 F2=2T; к=3 F3=3T;… Fk= кТ (при нулевой частоте — постоянная составляющая).

Пусть наша исходная функция, представляет собой сигнал, записанный в течение Т=1 сек. Тогда период первой гармоники будет равен длительности нашего сигнала Т1=Т=1 сек и частота гармоники равна 1 Гц. Период второй гармоники будет равен длительности сигнала, деленной на 2 (Т2=Т/2=0,5 сек) и частота равна 2 Гц. Для третьей гармоники Т3=Т/3 сек и частота равна 3 Гц. И так далее.

Шаг между гармониками в этом случае равен 1 Гц.

Таким образом сигнал длительностью 1 сек можно разложить на гармонические составляющие (получить спектр) с разрешением по частоте 1 Гц.
Чтобы увеличить разрешение в 2 раза до 0,5 Гц — надо увеличить длительность измерения в 2 раза — до 2 сек. Сигнал длительностью 10 сек можно разложить на гармонические составляющие (получить спектр) с разрешением по частоте 0,1 Гц. Других способов увеличить разрешение по частоте нет.

Существует способ искусственного увеличения длительности сигнала путем добавления нулей к массиву отсчетов. Но реальную разрешающую способность по частоте он не увеличивает.

3. Дискретные сигналы и дискретное преобразование Фурье

С развитием цифровой техники изменились и способы хранения данных измерений (сигналов). Если раньше сигнал мог записываться на магнитофон и храниться на ленте в аналоговом виде, то сейчас сигналы оцифровываются и хранятся в файлах в памяти компьютера в виде набора чисел (отсчетов).

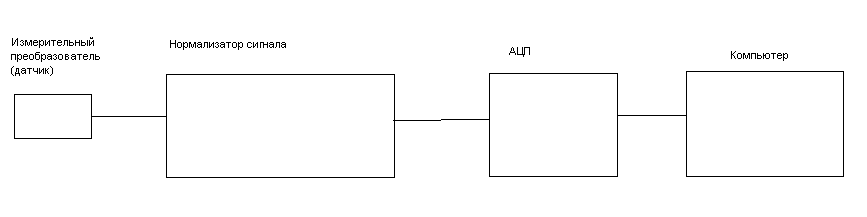
Обычная схема измерения и оцифровки сигнала выглядит следующим образом.

рис.9 Схема измерительного канала

Сигнал с измерительного преобразователя поступает на АЦП в течение периода времени Т. Полученные за время Т отсчеты сигнала (выборка) передаются в компьютер и сохраняются в памяти.

рис.10 Оцифрованный сигнал — N отсчетов полученных за время Т

Какие требования выдвигаются к параметрам оцифровки сигнала? Устройство, преобразующее входной аналоговый сигнал в дискретный код (цифровой сигнал) называется аналого-цифровой преобразователь (АЦП, англ. Analog-to-digital converter, ADC) ( Wiki).

Одним из основных параметров АЦП является максимальная частота дискретизации (или частота семплирования, англ. sample rate) — частота взятия отсчетов непрерывного во времени сигнала при его дискретизации. Измеряется в герцах. (( Wiki))

Согласно теореме Котельникова, если непрерывный сигнал имеет спектр, ограниченный частотой Fмакс, то он может быть полностью и однозначно восстановлен по его дискретным отсчетам, взятым через интервалы времени 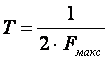, т.е. с частотой Fd ≥ 2*Fмакс, где Fd — частота дискретизации; Fмакс — максимальная частота спектра сигнала. Другими слова частота оцифровки сигнала (частота дискретизации АЦП) должна как минимум в 2 раза превышать максимальную частоту сигнала, который мы хотим измерить.

А что будет, если мы будем брать отсчеты с меньшей частотой, чем требуется по теореме Котельникова?

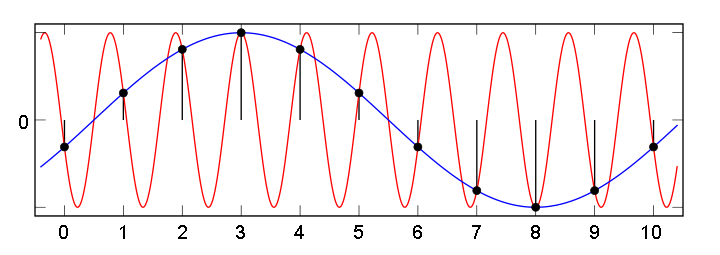
В этом случае возникает эффект «алиасинга» (он же стробоскопический эффект, муаровый эффект), при котором сигнал высокой частоты после оцифровки превращается в сигнал низкой частоты, которого на самом деле не существует. На рис. 11 красная синусоида высокой частоты — это реальный сигнал. Синяя синусоида более низкой частоты — фиктивный сигнал, возникающий вследствие того, за время взятия отсчета успевает пройти больше, чем пол-периода высокочастотного сигнала.

Рис. 11. Появление ложного сигнала низкой частоты при недостаточно высокой частоте дискретизации

Чтобы избежать эффекта алиасинга перед АЦП ставят специальный антиалиасинговый фильтр — ФНЧ (фильтр нижних частот), который пропускает частоты ниже половины частоты дискретизации АЦП, а более высокие частоты зарезает.

Для того, чтобы вычислить спектр сигнала по его дискретным отсчетам используется дискретное преобразование Фурье (ДПФ). Отметим еще раз, что спектр дискретного сигнала «по определению» ограничен частотой Fмакс, меньшей половине частоты дискретизации Fd. Поэтому спектр дискретного сигнала может быть представлен суммой конечного числа гармоник, в отличие от бесконечной суммы для ряда Фурье непрерывного сигнала, спектр которого может быть неограничен. Согласно теореме Котельникова максимальная частота гармоники должна быть такой, чтобы на нее приходилось как минимум два отсчета, поэтому число гармоник равно половине числа отсчетов дискретного сигнала. То есть если в выборке имеется N отсчетов, то число гармоник в спектре будет равно N/2.

Рассмотрим теперь дискретное преобразование Фурье (ДПФ).

Сравнивая с рядом Фурье

видим, что они совпадают, за исключением того, что время в ДПФ имеет дискретный характер и число гармоник ограничено величиной N/2 — половиной числа отсчетов.

Формулы ДПФ записываются в безразмерных целых переменных k, s, где k – номера отсчетов сигнала, s – номера спектральных составляющих.
Величина s показывает количество полных колебаний гармоники на периоде Т (длительности измерения сигнала). Дискретное преобразование Фурье используется для нахождения амплитуд и фаз гармоник численным методом, т.е. «на компьютере»

Возвращаясь к результатам, полученным в начале. Как уже было сказано выше, при разложении в ряд Фурье непериодической функции (нашего сигнала), полученный ряд Фурье фактически соответствует периодической функции с периодом Т. (рис.12).

рис.12 Периодическая функция f(x) с периодом Т0, с периодом измерения Т>T0

Как видно на рис.12 функция f(x) периодическая с периодом Т0. Однако из-за того, что длительность измерительной выборки Т не совпадает с периодом функции Т0, функция, получаемая как ряд Фурье, имеет разрыв в точке Т. В результате спектр данной функции будет содержать большое количество высокочастотных гармоник. Если бы длительность измерительной выборки Т совпадала с периодом функции Т0, то в полученном после преобразования Фурье спектре присутствовала бы только первая гармоника (синусоида с периодом равным длительности выборки), поскольку функция f(x) представляет собой синусоиду.

Другими словами, программа ДПФ «не знает», что наш сигнал представляет собой «кусок синусоиды», а пытается представить в виде ряда периодическую функцию, которая имеет разрыв из-за нестыковки отдельных кусков синусоиды.

В результате в спектре появляются гармоники, которые должны в сумме изобразить форму функции, включая этот разрыв.

Таким образом, чтобы получить «правильный» спектр сигнала, являющегося суммой нескольких синусоид с разными периодами, необходимо чтобы на периоде измерения сигнала укладывалось целое число периодов каждой синусоиды. На практике это условие можно выполнить при достаточно большой длительности измерения сигнала.

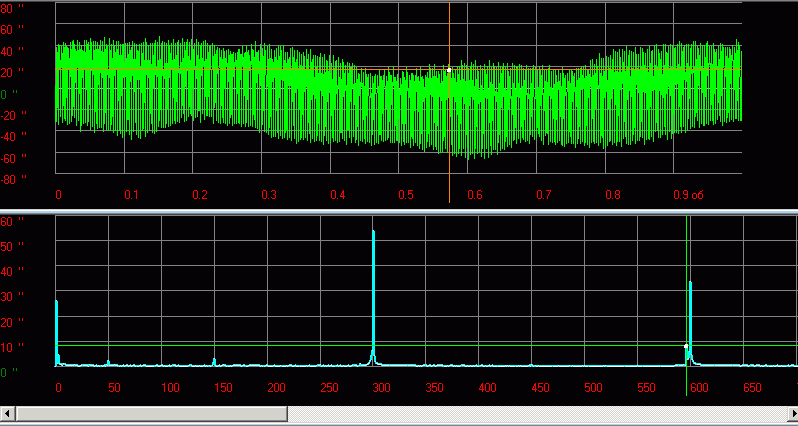
Рис.13 Пример функции и спектра сигнала кинематической погрешности редуктора

При меньшей длительности картина будет выглядеть «хуже»:

Рис.14 Пример функции и спектра сигнала вибрации ротора

На практике бывает сложно понять, где «реальные составляющие», а где «артефакты», вызванные некратностью периодов составляющих и длительности выборки сигнала или «скачками и разрывами» формы сигнала. Конечно слова «реальные составляющие» и «артефакты» не зря взяты в кавычки. Наличие на графике спектра множества гармоник не означает, что наш сигнал в реальности из них «состоит». Это все равно что считать, будто число 7 «состоит» из чисел 3 и 4. Число 7 можно представить в виде суммы чисел 3 и 4 — это правильно.

Так и наш сигнал… а вернее даже не «наш сигнал», а периодическую функцию, составленную путем повторения нашего сигнала (выборки) можно представить в виде суммы гармоник (синусоид) с определенными амплитудами и фазами. Но во многих важных для практики случаях (см. рисунки выше) действительно можно связать полученные в спектре гармоники и с реальными процессами, имеющими циклический характер и вносящими значительный вклад в форму сигнала.

Некоторые итоги

1. Реальный измеренный сигнал, длительностью T сек, оцифрованный АЦП, то есть представленный набором дискретных отсчетов (N штук), имеет дискретный непериодический спектр, представленный набором гармоник (N/2 штук).

2. Сигнал представлен набором действительных значений и его спектр представлен набором действительных значений. Частоты гармоник положительны. То, что математикам бывает удобнее представить спектр в комплексной форме с использованием отрицательных частот не значит, что «так правильно» и «так всегда надо делать».

3. Сигнал, измеренный на отрезке времени Т определен только на отрезке времени Т. Что было до того, как мы начали измерять сигнал, и что будет после того — науке это неизвестно. И в нашем случае — неинтересно. ДПФ ограниченного во времени сигнала дает его «настоящий» спектр, в том смысле, что при определенных условиях позволяет вычислить амплитуду и частоту его составляющих.

Использованные материалы и другие полезные материалы.

FourierScope — программа для построения радио сигналов и их спектрального анализа.
Graph — программа с открытым кодом, предназначенная для построения математических графиков.
ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ – КАК ЭТО ДЕЛАЕТСЯ
Дискретное преобразование Фурье (ДПФ)

При обсуждении переменного тока в одной из предыдущих статей (ссылка) мы познакомились с понятием гармонической (синусоидальной) функции. А бывают ли негармонические функции и сигналы, и как с ними работать? В этом нам и предстоит сегодня разобраться. Кроме того, мы рассмотрим важнейшее понятие – амплитудно-частотную характеристику (АЧХ) сигналов.

Гармонические и негармонические сигналы.

И для начала чуть подробнее разберемся, как классифицируются сигналы. В первую очередь, нас интересуют периодические сигналы. Их форма повторяется через определенный интервал времени T, называемый периодом. Периодические сигналы в свою очередь делятся на два больших класса – гармонические и негармонические. Гармонический сигнал – это сигнал, который можно описать следующей функцией:

Здесь A – амплитуда сигнала, w – циклическая частота, а phi – начальная фаза. Может возникнуть логичный вопрос – разве синусоидальный сигнал не является гармоническим? Конечно, является, дело в том, что sinalpha = cos(frac{pi}{2}medspace-medspace alpha) – то есть сигналы отличаются начальной фазой, соответственно, синусоидальный сигнал не противоречит определению, которое мы дали для гармонических колебаний.

Вторым подклассом периодических сигналов являются негармонические колебания. Вот пример негармонического сигнала:

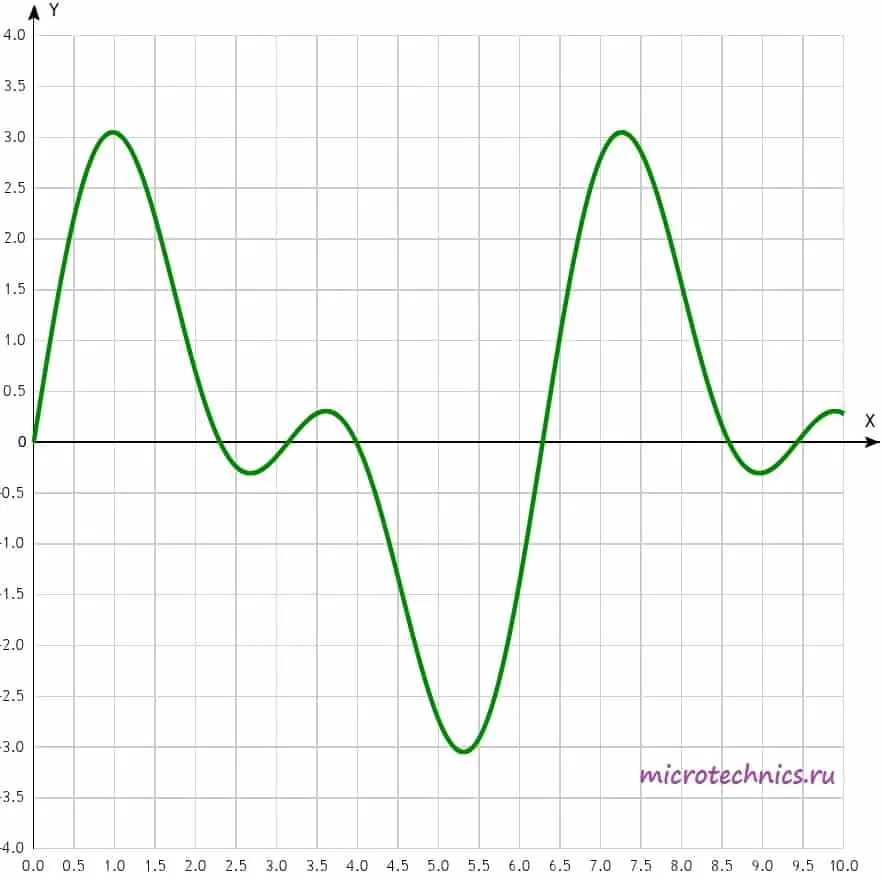
Как видите, несмотря на свой вид, сигнал остается периодическим, то есть его форма повторяется через интервал времени, равный периоду.

Для работы с такими сигналами и их исследования существует определенная методика, которая заключается в разложении сигнала в ряд Фурье. Суть состоит в том, что негармонический периодический сигнал (при выполнении определенных условий) можно представить в виде суммы гармонических колебаний с определенными амплитудами, частотами и начальными фазами. Важным нюансом является то, что все гармонические колебания, которые участвуют в суммировании, должны иметь частоты, кратные частоте исходного негармонического сигнала. Возможно это пока не совсем понятно, так что рассмотрим практический пример и разберемся подробнее. И для примера используем сигнал, который изображен на рисунке чуть выше. Его можно представить следующим образом:

u(t) = u_1(t) + u_2(t) = 2 sin(t) + 1.5 sin(2t)

Давайте изобразим все эти сигналы на одном графике:

Функции u_1(t), u_2(t) называют гармониками сигнала, а ту из них, период которой равен периоду негармонического сигнала, называют первой или основной гармоникой. В данном случае первой гармоникой является функция u_1(t) (ее частота равна частоте исследуемого негармонического сигнала, соответственно, равны и их периоды). А функция u_2(t) = 1.5 sin(2t) представляет из себя ни что иное как вторую гармонику сигнала (ее частота в два раза больше). В общем случае, негармонический сигнал раскладывается на бесконечное число гармоник:

u(t) = U_0 + sum_{i=0}^{infty}{U_{k}thinspace sin(thinspace kwt + phi_kthinspace )}

Здесь U_k – амплитуда, а phi_k – начальная фаза k-ой гармоники. Как мы уже упомянули чуть ранее, частоты всех гармоник кратны частоте первой гармоники, собственно, это мы и наблюдаем в данной формуле. U_0 – это нулевая гармоника, ее частота равна 0, она равна среднему значению функции за период. Почему среднему? Смотрите – среднее значения функции синуса за период равно 0, а значит при усреднении в этой формуле все слагаемые, кроме U_0 будут равны 0 👍

Амплитудный спектр сигнала.

Совокупность всех гармонических составляющих негармонического сигнала называют спектром этого сигнала. Различают фазовый и амплитудный спектр сигнала:

• фазовый спектр сигнала – совокупность начальных фаз всех гармоник
• амплитудный спектр сигнала – амплитуды всех гармоник, из которых складывается негармонический сигнал

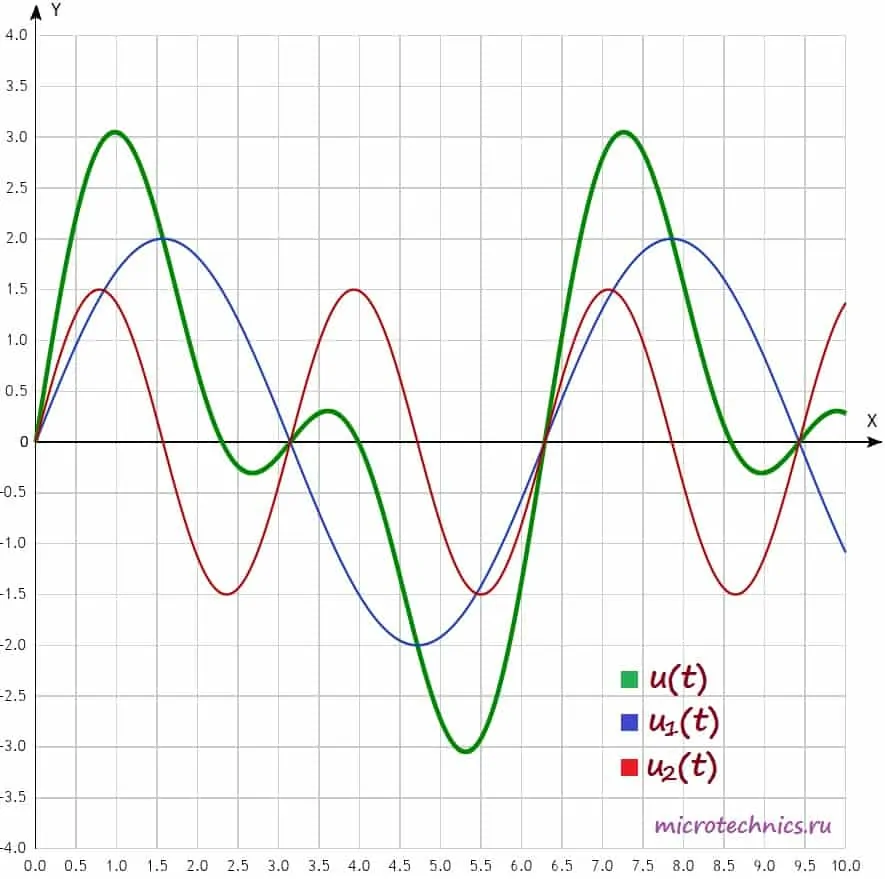
Давайте рассмотрим амплитудный спектр подробнее. Для визуального изображения спектра используют диаграммы, представляющие из себя набор вертикальных линий определенной длины (длина зависит от амплитуды сигналов). На горизонтальной оси диаграммы откладываются частоты гармоник:

При этом на горизонтальной оси могут откладываться как частоты в Гц, так и просто номера гармоник, как в данном случае. А по вертикальной оси – амплитуды гармоник, тут все понятно. Давайте построим амплитудный спектр сигнала для негармонического колебания, которое мы рассматривали в качестве примера в самом начале статьи. Напоминаю, что его разложение в ряд Фурье выглядит следующим образом:

u(t) = u_1(t) + u_2(t) = 2 sin(t) + 1.5 sin(2t)

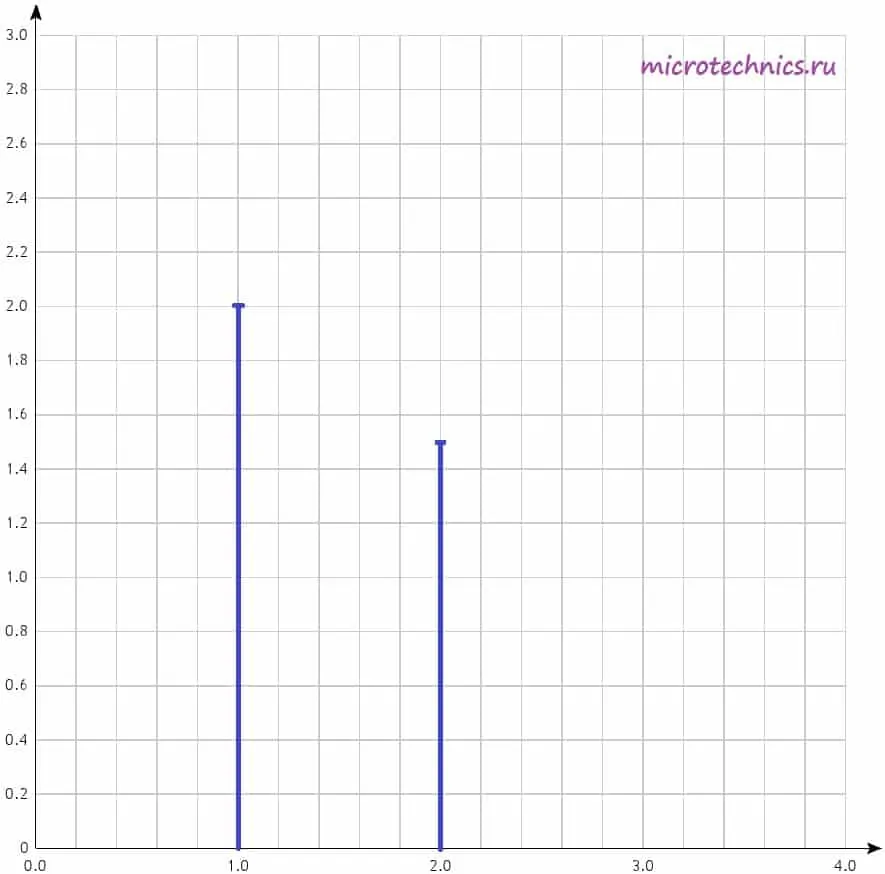
У нас есть две гармоники, амплитуды которых равны, соответственно, 2 и 1.5. Поэтому на диаграмме две линии, длины которых соответствуют амплитудам гармонических колебаний. Фазовый спектр сигнала строится аналогично, за той лишь разницей, что используются начальные фазы гармоник, а не амплитуды.

Итак, с построением и анализом амплитудного спектра сигнала мы разобрались. Давайте перейдем к следующей теме сегодняшней статьи – к понятию амплитудно-частотной характеристики.

Амплитудно-частотная характеристика (АЧХ).

АЧХ является важнейшей характеристикой многих цепей и устройств – фильтров, усилителей звука и т. д. Даже простые наушники имеют свою собственную амплитудно-частотную характеристику. Проанализируем, какой смысл она в себе несет…

АЧХ – это зависимость амплитуды выходного сигнала от частоты входного сигнала. Как мы выяснили в первой части статьи, негармонический периодический сигнал можно разложить в ряд Фурье. Но мы сейчас рассмотрим, в первую очередь, аудио-сигнал, и выглядит он следующим образом:

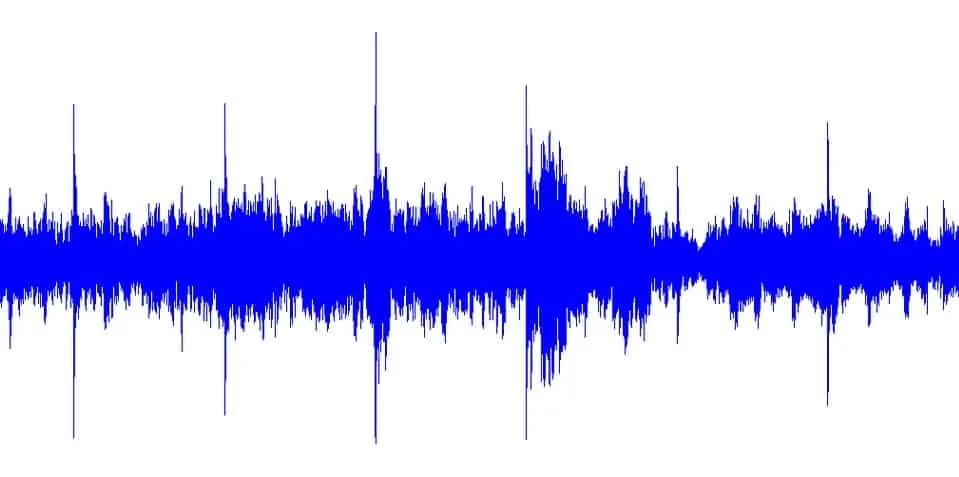
Как видите, ни о какой периодичности здесь не идет и речи. Но, к счастью, существуют специальные алгоритмы, которые позволяют представить звуковой сигнал в виде спектра входящих в него частот. Мы сейчас не будем подробно разбирать эти алгоритмы, это тема для отдельной статьи. Просто примем тот факт, что они позволяют нам осуществить такое преобразование.

Соответственно, мы можем построить диаграмму амплитудного спектра такого сигнала. А пройдя через какую-либо цепь (к примеру, через наушники при воспроизведении звука) сигнал будет изменен. Так вот амплитудно-частотная характеристика как раз и показывает, какие изменения будет претерпевать входной сигнал при прохождении через ту или иную цепь. Давайте детально обсудим этот момент.

Итак, на входе мы имеем ряд гармоник. Амплитудная-частотная характеристика показывает, как изменится амплитуда той или иной гармоники при прохождении через цепь. Рассмотрим пример АЧХ:

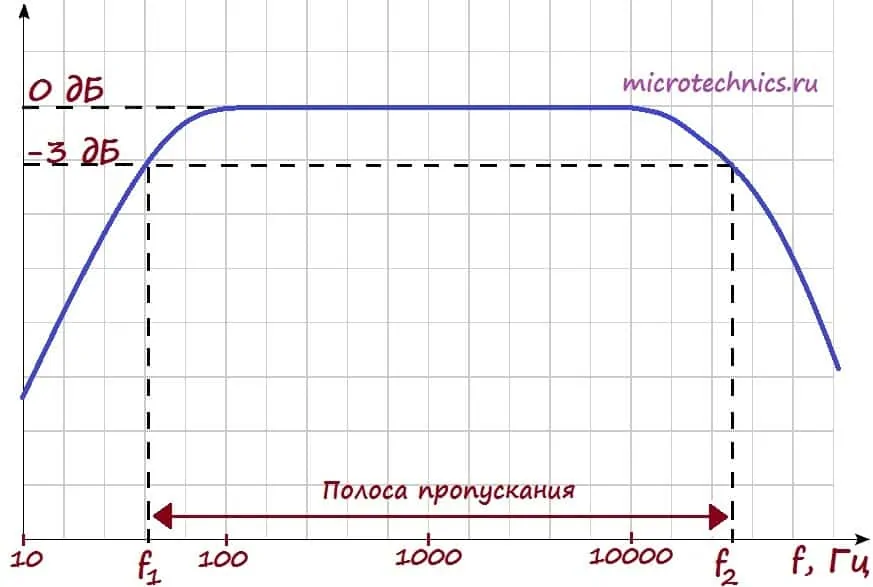
Разбираем поэтапно, что тут изображено. Начнем с осей графика АЧХ. По оси y мы откладываем величину выходного напряжения (или коэффициента усиления, как на данном рисунке). Коэффициент усиления мы считаем в дБ, соответственно величина, равная 0 дБ, соответствует усилению в 1 раз, то есть амплитуда сигнала остается неизменной.

По оси x откладываются частоты входного сигнала. Таким образом, в рассматриваемом случае для всех гармоник, частоты которых лежат в интервале от 100 до 10000 Гц, амплитуда не изменится. А сигналы всех остальных гармоник будут ослаблены.

На графике отдельно отмечены частоты f_1 и f_2. Их отличительной особенностью является то, что сигнал гармоник данных частот будет ослаблен в 1.41 раза (3 дБ) по напряжению. Это соответствует уменьшению по мощности в 2 раза . Полосу частот между f_1 и f_2 называют полосой пропускания. Получается следующая ситуация – сигналы всех гармоник, частоты которых лежат в пределах полосы пропускания устройства/цепи будут ослаблены менее, чем в 2 раза по мощности.

Практические примеры АЧХ аудио-устройств.

Частотный диапазон аудио-устройств обычно разбивают на низкие, средние и высокие частоты. Приблизительно это выглядит так:

• 20 Гц – 160 Гц – область низких частот
• 160 Гц – 1.28 КГц – область средних частот
• 1.28 КГц – 20.5 КГц – область высоких частот

Именно такую терминологию обычно можно встретить в разных программах-эквалайзерах, используемых для настройки звука. Теперь вы знаете, что красивые графики из таких программ являются именно амплитудно-частотными характеристиками, с которыми мы познакомились в сегодняшней статье. И в завершение статьи посмотрим на пару примеров АЧХ:

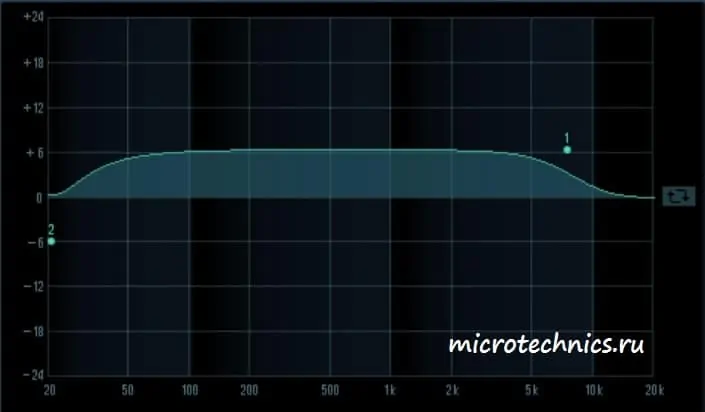
Здесь мы можем видеть амплитудно-частотную характеристику усилителя. Причем усилены будут преимущественно средние частоты диапазона.

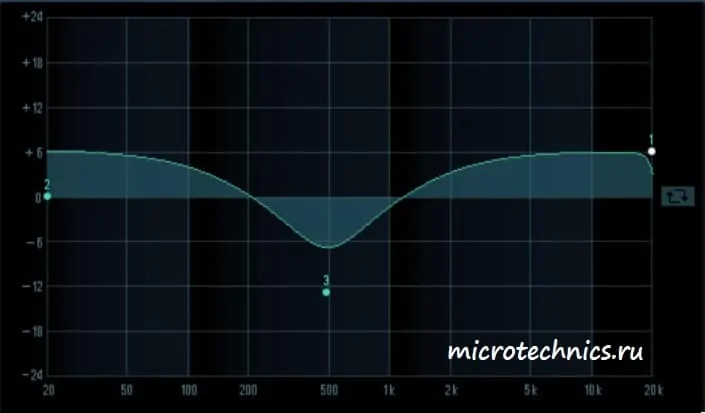
Во втором случае ситуация совсем другая – низкие и верхние частоты усиливаются, а в области средних частот для гармоник с частотой 500 Гц мы наблюдаем значительное ослабление.

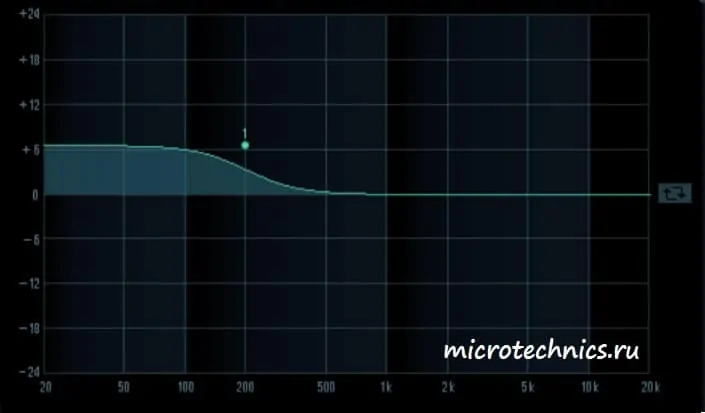
А теперь усиливаются только низкие частоты. Аудио-аппаратура с такой АЧХ будет обладать высоким уровнем басов.

На этом мы и заканчиваем нашу сегодняшнюю статью. Спасибо за внимание и ждем вас на нашем сайте снова 🤝

Как нам хорошо известно, сетевое напряжение имеет синусоидальную форму и частоту равную 50 Гц.

Это в идеале, но на практике так бывает далеко не всегда.

И дело здесь в гармонических составляющих сети – высших гармониках, представляющих из себя частотные сигналы, отличающиеся от основной частоты, и вносящих искажения в синусоидальную форму питающего напряжения, а это в свою очередь становится причиной ухудшения качества электроэнергии, нарушению нормальной работы электропотребителей и т.д.

Откуда же берутся эти гармонические составляющие?

Дело в том, что в цепях с линейной нагрузкой, к которым можно отнести сопротивление, индуктивность, емкость, протекающий через нагрузку ток пропорционален прикладываемому напряжению и следовательно синусоидальной форме сигнала напряжения соответствует токовая синусоида, поэтому разность фаз между ними равна нулю. А вот в случае, если наблюдается нелинейная зависимость протекающего тока от приложенного напряжения, синусоидальная форма сигнала искажается.

Связано это в первую очередь с ростом количества электрооборудования, имеющего нелинейные характеристики, вызванные наличием в схемотехнике полупроводниковых элементов. Наиболее “проблемными” в этом плане являются тиристорные регуляторы, преобразователи частоты, источники бесперебойного питания, электронные балласты, сварочные аппараты, электродуговые печи и другое оборудование с импульсными источниками питания.

Это приводит к возникновению импульсных токов, содержащих большое количество гармонических составляющих, так называемых высших гармоник, отличающихся от основной гармоники, которые затем попадают в электрические сети и вносят искажения. Гармоники образуются на частотах, кратных основной. Так, первая (основная) гармоника имеет частоту 50 Гц, частота гармоники 3-го порядка будет равна 150 Гц, частота гармоники 5-го порядка – 250 Гц и т.д. Получается, что реальное напряжение в сети представляет собой сумму основного синусоидального сигнала и его гармонических составляющих.

Надо учитывать, что полностью избавиться от влияния гармонических составляющих невозможно, и пока уровень гармоник не превышает допустимых норм, в принципе можно не беспокоиться о каких-то серьезным последствиях.

Согласно ГОСТ 13109-97, нормально допустимое значение коэффициентов гармонических составляющих напряжения для сетей 0,38 кВ составляет 8 %, а предельно допустимое – 12 %. Также в этом ГОСТ приведены допустимые значения для каждой n-ой гармонической составляющей, например для 3-ей гармоники это 5%, для 5-ой гармоники – 6,0 %, для 7-ой гармоники – 5 % и т.д. Считается, что наибольшие искажения в синусоидальный сигнал вносят гармоники 3, 5, 7 порядка.

Немного расчётов

Параметр, указывающий на уровень влияния нелинейных искажений, или по другому степень отличия формы сигнала от синусоидальной, называется коэффициентом нелинейных искажений Ku (THD – Total Harmonic Distorsions).

U (1) – действующее значение напряжения 1-ой гармоники

U(2), U(3) … U(40) – действующие значения напряжения высших гармоник.

Таким образом можно определить общую долю суммарного напряжения высших гармоник по отношению к напряжению основной частоты.

Еще одним параметром является коэффициент n-ой гармонической составляющей напряжения.

n – номер гармонической составляющей, кратной основной частоте

По этой формуле вычисляется вклад конкретной гармоники в общие искажения.

Основные характеристики гармоник

Все гармоники можно разделить по трем основным характеристикам – порядковому номеру, частоте и типу последовательности.

• Порядковый номер гармоники – это число,показывающее во сколько раз частота гармонической составляющей превышает частоту основной гармоники.
• Частота гармоники определяется путем умножения порядкового номера гармоники на значение основной частоты – 50 Гц.
• По типу последовательности разделяют гармоники прямой, обратной и нулевой последовательности. Гармоники 4, 7, 10, 13 и т. д. порядка образуют симметричную систему напряжений прямой последовательности, то есть совпадающей с последовательностью фаз первой гармоники. Гармоники 2, 5, 8, 11, 14 и т.д. образуют системы напряжений обратной последовательности по отношению к основной частоте. Гармоники с порядковым номером, кратным третьей гармоники (3, 6, 9, 12 и.д.) имеют нулевой порядок следования фаз, т.е. совпадают, и, следовательно, образуют симметричные системы нулевой последовательности.

Последствия возникновения гармоник

Какие же проблемы приносят гармонические составляющие в случае отклонения от предельно допустимых показателей?

На самом деле негативных воздействий немало, это увеличение потерь в сетях, перегрев трансформаторов,перегрузки на нейтральных проводах, гармонические шумы, искажение формы синусоидальной кривой, перегрузка и следовательно уменьшение срока службы конденсаторов коррекции коэффициента мощности, поверхностный эффект. И это еще перечислены не все негативные последствия данного эффекта. Все эти факторы приводят в конечном итоге к экономическим, энергетическим потерям и сокращению срока службы оборудования.

Поэтому в случае увеличения количества гармоник и их выхода за допустимые пределы, необходимо задуматься о принятии решений для снижения их уровня, при этом предварительно проводятся измерения гармонических искажений, по результату которых уже определяются необходимые меры .

Измерение показателей гармоник в сети

Для анализа качества электросети и выявления высших гармоник применяются, в частности, многофункциональные измерительные приборы или по другому анализаторы качества электроэнергии.

Они позволяют получать подробную информацию по всем основным характеристикам качества электроэнергии, таким как:

• коэффициент мощности
• коэффициент амплитуды
• среднеквадратичные значения тока и напряжения
• значения активной, реактивной и полной мощности
• активной и реактивной энергии в прямом и обратном направлении
• суммарный коэффициент гармоник THD тока и напряжения
• коэффициент n-й гармонической составляющей напряжения
• дисбаланс напряжения

И целый ряд других параметров, которые по совокупности позволяют получить точную оценку не только гармонических величин, но и провести полный анализ состояния сетей.

Кроме этого, анализаторы имеют дополнительные функции, такие как ведение журнала событий, проверка последовательности чередования фаз, передача данных на верхний уровень по интерфейсу RS-485 или Ethernet, светодиодная индикация, дискретные входы и выходы.

Способы уменьшения гармонических составляющих

На основании полученных данных можно принимать решения о внедрении средств, направленных на уменьшение гармонических составляющих.

К основным способам уменьшения гармоник относятся разделение линейных и нелинейных нагрузок, обеспечение симметричного режима работы трехфазной системы, снижение полного сопротивления распределительной сети за счет увеличения сечения кабелей, применение линейных дросселей, применение изолирующих трансформаторов с обмотками «треугольник» и «звезда», применение пассивных и активных фильтров.

Одним из наиболее простых способов снижения уровня высших гармоник является установка линейных дросселей переменного тока. В частности, такой способ фильтрации широко применяется для подавления помех, возникающих при работе частотных преобразователей.

Дроссель имеет малое значение индуктивного сопротивления на основной частоте 50 Гц и большое значение сопротивления для высших гармоник, что приводит к их ослаблению. Помимо дросселей переменного тока, для частотных преобразователей могут применяться и дроссели звена постоянного тока.

Помимо дросселей широко применяются пассивные и активные фильтры.

Пассивный фильтр гармоник

Пассивные фильтры строятся на основе индуктивно-емкостной схемы (LC-фильтры), состоящей из продольных индуктивностей и поперечной цепи, состоящей из последовательно включенных индуктивности и емкости которые образуют последовательный колебательный контур, настроенный на определенную гармонику. Если необходимо уменьшение коэффициента искажения по нескольким гармоникам, можно использовать несколько параллельно включенных фильтров. Такой метод часто используется в цепях с источниками бесперебойного питания ( UPS).

Недостатком такого метода является его ограниченный только определенными гармониками эффект, поэтому для подавления всего спектра гармонических составляющих в сети используются активные фильтры.

Активный фильтр гармоник

Активный фильтр гармоник (АФГ) представляет собой электронное устройство, можно сказать является управляемым источником тока, подключаемым параллельно с нагрузкой, генерирующей высшие гармоники. Принцип действия основан на анализе гармоник нелинейной нагрузки и генерировании в распределительную сеть таких же гармоник, но противофазе. В результате высшие гармонические составляющие нейтрализуются в точке подключения фильтра и на выходе получается почти синусоидальная форма.

Такой метод благодаря своей эффективности является одним из наиболее действенных способов подавления высших гармоник, но не самым дешевым. Его применение оправдано там, где наблюдается большой уровень искажений.