Как найти газовую постоянную для газа

Универса́льная га́зовая постоя́нная — константа, численно равная работе расширения одного моля идеального газа в изобарном процессе при увеличении температуры на 1 К. Равна произведению постоянной Больцмана на число Авогадро. Обозначается латинской буквой R.

Общая информация[править | править код]

И. П. Алымов (1865)^[1][2][3], Цейнер (1866)^[4], Гульдберг (1867)^[5], Горстман (1873)^[6] и Д. И. Менделеев (1874)^[7][2][3] пришли к выводу, что произведение индивидуальной для каждого газа постоянной в уравнении Клапейрона на молекулярный вес μ газа должно быть постоянной для всех газов величиной. Д. И. Менделеев вычислил^[8][9] значение константы R, используя закон Авогадро, согласно которому 1 моль различных газов при одинаковом давлении и температуре занимает одинаковый объём

Входит в уравнение состояния идеального газа
в формулу для коэффициента диффузии сферических броуновских частиц
и в ряд других уравнений молекулярно-кинетической теории.

В Международной системе единиц (СИ) универсальная газовая постоянная, в силу точно установленных численных значений постоянных Авогадро и Больцмана, в точности равна

R = 8,314 462 618 153 24 Дж/(моль∙К).

В системе СГС универсальная газовая постоянная равна R = 83 144 626,181 532 4 эрг/(моль∙К) (точно).

Универсальная газовая постоянная равна разности молярных теплоёмкостей идеального газа при постоянном давлении и постоянном объёме: Кроме того, поскольку отношение теплоёмкостей данного идеального газа является его показателем адиабаты можно записать следующие соотношения:

У идеального газа показатель адиабаты связан с числом степеней свободы f молекулы соотношением что позволяет сразу вычислять молярные теплоёмкости газов, близких к идеальным. Например, для воздуха (в основном двухатомного газа, молекулы которого при комнатной температуре обладают тремя поступательными и двумя вращательными степенями свободы, f = 3+2 = 5) показатель адиабаты γ = 1 + 2/5 = 7/5, откуда Для аргона (одноатомного газа) у молекулы есть лишь три поступательные степени свободы, откуда γ = 1 + 2/3 = 5/3, а теплоёмкости

Эти соотношения обусловлены законом равнораспределения энергии по степеням свободы, утверждающим, что в тепловом равновесии при температуре T на одну степень свободы вращательного и поступательного движения молекулы приходится в среднем энергия, равная (1/2)kT, а на одну колебательную степень свободы — энергия kT^[10]; здесь k — постоянная Больцмана. Для большинства двухатомных газов при комнатной температуре колебательные степени свободы не возбуждаются (это проявление квантового характера осцилляций молекулы), и их не нужно учитывать. При увеличении температуры на 1 К при постоянном объёме энергия каждой молекулы газа по каждой кинетической степени свободы в среднем увеличивается на k/2, а энергия 1 моля газа (число Авогадро молекул, N_A) — на N_Ak/2. Так, энергия молекулы одноатомного газа увеличивается на , а энергия моля такого газа — на Отсюда становится понятной связь между универсальной газовой константой, постоянной Больцмана и числом Авогадро:

Универсальная газовая постоянная возникает и в приложениях термодинамики, относящихся к жидкостям и твёрдым телам. Так, эмпирический закон Дюлонга — Пти утверждает, что при комнатной температуре молярная теплоёмкость твёрдых простых веществ близка к 3R. Он объясняется тем, что атом в кристаллической решётке имеет три колебательные степени свободы, то есть согласно закону равнораспределения на каждый атом приходится в среднем 3kT/2 кинетической и столько же потенциальной энергии. Отсюда моль атомов обладает тепловой энергией Этот закон выполняется лишь при абсолютных температурах, значительно превышающих так называемую температуру Дебая для данного вещества, которая определяет необходимость учёта квантовой статистики при низких температурах.

Иногда рассматривается также индивидуальная газовая постоянная конкретного газа, равная отношению R к молекулярной массе данного газа (или к средней молекулярной массе смеси газов): R′ = R / μ. Для сухого воздуха R′ ≈ 287 Дж/(кг∙К), для водорода 4125 Дж/(кг∙К).

Связь между газовыми константами[править | править код]

Как показано выше, универсальная газовая постоянная выражается через произведение постоянной Больцмана на число Авогадро^[11]:

Постоянную Больцмана используют в формулах, описывающих изучаемое явление или поведение рассматриваемого объекта с микроскопической точки зрения (см. Молекулярно-кинетическая теория, Статистическая физика, Физическая кинетика), тогда как универсальная газовая постоянная более удобна при расчетах, касающихся макроскопических систем, когда число частиц задано в молях.

См. также[править | править код]

• Постоянная Больцмана
• Число Авогадро
• Уравнение состояния идеального газа

Примечания[править | править код]

Литература[править | править код]

• Partington J. R. A Text-book of Thermodynamics (with Special Reference to Chemistry). — London: Constable & Company LTD, 1913. — x + 544 p.
• Partington J. R. An Advanced Treatise on Physical Chemistry. Vol. 1. Fundamental Principles. The Properties of Gases. — London — New York — Toronto: Longmans, Green and Co, 1949. — xlii + 943 p.
• Zeuner G. Grundzüge der mechanischen Wärmetheorie. — 2. vollständig umgearbeitete Auflage. — Leipzig: Verlag von Arthur Felix, 1866. — xvi + 568 + xxv p.
• Алымов И. Научные выводы относительно водяного пара // Морской сборник. — 1865. — Т. 77, № 3. — С. 87—113.
• Больцмана постоянная // Физическая энциклопедия. — 1988. — Т. 1. — С. 222.
• Гельфер Я. М. История и методология термодинамики и статистической физики. — 2-е изд., перераб. и доп. — М.: Высшая школа, 1981. — 536 с.
• Голоушкин В. Н. Уравнение состояния идеального газа Д.И. Менделеева // Успехи физических наук. — 1951. — Т. 45, № 4. — С. 616—621. — doi:10.3367/UFNr.0045.195112c.0616.
• Кипнис А. Я. К истории установления уравнения состояния идеального газа // Вопросы истории естествознания и техники. — Изд-во АН СССР, 1962. — № 13. — С. 91—94.

From Wikipedia, the free encyclopedia

Value of R[1]	Unit
SI units
8.31446261815324	J⋅K−1⋅mol−1
8.31446261815324	m3⋅Pa⋅K−1⋅mol−1
8.31446261815324	kg⋅m2⋅s−2⋅K−1⋅mol−1
Other common units
8314.46261815324	L⋅Pa⋅K−1⋅mol−1
8.31446261815324	L⋅kPa⋅K−1⋅mol−1
0.0831446261815324	L⋅bar⋅K−1⋅mol−1
8.31446261815324×107	erg⋅K−1⋅mol−1
0.730240507295273	atm⋅ft3⋅lbmol−1⋅°R−1
10.731577089016	psi⋅ft3⋅lbmol−1⋅°R−1
1.985875279009	BTU⋅lbmol−1⋅°R−1
297.031214	inH2O⋅ft3⋅lbmol−1⋅°R−1
554.984319180	torr⋅ft3⋅lbmol−1⋅°R−1
0.082057366080960	L⋅atm⋅K−1⋅mol−1
62.363598221529	L⋅Torr⋅K−1⋅mol−1
1.98720425864083…	cal⋅K−1⋅mol−1
8.20573660809596…×10−5	m3⋅atm⋅K−1⋅mol−1

The molar gas constant (also known as the gas constant, universal gas constant, or ideal gas constant) is denoted by the symbol R or R. It is the molar equivalent to the Boltzmann constant, expressed in units of energy per temperature increment per amount of substance, i.e. the pressure–volume product, rather than energy per temperature increment per particle. The constant is also a combination of the constants from Boyle’s law, Charles’s law, Avogadro’s law, and Gay-Lussac’s law. It is a physical constant that is featured in many fundamental equations in the physical sciences, such as the ideal gas law, the Arrhenius equation, and the Nernst equation.

The gas constant is the constant of proportionality that relates the energy scale in physics to the temperature scale and the scale used for amount of substance. Thus, the value of the gas constant ultimately derives from historical decisions and accidents in the setting of units of energy, temperature and amount of substance. The Boltzmann constant and the Avogadro constant were similarly determined, which separately relate energy to temperature and particle count to amount of substance.

The gas constant R is defined as the Avogadro constant N_A multiplied by the Boltzmann constant k (or k_B):

Since the 2019 redefinition of SI base units, both N_A and k are defined with exact numerical values when expressed in SI units.^[2] As a consequence, the SI value of the molar gas constant is exactly 8.31446261815324 J⋅K⁻¹⋅mol⁻¹.

Some have suggested that it might be appropriate to name the symbol R the Regnault constant in honour of the French chemist Henri Victor Regnault, whose accurate experimental data were used to calculate the early value of the constant. However, the origin of the letter R to represent the constant is elusive. The universal gas constant was apparently introduced independently by Clausius’ student, A.F. Horstmann (1873)^[3][4]
and Dmitri Mendeleev who reported it first on Sep. 12, 1874.^[5]
Using his extensive measurements of the properties of gases,^[6][7]
Mendeleev also calculated it with high precision, within 0.3% of its modern value.^[8]

The gas constant occurs in the ideal gas law:

where P is the absolute pressure, V is the volume of gas, n is the amount of substance, m is the mass, and T is the thermodynamic temperature. R_specific is the mass-specific gas constant. The gas constant is expressed in the same unit as are molar entropy and molar heat.

Dimensions[edit]

From the ideal gas law PV = nRT we get:

where P is pressure, V is volume, n is number of moles of a given substance, and T is temperature.

As pressure is defined as force per area of measurement, the gas equation can also be written as:

Area and volume are (length)² and (length)³ respectively. Therefore:

Since force × length = work:

The physical significance of R is work per degree per mole. It may be expressed in any set of units representing work or energy (such as joules), units representing degrees of temperature on an absolute scale (such as kelvin or rankine), and any system of units designating a mole or a similar pure number that allows an equation of macroscopic mass and fundamental particle numbers in a system, such as an ideal gas (see Avogadro constant).

Instead of a mole the constant can be expressed by considering the normal cubic meter.

Otherwise, we can also say that:

Therefore, we can write R as:

And so, in terms of SI base units:

R = 8.314462618… kg⋅m²⋅s⁻²⋅K⁻¹⋅mol⁻¹.

Relationship with the Boltzmann constant[edit]

The Boltzmann constant k_B (alternatively k) may be used in place of the molar gas constant by working in pure particle count, N, rather than amount of substance, n, since

where N_A is the Avogadro constant.
For example, the ideal gas law in terms of the Boltzmann constant is

where N is the number of particles (molecules in this case), or to generalize to an inhomogeneous system the local form holds:

where ρ_N = N/V is the number density.

Measurement and replacement with defined value[edit]

As of 2006, the most precise measurement of R had been obtained by measuring the speed of sound c_a(P, T) in argon at the temperature T of the triple point of water at different pressures P, and extrapolating to the zero-pressure limit c_a(0, T). The value of R is then obtained from the relation

where:

• γ₀ is the heat capacity ratio (5/3 for monatomic gases such as argon);
• T is the temperature, T_TPW = 273.16 K by the definition of the kelvin at that time;
• A_r(Ar) is the relative atomic mass of argon and M_u = 10⁻³ kg⋅mol⁻¹ as defined at the time.

However, following the 2019 redefinition of the SI base units, R now has an exact value defined in terms of other exactly defined physical constants.

Specific gas constant[edit]

Rspecific for dry air	Unit
287.052874	J⋅kg−1⋅K−1
53.3523	ft⋅lbf⋅lb−1⋅°R−1
1,716.46	ft⋅lbf⋅slug−1⋅°R−1
Based on a mean molar mass for dry air of 28.964917 g/mol.

The specific gas constant of a gas or a mixture of gases (R_specific) is given by the molar gas constant divided by the molar mass (M) of the gas or mixture.

Just as the molar gas constant can be related to the Boltzmann constant, so can the specific gas constant by dividing the Boltzmann constant by the molecular mass of the gas.

Another important relationship comes from thermodynamics. Mayer’s relation relates the specific gas constant to the specific heat capacities for a calorically perfect gas and a thermally perfect gas.

where c_p is the specific heat capacity for a constant pressure and c_v is the specific heat capacity for a constant volume.^[9]

It is common, especially in engineering applications, to represent the specific gas constant by the symbol R. In such cases, the universal gas constant is usually given a different symbol such as R to distinguish it. In any case, the context and/or unit of the gas constant should make it clear as to whether the universal or specific gas constant is being referred to. ^[10]

In case of air, using the perfect gas law and the standard sea-level conditions (SSL) (air density ρ₀ = 1.225 kg/m³, temperature T₀ = 288.15 K and pressure p₀ = 101325 Pa), we have that R_air = P₀/(ρ₀T₀) = 287.052874247 J·kg⁻¹·K⁻¹. Then the molar mass of air is computed by M₀ = R/R_air = 28.964917 g/mol.^[11]

U.S. Standard Atmosphere[edit]

The U.S. Standard Atmosphere, 1976 (USSA1976) defines the gas constant R^∗ as:^[12][13]

R^∗ = 8.31432×10³ N⋅m⋅kmol⁻¹⋅K⁻¹ = 8.31432 J⋅K⁻¹⋅mol⁻¹.

Note the use of kilomoles, with the resulting factor of 1000 in the constant. The USSA1976 acknowledges that this value is not consistent with the cited values for the Avogadro constant and the Boltzmann constant.^[13] This disparity is not a significant departure from accuracy, and USSA1976 uses this value of R^∗ for all the calculations of the standard atmosphere. When using the ISO value of R, the calculated pressure increases by only 0.62 pascal at 11 kilometers (the equivalent of a difference of only 17.4 centimeters or 6.8 inches) and 0.292 Pa at 20 km (the equivalent of a difference of only 33.8 cm or 13.2 in).

Also note that this was well before the 2019 SI redefinition, through which the constant was given an exact value.

References[edit]

External links[edit]

• Ideal gas calculator Archived 2012-07-15 at the Wayback Machine – Ideal gas calculator provides the correct information for the moles of gas involved.
• Individual Gas Constants and the Universal Gas Constant – Engineering Toolbox

В физике мы частенько встречаемся с такой штукой, как универсальная газовая постоянная. Вроде как и понятно, что её значение равно 8,31 Дж/Моль*градус.

Используется она преимущественно в задачах про газы и газовые законы. Но пытливые умы обязательно спросят…А зачем всё это и почему универсальная?

Для начала начнем со стандартного определения из учебника:

Универсальная газовая постоянная — константа, численно равная работе расширения одного моля идеального газа в изобарном процессе при увеличении температуры на 1 К. Равна произведению постоянной Больцмана на число Авогадро. Обозначается латинской буквой R.

Разбираем определение по атомам

Слово константа оно и понятно без лишних комментариев. В физике оно означает нечто типа “неизменная не при каких условиях величина“. Скажем, масса гири 10 кг и при нормальных условиях этот параметр не изменится, если не отпилить от гири кусок.

Численно равная – это просто красивая формулировка, которая означает что одно число равно другому числу.

Одного моля… – что такое моль мы наверное помним. Это количество вещества. Такая единица измерения объема. Для тех, кто не помнит, отметим, что моль – это количество вещества массой равной его молекулярной массе. Например, есть молекула водорода, состоящая из двух атомов. У неё есть стандартная масса. Значит, чтобы взять 1 моль водорода, нужно взять массу водорода, равную массе 1 молекулы этого водорода. Для каждого вещества это свой объем.

Идеальный газ – это несуществующий в природе газ. Его упрощенная модель, которая не учитывает взаимодействие между самим частицами газа, кроме их соударений друг с другом или при ударе об стенки. Почему модель? Потому что если брать газ реальный, то крыша может натурально поехать. Для упрощения мы рассматриваем модель.

Изобарный процесс – это процесс, который протекает при постоянном давлении. Скажем, если кипятить воду в открытой кастрюле, то процесс изобарный. Давление постоянное, так как крышки нет, а температура с объемом могут изменяться.

Про число Авогадро мы писали отдельно в этом материале. Повторяться уже не будем.

А вот про постоянную Больцмана вспомним! Это физическая постоянная, определяющая связь между температурой и энергией. Грубо говоря, благодаря этому значению можно рассчитать, насколько вырастет энергия газа при нагреве. Ну а равна она 1,38*10^-23 Дж/К.

Как всё это увязать в голове

Здорово…Теперь мы все термины знаем. Но всё равно непонятно, для чего нужна газовая постоянная. Попробуем сказать понятными словами тоже самое.

Если увеличить температуру на один кельвин при неизменном давлении процесса, то газ расширяется и при этом расширении системой (газом) совершается работа (или затрачивается энергия), равная универсальной газовой постоянной или 8,31 Дж.

Ну так-то вроде теперь всё понятно! Кроме того, для чего это знать…

Для чего нужна универсальная газовая постоянная

Нужна эта величина для упрощения расчётов. Она так и будет мелькать во всем курсе физики. Физический смысл мы уже знаем.

Эта величина используется всегда, когда речь заходит о процессах, где есть работа при изменении состояния газов. Скажем, когда нужно рассчитать изменение термодинамических параметров если изменился один из них. Выведение этой величины в единую газовую постоянную упрощает дальнейшие расчёты.

Универсальная газовая постоянная удобна при расчетах, касающихся макроскопических систем, когда число частиц задано в молях.

————

Обязательно оцените статью лайком и подпишитесь на проект! Это очень важно для развития канала. Виноваты странные алгоритмы Дзена!

————-

Советую также прочитать на нашем канале:

—–

Смотрите нас на YouTube и присоединяйтесь к нашему Телеграм!

Удельная газовая
постоянная однородного газа, заменяющего
смесь, называется газовой постоянной
смеси R_см,
Дж / (кг·К):

,

или окончательно

.

Через мольные доли
газовая постоянная смеси вычисляется
следующим образом:

,
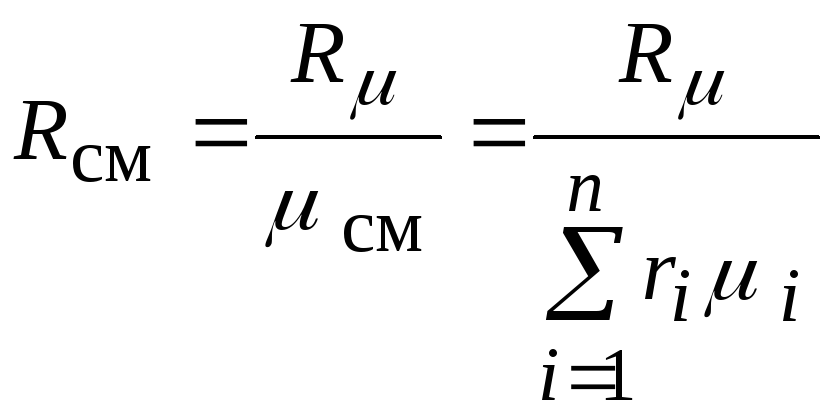или окончательно

.

С использованием

можно получить формулу для вычисления
парциального давления идеального газа

через его массовую долю.

Т. к. и
,

то разделив эти
выражения друг на друга получим:

,

откуда

Из последнего
выражения можно получить удобную
формулу, связывающую мольные и массовые
доли идеального газа.

Т. к. ,

то

1.4.8. Плотность смеси газов

Плотность однородного
газа, заменяющего
смесь, называется плотностью смеси:

В справочниках
обычно приводится без объяснений
следующая формула для плотности смеси:

В то же время в
технической литературе встречаются
формулы вида

С вычислением
плотности смеси через плотности
компонентов связано наибольшее число
студенческих ошибок. Дело в том, что
значение плотности
-го
компонента можноформальнополучить из двух формул:

и

Т.
к.
,
то значенияизаметно отличаются друг от друга.

Проясним вопрос
с вычислением плотности смеси.

По определению
и,
тогда.

Но
и

Т.
о. в последней формуле плотность i-го
газавычисляется как плотность этого газа,
находящегося в количествекилограммовв объеме(парциальном объеме) при давлении
смеси
и температуре смеси .

Такое толкование
плотности компонентов смеси используется,
в частности, при расчетеобъемов
продуктов сгорания топлива.

Если плотность
i-го газа в смеси
вычислять через его парциальное давление

,
то

Т.
о. в этой формуле плотность i-го
газа– это плотность газа массой,
находящегося вобъеме (объем
смеси) при его парциальном давлении и температуре(температуре смеси).

Такое толкование
плотности компонентов смеси, в частности,
используется при определении абсолютной
и относительной влажности воздуха.

1.4.9. Энтропия смеси идеальных газов

Как указано в
параграфе 1.4.1., энтропия 1 кг
–
компонентной смеси идеальных газов
(удельная энтропия смеси)S_см
, Дж / (К · кг), определяется по
следующей формуле:

,

где: –
энтропия 1 кгi-го газа.

Из
курса общей термодинамики известно:

,

где: –
массовая изобарная теплоемкостьi-го
газа.

Окончательно
удельная энтропия
-компонентной
смеси может быть вычислена по следующей
формуле:

1.4.10. Теплоемкость газовой смеси

По определению,
теплоемкость – это количество теплоты,
которое необходимо для изменения
температуры единицы количества вещества

(
)
на один градус.

Т. к. температура
всех газов в смеси одинакова, то
теплоемкость смеси, складывается из
теплоемкостей всех компонентов, взятых
в долях, соответствующих способу задания
смеси:

– массовая (удельная)
теплоемкость, Дж / (кг·К);

– мольная теплоемкость,
Дж / (кмоль·К);

– объемная
теплоемкость, Дж / (м³·К).

где: – массовая, мольная и объемная теплоемкостиi-го компонента.

Газовая постоянная смеси газов.

Газовая постоянная смеси газов.

• Газовая постоянная смешанного газа Смешанный газ следует уравнению состояния-pV = mRT и R = pV / mT. Из Формулы (3-2″) n = gtRi / R и 2G / = ZgiRi / R = 1, из которых^ Р = организации стандартов Ирана ’= ^ + g2R2 + … + гнрн. ■(3-3)） Газовая постоянная смешанного газа равна сумме массовой доли каждого газа и произведения этой

газовой постоянной. Еще одно уравнение, определяющее газовую постоянную смеси Р = 2giRi-Ф 8314.2(г,/ ^ + ГДж <он + … + г меня. по известной средней молекулярной массе смеси. Людмила Фирмаль

отдельных газов определяется тем же уравнением, но там вводится фактическая молекулярная масса каждого газа. Если указан объемный состав смеси, (3-2 ’） gi =(RiRiYi и Xg,= RZn / Rt = 1. И затем… R—V = 1 KrJR, + rJR,+; • • + rn! Дипломированная медсестра.) •(3-6)）Средняя молекулярная масса газовой смеси Средняя молекулярная масса является условной величиной, которая относится

к однородному газу, в котором число молекул и общая масса равны числу молекул и массе смешанного газа. Если известна газовая постоянная смеси、 С-8314.2 / Р•. (3-7） И. Я — = 8314.2%/?+ 2 + … + gntfn). Газовая постоянная Rlt R2t …Заменив Rn величиной из уравнения Клапейрона, получим формулу средней молекулярной массы, если смесь задана массовой долей. х = л / (&//ИИ + gjpt + … + W-(3: 8） Если

• смесь указана в объемной доле, то из Формулы (3-6): Р = H2rJRi = 8314.2 / 2rf | если. С / ? ’8 314,2 / Форекс ’ И затем… •[Л= Srijij = rjfij +Г2[Л2+ … +Гпсп. (3-9） Средняя молекулярная масса газовой смеси равна сумме продуктов объемной доли по молекулярной массе отдельных газов, входящих в состав смеси.Парциальное давление Если известны основные параметры газа, то парциальное давление

газа можно определить по массовой доле уравнения Клапейрона. Л = п =(3-10） В. г-н р. Привет.. чтобы найти парциальное давление каждого газа при определении смеси по объемной доле. ПТВ = ПВЛ и Pi = Р ^ = РТП. (3-11） Парциальное давление каждого газа равно произведению полного давления смешанного газа на объемную долю. Формула (3-

Вы можете использовать закон Бойля-Марриотта Людмила Фирмаль

11)обычно используется при техническом расчете и испытаниях теплового оборудования. Объемная доля газа определяется специальным прибором — газоанализатором. Управление вопросами и примерами в главе 3 1.Что такое смешанный газ? 2.Дайте Далтону формулировку закона. • * 3.Что называется парциальным давлением?

4.Что называется массой, объемом и молярной долей? 5.Так называемая частичная, или. Ты убавил громкость? Какова связь между удельным объемом, плотностью, молекулярной массой и постоянной газа? 7.Почему молекулярная масса смеси называется средней молекулярной массой? * 8.Как. Пересчет массового состава в объем и пересчет объема в объем? 9., Как определяется газовая

постоянная смеси по массовой доле и объемной доле? — В J0.Как парциальное давление газа в смеси определяется массовой долей и объемной долей? 11.Как определяется средняя молекулярная масса смеси газов? Пример 3-1.Если мы предположим, что объем сухого воздуха составляет 21% 02 и 79% N2, мы получим среднюю молекулярную массу сухого воздуха. По Формуле (3-9)、 = РЛ іх +

r2fx3= 32-0.210 + 28.016-0.79 = 28.93 Пример 3-2 определяет газовую постоянную, плотность и парциальное давление смеси, состоящей из 20 массовых долей воздуха и 1 массовой доли легкого газа. Плотность легкого газа при температуре 273°К и давлении 101325 ″ Li2 ″ равна 0,52 кг Газовая постоянная легкого газа определяется по формуле Клапейрона. U1325 = 7и Джей!(Кг-град). J 0,52-273 В и’

Газовая постоянная воздуха составляет 287.04 Дж! Это хорошая идея. Газовая постоянная смешанного газа определяется по формуле (3-3): R = + g2R2= 287.04-20 / 21 + 714-1 / 21 = 306.3 j /(кг> град). Плотность смеси определяется уравнением Клапейрона: p = p / RT = 101325:306,30-273 = 1,21 кг / М9.Парциальное давление определяется по формуле (3-11). = 101325 — = 90100 nCl Ри Р. 21,306. 3 ′ Парциальное давление газа лампы = = — — — — ^- =11225 Н(м G2 G62 I 21 306.30

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Способы задания состава газовой смеси

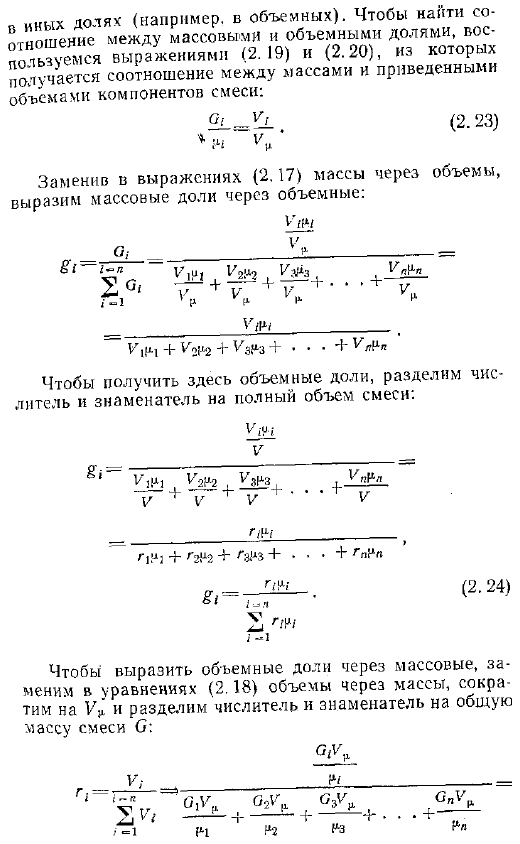
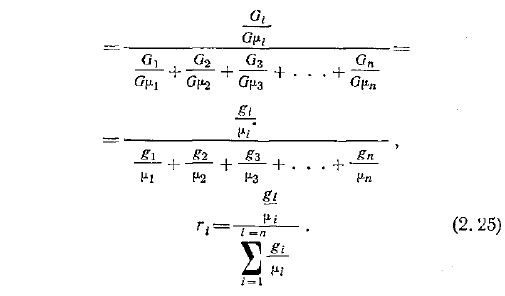
Способы задания состава газовой смеси

• Газовая постоянная, содержащаяся в формуле Клапейрона, может быть определена по формуле 2.12 только в том случае, если молекулярная масса газа равна p. молекулярная масса химически чистого газа может быть легко вычислена, если химическая формула газа равна. Сделайте это, суммируя атомные массы всех химических элементов, составляющих молекулу газа, с учетом количества элементарных атомов в молекуле газа. molecule.

Например, молекулярная масса углекислого газа CO2 Co, — s 2p-0 12 2 1 b-44 кг I кмоль. Однако в теплотехнических расчетах чаще всего приходится работать со смесями, состоящими из нескольких газов, а не с чистыми газами. Это воздух, содержащий азот, кислород, аргон, углекислый газ, водяной пар, продукты сгорания топлива или другие mixtures. In в этом случае, зная состав смеси, необходимо уметь определять молекулярные свойства смеси относительную молекулярную массу и газовую постоянную. Состав смеси может быть определен по массе, объему или молярной доле. Установите смесь в массовую долю. Массовая доля газа в смеси — это отношение массы конкретного газа к массе всей смеси.

В особых условиях (например, при измерении температуры газа в печах) для уменьшения погрешностей экранировки недостаточно. Людмила Фирмаль

Смесь газов с массой 6 масса 32, p 7н-массовая доля этих газов 2.17 Смесь com — л. Где ez, y P-массовая доля газа c — общая масса смеси, равная сумме масс центнера. О О1 О2 63. гол-2 1-1 Сумма всех массовых долей всех компонентов равна 1. 1-р 2 3 е 1-1 1 Установите смесь по объемной доле. Объемная доля газа в смеси — это отношение приведенного объема компонента к объему всей смеси. Уменьшенный объем — это объем, который занимали компоненты смеси до смешивания, и находится при том же давлении и температуре, в которых находится смесь. Сумма всех объемов, которые появляются, будет равна общему объему смеси. л 21 г- I-1 Подобный этому рН — , 2.18 Совместное использование компонентов.

• Где РТ Р2, Р3,. , ha объем И e 2, V3 уменьшенный объем компонента l3. Y — общий объем для смеси. Сумма объемных долей всех компонентов равна 1. 1 — н Г −24-2424-Х3. — — 2Г 1- г 1 Установите состав смеси с мольной фракцией. Молярная доля газа в смеси — это отношение молярного числа конкретного газа к общему молярному числу всех газов в смеси. Молярное число газа может быть определено параметрами P и T, путем деления массы газа на его молекулярную массу или объема восстановленного газа на молярный объем. М — кмоль, 2.19 Д 1 ххол. 2. Двадцать 1 гр. В Формуле 2.20 обозначение компонента I не присваивается количеству.

Это связано с тем, что это количество одинаково для всех газов, согласно закону Авогадро. Поэтому молярная доля выражается соотношением Л1 Здесь, через L4, указывается общее количество молей всех компонентов. В идеальной смеси газов объем и молярные доли будут равны друг другу. Согласно уравнению 2.21, подставим число молей, выраженное в объеме согласно уравнению 2.20. Умножение на Л. Все члены числителя и знаменателя значение дроби не изменяется ВИ, ВИ, ВИ гр 2.22 У1 2 Ч-Уд В 2 Часто состав смеси задается в 1 доле например, по массе, но нужно знать состав других долей например, по объему.

Уравнение (14-40) показывает, что для уменьшения ошибки надо, чтобы все члены уравнения, относящиеся к излучению, были малы. Людмила Фирмаль

Чтобы найти соотношение массовой доли и объемной доли, по уравнениям 2.19 и 2.20 получаем соотношение между массой и уменьшающимся объемом смешиваемого компонента. Да. ч у Если заменить массу в Формуле 2.17 на объем, то по объему мы будем представлять массовую долю. ыы В П. U lnl В — В Г Лодзь. 2.23 2. , 4 г 3Н-Е Л Х Чтобы получить здесь объемную долю, разделите числитель и знаменатель на общий объем смеси. У В 1ч. 1, Ch2r 2 Ulns, D. В В В — В ЦУП Г Гг21 2 гэнз глг п 2.24 Чтобы выразить объемную долю по массе, в Формуле 2.18 уменьшите объемную долю на 1U и разделите числитель и знаменатель на общую массу смеси О о ХДС В середине 11 ода ый, ый, rSp1Y я н 0 1 Л 1ч 2. 3.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник