Алгоритм решения задач
по определению поясного и местного времени.
Определение поясного времени
Задача:
Определите поясное время Магадана, если в Москве 6 часов.
Действия:
1.
Определите, в каком часовом поясе находятся пункты
Москва
2; Магадан 10;
2 .Определите
на сколько разница во времени между пунктам
10
-2 =8 (разница между пунктами во времени)
3.
Вычислите поясное время (определите какой пункт восточнее, какой западнее.)
Магадан восточнее, значит там времени больше следовательно, к Московскому времени
нужно прибавить разницу во времени . 6 +8 = 14 часов
Ответ:
Поясное время Магадана 14 часов.
Определение местного времени
Задача:
Определите местное время в Магадане, если в Москве 6часов.
Действия:
1.
Определите географическую долготу пунктов
Москва
37° в.д ; Магадан 151° в.д;
2.
Вычислите разницу в градусах между пунктами
151°-37°=114°
3.
Вычислить разницу во времени между пунктами
114
х 4 =456:60= 7,6 часа (это 7 часов 36 минут т.к 0,6 часа х 60 минут = 36 минут)
4.
Определить местное время (сложить время Москвы и разницу во времени.)
6 +7
ч. 36 мин = 13 ч.36 мин
Ответ:
Местное время в Магадане13 ч.36 мин
Примечания:
0,1
часа – 6 минут
0,2
часа -12 минут
0,3
часа -18 минут и.т д
Задания
на определение поясного времени
Самолет
вылетел из Читы ( 8-й часовой пояс ) в Мурманск ( 2-й часовой пояс ) в 22 ч.
В
Мурманске самолет приземлился в 21 ч. Сколько времени самолет находился в
полете?
Решение:
Для ответа на
задание нужно определить разницу во времени в двух городах. Известно, что время
каждого часового пояса отличается на 1 ч. Для Читы и Мурманска разница
составляет
(
8 – 2 = 6 ) 6 ч. Зная, что Чита находится восточнее Мурманска, делаем вывод о
том, что в Чите
времени
на 6 ч. больше, чем в Мурманске. Значит самолет вылетел из Читы, когда в
Мурманске было ( 22 – 6 = 16 ) 16 ч., а приземлился в Мурманске в 21 ч.
Соответственно он находился в полете 5 ч.
Задания:
1.
Самолет вылетел из Читы ( 8-й часовой пояс ) в Мурманск ( 2-й часовой пояс ) в
15 ч по местному времени. Время полета из Читы до Мурманска 5 ч. Сколько
времени будет в Мурманске, когда самолет приземлится? Ответ: 14 ч.
2.
Определите, когда по московскому времени совершит посадку в Москве ( 2-й
часовой пояс )
самолет,
вылетевший из Екатеринбурга ( 4-й часовой пояс ) в 11 ч по местному времени и
находившийся в полете 2 ч. Ответ: 11 ч.
3.
Определите, когда по московскому времени совершит посадку в Москве ( 2-й
часовой пояс )
Самолет,
вылетевший из Новосибирска ( 5-й часовой пояс ) в 11 ч по местному времени и
находившийся в полете 5 ч. Ответ: 13 ч.
4.
Самолет вылетел в 9 ч из Москвы ( 2-й часовой пояс ) в Якутск ( 8-й часовой
пояс ) .
Когда
по местному времени совершит посадку в Якутске самолет, находившийся в полете 5
ч?
Ответ:
20 ч.
5.
Сколько времени ( с учетом декретного ) будет в Красноярске ( 6-й часовой пояс
), если в Лондоне полночь? Ответ: 7 ч.
6.
Сколько времени ( с учетом декретного ) будет в Мурманске ( 2-й часовой пояс ),
когда в Лондоне 12 ч дня? Ответ: 15 ч.
7.
Определите поясное время ( с учетом декретного ) Красноярска ( 6-й часовой пояс
), если в Лондоне 11 ч. Ответ: 18 ч.
8.
Сколько времени в Омске ( 5-й часовой пояс ), когда в Москве 15 ч? Ответ: 18 ч.
9.
Сколько времени, с учетом декретного, будет во Владивостоке ( 9-й часовой пояс
), когда в Лондоне полночь? Ответ: 10 ч.
Для
решения задач на определение поясного времени необходимо: внимательно изучить
карту часовых поясов России и мира. Обратить внимание на разницу во времени на
территории России и мира, иметь четкое представление о поясном, декретном,
московском времени; помнить расположение линии перемены дат.
Основные
тезисы темы: часовые пояса мира.
– В каждом часовом
поясе время исчисляется по меридиану, проходящему по его середине. Это время
называется поясным. Оно отличается от времени соседнего пояса ровно на один
час. Отсчет поясов ведется с запада на восток. За нулевой принят пояс, по оси
которого проходит Гринвичский меридиан.
– Местное
время-это время на одном меридиане в каждой его точке.
– Территория
России располагается в пределах 11 часовых поясов, со 2 Московского по 12.
Одиннадцать часов разделяют Калининградскую область от Чукотки на востоке.
– Линия перемены
дат. Для того чтобы избежать путаницы с сутками года, международным соглашением
установлена линия перемены дат. Она проведена по географическим картам
приблизительно по 180-му меридиану в обход суши. Если мы пересечем эту линию с
запада на восток, то мы совершим Т+1 оборот, т.е. Т+1 сутки, и, как ни странно,
приедем во вчерашний день. Следовательно ,пересекая эту линию с запада на
восток, мы должны считать одни и те же сутки два раза. При пересечении линии
перемены дат с востока на запад, наоборот, пропускать один день.
– Декретное время.
Специальным постановлением ( декретом ) Совета Народных Комиссаров в 1930 году
поясное время на территории страны было переведено на один час вперед. Это было
сделано для более эффективного, полного использования дневного времени суток.
– Летнее время.
Продолжительность дня летом увеличивается. По всей стране в последнее
воскресенье марта вводится летнее время: стрелки часов переводятся на один час
назад. Осенью, в последнее воскресенье октября , летнее время отменяется.
Задачи
на определение поясного времени.
1. Определите
летнее время в Якутске, в Магадане, если в Москве 10 часов утра?
2. Определить
время в Бразилии, если в Москве 8 часов?
3. По какой
системе пришлось бы измерять время на Земле, если бы она не вращалась вокруг
своей оси?
4. Теплоход,
отплывший из Владивостока в субботу 24 мая, прибыл в Сан-Франциско ( США )
ровно через 15 суток. Какого числа, в какой месяц и день недели он прибыл в
Сан-Франциско?
5. На нулевом
меридиане полдень, а на корабле 17-00. В каком океане плывет корабль?
6. Если в Лондоне
12-00, который час по поясному времени в Москве и Владивостоке?
7. Который час в
Магадане по местному времени, если на линии Гринвичского меридиана
12-00?
8. Житель Аляски
прилетел на Чукотку. На сколько часов ему надо перевести стрелки?
9. Сколько раз в
нашей стране можно встречать Новый год?
Решение
задач на местное и поясное время.
Задача
№1.
На 30° в.д. среда,
1 января, 18 час местного времени. Какой день недели, число и время на 180 меридиане?
Решение:
1.Находим разницу
в градусах и во времени между 30° в.д. и 180 – градусным меридианом:
180°-
30°в.д = 150°: 15°/час = 10 часов (это разница во времени).
Так как 180
меридиан распложен восточнее 30° в.д., то к местному времени 30° в.д. (18
часов) нужно прибавить разницу во времени т.е. 10 часов:
18
час+10 час = 28 час (1 сутки и 4 часа).
Значит,
на 180 меридиане будут новые сутки, т.е. 2 января.
Ответ:
На
180 меридиане будет 2 января, четверг, 4 часа утра.
Задача
№2.
В Киеве поясное
время – 12 час. В пункте А местное время – 9 часов, а в пункте Б – 14 часов.
Определите
географическую долготу пунктов А и Б.
Решение:
Долгота
Киева – 31° в.д.
Для
пункта «А»
1)12
часов – 9 часов = 3 часа;
2)3
часа×15° = 45°;
3)45°
– 31° = 14°з.д.
Для
пункта «Б»
1)14
часов – 12 часов = 2 часа;
2)2
часа×15° = 30°;
3)31°+30°
= 61°в.д.
Ответ:
Долгота
пункта А – 14°з.д., долгота пункта Б – 61° в.д.
Задача
№3.
На 180 меридиане –
понедельник, 15 мая, 15 часов местного времени. Какое число, день недели и
местное время на: 45° в.д., 150° в.д., 0° долготы, 15°з.д., 170°з.д.
Решение:
а)180° – 45° = 135
: 15/час = 9 часов
9 часов – разница
во времени между 180° меридианом и 45° в.д. Так как 45° в.д. находится
восточнее 180° меридиана, то
15 часов – 9 часов
= 6 часов утра 15 мая, понедельник..
Ответ:
На 45° в.д. 15 мая
понедельник, 6 часов утра.
б)180° – 150° в.д.
= 30°, 30° : 15/час = 2 часа,
15 часов – 2 часа
= 13 часов.
Ответ:
На 150° в.д. 15
мая, понедельник, 13 часов.
в)180° – 0° =
180°, 180° : 15/час = 12 часов
15 часов – 12
часов = 3 часа утра.
Ответ:
На 0° 15 мая,
понедельник, 3 часа утра.
г)180° + 15°з.д. =
195°, 195° : 15/час = 13
учитывая
направление вращения Земли с запада на восток:
15 часов – 13
часов = 26 часов или 2 часа утра, 15 мая, понедельник.
Ответ:
На 15°з.д. 15 мая,
понедельник, 2 часа утра.
д)180° – 170°з.д.
= 10° × 4мин= 40 минут
15 часов + 40
минут = 15 часов 40 минут.
Ответ:
На 170°з.д. – 14
мая, воскресенье, 15 часов 40 минут.
Задача
№4.
Самолёт вылетел из
Претории (ΙΙ часовой пояс) в 15 часов 1 – го декабря и полетел на
северо-восток. Через 9 часов он пересёк 180-й меридиан, а ещё через 2 часа
приземлился в Гонолулу (14 часовой пояс). Который час и какое число будет в
Гонолулу в момент приземления.
Решение:
1.Определить
разницу во времени между городами
24 – 14 – 2 = 12
часов
2.Определить время
в Гонолулу в момент приземления из Претории. Так как Гонолулу находится
западнее, то
15 – 12 = 3 часа
3.Поясное время в
Гонолулу в момент приземления самолёта
3 + 9 + 2 = 14
часов.
Ответ:
В Гонолулу 14
часов 1 декабря.
Высота
солнца над горизонтом.
Определение
географических координат.
Задача
№1.
Определите
географическую широту города, если известно, что в дни равноденствия солнце в
полдень стоит над горизонтом на высоте 63° (тень падает на юг).
Решение:
Пункт находится в
южном полушарии. Высота солнца в дни равноденствия определяют по формуле h
= 90° – φ. Определите широту пункта φ = 90° – 63° = 27°ю.ш.
Задача
№2.
На какой
географической широте расположен город А, если солнце в полдень 22 декабря
(тень падает на юг) находится на высоте 70° над горизонтом.
Решение:
Из условия задачи
следует, что пункт А расположен в южном полушарии, так как тень падает на юг.
Высота солнца для летнего солнцестояния (22 декабря – в южном полушарии лето)
определяется по формуле h = 90° – φ + 23°
30′
Из этой формулы
можно найти φ широту места т.е. города А
φ = 90° – 70° +
23°30′ = 43°30’ю.ш.
Ответ:
Географическая
широта города А = 43°30’ю.ш.
Задача
№3.
Определите
географические координаты города – столицы, расположенной на запад от Киева на
27°30′. Полярную звезду в этом месте видно на расстоянии 54° от точки зенита.
Решение:
1.Долгота Киева
30°30′ в.д. Можем найти географическую долготу города
λ =
30°30′ – 27°30′ = 3° в.д.
2.В северном
полушарии географическая широта любой точки равна углу между Полярной звездой и
линией горизонта. Находим географическую широту:
φ = 90° –
54° = 36°с.ш.
Ответ:
Географические
координаты 36°с.ш. и 3°в.д.
Задача
№4.
В городе – столице
островного государства солнце в течение суток выше всего находится над
горизонтом в 4 часа по Гринвичу. В течении года высота солнца изменяется от 52°
до 90°. Назовите город и государство.
Решение:
1.Определите
часовой пояс города:
12 часов
– 4 часа = 8 часовой пояс
2.Определите
географическую долготу зная, что через каждые 15° разница во времени 1 час.
8 часов
× 15° = 120° в.д.
3.город расположен
между тропиками, так как солнце может быть в зените (90°) min
угол падения солнечных лучей 52° даёт возможность определить географическую
широту в период зимнего солнцестояния
φ = 90°
– 52° – 23,5° = 14,5°
Город имеет
географические координаты 14,5°с.ш. и 120°в.д.
Ответ:
г. Манила,
Филиппины.
Так как Земля вращается вокруг своей оси, Солнце встаёт и заходит в разных частях нашей планеты в разное время. Но для точек, расположенных на одном меридиане, время одинаково. Это время называют местным.
Местное время — время, определяемое для данного места на Земле; зависит от географической долготы места и одинаково для всех точек на одном меридиане.
Пользоваться местным временем в быту невозможно, так как на каждом меридиане было бы своё собственное время. Для удобства Землю условно поделили на (24) часовых пояса.
Географический часовой пояс — условная полоса на земной поверхности шириной ровно (15°).

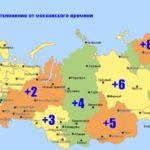
Часовые пояса
При переходе из одного часового пояса в другой значения минут и секунд (времени) сохраняются, изменяется лишь значение часов. Хотя существуют некоторые страны, в которых местное время отличается от всемирного не только на целое количество часов, но ещё дополнительно на (30) или (45) мин.
Для того чтобы определить, какова разница во времени между двумя населёнными пунктами или другими географическими точками, необходимо для начала определить, к какому часовому поясу принадлежит каждая из них. После этого осуществить необходимый расчёт будет довольно просто. Например, нам требуется вычислить разницу во времени между Новосибирском и Рио-де-Жанейро. Для этого достаточно знать, что Новосибирск находится в часовом поясе (UTC+7), а Рио-де-Жанейро — (UTC-3). Отсюда следует, что разница во времени между этими городами составляет (10) часов. Например, когда в Новосибирске — (10) часов утра, в Рио наступает полночь. Аналогичным образом можно определить разницу во времени для всех других случаев.
Средним меридианом нулевого часового пояса считается Гринвичский (нулевой) меридиан.
Всемирное время (мировое время) — среднее солнечное время начального меридиана.
В (12)-ом часовом поясе, примерно по меридиану (180°), условно проведена линия перемены дат.
Линия перемены дат — условная линия на поверхности земного шара, проходящая от полюса до полюса, по разные стороны которой местное время различается на сутки.
Время на территориях, которые расположены на запад и восток от этой линии, различается ровно на (24) часа. Каждый пересекающий линию перемены дат с востока на запад должен перевести календарь на один день вперёд.
- Участники первого кругосветного путешествия «потеряли» один день, потому что пересекли линию перемены даты в направлении из Америки в Азию.
- В романе «Вокруг света за (80) дней» Филеас Фогг сначала думал, что проиграл пари, прибыв в Лондон на день позже срока, а на самом деле у него в запасе был один день, так как он пересёк линию перемены даты на пути из Азии в Америку.

Упрощённая иллюстрация связи между линией даты, датой и временем дня. Соседние даты отличаются друг от друга цветом
Источники:
Рис. 1. Часовые пояса. © ЯКласс.
Рис. 2. Упрощённая иллюстрация связи между линией даты, датой и временем дня. Автор: Arnaudf — собственная работа, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=16454753.
 Задач и на определение местного времени. Задачи на определение географической долготы, если известно точное время, и наоборот — определение местного времени, если известна географическая долгота, как правило, не вызывают особой сложности. Чтобы определить географическую долготу, нужно знать точное время пункта, географическую долготу которого мы собираемся определять, и местное время любого пункта, долгота которого нам известна.
Задач и на определение местного времени. Задачи на определение географической долготы, если известно точное время, и наоборот — определение местного времени, если известна географическая долгота, как правило, не вызывают особой сложности. Чтобы определить географическую долготу, нужно знать точное время пункта, географическую долготу которого мы собираемся определять, и местное время любого пункта, долгота которого нам известна.
Задача 1
Определите точное время пункта, расположенного восточнее на 45° от Лондона, в котором на данный момент полдень.
Решение
Если круг, величина которого составляет 360°, разделить на 24 часа, то получим 15°.
360° : 24 ч = 15°.
Итак, 1 час = 15°, а 45° = 3 ч (45 : 15° = 3).
Местное время пункта будет на 3 часа больше, чем время в Лондоне, потому что указанный пункт расположен восточнее.
Поскольку в Лондоне полдень, т. е. 12 часов, то в неизвестном пункте будет 15 часов (12 + 3 = 15).
Ответ
Местное время пункта составит 15 часов.
Задача 2
Определите географическую долготу пункта, если его местное время опережает местное время
Лондона на 1 час.
Решение
1 час — 15°, а географическая долгота Лондона — 0° долготы.
Поскольку местное время пункта опережает местное время Лондона, пункт расположен восточнее.
0° + 15° = 15° в. д. (географическая долгота пункта).
Ответ
Географическая долгота пункта — 15° в. д.
Задача 3
Определите точное время на нулевом меридиане, если на 180° меридиане по местному времени 24 часа.
Решение
- Определяем разницу в градусах:
180° – 0° = 180°.
- Определяем разницу во времени:
180°: 15° = 12 часов.
- Определяем время на нулевом меридиане:
24 часа – 12 часов = 12 часов.
Ответ
Местное время на нулевом меридиане будет составлять 12 часов.
Солнце всегда освещает только половину земного шара: на одном полушарии — день, а на другом в это время ночь, соответственно всегда есть точки, где в данный момент полдень и Солнце находится в верхней кульминации. По мере того как Земля вращается вокруг оси, полдень наступает в тех местах, которые лежат всё западнее. По положению Солнца (или звёзд) на небе определяется местное время для любой точки земного шара. Местное время в двух пунктах (T1 и T2) отличается ровно на столько, на сколько отличается их географическая долгота:
T1 – T2 = λ1 – λ2.
Ясно, что полдень наступает в данном пункте Земли позже, чем в другом, ровно на столько, сколько времени нужно планете, чтобы повернуться на угол, соответствующий разности их долгот. Так, например, в Санкт-Петербурге, который находится на 8°45ʹ западнее Москвы, полдень наступает на 35 мин позднее.
Определив из наблюдений местное время в данном пункте и сравнив его с местным временем другого, географическая долгота которого известна, можно вычислить географическую долготу пункта наблюдения. Условились отсчитывать долготу от начального (нулевого) меридиана, проходящего через Гринвичскую обсерваторию. Местное время этого меридиана называют всемирным временем — Universal Time (UT). Тогда
T1 = UT + λ1,
иначе говоря, местное время любого пункта равно всемирному времени в этот момент плюс долгота данного пункта от начального меридиана, выраженная в часовой мере.
До недавнего времени, принимая эти сигналы и определяя местное время по моментам кульминации звёзд, вычисляли точные координаты любого пункта земной поверхности. Сейчас точная навигация осуществляется средствами спутниковых систем ГЛОНАСС и GPS (Global Positioning System). Пункты с точно определёнными координатами служат опорными точками при составлении карт, прокладке трасс газопроводов, автомобильных и железных дорог, строительстве крупных объектов и ряде других работ. Сигналы точного времени, наряду с другими средствами (радиомаяками, навигационными спутниками и т. п.), необходимы в авиационной и морской навигации.
Если бы в своей повседневной жизни мы пользовались местным временем, то по мере передвижения на запад или восток приходилось бы непрерывно передвигать стрелки часов. Возникающие при этом неудобства столь очевидны, что в настоящее время практически всё население земного шара пользуется поясным временем.
Поясная система счёта времени была предложена в 1884 г. Согласно этой системе весь земной шар был разделён по долготе на 24 часовых пояса (по числу часов в сутках), каждый из которых занимает примерно 15°. По сути дела, счёт времени по этой системе ведётся только на 24 основных меридианах, отстоящих друг от друга на 15° по долготе. Время на этих меридианах, которые расположены примерно посередине каждого часового пояса, отличается ровно на один час. Местное время основного меридиана данного пояса называется поясным временем. По нему ведётся счёт времени на всей территории, относящейся к этому часовому поясу. Поясное время, которое принято в конкретном пункте, отличается от всемирного на число часов, равных номеру его часового пояса:
T = UT + n,
где UT — всемирное время, а n — номер часового пояса.
Границами часовых поясов являются линии, которые идут от Северного полюса Земли до Южного и отстоят приблизительно на 7,5° от основных меридианов. Эти границы далеко не всегда проходят строго по меридианам, а проведены по административным границам областей или других регионов так, чтобы на всей их территории действовало одно и то же время (рис. 2.18). Естественно, например, что Москва живёт по времени одного (второго) часового пояса. Если же формально следовать принятому правилу деления на часовые пояса, то нужно было бы провести границу пояса так, что город оказался бы разделённым на две неравные части.
В нашей стране поясное время было введено с 1 июля 1919 г. С тех пор границы часовых поясов неоднократно пересматривались и изменялись.
В конце XX в. в России несколько раз вводилось и затем отменялось декретное время, которое на 1 ч опережает поясное. В январе 1992 г. оно было в последний раз установлено, и теперь в повседневной жизни мы снова используем это время, называя его местным временем.
Многие страны весной переходят на «летнее время», переводя стрелки часов на 1 ч вперёд по отношению к «зимнему времени», к которому они возвращаются поздней осенью.
В России с апреля 2011 г. такая операция не проводится. До октября 2014 г. местное время на 1 ч опережало декретное и, в частности, в Москве было равно всемирному времени, увеличенному на 4 ч. С октября 2014 г. в России было возвращено декретное время, и разница между московским и всемирным временем стала равной 3 ч.
Календарь
Система счёта длительных промежутков времени, согласно которой устанавливается определённая продолжительность месяцев, их порядок в году и начальный момент отсчёта лет, называется календарём. Календарь, которым мы пользуемся в настоящее время, создан в результате длительных поисков наиболее удобной для этих целей системы. На протяжении истории человечества существовало более 200 различных календарей.
Уже на первом этапе развития цивилизации некоторые народы стали пользоваться лунными календарями. В этих календарях чередовались месяцы продолжительностью 29 и 30 суток. Началом месяца всегда считалось новолуние. Временной интервал между последовательными новолуниями составляет 29,5 суток — такова периодичность смены фаз Луны, связанная с её обращением вокруг Земли. При таком календаре не получается полного согласования с продолжительностью года, которая составляет приблизительно 365,25 суток. Двенадцать лунных месяцев содержат всего 354 дня. Для устранения несогласованности между лунным и солнечным годом в различных лунных календарях были предложены необходимые поправки.
В солнечном календаре за основу берётся продолжительность тропического года, который представляет собой промежуток времени между двумя последовательными прохождениями центра Солнца через точку весеннего равноденствия. Тропический год составляет 365 суток 5 часов 48 минут 46,1 секунды. Поскольку число суток в году не может быть дробным, во всех календарях большая часть лет содержит 365 суток и вводится правило, по которому определённые годы имеют продолжительность на сутки больше. В зависимости от этого средняя продолжительность года по тому или иному календарю в большей или меньшей степени приближается к продолжительности тропического года.
В Древнем Египте в V тысячелетии до н. э. был введён календарь, который состоял из 12 месяцев по 30 дней в каждом и дополнительных 5 дней в конце года. Такой календарь давал ежегодно отставание в 0,25 суток, или 1 год за 1460 лет.
Непосредственный предшественник современного календаря был разработан в Древнем Риме по приказу императора Юлия Цезаря и потому получил название юлианского. Год, согласно этому календарю, состоял из 12 месяцев и содержал 365 или 366 суток. Лишние сутки добавлялись каждые четыре года: такие годы, номер которых делится на четыре, получили название високосных.
С учётом високосных лет продолжительность года по юлианскому календарю (старому стилю) отличалась от продолжительности тропического года на 11 минут 14 секунд, что давало ошибку в 1 сутки за 128 лет, или 3 суток примерно за 400 лет. Юлианский календарь был принят в качестве христианского в 325 г. н. э., и ко второй половине XVI в. расхождение достигло уже 10 суток.
В России новый стиль был введён только с 1 февраля 1918 г. К этому времени между ним и старым стилем накопилась разница в 13 дней. Эта разница сохранится до 2100 г., который по старому стилю должен был бы считаться високосным, а по новому — простым. Различие между старым и новым стилем обычно указывается, когда мы имеем дело с событиями, относящимися к прошлому. Так, например, мы говорим, что К. Э. Циолковский родился 5 (17) сентября 1857 г.
Нумерация лет как по новому, так и по старому стилю ведётся от года Рождества Христова, наступления новой эры. В России новая эра была введена указом Петра I, согласно которому после 31 декабря 7208 г. «от сотворения мира» наступило 1 января 1700 г. от Рождества Христова.
1. Измерение времени. Вся наша жизнь связана со временем и регулируется периодической сменой дня и ночи, а также времён года. На этих природных повторяющихся явлениях базируются основные единицы измерения времени — сутки, месяц, год. Широко используемая единица для измерения времени — сутки — связана с периодом вращения Земли вокруг своей оси.
Момент верхней кульминации центра Солнца называется истинным полднем, момент нижней кульминации — истинной полночью. Промежуток времени между двумя последовательными одноимёнными кульминациями центра Солнца называется истинными солнечными сутками. Время, прошедшее от момента нижней кульминации центра солнечного диска до любого другого его положения на одном и том же географическом меридиане, называется истинным солнечным временем (T¤).
Необходимо отметить, что истинные солнечные сутки периодически меняют свою продолжительность. Это вызывается двумя причинами: во-первых, наклоном плоскости эклиптики к плоскости небесного экватора, во-вторых, эллиптической формой орбиты Земли. Когда Земля находится на участке эллипса, расположенном ближе к Солнцу (на рис. 18 это положение показано слева), то она движется быстрее. Через полгода Земля окажется в противоположной части эллипса и будет перемещаться по орбите медленнее. Неравномерное движение Земли по своей орбите вызывает неравномерное видимое перемещение Солнца по небесной сфере, т. е. в разное время года Солнце перемещается с различной скоростью. Поэтому продолжительность истинных солнечных суток постоянно меняется и пользоваться ими в качестве единицы измерения времени неудобно. По этой причине в повседневной жизни используются не истинные, а средние солнечные сутки, продолжительность которых принята постоянной. Устанавливаются они по движению среднего экваториального Солнца — воображаемой точки, которая движется равномерно по небесному экватору и в точках весеннего и осеннего равноденствия совпадает с центром истинного Солнца. Верхнюю кульминацию среднего экваториального Солнца называют средним полднем, а промежуток времени между двумя последовательными средними полднями — средними солнечными сутками. Продолжительность их всегда одинакова. Средние солнечные сутки делят на 24 часа. Каждый час среднего солнечного времени в свою очередь делится на 60 минут, а каждая минута — на 60 секунд. За начало средних солнечных суток принимается средняя полночь, т. е. момент нижней кульминации среднего экваториального Солнца. Время, протёкшее от момента нижней кульминации среднего экваториального Солнца до любого другого его положения на одном и том же географическом меридиане, называется средним солнечным временем (Тср).

Разность между средним солнечным временем и истинным солнечным временем в один и тот же момент называется уравнением времени. Оно обозначается греческой буквой п. Можно записать следующее равенство:
![]() Величина уравнения времени п обычно приводится в астрономических календарях. Приблизительно её можно найти по графику (рис. 19), из которого видно, что четыре раза в год уравнение времени п равно нулю. Это происходит примерно 14 апреля, 14 июня, 2 сентября и 24 декабря. Уравнение времени п принимает наибольшие численные значения около 14 февраля (h = +14 мин) и 3 ноября (h = -16 мин).
Величина уравнения времени п обычно приводится в астрономических календарях. Приблизительно её можно найти по графику (рис. 19), из которого видно, что четыре раза в год уравнение времени п равно нулю. Это происходит примерно 14 апреля, 14 июня, 2 сентября и 24 декабря. Уравнение времени п принимает наибольшие численные значения около 14 февраля (h = +14 мин) и 3 ноября (h = -16 мин).
Различают также звёздные сутки (около 23 ч 56 мин 4 с). Звёздные сутки равны промежутку времени между двумя последовательными одноимёнными кульминациями точки весеннего равноденствия. Момент верхней кульминации этой точки, принимаемый за начало звёздных суток, считается 0 часов звёздного времени. Время, протёкшее от момента верхней кульминации точки весеннего равноденствия до любого другого её положения на одном и том же географическом меридиане, называется звёздным временем.

Рисунок 19 — График уравнения времени
2. Определение географической долготы. Измерение времени солнечными сутками связано с географическим меридианом. Время, измеренное на данном меридиане, называется местным временем данного меридиана, и оно одинаково для всех пунктов, находящихся на нём. Кульминация любой точки небесной сферы происходит в разное время на разных меридианах земного шара. Причём, чем восточнее земной меридиан, тем раньше в пунктах, лежащих на нём, происходит кульминация или начинаются сутки. Так как Земля за каждый час поворачивается на 15°, то разность времени двух пунктов в один час соответствует и разности долгот в 15° (в часовой мере 1 час). Отсюда можно сделать вывод: разность местного времени двух пунктов на Земле численно равна разности значений долготы, выраженных в часовой мере. Для пунктов земной поверхности, расположенных на географических долготах l1 и l2, получим:
![]() Формула (1)
Формула (1)
За начальный (нулевой) меридиан для отсчёта географической долготы принят меридиан, проходящий через Гринвичскую обсерваторию близ Лондона. Местное среднее солнечное время Гринвичского меридиана называется всемирным временем. Все сигналы точного времени соответствуют минутам и секундам всемирного времени. В астрономических календарях и ежегодниках моменты большинства явлений указываются по всемирному времени. Моменты этих явлений по местному времени какого-либо пункта легко определить, зная долготу этого пункта от Гринвича.
Если в данный момент на Гринвичском меридиане всемирное время будет Т0, то в местности с географической долготой l будет Тl. Следовательно, формула (1) при l0 = 0 примет вид:
 Формула 2)
Формула 2)
Данная формула позволяет находить географическую долготу по всемирному времени (Т0) и местному времени (Тl), которое определяется из астрономических наблюдений. С другой стороны, зная долготу места наблюдения (l) и всемирное время (Т0), можно определить местное время (Тl):

Различие между местным временем даже не очень далеко расположенных друг от друга населённых пунктов создаёт неудобства в повседневной жизни. Так, например, местное время в Бресте и Витебске отличается на 26 мин. Жители этих городов, приезжая друг к другу в гости, должны были бы постоянно переводить стрелки часов. Отсюда возникла необходимость введения поясной системы счёта времени. Согласно этой системе, весь земной шар разделён на 24 часовых пояса, каждый из которых простирается по долготе на 15° (или 1 ч). Часовой пояс Гринвичского меридиана считается нулевым. Остальным поясам в направлении от нулевого на восток присвоены номера от 1 до 23. В пределах одного пояса во всех пунктах в каждый момент поясное время одинаково. В соседних поясах оно отличается ровно на один час. Границы поясов в малонаселённых местах, на морях и океанах проходят по меридианам, отстоящим на 7,5° к востоку и западу от центрального меридиана данного часового пояса. В остальных районах границы поясов для большего удобства проведены по государственным и административным границам, горным хребтам, рекам и другим естественным рубежам.
Зная всемирное время (Т0) и номер пояса данного места (n), можно найти поясное время:
![]() Формула (3)
Формула (3)
Исключив из формул (1) и (3) Т0, получим соотношение, позволяющее определять географическую долготу по поясному времени (Тn) и времени для местности с географической долготой l (Тl):
 Формула (4)
Формула (4)

Фильм. Измерение времени.
В целях экономии и рационального распределения электроэнергии в течение суток на летний период в некоторых странах весной стрелки часов переводят на час вперёд — вводят летнее время, а осенью снова на час назад.
Существует граница, открывающая новую дату и день недели. Международная линия перемены дат проходит через Берингов пролив между островами Тихого океана от Северного полюса до Южного полюса (меридиан 180°).
Более надёжным и удобным временем считается атомное время, которое было введено Международным комитетом мер и весов в 1964 г. За эталон приняты атомные (квантовые) часы. По таким часам секунда — это промежуток времени, за который проходит 9 192 631 770 колебаний электромагнитной волны, излучаемой атомом цезия. С 1 января 1972 г. все страны земного шара ведут счёт времени по атомным часам.
Атомное время очень удобно для исследования Земли, потому что с его помощью можно изучать неравномерности во вращении нашей планеты. Ошибка хода атомных часов невелика — примерно 1 с за 50 тыс. лет.
3. Календарь. Календарь — это система счёта длительных промежутков времени, в основе которой лежат периодические астрономические явления: вращение Земли вокруг оси, изменение лунных фаз, обращение Земли вокруг Солнца. Любая календарная система опирается на три основные единицы измерения времени, а именно: средние солнечные сутки, синодический (или лунный) месяц и тропический (или солнечный) год.
Рис. 20. Антикитерский механизм (фрагмент, найденный археологами, и воссозданная на его основе модель)
Синодический месяц — это промежуток времени между двумя последовательными одинаковыми фазами Луны. Он равен 29,5306 суток. Тропический год — промежуток времени между двумя последовательными прохождениями центра Солнца через точку весеннего равноденствия. Он равен 365,2422 суток. Из-за медленного движения точки весеннего равноденствия навстречу Солнцу, вызванного прецессией, Солнце оказывается в той же точке неба относительно звёзд через промежуток времени на 20 мин 28 с больший, чем тропический год. Он называется звёздным годом и содержит 365,2564 средних солнечных суток.
Синодический месяц и тропический год не содержат целого числа средних солнечных суток, поэтому невозможно подобрать такое целое число тропических лет, в которых содержалось бы целое число синодических месяцев и целое число средних солнечных суток. Стремление согласовать между собой сутки, месяц и год привело к тому, что в разные эпохи у различных народов было создано много видов календарей, которые можно условно разделить на три типа: лунные, лунно-солнечные и солнечные. На рисунке 20 показано механическое приспособление, созданное древнегреческими астрономами во II в. до н. э. для расчёта движения Луны, Солнца и планет в календарных целях.

Рисунок 21 — Древний римский календарь
В лунном календаре год делится на 12 месяцев, содержащих попеременно 30 или 29 суток. Всего в лунном календаре 354 или 355 средних солнечных суток, т. е. он короче солнечного года примерно на 10 суток. Этот календарь получил широкое распространение в странах Ближнего Востока и принят в современном исламском мире. Из-за того что лунный год имеет меньше дней, чем тропический, у мусульман начало года постоянно перемещается по сезонам и выпадает то на весну, то на лето, то на зиму, то на осень.
Лунно-солнечные календари наиболее сложные. В них сумма некоторого количества лунных месяцев приблизительно соответствует продолжительности тропического года. В основе этих календарей лежит соотношение: 19 солнечных лет равны 235 лунным месяцам (с ошибкой около 2 ч). Год делится на 12 месяцев, каждый из которых начинается с новолуния. В настоящее время такая система сохранилась в еврейском календаре. Он содержит 12 или 13 месяцев в году. Продолжительность некоторых месяцев каждый год меняется, начало года всегда приходится на осень, но не совпадает с одной и той же датой григорианского календаря.
Римляне первоначально исчисляли время лунными годами. Новый год начинался 1 марта. До сих пор некоторые месяцы современного календаря называются в соответствии с этой традицией: сентябрь — «седьмой», декабрь — «десятый» и т. д. Впоследствии первый день года был перенесён римлянами на 1 января, так как с 153 г. до н. э. в этот день вступали в должность консулы (рис. 21).

Рисунок 22 — Медаль, выпущенная в память о введении григорианского календаря
Одним из первых солнечных календарей считается египетский, созданный в 4-м тыс. до н. э. По этому календарю год состоял из 12 месяцев по 30 дней в каждом, а в конце года добавлялось ещё 5 праздничных дней. Современный календарь берёт начало от солнечного римского календаря, появившегося в результате реформы Юлия Цезаря (отсюда его название — юлианский), проведённой 1 января 45 г. до н. э. Средняя продолжительность года, согласно этому календарю, была равна 365,25 суток, что соответствовало известной в то время длине тропического года. Для удобства три года подряд считали по 365 дней, а на четвёртый (високосный) добавляли лишние сутки — 366 дней. Год состоял из 12 месяцев: нечётные месяцы — 31 день, чётные — 30 дней; только февраль простого, невисокосного, года содержал 28 дней.
Вследствие того что продолжительность юлианского года длиннее тропического на 11 мин 15 с, за 128 лет накапливалась ошибка в целые сутки, а за 400 лет — около трёх суток. С течением времени календарь запаздывал всё больше и больше. Поэтому в конце XVI в. весеннее равноденствие наступало не 21, а 11 марта. Ошибка была исправлена в 1582 г., когда глава католической церкви папа Григорий ХШ создал специальную комиссию по реформе календаря, передвинувшую счёт дней на 10 суток вперёд и вернувшую весеннее равноденствие на 21 марта. Исправленный календарь получил название григорианского календаря или календаря нового стиля. В честь его введения была отчеканена памятная медаль (рис. 22). Систему счёта времени по юлианскому календарю сейчас называют старым стилем.
Високосный год в григорианском календаре — каждый четвёртый, за исключением годов с целым числом столетий (например, 1700, 1800). Такой год считается високосным только тогда, когда число сотен делится на 4 без остатка.
В России этот календарь был введён со среды 31 января 1918 г. Следующий день уже был 14 февраля, так как к тому времени календарная разница между новым и старым стилем достигла 13 дней. Это различие в 13 суток будет сохраняться до 15 февраля 2100 г. по старому стилю, или до 28 февраля 2100 г. по новому стилю. После этой даты оно увеличится на одни сутки и станет равным 14 суткам.
Григорианский календарный год длиннее солнечного года на 26 с. Лишние сутки накопятся только в L в. н. э., потому что разница в один день набегает за 3280 лет.
Необходимо отметить, что и григорианский календарь не лишён недостатков: неодинаковая продолжительность месяцев, неравные кварталы, несогласованность чисел месяцев с днями недели.
Много вопросов вызывают и привычные названия месяцев. Так, июль назван в память о римском императоре Юлии Цезаре, август — в честь римского императора Октавиана Августа. Остальные месяцы календаря получили свои названия по-разному: например, январь — в честь римского бога Януса, февраль — в честь ежегодных языческих обрядов очищения, март — по имени бога Марса, май — богини Майи, июнь — богини Юноны. Названия «сентябрь», «октябрь», «ноябрь», «декабрь» переводятся с латинского языка соответственно как «седьмой», «восьмой», «девятый», «десятый» и в настоящее время не соответствуют этой нумерации.
Кроме счёта месяцев в годах, следует вести счёт и самим годам. Для этой цели издревле использовались эры, т. е. длительные промежутки счёта лет. Эрой называется исходный пункт каждого летоисчисления. У разных народов эры были разные и связывались с какими-либо знаменательными событиями или с годами правления царей и императоров.
В Риме использовалась эра от основания Рима (753 г. до н. э.) и счёт годов от назначения консулов. В средневековой Европе была распространена эра Диоклетиана, считавшаяся от восшествия на престол императора Диоклетиана (29 августа 284 г. н. э.). Она применялась до XV в.
В Древней Греции применялась эра Олимпиад (начало 776 г. до н. э.). Олимпиады проводились раз в четыре года.
Иудеи отсчитывают начало эры от сотворения мира — от 3761 г. до н. э.
Христиане использовали эру от сотворения мира, принимая начало в 5508 г. до н. э. Эру от Рождества Христова рассчитал папский архивариус Дионисий Малый в 525 г. Он приравнял 248 г. эры Диоклетиана к 532 г. от рождения Христа. Эра от Рождества Христова, или новая эра (наша эра), частично начала применяться с Х в., а повсеместно в католических странах — лишь с XV в. В России она была введена в 1700 г. указом Петра I, согласно которому после 31 декабря 7208 г. от сотворения мира наступило 1 января 1700 г.
Мусульмане всего мира используют свою эру, которая называется хиджра и ведёт счёт лет от даты переселения пророка Мухаммеда из Мекки в Медину, что произошло в сентябре 622 г. н. э.
Главные выводы 1. Промежуток времени между двумя последовательными одноимёнными кульминациями центра солнечного диска на одном и том же географическом меридиане называется истинными солнечными сутками. 2. Из-за неравномерности истинных солнечных суток в повседневной жизни используются средние солнечные сутки, продолжительность которых постоянна. 3. Звёздные сутки — промежуток времени между двумя последовательными одноимёнными кульминациями точки весеннего равноденствия на одном и том же географическом меридиане. 4. Географическая долгота данной местности определяется разностью между местным и всемирным временем. 5. Календарь — это система счёта длительных промежутков времени, в основе которой лежат периодические астрономические явления. Мы живём по григорианскому календарю.
Контрольные вопросы и задания
1. Чем отличаются истинные солнечные сутки от средних солнечных суток?
2. Что называют звездными сутками?
3. Что понимают под уравнением времени?
4. Что понимают под всемирным временем?
5. Что понимают под линией перемены дат? Где она проходит?
6. Назовите календарные системы. На каких принципах они строятся?
7. В чем состоит отличие григорианского календаря от юлианского?
8. Почему нельзя создать абсолютно точный календарь?
9. Найдите разницу в местном времени для городов Гродно и Могилев.
10. В местный полдень капитан корабля отметил 14 ч 13 мин 46 с по хронометру, идущему по гринвичскому времени. Определите географическую долготу корабля.
11. 22 июня наблюдатель определил, что средний местный полдень наступил в 8 ч 40 мин всемирного времени, а высота Солнца в этот момент была равна 62°10′. Склонение Солнца в этот день δ = +23°26′. Определите географические координаты наблюдателя.
Проверь себя
Выбор тем
