Как найти геометрический момент инерции - Сайт, где вы сможете решить свои вопросы

Момент инерции
${displaystyle J=int limits _{(m)}r^{2}mathrm {d} m}$
Размерность	L²M
Единицы измерения
СИ	кг·м²
СГС	г·см²

Моме́нт ине́рции — тензорная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле. Момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества, которое, формально, может представлять собой не обязательно ось вращения (т.е. прямую), но и точку или плоскость. В последних случаях говорят о моменте инерции относительно точки или плоскости, а возникать такие величины могут в формальных вычислениях, например, при расчете тензора инерции.

Единица измерения в Международной системе единиц (СИ): кг·м².

Обозначение: I или J.

Различают несколько моментов инерции — в зависимости от типа базового множества до которого отсчитываются расстояния от элементарных масс.

Осевой момент инерции[править | править код]

Осевые моменты инерции некоторых тел

Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина J_a, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси^[1]:

${displaystyle J_{a}=sum _{i=1}^{n}m_{i}r_{i}^{2},}$

где:

m_i — масса i-й точки,
r_i — расстояние от i-й точки до оси.

Осевой момент инерции тела J_a является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.

${displaystyle J_{a}=int limits _{(m)}r^{2}dm=int limits _{(V)}rho r^{2}dV,}$

где:

dm = ρ dV — масса малого элемента объёма тела dV,

ρ — плотность,

r — расстояние от элемента dV до оси a.

Если тело однородно, то есть его плотность всюду одинакова, то

${displaystyle J_{a}=rho int limits _{(V)}r^{2}dV.}$

Теорема Гюйгенса — Штейнера[править | править код]

Момент инерции твёрдого тела относительно какой-либо оси зависит от массы, формы и размеров тела, а также и от положения тела по отношению к этой оси. Согласно теореме Гюйгенса — Штейнера, момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела J_c относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями^[1]:

${displaystyle J=J_{c}+md^{2},}$

где m — полная масса тела.

Например, момент инерции стержня относительно оси, проходящей через его конец, равен:

${displaystyle J=J_{c}+md^{2}={frac {1}{12}}ml^{2}+mleft({frac {l}{2}}right)^{2}={frac {1}{3}}ml^{2}.}$

Осевые моменты инерции некоторых тел[править | править код]

Моменты инерции однородных тел простейшей формы относительно некоторых осей вращения

Описание	Положение оси a	Момент инерции J_a
Материальная точка массы m	На расстоянии r от точки, неподвижная	$mr^{2}$
Полый тонкостенный цилиндр или кольцо радиуса r и массы m	Ось цилиндра	$mr^{2}$
Сплошной цилиндр или диск радиуса r и массы m	Ось цилиндра	${frac {1}{2}}mr^{2}$
Полый толстостенный цилиндр массы m с внешним радиусом r₂ и внутренним радиусом r₁	Ось цилиндра	$m{frac {r_{2}^{2}+r_{1}^{2}}{2}}$ ^{[Комм 1]}
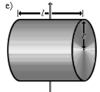
Сплошной цилиндр длины l, радиуса r и массы m	Ось перпендикулярна образующей цилиндра и проходит через его центр масс	${1 over 4}mcdot r^{2}+{1 over 12}mcdot l^{2}$
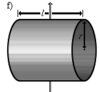
Полый тонкостенный цилиндр (кольцо) длины l, радиуса r и массы m	Ось перпендикулярна к цилиндру и проходит через его центр масс	${1 over 2}mcdot r^{2}+{1 over 12}mcdot l^{2}$
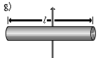
Прямой тонкий стержень длины l и массы m	Ось перпендикулярна к стержню и проходит через его центр масс	${frac {1}{12}}ml^{2}$
Прямой тонкий стержень длины l и массы m	Ось перпендикулярна к стержню и проходит через его конец	${frac {1}{3}}ml^{2}$
Тонкостенная сфера радиуса r и массы m	Ось проходит через центр сферы	${frac {2}{3}}mr^{2}$
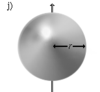
Шар радиуса r и массы m	Ось проходит через центр шара	${frac {2}{5}}mr^{2}$
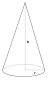
Конус радиуса r и массы m	Ось конуса	${frac {3}{10}}mr^{2}$
Равнобедренный треугольник с высотой h, основанием a и массой m	Ось перпендикулярна плоскости треугольника и проходит через вершину (при высоте)	${frac {1}{24}}m(a^{2}+12h^{2})$
Правильный треугольник со стороной a и массой m	Ось перпендикулярна плоскости треугольника и проходит через центр масс	${frac {1}{12}}ma^{2}$
Квадрат со стороной a и массой m	Ось перпендикулярна плоскости квадрата и проходит через центр масс	${frac {1}{6}}ma^{2}$
Прямоугольник со сторонами a и b и массой m	Ось перпендикулярна плоскости прямоугольника и проходит через центр масс	${frac {1}{12}}m(a^{2}+b^{2})$
Правильный n-угольник радиуса r и массой m	Ось перпендикулярна плоскости и проходит через центр масс	${displaystyle {frac {mr^{2}}{6}}left[1+2cos(pi /n)^{2}right]}$
Тор (полый) с радиусом направляющей окружности R, радиусом образующей окружности r и массой m	Ось перпендикулярна плоскости направляющей окружности тора и проходит через центр масс	${displaystyle I=mleft({frac {3}{4}},r^{2}+R^{2}right)}$

Вывод формул[править | править код]

Тонкостенный цилиндр (кольцо, обруч)

Вывод формулы

Момент инерции тела равен сумме моментов инерции составляющих его частей. Разобьём тонкостенный цилиндр на элементы с массой dm и моментами инерции dJ_i. Тогда

${displaystyle J=sum dJ_{i}=sum R_{i}^{2}dm.qquad (1).}$

Поскольку все элементы тонкостенного цилиндра находятся на одинаковом расстоянии от оси вращения, формула (1) преобразуется к виду

$J=sum R^{2}dm=R^{2}sum dm=mR^{2}.$

Толстостенный цилиндр (кольцо, обруч)

Вывод формулы

Пусть имеется однородное кольцо с внешним радиусом R, внутренним радиусом R₁, толщиной h и плотностью ρ. Разобьём его на тонкие кольца толщиной dr. Масса и момент инерции тонкого кольца радиуса r составит

$dm=rho dV=rho cdot 2pi rhdr;qquad dJ=r^{2}dm=2pi rho hr^{3}dr.$

Момент инерции толстого кольца найдём как интеграл

$J=int _{R_{1}}^{R}dJ=2pi rho hint _{R_{1}}^{R}r^{3}dr=$

${displaystyle =2pi rho hleft.{frac {r^{4}}{4}}right|_{R_{1}}^{R}={frac {1}{2}}pi rho hleft(R^{4}-R_{1}^{4}right)={frac {1}{2}}pi rho hleft(R^{2}-R_{1}^{2}right)left(R^{2}+R_{1}^{2}right).}$

Поскольку объём и масса кольца равны

$V=pi left(R^{2}-R_{1}^{2}right)h;qquad m=rho V=pi rho left(R^{2}-R_{1}^{2}right)h,$

получаем окончательную формулу для момента инерции кольца

$J={frac {1}{2}}mleft(R^{2}+R_{1}^{2}right).$

Однородный диск (сплошной цилиндр)

Вывод формулы

Рассматривая цилиндр (диск) как кольцо с нулевым внутренним радиусом (R₁ = 0), получим формулу для момента инерции цилиндра (диска):

$J={frac {1}{2}}mR^{2}.$

Сплошной конус

Вывод формулы

Разобьём конус на тонкие диски толщиной dh, перпендикулярные оси конуса. Радиус такого диска равен

$r={frac {Rh}{H}},$

где R – радиус основания конуса, H – высота конуса, h – расстояние от вершины конуса до диска.
Масса и момент инерции такого диска составят

$dm=rho dV=rho cdot pi r^{2}dh;$

$dJ={frac {1}{2}}r^{2}dm={frac {1}{2}}pi rho r^{4}dh={frac {1}{2}}pi rho left({frac {Rh}{H}}right)^{4}dh;$

Интегрируя, получим

${begin{aligned}J=int _{0}^{H}dJ={frac {1}{2}}pi rho left({frac {R}{H}}right)^{4}int _{0}^{H}h^{4}dh={frac {1}{2}}pi rho left({frac {R}{H}}right)^{4}left.{frac {h^{5}}{5}}right|_{0}^{H}=={frac {1}{10}}pi rho R^{4}H=left(rho cdot {frac {1}{3}}pi R^{2}Hright){frac {3}{10}}R^{2}={frac {3}{10}}mR^{2}.end{aligned}}$

Сплошной однородный шар

Вывод формулы

Разобьём шар на тонкие диски толщиной dh, перпендикулярные оси вращения. Радиус такого диска, расположенного на высоте h от центра сферы, найдём по формуле

$r={sqrt {R^{2}-h^{2}}}.$

Масса и момент инерции такого диска составят

$dm=rho dV=rho cdot pi r^{2}dh;$

$dJ={frac {1}{2}}r^{2}dm={frac {1}{2}}pi rho r^{4}dh={frac {1}{2}}pi rho left(R^{2}-h^{2}right)^{2}dh={frac {1}{2}}pi rho left(R^{4}-2R^{2}h^{2}+h^{4}right)dh.$

Момент инерции шара найдём интегрированием:

${begin{aligned}J&=int _{-R}^{R}dJ=2int _{0}^{R}dJ=pi rho int _{0}^{R}left(R^{4}-2R^{2}h^{2}+h^{4}right)dh=\&=pi rho left.left(R^{4}h-{frac {2}{3}}R^{2}h^{3}+{frac {1}{5}}h^{5}right)right|_{0}^{R}=pi rho left(R^{5}-{frac {2}{3}}R^{5}+{frac {1}{5}}R^{5}right)={frac {8}{15}}pi rho R^{5}=\&=left({frac {4}{3}}pi R^{3}rho right)cdot {frac {2}{5}}R^{2}={frac {2}{5}}mR^{2}.end{aligned}}$

Тонкостенная сфера

Вывод формулы

Для вывода воспользуемся формулой момента инерции однородного шара радиуса R:

$J_{0}={frac {2}{5}}MR^{2}={frac {8}{15}}pi rho R^{5}.$

Вычислим, насколько изменится момент инерции шара, если при неизменной плотности ρ его радиус увеличится на бесконечно малую величину dR.

${displaystyle {begin{aligned}J&={frac {dJ_{0}}{dR}}dR={frac {d}{dR}}left({frac {8}{15}}pi rho R^{5}right)dR=\&={frac {8}{3}}pi rho R^{4}dR=left(rho cdot 4pi R^{2}dRright){frac {2}{3}}R^{2}={frac {2}{3}}mR^{2}.end{aligned}}}$

Тонкий стержень (ось проходит через центр)

Вывод формулы

Разобьём стержень на малые фрагменты длиной dr. Масса и момент инерции такого фрагмента равна

$dm={frac {mdr}{l}};qquad dJ=r^{2}dm={frac {mr^{2}dr}{l}}.$

Интегрируя, получим

$J=int _{-l/2}^{l/2}dJ=2int _{0}^{l/2}dJ={frac {2m}{l}}int _{0}^{l/2}r^{2}dr={frac {2m}{l}}left.{frac {r^{3}}{3}}right|_{0}^{l/2}={frac {2m}{l}}{frac {l^{3}}{24}}={frac {1}{12}}ml^{2}.$

Тонкий стержень (ось проходит через конец)

Вывод формулы

При перемещении оси вращения из середины стержня на его конец, центр тяжести стержня перемещается относительно оси на расстояние ^l⁄₂. По теореме Штейнера новый момент инерции будет равен

$J=J_{0}+mr^{2}=J_{0}+mleft({frac {l}{2}}right)^{2}={frac {1}{12}}ml^{2}+{frac {1}{4}}ml^{2}={frac {1}{3}}ml^{2}.$

Безразмерные моменты инерции планет и их спутников^[2]^[3]^[4]

Безразмерные моменты инерции планет и спутников[править | править код]

Большое значение для исследований внутренней структуры планет и их спутников имеют их безразмерные моменты инерции. Безразмерный момент инерции тела радиуса r и массы m равен отношению его момента инерции относительно оси вращения к моменту инерции материальной точки той же массы относительно неподвижной оси вращения, расположенной на расстоянии r (равному mr²). Эта величина отражает распределение массы по глубине. Одним из методов её измерения у планет и спутников является определение доплеровского смещения радиосигнала, передаваемого АМС, пролетающей около данной планеты или спутника. Для тонкостенной сферы безразмерный момент инерции равен 2/3 (~0,67), для однородного шара — 0,4, и вообще тем меньше, чем большая масса тела сосредоточена у его центра. Например, у Луны безразмерный момент инерции близок к 0,4 (равен 0,391), поэтому предполагают, что она относительно однородна, её плотность с глубиной меняется мало. Безразмерный момент инерции Земли меньше, чем у однородного шара (равен 0,335), что является аргументом в пользу существования у неё плотного ядра^[5]^[6].

Центробежный момент инерции[править | править код]

Центробежными моментами инерции тела по отношению к осям прямоугольной декартовой системы координат называются следующие величины^[1]^[7]:

${displaystyle J_{xy}=int limits _{(m)}xydm=int limits _{(V)}xyrho dV,}$

${displaystyle J_{xz}=int limits _{(m)}xzdm=int limits _{(V)}xzrho dV,}$

${displaystyle J_{yz}=int limits _{(m)}yzdm=int limits _{(V)}yzrho dV,}$

где x, y и z — координаты малого элемента тела объёмом dV, плотностью ρ и массой dm.

Ось OX называется главной осью инерции тела, если центробежные моменты инерции J_xy и J_xz одновременно равны нулю. Через каждую точку тела можно провести три главные оси инерции. Эти оси взаимно перпендикулярны друг другу. Моменты инерции тела относительно трёх главных осей инерции, проведённых в произвольной точке O тела, называются главными моментами инерции данного тела^[7].

Главные оси инерции, проходящие через центр масс тела, называются главными центральными осями инерции тела, а моменты инерции относительно этих осей — его главными центральными моментами инерции. Ось симметрии однородного тела всегда является одной из его главных центральных осей инерции^[7].

Геометрические моменты инерции[править | править код]

Геометрический момент инерции объёма относительно оси — геометрическая характеристика тела, выражаемая формулой^[8]:

${displaystyle J_{Va}=int limits _{(V)}r^{2}dV,}$

где, как и ранее r — расстояние от элемента dV до оси a.

Размерность J_Va — длина в пятой степени ( $mathrm {dim} J_{Va}=mathrm {L^{5}}$ ), соответственно единица измерения СИ — м⁵.

Геометрический момент инерции площади относительно оси — геометрическая характеристика тела, выражаемая формулой^[8]:

${displaystyle J_{Sa}=int limits _{(S)}r^{2}dS,}$

где интегрирование выполняется по поверхности S, а dS — элемент этой поверхности.

Размерность J_Sa — длина в четвёртой степени ( $mathrm {dim} J_{Sa}=mathrm {L^{4}}$ ), соответственно единица измерения СИ — м⁴. В строительных расчетах, литературе и сортаментах металлопроката часто указывается в см⁴.

Через геометрический момент инерции площади выражается момент сопротивления сечения:

${displaystyle W={frac {J_{Sa}}{r_{max}}}.}$

Здесь r_max — максимальное расстояние от поверхности до оси.

Геометрические моменты инерции площади некоторых фигур
Прямоугольника высотой и шириной :	$J_{y}={frac {bh^{3}}{12}}$ $J_{z}={frac {hb^{3}}{12}}$
Прямоугольного коробчатого сечения высотой и шириной по внешним контурам и , а по внутренним и соответственно	$J_{z}={frac {BH^{3}}{12}}-{frac {bh^{3}}{12}}={frac {1}{12}}(BH^{3}-bh^{3})$ $J_{y}={frac {HB^{3}}{12}}-{frac {hb^{3}}{12}}={frac {1}{12}}(HB^{3}-hb^{3})$
Круга диаметром	$J_{y}=J_{z}={frac {pi d^{4}}{64}}$

Геометрические моменты инерции площади некоторых фигур

Прямоугольника высотой

и шириной

$J_{y}={frac {bh^{3}}{12}}$

$J_{z}={frac {hb^{3}}{12}}$

Прямоугольного коробчатого сечения высотой и шириной по внешним контурам

, а по внутренним

соответственно

$J_{z}={frac {BH^{3}}{12}}-{frac {bh^{3}}{12}}={frac {1}{12}}(BH^{3}-bh^{3})$

$J_{y}={frac {HB^{3}}{12}}-{frac {hb^{3}}{12}}={frac {1}{12}}(HB^{3}-hb^{3})$

Круга диаметром

$J_{y}=J_{z}={frac {pi d^{4}}{64}}$

Момент инерции относительно плоскости[править | править код]

Моментом инерции твёрдого тела относительно некоторой плоскости называют скалярную величину, равную сумме произведений массы каждой точки тела на квадрат расстояния от этой точки до рассматриваемой плоскости^[9].

Если через произвольную точку провести координатные оси x,y,z , то моменты инерции относительно координатных плоскостей xOy , yOz и zOx будут выражаться формулами:

${displaystyle J_{xOy}=sum _{i=1}^{n}m_{i}z_{i}^{2} ,}$

${displaystyle J_{yOz}=sum _{i=1}^{n}m_{i}x_{i}^{2} ,}$

${displaystyle J_{zOx}=sum _{i=1}^{n}m_{i}y_{i}^{2} .}$

В случае сплошного тела суммирование заменяется интегрированием.

Центральный момент инерции[править | править код]

Центральный момент инерции (момент инерции относительно точки O, момент инерции относительно полюса, полярный момент инерции) ${displaystyle J_{O}}$ — это величина, определяемая выражением^[9]:

${displaystyle J_{a}=int limits _{(m)}r^{2}dm=int limits _{(V)}rho r^{2}dV,}$

где:

Центральный момент инерции можно выразить через главные осевые моменты инерции, а также через моменты инерции относительно плоскостей^[9]:

${displaystyle J_{O}={frac {1}{2}}left(J_{x}+J_{y}+J_{z}right),}$

${displaystyle J_{O}=J_{xOy}+J_{yOz}+J_{xOz}.}$

Тензор инерции и эллипсоид инерции[править | править код]

Момент инерции тела относительно произвольной оси, проходящей через центр масс и имеющей направление, заданное единичным вектором ${displaystyle {vec {s}}=leftVert s_{x},s_{y},s_{z}rightVert ^{T},leftvert {vec {s}}rightvert =1}$ , можно представить в виде квадратичной (билинейной) формы:

${displaystyle I_{s}={vec {s}}^{T}cdot {hat {J}}cdot {vec {s}},qquad }$

(1)

где — тензор инерции. Матрица тензора инерции симметрична, имеет размеры и состоит из компонент центробежных моментов:

${displaystyle {hat {J}}=leftVert {begin{array}{ccc}J_{xx}&-J_{xy}&-J_{xz}\-J_{yx}&J_{yy}&-J_{yz}\-J_{zx}&-J_{zy}&J_{zz}end{array}}rightVert ,}$

${displaystyle J_{xy}=J_{yx},quad J_{xz}=J_{zx},quad J_{zy}=J_{yz},quad }$

${displaystyle J_{xx}=int limits _{(m)}(y^{2}+z^{2})dm,quad J_{yy}=int limits _{(m)}(x^{2}+z^{2})dm,quad J_{zz}=int limits _{(m)}(x^{2}+y^{2})dm.}$

Выбором соответствующей системы координат матрица тензора инерции может быть приведена к диагональному виду. Для этого нужно решить задачу о собственных значениях для матрицы тензора :

${displaystyle {hat {J}}_{d}={hat {Q}}^{T}cdot {hat {J}}cdot {hat {Q}},}$

${displaystyle {hat {J}}_{d}=leftVert {begin{array}{ccc}J_{X}&0&0\0&J_{Y}&0\0&0&J_{Z}end{array}}rightVert ,}$

где — ортогональная матрица перехода в собственный базис тензора инерции. В собственном базисе координатные оси направлены вдоль главных осей тензора инерции, а также совпадают с главными полуосями эллипсоида тензора инерции. Величины ${displaystyle J_{X},J_{Y},J_{Z}}$ — главные моменты инерции. Выражение (1) в собственной системе координат имеет вид:

${displaystyle I_{s}=J_{X}cdot s_{x}^{2}+J_{Y}cdot s_{y}^{2}+J_{Z}cdot s_{z}^{2},}$

откуда получается уравнение эллипсоида в собственных координатах. Разделив обе части уравнения на ${displaystyle I_{s}}$

${displaystyle left({s_{x} over {sqrt {I_{s}}}}right)^{2}cdot J_{X}+left({s_{y} over {sqrt {I_{s}}}}right)^{2}cdot J_{Y}+left({s_{z} over {sqrt {I_{s}}}}right)^{2}cdot J_{Z}=1}$

и произведя замены:

${displaystyle xi ={s_{x} over {sqrt {I_{s}}}},eta ={s_{y} over {sqrt {I_{s}}}},zeta ={s_{z} over {sqrt {I_{s}}}},}$

получаем канонический вид уравнения эллипсоида в координатах :

${displaystyle xi ^{2}cdot J_{X}+eta ^{2}cdot J_{Y}+zeta ^{2}cdot J_{Z}=1.}$

Расстояние от центра эллипсоида до некоторой его точки связано со значением момента инерции тела вдоль прямой, проходящей через центр эллипсоида и эту точку:

${displaystyle r^{2}=xi ^{2}+eta ^{2}+zeta ^{2}=left({s_{x} over {sqrt {I_{s}}}}right)^{2}+left({s_{y} over {sqrt {I_{s}}}}right)^{2}+left({s_{z} over {sqrt {I_{s}}}}right)^{2}={1 over I_{s}}.}$

См. также[править | править код]

Кинематика твёрдого тела
Метод главных компонент
Сопротивление материалов
Теорема Штейнера
Теорема Кёнига (механика)
Механические приложения тройного интеграла
Механические приложения двойного интеграла
Полярный момент инерции
Список моментов инерции
Момент силы
Момент импульса

Комментарии[править | править код]

↑ При получении этой формулы путём вычитания момента инерции сплошного цилиндра радиусом r₁ из цилиндра радиусом r₂ необходимо обратить внимание, что их массы при этом не будут одинаковыми или равны m. При этом должно выполняться условие ${displaystyle m_{2}-m_{1}=m}$ . Из формулы для массы соответствующего цилиндра можно определить, что в этом случае ${displaystyle m_{1}=m{frac {r_{1}^{2}}{r_{2}^{2}-r_{1}^{2}}}}$ и ${displaystyle m_{2}=m{frac {r_{2}^{2}}{r_{2}^{2}-r_{1}^{2}}}}$ . В правильности использования знака «+» в этой формуле также можно убедиться, если сравнить моменты инерции полого толстостенного и сплошного цилиндров с одинаковыми массами. Действительно, у первого из этих цилиндров масса в среднем сосредоточена дальше от оси, чем у второго, поэтому и момент инерции этого цилиндра должен быть больше, чем у сплошного. Именно такое соотношение моментов инерции и обеспечивает знак «+». С другой стороны, в пределе при стремлении r₁ к r₂ формула для полого толстостенного цилиндра должна приобрести тот же вид, что и формула для полого тонкостенного цилиндра. Очевидно, что такой переход происходит только при использовании формулы со знаком «+».

Примечания[править | править код]

↑ ¹ ² ³ Тарг С. М. Момент инерции // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1992. — Т. 3. — С. 206—207. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.
↑ Planetary Fact Sheet. Дата обращения: 31 августа 2010. Архивировано 14 марта 2016 года.
↑ Showman, Adam P.; Malhotra, Renu. The Galilean Satellites (англ.) // Science. — 1999. — Vol. 286, no. 5437. — P. 77—84. — doi:10.1126/science.286.5437.77. — PMID 10506564.
↑ Margot, Jean-Luc; et al. Mercury’s moment of inertia from spin and gravity data (англ.) // Journal of Geophysical Research (англ.) (рус. : journal. — 2012. — Vol. 117. — doi:10.1029/2012JE004161.
↑ Галкин И.Н. Внеземная сейсмология. — М.: Наука, 1988. — С. 42-73. — 195 с. — (Планета Земля и Вселенная). — 15 000 экз. — ISBN 502005951X.
↑ Пантелеев В. Л. Физика Земли и планет. Гл. 3.4 — Гравитационное поле планеты. Дата обращения: 31 августа 2010. Архивировано 3 октября 2013 года.
↑ ¹ ² ³ Тарг С. М. Краткий курс теоретической механики. — М.: «Высшая школа», 1995. — С. 269—271. — 416 с. — ISBN 5-06-003117-9.
↑ ¹ ² Бухгольц Н. Н. Основной курс теоретической механики. — 4-е изд. — М.: «Наука», 1966. — Т. 2. — С. 131.
↑ ¹ ² ³ Яблонский А. А. Динамика // Курс теоретической механики. — 3-е изд. — М.: «Высшая школа», 1966. — Т. II. — С. 102—103. — 411 с.

Литература[править | править код]

Матвеев. А. Н. Механика и теория относительности. М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.)
Трофимова Т. И. Курс физики. — 7-е изд. — М.: Высшая школа, 2001. — 542 с.
Алешкевич В. А., Деденко Л. Г., Караваев В. А. Механика твердого тела. Лекции. Архивная копия от 7 января 2014 на Wayback Machine Издательство Физического факультета МГУ, 1997.
Павленко Ю. Г. Лекции по теоретической механике. М.: ФИЗМАТЛИТ, 2002. — 392с.
Яворский Б. М., Детлаф А. А. Физика для школьников старших классов и поступающих в вузы: учебное пособие — М.: Дрофа, 2002, 800с. ISBN 5-7107-5956-3
Сивухин Д. В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560 с.
Беляев Н. М. Сопротивление материалов. Главная редакция физико-математической литературы изд-ва «Наука», 1976. — 608 с.

Ссылки[править | править код]

Определение момента инерции тел простой формы.

Источник

В прошлый раз мы поговорили о такой величине, как статические моменты. Теперь можем двигаться дальше: сегодня на повестке моменты инерции.

Внимательный читатель уже может возмутиться:
“И зачем мы изучаем эти моменты? Какой в этом прок?
Причём же тут инерция, если сопромат — по сути статика?»

На первый вопрос у меня есть два ответа — краткий и не очень. Пока ограничусь кратким:

Статические моменты и моменты инерции широко используются для определения нормальных и касательных напряжений, определении прогибов и деформаций конструкций. Читая о том, как все это вычислить, вы будете сталкиваться с геометрическими характеристиками постоянно. Поэтому лучше сразу понимать, о чем идёт речь, а, при необходимости, подсматривать тут.

В изгибаемом элементе от момента сил возникают напряжения, для определения которых нам и нужен момент инерции (хотя и опосредованно. Впрочем, если вы читали статью про моменты, то это уже знаете). При этом сам элемент деформируется, и величина этих деформаций (прогибов) также определяется с помощью момента инерции.

Для ответа на второй вопрос перейдем уже к моментам инерции.

Что такое момент инерции

Рисунок 1. Поперечное сечение стержня. Где-то я его уже видел…

Суть и смысл моментов инерции в общем случае походит на статические моменты, однако корни нужно искать в описании вращения тела. Для вращательного движения одного только значения массы тела недостаточно, требуется еще знать распределение этой массы в теле. Рассмотрим вращающееся тело, как совокупность точек с предельно малыми размером и массой, которые находятся на расстояниях Ri (от нуля до R):

Где:
T — кинетическая энергия;
J — момент инерции;
m — масса;
v — скорость;
w — угловая скорость;
R — радиус;

Тут видно, что также, как в формуле кинетической энергии при линейном движении мера инертности — масса, при вращательном движении мера инертности — момент инерции. Впрочем, я немного забегаю вперёд.

Угловая скорость вращающегося тела — угол поворота, пройденный за единицу времени

Тут начальный угол поворота φ₀ может быть равен нулю, если мы рассматриваем начало движения.

Линейная скорость тела:

где r — расстояние от рассматриваемой точки до оси вращения

Ускорение вращающегося тела (а нас интересует нормальное) тогда:

Я не буду затрагивать динамику вращающегося тела, и расскажу только о жизненно необходимом.

Сила (которая по второму закону Ньютона — произведение массы на ускорение):

и момент:

И вот тут вспомним уже третий закон Ньютона — действию всегда есть равное и противоположное противодействие, а значит действию найденного нами момента будет сопротивляться — момент инерции.

Вспомним также, что, как и со статическими моментами, на разные точки тела, удаленные от оси вращения на разные расстояния будет действовать разный момент, а общий момент можно получить их просуммировав:

При этом значения вращающего момента и момента инерции будут равны, а сами моменты направлены в противоположные стороны. При постоянной угловой скорости вращения, например w = 1, основными величинами, характеризующими вращающий момент или момент инерции будут масса материальных точек, составляющих тело, и расстояния от этих точек до оси вращения. Но, как я уже показал, рассказывая про статические моменты, массу точек для изотропных (в данном случае имеющих одинаковую плотность) объектов можно выносить за скобки и рассматривать исключительно геометрию. Формула момента инерции примет следующий вид:

Почему I_р? Потому что мы с вами оперировали радиусом и углом поворота (в формуле угловой скорости) — т.е. использовали полярную систему отсчета (что и демонстрирует индекс p).

Таким образом момент инерции является мерой инертности тела при вращательном движении, подобно тому как масса является мерой инертности тела при поступательном прямолинейном движении.

Как найти момент инерции

Чтобы немного упростить себе операции со всеми этими величинами перейдем к родной и понятной системе отсчета: перпендикулярным осям X и Y. Возьмем случайное сечение стержня и рассмотрим интегралы, как мы уже делали со статическими моментами:

Первые два интеграла называются осевыми моментами инерции относительно осей x и y, а третий — центробежным моментом инерции сечения относительно осей x, y. Теперь рассмотрим случай параллельного переноса осей , не вдаваясь глубоко в вычисление интегралов.

Для осей x₁=x+a, y₁=y+b моменты инерции будут равны:

Если вы, как и часть прочитавших эту статью перед публикацией, не имеете черного пояса и седьмого дана в интегральных преобразованиях, то:

т.к.

Тут первый интеграл — Ix1, второй интеграл — Sx1, а третий раскрывается в площадь при нулевом свободном члене.

Надеюсь, понятно, что при параллельном переносе по y изменяется только ось (буква).

В последнем случае мы рассматриваем перенос по обеим осям сразу.

Где:
Ix — очевидно, момент инерции относительно оси x
Sx — статический момент сечения относительно оси y
F — площадь сечения

А теперь предположим, что некие оси x₁ и y₁ являются центральными, тогда и выражения упрощаются и принимают вид:

Немного проясню обозначение осей:

Центральными называются оси, проходящие через центр тяжести фигуры, т. е. статические моменты относительно этих осей равны нулю.

Главными называются оси, в которых центробежный момент инерции (I_xy) равен нулю. Если фигура имеет хотя бы одну ось симметрии, то эта ось является главной осью.

Оси, относительно которых центробежный момент инерции равен нулю, а осевые моменты инерции принимают экстремальные значения называются главными осями. Если эти оси являются также и центральными, то они называются главными центральными осями. Осевые моменты инерции относительно главных осей называются главными моментами инерции.

И теперь можно уже коснуться практики: речь о моментах инерции простых сечений.

Момент инерции прямоугольника

Определим осевые моменты инерции прямоугольника со сторонами b и h относительно осей x и y, проходящих через его центр тяжести. В качестве элементарной площадки dA возьмем полоску шириной b и высотой . Тогда будем иметь:

Не прибегая к вычислениям, замечу, что для момента инерции относительно оси Y изменится только положение сторон b и h. Следовательно:

Момент инерции квадрата

Прямоугольник со сторонами b=h=a. Следовательно:

Момент инерции круга

Тут воспользуемся полярным моментом инерции относительно центра круга. Определим его, как сумму колец с толщиной dp:

Момент инерции кольца

А здесь – явная аналогия с моментом инерции круга:

Как мы видим, момент инерции кольца это разность моментов инерции большего и меньшего кругов.

Пример нахождения момента инерции тавра

Найдём осевые моменты инерции тавра (рисунок 5), приведенного на рисунке, относительно центральных осей x_c и y_c.

Рисунок 8. Тавр, положение осей

Так как оси x₁ и x₂ являются центральными осями для простых фигур в виде прямоугольников, для определения момента инерции фигуры относительно оси x_c воспользуемся формулой.

Момент инерции относительно оси y_c получим путем сложения моментов инерции простых фигур относительно этой же оси, так как ось y_c является общей центральной осью для простых фигур и для всей фигуры.

Центробежный момент инерции относительно осей x_c и y_c равен нулю, так как ось инерции y_c является главной осью (осью симметрии фигуры).

Обобщение и подведение итогов

Момент инерции является мерой инертности тела при вращательном движении, подобно тому как масса является мерой инертности тела при поступательном прямолинейном движении. В статике момент инерции применяется в определении прогибов, расчетах конструкций на касательные и нормальные напряжения. Момент инерции также, как и статические моменты, характеризует положение осей относительно сечения элемента. Так у нас появляются:

Центральные оси, проходящие через центр тяжести фигуры, т. е. статические моменты относительно этих осей равны нулю.

Главные оси, в которых центробежный момент инерции (I_xy) равен нулю, а осевые моменты инерции — максимальны. Если фигура имеет хотя бы одну ось симметрии, то эта ось является главной осью.

При этом главные и центральные оси могут совпадать!

Список использованных источников

Александров А.В. Сопротивление материалов: Учеб. для ВУЗов/ А.В. Александров, В.Д. Потапов, Б.П. Державин; под ред. А.В. Александрова – 3-е изд. испр. – М.: Высш. шк., 2003. – 560 с.: ил. ISBN 5-06-003732-0
Дарков А.В., Шпиро Г.С. Сопротивление материалов – Учеб. для техн. вузов – 5-е изд. перераб. и дополн. – М.: Высш. шк., 1989 – 624 с. ил.
Г.И. Беликов. Геометрические характеристики поперечных сечений стержней. Учебно-практическое пособие. — Волгоград: ВолгГАСУ, 2015. — 56 с. — ISBN 978-5-98276-752-3

Автор: Марк Ершов
Редактор, факт-чекер: К.А.Овчинников

5 413

Источник

Часто мы слышим выражения: «он инертный», «двигаться по инерции», «момент инерции». В переносном значении слово «инерция» может трактоваться как отсутствие инициативы и действий. Нас же интересует прямое значение.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Что такое инерция

Согласно определению инерция в физике – это способность тел сохранять состояние покоя или движения в отсутствие действия внешних сил.

Если с самим понятием инерции все понятно на интуитивном уровне, то момент инерции – отдельный вопрос. Согласитесь, сложно представить в уме, что это такое. В этой статье Вы научитесь решать базовые задачи на тему «Момент инерции».

Определение момента инерции

Из школьного курса известно, что масса – мера инертности тела. Если мы толкнем две тележки разной массы, то остановить сложнее будет ту, которая тяжелее. То есть чем больше масса, тем большее внешнее воздействие необходимо, чтобы изменить движение тела. Рассмотренное относится к поступательному движению, когда тележка из примера движется по прямой.

По аналогии с массой и поступательным движением момент инерции – это мера инертности тела при вращательном движении вокруг оси.

Момент инерции – скалярная физическая величина, мера инертности тела при вращении вокруг оси. Обозначается буквой J и в системе СИ измеряется в килограммах, умноженных на квадратный метр.

Как посчитать момент инерции? Есть общая формула, по которой в физике вычисляется момент инерции любого тела. Если тело разбить на бесконечно малые кусочки массой dm, то момент инерции будет равен сумме произведений этих элементарных масс на квадрат расстояния до оси вращения.

Это общая формула для момента инерции в физике. Для материальной точки массы m, вращающейся вокруг оси на расстоянии r от нее, данная формула принимает вид:

Теорема Штейнера

От чего зависит момент инерции? От массы, положения оси вращения, формы и размеров тела.

Теорема Гюйгенса-Штейнера – очень важная теорема, которую часто используют при решении задач.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Теорема Гюйгенса-Штейнера гласит:

Момент инерции тела относительно произвольной оси равняется сумме момента инерции тела относительно оси, проходящей через центр масс параллельно произвольной оси и произведения массы тела на квадрат расстояния между осями.

Для тех, кто не хочет постоянно интегрировать при решении задач на нахождение момента инерции, приведем рисунок с указанием моментов инерции некоторых однородных тел, которые часто встречаются в задачах:

Пример решения задачи на нахождение момента инерции

Рассмотрим два примера. Первая задача – на нахождение момента инерции. Вторая задача – на использование теоремы Гюйгенса-Штейнера.

Задача 1. Найти момент инерции однородного диска массы m и радиуса R. Ось вращения проходит через центр диска.

Решение:

Разобьем диск на бесконечно тонкие кольца, радиус которых меняется от 0 до R и рассмотрим одно такое кольцо. Пусть его радиус – r, а масса – dm. Тогда момент инерции кольца:

Массу кольца можно представить в виде:

Здесь dz – высота кольца. Подставим массу в формулу для момента инерции и проинтегрируем:

В итоге получилась формула для момента инерции абсолютного тонкого диска или цилиндра.

Задача 2. Пусть опять есть диск массы m и радиуса R. Теперь нужно найти момент инерции диска относительно оси, проходящей через середину одного из его радиусов.

Решение:

Момент инерции диска относительно оси, проходящей через центр масс, известен из предыдущей задачи. Применим теорему Штейнера и найдем:

Кстати, в нашем блоге Вы можете найти и другие полезные материалы по физике и решению задач.

Надеемся, что Вы найдете в статье что-то полезное для себя. Если в процессе расчета тензора инерции возникают трудности, не забывайте о студенческом сервисе. Наши специалисты проконсультируют по любому вопросу и помогут решить задачу в считанные минуты.

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник

Содержание:

Геометрия масс:

Центр масс

При рассмотрении движения твердых тел и других механических систем важное значение имеет точка, называемая центром масс. Если механическая система состоит из конечного числа материальных точек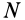

где 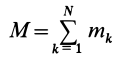— масса системы. Обозначая декартовы координаты материальных точек 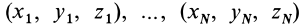, из (1) проецированием на декартовы оси координат получим следующие формулы для координат центра масс:

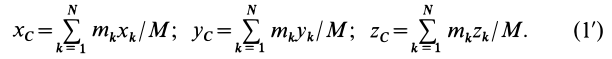
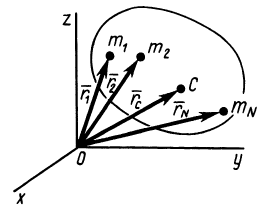
Рис. 21

Центр масс является не материальной точкой, а геометрической. Он может не совпадать ни с одной материальной точкой системы, как, например, в случае кольца. Центр масс системы характеризует распределение масс в системе.

Векторная величина 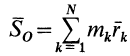называется статическим моментом массы относительно точки . Скалярная величина 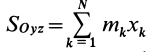называется статическим моментом

массы относительно координатной плоскости 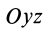. Величины 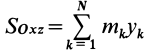и 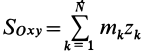являются соответственно статическими моментами массы относительно координатных плоскосте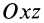й и .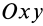

Радиус-вектор и координаты центра масс через статические моменты массы выражаются формулами

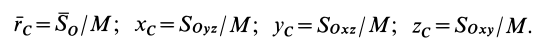
Если механическая система представляет собой сплошное тело, то его разбивают на элементарные частицы с бесконечно малыми массами 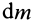и с изменяющимися от частицы к частице радиусом-вектором .

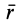Суммы в пределе переходят в интегралы. Формулы (1) и (Г) принимают форму

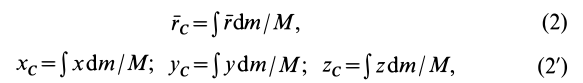
где 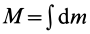— масса тела.

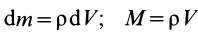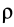Для однородных сплошных тел , где — плотность тела, общая для всех элементарных частиц; 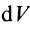—объем элементарной частицы; 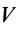—объем тела.

Для тел типа тонкого листа, которые можно принять за однородные материальные поверхности, 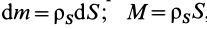, где 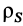— поверхностная плотность; 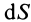—площадь поверхности элементарной частицы; 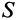—площадь поверхности.

Для тонкой проволоки, которую можно принять за отрезок линии, 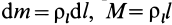, где 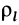— линейная плотность; 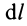—длина элемента линии; 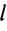—длина отрезка линии.

В этих случаях определение центра масс тел сводится к вычислению центра масс объемов, площадей и длин линий соответственно.

Моменты инерции

Для характеристики распределения масс в телах при рассмотрении вращательных движений требуется ввести понятия моментов инерции.

Моменты инерции относительно точки и оси

Моментом инерции механической системы, состоящей из 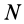материальных точек, относительно точки 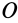называется сумма произведений масс этих точек на квадраты их расстояний до точки 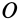(рис. 22), т. е.

Момент инерции относительно точки часто называют полярным моментом инерции. В случае сплошного тела сумма переходит в интеграл и для полярного момента инерции имеем

где 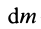— масса элементарной частицы тела, принимаемой в пределе за точку; 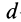—ее расстояние до точки .

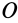Моментом инерции 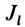системы материальных точек относительно оси 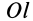называется сумма произведений масс этих точек на квадраты их расстояний 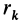до оси 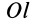(рис. 22), т. е.

Рис. 22

В частном случае сплошного тела сумму следует заменить интегралом:

Моменты инерции одинаковых по форме однородных тел, изготовленных из разных материалов, отличаются друг от друга. Характеристикой, не зависящей от массы материала, является радиус инерции. Радиус инерции 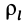относительно оси 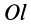определяется по формуле

где 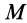—масса тела.

Момент инерции относительно оси через радиус инерции относительно этой оси определяется выражением

В справочниках по моментам инерции приводят таблицы значений радиусов инерции различных тел.

Формула (5′) позволяет считать радиус инерции тела относительно оси расстоянием от этой оси до такой точки, в которой следует поместить массу тела, чтобы ее момент инерции оказался равным моменту инерции тела относительно рассматриваемой оси.

Моменты инерции относительно оси и точки имеют одинаковую размерность — произведение массы на квадрат длины .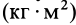

Кроме моментов инерции относительно точки и оси используются также моменты инерции относительно плоскостей и центробежные моменты инерции. Эти моменты инерции удобно рассмотреть относительно координатных плоскостей и осей декартовой системы координат.

Моменты инерции относительно осей координат

Моменты инерции относительно декартовых осей координат 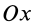, 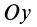и 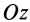и их начала — точки 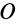(рис. 23) — определяются выражениями

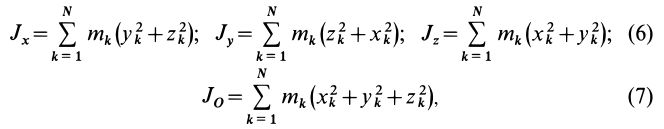
где 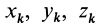— координаты материальных точек системы. Для сплошных тел эти формулы примут вид

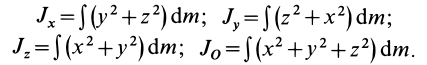
Из приведенных формул следует зависимость

Если через точку 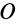провести другую систему декартовых осей координат 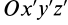, то для них по формуле (8) получим

Из сравнения (8) и (8′) следует, что

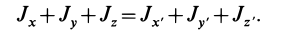
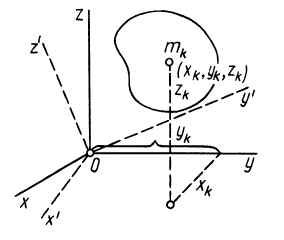
Рис. 23

Сумма моментов инерции относительно декартовых осей координат не зависит от ориентации этих осей в рассматриваемой точке, т. е. является величиной, инвариантной по отношению к направлению осей координат.

Для осей координат 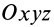можно определить следующие три центробежных момента инерции:

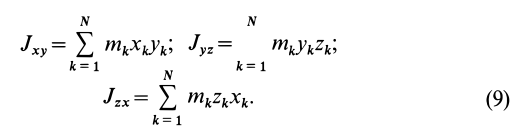
Центробежные моменты инерции часто называют произведениями инерции.

Моменты инерции относительно осей и точек — величины положительные, так как в них входят квадраты координат. Центробежные моменты инерции содержат произведения координат и могут быть как положительными, так и отрицательными.

Центробежные моменты инерции имеют важное значение при рассмотрении давлений на подшипники при вращении твердого тела вокруг неподвижной оси и в других случаях.

Кроме рассмотренных моментов инерции иногда используются моменты инерции относительно координатных плоскостей 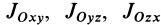, которые определяются выражениями

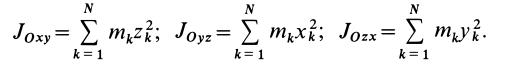
Теорема о моментах инерции относительно параллельных осей (теорема Штейнера)

Установим зависимость между моментами инерции системы относительно параллельных осей, одна из которых проходит через центр масс. Пусть имеем две системы прямоугольных, взаимно параллельных осей координат 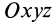и 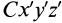. Начало системы координат 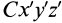находится в” центре масс системы (рис. 24).

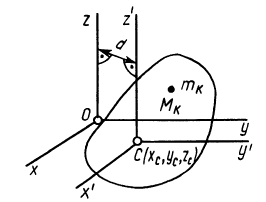
Рис. 24

По определению момента инерции относительно оси имеем

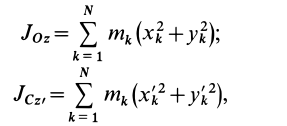
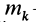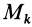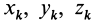где — масса точки , а и 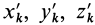— координаты этой точки относительно систем координат 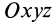и 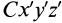соответственно. Если обозначить 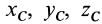координаты центра масс относительно системы координат 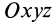, то для взаимно параллельных осей координаты одной и той же точки 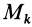связаны соотношениями параллельного переноса

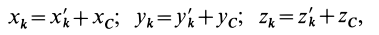
Подставим эти значения координат в выражение момента инерции 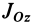. После преобразований получим

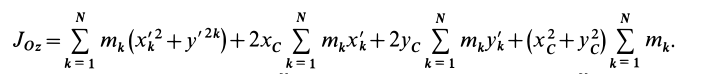
В этом соотношении 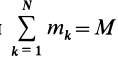—масса системы, 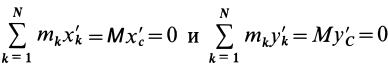, так как 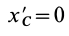и 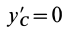вследствие k = 1

того, что по условию центр масс находится в начале координат этой системы координат.

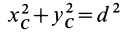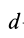Величина , где —расстояние между осям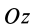и и 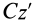. Окончательно

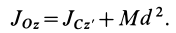
Связь моментов инерции относительно двух параллельных осей, одна из которых проходит через центр масс, составляет содержание так называемой теоремы Штейнера или Гюйгенса— Штейнера: момент инерции системы относительно какой-либо оси равен моменту инерции относительно параллельной оси, проходящей через центр масс, плюс произведение массы системы на квадрат расстояния между этими осями.

Из теоремы Штейнера следует, что для совокупности параллельных осей момент инерции является наименьшим относительно оси, проходящей через центр масс.

Если взять ось 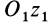параллельной 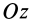, то для нее получим

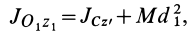
где 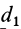— расстояние между параллельными осям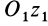и и .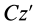

Исключая момент инерции 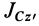из двух последних формул, получим зависимость моментов инерции относительно двух параллельных осей, не проходящих через центр масс:

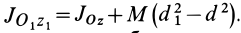
Установим изменение центробежных моментов инерции при параллельном переносе осей координат. Имеем

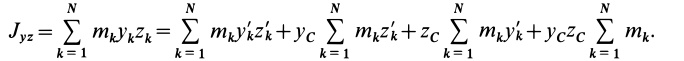
Учитывая, что 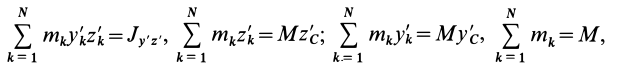получаем

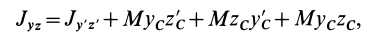
где 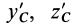— координаты центра масс относительно системы координат 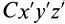. Аналогичные формулы получаются для двух других центробежных моментов инерции:

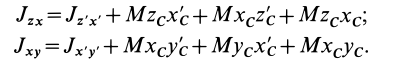
Так как начало системы координат 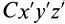находится в центре масс, то 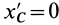, , 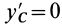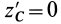и тогда

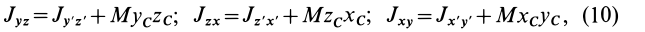
т. е. центробежные моменты инерции при параллельном переносе осей координат из любой точки в центре масс изменяются в соответствии с (10).

Если производится параллельный перенос осей 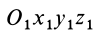из точки 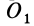в центр масс, то, согласно (10), имеем:

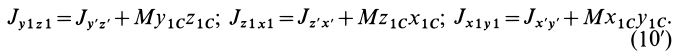
Исключая из (10) и (10′) центробежные моменты инерции Л’з” Лу, получим формулы для изменения центробежных моментов инерции при параллельном переносе осей координат из точки 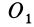в точку :

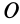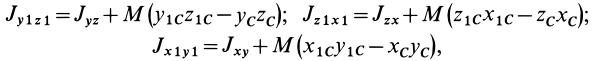
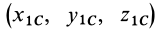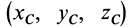где и — координаты центра масс в двух системах взаимно параллельных осей координат.

Моменты инерции простейших однородных тел

Моменты инерции тел сложной формы часто удается вычислить, если их предварительно разбить на тела простой формы. Моменты инерции сложных тел получают суммируя моменты инерции частей этих тел. Получим формулы для вычисления моментов инерции некоторых однородных простейших тел.

Однородный стержень

Имеем однородный стержень длиной 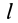и массой 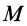(рис. 25). Направим по стержню ось 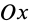. Вычислим момент инерции стержня относительно оси 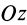, проходящей перпендикулярно стержню через его конец. Согласно определению момента инерции сплошного тела относительно оси, имеем

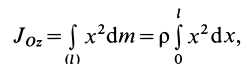
так как 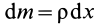, где 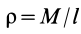—плотность стержня.

Вычисляя интеграл, получаем

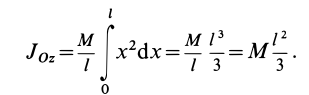
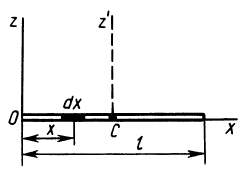
Рис. 25

Таким образом,

Момент инерции стержня относительно оси 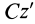, проходящей через центр масс и параллельной оси 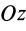, определяется по теореме Штейнера:

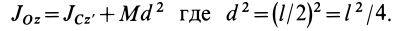
Следовательно,

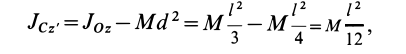
т. е.

Прямоугольная пластина

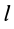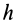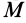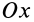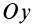Прямоугольная тонкая пластина имеет размеры и и массу (рис. 26). Оси и расположим в плоскости пластины, а ось 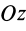—перпендикулярно ей. Для определения момента инерции пластины относительно оси 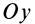разобьем пластину на элементарные полоски шириной 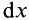и массой 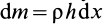и проинтегрируем по 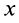от 0 до 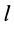. Получим

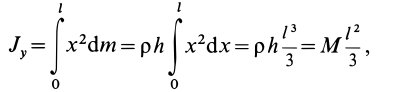
так как .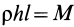

Аналогичные вычисления для оси 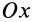дадут

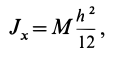
так как эта ось 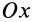проходит через середину пластины. Для определения момента инерции пластины относительно оси 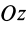следует предварительно вычислить момент инерции отдельной заштрихованной полоски относительно параллельной оси 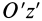по формуле (12) для стержня и применить затем теорему Штейнера. Для элементарной полоски имеем

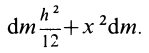
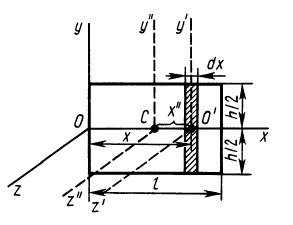
Рис. 26

Интегрируя это выражение в пределах от 0 до 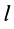, получим

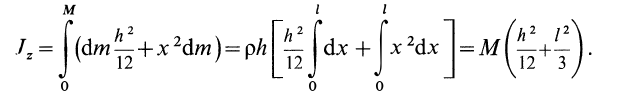
Итак, для моментов инерции пластины относительно осей координат получены следующие формулы:

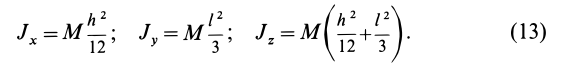
Круглый диск

Имеем тонкий однородный диск радиусом 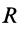и массой 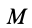(пис. 27). Вычислим момент его инерции 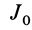относительно точки 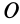. Этот момент инерции для тонкого диска совпадает с моментом инерции 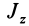относительно координатной оси 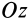, перпендикулярной плоскости диска. Разобьем диск на концентрические полоски шириной 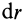, принимаемые в пределе за материальные окружности. Масса полоски равна ее площади 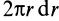, умноженной на плотность 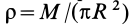, т.е. 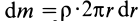. Момент одной полоски относительно точки 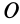равен . 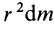Для всего диска

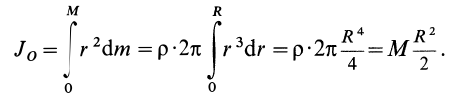
Таким образом,

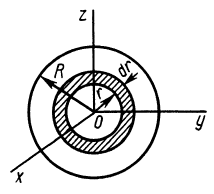
Рис. 27

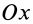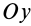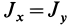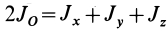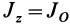Для осей координат и , расположенных в плоскости диска, в силу симметрии . Используя (8), имеем , но , поэтому

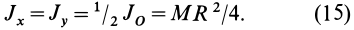
В случае тонкого проволочного кольца или круглого колеса, у которых масса распределена не по площади, а по его ободу, имеем

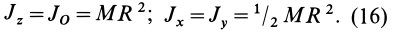
Круглый цилиндр

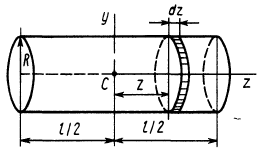
Рис. 28

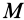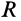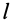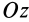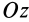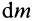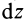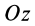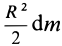Для круглого однородного цилиндра, масса которого , радиус и длина (рис. 28), вычислим прежде всего его момент инерции относительно продольной оси симметрии . Для этого разобьем цилиндр плоскостями, перпендикулярными оси , на тонкие диски массой и толщиной . Для такого диска момент инерции относительного оси равен . Для всего цилиндра

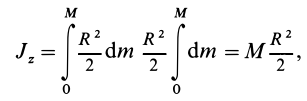
т.е.

Вычислим момент инерции цилиндра относительно его поперечной оси симметрии 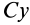. Для этого разобьем цилиндр поперечными сечениями, перпендикулярными его продольной оси, на элементарные диски толщиной 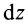. Момент инерции элементарного диска массой 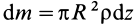относительно оси 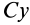, по теореме Штейнера, .

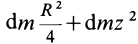Чтобы получить момент инерции всего цилиндра относительно оси 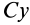, следует проинтегрировать полученное выражение по 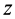в пределах от 0 до 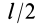и результат удвоить. Получим

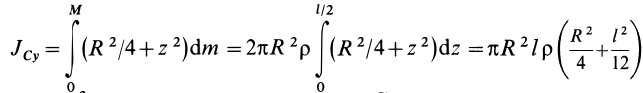
Но 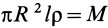— масса цилиндра. Следовательно,

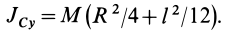
Таким образом, момент инерции цилиндра относительно его поперечной оси симметрии получается как сумма моментов инерции относительно этой оси диска и стержня, массы которых равны по отдельности массе цилиндра. Диск получается из цилиндра симметричным сжатием его с торцов до срединной плоскости при сохранении радиуса, а стержень — сжатием цилиндра в однородный стержень, расположенный по оси цилиндра, при сохранении длины.

Шар

Пусть масса шара 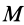, радиус 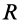(рис. 29). Разобьем шар на концентрические сферические слои радиусом 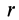и толщиной 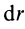. Масса такого слоя 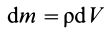, где 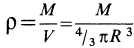; 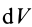—объем слоя, равный произведению площади поверхности сферы радиусом 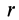на толщину слоя 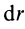, т.е. 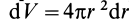. Таким образом, масса элементарного слоя 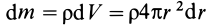. Для момента инерции шара относительно его центра 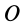имеем

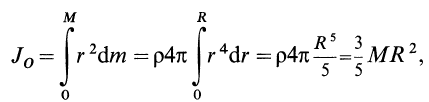
т.е.

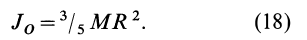
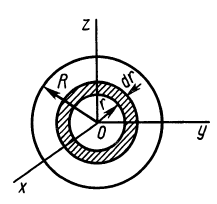
Рис. 29

Для осей координат, проходящих через центр шара, в силу симметрии 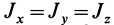. Но 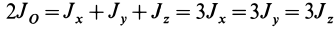. Следовательно,

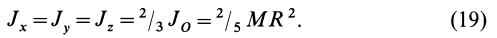
Моменты инерции относительно осей, проходящих через заданную точку

В заданной точке 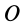выберем декартову систему осей координат 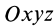. Ось 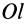образует с осями координат углы 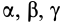(рис. 30). По определению момента инерции относительно оси 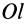имеем

или для сплошных тел

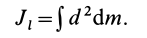
В дальнейшем используется определение (20). Сплошные тела считаются разбитыми на 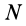малых частей, принимаемых за точки.

Из прямоугольного треугольника 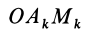получаем

где 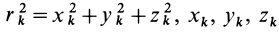— координаты точки 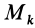. Отрезок 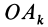является проекцией радиуса-вектора 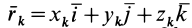на ось 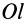. Для получения проекции вектора 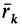на ось 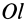его следует умножить скалярно на единичный вектор этой оси 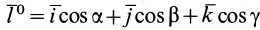. Имеем

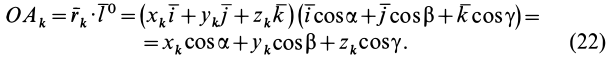
Умножая в (21) 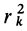, выраженный через координаты точки 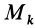, на единицу в виде 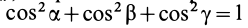и используя значение (22) для 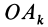, получим

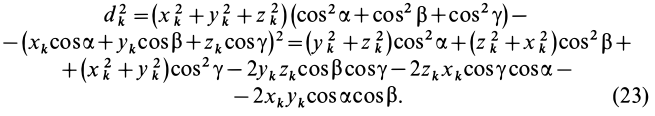
Подставляя (23) в (20) и вынося косинусы углов за знаки сумм, имеем

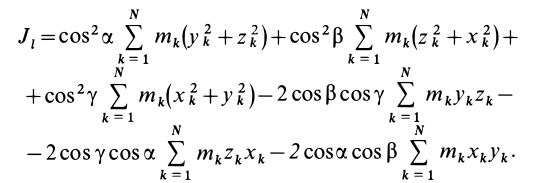
Учитывая, что

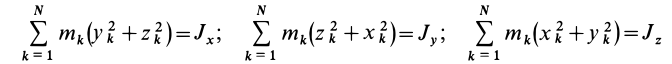
— моменты инерции относительно осей координат, а

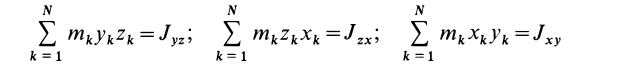
— центробежные моменты инерции относительно тех же осей, получим

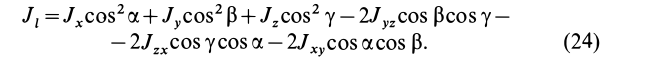
Для определения момента инерции 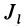, кроме углов 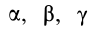, определяющих направление оси, необходимо знать в точке шесть моментов инерции: 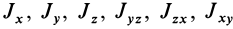. Их удобно расположить как элементы единой таблицы или матрицы:

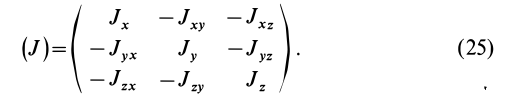
Матрица, или таблица (25), составленная из осевых и центробежных моментов инерции относительно декартовых осей координат, называется тензором инерции в точке . В тензоре инерции условились центробежные моменты инерции брать со знаком минус. Компоненты тензора инерции (отдельные осевые или центробежные моменты инерции) зависят не только от выбора точки, но и от ориентации осей координат в этой точке.

Для определения момента инерции относительно какой-либо оси, проходящей через заданную точку, для рассматриваемого тела необходимо иметь тензор инерции в этой точке и углы, определяющие направление оси с осями координат.

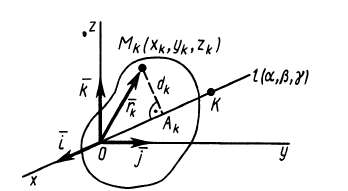
Рис. 30

Эллипсоид инерции

Для характеристики распределения моментов инерции тела относительно различных осей, проходящих через заданную точку, используется поверхность второго порядка — эллипсоид инерции. Для построения этой поверхности на каждой оси 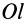(см. рис. 31), проходящей через точку , откладывают от этой точки отрезок

Геометрическое место концов отрезков 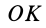расположится на поверхности, которая называется эллипсоидом инерции. Получим уравнение эллипсоида инерции. Для этого выразим косинусы углов 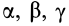через координаты 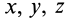точки 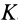. Имеем:

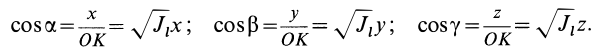
Подставляя эти значения косинусов углов в (24) и сокращая на 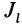, получим уравнение поверхности второго порядка:

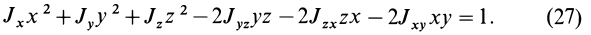
Это действительно уравнение эллипсоида, так как отрезок 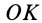имеет конечную длину для всех осей, для которых моменты инерции не обращаются в нуль. Другие поверхности второго порядка, например гиперболоиды и параболоиды, имеют бесконечно удаленные точки. Эллипсоид инерции вырождается в цилиндр для тела в виде прямолинейного отрезка, если точка расположена на самом отрезке. Для оси, направленной по этой прямой линии, момент инерции обращается в нуль и соответственно отрезок 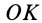равен бесконечности.

Для каждой точки имеется свой эллипсоид инерции. Эллипсоид инерции для центра масс тела называют центральным эллипсоидом инерции. Оси эллипсоида инерции (его сопряженные диаметры) называются главными осями инерции. В общем случае эллипсоид инерции имеет три взаимно перпендикулярные главные оси инерции. Они являются его осями симметрии.

В случае эллипсоида вращения все прямые, расположенные в экваториальной плоскости эллипсоида, перпендикулярной оси вращения, будут главными осями инерции. Для шара любая прямая, проходящая через его центр, есть главная ось инерции.

Моменты инерции относительно главных осей инерции называются главными моментами инерции, а относительно главных центральных осей инерции — главными центральными моментами инерции.

Если уравнение эллипсоида инерции отнести к его главным осям 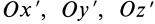, то оно примет вид

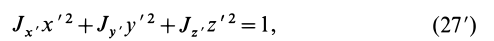
где 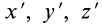—текущие координаты точки, расположенной на эллипсоиде инерции, относительно главных осей инерции;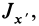 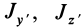— главные моменты инерции. Уравнение эллипсоида инерции (27′) не содержит слагаемых с произведениями координат точек. Поэтому центробежные моменты инерции относительно главных осей инерции равны нулю, т. е.

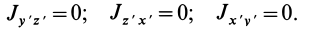
Справедливо и обратное утверждение: если центробежные моменты инерции относительно трех взаимно перпендикулярных осей равны нулю, то эти оси являются главными осями инерции. Обращение в нуль трех центробежных моментов инерции является необходимым и достаточным условием того, что соответствующие прямоугольные оси координат есть главные оси инерции.

Главные моменты инерции часто обозначают 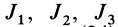, вместо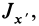 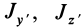. Для главных осей инерции формула (24) принимает форму

Заказать решение задач по теоретической механике

Свойства главных осей инерции

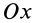Теорема 1. Если одна из декартовых осей координат, например (рис. 31), является главной осью инерции для точки , а две другие оси и 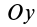— любые, то два центробежных момента инерции, содержащих индекс главной оси инерции , обращаются в нуль, т.е. 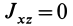и .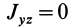

Главная ось инерции 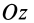является осью симметрии эллипсоида инерции. Поэтому каждой точке эллипсоида, например 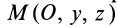, соответствует симметричная относительно этой оси точка 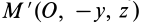. Подставляя в уравнение эллипсоида инерции (27) последовательно координаты этих точек, получим

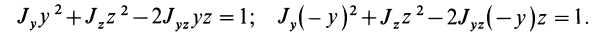
Вычитая из первого уравнения второе, имеем

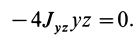
Так как всегда можно выбрать точки, для которых 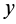и 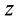отличны от нуля, то .

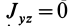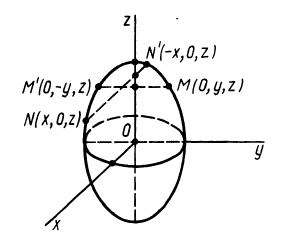
Рис. 31

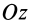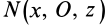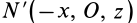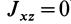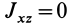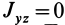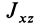Аналогичные рассуждения для двух симметричных относительно оси точек и приводят к заключению, что . В аналитической геометрии при исследовании уравнений поверхностей второго порядка доказывается обратное утверждение, что если и , то ось есть главная ось. Таким образом, обращение в нуль центробежных моментов инерции и 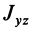является необходимым и достаточным условием, чтобы ось была главной осью инерции для точки .

Теорема 2. Если однородное тело имеет плоскость симметрии, то для любой точки, лежащей в этой плоскости, одна из главных осей инерции перпендикулярна плоскости симметрии, а две другие главные оси инерции расположены в этой плоскости.

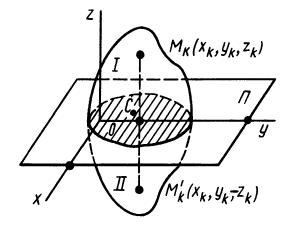
Рис. 32

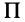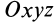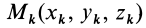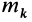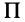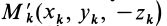Для доказательства теоремы выберем в плоскости симметрии точку и в ней оси прямоугольной системы координат , причем ось направим перпендикулярно плоскости симметрии (рис. 32). Тогда каждой точке тела массой соответствует симметричная относительно плоскости точка с такой же массой. Координаты точек 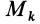и 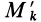отличаются только знаком у координат .

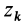Для центробежного момента инерции 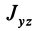имеем

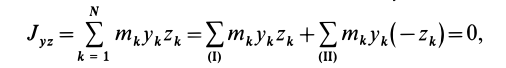
так как часть тела (I), соответствующая точкам с положительными координатами 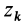, одинакова с частью тела (II), у которой точки имеют такие же координаты 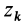, но со знаком минус. Аналогично доказывается, что

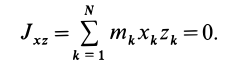
Так как центробежные моменты инерци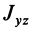и и 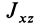обращаются в нуль, то ось есть главная ось инерции для точки . Другие две главные оси инерции перпендикулярны оси и, следовательно, расположены в плоскости симметрии.

Центр масс однородного симметричного тела находится в плоскости симметрии. Поэтому одна из главных центральных осей инерции перпендикулярна плоскости симметрии, а две другие расположены в этой плоскости.

Доказанная теорема справедлива и для неоднородного тела, имеющего плоскость материальной симметрии.

Теорема 3. Если однородное тело имеет ось симметрии или неоднородное тело имеет ось материальной симметрии, то эта ось является главной центральной осью инерции.

Теорема доказывается аналогично предыдущей. Для каждой точки тела 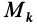с положительными координатами 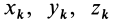и массой 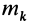существует симметричная относительно оси точка с такой же массой и такими же по величине, но отрицательными координатами 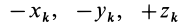, если осью симметрии является ось . Тогда

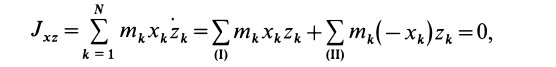
так как суммы по симметричным относительно оси частям тела (I) и (II) отличаются друг от друга только знаком у координаты .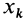

Аналогично доказывается, что .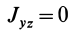

Таким образом, ось является главной осью инерции для любой точки, расположенной на оси симметрии тела. Она есть главная центральная ось инерции, так как центр масс находится на оси симметрии.

Теорема 4. Главные оси инерции для точки , расположенной на главной центральной оси инерции, параллельны главным центральным осям инерции (рис. 33).

Выберем в точке главной центральной оси инерции 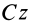систему декартовых осей координат 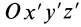, взаимно параллельных главным центральным осям инерции 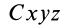. Тогда координаты точки тела 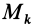в двух системах осей координат будут связаны между собой формулами параллельного переноса осей

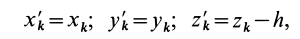
где 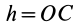. Используя эти формулы, вычисляем центробежные моменты инерци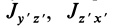и и 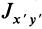. Имеем

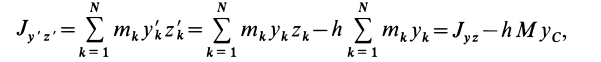
так как

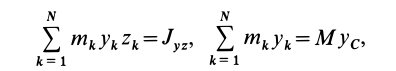
где 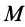—масса тела; 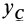— координата центра масс относительно системы координат 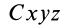. Аналогично получаем

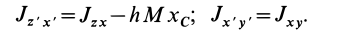
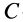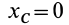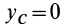Если — центр масс системы, то и . Для главных центральных осей инерции центробежные моменты инерции равны нулю, т. е.

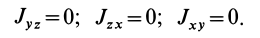
Используя полученные формулы при этих условиях, имеем:

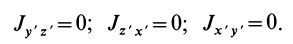
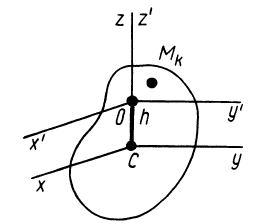
Рис. 33

Следовательно, оси 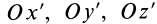есть главные оси инерции для произвольной точки 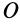, расположенной на главной центральной оси инерции 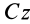. Теорема доказана.

Из доказанной теоремы в качестве следствия получаем: главная центральная ось инерции является главной осью инерции для всех своих точек. Действительно, главная ось инерции 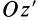для точки 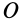, лежащей на главной центральной оси инерции 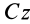, совпадает с этой осью. Главная ось инерции таким свойством не обладает. Главные оси инерции для точки 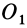, расположенной на главной оси инерции точки 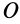, не параллельны главным осям инерции для этой точки. Они в общем случае повернуты относительно этих осей.

Определение главных моментов инерции и направления главных осей

Пусть известны компоненты тензора инерции в точке 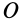относительно осей координат 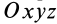. Для определения направления главных осей инерции в точке 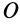используем уравнение эллипсоида инерции относительно этих осей

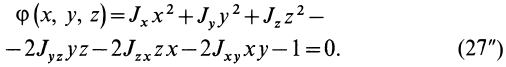
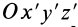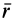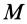Если оси координат являются главными осями инерции, то радиус-вектор точки эллипсоида инерции, расположенной на главной оси инерции, например оси 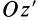(рис. 34), направлен по нормали к эллипсоиду, т. е. параллельно вектору 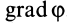, который, согласно его определению, вычисляется по формуле

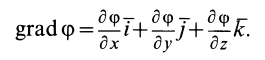
Параллельные векторы отличаются друг от друга скалярным множителем, который обозначим 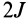. Тогда для параллельных векторов 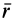и 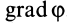и их проекций на оси координат имеем:

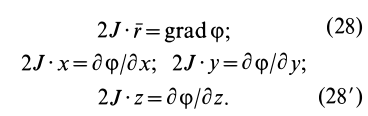
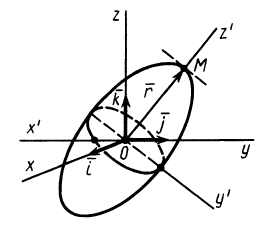
Рис. 34

В этих уравнениях 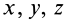являются координатами точки конца вектора 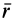, проведенного из точки 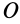вдоль какой-либо главной оси инерции для этой точки.

Для частных производных из (27′) получаем:

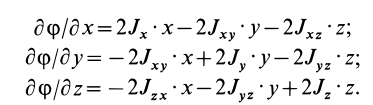
Подставляя их значения в (28′) и перенося все слагаемые в левую часть, после объединения и сокращения на общий множитель получим следующую систему уравнений для определения координат 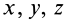точки 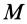, находящейся на главной оси инерции:

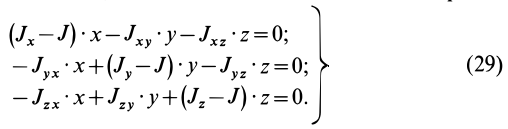
Так как (29) является однородной системой линейных уравнений, то отличные от нуля решения для координат 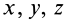получаются только при условии, что определитель этой системы равен нулю, т. е.

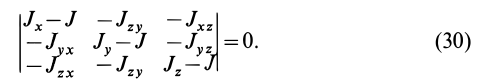
Это кубическое уравнение для определения 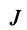называется уравнением собственных значений тензора инерции.

В общем случае имеется три различных действительных корня кубического уравнения 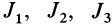, которые являются главными моментами инерции. Действительно, если ось 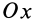совпадает с главной осью инерции, то для точки 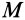эллипсоида инерции, расположенной на этой ос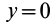и, и 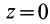. Первое уравнение (29) принимает вид

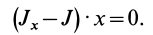
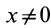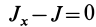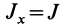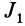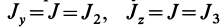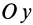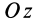Так как , то и , которое следует обозначить . Аналогично можно получить , если оси и — главные оси инерции.

Подставляя в (29) 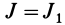получим только два независимых уравнения для определения координат точки 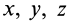эллипсоида инерции, соответствующих главной оси инерции, для которой главный момент инерции есть 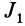. Третье уравнение системы будет следствием двух других уравнений, так как определитель этой системы равен нулю. Из (29) можно найти только две величины, например 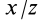и 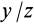. Они определят направление вектора вдоль главной оси инерции, момент инерции относительно которой есть 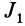. Модуль радиуса-вектора 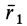остается неопределенным. Аналогично определяются направления векторов 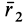и 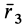вдоль двух других главных осей инерции, для которых главные моменты инерции равны 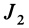и . Можно доказать, что векторы 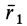, , 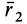, 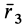направленные вдоль главных осей инерции, взаимно перпендикулярны.

Таким образом, если известен тензор инерции для осей , то можно определить как направление главных осей инерции, так и главные моменты инерции. Для главных осей инерции тензор инерции (25) принимает форму

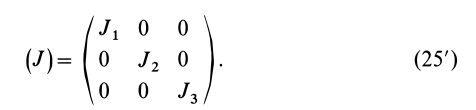
Выражение компонентов тензора инерции через главные моменты инерции

Определим компоненты тензора инерции в точке 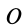относительно осей координат , если в этой точке известны главные моменты инерции относительно главных осей инерции 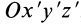, т. е. 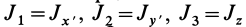. Предположим, что ориентация осей координат относительно главных осей инерции 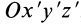задана таблицей углов:

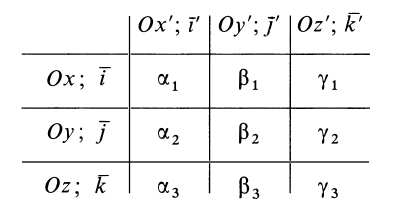
Осевые моменты инерции относительно осей 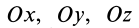через главные моменты инерции определяются по формуле (24′). Принимая последовательно за ось 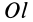оси координат 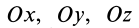, получим

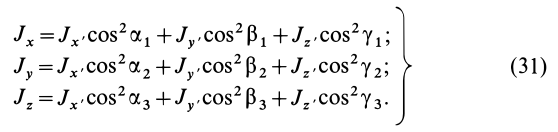
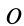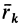Для выражения центробежных моментов инерции через главные моменты инерции используем формулы преобразования координат точек тела при повороте осей координат вокруг точки (рис. 35). Эти формулы получим проецированием на оси радиуса-вектора точки 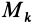, разложенного предварительно на составляющие, параллельные осям двух систем осей координат в точке 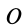. Имеем

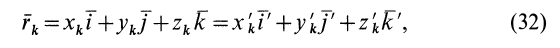
где 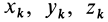— координаты точки 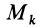относительно системы осей координат 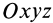, а 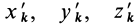— относительно 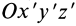. Проецирование вектора на какую-либо ось прямоугольной системы координат эквивалентно скалярному умножению этого вектора на единичный вектор оси. Умножая обе части (32) последовательно на единичные векторы осей координат 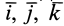и учитывая таблицу углов для осей, получим

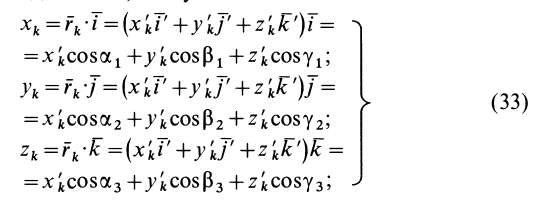
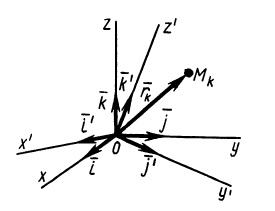
Рис. 35

Используя (33) для центробежного момента инерции 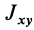, имеем

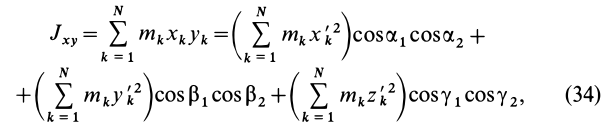
так как центробежные моменты инерции относительно главных осей инерции равны нулю, т. е.

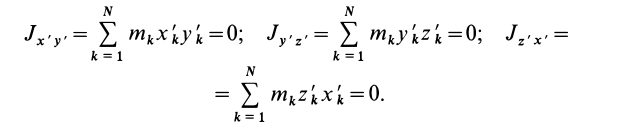
Оси координат 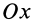и 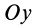взаимно перпендикулярны, поэтому косинусы их углов удовлетворяют условию

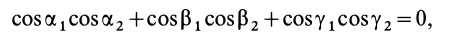
или

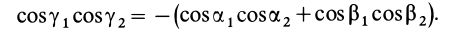
Используя это соотношение для исключения величины 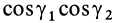и добавляя в первом слагаемом (34) под знаком суммы 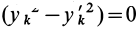, а во втором 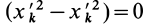, после объединения слагаемых с одинаковыми произведениями косинусов получим

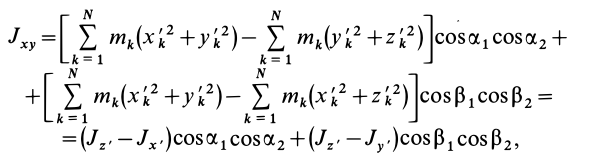
где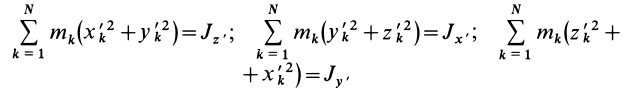

— главные моменты инерции. Аналогично получаются выражения для 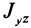и 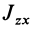. Итак имеем

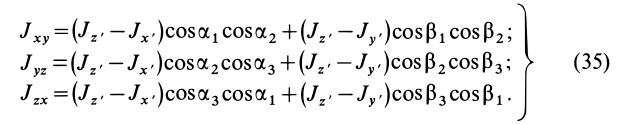
Формулы (31) и (35) дают выражения всех компонентов тензора инерции для осей координат 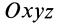через главные моменты инерции, если известны углы этих осей с главными осями инерции. В приложениях встречаются частные случаи, когда одна из осей координат 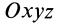совпадает с главной осью инерции.

Если ось 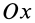совпадает с главной осью инерции 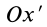(рис. 36), то 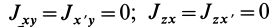. Это же можно получить из (35). Необходимые для вычисления углы соответственно равны:

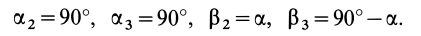
Из (35) имеем

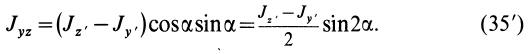
В формуле (35′) с полюсом следует брать главный момент инерции с индексом той оси, на положительное направление которой указывает дуговая стрелка поворота осей 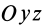на угол 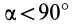до совпадения с осями 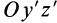. В рассматриваемом случае поворот осей 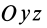вокруг 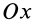до совпадения с главными осями производится от 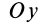оси к оси 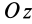; следовательно, с плюсом следует взять главный момент инерции 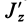и с минусом — .

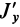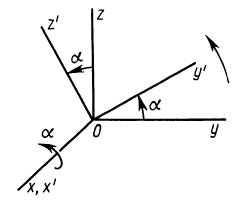
Рис. 36

Если оси расположены, как показано на рис. 37, то дуговая стрелка поворота осей 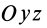до совпадения с главными осями инерции 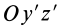на угол 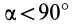направлена к отрицательному направлению оси 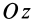. Поэтому в (35′) 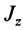, следует взять со знаком минус, а 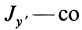знаком плюс, в чем нетрудно убедиться, используя (35) и таблицу углов. Имеем:

= 90°; р2 = а; Р3 = 90° + а;

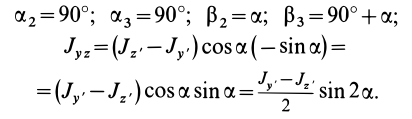
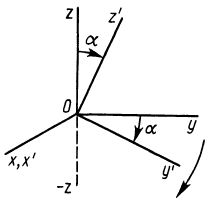
Рис. 37

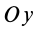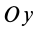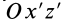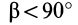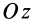Аналогично при совпадении осей с Оу’ и повороте осей Oxz вокруг до совпадения с осями на угол от к 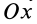в направлении против часовой стрелки имеем:

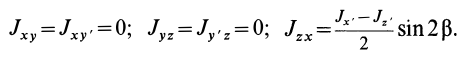
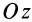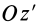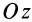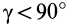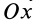При совпадении осей и и повороте осей вокруг на угол от к 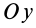против часовой стрелки получим:

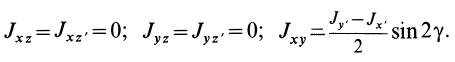
Свойства внутренних сил системы
Дифференциальное уравнение движения системы
Теоремы об изменении количества движения и о движении центра масс
Теорема об изменении кинетического момента
Прямолинейное движение точки
Криволинейное движение материальной точки
Движение несвободной материальной точки
Относительное движение материальной точки

Источник

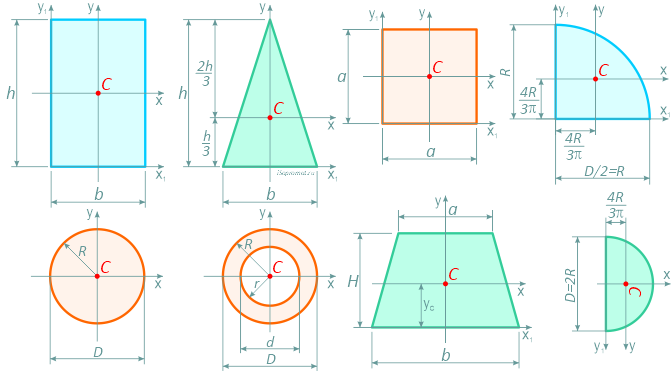
Формулы площадей, центров тяжести, осевых и полярных моментов инерции, моментов сопротивления и других геометрических характеристик основных простых фигур: прямоугольника, квадрата, равнобедренного и прямоугольного треугольника, круга, полукруга, четверти круга, кольцевого и тонкостенного сечений.

Обозначения в формулах:
C — положение центра тяжести фигуры;
A — площадь сечения;
I_x , I_y — осевые моменты инерции сечения относительно главных осей;
I_x1 , I_y1 — осевые моменты инерции относительно вспомогательных (смещённых) осей;
I_ρ — полярный момент инерции сечения;
W_x , W_y — осевые моменты сопротивления;
W_ρ — полярный момент сопротивления

Прямоугольник

Прямоугольник высотой h и шириной b.

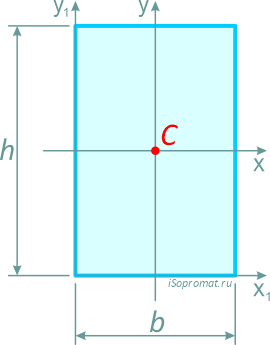
Центр тяжести прямоугольника в точке пересечения его диагоналей, на расстоянии половины высоты (h/2) по вертикали и половины ширины (b/2) по горизонтали.

Площадь

Центральные осевые моменты инерции прямоугольника

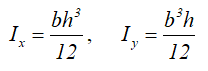
Моменты инерции относительно смещенных осей, проходящих через нижнюю левую точку

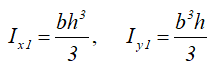
Осевые моменты сопротивления прямоугольного сечения

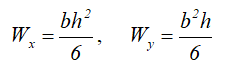
Квадрат

Квадрат — это частный случай прямоугольника, у которого высота равна ширине, т.е. h=b=a.

Центр тяжести квадрата находится так же на пересечении диагоналей — на расстоянии половины стороны (a/2) по высоте и ширине.

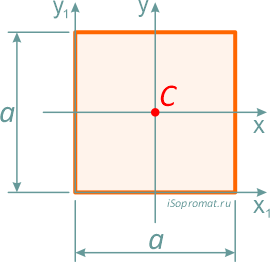
Площадь

Центральные осевые моменты инерции квадрата

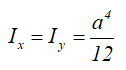
Моменты инерции относительно смещенных осей, проходящих через нижнюю левую точку

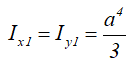
Осевой момент сопротивления квадратного сечения

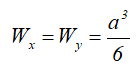
Треугольник равнобедренный

Равнобедренный треугольник высотой h и шириной основания b.

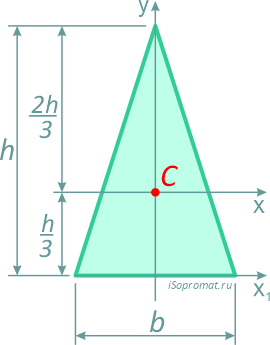
Центр тяжести треугольника располагается в точке пересечения его медиан на расстоянии 1/3 высоты от основания и 2/3 высоты от его вершин.

Площадь

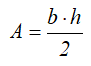
Центральные осевые моменты инерции треугольника

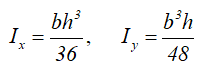
Момент инерции относительно смещенной оси x₁, проходящей через его основание

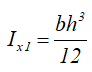
Прямоугольный треугольник

Прямоугольный треугольник высотой h и шириной основания b.

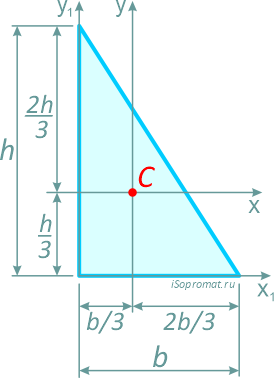
Центр тяжести прямоугольного треугольника располагается аналогично, на пересечении медиан на расстоянии 1/3 высоты от основания и 2/3 высоты от вершины.

Площадь

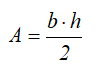
Центральные осевые моменты инерции прямоугольного треугольника

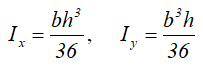
Моменты инерции относительно смещенных осей x₁ и y₁, проходящих через точку, соединяющую его катеты

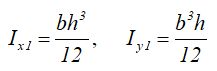
Трапеция

Равнобокая трапеция высотой H и шириной оснований: малого a и большого b.

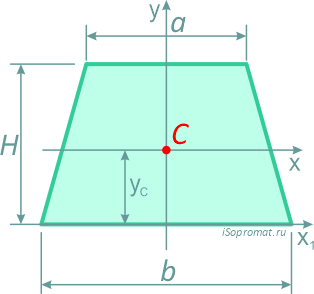
Площадь трапеции

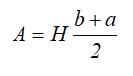
Центр тяжести на линии, соединяющей середины оснований трапеции, на высоте, определяемой по формуле:

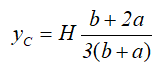
Круг

Круг диаметром D (d) или радиусом R (r)

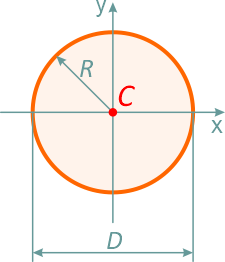
Площадь круга через его диаметр и радиус

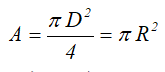
Центральные осевые и полярный моменты инерции круга

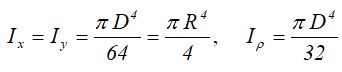
Осевые и полярный моменты сопротивления

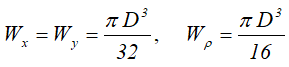
Полукруг

Половина круга диаметром D (d) или радиусом R (r)

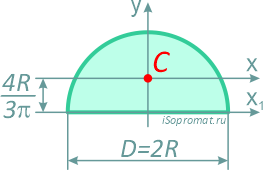
Площадь

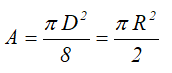
Осевые моменты инерции полукруга

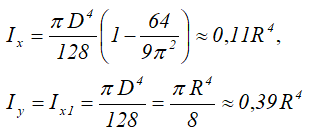
Четверть круга

Четверть круга диаметром D (d) или радиусом R (r)

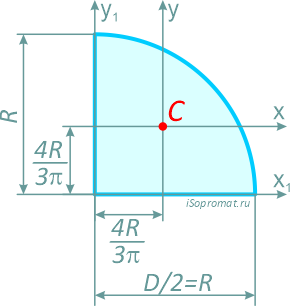
Площадь

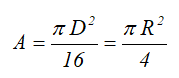
Центральные осевые моменты инерции четверти круга

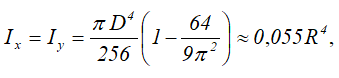
Моменты инерции относительно смещенных осей x₁ и y₁

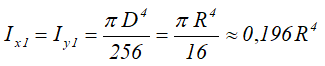
Кольцо

Кольцо с внешним диаметром D и внутренним d, (радиусами: внешним R и внутренним r)

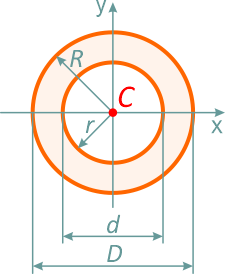
Отношение внутреннего диаметра (радиуса) к внешнему обозначается буквой c.

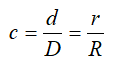
Площадь

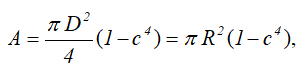
Центральные осевые и полярный моменты инерции кольца

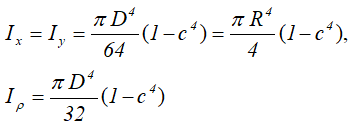
Осевые и полярный моменты сопротивления

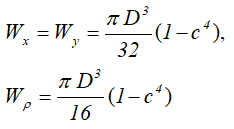
Тонкостенное сечение (труба)

Тонкостенный профиль (сечение трубы) средним радиусом R₀ и толщиной стенки трубы t при R₀>>t

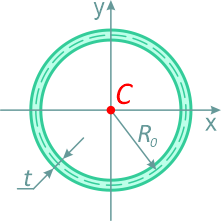
Площадь

Центральные осевые и полярный моменты инерции трубного сечения

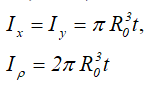
Осевые и полярный моменты сопротивления

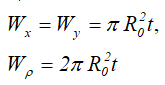
Пример определения координат центра тяжести сложной фигуры:

Другие видео

Смотрите также:
Определение координат центра тяжести сложных фигур
Геометрические характеристики сечений

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

Источник

Осевой момент инерции[править | править код]

Теорема Гюйгенса — Штейнера[править | править код]

Осевые моменты инерции некоторых тел[править | править код]

Вывод формул[править | править код]

Безразмерные моменты инерции планет и спутников[править | править код]

Центробежный момент инерции[править | править код]

Геометрические моменты инерции[править | править код]

Момент инерции относительно плоскости[править | править код]

Центральный момент инерции[править | править код]

Тензор инерции и эллипсоид инерции[править | править код]

См. также[править | править код]

Комментарии[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

Что такое момент инерции

Как найти момент инерции

Момент инерции прямоугольника

Момент инерции квадрата

Момент инерции круга

Пример нахождения момента инерции тавра

Обобщение и подведение итогов

Что такое инерция

Определение момента инерции

Теорема Штейнера

Пример решения задачи на нахождение момента инерции

Центр масс

Моменты инерции

Моменты инерции относительно точки и оси

Моменты инерции относительно осей координат

Теорема о моментах инерции относительно параллельных осей (теорема Штейнера)

Моменты инерции простейших однородных тел

Однородный стержень

Прямоугольная пластина

Круглый диск

Круглый цилиндр

Шар

Моменты инерции относительно осей, проходящих через заданную точку

Эллипсоид инерции

Свойства главных осей инерции

Определение главных моментов инерции и направления главных осей

Выражение компонентов тензора инерции через главные моменты инерции

Прямоугольник

Квадрат

Треугольник равнобедренный

Прямоугольный треугольник

Трапеция

Круг

Полукруг

Четверть круга

Кольцо

Тонкостенное сечение (труба)

Вам также может понравиться

Как найти мои подписки в телефоне самсунг

Как найти изменяемые ячейки

Как найти документ корректировка записей регистра

Добавить комментарий Отменить ответ