Как найти геометрическое место точек комплексного числа - Сайт, где вы сможете решить свои вопросы

Добавил:

Upload

Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Предмет:

Файл:

Комплексные числа и многочлены

.pdf

Скачиваний:

150

Добавлен:

18.04.2015

Размер:

527.62 Кб

Скачать

Для числа z = 1 a = 1, b = 0. Следовательно, ρ = 12 +02 =1 и по формуле

(1.1) находим

cos ϕ =1,

Эта

система имеет решение: ϕ = 0 . В итоге:

sin ϕ = 0.

1 =cos0 +isin 0 .

Пример 15. Представить в тригонометрической форме число z = –i.

Для него a = 0, b = –1. Следовательно, ρ =

02 +(−1)2 =1 и система (1.1)

cosϕ = 0,

ϕ = −

. Отсюда −i = cos(−

) +i sin(−

) .

имеет вид:

ϕ = −1

sin

Пример 16. Представить в тригонометрической форме число z = –1.

Для числа z = –1 a = –1, b = 0. Следовательно, ρ =

(−1)2 +02 =1 и система

cosϕ

= −1,

ϕ = π. Получаем

−1 = cos π+i sin π.

(1.1) имеет вид

ϕ = 0

sin

Пример 17. Представить в тригонометрической форме число z = 1 + i.

Для него a = 1, b = 1. Следовательно,

ρ =

12 +12 =

2 и по системе (1.1)

cosϕ =

. Значит, 1+i =

2(cos

+i sin

) .

ϕ =

sin ϕ =

Пример 18. Представить в тригонометрической форме число z = –5 + 7i.

Для него a = –5, b = 7. Следовательно, ρ =

(−5)2 +72 = 74

и система

−5

cosϕ =

Решением этой системы будет

(1.1) принимает вид

sin ϕ =

7 .

ϕ = π−arccos

5 . Тогда

−5 +7i =

74(cos(π−arccos

) +i sin(π−arccos

)).

3.1.6. Умножение и деление комплексных чисел. Формула Муавра

Пусть z = ρ1(cos ϕ+i sin ϕ);

w = ρ2 (cos ψ +i sin ψ) . Тогда верны формулы:

z w = ρ1 ρ2 (cos(ϕ+ψ) +isin(ϕ+ψ)) ,
	z	=	ρ1	(cos(ϕ−ψ) +isin(ϕ−ψ)),	(1.2)
	w
		ρ2
		zn = ρn (cos nϕ+isin nϕ) .	(1.3)

Последняя формула называется формулой Муавра [1, с. 190]. Она верна для любого натурального n.

	1+i	3	20

Пример 19. Вычислить:	1−i		.

Решение. Переведем числитель и знаменатель дроби из алгебраической

формы в тригонометрическую.

Для числа z1

=1+i

3 ρ =

12 +( 3)2 = 2 , ϕ = arctg

3 =

π.

Для числа

z2 =1 −i

ρ = 12 +(−1)2 = 2 , ϕ = arctg

−1

= −

. Таким

образом,

2(cos

+isin 3)

=[поформуле(1.2)] =

2(cos(−

4) +isin(−

4))

=2(cos(127π) +isin(127π)).

Витоге:

2)20

(cos(7π 20) +i sin(7π 20)) =

=[по формуле(1.3)] = (

= 210

35π

(cos 3 +i sin 3

) =[так как

=12π−

] =

= 2

(cos(− 3) +i sin(−

3)) = 2

(2 −

i) = 2

− 3i).

3.1.7. Задачи на построение областей на комплексной плоскости

Пример 20. Изобразить на комплексной плоскости числа, модуль

которых равен 1, т. е.

=1.

Решение.

Запишем

комплексное

число

алгебраической

форме

z = x + yi . По

условию

задачи

интерес представляют те числа,

модуль

которых равен 1, т.	е.		x + yi	=1. По определению модуля комплексного

числа	x2 + y2 =1.	Возведя обе части равенства в квадрат, получим
x2 + y2 =1. Данное	уравнение определяет на плоскости окружность с

центром в точке с координатами (0; 0) и радиусом, равным 1.

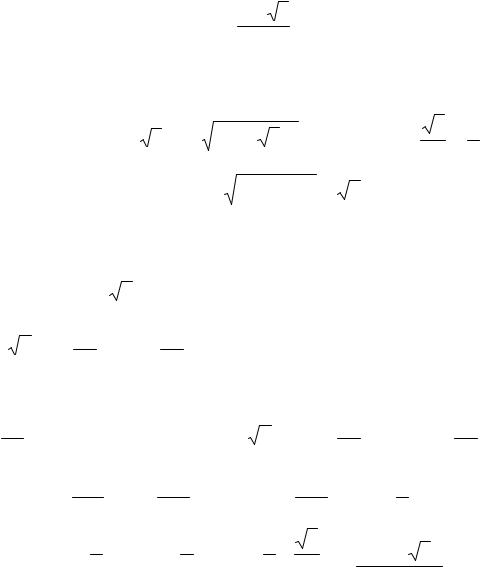
Пример 21. Найти геометрическое место точек, изображающих числа z, удовлетворяющие неравенству z −i ≤ 2.

Запишем комплексное число в общем виде z = x + yi . По условию задачи, интерес представляют те числа, модуль которых меньше или равен 2,


т. е.	x + yi −i		≤ 2. Сгруппируем под знаком модуля слагаемые, содержащие

i :		x +( y −1)i		≤ 2 . По определению модуля комплексного числа:

x2 + y2 ≤ 2 x2 + y2 ≤ 4 .

Данное уравнение определяет на плоскости круг с центром в точке с координатами (0; 1) и радиусом равным 2 (рис. 1.3).

Пример 22. Найти геометрическое место точек, изображающих числа z, удовлетворяющие неравенству Re z <1.

Re z – действительная часть числа z, неравенство можно записать как

x	<1, или	x <1	или −1 < x <1. Эта система определяет на плоскости

		x > −1

полосу, ограниченную прямыми x = 1 и x = –1. Причем, обе прямые нарисованы на штрихами, так как сами прямые в искомую область не входят из-за строгого знака неравенства (рис. 1.4).

	Y		Y
	3
	2		1
	1	–1	1	X

–1	1	X	–1
–1

	Рис. 1.3		Рис. 1.4

Пример 23. Найти геометрическое место точек, изображающих числа z,

z ≤ 2,

удовлетворяющие системе неравенств

Re z >1.

Как показано в примерах 20 и 21, неравенство z ≤ 2 определяет на

плоскости круг с центром в точке (0; 0) и радиусом, равным 2. Неравенство Re z >1, согласно примеру 22, определяет полуплоскость, ограниченную прямой x = 1 и находящуюся от нее справа. Так как неравенство Re z >1 строгое, то сама прямая x = 1 в область не входит и штрихами

пунктиром. Обе эти области изображены на рис. 1.5. Искомая область представляет собой пересечение двух данных областей (рис. 1.6).

–2

–1

2 X

–2

–1

2 X

–1

–2

Рис. 1.5

Рис. 1.6

Пример 24. Найти геометрическое место точек, изображающих числа z,

удовлетворяющие системе неравенств

z −1−i

π.

≤ arg z ≤

−

–1

Неравенство

z −1−i

определяет

–1

область вне круга с центром в точке (1; 1)

–2

радиусом

1. Так

как

неравенство

строгое,

то

сама окружность в

область

не

входит

Рис. 1.7	изображена штрихами (рис. 1.7).

	Y			Y
	2			2
	1			1
–1	1 2	3 X	–1	1 2	3 X
	–1			–1
	–2			–2
	Рис. 1.8			Рис. 1.9

Двойное неравенство − π4 ≤ arg z ≤ π4 определяет на плоскости область, в

которую входят комплексные числа с аргументами в интервале от − π4 до π4 .

Эта область представляет собой угол (рис. 1.8).

Искомая область представляет собой пересечение двух данных областей

(рис. 1.9).

3.1.8.Извлечение корня из комплексных чисел в тригонометрической форме

Определения и утверждения к 3.1.8 можно найти в [1, с. 191-192]. Комплексное число w = n z называется корнем n-й степени из

комплексного числа z, если z = wn .

Утверждение. При любом натуральном n > 1 и любом комплексном z существует ровно n различных чисел wk , таких, что wn = z :

w = n ρ(cos ϕ+ 2πk	+isin ϕ+ 2πk ),	(1.4)
k	n	n

где k = 0, 1, 2, …, n – 1.

Пример 25. Вычислить 4 −1 .

Решение. Для того чтобы воспользоваться формулой (1.4), необходимо представить число, стоящее под знаком корня, в тригонометрической форме.

Для числа z = -1 найдем его модуль и аргумент: ρ = 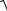(−1)2 +02 =1, ϕ = π. В

итоге −1 = cos π+isin π.

По формуле (1.4) w = 4	1(cos π+ 2πk	+isin π+ 2πk ) . Тогда:
k	4	4

w	= cos π+ 2π 0 +isin π+ 2π 0 = cos π +isin π =	2 +i	2 ,
0								4			4		4			4					2		2

w	= cos π+ 2π 1 +isin π+ 2π 1 = cos 3π +isin 3π = −		2 +i	2 ,
1								4			4				4				4					2	2

w	= cos π+ 2π 2 +isin π+ 2π 2 = cos 5π +isin 5π = −	2 −i		2 ,
2								4			4		4				4				2		2

w	= cos π+ 2π 3 +isin π+ 2π 3 = cos 7π +isin 7π =		2 −i		2.
3								4			4		4					4				2	2

		Пример 26. Вычислить 5 −32i .
		Решение. Для числа z = −32i найдем его модуль ρ и аргумент ϕ:
ρ =	02 +322		= 32 , ϕ = − π, так как число z = −32i лежит на
											2															−π			−π
отрицательной части мнимой оси. В итоге z = −32i = 32(cos		+i sin	) .
2
																				−π + 2πk		−π					2
																					+ 2πk
По формуле (1.4)	w = 5 32(cos	2				+isin		2					) ,

											k	5										5
где k = 0, 1, 2, 3, 4. Тогда:

w		= 2(cos	−π		+i sin	−π	),

0								10			10

w	= 2(cos 3π +i sin 3π),
1						10			10

w		= 2(cos 7π +i sin 7π),
2								10			10

w	= 2(cos	11π	+i sin	11π	) = 2(cos	−9π	+i sin	−9π	),

3								10			10						10					10

w	= 2(cos15π	+isin15π ) = 2(cos −π +isin −π ).
4								10			10				2					2

Для				w	и	w	аргументами	будут		−9π	и		−π	,		а	не			11π	и	15π

		3				4												10						2				10		10

соответственно, так как ϕ (−π; π].

Пример 27. Вычислить 3 − 2 + 2

3i .

Решение. Для числа

z = −2 + 2

модуль ρ и аргумент ϕ есть:

ρ = (−2)2 +(2

3)2 = 4 +

124 = 16 = 4

, ϕ =

2π

В итоге z = −2 + 2 3i = 4(cos

2π

+i sin

2π

) . По формуле (1.4)

2π

+2πk

2π

+2πk

= 3 4(cos

+i sin

), где k = 0, 1, 2. Тогда:

= 3 4(cos 2π

+isin 2π),

= 3 4(cos 2π

+isin 2π),

= 3 4(cos 8π

+isin 8π),

= 3 4(cos14π +isin14π) = 3 4(cos −4π +isin −4π).

Из формулы (1.4) видно, что аргументы корней wk отличаются на одну и ту же

величину 2nπ , а модули всех

корней одинаковые и равны n ρ. Значит, на комплексной плоскости все wk лежат на окружности с центром в начале

координат	и	радиусом	n ρ	на
одинаковом	расстоянии	друг	от
друга.	Для	примера	27
изображения		самого	числа
z = −2 + 2	3i	и его корней w0 ,	w1 ,

	Im z
	.z
	.w3	.w1
	1 *2 3 4 Re z
	–4 –3 –2 –1
		.w2 3 4

Рис. 1.10

w2 можно видеть на рис. 1.10.

2.МНОГОЧЛЕНЫ

2.1.Многочлены и действия над ними

Определения и утверждения к 2.1 можно найти в [1, с. 203-206].

Для действительной переменной x функция вида f (x) = axn , где a и x – действительные числа, а n – натуральное число или 0 (по-другому это можно записать как a R, n N {0}), называется одночленом с действительным коэффициентом.

Многочлен – это сумма одночленов, т.е. функция вида

g(x) = an xn + an−1xn−1	n
+…+ a1x + a0 = ∑ai xi .
	i=0

При этом an называется старшим коэффициентом и an ≠ 0 , a0 – свободным членом, n – степенью многочлена.

Многочлен тождественно равен 0 тогда и только тогда, когда все его коэффициенты равны 0.

Если в записи многочлена нет какой-либо степени неизвестного, это значит, что коэффициент при этой степени равен 0.

На множестве многочленов определены следующие действия: 1. Сложение.

Пример 28. f (x) = 3x4 −7x2 + x −3; g(x) = 2x3 +5x2 +3x − 2 . Найти f (x) + g(x) .

f (x) + g(x) =3x4 + 2x3 +(−7 +5)x2 +(1+3)x +(−3 +(−2)) =

=3x4 + 2x3 −2x2 + 4x −5.

2.Умножение.

Пример 29. f (x) = 2x2 − x +1; g(x) = 3x −1. Найти f (x) g(x) . f (x) g(x) = (2x2 − x +1)(3x −1) =

=2x2 3x +(−x) 3x +1 3x + 2x2 (−1) +(−x) (−1) +1 (−1) =

=6x3 −3x2 +3x −2x2 + x −1 = 6x3 −5x2 + 4x −1.

3. Деление с остатком.
Разделить	f (x) на	g(x)	–	значит записать	f (x)	в виде
f (x) = g(x)q(x) + r(x),	или	f (x)	= q(x) +	r(x)	. Последняя	запись
g(x)	g(x)

аналогична записи для чисел: 173 = 5 + 23 , или 17 = 5 3 + 2.

Теорема (о делении с остатком) [1, с. 206]. Для любых многочленов

f (x)	и g(x) ≠ 0 существуют, и притом единственные,	многочлены q(x) и
r(x) , такие, что
	f (x) = g(x) q(x) + r(x) .	(2.1)
При	этом степень r(x) меньше степени g(x) , q(x) –	неполное частное,
r(x)	– остаток. Разделить f (x) на g(x) – значит записать	f (x) в виде (2.1).

Для практического нахождения частного и остатка существует метод деления «уголком».

Пример 30. Выполнить «уголком» деление с остатком: f (x) = x3 −3x2 − x −1 на g(x) = x2 − 2x +1.

Решение. Запишем делимое f (x) и делитель g(x) как при делении многозначных чисел:

x3 −3x2 − x −1 x2 − 2x +1

Находим частное от деления старшего члена делимого на старший член

делителя ( x3 / x2 = x ) и записываем результат в графу частного: x3 −3x2 − x −1 x2 − 2x +1

Умножаем делитель на результат деления и записываем под делимым:

x3 −3x2 − x −1 x2 − 2x +1
x3 − 2x2 + x	x

Вычитаем из делимого результат умножения:

x3 −3x2 − x −1	x2 − 2x +1

x3 −2x2 + x		x

− x2 − 2x −1

Проверяем степень получившегося в результате вычитания многочлена. Если она меньше степени делителя, то процесс деления закончен, и полученный многочлен является остатком. В противном случае деление продолжается аналогично описанному ранее:

x3 −3x2 − x −1 x2 − 2x +1
x3 − 2x2 + x	x – 1

−x2 − 2x −1

−x2 + 2x −1

–4x

Так как степень полученного многочлена меньше степени делителя, то процесс деления закончен. В результате: q(x) = x – 1– неполное частное, а

r(x) = –4x – остаток.

Ответ: x3 −3x2 − x −1 = (x2 −2x +1)(x −1) +(−4x) , или

x3 −3x2 − x −1	= x −1	−		4x	.

x2	−2x +1		x2	−2x +1

Пример 31. Выполнить деление с остатком: 3x5 +1 на x2 −1. Решение. Запишем делимое и делитель как при делении многозначных

чисел. Если в записи многочлена отсутствует одна или несколько степеней, то при записи, для удобства вычислений, следует на их места записать нули:

3x5 + 0x4 + 0x3 + 0x2 + 0x +1		x2 −1

3x5	−3x3			3x3 +3x

		3x3 + 0x2 + 0x
		3x3	−3x

3x +1

Получившиеся в результате умножения многочлены удобнее записывать, располагая слагаемые в соответствии с их степенями. Так как степень полученного многочлена меньше степени делителя, то процесс деления

закончен. В результате: q(x) =3x3 +3x – неполное частное, а r(x) = 3x + 1	–
остаток.
Ответ: 3x5 +1 = (x2 −1)(3x3 +3x) + (3x +1) , или 3x5 +1 = 3x3 +3x + 3x +1 .
x2 −1	x2 −1
Пример 32. Делится ли нацело многочлен	x4 + 4x3 − 2x −8 на
многочлен x3 − 2 ?

Решение. Разделим один многочлен на другой «уголком».

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Алгебра и начала математического анализа, 11 класс

Урок №39. Геометрическая интерпретация комплексного числа.

Перечень вопросов, рассматриваемых в теме

изображение комплексного числа на плоскости- точками;
изображение комплексного числа на плоскости- векторами;

3) определение модуля комплексного числа.

Глоссарий по теме:

а) Комплексные числа изображают точками плоскости по следующему правилу: a + bi = M (a; b)

б) Комплексное число можно изобразить вектором, который имеет начало в точке О и конец в данной точке

Длина радиус-вектора, изображающего комплексное число z=a+bi, называется модулем этого комплексного числа.

Модуль любого ненулевого комплексного числа есть положительное число. Модули комплексно сопряженных чисел равны. Модуль произведения/частного двух комплексных чисел равен произведению/частному модулей каждого из чисел.

Модуль вычисляется по формуле:

То есть модуль есть сумма квадратов действительной и мнимой частей заданного числа.

Основная литература:

Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.

Дополнительная литература:

Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2017.

Теоретический материал для самостоятельного изучения

Геометрическое изображение комплексных чисел.

а) Комплексные числа изображаются точками плоскости по следующему правилу: a + bi = M (a; b) (рис.1).

Рисунок 1

б) Комплексное число можно изобразить вектором, который имеет начало в точке О и конец в данной точке (рис.2).

Рисунок 2

Пример. Постройте точки, изображающие комплексные числа: 1; – i; – 1 + i; 2 – 3i (рис.3).

Рисунок 3

Модуль комплексного числа

Как отмечалось выше, комплексное число также можно изображать радиус-вектором (рис. 4).

Длина радиус-вектора, изображающего комплексное число z=a+bi, называется модулем этого комплексного числа.

Модуль вычисляется по формуле:

То есть модуль есть сумма квадратов действительной и мнимой частей заданного числа.

Иногда еще модуль комплексного числа обозначается как r или ρ.

Разбор решения заданий тренировочного модуля

№1. Тип задания: единичный выбор

Найдите модуль комплексного числа z=5-3i

Решим данное задание, используя определение модуля.

Т.к. Re z=5, Im z= -3, то искомое значение

Верный ответ: 2.

№2. Тип задания: рисование.

Изобразите вектором на комплексной плоскости точку z=2+3i

Решение:

Разобьем z=2+3i на две части: z₁=2 и z₂= 3i. Отметим на плоскости точки О и А, соединим их:

Источник

Лекция

Тригонометрическая
форма комплексного числа

План

1.Геометрическое
изображение комплексных чисел.

2.Тригонометрическая
запись комплексных чисел.

3.Действия над
комплексными числами в тригонометрической форме.

Геометрическое
изображение комплексных чисел.

а) Комплексные числа
изображают точками плоскости по следующему правилу: a
+ bi = M
(a;
b)
(рис.1).

Рисунок 1

б) Комплексное число
можно изобразить вектором, который имеет начало в точке О и конец в
данной точке (рис.2).

Рисунок 2

Пример 7. Постройте
точки, изображающие комплексные числа: 1; – i;
– 1 + i; 2 – 3i
(рис.3).

Рисунок 3

Тригонометрическая
запись комплексных чисел.

Комплексное число z
= a + bi
можно задать с помощью радиус – вектора с координатами (a;
b)
(рис.4).

Рисунок
4

Определение.
Длина вектора ,
изображающего комплексное число z,
называется модулем этого числа и обозначается или r.

Для любого комплексного
числа z его модуль r
= | z |
определяется однозначно по формуле .

Определение.
Величина угла между положительным направлением действительной оси и вектором , изображающим комплексное
число, называется аргументом этого комплексного числа и обозначается Аrg z
или φ.

Аргумент комплексного
числа z = 0
не определен. Аргумент комплексного числа z
≠ 0 – величина многозначная и определяется с точностью до слагаемого 2πк
(к = 0; – 1; 1; – 2; 2; …): Arg z
= arg z
+ 2πк, где arg z
– главное значение аргумента, заключенное в промежутке (-π; π],
то есть -π < arg z
≤ π (иногда в качестве главного значения
аргумента берут величину, принадлежащую промежутку
[0; 2π)).

a = r · cos φ, b = r ·
sin φ.

Следовательно,
комплексное число z
= a + bi
можно записать в виде: z
= r · cos φ
+ i r
· sin φ
или z
= r · (cos
φ + i sin
φ).

Такая запись комплексного
числа называется тригонометрической формой комплексного числа.

Пример 8. Представить в
тригонометрической форме комплексное число 1– i.

a = 1, b = -1.

φ
= .

1 – i
= (cos +
i sin ).

Действия
над комплексными числами в тригонометрической форме.

1) Умножение.

Пусть два числа
заданы и в алгебраической и в тригонометрической формах: z₁= a₁
+ b₁i
= r₁(cos φ₁
+ i sin φ₁),

z₂
= a₂ + b₂i = r₂ (cos φ₂ + i sin φ₂).

На основании исходного
определения правила умножения и формулы косинуса и синуса суммы
получаем:

z_1·z₂
= r_{1 ·}r₂ (cos (φ₁
+ φ₂)
+ i sin (φ₁
+ φ₂));
r_{1 ·}r₂>0.

Умножение комплексных
чисел в тригонометрической форме обладает следующими свойствами:

1º. Коммутативность: z₁z₂
= z₂z₁

2º. Ассоциативность: (z₁z₂)
z₃
= z₁
(z₂
z₃).

Пример 9. Найти
произведение комплексных чисел

z₁
= 2cos 50º + 2 i sin
50º, z₂
= cos 40º + i sin
40º.

Решение.
Тригонометрические формы этих чисел имеют вид:

z₁ = 2 · (cos
50º + i sin 50º), z₂ = 1· (cos 40º + i sin 40º). Тогда

z₁· z₂
= 1· 2 · (cos (50º + 40º) + i sin (50º + 40º)) = 2(cos 90º + i sin 90º) = = 2(0
+ i) = 2i.

2) Деление комплексных
чисел в тригонометрической форме.

Деление в поле
комплексных чисел на числа, отличные от нуля, всегда выполнимо. Если
числа z₁
и z₂ заданы в тригонометрической форме z₁
= r₁
(cos φ₁
+ i sin φ₁),
z₂
= r₂
(cos φ₂
+ i sin φ₂),
причем z₁≠
0, то комплексное число является
частным чисел z₁
и z₂(то есть z₁y
= z₂).

Пример 10. Найти частное
комплексных чисел z₁
= 2cos50º + 2i sin50º,
z₂
= cos40º + i sin40º.

Решение.
Тригонометрические формы этих чисел имеют вид:

z₁
= 2 · (cos50º + i sin50º), z₂ = 1· (cos40º + i sin40º).

Тогда
(cos
(50º – 40º) + i sin (50º – 40º)) = 2(cos10º + i sin10º).

3) Возведение в степень.

Определение.
n
– ой степенью комплексного числа z
называется комплексное число, получающееся в результате умножения числа z
самого на себя n
раз.

Число z
называется основанием степени, а натуральное число n
– показателем степени.

Возвести комплексное
число в n – ую степень можно по
формуле: z ⁿ
= (r ⁿ)
[cos
(nφ)
+ i sin
(nφ)].

Эту формулу при r
=1 часто называют формулой Муавра:

(cos φ + i sin φ) ⁿ
= cos (nφ) + i sin (nφ), n Î N.

Пример 11. Вычислите (1
+ i)¹⁰⁰.

Запишем комплексное число
1 + i в
тригонометрической форме.

a = 1, b = 1.

cos φ = , sin φ = , φ = .

(1+i)¹⁰⁰= [(cos + i sin)]¹⁰⁰= ()¹⁰⁰(cos·100 + i sin·100) = = 2⁵⁰(cos 25π +
i sin 25π) = 2⁵⁰(cos π + i sin π) = – 2⁵⁰.

4) Извлечение квадратного
корня из комплексного числа.

При извлечении
квадратного корня из комплексного числа a
+ bi имеем два случая:

если b
> о, то ;

если b
< о, то .

Так как из комплексного
числа всегда можно извлечь квадратный корень, то любое квадратное уравнение
всегда будет иметь решения во множестве комплексных чисел. Решения квадратного
уравнения ах² + bх
+ с = 0 можно найти по известной формуле:

Пример 12. Вычислите .

Так как b
< о, то воспользуемся формулой

= ,

= .

Упражнения

1.Записать
в тригонометрической
форме число

Т.к.то нужно взять равным.Значит,

2. Записать
в тригонометрической
форме число – 1 – і.

Тогда

3. Записать
в тригонометрической
форме число 1.Имеем
, или

4.Выполнить
действия

5. Представить следующие
комплексные числа в тригонометрическом виде:

1) 1, –1,
i, –i;

2) z
= 3 –
3i;

3) .

6. Даны числа

Вычислить: 1) ; 2) ; 3) ; 4) .

Вопросы для самопроверки:

1.Дать определение модуля
комплексного числа. Каков его геометрический смысл?

2. Комплексное число
умножили на 2. изменился модуль этого числа?

3. Почему равны модули
чисел: i; -i; 1; 1; 0?

4. Что такое аргумент
комплексного числа?

5. Как определить главное
значение аргумента числа z = a + bi?

6. Могут ли аргументом
комплексного числа быть одновременно углы а и -а?

7. Найти геометрическое
место точек плоскости, изображают комплексные числа с одинаковыми модулями.

8.Как размещаются на
плоскости точки, изображающие комплексные числа с одинаковыми аргументами?

9. Как представить
комплексное число вида а + bi
в тригонометрической форме? Как найти модуль и аргумент этого числа?

10. Как перейти от
тригонометрической формы комплексного числа в алгебраической?

11. Вывести правила
умножения и деления комплексных чисел, записанных в тригонометрической форме.

12. По какому правилу
выполняют действие возведения в степень комплексных чисел, записанных в
тригонометрической форме?

Источник

Re: Комплексные числа Z

Сообщение

Алексей » 02 май 2017, 22:06

Это не обычное уравнение Геометрическое место точек в данном случае – это множество точек комплексной плоскости, каждая из которых удовлетворяет заданным вам условиям. Итогом вашего решения должен стать рисунок. Уравнение вида (|z-z_0|=R) определяет множество точек, расположенных на окружности с центром в точке (z_0) и радиусом (R). А что касаемо главного значения аргумента, то ввиду условия (arg{z}in(-pi;pi]), в вашем случае получим: ( -pi<arg{z}<frac{pi}{3}). Это множество точек между двумя лучами, направленными из начала координат.

“Именно то, что наиболее естественно, менее всего подобает человеку.” Братья Стругацкие, “Хромая судьба”

Источник

Комплексные числа и геометрические узоры

Время на прочтение
6 мин

Количество просмотров 21K

Когда речь заходит о комплексных числах, в первую очередь вспоминают о преобразовании Фурье и прочих аспектах цифровой обработки сигналов. Однако у них есть и более наглядная интерпретация, геометрическая — как точки на плоскости, координатам которой соответствуют действительная и мнимая часть комплексного числа. Рассматривая некоторую кривую как совокупность таких точек, можно описать её как комплексную функцию действительной переменной.

▍ Окружность

Когда нам нужно начертить окружность в реальной жизни — мы берём циркуль и, уперев его одним (острым) концом, а другим (с грифелем) постепенно вращая, оставляем след на бумаге. В математике это делается аналогично — в роли циркуля выступает мнимая единица

$i$ , а в роли вращения — возведение её в степень переменной

$t$ , которую можно интерпретировать как момент времени (а в данном конкретном случае — как угол поворота). Здесь вектор описывает полный круг при изменении значения

$t$ от

$0$ до

$4 $ — что также удобно интерпретировать как четверти на координатной плоскости, когда при изменении целой части

$t$ одна из проекций на координатную ось меняет свой знак.

Возможно, выражение

$i^t$ кому-то может показаться несколько непривычным, поскольку оно не употребляется в традиционных учебниках математики. В таком случае можно использовать каноническую запись, перейдя к основанию

$e$ :

$i^t = e^{frac{i pi t}{2}}$ .

Также в качестве основания можно использовать минус единицу:

$i^t=(-1)^{t/2}$ , что часто используется в Wolfram Mathematica для описания единичных комплексных констант.

Разница между функциями

$e^{i t}$ ,

$ i^t$ состоит лишь в периоде

$t$ для полного оборота вектора по окружности —

$2 pi$ ,

$2$ или

$4$ ; а единицами измерения углов соответственно будут радианы, пол-обороты и кварт-обороты (квадранты). Запись с экспонентой является исторически первой, однако её сложно назвать наглядной — возведение в комплексную степень несколько контринтуитивно. В этой же статье вариант

$ i^t$ выбран по причине его большей компактности и наглядности.

▍ Эллипс

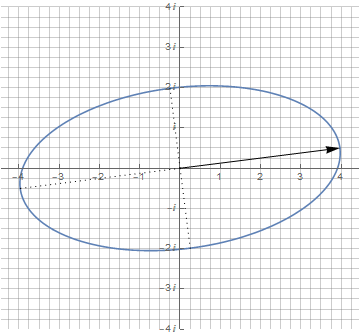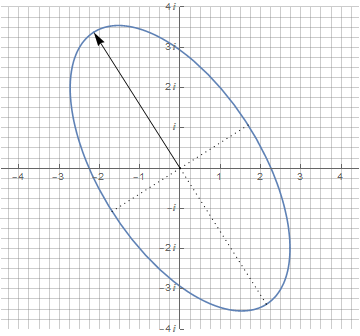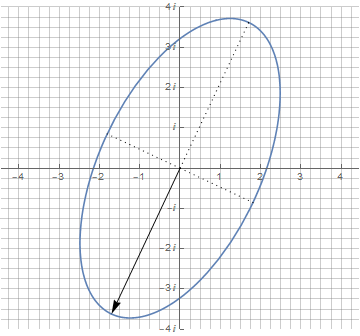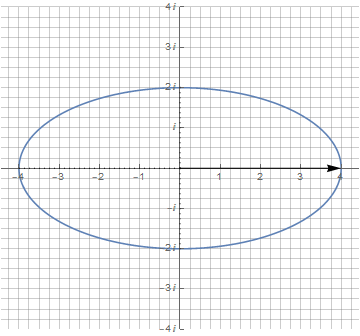
Эллипс можно начертить растягиванием окружности вдоль одной из осей. Но в таком случае это получится самый обычный параметрический график с участием тригонометрических функций, но без участия комплексных чисел. В комплексных же числах эллипс можно представить как сумму двух векторов разной длины и вращающихся с одной частотой, но в противоположные стороны:

$f(t) = i^{-t}+3 i^t$

Поскольку в комплексных числах результат суммы тоже не зависит от порядка слагаемых, эту же анимацию можно представить чуть по-другому:

Используя формулу в полярных координатах, можно начертить эллипс одним вектором, но с динамически изменяемой длиной:

$f(t)=i^t sqrt{frac{2 a^2 b^2}{left(b^2-a^2right) cos left(frac{2 pi t}{2}right)+a^2+b^2}},ato4,bto2$

Несмотря на то, что фигуры получаются одинаковыми, положение точки (и скорость) в каждый момент времени не совпадают, что хорошо видно на анимации. Поэтому производные этих эллипсов совпадать не будут:

Примечательно, что производная от эллипса, задаваемого суммой двух векторов, осталась тем же эллипсом с теми же пропорциями. Ну а теперь — самое главное преимущество комплексных чисел: чтобы повернуть эллипс на произвольный угол, достаточно просто умножить его на единичный вектор с необходимым углом поворота (phi):

$f(t)=i^{text{phi}} left(i^{-t}+3 i^tright)$

▍ Гипотрохоида и прочее

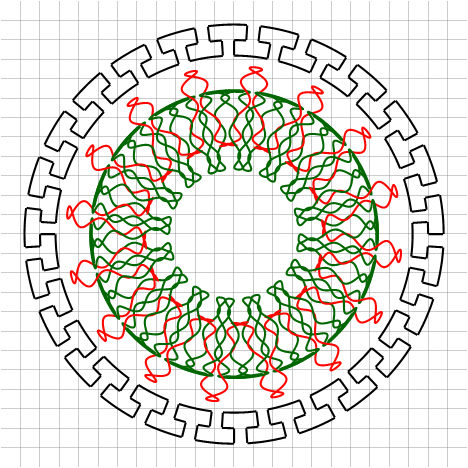
Усложнение получаемых фигур достигается усложнением их мат.модели. Достаточно изменить частоту второго вектора, и можно получить нечто более интересное, а именно — математическую модель спирографа:

$f(t) = i^{-t}+3 i^{t/3}$

$f(t)=i^{-t}+3 i^{frac{3 t}{4}}$

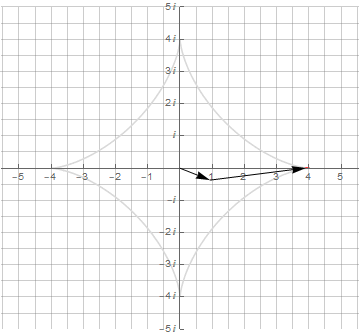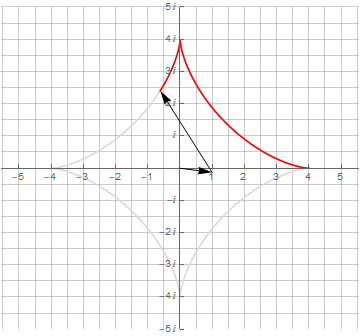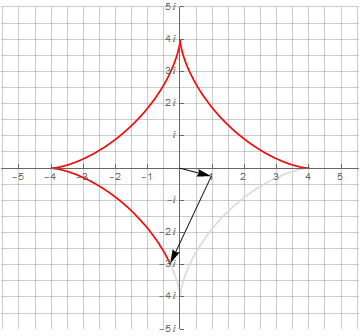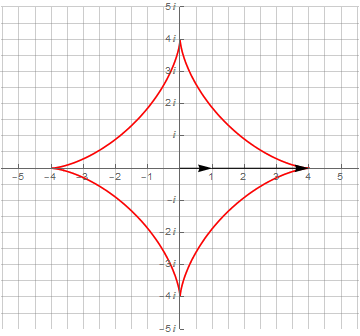
Здесь необходимо обратить внимание на то, что для получения замкнутой кривой одного оборота по окружности оказалось недостаточно — их потребовалось уже 3 и 4 соответственно. Это явилось следствием того, что период второго вектора не укладывается нацело в период первого вектора.

Можно и дальше добавлять векторы и получать всё более и более сложные фигуры:

$f(t)=i left(i^{-t}+1.9 i^{frac{2 t}{3}}+i^{-2 t}right)$

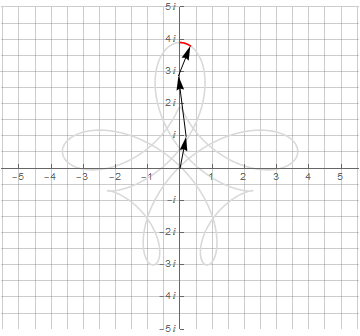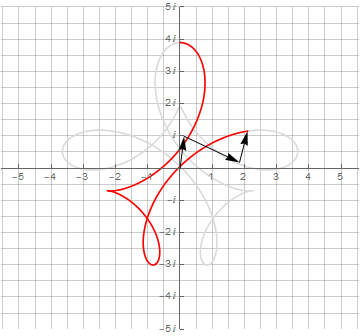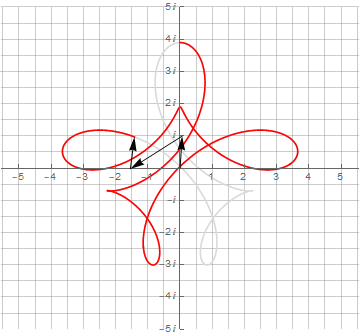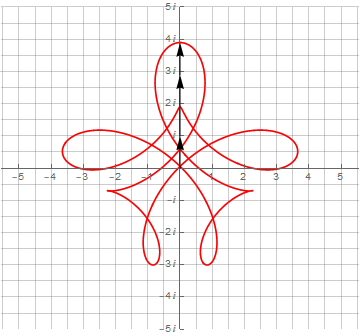
▍ Синусы и синусоидные ленты

Давайте немного отвлечёмся от окружностей и начертим синус. Традиционная запись синусоиды выглядит так:

В комплекcном виде формула для синусоды выглядит ненамного сложнее

а график, естественно, выглядит аналогично:

Легко видеть, как была получена это формула — правую часть равенства мы умножили на мнимую единицу, знак равенства заменили на плюс, а

$x$ и

$y$ заменили на одну и ту же параметрическую переменную —

$t$ . Принципиальная разница между этими формулами получилась в том, что теперь можно взять и повернуть синусоиду, просто умножив её на единичный вектор с нужным углом наклона (здесь 45°). Подобные трансформации синусодиды могут потребоваться для того, чтобы направлять её вдоль заданных кривых:

В параметрической форме записи можно модулировать координаты, получая таким образом различные деформации синусоиды, на первый взгляд не имеющих ничего общего с оригиналом:

$f(t)=t+frac{3}{8} sin (2 pi t)+i cos (pi t)$

$f(t)=3 t+i^t-frac{7}{5} i^{3 t}+3 i^t$

$f(t) = 3 t+i^t+frac{39}{20} i^{3 t}+3 i^t$

$f(t) = t+2 sin (t)+sin (2 t)+i left(3 cos left(frac{3 t}{2}right)right)$

Количество синусоид можно увеличивать, добиваясь эффекта заполнения пространства за счёт равномерного сдвига фаз между ними:

$f(t) = t+i cos left(frac{2 pi j}{n}+pi tright)$

Здесь

$n$ — количество синусоид, а

$j$ — порядковый номер синусоиды.

Смещение можно задавать и просто смещением координат — как по одной координате, так и по двум:

$f(t) =t+frac{3}{8} sin (2 pi t)+frac{2 j}{n}+i cos (pi t)$

$f(t) =t+frac{3}{8} sin (2 pi t)+frac{4 j}{n}+i cos (pi t)+i j$

▍ Розетты

Теперь можно попробовать и более сложные варианты — добавить фигурам заполнения. Есть два пути для этого:
1) взять центральную кривую, от которой в обе стороны осциллирует синусоида. Это творческий метод, поскольку внутренняя и внешняя огибающие будут зависеть от множества параметров и могут оказаться весьма неожиданными. Здесь также дополнительной сложностью будет вычисление нормали для синусоидной ленты. Несмотря на то, что её легко вычислить дифференцированием нашей кривой (и умножением на мнимую единицу) с последующей нормировкой функцией

, более интересные варианты получаются заданием её явным образом, в простейшем случае — нормалью к окружности.
2) явно задать внутреннюю и внешние огибающие, а конкретную точку между ними находить интерполяцией всё той же синусоидой. Этот вариант чуть сложнее, зато более предсказуемый.

Начнём с простого:

$f(t) =i^{-t}+3 i^t+i^t sin left(frac{8 pi t}{5}right)$

Обратите внимание: здесь мы не использовали синусоидную ленту — а обошлись лишь одной синусоидой, с некратным периодом 8/5. Для того, чтобы она замкнулась, потребовалось 5 полных оборотов (да, совпадение со знаменателем периода не случайно). Также обратите внимание, что направляющая для синусоиды не перпендикулярна центральной линии — потому что это условие в неё и не закладывалось. А если мы захотим его заложить — то потребуется продифференцировать кривую и повернуть её на 90° умножением на мнимую единицу:

$(i^{-t}+3 i^t)'=frac{pi i^{-t}}{2}-frac{3 pi i^t}{2}$

Как видно, получился тоже эллипс, только с другим масштабом (и сдвигом фазы на 90° что в нашем случае значения не имеет). Используя эту функцию (с коррекцией масштаба) в качестве направляющей для синусоидной ленты получим следующую формулу:

$f(t) = frac{1}{4} left(i^{-t}-3 i^tright) sin left(frac{2 pi j}{n}+4 pi tright)+i^{-t}+3 i^t$

Последний штрих — нормировать длину направляющей к единице, чтобы ширина заполняющей ленты была одинаковой (или явно заданной амплитуды). Сделать это можно функцией

$sgn$ или, что то же самое, через деление на абсолютное значение (которое считается как квадратный корень суммы квадратов мнимой и действительной части).

$f(t) = i^{-t}+3 i^t+frac{left(i^{-t}-3 i^tright)}{left| i^{-t}-3 i^tright| }sin left(frac{2 pi j}{n}+4 pi tright)$

Ну и напоследок — несколько примеров «творческих» орнаментов, полученных просто случайным подбором параметров:

$f(t) = left(2 i^t-i^{-t}right) left(cos left(5 pi left(k+frac{t}{2}right)right)+frac{1}{2} cos left(11 pi left(k+frac{t}{2}right)right)right)+8 i^t+i^{-t}$

$f(t) = left(3 i^t+i^{-3 t}right) left(cos left(7 pi left(k+frac{t}{2}right)right)+frac{1}{2} cos left(7 pi left(k+frac{t}{2}right)right)right)+8 i^t+i^{-3 t}$

$f(t) = i^t left(cos left(20 pi left(k+frac{t}{2}right)right)+cos left(16 pi left(k+frac{t}{2}right)right)right)+4 i^t$

▍ Розетты с интерполяцией

Для второго подхода, интерполяцией между двумя явно заданными огибающими, потребуется вспомогательная функция для изменения масштаба:

$f(x) = frac{y_{max } left(x-x_{min }right)+left(x_{max }-xright) y_{min }}{x_{max }-x_{min }}$

в которой при изменении

$x$ в диапазоне от

$x_{min}$ до

$x_{max}$ результат функции изменяется соответственно в диапазоне от

$y_{min}$ до

$y_{max}$ . Во многих системах компьютерной алгебры существуют уже предопределённые функции для этого, и в частности в Wolfram Мathematica ею является функция

$Rescaleleft[x,left{x_{min },x_{max }right},left{y_{min },y_{max }right}right]$ . Далее мы будем пользоваться таким же синтаксисом — группируя входные и выходные границы в фигурные скобки, для наглядности.

Итак, если в качестве границ взять эллипс и круг, то получится что-то вроде этого:

$f(t) = Rescaleleft[cos left(frac{13 pi t}{5}right),{-1,1},left{i^t,i^{-t}+3 i^tright}right]$

Эту формулу можно записать явным образом без использования функции

, подставив аргументы в её определение и упростив:

$f(t) = frac{1}{2} i^{-t} left(4 i^{2 t}+left(1+2 i^{2 t}right) cos left(frac{13 pi t}{5}right)+1right)$

Однако в таком случае логика работы этой формулы становится намного менее очевидной, и вносить в неё изменения исходя из изначальной логики построения становится намного сложнее.

Поскольку огибающие нам точно известны, то такие фигуры можно комбинировать, использовав одну и ту же огибающую для соседних фигур:

$f_1(t) = Rescaleleft[cos left(frac{13 pi t}{5}right),{-1,1},left{i^t,8 i^t sqrt{frac{2}{20-12 cos (pi t)}}right}right]$

$f_2(t) = Rescaleleft[cos left(frac{13 pi t}{5}right),{1,-1},left{3i^t,8 i^t sqrt{frac{2}{20-12 cos (pi t)}}right}right]$

Или чуть сложнее:

$small f_1(t) =Rescaleleft[cos left(frac{24 pi t}{5}right),{-1,1},left{i^t-frac{2 i^{5 t}}{35}+frac{i^{9 t}}{189},2 left(frac{3 i^{-5 t}}{70}+frac{i^{-t}}{4}+i^t+frac{i^{9 t}}{252}right)right}right]$

$small f_2(t) =Rescaleleft[cos left(frac{24 pi t}{5}right),{-1,1},left{3 left(-frac{1}{12} i^{-3 t}+frac{i^{-t}}{4}+i^tright),2 left(frac{3 i^{-5 t}}{70}+frac{i^{-t}}{4}+i^t+frac{i^{9 t}}{252}right)right}right]$

Огибающие, вообще говоря, не обязаны быть гладкими. Используя ранее выведенную формулу, в качестве огибающих можно использовать и многоугольники:

$f(t) = Rescaleleft[cos left(frac{33 pi t}{5}right),{-1,1},left{2 i^t,frac{i^t left(i^{n t}right)^{1/n}}{1+left(i^{n t}right)^{2/n}}right}right],n to 3$

Огибающие можно сделать более выраженными, если синусоиду немного «оквадратить»:

$f(t) = sin left(frac{1}{2} pi sin (t)right)$

$f(t) = -i text{Rescale}left[sin left(frac{1}{2} pi sin left(frac{31 pi t}{5}right)right),{-1,1},left{frac{i^t left(i^{4 t}right)^{1/4}}{1+left(i^{4 t}right)^{2/4}},frac{2 left(i^t left(i^{5 t}right)^{1/5}right)}{1+left(i^{5 t}right)^{2/5}}right}right]$

Можно пойти ещё дальше по пути выпрямления и вместо заполнения синусоидой просто использовать прямые отрезки:

$f(t) = i^t csc left(frac{1}{5} left(pi -sin ^{-1}left(sin left(frac{5 pi t}{2}right)right)right)right)$

▍ Бордюры

Вместо того, чтобы строить синусоидные ленты очевидным способом, их тоже можно получать интерполяцией между двумя прямыми:

$f(t) = Rescaleleft[cos left(pi left(frac{j}{n}+tright)right),{-1,1},{t-i,t+i}right]$

Если эту формулу символьно вычислить и упростить, то получим уже известную формулу синусоиды в параметрическом виде:

$f(t)=t+i cos left(pi left(frac{j}{n}+tright)right)$

Запись через функцию

позволяет более просто контролировать границы ленты для того, чтобы их можно было собирать как пазл. Например, сделав одну сторону короче другой, можно получить угол в 45° и собрать рамку:

$f(t)=Rescaleleft[cos left(pi left(frac{j}{n}+tright)right),{-1,1},{2 t,t+i}right],-1leq tleq 1$

В качестве границ интерполяции можно брать и любые другие кривые:

$f(t)=Rescaleleft[cos left(pi left(frac{j}{n}+tright)right),{-1,1},left{t,t+frac{1}{2} i cos (pi t)+iright}right]$

$f(t)=Rescaleleft[cos left(pi left(frac{j}{n}+tright)right),{-1,1},left{t-frac{1}{5} sin (pi t),t+frac{1}{2} i cos (pi t+sin (pi t))+iright}right]$

$f(t)=Rescaleleft[cos left(pi left(frac{j}{n}+tright)right),{-1,1},left{t-frac{1}{2} i cos left(frac{pi t}{3}right)-i,t+frac{1}{2} i cos (pi t)+iright}right]$

Можно добавить вариативности и заполнению, модулируя либо координаты границ интерполяции

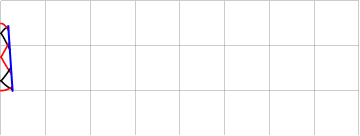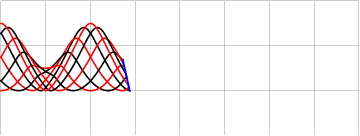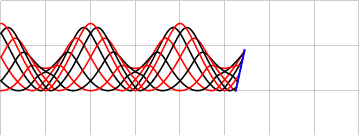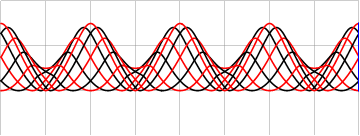
$f(t)=Rescaleleft[cos left(pi left(frac{j}{n}+tright)right),{-1,1},left{t+frac{1}{5} sin (pi t),t+frac{1}{2} i cos (pi t)+iright}right]$

$f(t) =Rescaleleft[cos left(pi left(frac{j}{n}+tright)right),{-1,1},left{t-frac{1}{5} sin (pi t),t+frac{1}{2} i cos (pi t)+iright}right]$

либо частоту заполняющей синусоиды

$f(t)=Rescaleleft[cos left(pi left(frac{j}{n}+tright)+cos (pi t)right),{-1,1},{t,t+i}right]$

$f(t)=Rescaleleft[cos left(pi left(frac{j}{n}+tright)+2 cos ^3(pi t)right),{-1,1},{t,t+i}right]$

▍ Заключение

Здесь были рассмотрены самые простые, базовые техники и фигуры. В качестве дальнейшего развития можно использовать и более сложные математические модели для описания огибающих, в том числе кусочно-непрерывные функции типа кривых Безье, и различные варианты их заполнения. Также комплексные числа можно использовать не только для графики как таковой, но и для описания траекторий различных механизмов типа механизма Чебышёва, что позволит аналитически находить оптимальные параметры и свойства таких механизмов. А если с комплексных чисел перейти на кватернионы — то можно рассматривать подобные построения и в 3Д-пространстве.

Разумеется, подобные задачи можно решать и без комплексных чисел — используя векторы и матричное исчисление, как собственно в основном все и делают. Однако комплексные числа представляются более подходящим инструментом для этого — как минимум более компактным, наглядным и с бОльшим простором для манипуляций, включая интегрирование/дифференцирование, разложение в ряд, преобразование Фурье и прочие инструменты функционального анализа. Впрочем, тема «комплексные числа vs. матрицы» выглядит довольно холиварной — поэтому и продолжить её предлагается уже в комментариях.

P.S. Скачать исходник статьи можно на GitHub.

Источник

Комплексные числа и многочлены

Re: Комплексные числа Z

Комплексные числа и геометрические узоры

▍ Окружность

▍ Эллипс

▍ Гипотрохоида и прочее

▍ Синусы и синусоидные ленты

▍ Розетты

▍ Розетты с интерполяцией

▍ Бордюры

▍ Заключение

Вам также может понравиться

Как найти человека в яндексе по нику

Как найти ручку в школе

Тренинг как найти друзей

Добавить комментарий Отменить ответ