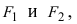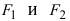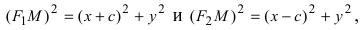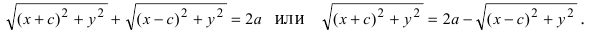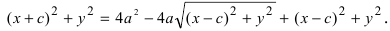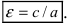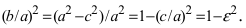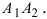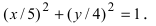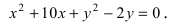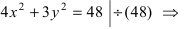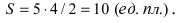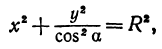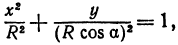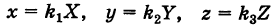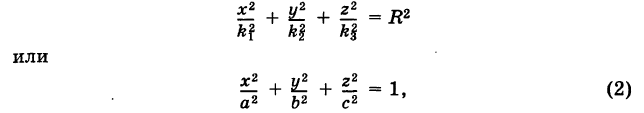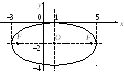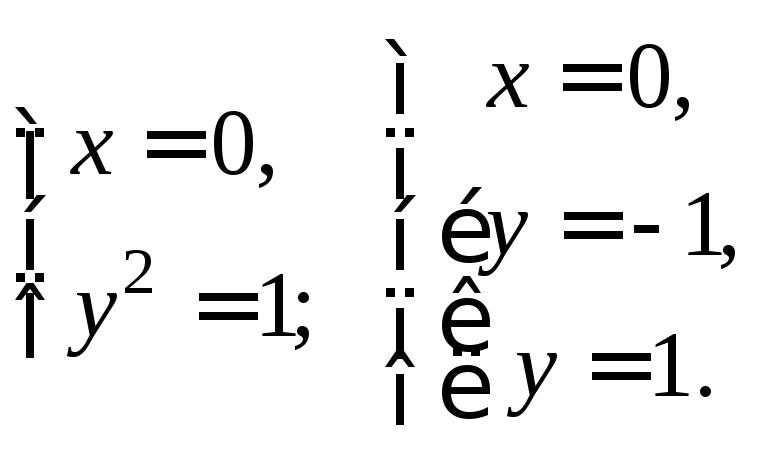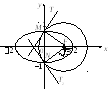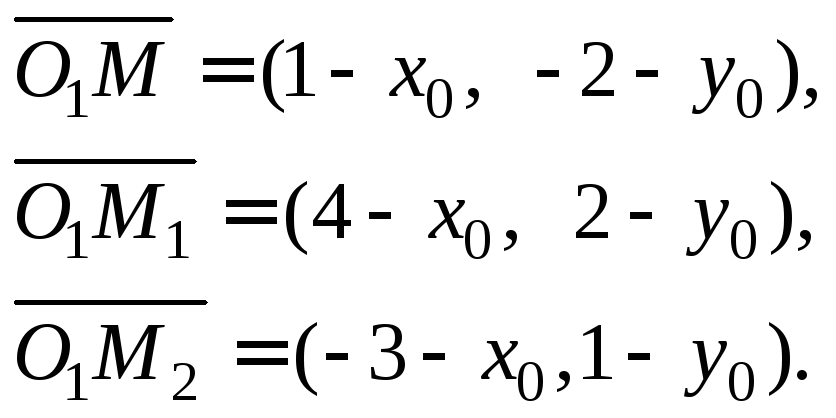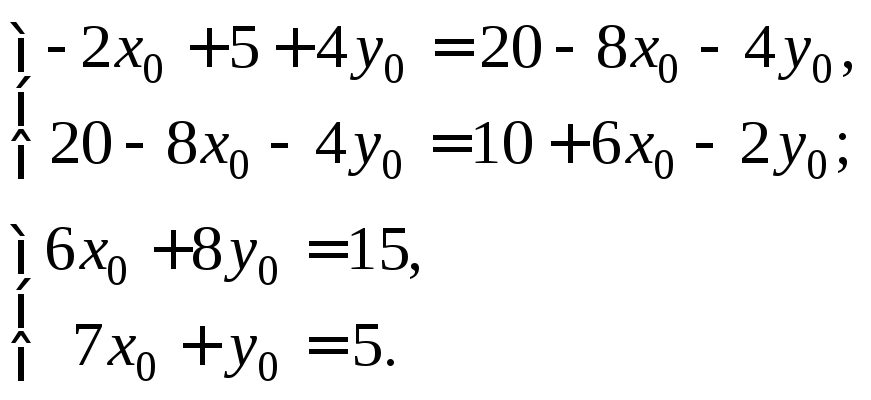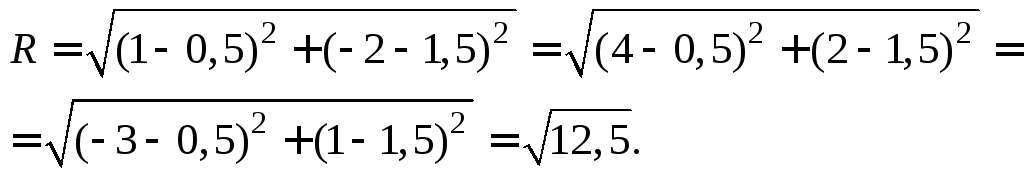Геометрические места точек
Геометрическим местом точек называют множество точек, заданное условием, являющимся и свойством, и признаком.
Другими словами, все точки из рассматриваемого геометрического места точек, и только они, удовлетворяют заданному условию.
Примеры геометрических мест точек (сокращённо ГМТ ) на плоскости представлены в следующей таблице, причём геометрические места точек изображаются в таблице красным цветом .
Определить геометрическое место точки по уравнению
Древнеегипетскую и вавилонскую культуру в области математики продолжали греки. Они не только усвоили весь опыт их геометрии, но и пошли гораздо дальше. Ученые древней Греции сумели привести в систему накопленные геометрические знания и, таким образом, заложить начала геометрии как дедуктивной науки.
Греческие купцы познакомились с восточной математикой, прокладывая торговые пути. Но люди Востока почти не занимались теорией, и греки быстро это обнаружили. Они задавались вопросами: почему в равнобедренном треугольнике два угла при основании равны; почему площадь треугольника равна половине площади прямоугольника при одинаковых основаниях и высотах?
К сожалению, не сохранилось первоисточников, описывающих ранний период развития греческой математики. Только благодаря восстановленным текстам четвертого столетия до нашей эры и трудам арабских ученых, которые были богаты переводами сочинений авторов античной Греции, мы располагаем изданиями Евклида, Архимеда, Аполлония и других великий людей. Но в этих произведениях уже представлена вполне развитая математическая наука.
Математика древней Греции прошла длительный и сложный путь развития, начиная с VI столетия до н.э. и по VI век. Историки науки выделяют три периода ее развития в соответствии с характером знаний:
- Накопление отдельных математических фактов и проблем (6 – 5B.B. до н.э.).
- Систематизация полученных знаний (4 – 3 в.в. до н.э.).
- Период вычислительной математики (3в. до н.э. – 6 в.).
Геометрическое место точек (ГМТ).
Определения.
Геометрическое место – термин, применявшийся в старой литературе по геометрии и до сих пор применяющийся в учебной литературе, для обозначения множества точек, удовлетворяющих некоторому условию, как правило, геометрического характера. Например: геометрическое место точек, равноудаленных от двух данных точек A и B – это серединный перпендикуляр к отрезку AB. Иногда говорят и о геометрическом месте прямых и других фигур.
Название связано с представлением о линии как о «месте», на котором располагаются точки.
Геометрическое Место Точек (ГМТ) – в геометрии траектория некоторой точки, перемещающейся в соответствии с данной формулой или условием. Например, круг является геометрическим местом точки, перемещающейся на плоскости так, что расстояние от места ее нахождения до центра остается неизменным.
Геометрическое место точек (ГМТ) – это множество точек, в которое попадают все точки, удовлетворяющие определенному условию, и только они.
Геометрическое место точек (ГМТ) – фигура речи в математике, употребляемая для определения геометрической фигуры как множества точек, обладающих некоторым свойством.
Примеры.
- Серединный перпендикуляр к отрезку есть геометрическое место точек, равноудалённых от концов отрезка.
- Окружность есть геометрическое место точек, равноудалённых от данной точки, называемой центром окружности.
- Парабола есть геометрическое место точек, равноудалённых от точки (называемой фокусом) и прямой (называемой директрисой).
Пример 1.
Срединный перпендикуляр любого отрезка есть геометрическое место точек (т.е. множество всех точек), равноудалённых от концов этого отрезка. Пусть PO перпендикулярно AB и AO = OB :
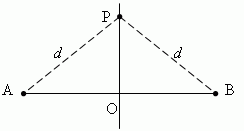
Тогда, расстояния от любой точки P, лежащей на срединном перпендикуляре PO, до концов A и B отрезка AB одинаковы и равны d .
Таким образом, каждая точка срединного перпендикуляра отрезка обладает следующим свойством: она равноудалена от концов отрезка.
Пример 2.
Биссектриса угла есть геометрическое место точек, равноудалённых от его сторон.
Пример 3.
Окружность есть геометрическое место точек (т.е. множество всех точек), равноудалённых от её центра ( на рис. показана одна из этих точек – А ).


Теоретическая часть.
Окружность – это геометрическое место точек (т.е. множество всех точек) на плоскости, равноудалённых от одной точки, называемой центром окружности. Отрезок, соединяющий центр окружности с какой-либо её точкой, называется радиусом и обозначается r или R. Часть плоскости, ограниченная окружностью, называется кругом. Часть окружности ( AmB, рис.1 ) называется дугой. Прямая PQ, проходящая через точки M и N окружности ( рис.1 ), называется секущей, а её отрезок MN, лежащий внутри окружности – хордой.
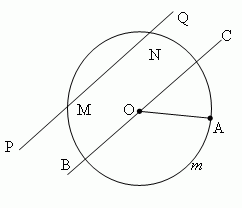
Хорда, проходящая через центр круга ( например, BC, рис 1), называется диаметром и обозначается d или D . Диаметр – это наибольшая хорда, равная двум радиусам (d = 2 r).
Касательная. Предположим, секущая PQ ( рис.2 ) проходит через точки K и M окружности. Предположим также, что точка M движется вдоль окружности, приближаясь к точке K. Тогда секущая PQ будет менять своё положение, вращаясь вокруг точки K. По мере приближения точки M к точке K секущая PQ будет стремиться к некоторому предельному положению АВ. Прямая AB называется касательной к окружности в точке K. Точка K называется точкой касания. Касательная и окружность имеют только одну общую точку – точку касания.
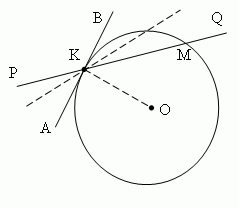
- Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания ( AB перпендикулярно OK, рис.2 ).
- Из точки, лежащей вне круга, можно провести две касательные к одной и той же окружности; их отрезки равны АВ=АС ( рис.3 ).

Сегмент – это часть круга, ограниченная дугой ACB и соответствующей хордой AB ( рис.4 ). Длина перпендикуляра CD, проведенного из середины хорды AB до пересечения с дугой ACB, называется высотой сегмента.

Сектор – это часть круга, ограниченная дугой AmB и двумя радиусами OA и OB, проведенными к концам этой дуги ( рис.5 ).
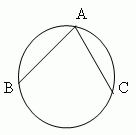
Центральный угол – угол, образованный двумя радиусами ( ∠AOB, рис.5 ). Вписанный угол – угол, образованный двумя хордами AB и AC, проведенными из их одной общей точки ( ∠BAC, рис.4 ). Описанный угол – угол, образованный двумя касательными AB и AC, проведенными из одной общей точки ( ∠BAC, рис.3 ).
Соотношения между элементами круга.
Вписанный угол ( ∠ABC, рис.7 ) равен половине центрального угла, опирающегося на ту же дугу AmC ( ∠AOC, рис.7 ). Поэтому, все вписанные углы ( рис.7 ), опирающиеся на одну и ту же дугу ( AmC, рис.7 ), равны. А так как центральный угол содержит то же количество градусов, что и его дуга ( AmC, рис.7 ), то любой вписанный угол измеряется половиной дуги, на которую он опирается ( в нашем случае AmC ).
рис. 7
Все вписанные углы, опирающиеся на полукруг (∠APB, ∠AQB, …, рис.8 ), прямые.
Угол (∠AOD, рис.9 ), образованный двумя хордами ( AB и CD ), измеряется полусуммой дуг, заключённых между его сторонами: ( AnD + CmB ) / 2 .
рис. 8 рис. 9
Угол (∠AOD, рис.10), образованный двумя секущими ( AO и OD ), измеряется полуразностью дуг, заключённых между его сторонами: ( AnD – BmC ) / 2.
Угол (∠DCB, рис.11), образованный касательной и хордой ( AB и CD ), измеряется половиной дуги, заключённой внутри него: CmD / 2.
Угол (∠BOC, рис.12), образованный касательной и секущей ( CO и BO ), измеряется полуразностью дуг, заключённых между его сторонами: ( BmC – CnD ) / 2 .
рис. 10 рис. 11
Описанный угол (∠AOC, рис.12), образованный двумя касательными ( CO и AO ), измеряется полуразностью дуг, заключенных между его сторонами: ( ABC – CDA ) / 2 .
Произведения отрезков хорд ( AB и CD, рис.13 или рис.14), на которые они делятся точкой пересечения, равны: AO · BO = CO · DO.
Квадрат касательной равен произведению секущей на её внешнюю часть ( рис.12): OA 2 = OB · OD. Это свойство можно рассматривать как частный случай рис.14.
рис. 13 рис. 14
Хорда ( AB , рис.15), перпендикулярная диаметру ( CD ), O пополам: AO = OB .
рис. 15
Интересный факт:
Поздравляем с Пи-раздником вас.
Выражаясь научным языком, число “Пи” – это отношение длины окружности к ее диаметру. Простая вроде бы вещь, но волнует умы математиков с глубокой древности. И продолжает волновать. До такой степени, что ученые – лет 20 назад – договорились отмечать праздник этого числа. И призвали присоединиться к торжествам всю прогрессивную общественность. Она присоединяется: ест круглые Пи-роги, вы-ПИ-вает, обязательно Пи-во и издает звуки Пи при встрече.
Фанаты будут соревноваться, вспоминая знаки числа “Пи”. И постараются превзойти рекорд 24-летнего китайского студента Лю Чао, который назвал по памяти без ошибок 68890 знаков. На это у него ушло 24 часа и 4 минуты.
Отправление торжеств назначено на 14 марта – дату, которая в американском написании выглядит как 3.14 – то есть, первыми тремя цифрами числа “Пи”.
По легенде, о числе “Пи” знали еще вавилонские жрецы. Использовали при строительстве Вавилонской башни. Но не смогли точно вычислить его значение и от этого не справились с проектом. Сам символ числа “Пи” впервые использовал в своих трудах в 1706 году математик Уильям Джон (William Jones). Но реально он прижился после 1737 года благодаря стараниям шведского математика Леонарда Эйлера (Leonhard Euler).
Отмечать праздник придумал американский физик Ларри Шо (Larry Shaw).
На вопрос, сколько знаков в числе “Пи” после запятой, точного ответа нет. Скорее всего, их бесконечное число. А главная особенность в том, что последовательность этих знаков не повторяется. Сегодня их известно 12411 триллионов. Обследовано 500 миллиардов. И повторений не найдено.
Как считают некоторые видные физики и математики, например Дэвид Бейли, Питер Борвин и Саймон Плофе (David Bailey, Peter Borewin, Simon Plouffe), их – повторений – не найти никому и никогда. Хоть испиши знаками всю Вселенную. Да хоть сколько Вселенных. И в этом ученые видят некую скрытую мистику. Полагают, что в числе “Пи” зашифрован бесконечный первородный хаос, ставший потом гармонией. Или какая-то загадочная информация.
- Сформулируйте определение окружности и круга?
- С какими новыми понятиями вы познакомились?
- Что называется геометрическим местом точек?
- Какая разница между диаметром и радиусом?
- Как найти радиус окружности какая описана около треугольника?
Список использованных источников:
- Урок на тему “Наглядная геометрия” Автор: Самылина Марина Валентиновна., г. Киев
- Савин А.П. Метод геометрических мест /Факультативный курс по математике: Учебное пособие для 7-9 классов средней школы. Сост. И.Л. Никольская. – М.: Просвещение, с. 74.
- Смирнова И.М., Смирнов В.А. Геометрия: Учебник для 7-9 классов общеобразовательных учреждений. – М.: Мнемозина, 2005, с. 84.
- Шарыгин И.Ф. Геометрия. 7-9 классы: Учебник для общеобразовательных учебных заведений. – М.: Дрофа, с. 76.
- Мазур К. И. «Решение основных конкурсных задач по математике сборника под редакцией М. И. Сканави»
Поставить вопрос о современном образовании, выразить идею или решить назревшую проблему Вы можете на Образовательном форуме, где на международном уровне собирается образовательный совет свежей мысли и действия. Создав блог, Вы не только повысите свой статус, как компетентного преподавателя, а и сделаете весомый вклад в развитие школы будущего. Гильдия Лидеров Образования открывает двери для специалистов высшего ранга и приглашает к сотрудничеству в направлении создания лучших в мире школ.
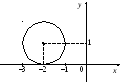
Определить геометрическое место точки по уравнению
Задание 5. Изобразить геометрическое место точек, заданных уравнением
б) в пространстве
Решение. а) Данное уравнение есть общее уравнение кривой второго порядка. Методом выделения полного квадрата приведём его к каноническому виду:
Это уравнение эллипса с центром в точке . Ось по Х равна ось по У равна
В пространстве заданному уравнению соответствует эллиптический цилиндр, направляющей линией которого является полученный в пункте а) эллипс. Направляющая расположена в плоскости Oxy, а образующие – прямые, параллельные оси Oz
[spoiler title=”источники:”]
http://edufuture.biz/index.php?title=%D0%93%D0%B5%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%BE%D0%B5_%D0%BC%D0%B5%D1%81%D1%82%D0%BE_%D1%82%D0%BE%D1%87%D0%B5%D0%BA._%D0%9F%D0%BE%D0%BB%D0%BD%D1%8B%D0%B5_%D1%83%D1%80%D0%BE%D0%BA%D0%B8
http://an-site.ru/kr/m06.htm
[/spoiler]
Геометрические места точек
Геометрическим местом точек называют множество точек, заданное условием, являющимся и свойством, и признаком.
Другими словами, все точки из рассматриваемого геометрического места точек, и только они, удовлетворяют заданному условию.
Примеры геометрических мест точек (сокращённо ГМТ ) на плоскости представлены в следующей таблице, причём геометрические места точек изображаются в таблице красным цветом .
Уравнение линии как геометрического места точек. Различные виды уравнений прямой. Исследование общего уравнения прямой. Построение прямой по ее уравнению
Уравнением линии называется уравнение с переменными x и y, которому удовлетворяют координаты любой точки этой линии и только они.
Входящие в уравнение линии переменные x и y называются текущими координатами, а буквенные постоянные — параметрами.
Чтобы составить уравнение линии как геометрического места точек, обладающих одинаковым свойством, нужно:
1) взять произвольную (текущую) точку M(x, y) линии;
2) записать равенством общее свойство всех точек M линии;
3) входящие в это равенство отрезки (и углы) выразить через текущие координаты точки M(x, y) и через данные в задаче.
В прямоугольных координатах уравнение прямой на плоскости задается в одном из следующих видов:
1. Уравнение прямой с угловым коэффициентом
где k — угловой коэффициент прямой, т. е. тангенс того угла, который прямая образует с положительным направлением оси Ox, причем этот угол отсчитывается от оси Ox к прямой против часовой стрелки, b — величина отрезка, отсекаемого прямой на оси ординат. При b = 0 уравнение (1) имеет вид y = kx и соответствующая ему прямая проходит через начало координат.
Уравнением (1) может быть определена любая прямая на плоскости, не перпендикулярная оси Ox.
Уравнение прямой с угловым коэффициентом разрешено относительно текущей координаты y.
2. Общее уравнение прямой
Частные случаи общего уравнения прямой:
а) Если C = 0, уравнение (2) будет иметь вид
и прямая, определяемая этим уравнением, проходит через начало координат, так как координаты начала координат x = 0, y = 0 удовлетворяют этому уравнению.
Геометрическое место точек
Геометрическое место точек (ГМТ) — это фигура, состоящая из всех точек плоскости, удовлетворяющих определённому условию.
Чтобы выяснить, что собой представляет некоторая фигура F — геометрическое место точек, удовлетворяющих заданному условию P, нужно доказать:
1) если определённая точка принадлежит фигуре F, то она удовлетворяет заданному условию P;
2) если определённая точка удовлетворяет заданному условию P, то она принадлежит фигуре F.
(то есть требуется доказать прямую теорему — свойство P точек, принадлежащих фигуре F, и обратную теорему — признак фигуры F: если точка удовлетворяет условию P, то она принадлежит F).
Геометрическое место точек, равноудалённых от данной точки — окружность.
Это следует непосредственно из определения окружности.
Некоторые теоремы о ГМТ
1) Геометрическим местом точек, равноудалённых от двух данных точек, является серединный перпендикуляр к отрезку, соединяющему эти точки.
2) Геометрическим местом точек, равноудалённых от сторон неразвёрнутого угла, является биссектриса этого угла.
3) Геометрическим местом точек, удалённых от данной прямой на расстояние h, состоит из двух прямых, параллельных данной прямой и отстоящих от неё на h.
4) Геометрическим местом точек, равноудалённых от двух параллельных прямых, является прямая, параллельная этим прямым и проходящая через середину их общего перпендикуляра.
Понятие ГМТ часто используют при решении задач на построение.
источники:
http://www.pm298.ru/reshenie/uravnpr.php
http://www.treugolniki.ru/geometricheskoe-mesto-tochek/
Эллипс:
Определение: Эллипсом называется геометрическое место точек, сумма расстояний от которых до двух выделенных точек
Получим каноническое уравнение эллипса. Выберем декартову систему координат так, чтобы фокусы
Рис. 29. Вывод уравнения эллипса.
Расстояние между фокусами (фокусное расстояние) равно 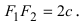
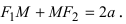
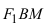
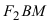
соответственно. Следовательно, согласно определению имеем
Возведем обе части равенства в квадрат, получим
Перенося квадратный корень в левую часть, а все остальное в правую часть равенства, находим 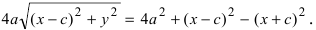
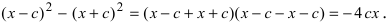
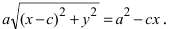
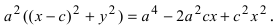
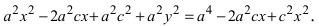
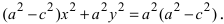
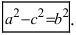
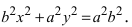
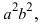
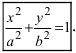
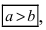
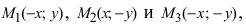
Определение: Найденные точки называются вершинами эллипса.
Рис. 30. Вершины, фокусы и параметры эллипса
Определение: Если 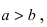
Определение: Эксцентриситетом эллипса называется отношение фокусного рас- стояния к большой полуоси эллипса
Из определения эксцентриситета эллипса следует, что он удовлетворяет двойному неравенству 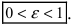
Если 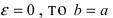
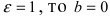
Пример:
Составить уравнение эллипса, если его большая полуось а = 5, а его эксцентриситет
Решение:
Исходя из понятия эксцентриситета, найдем абсциссу фокуса, т.е. параметр 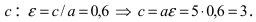
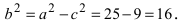
Пример:
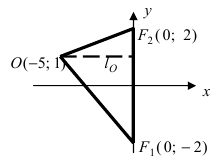
Найти площадь треугольника, две вершины которого находятся в фокусах эллипса 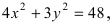
Решение:
Для определения координат фокусов эллипса и центра окружности преобразуем их уравнения к каноническому виду. Эллипс:
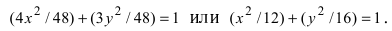
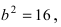
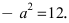
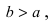
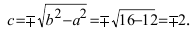
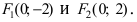
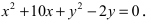
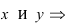
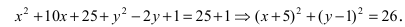
Построим в декартовой системе координат треугольник 
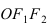
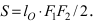
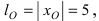
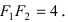
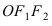
Эллипс в высшей математике
Рассмотрим уравнение
где 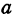
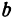
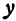
Отсюда видно, что уравнение (2) определяет две функции. Пока независимое переменное 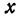
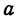
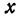
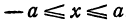
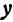
При 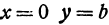
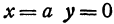
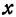

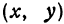
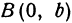
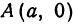
Полученная линия называется эллипсом. Число 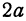
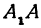
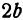
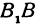
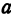
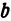
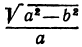
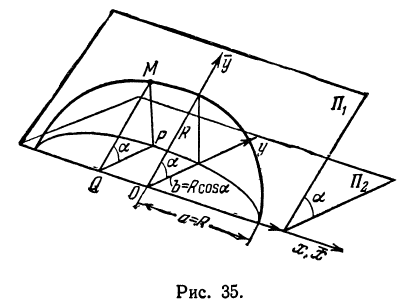
Пример:
Найти проекцию окружности на плоскость, не совпадающую с плоскостью окружности.
Решение:
Возьмем две плоскости, пересекающиеся под углом 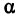
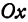
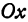
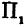
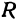
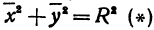
Пусть точка 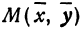
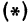
Обозначим проекцию точки 
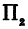
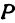
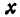
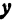
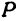

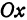
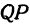
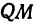
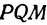
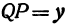
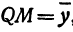
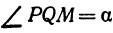
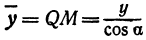

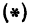
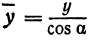
или
а это есть уравнение эллипса с полуосями 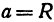
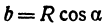
Таким образом, эллипс является проекцией окружности на плоскость, расположенную под углом к плоскости окружности.
Замечание. Окружность можно рассматривать как эллипс с равными полуосями.
Уравнение эллипсоида
Определение: Трехосным эллипсоидом называется поверхность, полученная в результате равномерной деформации (растяжения или сжатия) сферы по трем взаимно перпендикулярным направлениям.
Рассмотрим сферу радиуса R с центром в начале координат:
где Х, У, Z — текущие координаты точки сферы.
Пусть данная сфера подвергнута равномерной деформации в направлении координатных осей 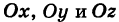
В результате сфера превратится в эллипсоид, а точка сферы М (X, У, Z) с текущими координатами Х, У, Z перейдет в точку эллипсоидам 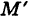
(рис. 206). Отсюда
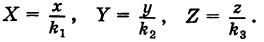
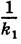
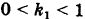
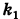
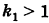
Подставляя эти формулы в уравнение (1), будем иметь
где 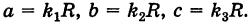
Величины 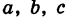
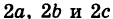
Если две полуоси эллипсоида равны между собой, то эллипсоид называется эллипсоидом вращения, так как может быть получен в результате вращения эллипса вокруг одной из его осей. Например, в геодезии считают поверхность земного шара эллипсоидом вращения с полуосями
а = b = 6377 км и с = 6356 км.
Если а = b = с, то эллипсоид превращается в сферу.
- Гипербола
- Парабола
- Многогранник
- Решение задач на вычисление площадей
- Шар в геометрии
- Правильные многогранники в геометрии
- Многогранники
- Окружность
Общие уравнения геометрических мест точек
Уравнением множества точек (уравнением г.м.т.) координатной плоскости называется равенство, связывающее координаты точек, верное для координат точек, принадлежащих множеству
, и неверное для координат точек, не принадлежащих
. Например, уравнение множества в аффинной системе координат
имеет вид:
(3.1)
в частности, в прямоугольной системе координат , а в полярной системе координат
(3.2)
где и
— некоторые функции двух аргументов.
Уравнения (3.1), (3.2) представляют собой аналитическую запись функциональной зависимости между координатами точек на плоскости, образующих геометрическое место точек. В частных случаях одна из координат может быть выражена через другую, т.е. одна координата задается как явная функция другой координаты. Тогда получается уравнение, разрешенное относительно этой координаты, например:
Заметим, что уравнениями вида в прямоугольной системе координат
могут быть заданы графики элементарных функций: степенных, тригонометрических, показательных, логарифмических.
Пример 3.1. Изобразить на координатной плоскости (в прямоугольной системе координат) множества точек, координаты которых удовлетворяют следующим уравнениям:
Решение. а) Уравнению удовлетворяют только те точки плоскости, у которых равны абсциссы и ординаты
. Эти точки лежат на биссектрисах
и
координатных углов (рис. 3.1, а).
б) Разлагая левую часть уравнения на множители, получаем уравнение , которое равносильно совокупности уравнений
Первому уравнению отвечают биссектрисы нечетных координатных углов, второму — биссектрисы четных координатных углов. Следовательно, заданному уравнению удовлетворяют только те точки, которые принадлежат хотя бы одной из указанных биссектрис (рис. 3.1, 6).
в) Уравнение равносильно системе уравнений
которая определяет единственную точку (начало координат) на плоскости (рис. 3.1, в).
г) Выражение есть квадрат расстояния от точки
до начала координат. Поэтому уравнению
(или
) удовлетворяют только те точки, которые удалены от точки
на расстояние, равное 1. Это множество точек является окружностью с центром в начале координат и радиусом 1 (рис.3.1,г).
д) Уравнению удовлетворяет каждая точка с неположительной абсциссой. Следовательно, множество решений этого уравнения представляет собой полуплоскость
, ограниченную осью ординат (рис.3.1,д).
е) Уравнение не имеет действительных решений, поэтому на координатной плоскости нет точек, удовлетворяющих этому уравнению.
Пример 3.2. На координатной плоскости (в прямоугольной системе координат) отмечены точки
и
. Вывести уравнения заданных множеств:
а) прямой (рис.3.2,а);
б) серединного перпендикуляра к отрезку (рис.3.2,б);
в) окружности с диаметром (рис.3.2,в).
Решение. а) Точка принадлежит прямой
тогда и только тогда, когда ее радиус-вектор
удовлетворяет условию
, где
— некоторое действительное число (см. Применение векторов в задачах). Записывая это векторное равенство в координатной форме, получаем
Исключая параметр из этой системы (например, подставляя во второе уравнение
), приходим к уравнению
или
.
б) Пусть произвольная точка плоскости. Эта точка принадлежит серединному перпендикуляру к отрезку
тогда и только тогда, когда
. Записывая это равенство в координатной форме, получаем
Возводя в квадрат и приводя подобные члены, приходим к уравнению .
в) Найдем радиус заданной окружности:
и координаты центра окружности — середины отрезка
, так как
. По определению точка
принадлежит этой окружности тогда и только тогда, когда
. Записывая это равенство в координатной форме, получаем
Возводя в квадрат и перенося все члены в левую часть равенства, получаем .
Пример 3.3. Изобразить на плоскости в полярной системе координат множества точек, координаты которых удовлетворяют следующим уравнениям:
а) (спираль Архимеда);
б) (кардиоида);
в) (лемниската Бернулли).
Решение. а) Построение выполняется по точкам при . Далее учитывается, что при каждом полном обороте полярный радиус увеличивается на
(рис.3.3-1).
б) Построение выполняется по точкам при , а затем продолжается симметрично полярной оси, так как замена
на
не изменяет уравнения (рис.3.3-2,а).
в) Построение выполняется по точкам при , а затем продолжается симметрично полярной оси и полюса
(рис.3.3-2,б).
Уравнения пересечений и объединений геометрических мест точек
Рассмотрим основные операции с множествами точек на координатной плоскости, заданными своими уравнениями.
Пусть множества и
в аффинной системе координат
заданы общими уравнениями
и
соответственно.
Пересечение множеств
и
состоит из точек, координаты которых удовлетворяют системе уравнений
Можно составить одно уравнение, равносильное этой системе, например:
Объединение множеств
и
состоит из точек, координаты которых удовлетворяют совокупности уравнений
равносильной одному уравнению, например:
.
Включение с алгебраической точки зрения означает, что уравнение
является следствием уравнения
, то есть
Равенство означает, что уравнения
и
равносильны (эквивалентны), то есть
В частности, равносильные уравнения, описывающие одно и то же геометрическое место точек, получаются при тождественных алгебраических преобразованиях равенств, например, при умножении обеих частей уравнения на отличное от нуля число, при приведении подобных членов, при переносе членов из одной части уравнения в другую с изменением знака на противоположный и т.п.
Полученные соотношения, сводящие операции с множествами на плоскости к алгебраическим операциям с уравнениями этих геометрических мест точек, не зависят от выбора системы координат. Например, в прямоугольной системе координат аналогичные соотношения получаем, полагая
и
, а в полярной системе координат
при
и
.
Параметрические уравнения геометрических мест точек
Функциональная зависимость между координатами точек плоскости, например в прямоугольной системе координат , может быть задана в параметрической форме, в которой обе координаты выражаются в виде функций вспомогательной переменной, называемой параметром:
(3.3)
где — параметр, принимающий действительные значения. Систему (3.3) называют параметрическим уравнением геометрического места точек.
Пример 3.4. Изобразить на координатной плоскости (в прямоугольной системе координат) множества точек, координаты которых удовлетворяют следующим параметрическим уравнениям:
Решение. 1) Исключим из заданной системы уравнений параметр . Возведя обе части каждого уравнения в квадрат и сложив почленно результаты, получим уравнение окружности
(см. пример 3.1 ,г). Параметром
служит величина угла поворота радиус-вектора изображающей точки, измеряемого от положительного направления оси абсцисс (рис.3.4,а).
2) Уравнения задают циклоиду — линию, которую описывает точка, принадлежащая окружности при качении этой окружности (без проскальзывания) по прямой (оси абсцисс). Построение одной арки циклоиды выполняется по точкам при . Затем эта арка “переносится” вдоль оси абсцисс (рис.3.4,б). Параметром
служит величина угла поворота радиуса катящейся окружности.
3) Уравнения задают астроиду (гипоциклоиду) — линию, которую описывает точка, принадлежащая окружности при качении этой окружности (без проскальзывания) по другой неподвижной окружности, касаясь ее внутренним образом. Астроида и обе окружности изображены на рис.3.4,в (астроида полужирной линией, неподвижная окружность сплошной, а подвижная — штриховой). Построение выполняется по точкам при , а затем продолжается симметрично координатным осям.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Эллипсом
называется геометрическое место точек
плоскости, координаты которых удовлетворяют
уравнению
(9.7)
где
(9.8)
Уравнение (9.7)
называется
каноническим
уравнением эллипса.
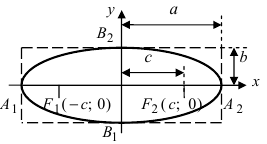
Параметры эллипса
Точки F1(–c,
0) и F2(c,
0), где
называютсяфокусами
эллипса,
при этом величина 2c
определяет междуфокусное
расстояние.
Точки А1(–а,
0), А2(а,
0), В1(0,
–b),
B2(0,
b)
называются вершинами
эллипса
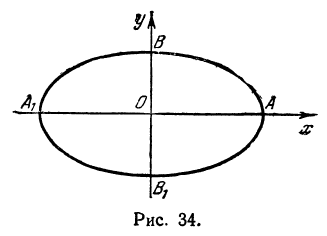
(рис. 9.2), при этом А1А2
= 2а
образует большую ось эллипса, а В1В2
– малую,
– центр эллипса.
Основные параметры
эллипса, характеризующие его форму:
ε
= с/a
– эксцентриситет
эллипса;
–фокальные
радиусы эллипса
(точка М
принадлежит эллипсу), причем r1
= a
+ εx,
r2
= a
– εx;
–директрисы
эллипса.
Рис. 9.2
Для эллипса
справедливо:
директрисы не пересекают границу и
внутреннюю область эллипса, а также
обладают свойством
Эксцентриситет
эллипса выражает его меру «сжатости».
Если b
> a
> 0, то
эллипс задается уравнением (9.7), для
которого вместо условия (9.8) выполняется
условие
.
(9.9)
Тогда 2а
– малая ось, 2b
– большая ось,
– фокусы (рис. 9.3). При этомr1
+ r2
= 2b,
ε
= c/b,
директрисы определяются уравнениями:
Рис. 9.3
При
условии
имеем (в виде частного случая эллипса)окружность
радиуса R
= a.
При этом с
= 0, а значит, ε = 0.
Точки эллипса
обладают характеристическим
свойством:
сумма расстояний от каждой из них до
фокусов есть величина постоянная, равная
2а
(рис. 9.2).
Для параметрического
задания эллипса
(формула (9.7)) в случаях выполнения условий
(9.8) и (9.9) в качестве параметра t
может быть взята величина угла между
радиус-вектором точки, лежащей на
эллипсе, и положительным направлением
оси Ox:
где
Если центр эллипса
с полуосями
находится в точке
то его уравнение имеет вид:
(9.10)
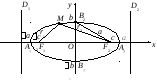
Пример 1.
Привести уравнение эллипса x2
+ 4y2
= 16 к каноническому виду и определить
его параметры. Изобразить эллипс.
Решение.
Разделим уравнение x2 + 4y2 = 16
на 16, после чего получим:
По виду полученного
уравнения заключаем, что это каноническое
уравнение эллипса (формула (9.7)), где а
= 4 – большая полуось, b
= 2 – малая полуось. Значит, вершинами
эллипса являются точки A1(–4, 0),
A2(4, 0),
B1(0, –2),
B2(0, 2).
Так как
– половина междуфокусного расстояния,
то точкиявляются фокусами эллипса. Вычислим
эксцентриситет:
Директрисы D1,
D2
описываются уравнениями:
Изображаем эллипс
(рис. 9.4).
Рис. 9.4
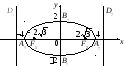
Пример 2.
Определить параметры эллипса
Решение.
Сравним данное уравнение с каноническим
уравнением эллипса
со смещенным центром. Находим центр
эллипсаС:
Большая полуось
малая полуось
прямые
– главные оси. Половина междуфокусного
расстоянияа значит, фокусы
Эксцентриситет
ДиректрисыD1
и D2
могут быть описаны с помощью уравнений:
(рис. 9.5).
Рис. 9.5
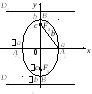
Пример 3.
Определить, какая кривая задается
уравнением, изобразить ее:
1) x2
+ y2
+ 4x
– 2y
+ 4 = 0; 2) x2
+ y2
+ 4x
– 2y
+ 6 = 0;
3) x2
+ 4y2
– 2x
+ 16y
+ 1 = 0; 4) x2
+ 4y2
– 2x
+ 16y
+ 17 = 0;
5)
Решение.
1) Приведем уравнение к каноническому
виду методом выделения полного квадрата
двучлена:
x2
+ y2
+ 4x
– 2y
+ 4 = 0;
(x2
+ 4x)
+ (y2
– 2y)
+ 4 = 0;
(x2
+ 4x
+ 4) – 4 + (y2
– 2y
+ 1) – 1 + 4 = 0;
(x
+ 2)2
+ (y
– 1)2
= 1.
Таким образом,
уравнение может быть приведено к виду
(x
+ 2)2
+ (y
– 1)2
= 1.
Это уравнение
окружности с центром в точке (–2, 1) и
радиусом R = 1
(рис. 9.6).
Рис. 9.6
2)
Выделяем полные квадраты двучленов в
левой части уравнения и получаем:
(x
+ 2)2
+ (y
– 1)2
= –1.
Это уравнение не
имеет смысла на множестве действительных
чисел, так как левая часть неотрицательна
при любых действительных значениях
переменных x
и y,
а правая – отрицательна. Поэтому говорят,
что это уравнение «мнимой окружности»
или оно задает пустое множество точек
плоскости.
3) Выделяем полные
квадраты:
x2
+ 4y2
– 2x
+ 16y
+ 1 = 0;
(x2
– 2x
+ 1) – 1 + 4(y2
+ 4y
+ 4) – 16 + 1 = 0;
(x
– 1)2
+ 4(y
+ 2)2
– 16 = 0;
(x
– 1)2
+ 4(y
+ 2)2
= 16.
Значит, уравнение
имеет вид:
или
Полученное
уравнение, а следовательно, и исходное
задают эллипс. Центр эллипса находится
в точке О1(1,
–2), главные оси задаются уравнениями
y
= –2, x
= 1, причем большая полуось а
= 4, малая полуось b
= 2 (рис. 9.7).
Рис. 9.7
4) После выделения
полных квадратов имеем:
(x
– 1)2
+ 4(y
+ 2)2
– 17 + 17 = 0 или (x
– 1)2
+ 4(y
+ 2)2
= 0.
Полученное уравнение
задает единственную точку плоскости с
координатами (1, –2).
5) Приведем уравнение
к каноническому виду:
Очевидно, оно
задает эллипс, центр которого находится
в точке
главные оси задаются уравнениями
причем большая полуось
малая полуось
(рис. 9.8).
Рис. 9.8
Пример 4.
Записать уравнение касательной к
окружности радиуса 2 с центром в
правом фокусе эллипса x2
+ 4y2
= 4 в точке пересечения с осью ординат.
Решение.
Уравнение эллипса приведем к каноническому
виду (9.7):
Значит,
и правый фокус –
Поэтому, искомое уравнение окружности
радиуса 2 имеет вид (рис. 9.9):
Окружность
пересекает ось ординат в точках,
координаты которых определяются из
системы уравнений:
Получаем:
Пусть это точки N
(0; –1) и М
(0; 1). Значит, можно построить две
касательные, обозначим их Т1
и Т2.
По известному свойству касательная
перпендикулярна радиусу, проведенному
в точку касания.
Пусть
Тогда
уравнение касательнойТ1
примет вид:
значит,
илиТ1:
Тогда уравнение
касательной Т2
примет вид:
значит,
илиТ2:
Рис. 9.9
Пример 5.
Записать уравнение окружности, проходящей
через точку М(1,
–2) и точки пересечения прямой x
– 7y
+ 10 = 0 с окружностью x2
+ y2
– 2x
+ 4y
– 20 = 0.
Решение.
Найдем точки пересечения прямой x
– 7y
+ 10 = 0 с окружностью x2
+ y2
– 2x
+ 4y
– 20 = 0, решив систему уравнений:
Выразим х
из первого уравнения системы:
x
= 7y
– 10.
Затем подставим
во второе:
(7y
– 10)2
+ y2
– 2(7y
– 10) + 4y
– 20 = 0.
Оно равносильно
уравнению
y2
– 3y
+ 2 = 0.
Используя формулы
корней квадратного уравнения, найдем
y1
= 1, y2
= 2, откуда x1
= –3, x2
= 4.
Итак, имеем три
точки, лежащие на окружности: M(1,
–2), M1(4,
2) и M2(–3,
1). Пусть О1(x0,
y0)
– центр окружности. Тогда
гдеR
– радиус окружности.
Найдем координаты
векторов:
Значит,
что равносильно
системе
Упрощаем ее:
Решая последнюю
систему, получаем ответ:
Таким образом,
центр окружности находится в точке
(0,5; 1,5), ее радиус
Тогда каноническое
уравнение искомой окружности имеет
вид:
Задания
Соседние файлы в папке Часть 2
- #
- #
- #
- #
- #
- #
- #
- #
- #