Как найти геометрическое место точек треугольника

Геометрические места точек

Геометрическим местом точек называют множество точек, заданное условием, являющимся и свойством, и признаком.

Другими словами, все точки из рассматриваемого геометрического места точек, и только они, удовлетворяют заданному условию.

Примеры геометрических мест точек (сокращённо ГМТ ) на плоскости представлены в следующей таблице, причём геометрические места точек изображаются в таблице красным цветом .

Планиметрия. Страница 3

1 2 3 4 5 6 7 8 9 10 11 12

1.Окружность

Окружностью называется фигура, состоящая из множества точек на плоскости, равноудаленных от данной точки.

Эта данная точка называется центром окружности. Расстояние от центра окружности до ее точек называется радиусом окружности.

Отрезок, соединяющий две точки окружности, называется хордой.

Если хорда проходит через центр окружности, то она называется диаметром. (Рис.1)

ОА – радиус
ВС – диаметр
DE – хорда

Рис.1 Окружность, радиус, диаметр, хорда.

2.Окружность, описанная около треугольника

Теорема: центр окружности, описанной около треугольника, является точкой пересечения перпендикуляров, опущенных на середины сторон данного треугольника.

Доказательство. Пусть АВС данный треугольник и точка О является центром окружности, описанной около данного треугольника. (Рис.2) Тогда отрезки ОА, ОВ, ОС равны как радиусы. Следовательно, треугольники Δ АОВ, Δ ВОС, Δ АОС – равнобедренные. А следовательно, и медианы, проведенные к серединам сторон ОК, ОЕ, ОD, являются одновременно биссектрисой и высотой. Поэтому предположение, что центр окружности, описанной около треугольника, является точкой пересечения высот, верно.

Рис.2 Теорема. Окружность, описанная около треугольника.

3.Окружность, вписанная в треугольник

Теорема. центр окружности, вписанной в треугольник, является точкой пересечения биссектрис, проведенных из его углов.

Доказательство. Пусть дан треугольник АВС. Точка О – центр вписанной окружности. (Рис. 3)

Тогда треугольник Δ АОЕ равен треугольнику Δ АОТ,
Δ СОЕ = Δ СОК,
Δ ВОК = Δ ВОТ.
Так как стороны ОА, ОВ, ОС у них общие. А ОК, ОЕ, ОТ как радиусы.
Следовательно:
∠ ЕАО = ∠ ТАО,
∠ ЕСО = ∠ КСО,
∠ КВО = ∠ ТВО.

Это значит, что точка О лежит на пересечении биссектрис АО, ВО, СО.

Рис.3 Теорема. Окружность, вписанная в треугольник.

4.Геометрическое место точек

Геометрическое место точек это фигура, которая представляет собой совокупность точек на плоскости, подчиняющихся определенному закону или обладающих определенным свойством.

Теорема. Геометрическим местом точек называется прямая, все точки которой равноудалены от двух данных точек, перпендикулярная отрезку, соединяющему эти точки и проходящая через его середину.

Доказательство. Пусть дан отрезок АС. Прямая А проходит через середину этого отрезка и перпендикулярна ему.(Рис. 4).

Тогда треугольники Δ АМВ и Δ СМВ равны. Так как сторона ВМ у них обшая, а стороны АМ и МС равны по условию. Следовательно точка В равноудалена от точек А и С.
Возьмем другую точку, например D, не лежащую на прямой а. Тогда сторона MD не принадлежит прямой а. А следовательно, углы AMD и DMC не равны т.к. не равны треугольники. Данное утверждение основано на том, что через точку, лежащую на прямой, можно провести только одну перпендикулярную ей прямую. И следовательно, расстояния от точки D до точек А и С не равны. Поэтому, для того чтобы расстояния от некой точки Х до двух данных точек были равны, необходимо чтобы она лежала на прямой а, которая перпендикулярна отрезку, соединяющего эти точки, и которая проходит через его середину.

Рис.4 Теорема. Геометрическое место точек.

Репетитор: Васильев Алексей Александрович

Предметы: математика, физика, информатика, экономика, программирование.

2000 руб / 120 мин – подготовка к ЕГЭ и ГИА для школьников. 3000 руб / 120 мин – индивидуально (базовый уровень). 2000 руб / 120 мин – студенты.

Тел. 8 916 461-50-69, email: alexey-it@ya.ru

Пример 1

Дана окружность с центром О. И проведена касательная а из точки С к этой окружности. Доказать, что точка К лежит на основании равнобедренного треугольника ОВС, если OB = 2R. (рис.5)

По условию прямая а есть касательная к окружности, следовательно радиус, проведенный к точке касания ОК, и который лежит на прямой с, составляет прямой угол с касательной. Так как ОВ = 2R и KB = R, то прямая а будет представлять собой геометрическое место точек, так как она перпендикулярна отрезку ОВ и проходит через его середину. А следовательно, треугольники ВКС и ОКС равны по первому признаку равенства треугольников. Отсюда можно сделать вывод, что точка К будет лежать на основании равнобедренного треугольника ВОС.

Рис.5 Задача. Дана окружность с центром О.

Пример 2

Докажите, что касательная к окружности не имеет с ней других общих точек, кроме точки касания. (Рис.6)

Доказательство:

Пусть дана окружность с центром в точке О. И прямая а, которая касается окружности в точке А. Допустим, что прямая а имеет еще одну точку касаная – точку В. Тогда радиус окружности, проведенный к точкам А и В образует угол с прямой а равный 90°.

Таким образом, в равнобедренном треугольнике АОВ углы при вершинах А и В равны 90°. А это невозможно. Следовательно, мы пришли к противоречию и прямая а не может касаться окружности в двух точках.

Рис.6 Задача. Касательная к окружности.

Пример 3

Точки А,В,С лежат на одной прямой, а точка О лежит вне этой прямой. Докажите, что треугольники АОВ и ВОС не могут быть равнобедренными с основаниями АВ и ВС. (Рис.7)

Доказательство:

Допустим, что треугольники АОВ и ВОС равнобедренные с основаниями АВ и ВС. Тогда Стороны АО, ВО и СО равны. Отсюда следует, что углы ОАВ, АВО, ОВС и ОСВ равны. И ∠АВО = ∠ОВС = 90°, так как эти углы являются смежными, а их сумма равна 180°.

Таким образом, в равнобедренных треугольниках АОВ и ВОС углы при вершинах А и С равны 90°. А это невозможно, потому, что тогда стороны АО, ВО и СО были бы параллельны, так как они перпендикулярны одной прямой АС. Следовательно, мы пришли к противоречию, и треугольники АОВ и ВОС не могут быть равнобедренными с основаниями АВ и ВС.

Рис.7 Задача. Даны три точки на прямой.

Пример 4

Окружности с центрами О и О₁ пересекаются в точках А и В. Докажите, что прямая АВ перпендикулярна прямой ОО₁ (Рис.8)

Доказательство:

Так как окружности пересекаются в точках А и В, то эти две точки принадлежат обеим окружностям. Следовательно, отрезок ОА = ОВ, как радиусы окружности с центром в точке О. А отрезок О₁А = О₁В, как радиусы окружности с центром в точке О₁.

Таким образом, треугольники ОАО₁ и ОВО₁ равны по третьему признаку равенства треугольников (по трем сторонам). А следовательно отрезки АС и ВС равны. И прямая ОО₁ является геометрическим местом точек для двух данных точек А и В. Т.е. любая точка прямой ОО₁ равноудалена от двух данных точек А и В. Следовательно, треугольники ОАС и ОВС равны, также как и треугольники АСО₁ и ВСО₁ по трем сторонам. А отсюда следует равенство углов при вершине С. Т.е. ∠ОСА = ∠ОСВ = ∠АСО₁ = ∠ВСО₁ = 90°.

Следовательно, можно сделать вывод, что прямая АВ перпендикулярна прямой ОО₁.

Рис.8 Задача. Окружности с центрами О и О₁.

Пример 5

Отрезок ВС пересекает прямую а в точке О. Расстояние от точек В и С до прямой а равны. Докажите, что точка О является серединой отрезка ВС (Рис.9)

Доказательство:

По условию задачи, расстояния от точек В и С до прямой а равны. Т.е. РС = BQ. Так как расстояние от точки до прямой представляет собой перпендикуляр, то два треугольника РОС и ВОQ, образованные двумя пересекающимися прямыми ВС и а, и перпендикулярами, опущенными на одну из них, равны по второму признаку равенства треугольников ( по стороне и двум прилегающим к ней углам: РС = BQ, углы при вершинах В и С равны как внутренние накрест лежащие, а углы при вершинах Р и Q прямые).

Из равенства треугольников РОС и ВОQ следует, что ВО = ОС.

Рис.9 Задача. Отрезок ВС пересекает прямую а .

Геометрическое место точек

Геометрическое место точек (ГМТ) — это фигура, состоящая из всех точек плоскости, удовлетворяющих определённому условию.

Чтобы выяснить, что собой представляет некоторая фигура F — геометрическое место точек, удовлетворяющих заданному условию P, нужно доказать:

1) если определённая точка принадлежит фигуре F, то она удовлетворяет заданному условию P;

2) если определённая точка удовлетворяет заданному условию P, то она принадлежит фигуре F.

(то есть требуется доказать прямую теорему — свойство P точек, принадлежащих фигуре F, и обратную теорему — признак фигуры F: если точка удовлетворяет условию P, то она принадлежит F).

Геометрическое место точек, равноудалённых от данной точки — окружность.

Это следует непосредственно из определения окружности.

Некоторые теоремы о ГМТ

1) Геометрическим местом точек, равноудалённых от двух данных точек, является серединный перпендикуляр к отрезку, соединяющему эти точки.

2) Геометрическим местом точек, равноудалённых от сторон неразвёрнутого угла, является биссектриса этого угла.

3) Геометрическим местом точек, удалённых от данной прямой на расстояние h, состоит из двух прямых, параллельных данной прямой и отстоящих от неё на h.

4) Геометрическим местом точек, равноудалённых от двух параллельных прямых, является прямая, параллельная этим прямым и проходящая через середину их общего перпендикуляра.

Понятие ГМТ часто используют при решении задач на построение.

[spoiler title=”источники:”]

http://www.mathtask.ru/0051-planimetry.php

[/spoiler]

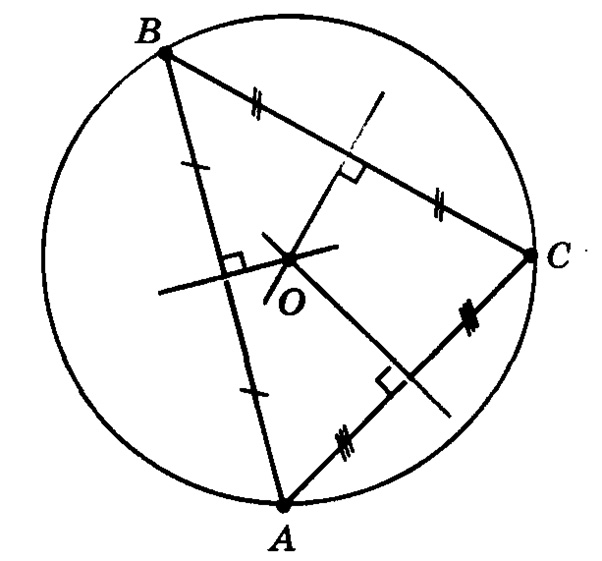
Мы знаем, что геометрическое место точек, которые равноудаленны от вершин треугольника, является центр описанной около треугольника окружности — этот центр является точкой пересечения серединных перпендикуляров к сторонам треугольника.

Найдем теперь геометрическое место точек, равноудаленных от сторон треугольника. Пусть дан треугольник DEF.

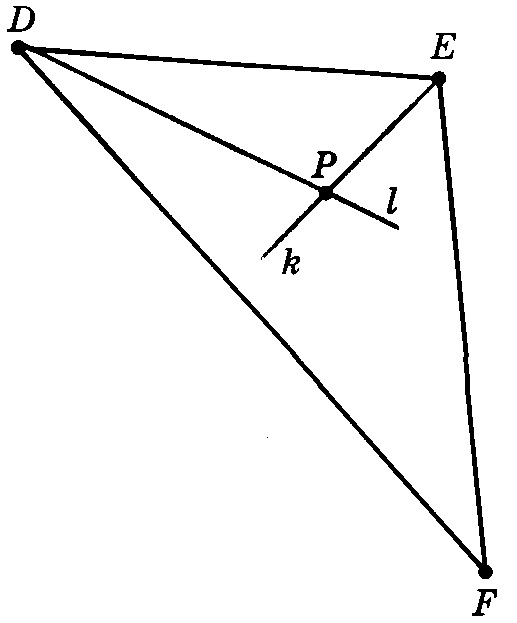
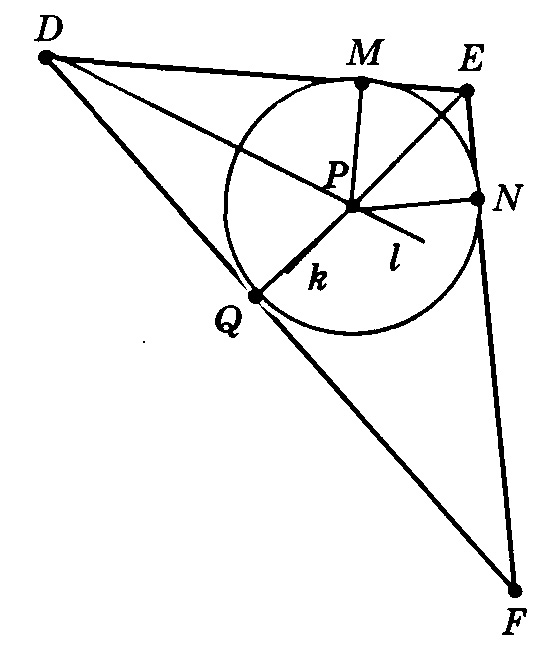
Геометрическим местом точек, равноудаленных от сторон DE и DF, является биссектриса l угла EDF, а геометрическим местом точек, равноудаленных от сторон DE и EF, — биссектриса k угла DEF. Каждая точка биссектрисы l равноудалена от сторон DE и DF, а каждая точка биссектрисы k — от сторон DE и EF. Тогда общая точка этих биссектрис — точка Р — равноудалена от всех трех сторон DE, DF и EF. Точка Р — искомое геометрическое место.

Перпендикуляры РМ, PN, PQ, опущенные из точки Р на стороны треугольника DEF, равны друг другу. Если построить окружность с центром Р и радиусом РМ, то она пройдет через все три точки М, N, Q. При этом, поскольку радиусы РМ, PN, PQ этой окружности перпендикулярны к сторонам DE, EF, FD треугольника DEF, то эти стороны являются касательными к проведенной окружности.

Содержание

Введение

Глава 1. Теоретические
основы изучения замечательных точек треугольника

1.1 Замечательные точки треугольника

1.2 Точка пересечения биссектрис

1.3 Точка пересечения высот треугольника

1.4 Точка пересечения медиан

1.5 Точка пересечения серединных перпендикуляров

Глава 2. Исследование
расположения центра описанной окружности треугольника

2.1 Геометрическое место
точек, равноудаленных от вершин треугольника при двух фиксированных точках

2.2 Геометрическое место
точек, равноудаленных от вершин треугольника при одной фиксированной точке

Заключение

Список литературы

Введение

В жизни часто
встречаются математические задачи, решение которых важно и необходимо для той
или иной практической деятельности в разных сферах общества. Наше исследование
посвящено решению практико-ориентированной задачи, которая рассматривает
вопрос, связанный с территориальным местоположением субъектов и о месте
нахождении того или иного объекта, равноудаленного от данных субъектов.

Постановка задачи: Пусть в Пензенской области есть три села,
администрации этих сел решили сделать совместный амбар для хранения зерна, но
возник вопрос: где нужно расположить амбар, чтобы путь от каждого села до
амбара был равным?

Если
принять сёла за точки, то решить задачу нам поможет геометрия и такая фигура, как треугольник. Треугольник
– геометрическая фигура, состоящая из трех точек,
не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки. Эта
фигура обладает немалым количеством различных свойств.

В данном проекте хотелось бы обратить
внимание на «замечательные точки треугольника». Замечательные точки
треугольника — точки, местоположение которых однозначно определяется
треугольником и не зависит от того, в каком порядке берутся стороны и вершины
треугольника.

На протяжении истории многие математики занимались данным
вопросом: Евклид, Архимед, Леонард
Эйлер, Ж. Понселе, Ш. Брианшон и другие. Они внесли большой вклад, показав
какие именно существуют замечательные точки, прямые в треугольнике.

В школьном курсе геометрии
рассматривают следующие из них:

1.     Точка пересечения биссектрис.

2.     Точка пересечения медиан.

3.     Точка пересечения высот.

4.     Точка   пересечения   серединных  
перпендикуляров.

Самым
удивительным свойством «замечательных точек треугольника» является то, что
некоторые из них связаны друг с другом определёнными соотношениями.

В
1765 году Эйлер доказал, что в любом треугольнике точка пересечения высот
треугольника – ортоцентр, барицентр и центр описанной окружности лежат на одной
прямой, названной позже «прямой Эйлера». В двадцатых годах XIX века французские
математики Ж. Понселе, Ш. Брианшон и другие установили независимо друг от друга
следующую теорему: основания медиан, основания высот и середины отрезков высот,
соединяющих ортоцентр с вершинами треугольника, лежат на одной и той же
окружности.

Эта
окружность называется «окружностью девяти точек», или «окружностью Фейербаха»,
или «окружностью Эйлера». К. Фейербах установил, что центр этой окружности
лежит на прямого Эйлера. Большой вклад в развитие геометрии треугольника внесли
математики XIX – XX веков Лемуан, Брокар, Тебо и другие. Существуют ещё другие
«замечательные точки треугольника». Это «точка Торричелли», «точка Лемуана»,
«точка Жергонна», «точка Нагеля».

Цель
исследовательской работы: исследовать ГМТ пересечения серединных
перпендикуляров треугольника в зависимости от фиксирования двух и одной точки.

Для
достижения поставленной цели в работе необходимо решить следующие задачи:

1.                
Изучить
необходимую литературу.

2.                
Изучить
классификацию замечательных точек треугольника.

3.                
Исследовать с помощью средств компьютерной среды
Математический конструктор зависимости между геометрическим местом точек (ГМТ),
полученным при движении одной из вершин треугольника и ГМТ, полученном при
движении двух вершин треугольника.

4.                
Провести анализ полученных данных и сделать
выводы.

Объект
исследования: треугольник и
центр описанной около треугольника окружности.

Предмет
исследования: зависимости в расположении центра описанной около треугольника
окружности.

Гипотеза: если
принять три села за три точки, условно соединить точки отрезками, получив тем
самым треугольник, то можно предположить, что решением нашей задачи будет
являться нахождение центра описанной около сел окружности.

Учебный предмет, в рамках которого
проводиться работа по проекту: геометрия.

Возраст учащихся: 8 класс

Тип проекта: исследовательский.

Методы исследования: изучение литературы,
моделирование, эксперимент, анализ и синтез.

Глава 1. Теоретические основы изучения
замечательных точек треугольника

1.1  
Замечательные точки треугольника

Прежде всего, следует изучить историю возникновения «замечательных
точек треугольника». В четвертой книге «Начал» Евклид решает задачу: «Вписать
круг в данный треугольник». Из решения вытекает, что три биссектрисы внутренних
углов треугольника пересекаются в одной точке – центре вписанного круга. Из
решения другой задачи Евклида вытекает, что перпендикуляры, восстановленные к
сторонам треугольника в их серединах, тоже пересекаются в одной точке – центре
описанного круга. В «Началах» не говорится о том, что и три высоты треугольника
пересекаются в одной точке, называемой ортоцентром (греческое слово «ортос»
означает «прямой», «правильный»). Это предложение было, однако, известно
Архимеду, Паппу, Проклу.

Четвертой особенной точкой треугольника является точка
пересечения медиан. Архимед доказал, что она является центром тяжести
(барицентром) треугольника. На вышеназванные четыре точки было обращено особое
внимание, и начиная с XVIII века они были названы “замечательными”
или “особенными” точками треугольника.

В школьном курсе геометрии
рассматривают следующие из них:

1.     Точка пересечения биссектрис.

2.     Точка пересечения медиан.

3.     Точка пересечения высот.

4.     Точка   пересечения   серединных  
перпендикуляров.

В 1765 году Эйлер доказал, что в любом треугольнике ортоцентр, барицентр
и центр описанной окружности лежат на одной прямой, названной позже
“прямой Эйлера”.

Теорема
была доказана в 1765 году Леонардо Эйлером, отсюда она и получила своё название
«Теорема Эйлера». В этом же году Эйлер обнаружил, что середины сторон треугольника
и основание его высот лежат на одной окружности. Впоследствии было обнаружено,
что на той же окружности лежат ещё три точки – середины отрезков, соединяющих
ортоцентр с вершинами треугольника. Это и есть «окружность 9 точек».   

Существуют
ещё другие «замечательные точки
треугольника». Это «точка Торричелли», «точка Лемуана», «точка
Жергонна», «точка Нагеля».

1.2  
Точка пересечения биссектрис

Биссектриса – это луч, который выходит из вершины
треугольника и делит ее ровно на две части. У треугольника
существуют три биссектрисы, соответствующие трём его вершинам.

Характеристическая
особенность точек, лежащих на биссектрисе угла: точка, лежащая на биссектрисе
угла равноудалена от его сторон.

Эта точка
всегда лежит внутри треугольника и является центром вписанной в треугольник окружности. Точка О – точка
пересечения биссектрис AA₁; BB₁;
CC₁
треугольника ABC, О – центр вписанной в треугольник ABC
окружности.

   
Теорема: Все
биссектрисы треугольника пересекаются в одной точке, которая называется
инцентром и является центром вписанной в треугольник окружности. Для
треугольника любого вида инцентр расположен внутри.

Рис.
1

1.3  
Точка пересечения высот треугольника

Высота
треугольника — перпендикуляр, опущенный из вершины треугольника на
противоположную сторону.

Точку пересечения высот называют ортоцентром. Точка пересечения высот может
лежать как внутри треугольника, так и вне его, и на его сторонах; AE;
CF; BD–
высоты треугольника ABC => точка О – точка пересечения высот.

Теорема: Высоты треугольника или их продолжения пересекаются в одной точке,
которая называется ортоцентром. Ортоцентр может располагаться: внутри
треугольника, вне его или совпадать с вершиной, соответственно в остроугольном,
тупоугольном и прямоугольном треугольнике.

Рис.
2

1.4  

Точка пересечения медиан

Медиана – это отрезок,
соединяющий вершину треугольника с серединой стороны, расположенной напротив
данной вершины.

Точка пересечения медиан всегда лежит внутри треугольника. Эта точка обладает
замечательным свойством, она делит каждую медиану на отрезки, отношение длин которых равно 2:1,
если считать отрезки от вершин треугольника.
Эту точку также называют центром масс треугольника или центроидом.

Теорема: Все медианы треугольника
пересекаются в одной точке, которая называется центроидом и делятся точкой
пересечения в отношении 2:1, считая от вершины. Для треугольника любого вида
центроид расположен внутри. Центроид является центром тяжести треугольника.

Рис.
3

1.5  Точка пересечения серединных перпендикуляров

Серединный
перпендикуляр к отрезку — это прямая, перпендикулярная данному отрезку и проходящая через
его середину.

Серединным перпендикуляром называется перпендикуляр,
проведённый к середине стороны треугольника. Точка пересечения серединных
перпендикуляров является центром описанной окружности. Эта точка может лежать
как внутри треугольника, так и вне его и на его сторонах. LO, МО, КО –
серединные перпендикуляры, О – точка их пересечения => точка О – центр описанной
окружности.   

Теорема: Серединные перпендикуляры треугольника пересекаются в одной точке,
которая является центром описанной около него окружности. Она может
располагаться внутри треугольника, вне его или лежать на его стороне.

Рис.
4

Глава 2. Исследование расположения центра
описанной окружности треугольника

Если
принять три села за три точки, условно соединить точки отрезками, получив тем
самым треугольник, то исходя из вышесказанного, можно сделать вывод, что
решением нашей задачи будет являться нахождение центра описанной около сел
окружности, в этой точке и необходимо расположить амбар, так как центр
описанной около треугольника окружности действительно равноудален от вершин
треугольника, то есть наш амбар таким образом будет находиться на одинаковом
расстоянии от каждого села.

Возникает
вопрос: где необходимо расположить амбар, если изменить расстояние между
селами, то есть какую траекторию будет описывать центр описанной около
треугольника окружности при изменении расстояний между вершинами треугольника.

Гипотеза:
центр описанной около треугольника окружности при изменении расстояний между
вершинами треугольника будет описывать кривую второго порядка.

Для
ответа на данный вопрос воспользуемся возможностями интерактивными средствами
образовательного назначения – Математический конструктор.

2.1 Геометрическое место точек,
равноудаленных от вершин треугольника при двух фиксированных точках

Проанализируем,
где будет находиться центр описанной окружности при двух фиксированных вершинах
и одной вершине, движущейся по окружности.

1.     Строим отрезок AB,
из точки A строим окружность произвольного радиуса.

2.     На полученной окружности выбираем
произвольную точку C.

3.     Соединяем отрезками точки A,
B, C,
получаем треугольник ABC.

4.     В полученном треугольнике строим
серединные перпендикуляры.

5.     Обозначаем за O
точку пересечения серединных перпендикуляров, которая будет являться центром
описанной около треугольника окружности.

6.     Описываем около треугольника окружность.

7.     Анимируем точку С, точка О будет оставлять
след.

8.     Получаем следующий результат (рис 5).

Рис.
5

В результате построения мы получили, что геометрическим
местом точки, равноудаленной от вершин треугольника при двух фиксированных
точках, будет являться прямая.

2.2
Геометрическое место точек,
равноудаленных от вершин треугольника при одной фиксированной точке

Проанализируем,
где будет находиться центр описанной окружности при одной фиксированной вершине
и двух вершинах, движущихся по окружности.

1.     Строим отрезок AE, из точки Aи из точки Eстроим
окружности произвольного радиуса.

2.     На полученных окружностях выбираем
произвольные точки BиC.

3.     Соединяем отрезками точки A, B, C,
получаем треугольник ABC.

4.     В полученном треугольнике строим
серединные перпендикуляры.

5.     Обозначаем за O точку пересечения
серединных перпендикуляров, которая будет являться центром описанной около
треугольника окружности.

6.     Описываем около треугольника окружность.

7.     Анимируем точки B и С, точка О будет
оставлять след.

8.     Получаем следующий результат (рис 6).

Рис.
6

В результате построения мы получили
траекторию движения точек не носящую определенного названия, тем самым можно
сказать о том, что геометрическое место точки, равноудаленной от вершин
треугольника при одной фиксированной точке, определить невозможно.

Заключение

В
результате проделанной работы нами была изучена необходимая литература,
классификация замечательных точек треугольника. Мы исследовали с помощью средств
компьютерной среды Математический конструктор зависимости в расположении центра
описанной окружности при движении одной или двух вершин треугольника. А также
провели анализ полученных данных и сделали выводы:

1.     ГМТ, описываемое центром
пересечения серединных перпендикуляров при двух фиксированных вершинах,
является прямая.

2.     ГМТ, описываемое центром
пересечения серединных перпендикуляров при одной фиксированной вершине,
является незамкнутая кривая.

Таким
образом, основная гипотеза проекта: если принять три села за три точки,
условно соединить точки отрезками, получив тем самым треугольник, то можно
предположить, что решением нашей задачи будет являться нахождение центра
описанной около сел окружности, подтвердилась.

При изменении условий основной задачи, а
именно, центр описанной около треугольника окружности при изменении расстояний
между вершинами треугольника будет описывать кривую второго порядка, не
подтвердилась.

Эти факты были исследованы нами с
помощью интерактивных средств образовательного назначения (Математический
конструктор), тем самым упрощая задачу проверки гипотезы по двум заданным
условиям рассматриваемой задачи.

В
качестве перспективы развития проекта можно изменить условия задачи, а именно: где будет находиться центр описанной
окружности при трех вершинах, движущихся по окружности. А также рассмотреть
движение точек не по окружности, а по эллипсу.

Список литературы

1.     Атанасян, Л.С. Учебник «Геометрия 7-9 классы / Л.С. Атанасян и др. –
М.: Мнемозина, 2015. – 384 с.

2.      Понарин, Я. П. Элементарная геометрия. В 2 т. / Я.П. Понарин.–М.:
МЦНМО, 2004. – 48 – 50 с.

3.     Математический конструктор онлайн [сайт] URL: https://obr.1c.ru/mathkit/

Определение

Геометрическое место точек (ГМТ) — это фигура, состоящая из всех точек плоскости, удовлетворяющих определённому условию.

Чтобы выяснить, что собой представляет некоторая фигура F — геометрическое место точек, удовлетворяющих заданному условию P, нужно доказать:

1) если определённая точка принадлежит фигуре F, то она удовлетворяет заданному условию P;

2) если определённая точка удовлетворяет заданному условию P, то она принадлежит фигуре F.

(то есть требуется доказать прямую теорему — свойство P точек, принадлежащих фигуре F, и обратную теорему — признак фигуры F: если точка удовлетворяет условию P, то она принадлежит F).

Геометрическое место точек, равноудалённых от данной точки — окружность.

Это следует непосредственно из определения окружности.

Некоторые теоремы о ГМТ

1) Геометрическим местом точек, равноудалённых от двух данных точек, является серединный перпендикуляр к отрезку, соединяющему эти точки.

2) Геометрическим местом точек, равноудалённых от сторон неразвёрнутого угла, является биссектриса этого угла.

3) Геометрическим местом точек, удалённых от данной прямой на расстояние h, состоит из двух прямых, параллельных данной прямой и отстоящих от неё на h.

4) Геометрическим местом точек, равноудалённых от двух параллельных прямых, является прямая, параллельная этим прямым и проходящая через середину их общего перпендикуляра.

Теорема 1 — свойство серединного перпендикуляра.

Теорема 2 —  свойство биссектрисы угла.

Понятие ГМТ часто используют при решении задач на построение.

• Альфашкола
• Уроки по математике
• Геометрия
• Геометрические места точек

Геометрические места точек – онлайн урок

К сожалению, информация по данному уроку пока отсутствует.

Отзывы:

Хороший преподаватель. Всё очень нравится!

Тамара Анатольевна – высокопрофессиональный педагог. Ее занятия очень хорошо спланированы и выполнены. Энн была на 100% вовлечена во время занятия. Очень спокойная и дружелюбная атмосфера помогла ей почувствовать себя увереннее. Энн добилась больших успехов. Спасибо большое, Тамара Анатольевна! Энн и семья.

Алексей Сергеевич замечательный педагог! Очень доступно объясняет материал и интересно ведёт уроки!!!

Похожие уроки