Классическое
определение вероятности основывается
на том, что число всех возможных случаев
конечно. Если распределение возможных
исходов испытания непрерывно и бесконечно,
то при решении задач часто используется
понятие геометрической
вероятности.
Полагают,
что имеется область Ω и в ней область
A.
На Ω наудачу бросается точка. Событие
А – попадание точки в область А.
Геометрической
вероятностью
события А называется отношение меры
области, благоприятствующей появлению
события А, к мере всей области Ω, т.е.
P(A)
=
;
Область
Ω может быть одномерной, двумерной,
трехмерной и n-мерной.
Пример.
В круг радиуса R=50
бросается точка. Найти вероятность ее
попадания во вписанный в круг квадрат.
Решение.
P(A) =
=
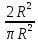
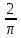; ( R =
; a =
)
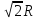6. Сумма событий и ее свойства. Примеры.
Суммой
нескольких событий называется событие,
состоящее в наступлении хотя бы одного
из данных событий.
Если
А и В — совместные события, то их сумма
А + В обозначает наступление или события
А, или события В, или обоих событий
вместе. Если А и В — несовместные события,
то их сумма А + В означает наступление
или события А, или события В.
Свойства:
-
А
+ В = В + А – коммутативность сложения. -
А
+ (В + С) = (А + В) + С – ассоциативность
сложения. -
А(В
+ С) = (А+В)(А+С) – законы дистрибутивности.
Примеры.
1)
Событие
А – попадание в цель при первом выстреле,
событие В – попадание в цель при втором
выстреле, тогда событие С = А + В есть
попадание в цель вообще, безразлично
при
каком выстреле – при первом, при втором
или при обоих вместе.
2)
Если событие А –
появление карты червонной масти при
вынимании карты из колоды, событие В –
появление карты бубновой масти, то С
= А + В есть
появление карты красной масти, безразлично
– червонной или бубновой.
7. Теорема сложения вероятностей (с доказательством) и ее следствия. Примеры. 8 Произведение событий и его свойства.
9. Условная вероятность. Зависимые и независимые события. Теорема умножения вероятностей (с доказательством). Примеры
Вероятность
Р(В) как мера степени объективной
возможности наступления события В имеет
смысл при выполнении определенного
комплекса условий. При изменении условий
вероятность события В может измениться.
Так, если к комплексу условий, при котором
изучалась вероятность р(В), добавить
новое условие А, то полученная вероятность
события В, найденная при условии, что
событие А произошло, называется условной
вероятностью события В и обозначается
РА(В), или Р(В/А), или Р(В/А).
Теорема
Умножения вероятностей принимает
наиболее простой вид, когда события,
образующие произведение, независимы.
Событие
В называется независимым от события А,
если его вероятность не меняется от
того, произошло событие А или нет, т.е.
РА(В)=Р(В)
В
противном случае, если РА(В) не равно
Р(В) событие В называется зависимым от
А.
Несколько
событий А,В,М… называются независимыми
в совокупности, если независимы любые
два из них и независимо любое из данных
событий и любые комбинации (произведения)
остальных событий. В противном случае
события А,В,М называются зависимыми.
Вероятность
произведения двух или нескольких
независимых событий равна произведению
вероятностей этих событий.
10.
Формулы полной вероятности и Байеса.
Примеры.
ФОРМУЛА
ПОЛНОЙ ВЕРОЯТНОСТИ
Пусть
события H1 , H2 ,K, Hn образуют полную группу
попарно несовместных событий. Такие
события называются гипотезами. Пусть
событие A происходит вместе с гипотезами
H1 , H2 ,K, Hn. Тогда для вероятности события
A справедлива формула
P(
A)
P(H1
)
PH
(
A)
P(H2
)
PH
(
A)
K
P(Hn
)
PH
(
A)
.
1 2 n
Доказательство. A
AH1
AH2
K
AHn
.
Так
как
H1
,
H2
,K,
Hnпопарно
несовместные, тоAH1 ,
AH2
,K,
AHn
также попарно
несовместные. По правилу сложения
вероятностей имеем
P(
A)
P(
AHi
)
P(Hi
)
PHi(
A)
.
Что и требовалось доказать.
Пример. На город примерно 100 дней в году
дует ветер с севера и 200 дней в году – с
запада. Промышленные предприятия,
расположенные на севере, производят
выброс вредных веществ каждый третий
день, а расположенные на западе – в
последний день каждой недели. Как часто
город подвергается воздействию вредных
выбросов?
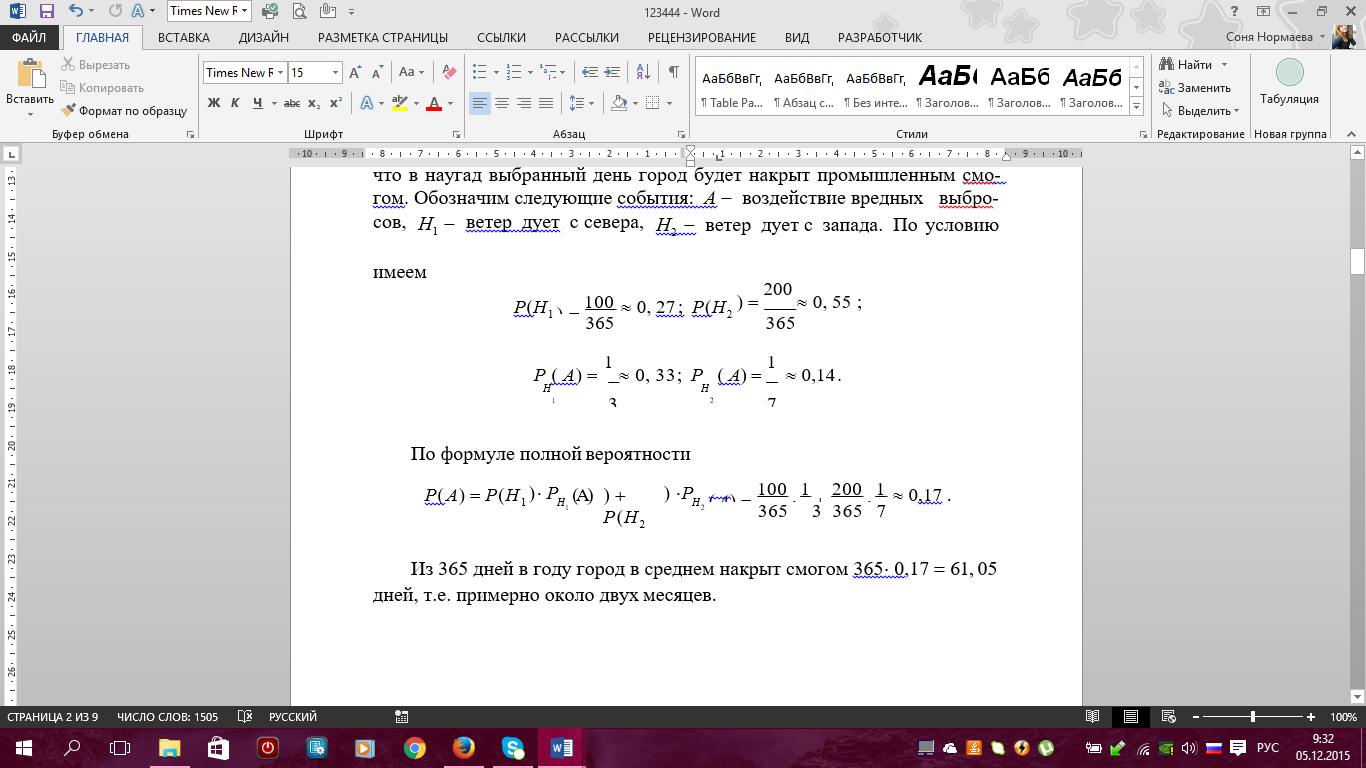
Решение. Другими словами, нужно вычислить
вероятность того, что в наугад выбранный
день город будет накрыт промышленным
смогом. Обозначим следующие события: A
воздействие вредных выбросов, H1
ветер дует с севера,H2
ветер дует с запада. По условию имеем
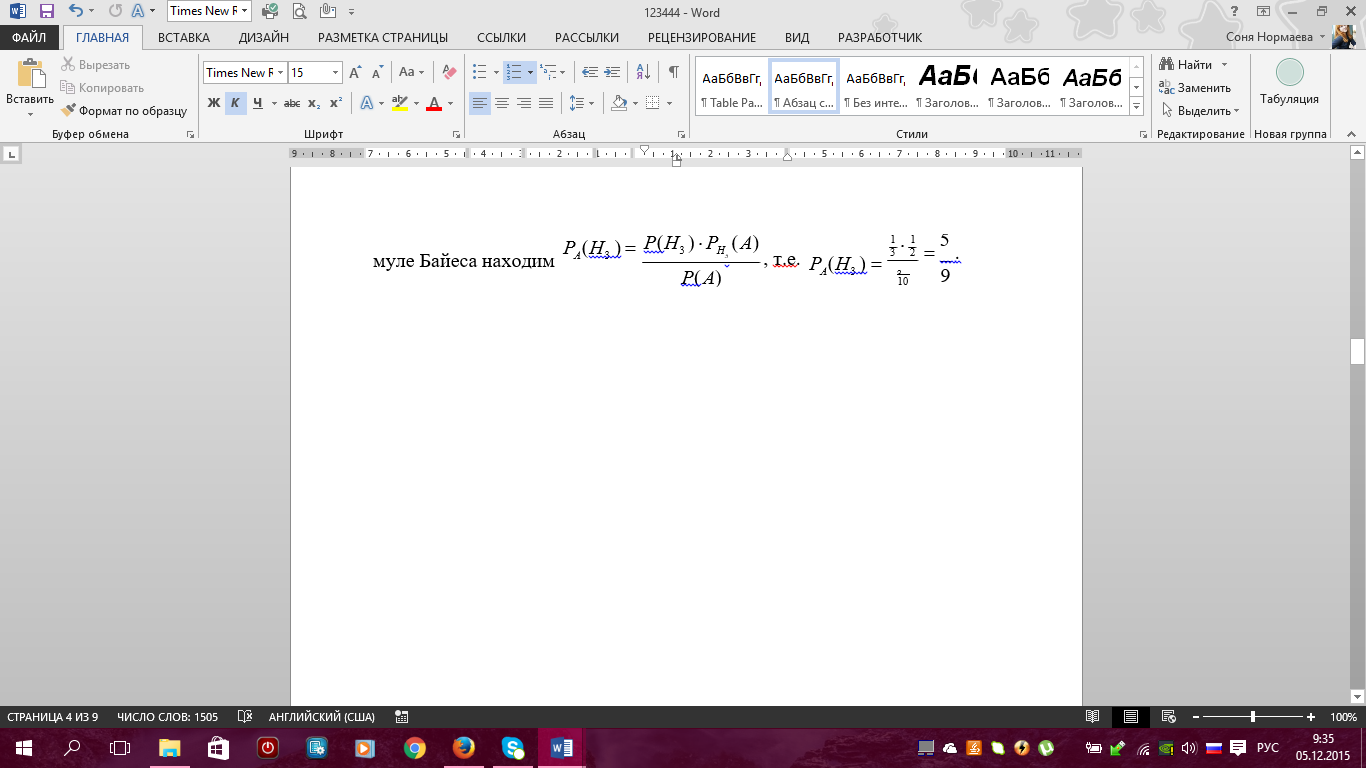
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Геометрическая вероятность
- Геометрическая вероятность на прямой
- Геометрическая вероятность на плоскости
- Геометрическая вероятность в пространстве
- Примеры
Понятие геометрической вероятности было сформулировано в §37 данного справочника. В этом параграфе мы рассмотрим различные задачи, при решении которых используется геометрическая вероятность.
п.1. Геометрическая вероятность на прямой
В одномерном случае пространству всех событий соответствует длина отрезка Ω ↔ L. Событие A ↔ lA – попадание в отрезок lA ≤ L.
Тогда вероятность события A $$ mathrm{ P(A)=frac{l_A}{L} } $$ Говорят, что мерой множеств событий в одномерном случае является длина.
Например:
Оптический кабель длиной 1 м случайно разрезают ножницами. Какова вероятность того, что длина обрезка составляет не меньше 80 см? 
Чтобы получить обрезок не менее 80 см, нужно попасть ножницами в отрезок 20 см справа или слева куска кабеля. Вероятности попадания (mathrm{P_{text{справа}}=frac{l_A}{L}, P_{text{слева}}=frac{l_A}{L}}). По правилу суммы, искомая вероятность при L=100 см, lA=20 см $$ mathrm{ P_{text{справа}}+P_{text{слева}}=frac{2l_A}{L}, P=frac{2cdot 20}{100}=0,4 } $$ Ответ: 0,4.
п.2. Геометрическая вероятность на плоскости
В двумерном случае пространству всех событий соответствует площадь некоторой замкнутой области Ω ↔ SΩ.
Событие A ↔ sA – попадание в замкнутую подобласть с площадью sA ≤ SΩ.
Тогда вероятность события A $$ mathrm{ P(A)=frac{s_A}{S_{Omega}} } $$ Говорят, что мерой множеств событий в двумерном случае является площадь.
Например:
Два друга договорились встретиться между 14 и 15 часами. Каждый может прийти в любой момент в течение назначенного часа. Тот, кто пришёл первым, ждёт другого в течение 15 минут, а затем уходит. Чему равна вероятность встречи? 
Пусть 0≤x≤60 (мин) и 0≤y≤60 (мин) – моменты прихода первого и второго друга соответственно. Тогда пространство событий – квадрат 60х60.
Область ожидания: |x–y|≤15. Раскроем модуль: –15≤x–y≤15. Получаем систему: (left{ begin{array}{ l} mathrm{yleq x+15} &\ mathrm{ygeq x-15} & end{array}right. ). На графике – это зелёная полоса. Событие A – встреча состоялась – соответствует площади зеленой полосы. Получаем: begin{gather*} mathrm{ S_{Omega}=60cdot 60=3600, s_A=3600-2S_{Delta}=3600-2cdot frac{1}{2}cdot 45^2=1575 }\ mathrm{ P(A)=frac{s_A}{S_{Omega}}=frac{1575}{3600}=frac{7}{16}=0,4375 } end{gather*} Ответ: 0,4375.
п.3. Геометрическая вероятность в пространстве
В трёхмерном случае пространству всех событий соответствует объём некоторой замкнутой области Ω ↔ VΩ.
Событие A ↔ vA – попадание в замкнутую подобласть с объёмом vA ≤ VΩ.
Тогда вероятность события A $$ mathrm{ P(A)=frac{v_A}{V_{Omega}} } $$ Говорят, что мерой множеств событий в трёхмерном случае является объём.
Например:
Телескоп находится на космической станции. В каждый момент времени он случайно направлен в одну из сторон и наблюдает часть неба. Пусть телескоп способен регистрировать все объекты в радиусе 10000 км. Какова вероятность, что он заметит астероид радиусом 100 км, залетевший в область регистрации? 
Пространству всех событий соответствует сфера объемом: $$ mathrm{ V_{Omega}=frac{4}{3}pi R^3, R=10000 text{км} } $$ Событие A – астероид замечен – соответствует объему астероида: $$ mathrm{ v_{A}=frac{4}{3}pi R^3, R=100 text{км} } $$ Вероятность того, что астероид будет замечен: $$ mathrm{ P(A)=frac{v_{A}}{V_{Omega}}=frac{frac{4}{3}pi R^3}{frac{4}{3}pi R^3}=left(frac{r}{R}right)^3, P(A)=left(frac{100}{10000}right)^3=10^{-6}=0,000001 } $$ Ответ: 0,000001.
п.4. Примеры
Пример 1. Для игры в «Дартс» используется круглая мишень радиусом 40 см. Центральный круг – «десятка» – имеет радиус 4 см. Если игрок всегда попадает в мишень в любую точку с одинаковой вероятностью, какова вероятность попасть в «десятку»?
Мерой для этой задачи является площадь.
Пространство всех событий – круг радиусом R = 40 см. Его площадь (mathrm{ S_{Omega;}=pi R^2}).
Событие A – попадание в «десятку» – круг радиусом r = 4 см. Его площадь (mathrm{ s_{A}=pi r^2}).
Вероятность попадания: $$ mathrm{ P(A)=frac{s_{A}}{S_{Omega}}=frac{pi r^2}{pi R^2}=left(frac{r}{R}right)^2, P(A)=left(frac{4}{40}right)^2=0,01 } $$ Ответ: 0,01.
Пример 2. В правильный треугольник вписан полукруг. В треугольник случайно ставятся точки. Какова вероятность, что точка попадет в полукруг?
Мерой в данной задаче является площадь.
Пусть сторона треугольника a. Тогда пространство всех событий – треугольник площадью (mathrm{ S_{Omega}=frac{sqrt{3}}{4}a^2}).
Найдем радиус вписанного полукруга.
ΔCOB ~ ΔOEB – по двум углам. $$ mathrm{ frac{CO}{OE}=frac{CB}{OB}Rightarrowfrac{acdot sin60^{circ}}{r}=frac{a}{a/2}Rightarrow r=frac{a}{2}cdot sin60^{circ}=frac{sqrt{3}}{4}a } $$ Площадь вписанного полукруга: (mathrm{ s_{A}=frac{pi r^2}{2}=frac{pi}{2}left(frac{sqrt{3}}{4}aright)^2=frac{3pi}{32}a^2}).
Вероятность попасть в полукруг: $$ mathrm{ P(A)=frac{s_{A}}{S_{Omega}}=frac{frac{3pi}{32}a^2}{frac{sqrt{3}}{4}a^2}=frac{sqrt{3}}{8}pi approx 0,68 } $$ Ответ: (mathrm{ frac{sqrt{3}}{8}pi approx 0,68. })
Пример 3. На отрезке [0; 1] случайным образом выбирается точка. Найдите вероятность того, что её координата x удовлетворяет условиям:
1) x2 > 0,64
2) (left{ begin{array}{ l} mathrm{0,3x^2leq 0,027} &\ mathrm{2x^2geq 0,08} & end{array}right. )
1) (mathrm{x^2geq 0,64Rightarrow (x^2-0,64)geq 0Rightarrow (x-0,8)(x+0,8)geq 0Rightarrow} left{ begin{array}{ l} mathrm{xleq -0,8} &\ mathrm{xgeq 0,8} & end{array}right. )
Учитывая x ∈ [0; 1], получаем: $$ left{ begin{array}{ l} mathrm{0leq xleq 1} &\ left[ begin{array}{ l} mathrm{xleq -0,8Rightarrow 0,8leq xleq 1} &\ mathrm{xgeq 0,8} & end{array}right.& end{array}right. $$ Мерой в данной задаче является длина: LΩ = 1, lA = 1 – 0,8 = 0,2
Вероятность выбора точки при данных условиях: ( mathrm{P(A)=frac{0,2}{1}=0,2} )
begin{gather*} 2) left{ begin{array}{ l} mathrm{0,3x^2leq 0,027} &\ mathrm{2x^2geq 0,08} & end{array}right. Rightarrow left{ begin{array}{ l} mathrm{x^2leq 0,009} &\ mathrm{x^2geq 0,004} & end{array}right. Rightarrow left{ begin{array}{ l} mathrm{x^2-0,009leq 0} &\ mathrm{x^2-0,004geq 0} & end{array}right. Rightarrow left{ begin{array}{ l} mathrm{(x-0,3)(x+0,3)leq 0} &\ mathrm{(x-0,2)(x+0,2)geq 0} & end{array}right. Rightarrow \ Rightarrow left{ begin{array}{ l} mathrm{-0,3leq xleq 0,3} &\ left[ begin{array}{ l} mathrm{xleq -0,2} &\ mathrm{xgeq 0,2} & end{array}right.& end{array}right. Rightarrow left[ begin{array}{ l} mathrm{-0,3leq xleq -0,2} &\ mathrm{0,2leq xleq 0,3} & end{array}right. end{gather*} Учитывая x ∈ [0; 1], получаем: $$ left{ begin{array}{ l} mathrm{0leq xleq 1} &\ left[ begin{array}{ l} mathrm{-0,3leq xleq -0,2} &\ mathrm{0,2leq xleq 0,3} & end{array}right.& end{array}right. Rightarrow 0,2 leq x leq 0,3 $$ Мерой в данной задаче является длина: LΩ = 1, lA = 0,3 – 0,2 = 0,1
Вероятность выбора точки при данных условиях: (mathrm{P(A)=frac{0,1}{1}=0,1})
Ответ: 1) 0,2; 2) 0,1.
Пример 4. В сито, наполненное до краёв зерном, уронили жемчужину. Сито представляет собой цилиндр радиусом 20 см и высотой 12 см.
1) Какова вероятность случайно зачерпнуть горсть зерна вместе с жемчужиной, если объём горсти 0,1 л?
2) Если после неудачной попытки, высыпать зерно из горсти обратно в сито, перемешать, и снова зачерпнуть горсть, изменится ли вероятность?
3) Если после неудачной попытки, высыпать зерно из горсти в сторону и зачерпнуть следующую горсть, изменится ли вероятность?
4) Сколько «неудачных» горстей нужно отсыпать в сторону, чтобы вероятность удачи для следующей попытки превысила 1/3?
1) Мерой для этой задачи является объём.
Пространство всех событий – все возможные точки, где может оказаться жемчужина – это цилиндрическое сито, объемом
VΩ = πR2h, R = 20 см = 2 дм, h = 12 см = 1,2 дм
VΩ = π · 22 · 1,2 = 4,8 π дм3 = 4,8 π л
Событие A – зачерпнуть жемчужину в горсти объемом vA = 0,1 л
Вероятность: $$ mathrm{ P(A)=frac{v_{A}}{V_{Omega}}, P(A)=frac{0,1}{4,8pi} approx 0,0066 } $$ 2) Если высыпать зерно обратно из горсти и перемешать, то пространство всех событий останется тем же, VΩ = 4,8π л. Вероятность не изменится.
3) Если высыпать зерно в сторону, пространство всех событий уменьшится:
V‘Ω = VΩ – vA = (4,8π – 0,1) л
Вероятность увеличится: $$ mathrm{ P(A)=frac{v_{A}}{V_{Omega}^{‘}}, P(A)=frac{0,1}{4,8pi -0,1} approx 0,0071 } $$
4) После того, как мы отсыпаем N горстей, пространство всех событий $$ mathrm{ V_{Omega}^{”} = V_{Omega}-Nv_{A}=(4,8pi-0,1N) text{л} } $$ По условию: $$ mathrm{ P(A)frac{0,1}{4,8pi -0,1N}geq frac13 } $$ Получаем: (mathrm{4,8pi -0,1Nlt 0,3Rightarrow Ngt frac{4,8pi-0,3}{0,1}=147,8})
N = 148.
Ответ: 1) 0,0066; 2) нет; 3) увеличится, 0,0071; 4) 148.
Пример 5. Загадываются два действительных числа от 0 до 4.
1) Какова вероятность, что их сумма больше 3?
2) Какова вероятность, что их разность меньше 1?
По условию 0 ≤ x ≤ 4, 0 ≤ y ≤ 4
Мерой для этой задачи является площадь.
Пространство всех событий: квадрат 4х4, SΩ = 42 = 16.
Ответ: (mathrm{ 1) frac{23}{32}; 2) frac{7}{16}. })
Полезная страница? Сохрани или расскажи друзьям
Пусть случайное испытание можно представить себе как бросание точки наудачу в некоторую геометрическую область G (на прямой, плоскости или пространстве). Элементарные исходы – это отдельные точки G, любое событие A – это подмножество этой области, пространства элементарных исходов G.
Если для простоты считать, что все точки G «равноправны» (выбор точек равномерен внутри области), то вероятность попадания точки в некоторое подмножество пропорционально его мере (длине, площади, объему) и не зависит от его расположения и формы.
Геометрическая вероятность события А определяется отношением:
$$
P(A)=frac{m(A)}{m(G)},
$$
где $m(G)$, $m(A)$ – геометрические меры (длины, площади или объемы) всего пространства элементарных исходов $G$ и события $А$ соответственно.
Чаще всего, в одномерном случае речь будет идти о длинах отрезков, в двумерном – о площадях фигур, в трехмерном – об объемах тел.
При этом, некоторые задачи сразу имеют геометрическую интерпретацию (первый пример), а другие выглядят как задачи “про жизнь”, самая распространенная из них – задача о встрече (второй пример).
Основная сложность при решении задач такого типа – построить математическую модель эксперимента, нужным образом выбрать пространство элементарных исходов, обозначить событие, выразить его математически как некоторую область. К сожалению, единого рецепта решения подобых заданий нет, нужно “набить” руку на разных задачах (см. примеры тут, например).
Примеры решений на геометрическую вероятность
Пример. На плоскость, разграфленную параллельными полосами шириной $2d$, расстояние между осевыми линиями которых равно $2D$, наудачу брошен круг радиуса $r$ ($r+dlt D$). Найти вероятность того, что круг пересечет некоторую полосу.
Решение. В качестве элементарного исхода этого испытания будем считать расстояние $x$ от центра круга до осевой линии ближайшей к кругу полосы (ее обозначим за 0). Тогда все пространство элементарных исходов – это отрезок, равный половине расстояния между осями полос $G={x: 0le x le D}$. Его мера – это длина отрезка, то есть $m(G)=D$.
Рассмотрим теперь случаи, благоприятствующие событию $A$ = (Круг пересечет полосу), и найдем меру соответствующей области точек. На чертеже выше покажем различные варианты выпадения круга.
Пересечение круга с полосой очевидно произойдет в том случае, если его центр попадет в полосу (точнее, ее половину), т.е. координата центра круга удовлетворяет неравенству $0 le x le d$, длина этого отрезка $d$.
Также круг пересечет полосу, если его центр будет находится от края полосы на расстоянии меньшем чем радиус (если равен радиусу – круг коснется полосы, если больше – то отстоит от полосы), т.е. когда $d le x le d+r$ (длина этого отрезка $r$).
Тогда вероятность события $A$ по геометрическому определению вероятности:
$$
P(A)=frac{d+r}{D}.
$$
Пример. Два человека договорились встретиться в определенном месте от 17 до 18 часов. При этом каждый обязался после прихода на место встречи ожидать другого 30 минут. Какова вероятность встречи этих людей, если каждый из них равновозможно придет в течение указанного интервала времени?
Решение. Обозначим моменты прихода первого и второго человека за $x$ и $y$. Так как они приходят в промежуток длительности 60 минут (от 17 до 18 часов), то справедливы следующие условия: $0 le x le 60$ и $0 le y le 60$.
Рассмотрим прямоугольную систему координат $xOy$. В этой системе координат всем возможным значениям времени прихода людей соответствуют точки квадрата со стороной 60.
Лица встретятся, если один человек придет раньше, чем уйдет другой, то есть если $y lt x+30$, когда $y gt x$ (второй пришел позже первого, но не позже чем через 30 минут от него) и $x lt y+30$, когда $y lt x$ (первый пришел позже второго, не но позже чем через 30 минут).
Более компактно запишем условия
$$
x lt y lt x+30 quad text{ или } quad x-30 lt y lt x. quad (*)
$$
Построим прямые $y=x$, $y=x-30$, $y=x+30$ и закрасим область, лежащую внутри квадрата, точки которой удовлетворяют условиям (*). Точки этой фигуры (серый шестиугольник в центре) являются благоприятствующими событию $A$ =(люди встретятся).
Тогда искомая вероятность встречи по геометрическому определению вероятности равна отношению площади этой фигуры к площади квадрата:
$$
P=frac{60^2-1/2cdot 30^2-1/2cdot 30^2}{60^2}=frac{3600-900}{3600}=frac{3}{4}=0,75.
$$
Больше примеров на геометрическую вероятность
Геометрические вероятности:
Область применения классического определения вероятности – испытания с конечным числом равновозможных исходов. Существенным является условие равновозможности. От конечности числа исходов опыта можно отказаться и определять вероятности не с помощью числа исходов, 27 а с помощью отношения длин, площадей и т.д., но при сохранении условия равновозможности.
Геометрическое определение вероятности
Пусть область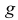 
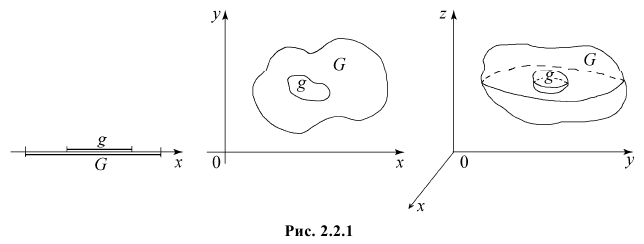
Если равновозможно попадание точки в любую точку области G, то вероятность попасть в область 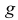равна отношению меры области 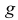к мере области G:
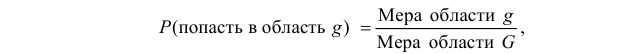
где «мера» – означает: 1) длину, если область G часть прямой или кривой линии; 2) площадь, если G часть плоскости; 3) объем, если G часть пространства, и т.д. в зависимости от характера области G.
Пример:
Две радиостанции течение часа независимо друг от друга должны передать сообщения длительностью 10 мин. и 20 мин. соответственно. Какова вероятность того, что сообщения не перекроются по времени.
Решение. Пусть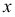 
– момент начала сообщения первой радиостанции, а 
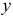– момент начала второго сообщения. Для того чтобы сообщения уложились в отведенный час, должны выполняться условия: 
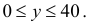Сообщения не перекроются во времени, если выполнятся условия: 
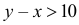и у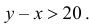 
Этим условиям удовлетворяют точки заштрихованных областей, изображенных на рис. 2.2.2.
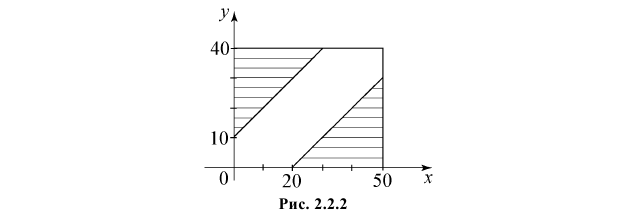
Так как все положения точки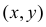 
в прямоугольнике 
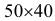равновозможны, то искомая вероятность равна отношению заштрихованной площади, которая равна 
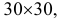к площади прямоугольника. Поэтому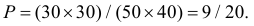 
Ответ.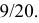 
Пример:
В треугольник с вершинами A(0;0), B(4;0) и C(0;2) наугад брошена точка, причем все положения точки в этом треугольнике равновозможны. Найдите вероятность того, что координаты точки X и Y будут удовлетворять неравенству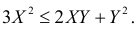 
Решение. Полагая в квадратном трехчлене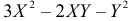 
переменной величиной X, а Y коэффициентом, найдем корни трехчлена X=Y и 
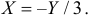Тогда неравенство 
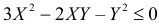можно записать в виде 
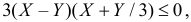или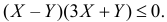 
Последнее неравенство равносильно совокупности неравенств:
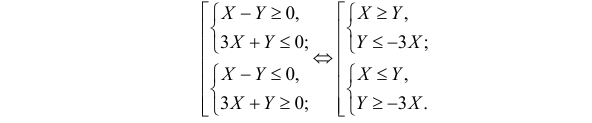
Точки плоскости, координаты которых удовлетворяют этой совокупности систем неравенств, на рис. 2.2.3 выделены штриховкой. Часть из них содержится в треугольнике ABC.
Так как по условию все положения точки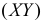 
в треугольнике ABC равновозможны, то по геометрическому определению вероятности искомая вероятность равна отношению площади заштрихованного треугольника AEC к площади треугольника ABC.
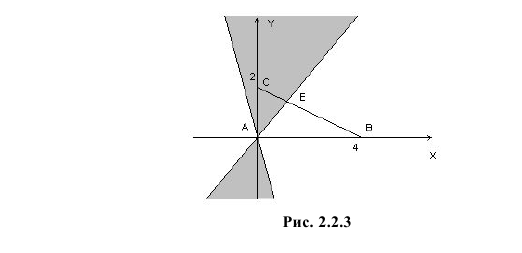
Площадь треугольника ABC равна половине произведения AB на AC, т.е. равна 4. Линия BC имеет уравнение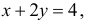 
а линия AE определяется уравнением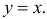 
Их точка пересечения имеет координаты E(4/3;4/3). Абсцисса точки E равна высоте треугольника AEC, опущенной на сторону AC. Поэтому площадь треугольника AEC равна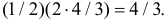 
Поэтому искомая вероятность равна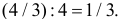 
Ответ. 1/3.
Пример:
Координаты случайной точки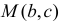 
в треугольнике, ограниченном осями координат и прямой 
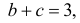служат коэффициентами квадратного уравнения 
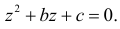Полагая все положения случайной точки в указанном треугольнике равновозможными, найти вероятность того, что уравнение имеет два действительных корня.
Решение. Пусть А – интересующее нас событие. Уравнение имеет действительные корни, если его дискриминант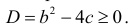 
Это неравенство будет выполнено, если случайная точка М попадет в треугольнике ниже кривой 
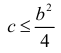(на рис. 2.2.4 заштрихованная область). Точка пересечения линий 
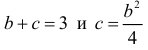имеет координаты (2;1). Поэтому площадь заштрихованной фигуры на рис. 2.2.4 равна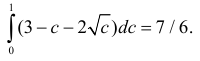 
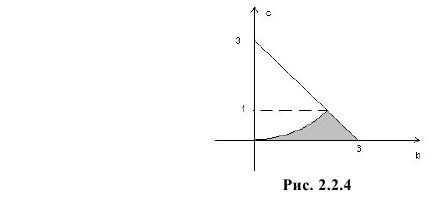
Так как площадь всего треугольника равна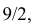 
то по геометрическому определению вероятности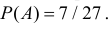 
Ответ.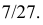 
Пример:
Плоскость разграфлена параллельными прямыми, отстоящими друг от друга на расстояние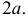 
Острый угол ромба равен 60°, а наибольшая диагональ равна 
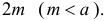Ромб наугад бросают на плоскость. Какова вероятность того, что ромб пересечет одну из прямых?
Решение. Бросание ромба «наугад» подразумевает, что центр ромба с равными шансами может оказаться на любом расстоянии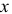 
(в пределах от 0 до 
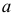) от ближайшей прямой, а значения угла 
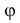между наибольшей диагональю и ближайшей прямой равновозможны в пределах от 
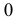до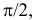 
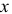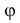при этом и независимы. Заметим, что расстояние от центра ромба до его стороны равно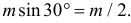 
Если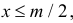 
то ромб несомненно пересечет ближайшую прямую. Если же 
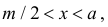то для пересечения ближайшей прямой необходимо и достаточно, чтобы 
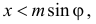т.е. проекция половины наибольшей диагонали на перпендикуляр к прямой должна быть больше расстояния от центра ромба до прямой (см. рис. 2.2.5).
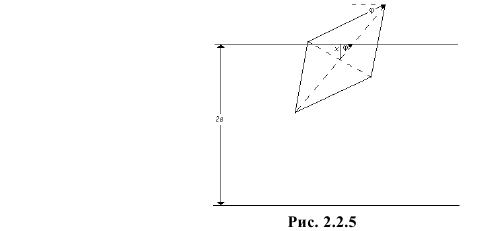
Названные условия выполняются в заштрихованной области на рис. 2.2.6. Графики функци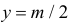й 
и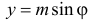 
пересекаются в точках, в которых 
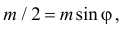т.е. пр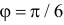и 
и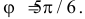 
Поэтому заштрихованная площадь равна
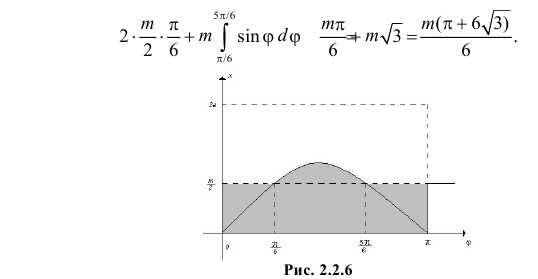
Любое положение ромба относительно ближайшей прямой можно охарактеризовать точкой в прямоугольнике со сторонам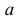и 
и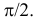 
Поскольку все положения ромба относительно ближайшей прямой равновозможны, то по геометрическому определению вероятности искомая вероятность равна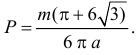 
Ответ.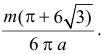 
Пример:
Наудачу взяты два положительных числах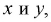 
причем 
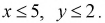Найти вероятность того, что 
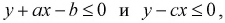если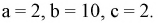 
Подставляя значения коэффициентов в неравенства, получаем
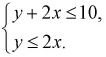
Строим на рис. 1.8 оси координат и область, которая определяет пространство элементарных событий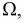 
она задается неравенствами 
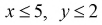и отображается на рисунке 1.8 прямоугольником.
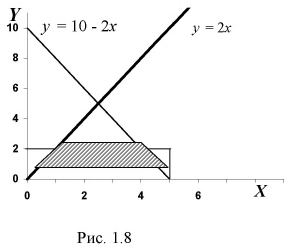
Площадь прямоугольника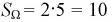 
[условных единиц]. Область благоприятствующих исходов определяется неравенствами 
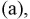поэтому строим на рисунке прямые, которые задаются из неравенств 
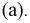Заштрихованная на рисунке 1.8 область описывает благоприятствующие исходы (с учетом всех возможных значений) и является трапецией, площадь которой 
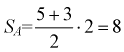[условных единиц]. Тогда вероятность события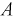 
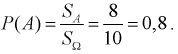
Пример:
Найти вероятность того, что на экране радиолокатора отметка от цели появится в кружке радиусом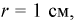 
на азимуте 
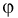ноль градусов, на расстоянии 
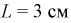от центра экрана, если радиус экрана равен 30 см.
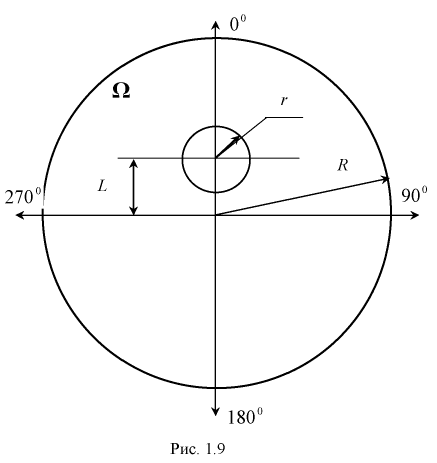
Экран радиолокатора, рис. 1.9, представляет собой электронно-лучевую трубку с радиальной разверткой, в которой от центра до края экрана движется электронный луч и после достижения края движение луча опять начинается от центра к краю, но с некоторым смещением по азимуту. Это перемещение луча от центра экрана соответствует началу излучения радиоимпульса антенного радиолокатора, который укреплен на боковой стенке кабины с передающим устройством, а кабина, в свою очередь, вращается вокруг вертикальной оси, что соответствует смещению луча на экране по азимуту. И когда радиоимпульс отражается от цели, на экране радиолокатора вспыхивает яркая точка. По положению этой точки на экране легко определить расстояние до цели и ее азимут.
Зная геометрическое определение вероятности, можно сразу сказать, что вероятность появления отметки от цели в кружке радиусом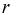 
зависит только от отношения площадей и не зависит ни от формы области благоприятствующих исходов, ни от места ее расположения. Поэтому в этой задаче есть избыточная информация – расстояние 
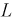и азимут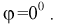 
Определяем область благоприятствующих исходов, которой является кружок радиусом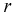 
и площадью – 
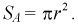Пространство элементарных событий 
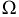– это область экрана, его площадь 
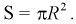Тогда
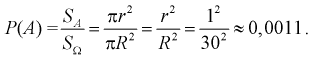
- Теоремы сложения и умножения вероятностей
- Формула полной вероятности
- Повторные независимые испытания
- Простейший (пуассоновский) поток событий
- Комбинаторика – правила, формулы и примеры
- Классическое определение вероятности
- Элементы теории ошибок
- Методы математической статистики
Геометрическая вероятность
4 июля 2011
Классическое определение вероятности связано с понятием элементарного события. Рассматривается некий набор Ω равновероятных событий Ai, которые в совокупности дают достоверное событие. И тогда все хорошо: всякое событие разбивается на элементарные, после чего считается его вероятность.
Однако, далеко не всегда исходный набор Ω (т.е. пространство всех элементарных событий) является конечным. Например, в качестве Ω можно взять ограниченное множество точек на плоскости или отрезок на прямой.
В качестве события A можно рассмотреть любую подобласть области Ω. Например, фигуру внутри исходной фигуры на плоскости или отрезок, лежащий внутри исходного отрезка на прямой.
Заметим, что элементарным событием на таком множестве может быть только точка. В самом деле, если множество содержит более одной точки, его можно разбить на два непустых подмножества. Следовательно, такое множество уже неэлементарно.
Теперь определим вероятность. Тут тоже все легко: вероятность «попадания» в каждую конкретную точку равна нулю. Иначе получим бесконечную сумму одинаковых положительных слагаемых (ведь элементарные события равновероятны), которые в сумме по-любому больше P(Ω) = 1.
Итак, элементарные события для бесконечных областей Ω — это отдельные точки, причем вероятность «попадания» в любую из них равна нулю. Но как искать вероятность неэлементарного события, которое, подобно Ω, содержит бесконечное множество точек? Вот мы и пришли к определению геометрической вероятности.
Геометрическая вероятность события A, являющегося подмножеством множества Ω точек на прямой или плоскости — это отношение площади фигуры A к площади всего множества Ω:
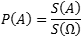
Задача. Мишень имеет форму окружности радиуса 4. Какова вероятность попадания в ее правую половину, если попадание в любую точку мишени равновероятно? При этом промахи мимо мишени исключены.
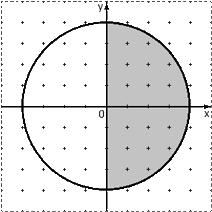
Взглянем на картинку: нас устроит любая точка из правого полукруга. Очевидно, площадь S(A) этого полукруга составляет ровно половину площади всего круга, поэтому имеем:
Как видите, ничего сложного в геометрической вероятности нет. Однако даже в Москве многие репетиторы по высшей математике стараются обойти эту тему стороной, поскольку считают ее необязательной. Результат — непонимание материала и, как следствие, проблемы на экзамене по теории вероятностей.
Чтобы наглядно представить себе, что такое геометрическая вероятность, возьмите лист бумаги и начертите произвольную фигуру. Треугольник, квадрат или окружность — что угодно. Затем возьмите острый, хорошо заточенный карандаш и ткните им в любую точку фигуры. Повторите этот нехитрый процесс несколько раз. Если исключить попадания за пределами фигуры, то получится вот что:
- Вероятность попадания в фигуру равна P(Ω) = 1. Это вполне логично, поскольку вся наша фигура — это и есть пространство элементарных событий Ω;
- Если некоторую точку (элементарное событие) отметить заранее, то вероятность попадания именно в нее равна нулю. Даже если специально «целиться», точного попадания не будет. Ошибка составит тысячные доли миллиметра, но не ноль;
- Теперь возьмем две точки. Вероятность попадания в любую из них все равно ноль. Аналогично, если взять 3 точки. Или пять — без разницы.
Этот опыт показывает, что конечная сумма нулевых слагаемых всегда равна нулю. Но что происходит, когда слагаемых становится бесконечно много? Здесь ситуация не так однозначна, и возможны три варианта:
- Сумма равна нулю, как и для конечного набора точек. Если в нашем опыте отмечать точки до бесконечности, вероятность попадания в их объединение все равно нулевая;
- Сумма равна некоторому положительному числу — этот случай принципиально отличается от первого. Здесь и возникает геометрическая вероятность;
- Сумма равна бесконечности — бывает и такое, но сейчас нас это не интересует.
Почему так происходит? Механизм возникновения положительных чисел и бесконечностей связан с понятием счетности множества. Кроме того, надо понимать, что такое мера Лебега. Впрочем, эти знания действительно нужны вам, только если вы учитесь на математика.
Смотрите также:
- Формула полной вероятности
- Схема Бернулли. Примеры решения задач
- Умножение и деление дробей
- Не пишите единицы измерения в задаче B12
- Изюм и виноград (смеси и сплавы)
- ЕГЭ 2022, задание 6. Касательная к графику функции
