Как найти гидравлический диаметр трубы – Сайт, где вы сможете решить свои вопросы

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 17 сентября 2018 года; проверки требуют 10 правок.

Гидравлический (эквивалентный) диаметр — мера эффективности русла в пропускании потока жидкости, равняется такому диаметру трубы, которая будет создавать эквивалентное сопротивление потоку, что и русло с площадью сечения потока $A$ и смоченным периметром $P$ . Чем меньше гидравлический диаметр, тем бо́льшее сопротивление потоку оказывает русло (при одинаковой площади поперечного сечения потока).

Нахождение[править | править код]

Определяется по формуле:

${displaystyle D_{Gamma }={frac {4A}{P}}}$

где A — площадь поперечного сечения потока жидкости и P — смоченный периметр (см. ниже) поперечного сечения потока.

1) Для трубы круглого поперечного сечения, полностью (без пустот) заполненной жидкостью, эта формула принимает вид:

${displaystyle D_{Gamma }={frac {4{frac {pi D^{2}}{4}}}{pi D}}=D}$

То есть, для круглого сечения гидравлический диаметр равен геометрическому диаметру.

2) Для кольца гидравлический диаметр равен:

${displaystyle D_{Gamma }={frac {4cdot 0{,}25pi (D^{2}-d^{2})}{pi (D+d)}}=D-d}$

где $D$ — наружный диаметр кольца, $d$ — внутренний диаметр кольца.

3) Для каналов прямоугольного сечения гидравлический диаметр определяют по формуле:

${displaystyle D_{Gamma }={frac {2ab}{(a+b)}}}$

где a — уровень заполнения канала и b — ширина канала.

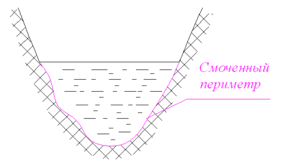
Смоченный периметр[править | править код]

Пояснение понятия «смоченный периметр».

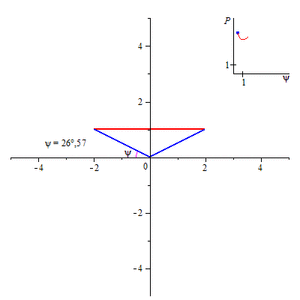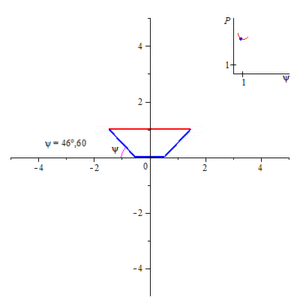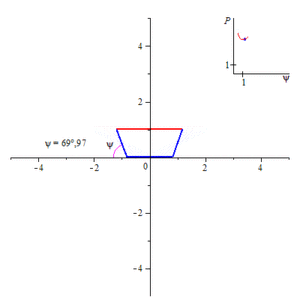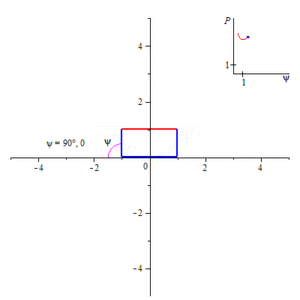
Изменение смоченного периметра (синий) канала в форме равнобедренной трапеции в зависимости от угла откоса ѱ.

Смоченный периметр — длина части границы канала, касающейся жидкости.

Понятие смоченного периметра имеет большое значение при проектировании каналов. Расход воды равен произведению площади поперечного сечения канала на скорость течения. Скорость же течения, по формуле Шези, при постоянной площади сечения канала и гидравлическом уклоне, прямо пропорциональна квадратному корню из гидравлического радиуса, то есть обратно пропорциональна квадратному корню из смоченного периметра. Поэтому при заданной площади поперечного сечения стараются минимизировать смоченный периметр, чтобы увеличить скорость течения, а, следовательно, и расход воды. Поперечное сечение канала обычно представляет собой равнобедренную трапецию, нижнее основание которой меньше верхнего. Смоченный периметр такого канала равен сумме нижнего основания и боковых сторон этой трапеции. Считая площадь такой трапеции заданной, находят минимум смоченного периметра в зависимости либо от угла откоса (угол, смежный углу при нижнем основании) при постоянной глубине (то есть высоте трапеции), либо от глубины при постоянном угле откоса. В первом случае наименьший смоченный периметр будет при угле откоса, равном 60°^[1].

Гидравлический радиус[править | править код]

Существует также понятие «гидравлический радиус». Несмотря на своё название, гидравлический диаметр не равен двум гидравлическим радиусам.

Гидравлический радиус вычисляется по формуле:

${displaystyle R_{h}={frac {A}{P}}}$ ,

где:

A — площадь поперечного сечения (м²)
P — смоченный периметр (м)

См. также[править | править код]

Формула Дарси-Вейсбаха

Примечания[править | править код]

↑ Попов Г.Н. Как применялась и применяется тригонометрия на практике. — 2-е изд. — Государственное учебно-педагогическое издательство, 1931. — С. 73—82. — 88 с. — (Рабочая библиотека по математике для школ II ступени). Архивная копия от 26 июня 2013 на Wayback Machine Архивированная копия. Дата обращения: 17 ноября 2016. Архивировано 26 июня 2013 года.

Литература[править | править код]

Ю. И. Дытнерский. Процессы и аппараты химической технологии. Часть 1. Теоретические основы процессов химической технологии. — М.: Химия, 1995. — 400 с. — 6500 экз. — ISBN 5-7245-1006-5.

Источник

Гидравлический диаметр (эквивалентный диаметр) —: это отношение учетверенной площади живого сечения потока к смоченному периметру.

Общие сведения

Гидравлический диаметр (эквивалентный диаметр) обычно обозначается — d_г, d_h,D_г. Широко применяется при гидравлических и аэродинамических расчетах различных систем, где формой сечения каналов не является окружность. Гидравлический (эквивалентный) диаметр может служит мерой эффективности системы в пропускании потока жидкости или газа.

Формулы расчет гидравлического диаметра (эквивалентного диаметра). Калькуляторы гидравлического диаметра (эквивалентного диаметра).

Классическая формула гидравлического диаметра (эквивалентного диаметра)

D_г=(4*S)/P,

где S— площадь поперечного сечения потока жидкости или газа; P — смоченный периметр поперечного сечения потока.

Гидравлический диаметр (эквивалентный диаметр) круглого сечения (например: воздуховоды, трубы, дымоходы и т.п)

Совпадает с геометрическим диметром, т.е. D_г=D_вн, где D_вн — внутренний диаметр круглого сечения воздуховода, трубы и т.п.

Гидравлический диаметр (эквивалентный диаметр) сечения в виде кольца (например: труба в трубе и т.п.)

D_г=2(r₂-r₃),

где r₂— внутренний радиус внешней трубы, воздуховода и т.п.; r₃ — внешний радиус внутренний трубы, воздуховода и т.п.

Гидравлический диаметр (эквивалентный диаметр) прямоугольного сечения (например: трубы квадратного сечения, дымоходы и т.п.)

D_г=2*a*b/(a+b),

где a— первая сторона прямоугольного сечения; b — вторая сторона прямоугольного сечения.

Видеоматериал по теме «Гидравлический диаметр (эквивалентный диаметр)»

Примечание

Смоченный периметр —: длина части границы канала, касающейся жидкости.

Поделиться ссылкой:

Источник

Содержание

Определение гидравлического диаметра

Круг является самой простой формой, поэтому проще всего производить вычисления при работе с круглыми поперечными сечениями. Когда жидкость течет по некруглому каналу, мы переводим поперечное сечение в круглое для удобства расчетов. Этот недавно полученный диаметр круглого поперечного сечения называется гидравлический диаметр. Обозначается как D_h. Следовательно, мы можем получить те же результаты для некруглого воздуховода, что и для круглого воздуховода, используя концепцию гидравлического диаметра.

Уравнение гидравлического диаметра

Гидравлический диаметр можно найти по формуле, приведенной ниже:

Дч = 4А/П

Где,
D_hгидравлический диаметр
A – площадь некруглого поперечного сечения
P – смоченный периметр некруглого поперечного сечения

Гидравлический диаметр зависит от гидравлического радиуса R_h, который можно найти, разделив площадь поперечного сечения A на смоченный периметр P.

Отметим, что D_h= 4R_hЭто соотношение отличается от обычного соотношения между диаметром и радиусом (т.е. D = 2R). Эта разница возникает только при преобразовании некруглых сечений в круглые.

Примечание. Закон сохранения количества движения соблюдается при расчете гидравлического диаметра. Кроме того, гидравлический диаметр отличается от обычного диаметра. D_h то же самое только для круглых каналов.

гидравлический диаметр

Простое представление гидравлического диаметра

Гидравлический диаметр и число Рейнольдса

Число Рейнольдса используется в гидромеханике и теплопередача, чтобы найти тип потока, ламинарный или турбулентный. Гидравлический диаметр используется в формуле для расчета числа Рейнольдса.
Число Рейнольдса – это отношение сил инерции к силам вязкости. Это безразмерное число названо в честь ирландского ученого Осборна Рейнольдса, который популяризировал эту концепцию в 1883 году.

Это число показывает влияние вязкости на контроль скорости течения жидкости. Линейный профиль вязкости развивается при ламинарном течении. При ламинарном течении жидкость течет так, как будто она течет параллельными слоями. Эти слои не пересекаются друг с другом и перемещаются без каких-либо разрывов между ними. Этот тип потока обычно происходит на малых скоростях. При малых скоростях смешивания двух слоев не происходит и жидкость течет слоями, наложенными друг на друга.

Ламинарный поток помогает нам измерять поток высоковязких жидкостей, поскольку этот тип потока дает линейную зависимость между скоростью потока и падение давления. Благоприятный условия ламинарного течения высокая вязкость и низкая скорость. При более высоких скоростях частицы жидкости начинают вести себя по-другому, что приводит к перемешиванию слоев жидкости. Такое перемешивание приводит к возникновению турбулентности, отсюда и название турбулентного течения. Турбулентный поток желателен, когда требуется надлежащее перемешивание жидкости. Одним из таких примеров является смешивание топлива с окислителем в ракетных двигателях. Турбулентность способствует тщательному перемешиванию жидкости.
Число Рейнольдса можно рассчитать из уравнения, приведенного ниже:

Где,
Re – число Рейнольдса
u – средняя скорость (в м / с)
ν – кинематическая вязкость (в м²/ с)
Dh – гидравлический диаметр (в м)

В круглой трубе
Ламинарный поток, Re <2000
Переходный поток, 2000 <Re <4000
Турбулентный поток, Re> 4000

Для плоской тарелки
Ламинарный поток, Re <5,00,000
Турбулентный поток, Re > 5,00,000 XNUMX XNUMX

Гидравлический диаметр круглой трубы | гидравлический диаметр цилиндра

Круглые трубы чаще всего используются для транспортировки жидкости / газа из одного места в другое (даже на большие расстояния). Водопроводы – это реальный пример круглых каналов, которые используются для транспортировки жидкости. Эти трубы могут проходить на большие расстояния, например, от станций фильтрации воды до домов, а также на короткие расстояния, например, от резервуара с грунтовой водой до резервуара для воды на террасе. Гидравлический диаметр круглой трубы определяется следующим образом:

Dh = 4πR²/2πR = 2R

Где,
R – радиус круглого сечения.

Гидравлический диаметр прямоугольного воздуховода

Прямоугольные воздуховоды используются, когда возникает проблема с зазором. Кроме того, прямоугольные воздуховоды просты в изготовлении и снижают потери давления. В кондиционерах используются прямоугольные воздуховоды, чтобы избежать потерь давления. Гидравлический диаметр прямоугольного воздуховода определяется по формуле:

Dh = 4ab/2(a+b) = 2ab/ a+b

Где,

a и b – длины большей и меньшей сторон.

Для квадратного сечения

a = b

Дх = 2а²/2а = а

Где,
а – длина каждой стороны квадрата.

Гидравлический диаметр затрубного пространства

Иногда для увеличения / уменьшения скорости теплопередачи через кольцевую трубу пропускают две жидкости, так что одна жидкость выходит за пределы другой. На скорость теплопередачи влияет действие двух жидкостей. Гидравлический диаметр кольцевого пространства определяется по формуле:

$Dh=\frac{4(\frac{\Pi }{4})(D^{2}-d^{2})}{\Pi (D+d)}=D-d$

Где D и d – диаметры внешнего и внутреннего круга соответственно.

Гидравлический диаметр треугольника

$Dh=\frac{(\frac{\sqrt{3}}{4})l^{2}}{3l}=\frac{l}{4\sqrt{3}}$

Где,
l – длина каждой стороны.

Гидравлический диаметр эллипса

Дх = 4wh(64-16е²)/ш+ч(64-3е⁴)

Где, е = что/ш+ч

Гидравлический диаметр пластинчатого теплообменника | гидравлический диаметр кожухотрубного теплообменника

Теплообменники – это тепловые устройства, используемые для передачи тепла от одной жидкости к другой с целью уменьшения / увеличения температуры жидкости по желанию. Существует множество типов теплообменников, из которых наиболее часто используются пластинчатые и кожухотрубные теплообменники. Жидкости могут проходить через теплообменник двумя способами. В первом типе и горячие, и холодные жидкости нагнетаются в одном и том же направлении, поэтому он называется теплообменником с параллельным потоком. Во втором типе жидкости проходят через трубку в противоположных направлениях, поэтому он называется противоточным теплообменником.

Исходя из этого и спроектированы испаритель и конденсатор. В испарителе температура горячей жидкости остается неизменной, в то время как холодная жидкость становится теплее. В конденсаторе температура холодной жидкости остается прежней, а температура более горячей жидкости снижается.

Скорость передачи в теплообменнике определяется следующим соотношением:

Для горячей жидкости: Q_h = м_h C_ph (T_hi – Т_ho )
Для холодной жидкости: Q_c = м_cC_pc (T_co – Т_ci )

Сохраняя энергию,
Тепло, потерянное горячей жидкостью = тепло, полученное холодной жидкостью.
=> Q_h = Q_cГде,
Q_h означает потерю тепла горячей жидкостью
Q_c обозначает тепло, получаемое холодной жидкостью
T_hi температура горячей жидкости на входе
T_ho температура горячей жидкости на выходе
T_ci температура холодной жидкости на входе
T_co температура холодной жидкости на выходе
m_h масса горячей жидкости (в кг)
m_c масса холодной жидкости (в кг)
C_ph – удельная теплоемкость горячей жидкости (в Дж / К-кг)
C_pc – удельная теплоемкость холодной жидкости (в Дж / К-кг)

В пластинчатых теплообменниках тепло проходит через секцию и разделяет горячую и холодную жидкости. Этот тип теплообменника используется во многих промышленных приложениях. Они используются в Тепловой насос, системы охлаждения масла, система охлаждения двигателя, системы хранения тепла и т. д.
Пластинчатый теплообменник имеет прямоугольное / квадратное поперечное сечение, следовательно, гидравлический диаметр определяется следующим образом:

Дч = 2аб/а+б

Где,
a и b – длина более короткой стороны и более длинной стороны соответственно.

Пластинчатый теплообменник
Изображение кредита: https://commons.wikimedia.org/wiki/File:Plate_frame_1.svg

В оболочке и трубке тип теплообменник, трубы установлены в цилиндрической оболочке. По этим трубкам проходят как горячие, так и холодные жидкости таким образом, что одна жидкость течет вне другой жидкости. За счет этого происходит передача тепла от одной жидкости к другой. Теплообменник кожухового типа широко используется в промышленности, в основном в химических процессах и применениях, где требуется высокое давление.
Оболочка трубы теплообменник имеет кольцевое поперечное сечение, следовательно, гидравлический диаметр определяется выражением

D_h= Dd

Кожухотрубный теплообменник
Изображение кредита: Теплообменник прямотрубный 2-х ходовой

Эквивалентный диаметр и гидравлический диаметр

Эквивалентный диаметр и гидравлический диаметр различаются по значениям. Диаметр круглого воздуховода, который дает то же самое давление потери в прямоугольном канале для равного расхода называются эквивалентным диаметром. Несмотря на то, что круглые воздуховоды имеют наименьшую площадь поверхности для данной потери давления, они не подходят для изготовления. Прямоугольные воздуховоды просты в изготовлении, поэтому они используются в практических случаях. Когда скорость потока и падение давления известно, то для проектирования прямоугольного воздуховода мы используем диаграмму трения, чтобы найти эквивалентный диаметр, а затем требуемые размеры, фиксируя определенные параметры, такие как соотношение сторон или длина любой стороны.

Отношение длины более короткой стороны к более длинной стороне называется соотношением сторон.

АР = а/б

Мы можем найти эквивалентный диаметр по уравнению эквивалентного диаметра Хюбшера. Это показано ниже –
De = 1.30 (аб)^0.625/(а+б)^0.25

Где,

a и b – длина более короткой стороны и длинной стороны соответственно.

Недавние исследования пришли к выводу, что эквивалентный диаметр, полученный из эмпирических соотношений, не является надежным при расчете потерь давления в трубах. Следовательно, мы используем гидравлический диаметр во всех случаях.

В чем разница между гидравлическим диаметром, эквивалентным диаметром и характеристической длиной в гидромеханике и теплопередаче?

Гидравлический диаметр, как обсуждалось ранее, представляет собой новый диаметр, полученный из некруглого воздуховода, так что характеристики потока остаются такими же. Гидравлический диаметр используется для расчета числа Рейнольдса, которое помогает нам понять, является ли поток ламинарным, переходным или турбулентным.

Диаметр круглого воздуховода, который дает то же самое давление потери в прямоугольном канале для равного расхода называются эквивалентным диаметром.

Потеря давления в трубе определяется уравнением Дарси-Вейсбаха:

$\Delta p=\frac{\rho flv^{2}}{2D}$

Где,

ρ – плотность жидкости (кг / м ^ 3)
D – гидравлический диаметр трубы (в м)
l – длина трубы (в м)
v – средняя скорость потока (в м / с). Характеристическая длина – это, по сути, объем системы, деленный на ее площадь поверхности.
В некоторых случаях он может быть равен гидравлическому диаметру.

Математически,

L_c V =_{поверхность}/A_{поверхность}

Для квадратного воздуховода
L_c = a

Для прямоугольного воздуховода

Lc = 2ab/a+b

В теплопередаче характеристическая длина используется для расчета числа Нуссельта. Отношение конвективной теплопередачи к кондуктивной теплопередаче называется числом Нуссельта. Он показывает, какой тип теплопередачи преобладает.
Число Нуссельта, Nu определяется как

Nu = hLc/k

где,
h – конвективное тепловое сопротивление
L – характерная длина
k это теплопроводность

Число Нуссельта, равное 1, представляет теплопередача при чистой теплопроводности по мере увеличения числа Нуссельта теплопередача за счет конвекции продолжает увеличиваться. При значении числа Нуссельта, приближающемся к 100-1000, преобладает конвективный теплообмен. Значение числа Нуссельта не может быть меньше 1, оно может быть больше 1 или равно 1. Значение числа Нуссельта всегда постоянно для полностью развитых ламинарный поток. Для сложной формы вычисляются локальные числа Нуссельта для поверхности, а затем вычисляется среднее число Нуссельта с использованием этих локальных чисел Нуссельта. Среднее число Нуссельта используется для получения дальнейших выводов.

В чем разница между гидравлическим радиусом и гидравлической глубиной / средней гидравлической глубиной?

Существует заблуждение, что гидравлический радиус и гидравлическая глубина одинаковы. Оба они имеют разное значение и имеют индивидуальное значение при измерении свойств жидкости. Понятие гидравлического радиуса и гидравлической глубины подробно обсуждается ниже.

Отношение площади поперечного сечения потока к смоченному периметру называется гидравлическим радиусом.
R_h = A / P

Отношение площади поперечного сечения потока к свободной поверхности воды или ширине верхней поверхности называется гидравлической глубиной.

H_d = A / T

где,

A – площадь поперечного сечения потока
T – ширина до верхней или свободной поверхности.

Математически средняя гидравлическая глубина и гидравлический радиус одинаковы.

Каково физическое значение гидравлического диаметра в науках о жидкости и теплоте?

На практике число Рейнольда используется для проверки поведения или характера потока жидкости. Это, в свою очередь, помогает нам найти число Нуссельта, которое затем используется для определения скорости передачи тепла из закрытого трубопровода.
Следовательно, число Рейнольдса – очень важное безразмерное число, которое играет жизненно важную роль как в науках о жидкости, так и в тепловых науках. Но чтобы найти число Рейнольда, сначала нам нужно найти гидравлический диаметр закрытого водовода. Для некруглого поперечного сечения гидравлический диаметр обеспечивает такое значение диаметра, что его характеристики потока эквивалентны характеристикам круглого поперечного сечения.

Отношение конвективной теплопередачи к кондуктивной теплопередаче называется числом Нуссельта.

Число Нуссельта определяется следующим соотношением:

Для ламинарный поток: Nu = 0.332 Re^0.5 Pr^0.33
Для турбулентного потока: Nu = 0.039 Re^0.8 Pr^0.33

Где,
Re обозначает число Рейнольдса
Pr обозначает число Прандтля

Отношение коэффициента диффузии по импульсу к коэффициенту температуропроводности называется Число Прандтля. Он назван в честь немецкого ученого Людвига Прандтля. Это безразмерное число помогает нам в вычислениях, связанных с принудительная и естественная конвекция тепла. Его значение состоит в том, что он помогает нам изучить связь между переносом импульса и способностью переноса тепла жидкостью.

Число Прандтля рассчитывается по формуле, приведенной ниже:

Pr = μCп / к

Где,
Pr – число Прандтля
µ является динамическим вязкость
Cp – теплоемкость

Обратите внимание, что число Нуссельта также можно найти с помощью соотношения: Nu = hLc / k, когда мы знаем значения конвективного и кондуктивного теплового сопротивления.

Проще говоря, гидравлический диаметр является основой для определения поведения потока и скорости потока. тепло переход от жидкости, которая течет в закрытом трубопроводе. При этом он также упрощает расчеты путем преобразования некруглого канала в круглый.

Источник

From Wikipedia, the free encyclopedia

The hydraulic diameter, D_H, is a commonly used term when handling flow in non-circular tubes and channels. Using this term, one can calculate many things in the same way as for a round tube. When the cross-section is uniform along the tube or channel length, it is defined as^[1]^[2]

${displaystyle D_{text{H}}={frac {4A}{P}},}$

where

A is the cross-sectional area of the flow,

P is the wetted perimeter of the cross-section.

More intuitively, the hydraulic diameter can be understood as a function of the hydraulic radius R_H, which is defined as the cross-sectional area of the channel divided by the wetted perimeter. Here, the wetted perimeter includes all surfaces acted upon by shear stress from the fluid.^[3]

${displaystyle R_{text{H}}={frac {A}{P}},}$

${displaystyle D_{text{H}}=4R_{text{H}},}$

Note that for the case of a circular pipe,

${displaystyle D_{text{H}}={frac {4pi R^{2}}{2pi R}}=2R}$

The need for the hydraulic diameter arises due to the use of a single dimension in case of dimensionless quantity such as Reynolds number, which prefer a single variable for flow analysis rather than the set of variables as listed in the table below.^{[This sentence needs work]} The Manning formula contains a quantity called the hydraulic radius. Despite what the name may suggest, the hydraulic diameter is not twice the hydraulic radius, but four times larger.

Hydraulic diameter is mainly used for calculations involving turbulent flow. Secondary flows can be observed in non-circular ducts as a result of turbulent shear stress in the turbulent flow. Hydraulic diameter is also used in calculation of heat transfer in internal-flow problems.^[4]

Non-uniform and non-circular cross-section channels[edit]

In the more general case, channels with non-uniform non-circular cross-sectional area, such as the Tesla valve, the hydraulic diameter is defined as:^[5]

${displaystyle D_{text{H}}={frac {4V}{S}},}$

where

V is the total wetted volume of the channel,

S is the total wetted surface area.

This definition is reduced to ${displaystyle {frac {4A}{P}}}$ for uniform non-circular cross-section channels, and ${displaystyle 2R}$ for circular pipes.

List of hydraulic diameters[edit]

Geometry	Hydraulic diameter	Comment
Circular tube	${displaystyle D_{text{H}}={frac {4cdot {frac {pi D^{2}}{4}}}{pi D}}=D}$	For a circular tube the hydraulic diameter is simply the diameter of the tube.
Annulus	${displaystyle D_{text{H}}={frac {4cdot {frac {pi (D_{text{out}}^{2}-D_{text{in}}^{2})}{4}}}{pi (D_{text{out}}+D_{text{in}})}}=D_{text{out}}-D_{text{in}}}$
Square duct	${displaystyle D_{text{H}}={frac {4a^{2}}{4a}}=a}$	here a represents the length of a side, not the cross sectional area
Rectangular duct (fully filled). The duct is closed so that the wetted perimeter consists of the 4 sides of the duct.	${displaystyle D_{text{H}}={frac {4ab}{2(a+b)}}={frac {2ab}{a+b}}}$	For the limiting case of a very wide duct, i.e. a slot of width b, where b ≫ a, then D_H = 2a.
Channel of water or partially filled rectangular duct. Open from top by definition so that the wetted perimeter consists of the 3 sides of the duct (2 on the side and the base).	${displaystyle D_{text{H}}={frac {4ab}{2a+b}}}$	For the limiting case of a very wide duct, i.e. a slot of width b, where b ≫ a, and a is the water depth, then D_H = 4a.

For a fully filled duct or pipe whose cross-section is a regular polygon, the hydraulic diameter is equivalent to the diameter $D$ of a circle inscribed within the wetted perimeter.
This can be seen as follows: The $N$ -sided regular polygon is a union of $N$ triangles, each of height ${displaystyle D/2}$ and base ${displaystyle B=Dtan(pi /N)}$ .
Each such triangle contributes ${displaystyle BD/4}$ to the total area and $B$ to the total perimeter, giving

${displaystyle D_{text{H}}=4{frac {NBD/4}{NB}}=D}$

for the hydraulic diameter.

References[edit]

^ Kudela, Henryk (May 2017). “Viscous flow in pipe” (PDF). p. 3.
^ “Hydraulic Diameter for Non-Circular Ducts” (PDF). May 2017. p. 2.
^ Frank M. White. Fluid Mechanics. Seventh Ed.
^ S. G. Kandlikar; Srinivas Garimella; Dongqing Li; Stéphane Colin; Michael R. King (2013). Heat transfer and fluid flow in minichannels and microchannels (2nd ed.). Oxford: Butterworth-Heinemann. doi:10.1016/C2011-0-07521-X. ISBN 978-0-08-098351-6. OCLC 862108729.
^ Nguyen, Quynh M.; Huang, Dean; Dean, Evan; Romanelli, Genievieve; Meyer, Charlotte; Ristroph, Leif (Oct 2020). “Tesla’s fluidic diode and the electronic-hydraulic analogy”. American Journal of Physics. 89 (4): 393–402. arXiv:2103.14813. doi:10.1119/10.0003395. S2CID 232401497.

Живое сечение, гидравлический радиус и смоченный периметр в гидравлике

Содержание:

Живое сечение
Смоченный периметр
Гидравлический радиус
- Гидравлический радиус для круглой трубы
Гидравлический диаметр

Живое сечение

Живым или нормальным называют сечение потока перпендикулярное направлению скорости течения (линиям тока).

Живое сечение потока жидкости

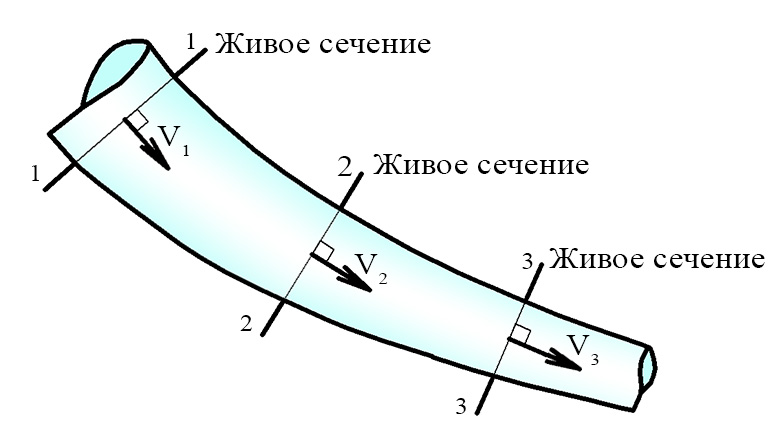
На рисунке изображен поток жидкости, в произвольных точках выбраны перпендикулярные направлениям скоростей живые сечения 1-1, 2-2, 3-3.

Смоченный периметр

Периметр контакта жидкости в данном живом сечении называют смоченным периметром (П, м).

Рассмотрим пример:

Определение смоченного периметра

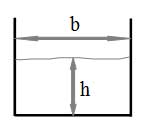
Для представленного сечения смоченный периметр можно определить по формуле:

П=2h+b

Гидравлический радиус

Отношение площади живого сечения (А, м²) к смоченному периметру (П, м) называют гидравлическим радиусом.

Rг=А/П, м

Гидравлический радиус для круглой трубы

Рассмотрим трубу с внутренним диаметром d, полностью заполненную жидкостью.

Определение гидравлического радиуса

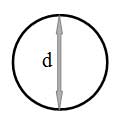
П=π d
A=π d2/4
Rг=d/4, м

Гидравлический диаметр

Для заполненной круглой трубы гидравлический диаметр можно определить по формуле:

Dг=4Rг, м

Нахождение[править | править код]

Смоченный периметр[править | править код]

Гидравлический радиус[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Общие сведения

Формулы расчет гидравлического диаметра (эквивалентного диаметра). Калькуляторы гидравлического диаметра (эквивалентного диаметра).

Классическая формула гидравлического диаметра (эквивалентного диаметра)

Гидравлический диаметр (эквивалентный диаметр) круглого сечения (например: воздуховоды, трубы, дымоходы и т.п)

Гидравлический диаметр (эквивалентный диаметр) сечения в виде кольца (например: труба в трубе и т.п.)

Гидравлический диаметр (эквивалентный диаметр) прямоугольного сечения (например: трубы квадратного сечения, дымоходы и т.п.)

Видеоматериал по теме «Гидравлический диаметр (эквивалентный диаметр)»

Примечание

Поделиться ссылкой:

Содержание

Определение гидравлического диаметра

Уравнение гидравлического диаметра

Гидравлический диаметр и число Рейнольдса

Гидравлический диаметр круглой трубы | гидравлический диаметр цилиндра

Гидравлический диаметр прямоугольного воздуховода

Гидравлический диаметр затрубного пространства

Гидравлический диаметр треугольника

Гидравлический диаметр эллипса

Гидравлический диаметр пластинчатого теплообменника | гидравлический диаметр кожухотрубного теплообменника

Эквивалентный диаметр и гидравлический диаметр

В чем разница между гидравлическим диаметром, эквивалентным диаметром и характеристической длиной в гидромеханике и теплопередаче?

В чем разница между гидравлическим радиусом и гидравлической глубиной / средней гидравлической глубиной?

Каково физическое значение гидравлического диаметра в науках о жидкости и теплоте?

Non-uniform and non-circular cross-section channels[edit]

List of hydraulic diameters[edit]

References[edit]

See also[edit]

Живое сечение, гидравлический радиус и смоченный периметр в гидравлике

Живое сечение

Смоченный периметр

Гидравлический радиус

Гидравлический радиус для круглой трубы

Гидравлический диаметр

Вам также может понравиться

Как найти блок сигнализации в автомобиле

Как найти учетную запись электронной почты

Как найти свои фейковые страницы в инстаграм

Добавить комментарий Отменить ответ