Рассмотрим
площадку ∆ω, на которую действует сила
∆Р
(рис.
5). Отношение p=∆Р/∆ω,
очевидно, представляет собой “напряжение”,
т. е. силу, приходящуюся на единицу
площади.
Так как при равновесии
жидкости ∆Р является сжимающей силой,
то р
представляет
собой среднее для данной площадки
напряжение
сжатия, которое называют средним
гидростатическим давлением
на площадке. Для
получения точного значения р
в данной
точке надо определить предел этого
отношения при
∆ω→0,
что
и определит гидростатическое давление
в данной точке:
![]() (24)
(24)
Размерность
[р]
равна
размерности напряжения, т. е.,
[р]=
[Па] или [кгс/м2].
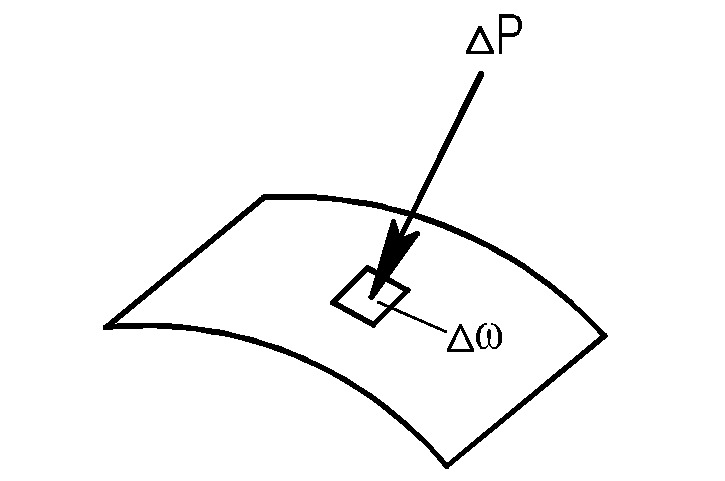
Рис. 5 – Сила, воздействующая
на единицу площади
Основная
теорема гидростатики. Величина
гидростатического
давления в данной точке не зависит от
ориентации в пространстве
площадки, на которой она расположена,
т. е.
px=py=pz=pn (25)
где рx,
ру,
pz
—
гидростатические давления по направлению
координатных
осей, а рп
—
то же, по произвольному
направлению п.
Для доказательства выберем внутри массы
жидкости, находящейся в равновесии,
объем в форме тетраэдра (рис. 6) и, полагая
его отвердевшим, напишем для него (как
для твердого тела)
условия равновесия в виде трех уравнений
проекций действующих сил и трех уравнений
моментов:
ΣX=0 и ΣMx=0 (26)
ΣY=0 и ΣMy=0 (27)
ΣZ=0 и ΣMz=0 (28)
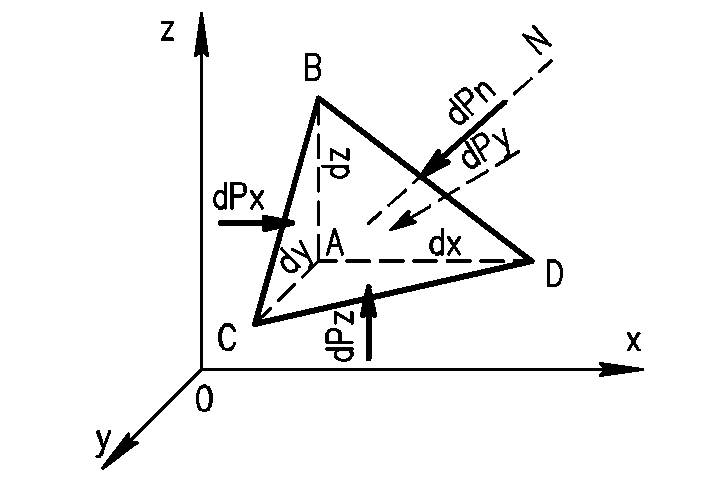
Рис. 6
– К теореме о независимости гидростатического
давления от направления
При уменьшении объема
тетраэдра в пределе до нуля система
действующих сил преобразуется в систему
сил, проходящих через
одну и ту же точку, и, таким образом,
уравнения моментов
теряют смысл.
Составим
уравнение проекций сил на ось Ох.
На рассматриваемый
тетраэдр действуют четыре поверхностные
силы (по числу граней тетраэдра),
направленные по нормалям
к соответствующим граням, и объемная
сила dF.
Проектируя
эти силы на ось Ох,
получим
![]() (29)
(29)
где
![]() ,
,![]() ,
,
так как
dω
cosα
представляет собой проекцию площадки
dω
на плоскость,
перпендикулярную оси Ох.
Объемная
сила dF=
dmj,
где dm
— масса тетраэдра, равная р1/6dxdydz,
а
j
— ускорение, создаваемое этой силой.
Тогда
dF
cosα
= dmj
cosα.
Введем
обозначение j·cos=X,
j·cos=У,
j·cos=Z,
где X,
Y
и
Z
— проекции ускорения внешней объемной
силы (эти обозначения
будут использоваться и далее).
После
соответствующих подстановок получим
уравнение
![]() (30)
(30)
– сокращая
которое на — dydz,
найдем
![]() (31)
(31)
Опуская
третье слагаемое как величину высшего
порядка малости
по сравнению с двумя первыми, получим
рх-рп=0
(32)
Очевидно,
по аналогии можем написать
рy-рn=0
ирz-рn=0
(33)
или, наконец,
рх=рy=рz=рn
(34)
что доказывает теорему.
Гидростатическое
давление в точке, будучи одинаковым по
любому направлению,
неодинаково в различных точках
пространства,
т. е. р
есть
функция координат: p=f(x,y,z).
3.3. Общие дифференциальные уравненияравновесия жидкости
Уравнение
Эйлера. Выберем
внутри покоящейся жидкости параллелепипед
с ребрами, расположенными параллельно
координатным
осям 0х,
0у
и
0z
(рис.
7) и равными соответственно dx,
dy
и
dz.
Составим
уравнения равновесия
этого параллелепипеда
в виде уравнений проекций сил
(согласно предыдущим рассуждениям
уравнения моментов теряют
смысл):ΣX=0,ΣY=0,ΣZ=0.
Проектируя
силы на ось 0х,
согласно
рис. 7, имеем
ΣX=dP-dP1+dF·cosα=0
(35)
Определим
каждое из слагаемых. Поверхностные
силы равны: dP=pdydz
и
dP1=p’dydz,
где
р
и
р‘
—
средние гидростатические давления
соответственно
на площадки ABCDA
и
A‘B‘C‘D‘A‘.
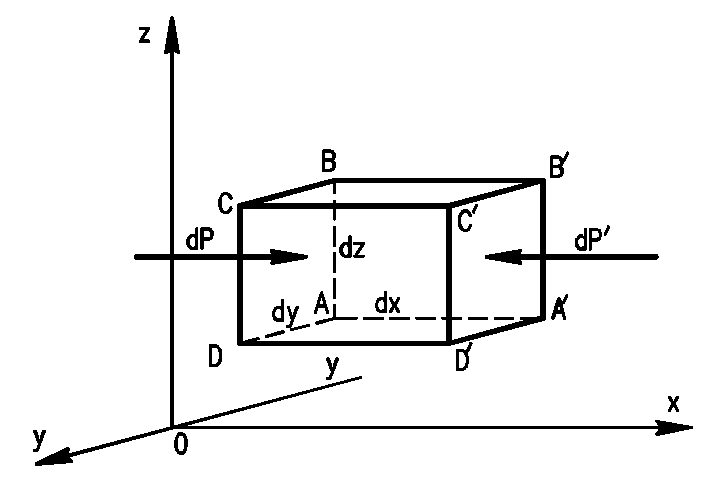
Рис. 7 – К выводу уравнений равновесия
жидкости
Так как
гидростатическое давление является
функцией координат,
среднее гидростатическое давление на
площадке A‘B‘C‘D‘A‘
будет равно:
![]() (36)
(36)
потому что при переходе от
площадки ABCDA
к площадке A‘B‘C‘D‘A‘
изменяется только
координата х.
Следовательно, сила
объемная
сила для массы dm=pdxdydz
равна:
dF
cos
α
= dmj
cos
α = dmX
= dx
dy
dzX.
Подставляя
в (35) значения слагаемых, запишем
![]() (37)
(37)
Раскрывая
скобки и (после приведения подобных
членов) сокращая
на dx
dy
dz,
получим
уравнение проекций сил на ось 0х
в
виде
![]() (38)
(38)
Аналогично
можно получить и уравнения проекций
сил на оси
Оу
и
Оz,
в результате чего система трех уравнений
равновесия жидкости
(уравнения Эйлера) запишется в виде
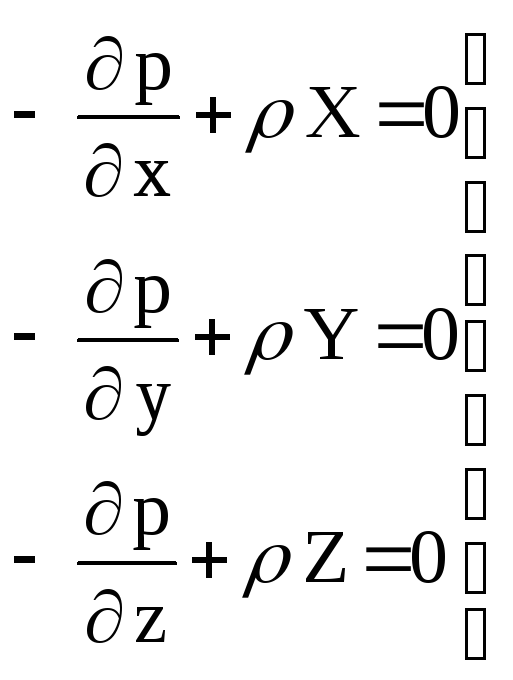 (39)
(39)
Основное
дифференциальное уравнение гидростатики.
Перепишем
уравнения Эйлера в несколько другом
порядке:
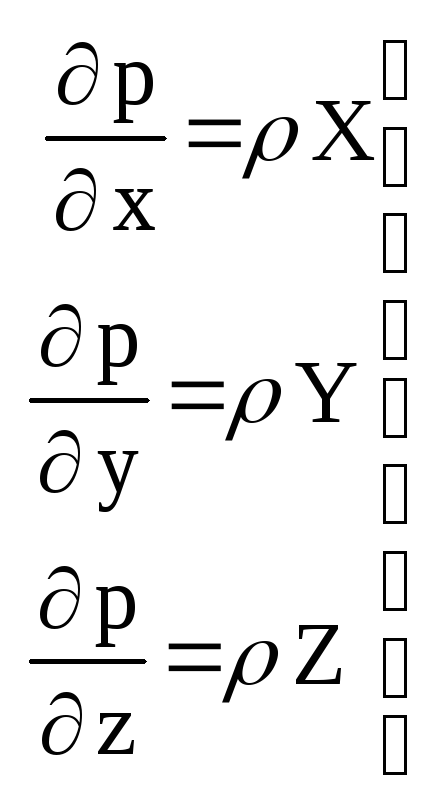 (40)
(40)
умножив
каждое из этих уравнений соответственно
на dx,
dy
и
dz
и
произведя сложение правых и левых частей
уравнений, получим
![]() (41)
(41)
Так как
гидростатическое давление р
зависит
только от трех независимых
переменных координат х,
у и
z,
левая
часть этого равенства
представляет собой полный дифференциал
функции p=f(х,у,z):
![]()
(42)
Делая
подстановку, находим окончательно
![]() (43)
(43)
Уравнение
(43) называется основным
дифференциальным уравнением гидростатики,
так
как его использование позволяет решать
основные задачи гидростатики.
Рассмотрим это уравнение более подробно.
Прежде
всего, отметим, что, так как dp
есть
полный дифференциал,
то выражение в скобках правой части
будет также полным
дифференциалом некоторой функции
координат,
т. е.
![]() (44)
(44)
Следовательно,
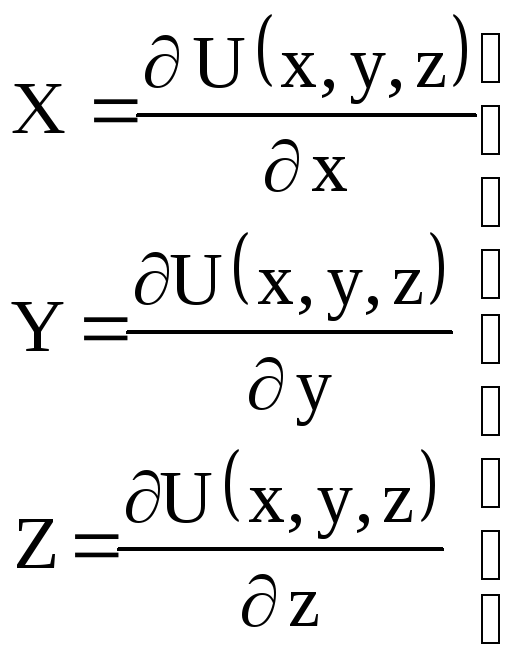 (45)
(45)
Здесь величины X,
Y
и Z,
т. е. проекции
ускорения объемной силы,
можно рассматривать как проекции самой
объемной силы, отнесенной к единице
массы данной жидкости, так как
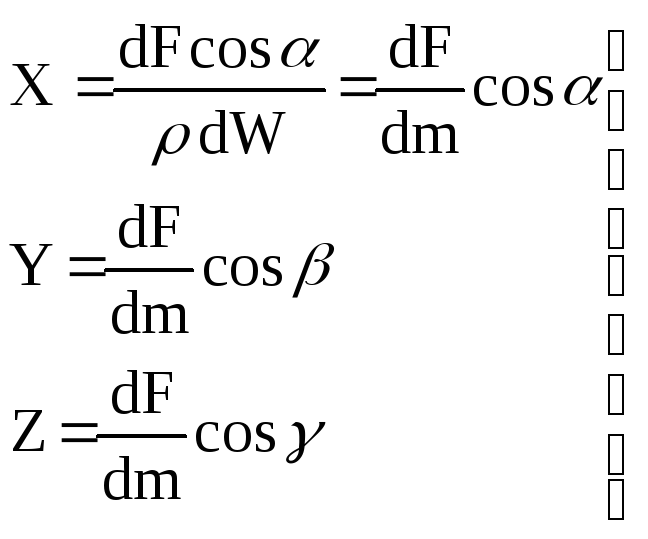 (46)
(46)
поэтому
функция U
(x,
у, z)
является
потенциалом сил или так
называемой “силовой функцией”.
Таким образом, равновесие
жидкости возможно, если объемные силы
имеют потенциал.
Правую
часть уравнения (43) можно рассматривать
и как уравнение
элементарной работы dT,
т.
е. можем написать
ρXdx+ρYdy+ρZdz=dT(47)
Действительно,
работа силы
![]() (силы, отнесенной к единице
(силы, отнесенной к единице
объема) на пути ds
(рис. 8) равна:
![]() (48)
(48)
где А
—
угол между направлением действия силы
dF/dW
и
линией
перемещения ds.
Но из (48) следует:
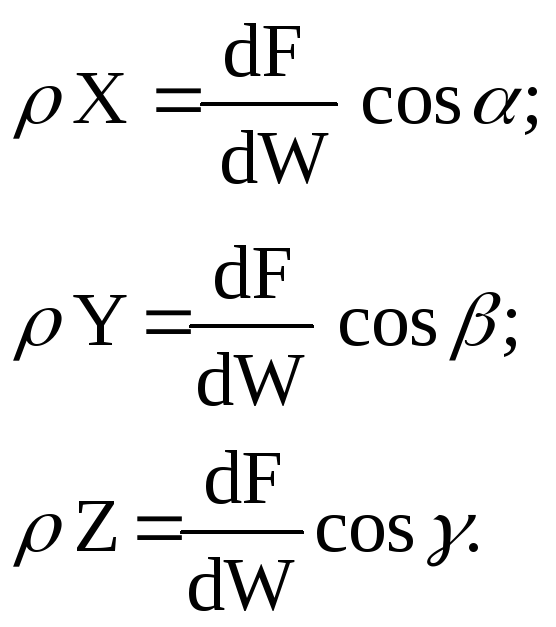 (49)
(49)
и
кроме
того
dx=ds
cos a; dy=ds cos b; dz=ds cos c.
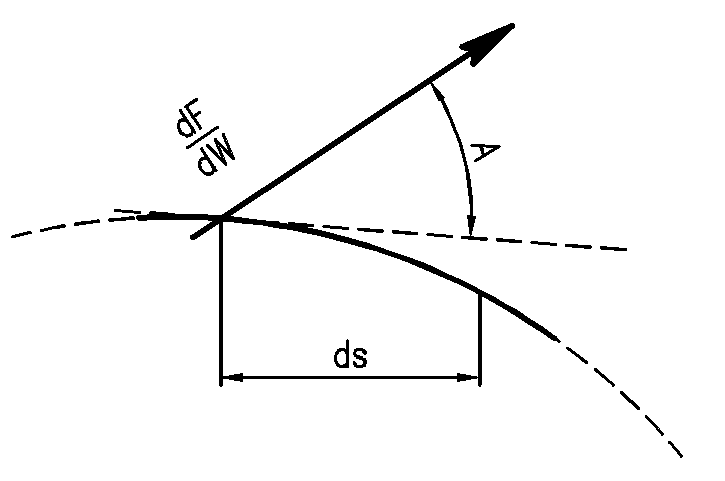
Рис 8 –
Работа силы dF/dW
на пути ds
С учетом
последнего слагаемые левой части
уравнения (47)
равны по отдельности:
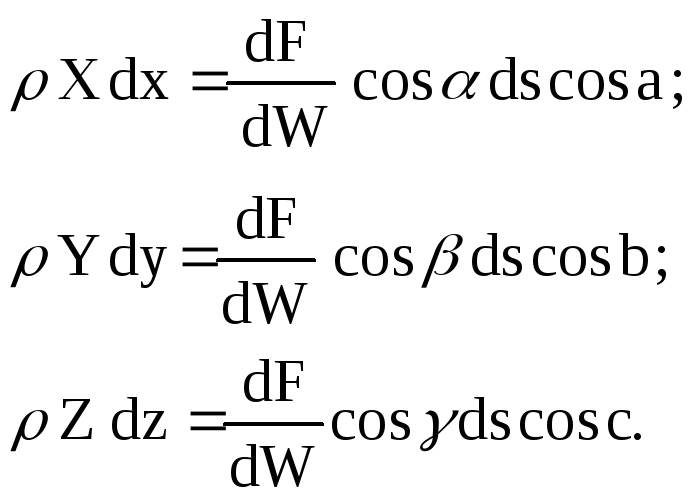 (50)
(50)
в сумме
![]()
Если
учесть, что cos
α
cos
a+cosβ
cos
b+cos
γ cos
с
=
cos
A,
приходим к
равенству:
![]() (51)
(51)
Это и
доказывает справедливость уравнения
(47).
Отсюда
заключаем, что изменение гидростатического
давления
dp
равно
работе внешних объемных сил, совершаемой
на пути изменения давления от р1
до
p2
(при
р2
– p1=dp).
Характеристическое
уравнение.
В основном дифференциальном
уравнении гидростатики (42) неизвестны
две величины: р
и
ρ (значения X,
Y
и
Z,
а
также координаты точки обычно заданы.)
Таким образом, для определенности
решения необходимо
иметь еще одно независимое уравнение,
в качестве которого используется
так называемое характеристическое
уравнение, определяющее
собой особенности данной жидкости.
Например,
рассматривая равновесие капельной
жидкости и считая
ее абсолютно несжимаемой, характеристическим
уравнением
будет условие
ρ =
const, (52)
а для
газа – уравнение Бойля-Мариотта p
=
RT,
или
p/=RT.
В общем
виде условия равновесия можно записать
в виде функции,
характеризующей особенности сжатия
данной жидкости:
ρ =
φ(Р,t°) (53)
Поверхность
уровня. Поверхностью
уровня называется такая
поверхность, все точки которой
имеют одно и то же
значение
рассматриваемой функции: например,
поверхность равной температуры
(изотермическая поверхность), поверхность
равного
потенциала и т. д.
Для
рассмотрения задач гидравлики важное
значение имеет поверхность равного
давления. Имея
в виду в дальнейшем изложении именно
поверхность равного
давления, будем условно называть ее
кратко поверхностью уровня.
Уравнение поверхности
уровня и свойства этой поверхности. Так
как во всех точках поверхности уровня
гидростатическое
давление одинаково, т. е. р =
const,
то dp=0
и из основного
дифференциального уравнения гидростатики
получим
ρ(Xdx+Ydy+Zdz)=0 (54)
Так как плотность ρ≠0, то
Xdx+Ydy+Zdz=0 (55)
где X,
Y
и
Z
— функции координат.
Уравнение (55) представляет
собой дифференциальное уравнение
поверхности, для которой р = const,
т. е. уравнение поверхности
уровня.
Рассмотрим
свойства
поверхности уровня:
-
Две
поверхности уровня не пересекаются
между собой. Действительно,
допустим, что поверхность давления р1
пересекается
с поверхностью давления р2,
тогда
в точках линии пересечения этих
поверхностей давление было бы одновременно
равным
и р1
и
р2,
что невозможно, так как р1≠р2.
Следовательно,
пересечение этих поверхностей невозможно.
-
Внешние
объемные силы направлены нормально к
поверхности
уровня. Подтвердить это положение можно
так. Работа силы
F.
на элементарном пути ds
согласно
(47) равна:
dT
=
ρ
(Xdx
+ Ydy
+ Zdz) (56)
Но для
поверхности уровня трехчлен в скобках
равен нулю поэтому
работа силы F
на
пути ds
вдоль
поверхности уровня равна
нулю (dT=0).
С другой
стороны, согласно рис. 8 работа силы
F=dT=F
cos
A
ds,
и
поскольку dT=0,
a
f≠0
и
ds≠0,
то
cos
A
должен
быть равен нулю, т. е. угол A=π/2.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
На чтение 7 мин Просмотров 5.3к.
В гидравлике есть несколько ключевых понятий. Центральное место отводится понятию гидростатического давления жидкости. Оно тесно связано с понятием напора жидкости, о котором будет сказано чуть позже.

Содержание
- Что такое
- В чем измеряется
- Шкала и виды давлений
- Формула расчета давления в открытом сосуде
- Давление жидкости в трубах и его нормативы
- Распределение давления жидкости в тубах
Что такое
Одно из широко распространенных определений гидростатического давления звучит так: «Гидростатическое давление в точке жидкости – это нормальное сжимающее напряжение, возникающее в покоящейся жидкости под действием поверхностных и массовых сил».
Напряжение – это понятие, широко используемое в курсе сопротивления материалов. Идея в следующем. В физике, мы знаем, есть понятие силы. Сила – векторная величина, характеризующая воздействие. Векторная – это значит, что представляется в виде вектора, т.е. стрелки в трехмерном пространстве. Эта сила может быть приложена в отдельной точке (сосредоточенная сила), или к поверхности (поверхностная), или ко всему телу (говорят, массовая / объемная). Поверхностные и массовые силы являются распределенными. Только такие и могут действовать на жидкость, так как она обладает функцией текучести (легко деформируется от любого воздействия).
Сила приложена к поверхности с какой-то конкретной площадью. В каждой точке этой поверхности возникнет напряжение, равное отношению силы к площади, это и есть понятие давления в физике.
В чем измеряется
В системе СИ единица измерения силы – Ньютон [Н], площади – квадратный метр [м2].

Отношение силы к площади: 1 Н / 1 м2 = 1 Па (Паскаль).
Паскаль является основной единицей измерения давления, но далеко не единственной. Ниже представлен пересчет единиц измерения давлений из одной в другую
100 000 Па = 0,1 МПа = 100 кПа ≈ 1 атм = 1 бар = 1 кгс/см2 = 14,5 psi ≈ 750 мм.рт.ст ≡ 750 Торр ≈ 10 м.вод.ст (м)
Шкала и виды давлений
Далее, принципиально важным моментом является так называемая шкала давлений или виды давлений. На рисунке ниже представлено, как взаимоувязаны такие понятия как абсолютное давление, абсолютный вакуум, частичный вакуум, избыточное или манометрическое давление.

Абсолютное давление – давление, отсчитываемое от нуля.
Абсолютный вакуум – ситуация, при которой на рассматриваемую точку ничего не действует, т.е. давление, равное 0 Па.
Атмосферное давление – давление, равное 1 атмосфере. Отношение веса (mg) вышележащего столба воздуха к площади его поперечного сечения. Атмосферное давление зависит от места, времени суток. Это один из параметров погоды. В прикладных инженерных дисциплинах обычно все отсчитывают именно от атмосферного давления, а не от абсолютного вакуума.

Частичный вакуум (или еще часто говорят – «величина вакуума», « разрежение» или «отрицательное избыточное давление» ). Частичный вакуум – недостаток давления до атмосферного. Максимально возможная на Земле величина вакуума как раз равняется одной атмосфере (~10 м.вод.ст.). Это означает, что у вас не получится попить воду через трубочку с расстояния 11 м при всем желании.
* на самом деле при нормальном для трубочек для напитков диаметре (~5-6 мм) эта величина будет гораздо меньше из-за гидравлических сопротивлений. Но даже через толстый шланг вы не сможете попить воду с глубины 11 м.
Если заменить вас на насос, а трубочку – на его всасывающий трубопровод, то ситуация принципиально не изменится. Поэтому воду из скважин добывают как правило именно скважинными насосами, которые опускаются непосредственно в воду, а не пытаются засасывать воду с поверхности земли.

Избыточное давление (или также еще называемое манометрическим)– превышение давления над атмосферным.
Приведем следующий пример. На данной фотографии показано измерение давления в автомобильной шине при помощи прибора манометра.
Манометр показывает именно избыточное давление. На этой фотографии видно, что избыточное давление в данной шине приблизительно 1,9 бар, т.е. 1,9 атм, т.е. 190 000 Па. Тогда абсолютное давление в этой шине – 290 000 Па. Если мы шину проткнем, то воздух начнет под разницей давлений выходить наружу до тех пор, пока давление внутри и снаружи шины не станет одинаковым, атмосферным. Тогда избыточное давление в шине будет равно 0.
Формула расчета давления в открытом сосуде

Теперь посмотрим, как определить гидростатическое давление в жидкости, находящейся в определенном объеме. Допустим, мы рассматриваем открытую бочку с водой.
На поверхности воды в бочке устанавливается атмосферное давление (обозначено маленькой буквой p с индексом «атм»). Соответственно, избыточное давление жидкости на поверхности равняется 0 Па. Теперь рассмотрим гидростатическое давление в точке X. Эта точка заглублена относительно поверхности воды на расстояние h, и за счет столба жидкости, гидростатическое давление в ней будет больше, чем на поверхности.
Давление в точке X (px) будет определяться, как давление на поверхности + давление, создаваемое столбом жидкости. Это называется основным уравнением гидростатики.

Для приблизительных расчетов можно принимать g = 10 м/с2. Плотность воды зависит от температуры, но для приблизительных расчетов может приниматься 1000 кг/м3.
При глубине h 2 м, абсолютное гидростатическое давление составит:
100 000 Па + 1000·10·2 Па = 100 000 Па +20 000 Па = 120 000 Па = 1,2 атм.
Избыточное давление жидкости – это значит за вычетом атмосферного: 120 000 – 100 000 = 20000 Па = 0,2 атм.

Таким образом, в избыточное давление в точке X определяется высотой столба жидкости. Форма емкости при этом никак не влияет. Если мы рассмотрим гигантский бассейн с глубиной 2 м, и трубку высотой 3 м, то гидростатическое давление на дне трубки будет больше, нежели на дне бассейна.
(Абсолютное гидростатическое давление на дне бассейна: 100000 + 1000*9,81*2 =
Абсолютное
Высота столба жидкости определяет давление, создаваемое этим столбом жидкости.pизб = ρgh.
Таким образом, гидростатическое давление можно выражать единицами длины (высоты): h = p / ρg
Например, рассмотрим, какое давление создает столб ртути высотой 750 мм:
p = ρgh = 13600 · 10 · 0,75 = 102 000 Па ≈ 100 000 Па, что отсылает нас к единицам измерения давления, рассмотренным ранее.
Т.е. 750 мм.рт.ст. = 100 000 Па.
По тому же принципу получается, что давление в 10 метров водяного столба равняется 100 000 Па:
1000 · 10 · 10 = 100 000 Па.
Выражение гидростатического давления в метрах водяного столба принципиально важно для водоснабжения, водоотведения, а также гидравлических расчетов отопления, гидротехнических расчетов и т. д.
Давление жидкости в трубах и его нормативы
Теперь посмотрим гидростатическое давление жидкости в трубопроводах. Что физически означает замеренное мастером давление в определенной точке (X) трубопровода? Манометр в данном случае показывает 2 кгс/см² (2 атм). Это избыточное давление в трубопроводе, оно эквивалентно 20 метрам водяного столба. Иными словами, если подсоединить к трубе вертикальную трубку, то вода в ней поднимется на величину избыточного давления, т.е. на высоту 20 м. Вертикальная трубка, которая сообщается с атмосферой (т.е. открытая) называются пьезометром.

Основная задача системы водоснабжения заключается в том, чтобы в требуемой точке вода имела необходимое избыточное давление. Например, согласно нормативному документу:
[ Постановление Правительства РФ от 06.05.2011 N 354 (ред. от 13.07.2019) «О предоставлении коммунальных услуг собственникам и пользователям помещений в многоквартирных домах и жилых домов» (вместе с «Правилами предоставления коммунальных услуг собственникам и пользователям помещений в многоквартирных домах и жилых домов») ] >>> давление в точке водоразбора должно быть не менее 3 м.вод.ст (0,03 МПа)

Под точкой водоразбора можно понимать место подключения смесителя (1). Эта точка находится приблизительно на расстоянии 1 м от пола, там же, где и подключение к стояку самой квартиры (2) . То есть давление примерно одинаково при закрытых кранах (вода не движется!). Давление регламентируется именно в этих точках, и, как указано выше, должно быть не меньше 3 — 6 м.вод.ст.
Однако необходимо отметить, что нормативно допустимая величина в 3 м.вод.ст – это совсем не много, так как современное сантехническое оборудование может требовать гидростатическое давление жидкости до 13 м.вод.ст в месте подключения для нормальной работы (подачи достаточного количества воды). Например, даже в старом СНиП по внутреннему водопроводу (СНиП 2.04.01-85*), указано, что при использовании аэратора на смесителе (сеточка, перекрывающая выходное отверстие), в точке подключения смесителя необходимо давление 5 м.вод.ст.
Распределение давления жидкости в тубах
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 21 июня 2020 года; проверки требуют 17 правок.
Гидростатическое давление — давление столба жидкости над условным уровнем.
Благодаря полной удобоподвижности своих частиц капельные и газообразные жидкости, находясь в покое, передают давление одинаково во все стороны; давление это действует на всякую часть плоскости, ограничивающей жидкость, с силой Р, пропорциональной величине w этой поверхности, и направленной по нормали к ней. Отношение P/w, то есть давление р на поверхность, равную единице, называется гидростатическим давлением[1].
Простое уравнение P = pw может действительно служить для точного вычисления давления на данную поверхность сосуда, газов и капельных жидкостей, находящихся при таких условиях, что часть давления, зависящая от собственного веса жидкостей, ничтожно мала по сравнению с давлением, передаваемым им извне. Сюда относятся почти все случаи давлений газов и расчеты давлений воды в гидравлических прессах и аккумуляторах[1].
Вычисление[править | править код]
В каждой жидкости существует давление, обусловленное её собственным весом 




Плотность жидкости 
Для бытовых расчетов можно принять, что с ростом глубины на каждые 10 метров пресной воды, давление увеличивается на 0,1 МПа (1 атмосфера).
История открытия[править | править код]
Это основное свойство жидкостей было открыто и проверено на опыте Блезом Паскалем в 1653 году.
Единица измерения[править | править код]
Единицей измерения давления в международной системе единиц является Паскаль. На практике гидростатическое давление часто измеряют в атмосферах, принимая за 1 атмосферу давление в 76 см ртутного столба, при температуре 0 °C при нормальном ускорении свободного падения 9,80665 м/с².
На основании гидростатического парадокса можно гидростатическое давление измерять также высотой столба ртути или воды, способного производить то же давление на единицу поверхности.
Свойства[править | править код]
Гидростатический парадокс[править | править код]

Гидростатическое давление на тело не зависит от направления.
Вычисление немного усложняется, когда надо узнать давление, производимое на не горизонтальную часть стенки сосуда вследствие тяжести налитой на него жидкости. Здесь причиной давления становится вес столбов жидкости, имеющих основанием каждую бесконечно малую частицу рассматриваемой поверхности, а высотой вертикальное расстояние от каждой такой частицы до свободной поверхности жидкости. Расстояния эти будут постоянны только для горизонтальных частей стенок и для бесконечно узких горизонтальных полосок, взятых на боковых стенках; к ним одним можно прилагать непосредственно формулу гидростатического давления. Для боковых же стенок надо суммировать, по правилам интегрального исчисления, давления на все горизонтальные элементы их поверхности; в результате получается общее правило: давление тяжелой жидкости на всякую плоскую стенку равняется весу столба этой жидкости, имеющему основанием площадь этой стенки, а высотой вертикальное расстояние её центра тяжести от свободной поверхности жидкости. Поэтому давление на дно сосуда будет зависеть только от величины поверхности этого дна, от высоты уровня жидкости в него налитой и от её плотности, от формы же сосуда оно зависеть не будет. Это положение известно под именем «гидростатического парадокса» и было разъяснено ещё Паскалем.
Действительно, оно кажется на первый взгляд неверным, потому что в сосудах с равными доньями, наполненными до равной высоты одной и той же жидкостью, вес её будет очень различный, если формы различны. Но вычисление и опыт (сделанный в первый раз Паскалем) показывают, что в сосуде, расширяющемся кверху, вес излишка жидкости поддерживается боковыми стенками и передается весам через их посредство, не действуя на дно, а в сосуде, суживающемся кверху, гидростатическое давление на боковые стенки действует снизу вверх и облегчает весы ровно на столько, сколько весило бы недостающее количество жидкости.
Закон Паскаля[править | править код]

Чем глубже, тем выше давление. (левая часть графика)
Гидростатическое давление жидкости с постоянной плотностью в однородном поле тяжести ( = несжимаемая жидкость) подчиняется закону Паскаля:
где:
— плотность [для пресной воды: ρ ≈ 1000 кг/м³]
— ускорение свободного падения [для Европы: g ≈ 9,81 м/с²]
— высота (здесь: жидкости) [м]
— [Па]
⇒ 
Примечания[править | править код]
- ↑ 1 2 Лермантов, 1893, с. 655.
- ↑ Давление столба жидкости. Формулы и расчеты онлайн — Интерактивный справочник формул. Дата обращения: 2 марта 2018. Архивировано 17 октября 2017 года.
- ↑ Пашков Н. Н., Долгачев Ф. М. Гидравлика. Основы гидрологии. – М., Энергия, 1977. – Тираж 25 000 экз. – с. 17
- ↑ Лев Давыдович Ландау, Евгений Михайлович Лифшиц: Статистическая физика. Часть I. с. 70.
Литература[править | править код]
- В. В. Лермантов. Гидростатическое давление // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1893. — Т. VIIIa. — С. 655—656.
Главная страница
Содержание
Введение
Основы гидростатики
Основы гидродинамики
Гидравлические сопротивления
Истечние жидкости из отверстий, насадков и из-под затворов
Гидравлический расчет простых трубопроводов
Гидравлические машины
Лекция 2. ОСНОВЫ ГИДРОСТАТИКИ
Гидравлика делится на два раздела: гидростатика и гидродинамика. Гидродинамика является более обширным
разделом и будет рассмотрена в последующих лекциях. В этой лекции будет рассмотрена гидростатика.
Гидростатикой называется раздел гидравлики, в котором рассматриваются законы равновесия жидкости
и их практическое применение.
В покоящейся жидкости всегда присутствует сила давления, которая называется гидростатическим давлением.
Жидкость оказывает силовое воздействие на дно и стенки сосуда. Частицы жидкости, расположенные в верхних
слоях водоема, испытывают меньшие силы сжатия, чем частицы жидкости, находящиеся у дна.
Рассмотрим резервуар с плоскими вертикальными стенками, наполненный жидкостью (рис.2.1, а). На дно
резервуара действует сила P равная весу налитой жидкости G = γ V, т.е. P = G.
Если эту силу P разделить на площадь дна Sabcd, то мы получим среднее гидростатическое
давление, действующее на дно резервуара.
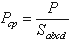
Гидростатическое давление обладает свойствами.
Свойство 1. В любой точке жидкости гидростатическое давление перпендикулярно площадке
касательной к выделенному объему и действует внутрь рассматриваемого объема жидкости.
Для доказательства этого утверждения вернемся к рис.2.1, а. Выделим на боковой стенке резервуара
площадку Sбок (заштриховано). Гидростатическое давление действует на эту площадку в виде
распределенной силы, которую можно заменить одной равнодействующей, которую обозначим P. Предположим,
что равнодействующая гидростатического давления P, действующая на эту площадку, приложена в точке
А и направлена к ней под углом φ (на рис. 2.1 обозначена штриховым отрезком со
стрелкой). Тогда сила реакции стенки R на жидкость будет иметь ту же самую величину, но
противоположное направление (сплошной отрезок со стрелкой). Указанный вектор R можно разложить на
два составляющих вектора: нормальный Rn (перпендикулярный к заштрихованной площадке) и
касательный Rτ к стенке.
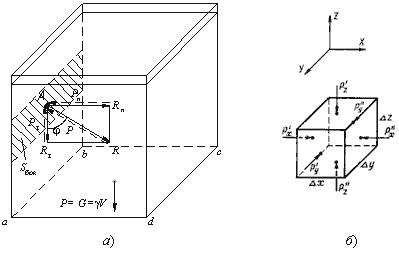
Рис. 2.1. Схема, иллюстрирующая свойства гидростатического давления
а – первое свойство; б – второе свойство
Сила нормального давления Rn вызывает в жидкости напряжения сжатия. Этим напряжениям
жидкость легко противостоит. Сила Rτ действующая на жидкость вдоль
стенки, должна была бы вызвать в жидкости касательные напряжения вдоль стенки и частицы должны были бы
перемещаться вниз. Но так как жидкость в резервуаре находится в состоянии покоя, то составляющая
Rτ отсутствует. Отсюда можно сделать вывод первого свойства
гидростатического давления.
Свойство 2. Гидростатическое давление неизменно во всех направлениях.
В жидкости, заполняющей какой-то резервуар, выделим элементарный кубик с очень малыми сторонами
Δx, Δy, Δz (рис.2.1, б). На каждую из боковых поверхностей будет
давить сила гидростатического давления, равная произведению соответствующего давления Px,
Py , Pz на элементарные площади. Обозначим вектора давлений,
действующие в положительном направлении (согласно указанным координатам) как P’x,
P’y, P’z, а вектора давлений, действующие в обратном направлении
соответственно P”x, P”y, P”z. Поскольку кубик
находится в равновесии, то можно записать равенства
P’xΔyΔz=P”xΔyΔz
P’yΔxΔz = P”yΔxΔz
P’zΔxΔy + γΔx, Δy, Δz = P”zΔxΔy
где γ – удельный вес жидкости;
Δx, Δy, Δz – объем кубика.
Сократив полученные равенства, найдем, что
P’x = P”x; P’y = P”y; P’z + γΔz = P”z
Членом третьего уравнения γΔz, как бесконечно малым по сравнению с P’z
и P”z, можно пренебречь и тогда окончательно
P’x = P”x; P’y = P”y; P’z=P”z
Вследствие того, что кубик не деформируется (не вытягивается вдоль одной из осей), надо полагать, что
давления по различным осям одинаковы, т.е.
P’x = P”x = P’y = P”y = P’z=P”z
Это доказывает второй свойство гидростатического давления.
Свойство 3. Гидростатическое давление в точке зависит от ее координат в пространстве.
Это положение не требует специального доказательства, так как ясно, что по мере увеличения погружения точки
давление в ней будет возрастать, а по мере уменьшения погружения уменьшаться. Третье свойство гидростатического
давления может быть записано в виде
P=f(x, y, z)
Рассмотрим распространенный случай равновесия жидкости, когда на нее действует только одна массовая сила –
сила тяжести, и получим уравнение, позволяющее находить гидростатическое давление в любой точке
рассматриваемого объема жидкости. Это уравнение называется основным уравнением гидростатики.
Пусть жидкость содержится в сосуде (рис.2.2) и на ее свободную поверхность действует давление P0
. Найдем гидростатическое давление P в произвольно взятой точке М, расположенной на
глубине h. Выделим около точки М элементарную горизонтальную площадку dS и построим на
ней вертикальный цилиндрический объем жидкости высотой h. Рассмотрим условие равновесия указанного
объема жидкости, выделенного из общей массы жидкости. Давление жидкости на нижнее основание цилиндра теперь
будет внешним и направлено по нормали внутрь объема, т.е. вверх.
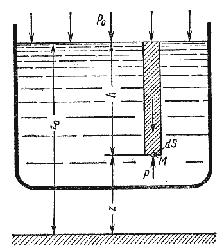
Рис. 2.2. Схема для вывода основного уравнения гидростатики
Запишем сумму сил, действующих на рассматриваемый объем в проекции на вертикальную ось:
PdS – P0 dS – ρghdS = 0
Последний член уравнения представляет собой вес жидкости, заключенный в рассматриваемом вертикальном цилиндре
объемом hdS. Силы давления по боковой поверхности цилиндра в уравнение не входят, т.к. они
перпендикулярны к этой поверхности и их проекции на вертикальную ось равны нулю. Сократив выражение на
dS и перегруппировав члены, найдем
P = P0 + ρgh = P0 + hγ
Полученное уравнение называют основным уравнением гидростатики. По нему можно посчитать давление в любой
точке покоящейся жидкости. Это давление, как видно из уравнения, складывается из двух величин: давления
P0 на внешней поверхности жидкости и давления, обусловленного весом вышележащих слоев
жидкости.
Из основного уравнения гидростатики видно, что какую бы точку в объеме всего сосуда мы не взяли, на нее
всегда будет действовать давление, приложенное к внешней поверхности P0. Другими словами
давление, приложенное к внешней поверхности жидкости, передается всем точкам этой жидкости по всем
направлениям одинаково. Это положение известно под названием закона Паскаля.
Поверхность, во всех точках которой давление одинаково, называется поверхностью уровня (подробно рассмотрим
в п.2.6). В обычных условиях поверхности уровня представляют собой горизонтальные плоскости.
Пусть мы имеем резервуар с наклонной правой стенкой, заполненный жидкостью с удельным весом γ. Ширина
стенки в направлении, перпендикулярном плоскости чертежа (от читателя), равна b
(рис.2.3). Стенка условно показана развернутой относительно оси АВ и заштрихована на рисунке. Построим
график изменения избыточного гидростатического давления на стенку АВ.
Так как избыточное гидростатическое давление изменяется по линейному закон P=γgh,
то для построения графика, называемого эпюрой давления, достаточно найти давление в двух точках, например
А и B.
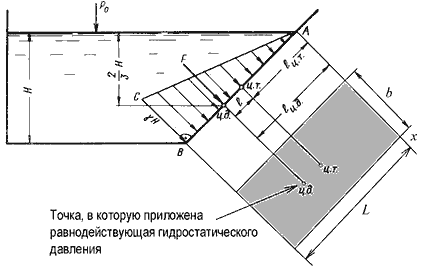
Рис. 2.3. Схема к определению равнодействующей гидростатического давления на плоскую
поверхность
Избыточное гидростатическое давление в точке А будет равно
PA = γh = γ·0 = 0
Соответственно давление в точке В:
PB = γh = γH
где H – глубина жидкости в резервуаре.
Согласно первому свойству гидростатического давления, оно всегда направлено по нормали к ограждающей
поверхности. Следовательно, гидростатическое давление в точке В, величина которого равна γH,
надо направлять перпендикулярно к стенке АВ. Соединив точку А с концом
отрезка γH, получим треугольную эпюру распределения давления АВС с прямым
углом в точке В. Среднее значение давления будет равно
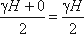
Если площадь наклонной стенки S=bL, то равнодействующая гидростатического давления равна
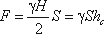
где hc = Н/2 – глубина погружения центра тяжести плоской поверхности под уровень жидкости.
Однако точка приложения равнодействующей гидростатического давления ц.д. не всегда будет совпадать
с центром тяжести плоской поверхности. Эта точка находится на расстоянии l от центра тяжести и равна
отношению момента инерции площадки относительно центральной оси к статическому моменту этой же площадки.
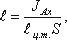
где JАx – момент инерции площади S относительно центральной оси, параллельной
Аx.
В частном случае, когда стенка имеет форму прямоугольника размерами bL и одна из его сторон лежит
на свободной поверхности с атмосферным давлением, центр давления ц.д. находится на расстоянии b/3
от нижней стороны.
Пусть жидкость заполняет резервуар, правая стенка которого представляет собой цилиндрическую криволинейную
поверхность АВС (рис.2.4), простирающуюся в направлении читателя на ширину b. Восстановим из
точки А перпендикуляр АО к свободной поверхности жидкости. Объем жидкости в отсеке АОСВ
находится в равновесии. Это значит, что силы, действующие на поверхности выделенного объема V, и
силы веса взаимно уравновешиваются.
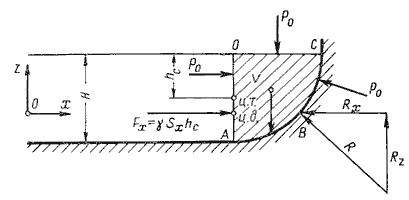
Рис. 2.4. Схема к определению равнодействующей гидростатического давления на
цилиндрическую поверхность
Представим, что выделенный объем V представляет собой твердое тело того же удельного веса, что и
жидкость (этот объем на рис.2.4 заштрихован). Левая поверхность этого объема (на чертеже вертикальная
стенка АО) имеет площадь Sx = bH, являющуюся проекцией криволинейной поверхности АВС на
плоскость yOz.
Cила гидростатического давления на площадь Sx равна Fx = γ
Sxhc.
С правой стороны на отсек будет действовать реакция R цилиндрической поверхности. Пусть точка
приложения и направление этой реакции будут таковы, как показано на рис.2.4. Реакцию R разложим на
две составляющие Rx и Rz.
Из действующих поверхностных сил осталось учесть только давление на свободной поверхности
Р0. Если резервуар открыт, то естественно, что давление Р0 одинаково
со всех сторон и поэтому взаимно уравновешивается.
На отсек АВСО будет действовать сила собственного веса G = γV, направленная вниз.
Спроецируем все силы на ось Ох:
Fx – Rx = 0 откуда Fx = Rx = γSxhc
Теперь спроецируем все силы на ось Оz:
Rx – G = 0 откуда Rx = G = γV
Составляющая силы гидростатического давления по оси Oy обращается в нуль, значит Ry = Fy = 0.
Таким образом, реакция цилиндрической поверхности в общем случае равна
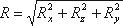
а поскольку реакция цилиндрической поверхности равна равнодействующей гидростатического давления R=F,
то делаем вывод, что
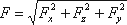
Тело, погруженное (полностью или частично) в жидкость, испытывает со стороны жидкости суммарное давление,
направленное снизу вверх и равное весу жидкости в объеме погруженной части тела.
Pвыт = ρжgVпогр
Для однородного тела плавающего на поверхности справедливо соотношение
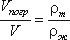
где: V – объем плавающего тела;
ρm – плотность тела.
Существующая теория плавающего тела довольно обширна, поэтому мы ограничимся рассмотрением лишь
гидравлической сущности этой теории.
Способность плавающего тела, выведенного из состояния равновесия, вновь возвращаться в это состояние
называется устойчивостью. Вес жидкости, взятой в объеме погруженной части судна называют
водоизмещением, а точку приложения равнодействующей давления (т.е. центр давления) – центром
водоизмещения. При нормальном положении судна центр тяжести С и центр водоизмещения d лежат
на одной вертикальной прямой O’-O”, представляющей ось симметрии судна и называемой осью плавания
(рис.2.5).
Пусть под влиянием внешних сил судно наклонилось на некоторый угол α, часть судна
KLM вышла из жидкости, а часть K’L’M’, наоборот, погрузилось в нее. При этом получили новое
положении центра водоизмещения d’. Приложим к точке d’ подъемную силу R и линию ее
действия продолжим до пересечения с осью симметрии O’-O”. Полученная точка m называется
метацентром, а отрезок mC = h называется метацентрической высотой. Будем считать h
положительным, если точка m лежит выше точки C, и отрицательным – в противном случае.
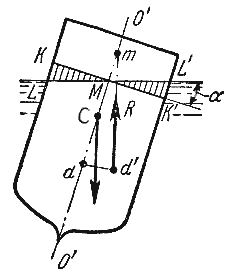
Рис. 2.5. Поперечный профиль судна
Теперь рассмотрим условия равновесия судна:
1) если h > 0, то судно возвращается в первоначальное положение;
2) если h = 0, то это случай безразличного равновесия;
3) если h<0, то это случай неостойчивого равновесия, при котором продолжается дальнейшее
опрокидывание судна.
Следовательно, чем ниже расположен центр тяжести и, чем больше метацентрическая высота, тем больше
будет остойчивость судна.
Как уже отмечалось выше, поверхность, во всех точках которой давление одинаково, называется поверхностью
уровня или поверхностью равного давления. При неравномерном или непрямолинейном движении на частицы
жидкости кроме силы тяжести действуют еще и силы инерции, причем если они постоянны по времени, то жидкость
принимает новое положение равновесия. Такое равновесие жидкости называется относительным покоем.
Рассмотрим два примера такого относительного покоя.
В первом примере определим поверхности уровня в жидкости, находящейся в цистерне, в то время как цистерна
движется по горизонтальному пути с постоянным ускорением a (рис.2.6).
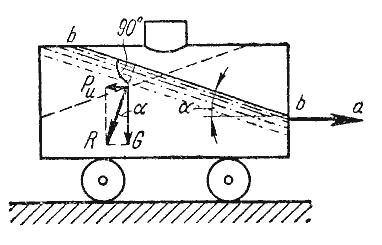
Рис. 2.6. Движение цистерны с ускорением
К каждой частице жидкости массы m должны быть в этом случае приложены ее вес G = mg и сила
инерции Pu, равная по величине ma. Равнодействующая 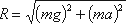
этих сил направлена к вертикали под углом α, тангенс которого равен
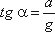
Так как свободная поверхность, как поверхность равного давления, должна быть нормальна к указанной
равнодействующей, то она в данном случае представит собой уже не горизонтальную плоскость, а наклонную,
составляющую угол α с горизонтом. Учитывая, что величина этого угла зависит только от
ускорений, приходим к выводу, что положение свободной поверхности не будет зависеть от рода находящейся в
цистерне жидкости. Любая другая поверхность уровня в жидкости также будет плоскостью, наклоненной к горизонту
под углом α. Если бы движение цистерны было не равноускоренным, а равнозамедленным,
направление ускорения изменилось бы на обратное, и наклон свободной поверхности обратился бы в другую сторону
(см. рис.2.6, пунктир).
В качестве второго примера рассмотрим часто встречающийся в практике случай относительного покоя жидкости
во вращающихся сосудах (например, в сепараторах и центрифугах, применяемых для разделения жидкостей). В этом
случае (рис.2.7) на любую частицу жидкости при ее относительном равновесии действуют массовые силы: сила
тяжести G = mg и центробежная сила Pu = mω2r, где r
– расстояние частицы от оси вращения, а ω – угловая скорость вращения сосуда.
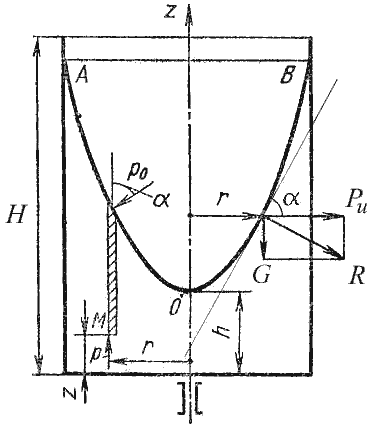
Рис. 2.7. Вращение сосуда с жидкостью
Поверхность жидкости также должна быть нормальна в каждой точке к равнодействующей этих сил R и
представит собой параболоид вращения. Из чертежа находим
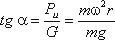
С другой стороны:
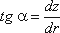
где z – координата рассматриваемой точки. Таким образом, получаем:
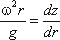
откуда
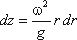
или после интегрирования
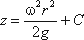
В точке пересечения кривой АОВ с осью вращения r = 0, z = h = C, поэтому окончательно будем
иметь
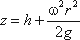
т.е. кривая АОВ является параболой, а свободная поверхность жидкости параболоидом. Такую же форму
имеют и другие поверхности уровня.
Для определения закона изменения давления во вращающейся жидкости в функции радиуса и высоты выделим
вертикальный цилиндрический объем жидкости с основанием в виде элементарной горизонтальной площадки dS
(точка М) на произвольном радиусе r и высоте z и запишем условие его равновесия в
вертикальном направлении. С учетом уравнения (2.11) будем иметь
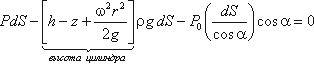
После сокращений получим
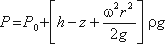
Это значит, что давление возрастает пропорционально радиусу r и уменьшается пропорционально
высоте z.
Проверить себя ( Тест )
Наверх страницы
Гидростатическое давление: формула и свойства.

Гидростатическое давление – это давление, производимое на жидкость силой тяжести.
Гидростатикой называется раздел гидравлики, в котором изучаются законы равновесия жидкостей и рассматривается практическое приложение этих законов.
Для того, чтобы понять гидростатику необходимо определиться в некоторых понятиях и определениях.
В этой статье мы подготовили для Вас, всю необходимую информацию о гидростатическом давлении, начиная от закона Паскаля и определения формулы гидростатического давления и до свойств давления и применения законов гидростатики в повседневной жизни.
Содержание статьи
- Закон Паскаля для гидростатики
- Определение и формула гидростатического давления
- Сила гидростатического давления
- Измерение гидростатического давления
- Свойства гидростатического давления + видеоматериалы
Закон Паскаля для гидростатики.
В 1653 году французским ученым Б. Паскалем был открыт закон, который принято называть основным законом гидростатики.
Звучит он так:
Давление на поверхность жидкости, произведенное внешними силами, передается в жидкости одинаково во всех направлениях.
Закон Паскаля легко понимается если взглянуть на молекулярное строение вещества. В жидкостях и газах молекулы обладают относительной свободой, они способны перемещаться друг относительно друга, в отличии от твердых тел. В твердых телах молекулы собраны в кристаллические решетки.
Относительная свобода, которой обладают молекулы жидкостей и газов, позволяет передавать давление производимое на жидкость или газ не только в направлении действия силы, но и во всех других направлениях.
Закон Паскаля для гидростатики нашел широкое распространение в промышленности. На этом законе основана работа гидроавтоматики, управляющей станками с ЧПУ, автомобилями и самолетами и многих других гидравлических машин.
Определение и формула гидростатического давления
Из описанного выше закона Паскаля вытекает, что:
Величина гидростатического давления не зависит от формы сосуда, в котором находится жидкость и определяется произведением
P = ρgh , где
ρ – плотность жидкости
g – ускорение свободного падения
h – глубина, на которой определяется давление.

Для иллюстрации этой формулы посмотрим на 3 сосуда разной формы.
Во всех трёх случаях давление жидкости на дно сосуда одинаково.
Полное давление жидкости в сосуде равно
P = P0 + ρgh, где
P0 – давление на поверхности жидкости. В большинстве случаев принимается равным атмосферному.
Сила гидростатического давления
Выделим в жидкости, находящейся в равновесии, некоторый объем, затем рассечем его произвольной плоскостью АВ на две части и мысленно отбросим одну из этих частей, например верхнюю. При этом мы должны приложить к плоскости АВ силы, действие которых будет эквивалентно действию отброшенной верхней части объема на оставшуюся нижнюю его часть.

Рассмотрим в плоскости сечения АВ замкнутый контур площадью ΔF, включающий в себя некоторую произвольную точку a. Пусть на эту площадь воздействует сила ΔP.
Тогда гидростатическое давление формула которого выглядит как
Рср = ΔP / ΔF
представляет собой силу, действующую на единицу площади, будет называться средним гидростатическим давлением или средним напряжением гидростатического давления по площади ΔF.
Истинное давление в разных точках этой площади может быть разным: в одних точках оно может быть больше, в других – меньше среднего гидростатического давления. Очевидно, что в общем случае среднее давление Рср будет тем меньше отличаться от истинного давления в точке а, чем меньше будет площадь ΔF, и в пределе среднее давление совпадет с истинным давлением в точке а.
Для жидкостей, находящихся в равновесии, гидростатическое давление жидкости аналогично напряжению сжатия в твердых телах.
Единицей измерения давления в системе СИ является ньютон на квадратный метр (Н/м2) – её называют паскалем (Па). Поскольку величина паскаля очень мала, часто применяют укрупненные единицы:
килоньютон на квадратный метр – 1кН/м2 = 1*103 Н/м2
меганьютон на квадратный метр – 1МН/м2 = 1*106 Н/м2
Давление равное 1*105 Н/м2 называется баром (бар).
В физической системе единицей намерения давления является дина на квадратный сантиметр (дина/м2), в технической системе – килограмм-сила на квадратный метр (кгс/м2). Практически давление жидкости обычно измеряют в кгс/см2, а давление равное 1 кгс/см2 называется технической атмосферой (ат).
Между всеми этими единицами существует следующее соотношение:
1ат = 1 кгс/см2 = 0,98 бар = 0,98 * 105 Па = 0,98 * 106дин = 104 кгс/м2
Следует помнить что между технической атмосферой (ат) и атмосферой физической (Ат) существует разница. 1 Ат = 1,033 кгс/см2 и представляет собой нормальное давление на уровне моря. Атмосферное давление зависит от высоты расположения места над уровнем моря.
Измерение гидростатического давления

На практике применяют различные способы учета величины гидростатического давления. Если при определении гидростатического давления принимается во внимание и атмосферное давление, действующее на свободную поверхность жидкости, его называют полным или абсолютным. В этом случае величина давления обычно измеряется в технических атмосферах, называемых абсолютными (ата).
Часто при учете давления атмосферное давление на свободной поверхности не принимают во внимание, определяя так называемое избыточное гидростатическое давление, или манометрическое давление, т.е. давление сверх атмосферного.
Манометрическое давление определяют как разность между абсолютным давлением в жидкости и давлением атмосферным.
Рман = Рабс – Ратм
и измеряют также в технических атмосферах, называемых в этом случае избыточными.
Случается, что гидростатическое давление в жидкости оказывается меньше атмосферного. В этом случае говорят, что в жидкости имеется вакуум. Величина вакуума равняется разнице между атмосферным и и абсолютным давлением в жидкости
Рвак = Ратм – Рабс
и измеряется в пределах от нуля до атмосферы.
Свойства гидростатического давления

Гидростатическое давление воды обладает двумя основными свойствами:
 Оно направлено по внутренней нормали к площади, на которую действует;
Оно направлено по внутренней нормали к площади, на которую действует;
 Величина давления в данной точке не зависит от направления (т.е. от ориентированности в пространстве площадки, на которой находится точка).
Величина давления в данной точке не зависит от направления (т.е. от ориентированности в пространстве площадки, на которой находится точка).
Первое свойство является простым следствием того положения, что в покоящейся жидкости отсутствуют касательные и растягивающие усилия.
Предположим, что гидростатическое давление направлено не по нормали, т.е. не перпендикулярно, а под некоторым углом к площадке. Тогда его можно разложить на две составляющие – нормальную и касательную. Наличие касательной составляющей из-за отсутствия в покоящейся жидкости сил сопротивления сдвигающим усилиям неизбежно привело бы к движению жидкости вдоль площадки, т.е. нарушило бы её равновесие.
Поэтому единственным возможным направлением гидростатического давления является его направление по нормали к площадке.
Если предположить что гидростатическое давление направлено не по внутренней, а по внешней нормали, т.е. не внутрь рассматриваемого объекта а наружу от него, то вследствие того, что жидкость не оказывает сопротивления растягивающим усилиям – частицы жидкости пришли бы в движение и её равновесие было бы нарушено.
Следовательно, гидростатическое давление воды всегда направлено по внутренней нормали и представляет собой сжимающее давление.
Из этого же правило следует, что если измениться давление в какой-то точке, то на такую же величину измениться давление в любой другой точке этой жидкости. В этом заключается закон Паскаля, который формулируется следующим образом: Давление производимое на жидкость, передается внутри жидкости во все стороны с одинаковой силой.
На применение этого закона основываются действие машин, работающих под гидростатическим давлением.
Ещё одним фактором влияющим на величину давления является вязкость жидкости, которой до недавнего времени приято было пренебрегать. С появлением агрегатов работающих на высоком давлении вязкость пришлось так же учитывать. Оказалось, что при изменении давления, вязкость некоторых жидкостей, таких как масла, может изменяться в несколько раз. А это уже определяет возможность использовать такие жидкости в качестве рабочей среды.


