Как найти гиперболу в математике - Сайт, где вы сможете решить свои вопросы

Что такое гипербола? Как построить гиперболу? (Для школьников (7-11 классов)).

Математическая гипербола.

Функция заданная формулой (y=frac{k}{x}), где к неравно 0. Число k называется коэффициентом обратной пропорциональности.
Определение гиперболы.
График функции (y=frac{k}{x}) называют гиперболой. Где х является независимой переменной, а у — зависимой.

Что нужно знать, чтобы построить гиперболу?
Теперь обсудим свойства гиперболы:

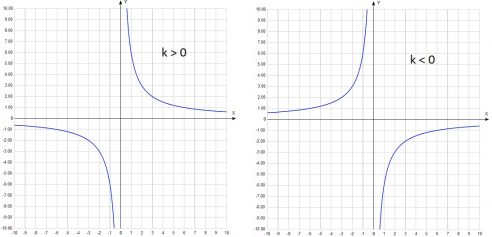
1. Ветви гиперболы. Если k>o, то ветви гиперболы находятся в 1 и 3 четверти. Если k<0, то ветви гиперболы находятся во 2 и 4 четверти.
гипербола, где k>0 ветви гиперболы находятся в 1 и 3 четверти

гипербола, где k<0 ветви гиперболы находятся во 2 и 4 четверти

2.Асимптоты гиперболы. Чтобы найти асимптоты гиперболы необходимо,иногда, уравнение гиперболы упростить. Рассмотрим на примере:
Пример №1:
$$y=frac{1}{x}$$
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому х не равен 0.
$$yneqcolor{red} {frac{1}{x}}+0$$
(frac{1}{x}) дробь отбрасываем, для того чтобы найти вторую асимптоту.
Остается простое число
y≠0 это вторая асимптота.
И так, асимптоты x≠0 и y≠0 в данном примере совпадают с осями координат OX и OY.
k=1, значит гипербола будет находится в первой и третьей четверти. k всегда находится в числители.
Построим примерный график гиперболы.

Пример №2:
$$y=frac{1}{x+2}-1$$
Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому х+2 неравен 0.
х+2≠0
х≠-2 это первая асимптота

Находим вторую асимптоту.

$$y=color{red} {frac{1}{x+2}}-1$$

Дробь (color{red} {frac{1}{x+2}}) отбрасываем
Остается y≠ -1 это вторая асимптота.

Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-2 и y≠-1):

Пример №3:

$$begin{align*}
&y=frac{2+x}{1+x} \\
&y=frac{color{red} {1+1}+x}{1+x} \\
&y=frac{1}{1+x}+frac{1+x}{1+x}\\
&y=frac{1}{1+x}+1\\
&y=frac{1}{color{red} {1+x}}+1
end{align*}$$

Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому 1+х неравен 0.
1+х≠0
х≠-1 это первая асимптота.

Находим вторую асимптоту.

$$y=color{red}{frac{1}{1+x}}+1$$

(color{red}{frac{1}{1+x}}) Дробь убираем.

Остается y≠1 это вторая асимптота.

Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-1 и y≠1):

3. У гиперболы есть центр симметрии относительно начала координат. Рассмотрим на примере:

$$y=frac{1}{x}$$

Возьмем точку А(1;1) с координатами, которая находится на графике у=1/х. На этом же графике лежит точка B(-1;-1). Видно, что точка А симметрична точке В относительна начала координат.

4. Оси симметрии гиперболы. У гиперболы две оси симметрии. Рассмотрим пример:

$$y=frac{1}{x}$$

Первой осью симметрии является прямая y=x. Посмотрим точки (0,5;2) и (2;0,5) и еще точки (-0,5;-2) и (-2;-0,5). Эти точки расположены по разные стороны данной прямой, но на равных расстояниях от нее, они симметричны относительно этой прямой.

Вторая ось симметрии это прямая y=-x.

5. Гипербола нечетная функция.

$$f(-x)=frac{1}{-x}=-frac{1}{x}=-f(x)$$

6. Область определения гиперболы и область значения гиперболы. Область определения смотрим по оси х. Область значения смотрим по оси у. Рассмотрим на примере:

$$y=frac{-1}{x-1}-1$$

а) Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому x-1 неравен 0.
x-1≠0
х≠1 это первая асимптота.

Находим вторую асимптоту.

$$y=color{red} {frac{-1}{x-1}}-1$$

Дробь (color{red} {frac{-1}{x-1}}) удаляем.

Остается y≠ -1 это вторая асимптота.

б) k=-1, значит ветви гиперболы будут находится во второй и четвертой четверти.

в) Возьмем несколько дополнительных точек и отметим их на графике.
х=0 y=0
x=-1 y=-0,5
x=2 y=-2
x=3 y=-1,5

г) Область определения смотрим по оси х. Графика гиперболы не существует по асимптоте х≠1, поэтому область определения будет находится
х ∈ (-∞;1)U(1;+∞).

д) Область значения смотрим по оси y. График гиперболы не существует по асимптоте y≠ -1, поэтому область значения будет находится
y ∈ (-∞;-1)U(-1;+∞).

е) функция возрастает на промежутке x ∈ (-∞;1)U(1;+∞).

7. Убывание и возрастание функции гиперболы. Если k>0, функция убывающая. Если k<0 функция возрастающая.

8. Для более точного построения взять несколько дополнительных точек. Пример смотреть в пункте №6.

Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
реклама

Источник

У этого термина существуют и другие значения, см. Гипербола.

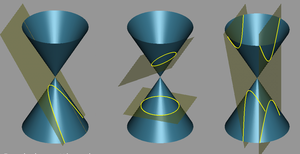
Сечения конусов плоскостью (с эксцентриситетом, большим единицы)

Гипе́рбола (др.-греч. ὑπερβολή, от ὑπερ — «верх» + βαλειν — «бросать») — геометрическое место точек M евклидовой плоскости, для которых абсолютное значение разности расстояний от M до двух выделенных точек $F_{1}$ и $F_{2}$ (называемых фокусами) постоянно. Точнее,

${bigl |}|F_{1}M|-|F_{2}M|{bigr |}=2a,$

причём $|F_{1}F_{2}|>2a>0.$

Наряду с эллипсом и параболой, гипербола является коническим сечением и квадрикой. Гипербола может быть определена как коническое сечение с эксцентриситетом, бо́льшим единицы.

История[править | править код]

Термин «гипербола» (греч. ὑπερβολή — избыток) был введён Аполлонием Пергским (ок. 262 год до н. э. — ок. 190 год до н. э.), поскольку задача о построении точки гиперболы сводится к задаче о приложении с избытком.

Определения[править | править код]

Гипербола может быть определена несколькими путями.

Коническое сечение[править | править код]

Три основных конических сечения

Гипербола может быть определена как множество точек, образуемое в результате сечения кругового конуса плоскостью, отсекающей обе части конуса. Другими результатами сечения конуса плоскостью являются парабола, эллипс, а также такие вырожденные случаи, как пересекающиеся и совпадающие прямые и точка, возникающие, когда секущая плоскость проходит через вершину конуса. В частности, пересекающиеся прямые можно считать вырожденной гиперболой, совпадающей со своими асимптотами.

Как геометрическое место точек[править | править код]

Через фокусы[править | править код]

Гипербола может быть определена как геометрическое место точек, абсолютная величина разности расстояний от которых до двух заданных точек, называемых фокусами, постоянна.

Для сравнения: кривая постоянной суммы расстояний от любой её точки до фокусов — эллипс, постоянного отношения — окружность Аполлония, постоянного произведения — овал Кассини.

Через директрису и фокус[править | править код]

Геометрическое место точек, для которых отношение расстояния до фокуса и до заданной прямой, называемой директрисой, постоянно и больше единицы, называется гиперболой. Заданная постоянная называется эксцентриситетом гиперболы.

Связанные определения[править | править код]

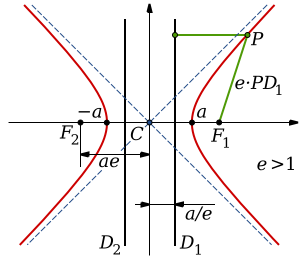
Асимптоты гиперболы (красные кривые), показанные голубым пунктиром, пересекаются в центре гиперболы, C. Два фокуса гиперболы обозначены как F₁ и F₂. Директрисы гиперболы обозначены линиями двойной толщины и обозначены D₁ и D₂. Эксцентриситет ε равен отношению расстояний точки P на гиперболе до фокуса и до соответствующей директрисы (показаны зелёным). Вершины гиперболы обозначены как ±a. Параметры гиперболы обозначают следующее:

a — расстояние от центра C до каждой из вершин
b — длина перпендикуляра к оси абсцисс, восставленного из каждой из вершин до пересечения с асимптотой
c — расстояние от центра C до любого из фокусов, F₁ и F₂,
θ — угол, образованный каждой из асимптот и осью, проведённой между вершинами

Гипербола состоит из двух отдельных кривых, которые называют ветвями.
Ближайшие друг к другу точки двух ветвей гиперболы называются вершинами.
Кратчайшее расстояние между двумя ветвями гиперболы называется большой осью гиперболы.
Середина большой оси называется центром гиперболы.
Расстояние от центра гиперболы до одной из вершин называется большой полуосью гиперболы.
- Обычно обозначается a.
Расстояние от центра гиперболы до одного из фокусов называется фокальным расстоянием.
- Обычно обозначается c.
Оба фокуса гиперболы лежат на продолжении большой оси на одинаковом расстоянии от центра гиперболы. Прямая, содержащая большую ось гиперболы, называется действительной, или поперечной, осью гиперболы.
Прямая, перпендикулярная действительной оси и проходящая через её центр, называется мнимой, или сопряжённой, осью гиперболы.
Отрезок между фокусом гиперболы и гиперболой, перпендикулярный её действительной оси, называется фокальным параметром.
Расстояние от фокуса до асимптоты гиперболы называется прицельным параметром.
- Обычно обозначается b.
В задачах, связанных с движением тел по гиперболическим траекториям, расстояние от фокуса до ближайшей вершины гиперболы называется перицентрическим расстоянием
- Обычно обозначается $r_{p}$ .

Соотношения[править | править код]

Для характеристик гиперболы, определённых выше, существуют следующие соотношения

${displaystyle c^{2}=a^{2}+b^{2}}$ .
.
${displaystyle b^{2}=a^{2}left(varepsilon ^{2}-1right)}$ .
${displaystyle r_{p}=aleft(varepsilon -1right)}$ .
${displaystyle a={frac {p}{varepsilon ^{2}-1}}}$ .
${displaystyle b={frac {p}{sqrt {varepsilon ^{2}-1}}}}$ .
${displaystyle c={frac {pvarepsilon }{varepsilon ^{2}-1}}}$ .
$p={frac {b^{2}}{a}}$ .

Равнобочная гипербола[править | править код]

Гиперболу, у которой a=b , называют равнобочной, или равносторонней.
Равнобочная гипербола в некоторой прямоугольной системе координат описывается уравнением

$xy=a^{2}/2,$

при этом фокусы гиперболы располагаются в точках (a, a) и (−a, −a).
Равнобочная гипербола является графиком обратной пропорциональности, задаваемой формулой

${displaystyle y={frac {k}{x}},quad kneq 0.}$

Эксцентриситет такой гиперболы равен .

Гипербола Киперта[править | править код]

Точка на гиперболе Киперта

Равнобочная гипербола как гипербола Киперта может быть определена через треугольники в трилинейных координатах^[1] в виде геометрического места точек (см. рис.):

Если три треугольника , и построены на сторонах треугольника , являются подобными, равнобедренными с основаниями на сторонах исходного треугольника, и одинаково расположенными (то есть все они построены либо с внешней стороны, либо с внутренней стороны), то прямые , и пересекаются в одной точке .

Если общий угол при основании равен theta , то вершины трёх треугольников имеют следующие трилинейные координаты:

{displaystyle X{big (}-sin theta :sin(C+theta ):sin(B+theta ){big )},}

{displaystyle Y{big (}sin(C+theta ):-sin theta :sin(A+theta ){big )},}

{displaystyle Z{big (}sin(B+theta ):sin(A+theta ):-sin theta {big )}.}

Уравнения[править | править код]

Декартовы координаты[править | править код]

Гипербола задаётся уравнением второй степени в декартовых координатах (x, y) на плоскости:

$A_{{xx}}x^{{2}}+2A_{{xy}}xy+A_{{yy}}y^{{2}}+2B_{{x}}x+2B_{{y}}y+C,=,0$

где коэффициенты A_xx, A_xy, A_yy, B_x, B_y, и C удовлетворяют следующему соотношению

${displaystyle D={begin{vmatrix}A_{xx}&A_{xy}\A_{xy}&A_{yy}end{vmatrix}}<0}$

$Delta :={begin{vmatrix}A_{{xx}}&A_{{xy}}&B_{{x}}\A_{{xy}}&A_{{yy}}&B_{{y}}\B_{{x}}&B_{{y}}&Cend{vmatrix}}not =0.$

Канонический вид[править | править код]

Перемещением центра гиперболы в начало координат и вращением её относительно центра уравнение гиперболы можно привести к каноническому виду:

${frac {{x}^{{2}}}{a^{{2}}}}-{frac {{y}^{{2}}}{b^{{2}}}}=1$

где — действительная полуось гиперболы; — мнимая полуось гиперболы^[2]. В этом случае эксцентриситет равен

${displaystyle varepsilon ={frac {c}{a}}={sqrt {1+{frac {b^{2}}{a^{2}}}}}.}$

Полярные координаты[править | править код]

Гипербола в полярных координатах

Если полюс находится в фокусе гиперболы, а вершина гиперболы лежит на продолжении полярной оси, то

$r={frac {p}{1-varepsilon cos varphi }}$

Если полюс находится в фокусе гиперболы, а полярная ось параллельна одной из асимптот, то

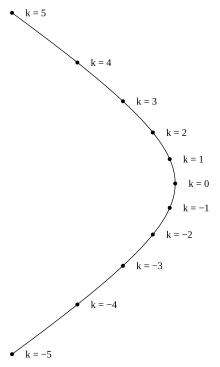
${frac {1}{r}}={frac {a}{b^{2}}}left(1-cos theta right)+{frac {1}{b}}sin theta$

Уравнения в параметрической форме[править | править код]

Подобно тому, как эллипс может быть представлен уравнениями в параметрической форме, в которые входят тригонометрические функции, гипербола в прямоугольной системе координат, центр которой совпадает с её центром, а ось абсцисс проходит через фокусы, может быть представлена уравнениями в параметрической форме, в которые входят гиперболические функции^[3].

${displaystyle {begin{cases}x=pm aoperatorname {ch} t,\y=boperatorname {sh} t,end{cases}}quad -infty <t<+infty .}$

В первом уравнении знак «+» соответствует правой ветви гиперболы, а «−» — её левой ветви.

Свойства[править | править код]

Оптическое свойство. Свет от источника, находящегося в одном из фокусов гиперболы, отражается второй ветвью гиперболы таким образом, что продолжения отраженных лучей пересекаются во втором фокусе.
Для любой точки, лежащей на гиперболе, отношение расстояний от этой точки до фокуса к расстоянию от этой же точки до директрисы есть величина постоянная.
Гипербола обладает зеркальной симметрией относительно действительной и мнимой осей, а также вращательной симметрией при повороте на угол 180° вокруг центра гиперболы.
Каждая гипербола имеет сопряжённую гиперболу, для которой действительная и мнимая оси меняются местами, но асимптоты остаются прежними. Сопряжённая гипербола не является результатом поворота начальной гиперболы на угол 90°; гиперболы различаются формой при .
Отрезок касательной в каждой точке гиперболы, заключенный между двумя асимптотами гиперболы, делится точкой касания пополам и отсекает от двух асимптот треугольник постоянной площади.

Асимптоты[править | править код]

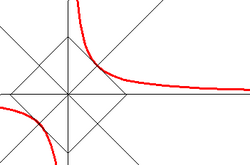
Две сопряжённые гиперболы (голубая и зелёная) обладают совпадающими асимптотами (красные). Эти гиперболы единичные и равнобочные, так как a = b = 1

Уравнения асимптот для гиперболы, заданной в каноническом виде

${frac {x^{2}}{a^{2}}}-{frac {y^{2}}{b^{2}}}=1$

выводятся следующим образом. Пусть . Предположим, что асимптота существует и имеет вид . Тогда

${displaystyle k=lim _{xto +infty }{frac {f(x)}{x}}=lim _{xto +infty }{frac {{frac {b}{a}}{sqrt {x^{2}-a^{2}}}}{x}}=lim _{xto +infty }{frac {b}{a}}left({frac {sqrt {x^{2}-a^{2}}}{x}}right)=lim _{xto +infty }{frac {b}{a}}left({sqrt {1-{frac {a^{2}}{x^{2}}}}}right)={frac {b}{a}},}$

${displaystyle l=lim _{xto +infty }left(f(x)-kxright)=lim _{xto +infty }{frac {b}{a}}left({sqrt {x^{2}-a^{2}}}-xright)=lim _{xto +infty }{frac {b}{a}}cdot {frac {a^{2}}{{sqrt {x^{2}-a^{2}}}+x}}=0.}$

Таким образом, уравнения двух асимптот имеют вид:

${displaystyle y=pm {frac {b}{a}}x}$

или

${displaystyle {frac {x}{a}}pm {frac {y}{b}}=0.}$

Диаметры и хорды[править | править код]

Диаметром гиперболы, как и всякого конического сечения, является прямая, проходящая через середины параллельных хорд. Каждому направлению параллельных хорд соответствует свой сопряжённый диаметр. Все диаметры гиперболы проходят через её центр. Диаметр, соответствующий хордам, параллельным мнимой оси, есть действительная ось; диаметр соответствующий хордам, параллельным действительной оси, есть мнимая ось.

Угловой коэффициент параллельных хорд и угловой коэффициент $k_{1}$ соответствующего диаметра связан соотношением

${displaystyle kcdot k_{1}=varepsilon ^{2}-1={frac {b^{2}}{a^{2}}}.}$

Если диаметр a делит пополам хорды, параллельные диаметру b, то диаметр b делит пополам хорды, параллельные диаметру a. Такие диаметры называются взаимно сопряжёнными. Главными диаметрами называются взаимно сопряжённые и взаимно перпендикулярные диаметры. У гиперболы есть только одна пара главных диаметров — действительная и мнимая оси.

Определение центра гиперболы

Касательная и нормаль[править | править код]

Поскольку гипербола является гладкой кривой, в каждой её точке (x₀, y₀) можно провести касательную и нормаль. Уравнение касательной к гиперболе, заданной каноническим уравнением, имеет вид:

${frac {xx_{0}}{a^{2}}}-{frac {yy_{0}}{b^{2}}}=1$

или, что то же самое,

$y=y_{0}+{frac {b^{2}x_{0}}{a^{2}y_{0}}}left(x-x_{0}right)$

Вывод уравнения касательной
Уравнение касательной произвольной плоской линии имеет вид $y-y_{0}=y'left(x_{0},y_{0}right)cdot left(x-x_{0}right)$ Каноническое уравнение гиперболы можно представить в виде пары функций $y=pm {sqrt {{frac {b^{2}}{a^{2}}}x^{2}-b^{2}}}$ . Тогда производная этих функций имеет вид $y'=pm {frac {{frac {b^{2}}{a^{2}}}x}{{sqrt {{frac {b^{2}}{a^{2}}}x^{2}-b^{2}}}}}={frac {b^{2}}{a^{2}}}{frac {x}{y}}$ . Подставив это уравнение в общее уравнение касательной, получим $y-y_{0}={frac {b^{2}}{a^{2}}}{frac {x_{0}}{y_{0}}}left(x-x_{0}right)$ ${frac {xx_{0}}{a^{2}}}-{frac {yy_{0}}{b^{2}}}={frac {x_{0}^{2}}{a^{2}}}-{frac {y_{0}^{2}}{b^{2}}}=1$

Вывод уравнения касательной

Уравнение касательной произвольной плоской линии имеет вид

$y-y_{0}=y'left(x_{0},y_{0}right)cdot left(x-x_{0}right)$

Каноническое уравнение гиперболы можно представить в виде пары функций

$y=pm {sqrt {{frac {b^{2}}{a^{2}}}x^{2}-b^{2}}}$

Тогда производная этих функций имеет вид

$y'=pm {frac {{frac {b^{2}}{a^{2}}}x}{{sqrt {{frac {b^{2}}{a^{2}}}x^{2}-b^{2}}}}}={frac {b^{2}}{a^{2}}}{frac {x}{y}}$

Подставив это уравнение в общее уравнение касательной, получим

$y-y_{0}={frac {b^{2}}{a^{2}}}{frac {x_{0}}{y_{0}}}left(x-x_{0}right)$

${frac {xx_{0}}{a^{2}}}-{frac {yy_{0}}{b^{2}}}={frac {x_{0}^{2}}{a^{2}}}-{frac {y_{0}^{2}}{b^{2}}}=1$

Уравнение нормали к гиперболе имеет вид:

$y=y_{0}-{frac {a^{2}}{b^{2}}}{frac {y_{0}}{x_{0}}}left(x-x_{0}right)$

Вывод уравнения нормали
Уравнение нормали произвольной плоской линии имеет вид $y-y_{0}={frac {1}{y'left(x_{0},y_{0}right)}}left(x_{0}-xright)$ . Каноническое уравнение гиперболы можно представить в виде пары функций $y=pm {sqrt {{frac {b^{2}}{a^{2}}}x^{2}-b^{2}}}$ . Тогда производная этих функций имеет вид $y'=pm {frac {{frac {b^{2}}{a^{2}}}x}{{sqrt {{frac {b^{2}}{a^{2}}}x^{2}-b^{2}}}}}={frac {b^{2}}{a^{2}}}{frac {x}{y}}$ . Подставив это уравнение в общее уравнение нормали, получим $y-y_{0}=-{frac {a^{2}}{b^{2}}}{frac {y_{0}}{x_{0}}}left(x-x_{0}right)$ .

Вывод уравнения нормали

Уравнение нормали произвольной плоской линии имеет вид

$y-y_{0}={frac {1}{y'left(x_{0},y_{0}right)}}left(x_{0}-xright)$

Каноническое уравнение гиперболы можно представить в виде пары функций

$y=pm {sqrt {{frac {b^{2}}{a^{2}}}x^{2}-b^{2}}}$

Тогда производная этих функций имеет вид

$y'=pm {frac {{frac {b^{2}}{a^{2}}}x}{{sqrt {{frac {b^{2}}{a^{2}}}x^{2}-b^{2}}}}}={frac {b^{2}}{a^{2}}}{frac {x}{y}}$

Подставив это уравнение в общее уравнение нормали, получим

$y-y_{0}=-{frac {a^{2}}{b^{2}}}{frac {y_{0}}{x_{0}}}left(x-x_{0}right)$

Кривизна и эволюта[править | править код]

Синим цветом показана гипербола. Зелёным цветом — эволюта правой ветви этой гиперболы (эволюта левой ветви вне рисунка. Красным цветом показан круг, соответствующий кривизне гиперболы в её вершине)

Кривизна гиперболы в каждой её точке (x, y) определяется из выражения:

$K={frac {ab}{left({frac {a^{2}}{b^{2}}}y^{2}+{frac {b^{2}}{a^{2}}}x^{2}right)^{{3/2}}}}$

Соответственно, радиус кривизны имеет вид:

$R={frac 1K}={frac {left({frac {a^{2}}{b^{2}}}y^{2}+{frac {b^{2}}{a^{2}}}x^{2}right)^{{3/2}}}{ab}}$

В частности, в точке (a, 0) радиус кривизны равен

$Rleft(a,0right)={frac {b^{2}}{a}}=p$

Вывод формулы для радиуса кривизны
Формула для радиуса кривизны плоской линии, заданной параметически, имеет вид: $R_{c}={frac {left(x'^{2} +y'^{2}right)^{{3/2}}}{left\|x'y''-x''y'right\|}}$ . Воспользуемся параметрическим представлением гиперболы: ${begin{cases}x=acdot {mathrm {ch}},(t)\y=bcdot {mathrm {sh}},(t)end{cases}}$ Тогда, первая производная x и y по t имеет вид ${begin{cases}x'=acdot {mathrm {sh}},(t)={frac {a}{b}}y\y'=bcdot {mathrm {ch}},(t)={frac {b}{a}}xend{cases}}$ , а вторая производная – ${begin{cases}x''=acdot {mathrm {ch}},(t)=x\y''=bcdot {mathrm {sh}},(t)=yend{cases}}$ Подставляя эти значения в формулу для кривизны получаем: $R_{c}={frac {left({frac {a^{2}}{b^{2}}}y^{2} +{frac {b^{2}}{a^{2}}}x^{2}right)^{{3/2}}}{left\|a{frac {y^{2}}{b}}-b{frac {x^{2}}{a}}right\|}}={frac {left({frac {a^{2}}{b^{2}}}y^{2} +{frac {b^{2}}{a^{2}}}x^{2}right)^{{3/2}}}{ableft\|{frac {y^{2}}{b}}-{frac {x^{2}}{a}}right\|}}={frac {left({frac {a^{2}}{b^{2}}}y^{2} +{frac {b^{2}}{a^{2}}}x^{2}right)^{{3/2}}}{ab}}$ .

Вывод формулы для радиуса кривизны

Формула для радиуса кривизны плоской линии, заданной параметически, имеет вид:

$R_{c}={frac {left(x'^{2} +y'^{2}right)^{{3/2}}}{left|x'y''-x''y'right|}}$

Воспользуемся параметрическим представлением гиперболы:

${begin{cases}x=acdot {mathrm {ch}},(t)\y=bcdot {mathrm {sh}},(t)end{cases}}$

Тогда, первая производная x и y по t имеет вид

${begin{cases}x'=acdot {mathrm {sh}},(t)={frac {a}{b}}y\y'=bcdot {mathrm {ch}},(t)={frac {b}{a}}xend{cases}}$

а вторая производная –

${begin{cases}x''=acdot {mathrm {ch}},(t)=x\y''=bcdot {mathrm {sh}},(t)=yend{cases}}$

Подставляя эти значения в формулу для кривизны получаем:

$R_{c}={frac {left({frac {a^{2}}{b^{2}}}y^{2} +{frac {b^{2}}{a^{2}}}x^{2}right)^{{3/2}}}{left|a{frac {y^{2}}{b}}-b{frac {x^{2}}{a}}right|}}={frac {left({frac {a^{2}}{b^{2}}}y^{2} +{frac {b^{2}}{a^{2}}}x^{2}right)^{{3/2}}}{ableft|{frac {y^{2}}{b}}-{frac {x^{2}}{a}}right|}}={frac {left({frac {a^{2}}{b^{2}}}y^{2} +{frac {b^{2}}{a^{2}}}x^{2}right)^{{3/2}}}{ab}}$

Координаты центров кривизны задаются парой уравнений:

${begin{cases}x_{c}={frac {x^{3}}{a^{2}}}left(1+{frac {b^{2}}{a^{2}}}right)\y_{c}=-{frac {y^{3}}{b^{2}}}left(1+{frac {a^{2}}{b^{2}}}right)end{cases}}$

Подставив в последнюю систему уравнений вместо x и y их значения из параметрического представления гиперболы, получим пару уравнений, задающих новую кривую, состоящую из центров кривизны гиперболы. Эта кривая называется эволютой гиперболы.

${begin{cases}x=pm a,{mathrm {ch}}^{3},tleft(1+{frac {b^{2}}{a^{2}}}right)\y=b,{mathrm {sh}}^{3},tleft(1+{frac {a^{2}}{b^{2}}}right)end{cases}}$

Эллиптическая система координат

Обобщение[править | править код]

Гипербола есть синусоидальная спираль при .

Применение[править | править код]

Семейство конфокальных (софокусных) гипербол вместе с семейством софокусных эллипсов образуют двумерную эллиптическую систему координат.

Другие ортогональные двумерные координатные системы, построенные с помощью гипербол, могут быть получены с помощью других конформных преобразований. Например, преобразование w = z² отображает декартовы координаты в два семейства ортогональных гипербол.

Инверсией гиперболы с центром, лежащим в её собственном центре, в фокусе или на вершине можно получить соответственно лемнискату Бернулли, улитку Паскаля или строфоиду.

Гиперболы можно видеть на многих солнечных часах. В течение любого дня года Солнце описывает окружность на небесной сфере, и его лучи, падающие на верхушку гномона солнечных часов, описывают конус света. Линия пересечения этого конуса с плоскостью горизонтальных или вертикальных солнечных часов является коническим сечением. На наиболее населённых широтах и в большую часть года это коническое сечение является гиперболой. На солнечных часах часто показаны линии, описываемые тенью от верхушки гномона в течение дня для нескольких дней года (например, дней летнего и зимнего солнцестояний), таким образом, на них часто можно видеть определённые гиперболы, вид которых различен для различных дней года и различных широт.

Гиперболы, соответствующие на плоскости траекториям первых межзвёздных объектов — 1I/Оумуамуа (зелёная линия) и 2I/Borisov (синия линия)

АМС, преодолевая притяжение основного влияющего на неё тела и далеко улетая от него, при отсутствии возмущений, должна двигаться по гиперболической траектории или параболической траектории, поскольку в таком случае теоретически возможно удаление до бесконечности от данного тела^[4]. В частности, гиперболическими относительно Солнца являются траектории АМС «Вояджер-1» и АМС «Вояджер-2», с эксцентриситетом 3,7 и 6,3 и большой полуосью 480,9 млн км и 601,1 млн км соответственно^[5]^[6]. Гиперболическая траектория небесного тела в Солнечной системе может указывать на его межзвёздное происхождение. В конце 2010-х годов были открыты первый межзвёздный астероид и первая межзвёздная комета^[7], их траектории — гиперболические. Однако известные ранее кометы с гиперболической траекторией небольшого эксцентриситета только собираются стать межзвёздными: испытав во время своей «жизни» в Солнечной системе возмущение от такой планеты, как Юпитер, они ложатся на межзвёздный курс^[8].

См. также[править | править код]

Гиперболоид
Гиперболы, описанные около треугольника
Каустика
Конические сечения
Кривая второго порядка
Окружность
Парабола
Эллипс
Кривая постоянной суммы расстояний между двумя точками — эллипс,
Кривая постоянной разности расстояний между двумя точками — гипербола,
Кривая постоянного отношения — окружность Аполлония,
Кривая постоянного произведения — овал Кассини.
Сглаженный восьмиугольник § Построение

Примечания[править | править код]

↑ Eddy, R. H. and Fritsch, R. The Conics of Ludwig Kiepert: A Comprehensive Lesson in the Geometry of the Triangle. Math. Mag. 67, pp. 188—205, 1994.
↑ Шнейдер В.Е. Краткий курс высшей математики. — Рипол Классик. — ISBN 9785458255349.
↑ Погорелов А. В. Геометрия. — М.: Наука, 1983. — С. 15—16. — 288 с.
↑ Сихарулидзе Ю. Г. Баллистика летательных аппаратов. — М.: Наука, 1982. — С. 162—163. — 5750 экз.
↑ Voyager – Hyperbolic Orbital Elements. НАСА. Дата обращения: 29 октября 2019. Архивировано 6 мая 2021 года.
↑ Ulivi P., Harland D. M. Robotic Exploration of the Solar System. Part I: The Golden Age 1957-1982. — Springer, Praxis, 2007. — P. 441. — ISBN 978-0-387-49326-8. Содержит эксцентриситет орбиты АМС «Вояджер-2» относительно Солнца после пролёта Нептуна.
↑ Naming of New Interstellar Visitor: 2I/Borisov. МАС (24 сентября 2019). Дата обращения: 24 сентября 2019. Архивировано 23 апреля 2020 года.
↑ Carl Sagan, Ann Druyan. Comet. — New York: Ballantine Books, 1997. — P. 104. — ISBN 0-345-41222-2.

Литература[править | править код]

Бронштейн И. Гипербола // Квант. — 1975. — № 3.
Граве Д. А. Гиперболы // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
Математическая энциклопедия (в 5 томах). М.: Советская энциклопедия, 1982.
Маркушевич А. И. Замечательные кривые // Популярные лекции по математике. — Гостехиздат, 1952. — Вып. 4. Архивировано 14 сентября 2008 года.

Источник

В данной публикации мы рассмотрим, что такое гипербола, приведем формулу, с помощью которой задается ее функция, а также на практических примерах разберем алгоритм построения данного вида графика.

Определение и функция гиперболы
Алгоритм построения гиперболы
- Пример 1
- Пример 2

Определение и функция гиперболы

Гипербола – это график функции обратной пропорциональности, которая в общем виде задается следующей формулой:

Здесь:

x – независимая переменная;
k ≠ 0;
при k > 0 гипербола расположена в I и III четвертях координатной плоскости;
при k < 0 график находится во II и IV четвертях.

На рисунке ниже изображен пример гиперболы.

Линии графика (зеленым цветом) называются его ветвями.
Оси абсцисс и ординат (Ox и Oy) являются асимптотами гиперболы, т.е. ветви бесконечно к ним приближаются, но никогда их не коснутся и не пересекут.
Ось симметрии (синим цветом) – это прямая:
- y = x (при k > 0)
- y = -x (при k < 0)

Смещение асимптот

Допустим у нас есть функция, заданная формулой:

В этом случае:

x = a – это вертикальная асимптота графика (при a ≠ 0) вместо оси Oy;
y = b – горизонтальная асимптота (при b ≠ 0) вместо оси Ox.

Канонический вид уравнения гиперболы (координатные оси совпадают с осями графика):

Алгоритм построения гиперболы

Пример 1

Дана функция y = ⁴/_x. Построим ее график.

Решение

Так как k > 0, следовательно, гипербола будет находиться в I и III координатных четвертях.

Чтобы построить график, сначала нужно составить таблицу соответствия значений x и y. То есть мы берем конкретное значение x, подставляем его в формулу функции и получаем y.


x	y	Расчет y
0,5	8	⁴ / _0,5 = 8
1	4	⁴ / ₁ = 4
2	2	⁴ / ₂ = 2
4	1	⁴ / ₄ = 1
8	0,5	⁴ / ₈ = 0,5

Теперь отмечаем найденные точки на координатной плоскости и соединяем их плавной линией, которая будет стремиться к осям координат. В итоге получится ветвь гиперболы, расположенная в первой четверти.

Чтобы построить ветвь в третьей четверти, вместо x в формулу подставляем -x. Так мы вычислим значения y.


x	y	Расчет y
-0,5	-8	⁴ / _-0,5 = -8
-1	-4	⁴ / _-1 = -4
-2	-2	⁴ / _-2 = -4
-4	-1	⁴ / _-4 = -1
-8	-0,5	⁴ / _-8 = -0,5

Соединив полученные точки получаем следующий результат. На этом построение гиперболы завершено.

Пример 2

Рассмотренный выше пример был одним из самых простых (без смещения асимптот). Давайте усложним задачу и построим гиперболу, заданную функцией ниже:

Решение

Так как k < 0, график будет располагаться во второй и четвертой четвертях.

Теперь определяемся с асимптотами, в нашем случае это x = 3 и y = 4 (см. информацию выше про их смещение).

Составим таблицу соответствия значений x и y.


x_{II четв.}	y_{II четв.}	x_{IV четв.}	y_{IV четв.}
-1	4,5	3,5	0
1	5	4	2
2	6	5	3
2,5	8	7	3.5

Остается только нанести рассчитанные точки на координатную плоскость и соединить их плавными линиями.

Источник

Определение

Графиком функции у=kx, где k≠0 число, а х – переменная, является кривая, которую называют гиперболой.

Гипербола имеет две ветви и может располагаться в 1 и 3 координатных четвертях, либо во 2 и 4. Это зависит от знака числа k. Рассмотрим данную кривую на рисунке, где показано ее расположение в зависимости от знака k.

Свойства гиперболы (у=kx)

График функции симметричен относительно начала координат (0;0). Поэтому функцию еще называют – обратная пропорциональность.

Область определения – любое число, кроме нуля.
Область значения – любое число, кроме нуля.
Функция не имеет наибольших или наименьших значений.

Построение графика функции

Для построения графика функции необходимо подбирать несколько положительных и несколько отрицательных значений переменной х, затем подставлять их в заданную функцию для вычисления значений у. После этого по найденным координатам построить точки и соединить их плавной линией. Рассмотрим построение графиков на примерах.

Построить график функции у=10x.

Для этого построим две таблицы для положительных и отрицательных значений х. Подбирать желательно такие значения х, чтобы число 10 на них делилось

х	1	2	4	5	10
у

х	–1	–2	–4	–5	–10
у

Теперь делим на эти числа 10, получим значения у:

х	1	2	4	5	10
у	10	5	2,5	2	1

х	–1	–2	–4	–5	–10
у	–10	–5	–2,5	–2	–1

Выполняем построение точек, они будут располагаться в первой и третьей координатных четвертях, так как число k положительное.

Теперь для построения гиперболы соединим точки плавной линией.

Построить график функции у=−5x.

Для этого построим также две таблицы для положительных и отрицательных значений х. Подбирать желательно такие значения х, чтобы число минус 5 на них делилось. Выполняем деление и получаем значения у. При делении обращаем внимание на знаки, чтобы не допускать ошибок.

х	1	2	5	10
у	–5	–2,5	–1	–0,5

х	–1	–2	–5	–10
у	5	2,5	1	0,5

Теперь отмечаем точки во 2 и 4 координатных четвертях (число k отрицательное) и соединяем их для получения ветвей гиперболы.

Задание OM1104o

Установите соответствие между графиками функций и формулами, которые их задают.

5oge 1) y = x²

2) y = x/2

3) y = 2/x

Для решения данной задачи необходимо знать вид графиков функций, а именно:

y = x² – парабола, в общем виде это y = ax²+bx+c, но в нашем случае b = c = 0, а а = 1

x/2 – прямая, в общем виде график прямой имеет вид y = ax + b, в нашем случае b = 0, а = 1/2

y = 2/x – гипербола, в общем виде график функции y = a/x + b, в данном примере b = 0, a = 2

Парабола изображена на рисунке А, гипербола на рисунке Б, а прямая – В.

Ответ:

А 1

Б 3

В 2

Ответ: 132

pазбирался: Даниил Романович | обсудить разбор

Задание OM1102o

Установите соответствие между функциями и их графиками.

Функции:

A) y = -3/x

Б) y = 3/x

В) y = 1/(3x)

Графики:

В данной ситуации можно воспользоваться двумя подходами — можно руководствоваться общими соображениями, а можно просто решить задачу подстановкой. Я рекомендую решать задачу общими соображениями, а проверять подстановкой.

Общие правила:

если уравнение гиперболы положительное (то есть не стоит знак -, как во втором и третьем случае), то график функции лежит в первой и третьей координатной четверти
если перед уравнением гиперболы стоит знак — (как в первом случае), то график лежит во второй и четвертой четвертях

Таким образом можно сразу определить, что первое уравнение соответствует графику под номером 2.

Второе правило, которым я пользуюсь, звучит так:

чем больше число в знаменателе гиперболы (рядом с x), тем сильнее гипербола жмется к осям координатной плоскости

и наоборот:

чем больше число в числителе уравнения гиперболы, тем слабее и медленнее график функции прижимается к осям

Следовательно, функция Б слабее прижимается к осям и ей соответствует график 3, а функции В соответствует график 1, так как она сильнее прижимается к осям.

Ответ:

A) 2

Б) 3

В) 1

Ответ: 231

pазбирался: Даниил Романович | обсудить разбор

Даниил Романович | Просмотров: 11.6k

Источник

История[править | править код]

Определения[править | править код]

Коническое сечение[править | править код]

Как геометрическое место точек[править | править код]

Через фокусы[править | править код]

Через директрису и фокус[править | править код]

Связанные определения[править | править код]

Соотношения[править | править код]

Равнобочная гипербола[править | править код]

Гипербола Киперта[править | править код]

Уравнения[править | править код]

Декартовы координаты[править | править код]

Канонический вид[править | править код]

Полярные координаты[править | править код]

Уравнения в параметрической форме[править | править код]

Свойства[править | править код]

Асимптоты[править | править код]

Диаметры и хорды[править | править код]

Касательная и нормаль[править | править код]

Кривизна и эволюта[править | править код]

Обобщение[править | править код]

Применение[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Определение и функция гиперболы

Алгоритм построения гиперболы

Пример 1

Пример 2

Свойства гиперболы (у=kx)

Построение графика функции

Вам также может понравиться

Нашел карту тинькофф как найти владельца

Как найти высоту вписанного равностороннего треугольника

Как найти хвост феи

Добавить комментарий Отменить ответ