Гипотенуза — сторона в прямоугольном треугольнике, находящаяся напротив прямого угла. Две других стороны — катеты. В прямоугольном треугольнике гипотенуза всегда длиннее катетов.

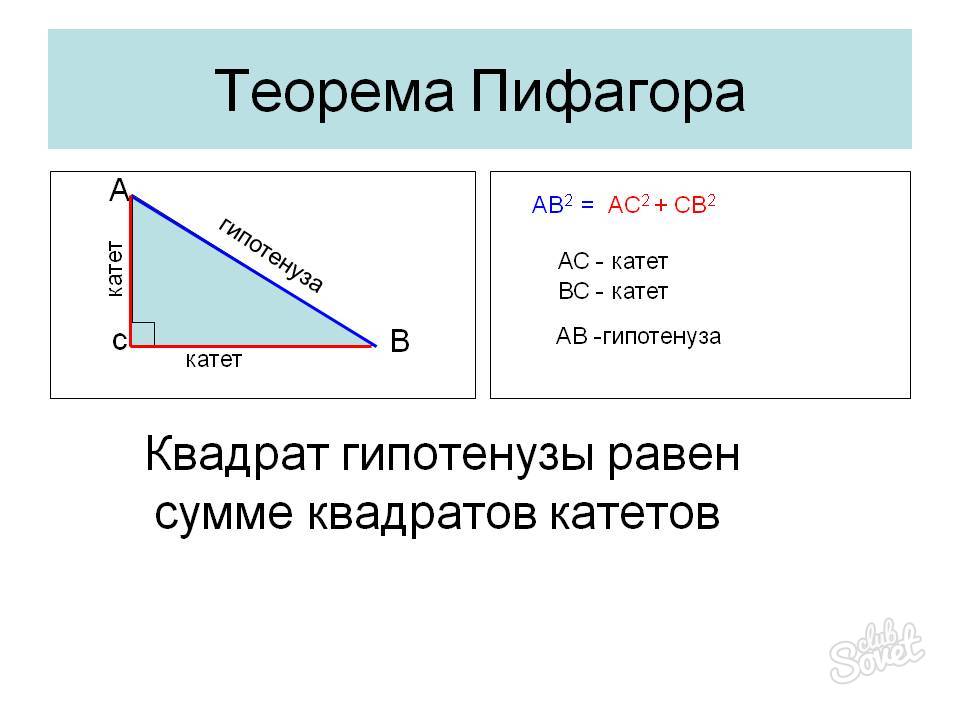
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов (формула: c² = a² + b², где c — гипотенуза, a и b — катеты). Очень часто для вычисления гипотенузы используется именно эта теорема.
Как найти гипотенузу?
Как найти гипотенузу, зная катеты?
Если известны оба катета (две другие стороны прямоугольного треугольника), можно применить Теорему Пифагора.
Теорема Пифагора — в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Формула: c² = a² + b² (при c — гипотенуза, a и b — катеты).
Например:

Один катет равен 3 см, другой — 4 см. Таким образом, а = 3, b = 4, подставляем в формулу:
c² = 3² + 4² <=> c² = 9 + 16 <=> c² = 25 <=> c = √25 <=> c = 5.
Ответ: длина гипотенузы 5 см (или x = 5).
Как найти катет в прямоугольном треугольнике
По той же формуле можно найти и длину одного неизвестного катета, нужно только немного её изменить:
Начальная формула: c² = a² + b² (при c — гипотенуза, a и b — катеты), и найти катет можно по этой:

Например: Один катет равен 3 см, а гипотенуза — 5 см. Нужно узнать длину второго катета.
Применяем формулу b = √c² — a² ⇔
b = √5² — 3² ⇔ b = √25 — 9 ⇔ b = √16 ⇔ b = 4.
Как найти гипотенузу, зная катет и угол?
Если есть противолежащий катет — теорема синусов
Если в условии задачи дан угол и противолежащий катет, то ищем гипотенузу по Теореме синусов: стороны треугольника пропорциональны синусам противолежащих углов.
Примечание: гипотенуза есть только в прямоугольном треугольнике, однако теорему синусов можно применять к любым треугольникам (не только к прямоугольным).
Формула:


Например:

Известна одна сторона треугольника 𝐴𝐶 = √2 и ∠β = 45º.
∠α = 90º (т.к. мы ищем гипотенузу, то второй угол в треугольнике прямой, значит имеет 90º).
Так как во всех треугольниках сумма всех углов равна 180º, то можем узнать оставшийся ∠c.
Значит: ∠c = 180º — (90º + 45º) = 45º.
Подставляем в формулу (a/sinα = b/sinβ = c/sinγ) известные:
BC/sin90º = AC/sin45º = AB/sin45º
В таблице вы найдёте значения для синуса:
| sin 45º | √2/2 |
| sin 60º | √3/2 |
| sin 90º | 1 |
В условии задачи нам дано: 𝐴𝐶 = √2, значит:
BC/sin90º = √2/sin45º = AB/sin45º
Подставляем значения синуса из таблицы:
BC/1 = √2/(√2/2) = AB/(√2/2) (забудем на время про катет AB) ⇔
BC = √2/(√2/2) ⇔ BC = 2 (гипотенуза равна 2)
Если хотите вычислить катет, уже зная другой катет и гипотенузу:
AB/(√2/2) = 2 ⇔ AB = √2
Ответ: гипотенуза BC равна 2 см, а катет AB √2 см.
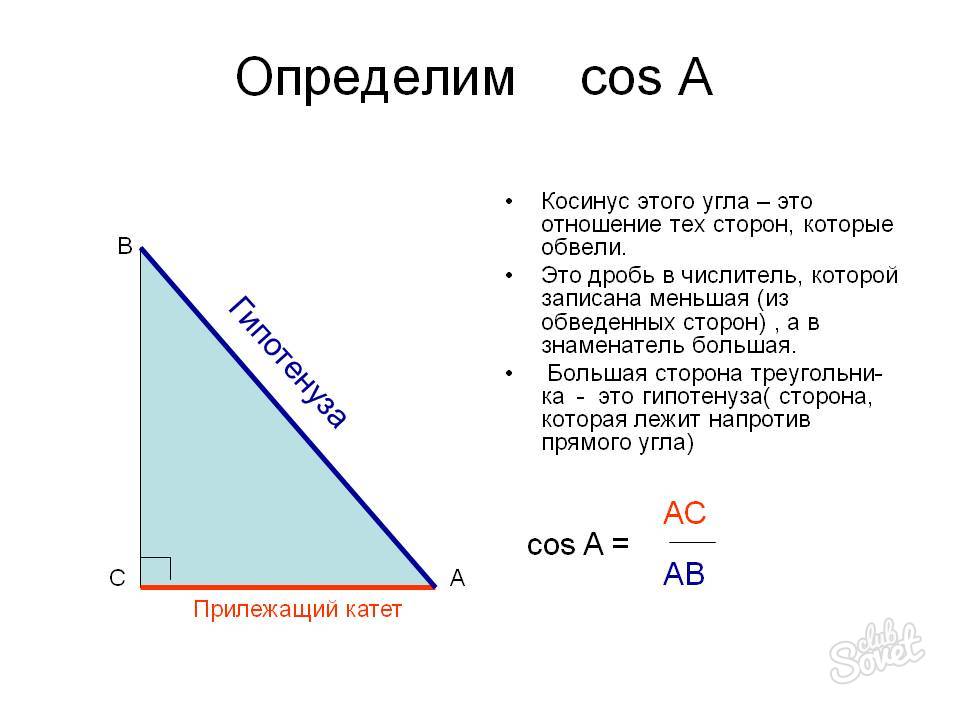
Если есть прилежащий катет — по косинусу
Если в условии задачи дан угол и прилежащий катет, то ищем гипотенузу по косинусу (в прямоугольном треугольнике, косинус острого угла (cos) — это отношение прилежащего катета (b) к гипотенузе(c), таким образом cos a = b/c, из этого получается c = b / cos α).
Т.е. гипотенуза (c) = прилежащий катет (b) / косинус угла или c = b / cos α.
Например:

Известна одна сторона треугольника AB = 1 и ∠β = 45º. Нужно вычислить гипотенузу (BC).
Помним, что гипотенуза (c) = прилежащий катет (b) / косинус угла или c = b / cos α. Т.е.: BC = AB / cosβ ⇔ BC = 1/ cos 45º.
Смотрим в таблице, чему равен cos 45º.
BC = 1/ (√2/2) = √2
Ответ: гипотенуза BC равна √2 см.
Как найти гипотенузу равнобедренного треугольника
В равнобедренном треугольнике есть гипотенуза только в том случае, если он одновременно и прямоугольный, т.к. гипотенуза есть только в прямоугольных треугольниках (и его основание будет гипотенузой).
Чтобы найти такую гипотенузу, нужно любой из двух одинаковых катетов возвести в квадрат, умножить на 2 и посчитать квадратный корень: b = √2a² (где b — гипотенуза, а — катет). Это следствие из теоремы Пифагора.
Например:

Катет равнобедренного треугольника равен 7см. Нужно найти гипотенузу.
Формула b = √2a². Подставляем:
b = √2*7² = √2*49 ≈ √98 ≈ 9.899
Если забудете эту формулу, можно использовать уже знакомую формулу Пифагора для гипотенузы (c² = a² + b²):
c² = a² + b²
c² = 7² + 7²
c² = 49 + 49
c² = 98
c = √98
c ≈ 9.899
Ответ: гипотенуза равна 9.899.
Узнайте больше про Теорему Пифагора, Теорему косинусов, а также, что такое Тангенс и Аксиома.
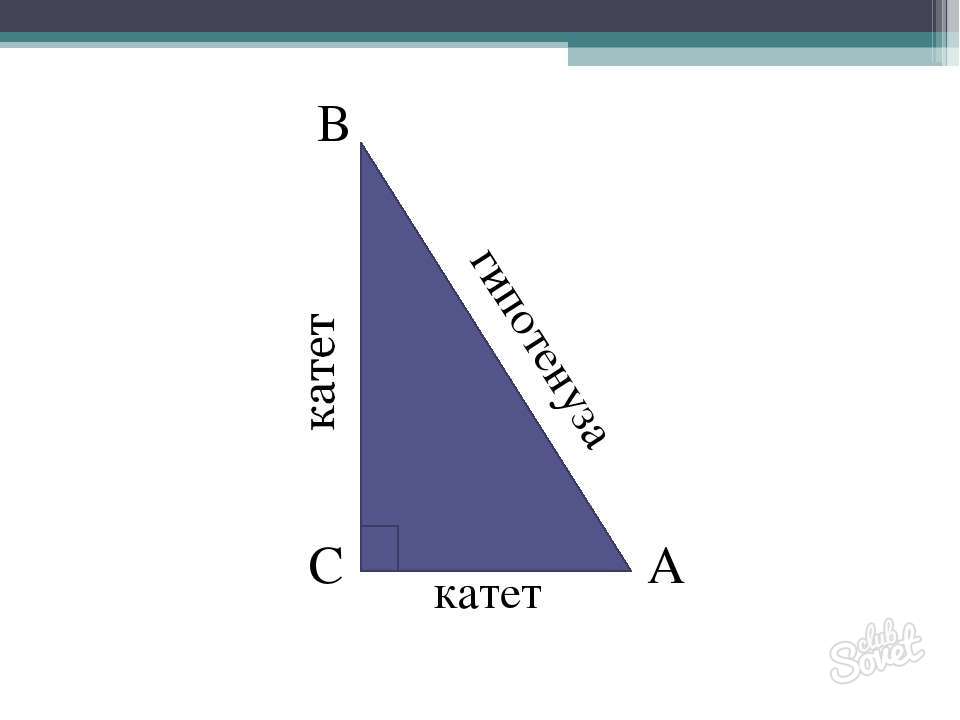
Как найти гипотенузу, если известны катеты
«А нам говорят, что катет короче гипотенузы…» Эти строки из известной песни, которая звучала в художественном фильме «Приключения электроника» действительно верны по геометрии Евклида. Ведь катеты – это две стороны, образующие угол, градусная мера которого равно 90 градусам. А гипотенуза – самая длинная «натянутая» сторона, которая соединяет два перпендикулярных друг другу катета, и лежит противоположно прямому углу. Именно поэтому найти гипотенузу по катетам можно только в прямоугольном треугольнике, и если бы катет был длиннее гипотенузы, то такой треугольник бы не существовал.
1
Как найти гипотенузу по теореме Пифагора, если известны оба катета
Теорема гласит, что квадрат гипотенузы – это есть ни что иное, как сумма квадратов катетов: x^2+y^2=z^2, где:
- х – первый катет;
- y – второй катет;
- z – гипотенуза.
Но необходимо найти просто гипотенузу, а не её квадрат. Для этого извлеките корень.
Алгоритм нахождения гипотенузы по двум известным катетам:
- Обозначьте для себя, где катеты, а где гипотенуза.
- Возведите первый катет в квадрат.
- Возведите второй катет в квадрат.
- Сложите полученные величины.
- Извлеките корень из числа, полученного в пункте 4.
2
Как найти гипотенузу через синус, если известен катет и острый угол, лежащий против него
Отношение известного катета к острому углу, лежащему против него, равно величине гипотенузы: a/sin A = c. Это следствие из определения синуса:
Отношение противолежащего катета к гипотенузе: sin А = а/с, где:
- a – первый катет;
- A – острый угол, противоположный катету;
- c- гипотенуза.
Алгоритм нахождения гипотенузы по теореме синусов:
- Обозначьте для себя известный катет и противоположный ему угол.
- Разделите катет на противоположный угол.
- Получите гипотенузу.
3
Как найти гипотенузу через косинус, если известен катет и острый угол, прилежащий ему
Отношение известного катета к острому прилежащему углу равно величине гипотенузы a/cos B = c. Это следствие из определения косинуса: отношение прилежащего катета к гипотенузе: cos B= a/с, где:
- a – второй катет;
- B – острый угол, прилежащий второму катету;
- с- гипотенуза.
Алгоритм нахождения гипотенузы по теореме косинусов:
- Обозначьте для себя известный катет и прилежащий ему угол.
- Разделите катет на прилежащий угол.
- Получите гипотенузу.
4
Как найти гипотенузу с помощью «египетского треугольника»
«Египетский треугольник» – это тройка чисел, зная которые вы сможете сэкономить время для нахождения гипотенузы или даже другого неизвестного катета. Треугольник имеет такое название, так как в Египте некоторые числа символизировали Богов и являлись основой при строении пирамид и других различных сооружений.
- Первая тройка чисел: 3-4-5. Катеты здесь равны 3 и 4. Тогда гипотенуза обязательно будет равняться 5. Проверка: (9+16=25).
- Вторая тройка чисел: 5-12-13. Здесь также катеты равняются 5 и 12. Следовательно, гипотенуза будет равняться 13. Проверка: (25+144=169).
Такие числа помогают даже тогда, когда они разделены или умножены на какое-нибудь одно число. Если катеты равны 3 и 4, то гипотенуза будет равняться 5. Если умножить эти числа на 2, то и гипотенуза умножится на 2. Например, тройка чисел 6-8-10 также будет подходить под теорему Пифагора и можно не высчитывать гипотенузу, если вы запомните такие тройки чисел.
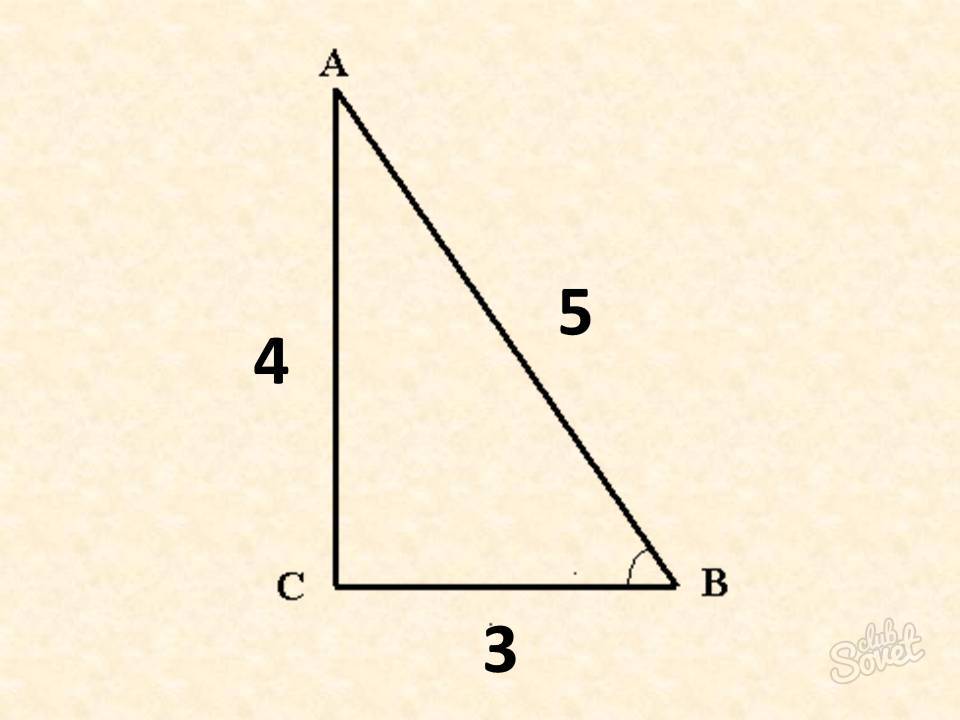
Таким образом, найти гипотенузу по известным катетам можно 4 способами. Самым оптимальным вариантом является теорема Пифагора, но также не помешало бы запомнить и тройки чисел, которые составляют “египетский треугольник”, ведь вы сможете сэкономить много времени, если вам попадутся такие значения.
Теорема Пифагора, Теорема косинусов, Формула
Теорема косинусов, формула
Квадрат стороны треугольника равен сумме квадратов двух других его сторон без удвоенного произведения одной из этих сторон на взятую на ней проекцию другой.
Если угол острый то справедлива формула
[ a^2 = b^2 + c^2 – 2bx ]
Если угол тупой то справедлива формула
[ a^2 = b^2 + c^2 + 2bx ]
Общая формула теоремы косинусов для всех случаев треугольников выглядит следующим образом:
[ a^2 = b^2 + c^2 – 2bccos(A) ]
Теорема Пифагора, Формула
Если угол прямой то справедлива формула
[ a^2 = b^2 + c^2 ]
Квадрат гипотенузы равен сумме квадратов катетов (это Теорема Пифагора).
Теорема Пифагора является частным случаем теоремы косинусов и часто применяется в разнообразных практических и теоретических вопросах.
Вычислить, найти сторону треугольника по Теореме Пифагора, Формула (4)
Теорема Пифагора, Теорема косинусов |
стр. 236 |
|---|
Здравствуйте, уважаемые читатели. В этой статье рассмотрим задачи по геометрии за 8 класс. Задачи на применение теоремы Пифагора, которые встречаются в 15 задании ОГЭ по математике.
Теорема Пифагора
Квадрат гипотенузы равен сумме квадратов катетов.
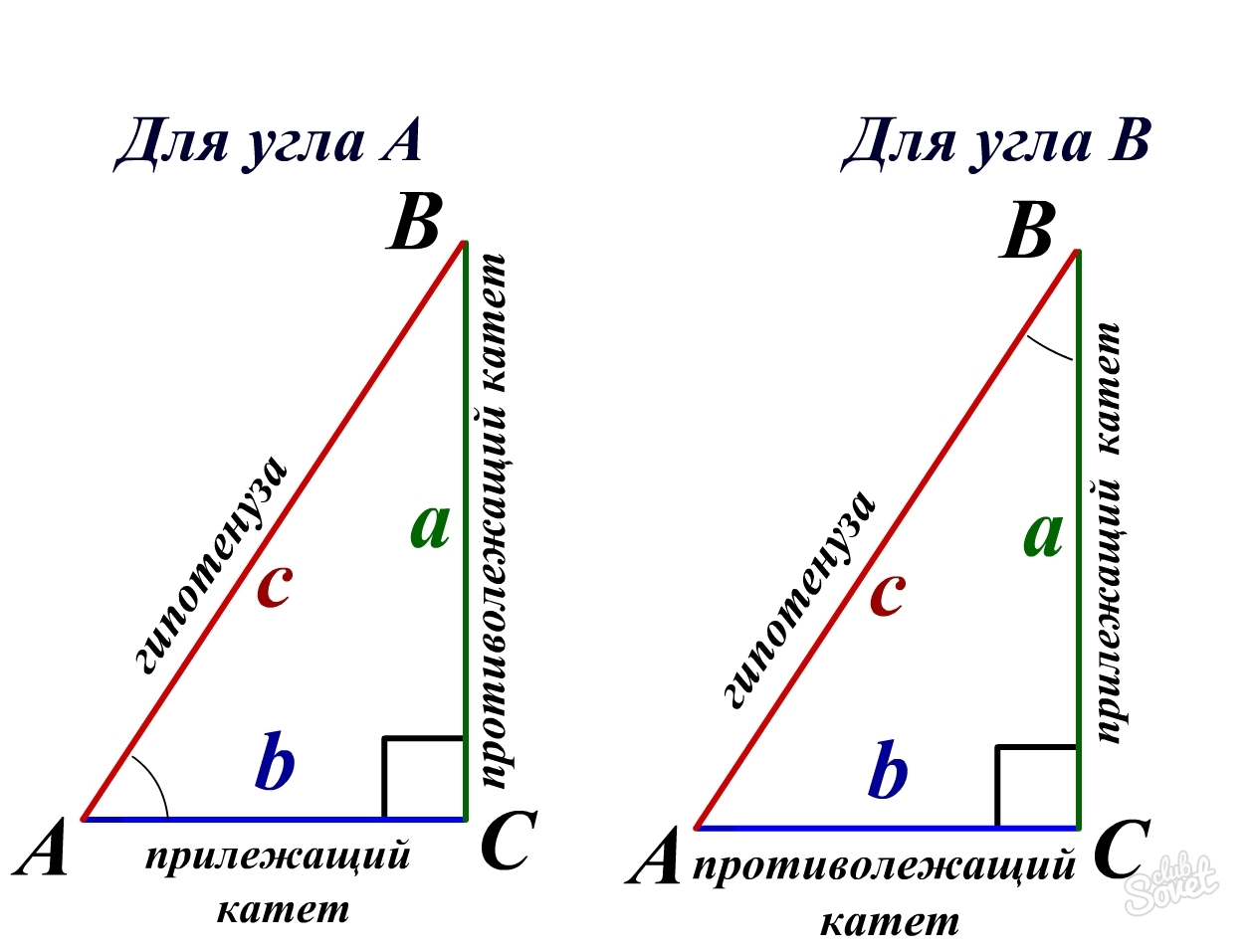
Примем условные обозначения: против угла С лежит сторона с (гипотенуза), против угла А сторона а и против угла В сторона в. Стороны а и в называются катетами
Стороны прямоугольного треугольника, которые образуют прямой угол, называются катетами.
Задача №1
Катеты прямоугольного треугольника равны 7 и 24. Найдите гипотенузу этого треугольника.
Решение
Задача №2
В прямоугольном треугольнике катет и гипотенуза равны 7 и 25 соответственно. Найдите другой катет этого треугольника.
Решение
В этой задаче можно воспользоваться формулой сокращенного умножения:
Задачи №3,4,5
Поскольку в равностороннем треугольнике медианы, биссектрисы и высоты совпадают, значит они равны. Отсюда следует, что задачи, представленные выше, одинаковые.
Решение
Способ №1 (по теореме Пифагора)
Обозначим треугольник буквами. Нам нужно найти сторону треугольника, значит будем находить сторону ВС. Так как BD – биссектриса, медиана и высота в равностороннем треугольнике, то пусть DC =x, тогда ВС = 2х. Решение представлено выше.
Способ №2 (через формулу равностороннего треугольника, которая дается в справочном материале на экзамене)
Формула дается для описанной и вписанной окружности в правильный треугольник. (Правильный=равносторонний).
По заданию нам нужно найти сторону, зная высоту равностороннего треугольника (высоты, медианы и биссектрисы в разностороннем (правильном) треугольнике совпадают).
Из этой формулы, выразим сторону треугольника:
Подставив значение в формулу, получаем:
Задачи 6,7,8
Поскольку в равностороннем треугольнике медианы, биссектрисы и высоты совпадают, значит они равны. Отсюда следует, что задачи, представленные выше, одинаковые. Найдем высоту в каждом треугольнике.
Решение
Общая формула для все этих задач выглядит следующим образом: (дается на экзамене в справочном материале)
Подставив значение стороны из каждой задачи, получаем следующие решения:
Задача №9
В треугольнике ABC известно, что AC=6, BC=8, угол C равен 90°. Найдите радиус описанной окружности этого треугольника
Решение
Радиус описанной окружности лежит на пересечении серединных перпендикуляров. Точка пересечения серединных перпендикуляров в прямоугольном треугольнике лежит на середине гипотенузы.
Значит для решения этой задачи, достаточно по теореме Пифагора найти гипотенузу и разделить на 2.
Теорема косинусов
Теорема косинусов это расширенная теорема Пифагора для произвольного треугольника. Выражение 2abCosC для прямоугольного треугольника равен 0, т.к. Cos90=0.
Задача 10.
В треугольнике ABC известно, что AB=8, BC=10, AC=12 . Найдите cosABC
Решение
Спасибо, что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог
Как найти,
гипотенузу или катеты в прямоугольном треугольнике.

a, b – катеты
c – гипотенуза
α, β – острые углы
Формулы для катета, (a):

Формулы для катета, (b):

Формулы для гипотенузы, (c):


Формулы сторон по теореме Пифагора, (a,b):



Вычислить длину неизвестной стороны через любые стороны и углы

b – сторона (основание)
a – равные стороны
α – углы при основании
β – угол образованный равными сторонами
Формулы длины стороны (основания), (b):


Формулы длины равных сторон , (a):


Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.

a, b, c – стороны произвольного треугольника
α, β, γ – противоположные углы
Формула длины через две стороны и угол (по теореме косинусов), (a):

* Внимательно, при подстановке в формулу, для тупого угла (α>90), cosα принимает отрицательное значение
Формула длины через сторону и два угла (по теореме синусов), (a):

В прямоугольном треугольнике катеты, являются высотами. Ортоцентр – точка пересечения высот, совпадает с вершиной прямого угла.

H – высота из прямого угла
a, b – катеты
с – гипотенуза
c1 , c2 – отрезки полученные от деления гипотенузы, высотой
α, β – углы при гипотенузе
Формула длины высоты через стороны, (H):

Формула длины высоты через гипотенузу и острые углы, (H):

Формула длины высоты через катет и угол, (H):

Формула длины высоты через составные отрезки гипотенузы , (H):

Высота– перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется – ортоцентр.
 H – высота треугольника
H – высота треугольника
a – сторона, основание
b, c – стороны
β, γ – углы при основании
p – полупериметр, p=(a+b+c)/2
R – радиус описанной окружности
S – площадь треугольника
Формула длины высоты через стороны, (H):

Формула длины высоты через сторону и угол, (H):

Формула длины высоты через сторону и площадь, (H):

Формула длины высоты через стороны и радиус, (H):

Медиана, отрезок |CO|, исходящий из вершины прямого угла BCA и делящий гипотенузу c, пополам.
Медиана в прямоугольном треугольнике (M), равна, радиусу описанной окружности (R).

M – медиана
R – радиус описанной окружности
O – центр описанной окружности
с – гипотенуза
a, b – катеты
α – острый угол CAB
Медиана равна радиусу и половине гипотенузы, (M):

Формула длины через катеты, (M):

Формула длины через катет и острый угол, (M):

Медиана – отрезок |AO|, который выходит из вершины A и делит противолежащею сторону c пополам.
Медиана делит треугольник ABC на два равных по площади треугольника AOC и ABO.

M – медиана, отрезок |AO|
c – сторона на которую ложится медиана
a, b – стороны треугольника
γ – угол CAB
Формула длины медианы через три стороны, (M):

Формула длины медианы через две стороны и угол между ними, (M):

Формула для вычисления высоты = биссектрисы = медианы.
В равностороннем треугольнике: все высоты, биссектрисы и медианы, равны. Точка их пересечения, является центром вписанной окружности.

L – высота=биссектриса=медиана
a – сторона треугольника
Формула длины высоты, биссектрисы и медианы равностороннего треугольника, (L):

Калькулятор – вычислить, найти медиану, биссектрису, высоту
Формулы для вычисления высоты, биссектрисы и медианы.
В равнобедренном треугольнике: высота, биссектриса и медиана, исходящие из угла образованного равными сторонами, один и тот же отрезок.

L – высота = биссектриса = медиана
a – одинаковые стороны треугольника
b – основание
α – равные углы при основании
β – угол образованный равными сторонами
Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):



Формула высоты, биссектрисы и медианы, через стороны, (L):

1. Найти по формулам длину биссектрисы из прямого угла на гипотенузу:

L – биссектриса, отрезок ME , исходящий из прямого угла (90 град)
a, b – катеты прямоугольного треугольника
с – гипотенуза
α – угол прилежащий к гипотенузе
Формула длины биссектрисы через катеты, ( L):

Формула длины биссектрисы через гипотенузу и угол, ( L):

2. Найти по формулам длину биссектрисы из острого угла на катет:

L – биссектриса, отрезок ME , исходящий из острого угла
a, b – катеты прямоугольного треугольника
с – гипотенуза
α, β – углы прилежащие к гипотенузе
Формулы длины биссектрисы через катет и угол, (L):


Формула длины биссектрисы через катет и гипотенузу, (L):


L– биссектриса, отрезок |OB|, который делит угол ABC пополам
a, b – стороны треугольника
с – сторона на которую опущена биссектриса
d, e – отрезки полученные делением биссектрисы
γ – угол ABC , разделенный биссектрисой пополам
p – полупериметр, p=(a+b+c)/2
Длина биссектрисы через две стороны и угол, (L):

Длина биссектрисы через полупериметр и стороны, (L):

Длина биссектрисы через три стороны, (L):

Длина биссектрисы через стороны и отрезки d, e, (L):


Точка пересечения всех трех биссектрис треугольника ABC, совпадает с центром О, вписанной окружности.
