Как найти гипотенузу при известном катете
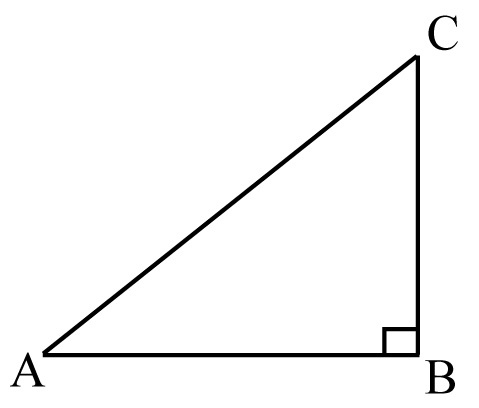
Катетами называют называют две стороны прямоугольного треугольника, образующие прямой угол. Противоположная прямому углу самая длинная сторона треугольника называется гипотенузой. Чтобы найти гипотенузу, нужно знать длину катетов.
Инструкция
Длины катетов и гипотенузы связаны соотношением, которое описывается теоремой Пифагора. Алгебраическая формулировка: “В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.”
Формула Пифагора выглядит так:
c2 = a2 + b2,
где с — длина гипотенузы, a и b — длины катетов.
Зная длины катетов, по теореме Пифагора можно найти гипотенузу прямоугольного треугольника:
c = √(a2 + b2).
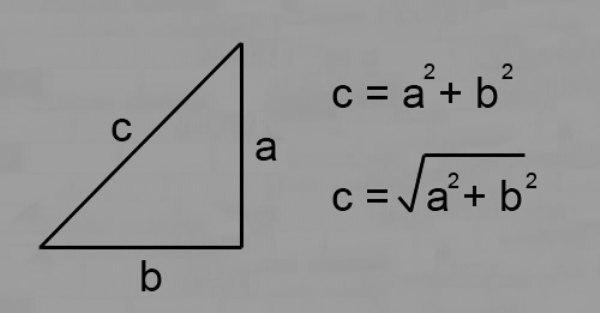
Пример. Длина одного из катетов равна 3 см, длина другого — 4 см. Сумма их квадратов равна 25 см²:
9 см² + 16 см² = 25 см².
Длина гипотенузы в нашем случае равна квадратному корню из 25 см² – 5 см. Стало быть, длина гипотенузы равняется 5 см.
Гипотенуза — сторона в прямоугольном треугольнике, находящаяся напротив прямого угла. Две других стороны — катеты. В прямоугольном треугольнике гипотенуза всегда длиннее катетов.

Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов (формула: c² = a² + b², где c — гипотенуза, a и b — катеты). Очень часто для вычисления гипотенузы используется именно эта теорема.
Как найти гипотенузу?
Как найти гипотенузу, зная катеты?
Если известны оба катета (две другие стороны прямоугольного треугольника), можно применить Теорему Пифагора.
Теорема Пифагора — в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Формула: c² = a² + b² (при c — гипотенуза, a и b — катеты).
Например:

Один катет равен 3 см, другой — 4 см. Таким образом, а = 3, b = 4, подставляем в формулу:
c² = 3² + 4² <=> c² = 9 + 16 <=> c² = 25 <=> c = √25 <=> c = 5.
Ответ: длина гипотенузы 5 см (или x = 5).
Как найти катет в прямоугольном треугольнике
По той же формуле можно найти и длину одного неизвестного катета, нужно только немного её изменить:
Начальная формула: c² = a² + b² (при c — гипотенуза, a и b — катеты), и найти катет можно по этой:

Например: Один катет равен 3 см, а гипотенуза — 5 см. Нужно узнать длину второго катета.
Применяем формулу b = √c² — a² ⇔
b = √5² — 3² ⇔ b = √25 — 9 ⇔ b = √16 ⇔ b = 4.
Как найти гипотенузу, зная катет и угол?
Если есть противолежащий катет — теорема синусов
Если в условии задачи дан угол и противолежащий катет, то ищем гипотенузу по Теореме синусов: стороны треугольника пропорциональны синусам противолежащих углов.
Примечание: гипотенуза есть только в прямоугольном треугольнике, однако теорему синусов можно применять к любым треугольникам (не только к прямоугольным).
Формула:


Например:

Известна одна сторона треугольника 𝐴𝐶 = √2 и ∠β = 45º.
∠α = 90º (т.к. мы ищем гипотенузу, то второй угол в треугольнике прямой, значит имеет 90º).
Так как во всех треугольниках сумма всех углов равна 180º, то можем узнать оставшийся ∠c.
Значит: ∠c = 180º — (90º + 45º) = 45º.
Подставляем в формулу (a/sinα = b/sinβ = c/sinγ) известные:
BC/sin90º = AC/sin45º = AB/sin45º
В таблице вы найдёте значения для синуса:
| sin 45º | √2/2 |
| sin 60º | √3/2 |
| sin 90º | 1 |
В условии задачи нам дано: 𝐴𝐶 = √2, значит:
BC/sin90º = √2/sin45º = AB/sin45º
Подставляем значения синуса из таблицы:
BC/1 = √2/(√2/2) = AB/(√2/2) (забудем на время про катет AB) ⇔
BC = √2/(√2/2) ⇔ BC = 2 (гипотенуза равна 2)
Если хотите вычислить катет, уже зная другой катет и гипотенузу:
AB/(√2/2) = 2 ⇔ AB = √2
Ответ: гипотенуза BC равна 2 см, а катет AB √2 см.
Если есть прилежащий катет — по косинусу
Если в условии задачи дан угол и прилежащий катет, то ищем гипотенузу по косинусу (в прямоугольном треугольнике, косинус острого угла (cos) — это отношение прилежащего катета (b) к гипотенузе(c), таким образом cos a = b/c, из этого получается c = b / cos α).
Т.е. гипотенуза (c) = прилежащий катет (b) / косинус угла или c = b / cos α.
Например:

Известна одна сторона треугольника AB = 1 и ∠β = 45º. Нужно вычислить гипотенузу (BC).
Помним, что гипотенуза (c) = прилежащий катет (b) / косинус угла или c = b / cos α. Т.е.: BC = AB / cosβ ⇔ BC = 1/ cos 45º.
Смотрим в таблице, чему равен cos 45º.
BC = 1/ (√2/2) = √2
Ответ: гипотенуза BC равна √2 см.
Как найти гипотенузу равнобедренного треугольника
В равнобедренном треугольнике есть гипотенуза только в том случае, если он одновременно и прямоугольный, т.к. гипотенуза есть только в прямоугольных треугольниках (и его основание будет гипотенузой).
Чтобы найти такую гипотенузу, нужно любой из двух одинаковых катетов возвести в квадрат, умножить на 2 и посчитать квадратный корень: b = √2a² (где b — гипотенуза, а — катет). Это следствие из теоремы Пифагора.
Например:

Катет равнобедренного треугольника равен 7см. Нужно найти гипотенузу.
Формула b = √2a². Подставляем:
b = √2*7² = √2*49 ≈ √98 ≈ 9.899
Если забудете эту формулу, можно использовать уже знакомую формулу Пифагора для гипотенузы (c² = a² + b²):
c² = a² + b²
c² = 7² + 7²
c² = 49 + 49
c² = 98
c = √98
c ≈ 9.899
Ответ: гипотенуза равна 9.899.
Узнайте больше про Теорему Пифагора, Теорему косинусов, а также, что такое Тангенс и Аксиома.
Как найти стороны прямоугольного треугольника
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как найти стороны прямоугольного треугольника
Чтобы посчитать стороны прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор

Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- для гипотенузы (с):
- длины катетов a и b
- длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
- для катета:
- длину гипотенузы (с) и длину одного из катетов
- длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
- длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
- длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)
Введите их в соответствующие поля и получите результат.
Найти гипотенузу (c)
Найти гипотенузу по двум катетам
Катет a =
Катет b =
Гипотенуза c =
0
Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b)?
Формула
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов:
c² = a² + b²
следовательно: c = √a² + b²
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:
c = √3² + 4² = √9 + 16 = √25 = 5 см
Найти гипотенузу по катету и прилежащему к нему острому углу
Катет (a или b) =
Прилежащий угол (β или α) =
Гипотенуза c =
0
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и прилежащий к нему угол?
Формула
c = a/cos(β) = b/cos(α)
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:
c = 2 / cos(60) = 2 / 0.5 = 4 см
Найти гипотенузу по катету и противолежащему к нему острому углу
Катет (a или b) =
Противолежащий угол (α или β) =
Гипотенуза c =
0
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол?
Формула
c = a/sin(α) = b/sin(β)
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:
c = 2 / sin(30) = 2 / 0.5 = 4 см
Найти гипотенузу по двум углам
Найти гипотенузу прямоугольного треугольника только по двум острым углам невозможно.
Найти катет
Найти катет по гипотенузе и катету
Гипотенуза c =
Катет (известный) =
Катет (искомый) =
0
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и второй катет?
Формула
a = √c² – b²
b = √c² – a²
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:
a = √5² – 4² = √25 – 16 = √9 = 3 см
Найти катет по гипотенузе и прилежащему к нему острому углу
Гипотенуза c =
Угол (прилежащий катету) = °
Катет =
0
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?
Формула
a = c ⋅ cos(β)
b = c ⋅ cos(α)
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:
b = 5 ⋅ cos(60) = 5 ⋅ 0.5 = 2.5 см
Найти катет по гипотенузе и противолежащему к нему острому углу
Гипотенуза c =
Угол (противолежащий катету) = °
Катет =
0
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?
Формула
a = c ⋅ sin(α)
b = c ⋅ sin(β)
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:
a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см
Найти катет по второму катету и прилежащему к нему острому углу
Катет (известный) =
Угол (прилежащий известному катету) = °
Катет (искомый) =
0
Чему равен один из катетов прямоугольного треугольника если известен другой катет и прилежащий к нему острый угол?
Формула
a = b ⋅ tg(α)
b = a ⋅ tg(β)
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:
b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см
Найти катет по второму катету и противолежащему к нему острому углу
Катет (известный) =
Угол (противолежащий известному катету) = °
Катет (искомый) =
0
Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?
Формула
a = b / tg(β)
b = a / tg(α)
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если катет b = 3 см, а ∠β = 35°:
a = 3 / tg(35) ≈ 3 / 0.7 ≈ 4.28 см
См. также
Содержание материала
- Треугольник
- Видео
- Почему гипотенуза — самая длинная сторона треугольника?
- Как найти высоту в прямоугольном треугольнике?
- под номером : известен катет и угол, который к нему прилежит
- В тригонометрии
- Прямоугольный треугольник
- под номером : по радиусу описанной окружности
- Гипотенуза формула, правила и примеры вычислений
- Гипотенуза равнобедренного треугольника
- Равносторонний треугольник
- Как найти угол между катетом и гипотенузой?
Треугольник
Треугольник – это фигура, состоящая из трех сторон и трех вершин. Стороны образуют три угла при трех вершинах.

Рис. 1. Треугольник
Для формулировки теорем требуется всем понятное обозначение сторон. Эти обозначения не должны быть классическими АВ или ВС, поскольку такие обозначения зависят от каждого конкретного ученика. Никто не вправе запретить решающему обозначать фигуру так, как это удобно лично ему. Например, именно по этой причине в математику было введено понятие основания треугольника. Вспомните, в равнобедренном треугольнике высота, проведенная к основанию, равняется биссектрисе и медиане. Формулировка четкая, понятная и простая для запоминания. Именно в этих целях и вводят дополнительные понятия.
Почему гипотенуза — самая длинная сторона треугольника?
Изучив рисунок выше и другие прямоугольные треугольники, вы заметите, что гипотенуза всегда является самой длинной стороной всех прямоугольных треугольников. Это просто потому, что он расположен напротив самого большого угла, угла 90 °.
это также можно доказать математически с помощью теоремы Пифагора:
a² + b² = c²
a² > b² , a² > c²
a > b , a > c
Как видите, результат вышеописанной операции состоит в том, что «a» (гипотенуза) больше двух других сторон.
Видео
Как найти высоту в прямоугольном треугольнике?
Примеры решения задач
| Задание | В прямоугольном треугольнике катеты равны см и см. Найти высоту , опущенную на гипотенузу . |
|---|---|
| Решение | Пусть катет см, а см (рис. 2). Тогда по теореме Пифагора гипотенуза см Площадь прямоугольного треугольника равна половине произведения катетов, т.е. Высоту найдем по формуле |
| Ответ | см |
под номером : известен катет и угол, который к нему прилежит
Для того чтобы узнать, как найти гипотенузу, потребуется вспомнить тригонометрические функции. А именно косинус. Для удобства будем считать, что даны катет «а» и прилежащий к нему угол α.
Теперь нужно вспомнить, что косинус угла прямоугольного треугольника равен отношению двух сторон. В числителе будет стоять значение катета, а в знаменателе — гипотенузы. Из этого следует, что последнюю можно будет сосчитать по формуле:
с = а / cos α.
В тригонометрии
Построим на плоскости прямоугольную систему координат с единичной (с радиусом, равным 1) окружностью с центром в точке (0; 0). B – пересечение угла α и кривой (рис. 4).

На оси абсцисс X отмечается cos α; на оси ординат Y – sin α.
В получившемся прямоугольном треугольнике отрезок 0B является гипотенузой. Учитывая доказанную теорему, выводим основное равенство математической дисциплины:
sin2α + cos2α = 1
Прямоугольный треугольник
Прямоугольный треугольник – это особенная фигура. Она имеет свои свойства и пропорции, один из углов такого треугольника всегда известен и равен 90 градусам, к тому же имеются специфические формулы площади и признаки равенства прямоугольных треугольников.

В Древней Греции прямоугольным треугольникам уделяли особое внимание. Эти фигуры были предметом изучения не только математики, но и мореходства. С помощью подобных прямоугольных треугольников греки определяли расстояния в море. А в древних Сиракузах на основе системы прямоугольных треугольников была создана система прицеливания, с помощью которой город долгое время отбивался от атак врагов.
Греки особое внимание уделяли точности формулировок и потому придумали для сторон треугольников особые названия: гипотенуза для стороны, лежащей напротив прямого угла и катеты для сторон, прилежащих к прямому углу.

Есть гипотенуза у равнобедренного треугольника? В общем случае, нет. В равнобедренном треугольнике есть только две боковые стороны и основание. Но если перед нами прямоугольный равнобедренный треугольник, то основание такого треугольника будет являться одновременно и гипотенузой. Найти ее можно как квадратный корень из удвоенного произведения квадрата катета – это следствие из теоремы Пифагора и равенства катетов, как боковых сторон равнобедренного треугольника.
$b=sqrt{2a^2}$ – где b это гипотенуза, а а – значение длины одного из катетов
под номером : по радиусу описанной окружности
Теперь, для того чтобы узнать, как найти гипотенузу, потребуется вспомнить свойство окружности, которая описана около прямоугольного треугольника. Оно гласит следующее. Центр окружности совпадает с серединой гипотенузы. Если сказать по-другому, то самая большая сторона прямоугольного треугольника равна диагонали окружности. То есть удвоенному радиусу. Формула для этой задачи будет выглядеть так:
с = 2 * r, где буквой r обозначен известный радиус.
Это все возможные способы того, как находить гипотенузу прямоугольного треугольника. Пользоваться в каждой конкретной задаче нужно тем методом, который больше подходит по набору данных.
Гипотенуза формула, правила и примеры вычислений
Слово «гипотенуза» со школьных времен у многих вызывает негативные ассоциации. Добавим загадочного и непонятного. Происходит от греческого «ὑποτείνουσα».
А ведь означает всего-навсего «вытянутый». И речь идет о простейшей форме треугольника – прямоугольной (рис. 1).

Гипотенузой называют сторону напротив прямого угла. Самую протяженную. В данном случае – с. Остальные составляющие – катеты.
Простыми фигурами интересовались древние строители Вавилона и Египта. А особенно – землемеры. Еще бы: ведь основа любой цивилизации – распределение угодий и налоги.
Считается, что теоретическая база была доказательно предложена Пифагором в V-м веке до н. э. Хотя, скорее всего, это было сделано ранее.
Гипотенуза равнобедренного треугольника
В такой фигуре катеты равны и являются сторонами прямого угла (рис. 5). Расчет гипотенузы c производится по формуле теоремы Пифагора.


Нетрудно заметить, что углы α = 45°. Поскольку сумма всех равна 180°.
Равносторонний треугольник
Стоит сказать и о равностороннем треугольнике, ведь это частный случай равнобедренного. Может ли существовать гипотенуза у равностороннего треугольника? Нет, поскольку гипотенуза возможна только в прямоугольном треугольнике, а в равностороннем треугольнике все углы всегда составляют 60 градусов, поэтому такой вариант невозможен вовсе.
Как найти угол между катетом и гипотенузой?
sin (α) = a/c Если известен катет, прилежащий искомому углу, и гипотенуза, можно вычислить косинус этого угла, как отношение прилежащего катета к гипотенузе. Затем в таблице косинусов находим величину угла.
Теги
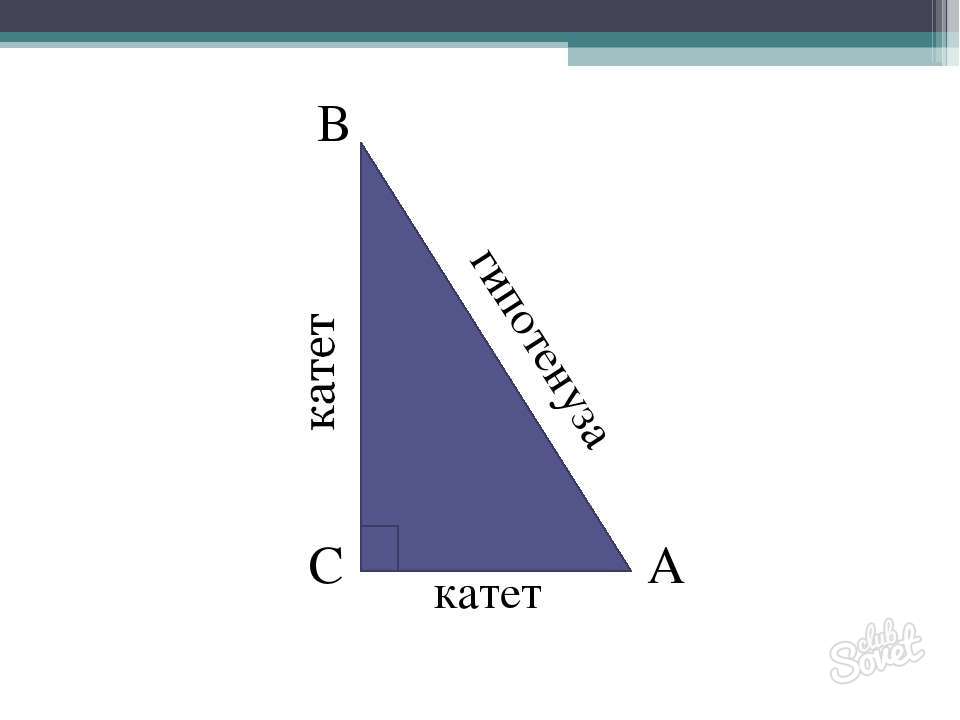
Как найти гипотенузу, если известны катеты
«А нам говорят, что катет короче гипотенузы…» Эти строки из известной песни, которая звучала в художественном фильме «Приключения электроника» действительно верны по геометрии Евклида. Ведь катеты – это две стороны, образующие угол, градусная мера которого равно 90 градусам. А гипотенуза – самая длинная «натянутая» сторона, которая соединяет два перпендикулярных друг другу катета, и лежит противоположно прямому углу. Именно поэтому найти гипотенузу по катетам можно только в прямоугольном треугольнике, и если бы катет был длиннее гипотенузы, то такой треугольник бы не существовал.
1
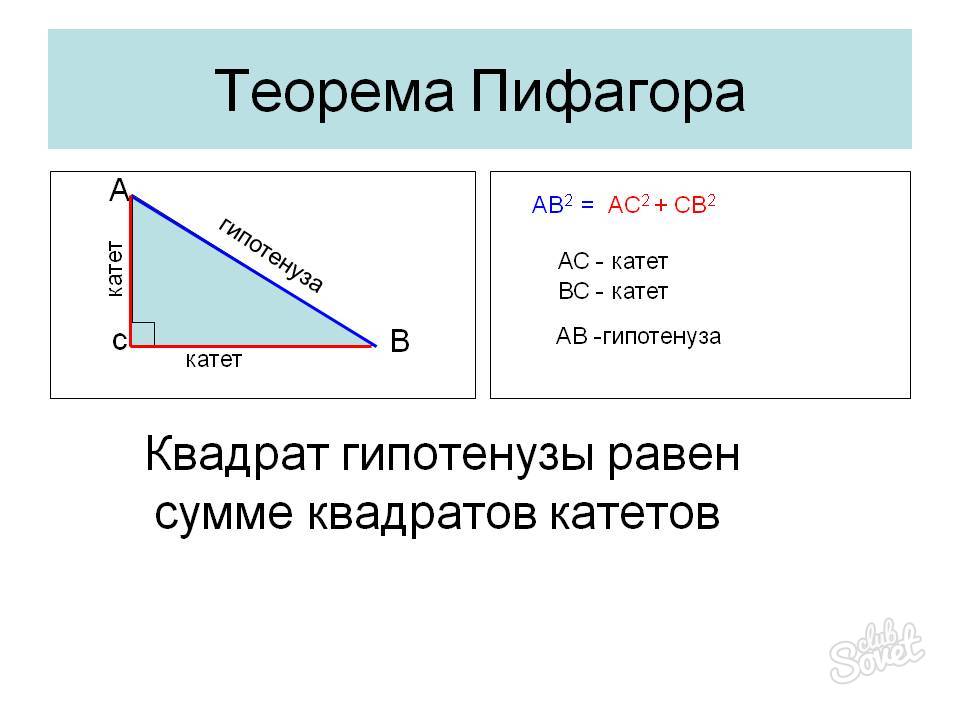
Как найти гипотенузу по теореме Пифагора, если известны оба катета
Теорема гласит, что квадрат гипотенузы – это есть ни что иное, как сумма квадратов катетов: x^2+y^2=z^2, где:
- х – первый катет;
- y – второй катет;
- z – гипотенуза.
Но необходимо найти просто гипотенузу, а не её квадрат. Для этого извлеките корень.
Алгоритм нахождения гипотенузы по двум известным катетам:
- Обозначьте для себя, где катеты, а где гипотенуза.
- Возведите первый катет в квадрат.
- Возведите второй катет в квадрат.
- Сложите полученные величины.
- Извлеките корень из числа, полученного в пункте 4.
2
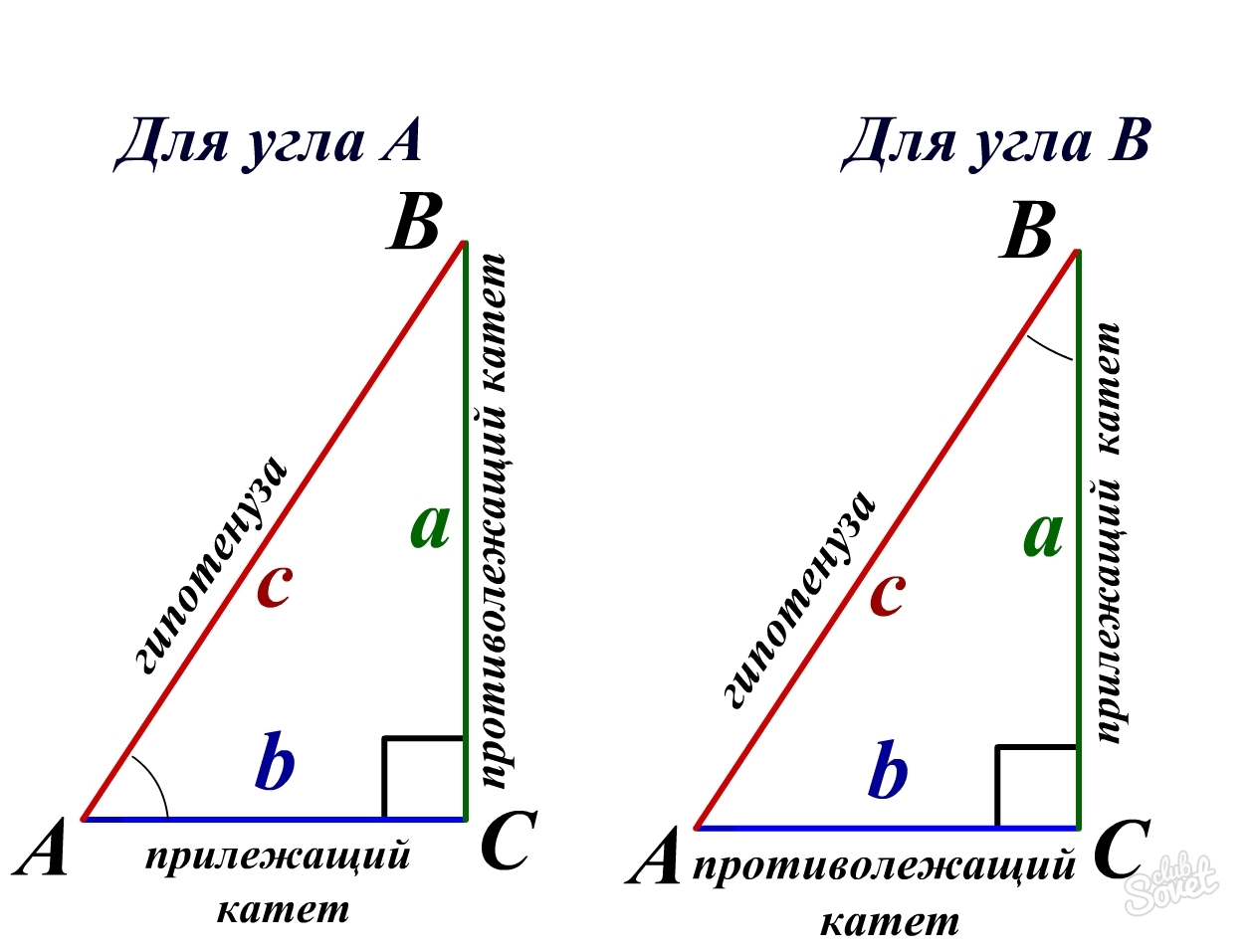
Как найти гипотенузу через синус, если известен катет и острый угол, лежащий против него
Отношение известного катета к острому углу, лежащему против него, равно величине гипотенузы: a/sin A = c. Это следствие из определения синуса:
Отношение противолежащего катета к гипотенузе: sin А = а/с, где:
- a – первый катет;
- A – острый угол, противоположный катету;
- c- гипотенуза.
Алгоритм нахождения гипотенузы по теореме синусов:
- Обозначьте для себя известный катет и противоположный ему угол.
- Разделите катет на противоположный угол.
- Получите гипотенузу.
3
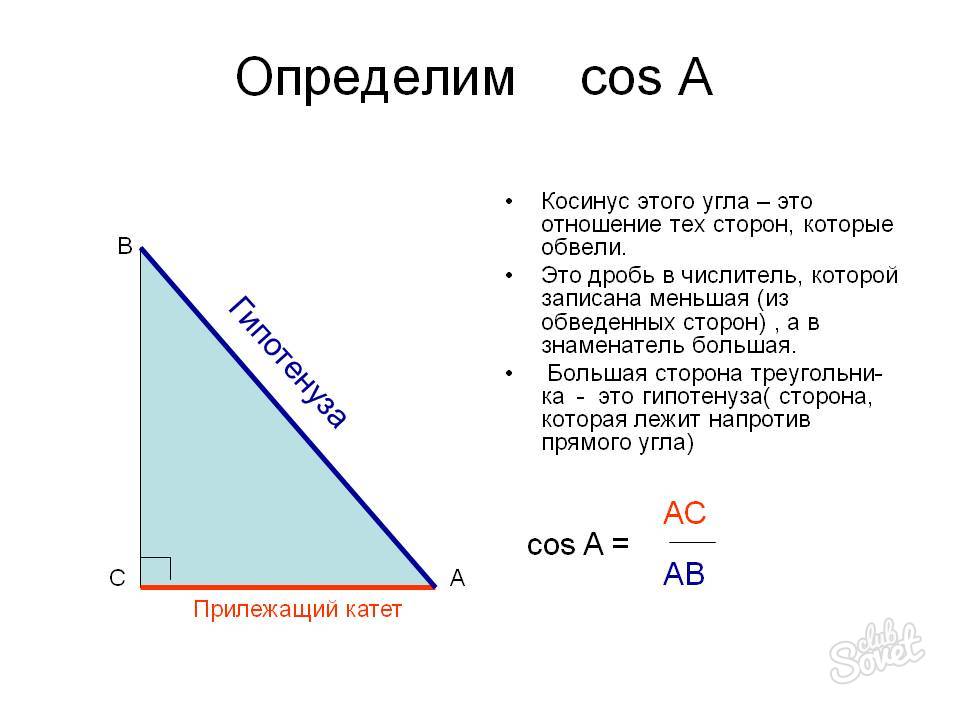
Как найти гипотенузу через косинус, если известен катет и острый угол, прилежащий ему
Отношение известного катета к острому прилежащему углу равно величине гипотенузы a/cos B = c. Это следствие из определения косинуса: отношение прилежащего катета к гипотенузе: cos B= a/с, где:
- a – второй катет;
- B – острый угол, прилежащий второму катету;
- с- гипотенуза.
Алгоритм нахождения гипотенузы по теореме косинусов:
- Обозначьте для себя известный катет и прилежащий ему угол.
- Разделите катет на прилежащий угол.
- Получите гипотенузу.
4
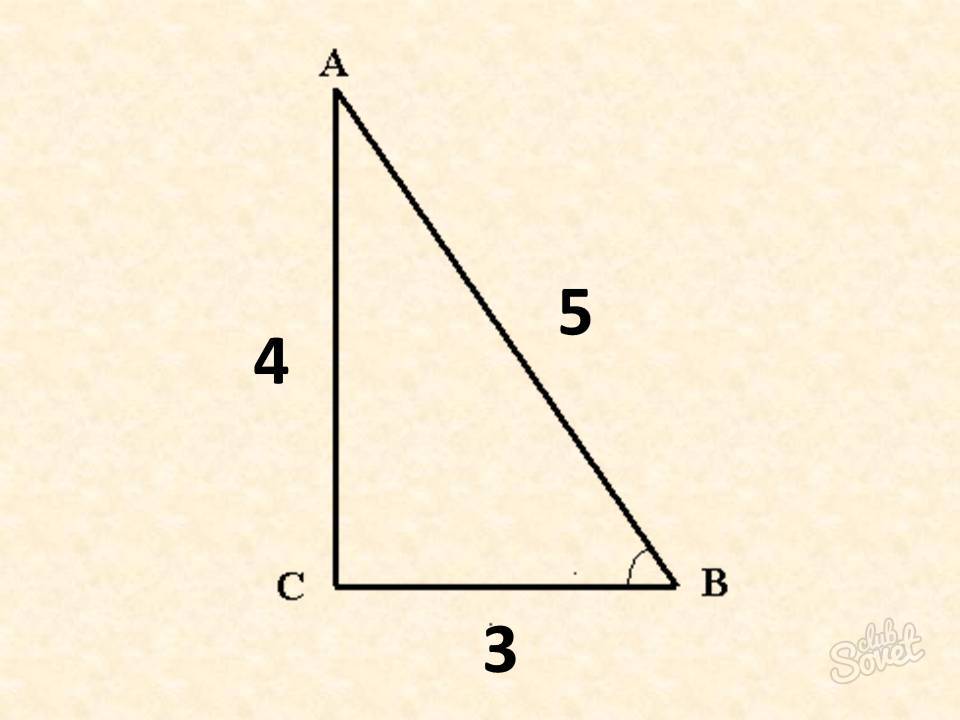
Как найти гипотенузу с помощью «египетского треугольника»
«Египетский треугольник» – это тройка чисел, зная которые вы сможете сэкономить время для нахождения гипотенузы или даже другого неизвестного катета. Треугольник имеет такое название, так как в Египте некоторые числа символизировали Богов и являлись основой при строении пирамид и других различных сооружений.
- Первая тройка чисел: 3-4-5. Катеты здесь равны 3 и 4. Тогда гипотенуза обязательно будет равняться 5. Проверка: (9+16=25).
- Вторая тройка чисел: 5-12-13. Здесь также катеты равняются 5 и 12. Следовательно, гипотенуза будет равняться 13. Проверка: (25+144=169).
Такие числа помогают даже тогда, когда они разделены или умножены на какое-нибудь одно число. Если катеты равны 3 и 4, то гипотенуза будет равняться 5. Если умножить эти числа на 2, то и гипотенуза умножится на 2. Например, тройка чисел 6-8-10 также будет подходить под теорему Пифагора и можно не высчитывать гипотенузу, если вы запомните такие тройки чисел.
Таким образом, найти гипотенузу по известным катетам можно 4 способами. Самым оптимальным вариантом является теорема Пифагора, но также не помешало бы запомнить и тройки чисел, которые составляют “египетский треугольник”, ведь вы сможете сэкономить много времени, если вам попадутся такие значения.
