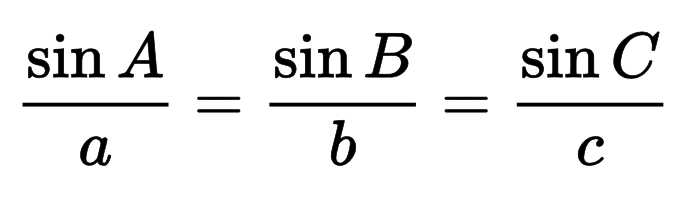Как найти стороны прямоугольного треугольника
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как найти стороны прямоугольного треугольника
Чтобы посчитать стороны прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- для гипотенузы (с):
- длины катетов a и b
- длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
- для катета:
- длину гипотенузы (с) и длину одного из катетов
- длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
- длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
- длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)
Введите их в соответствующие поля и получите результат.
Найти гипотенузу (c)
Найти гипотенузу по двум катетам
Катет a =
Катет b =
Гипотенуза c =
0
Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b)?
Формула
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов:
c² = a² + b²
следовательно: c = √a² + b²
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:
c = √3² + 4² = √9 + 16 = √25 = 5 см
Найти гипотенузу по катету и прилежащему к нему острому углу
Катет (a или b) =
Прилежащий угол (β или α) =
Гипотенуза c =
0
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и прилежащий к нему угол?
Формула
c = a/cos(β) = b/cos(α)
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:
c = 2 / cos(60) = 2 / 0.5 = 4 см
Найти гипотенузу по катету и противолежащему к нему острому углу
Катет (a или b) =
Противолежащий угол (α или β) =
Гипотенуза c =
0
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол?
Формула
c = a/sin(α) = b/sin(β)
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:
c = 2 / sin(30) = 2 / 0.5 = 4 см
Найти гипотенузу по двум углам
Найти гипотенузу прямоугольного треугольника только по двум острым углам невозможно.
Найти катет
Найти катет по гипотенузе и катету
Гипотенуза c =
Катет (известный) =
Катет (искомый) =
0
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и второй катет?
Формула
a = √c² – b²
b = √c² – a²
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:
a = √5² – 4² = √25 – 16 = √9 = 3 см
Найти катет по гипотенузе и прилежащему к нему острому углу
Гипотенуза c =
Угол (прилежащий катету) = °
Катет =
0
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?
Формула
a = c ⋅ cos(β)
b = c ⋅ cos(α)
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:
b = 5 ⋅ cos(60) = 5 ⋅ 0.5 = 2.5 см
Найти катет по гипотенузе и противолежащему к нему острому углу
Гипотенуза c =
Угол (противолежащий катету) = °
Катет =
0
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?
Формула
a = c ⋅ sin(α)
b = c ⋅ sin(β)
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:
a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см
Найти катет по второму катету и прилежащему к нему острому углу
Катет (известный) =
Угол (прилежащий известному катету) = °
Катет (искомый) =
0
Чему равен один из катетов прямоугольного треугольника если известен другой катет и прилежащий к нему острый угол?
Формула
a = b ⋅ tg(α)
b = a ⋅ tg(β)
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:
b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см
Найти катет по второму катету и противолежащему к нему острому углу
Катет (известный) =
Угол (противолежащий известному катету) = °
Катет (искомый) =
0
Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?
Формула
a = b / tg(β)
b = a / tg(α)
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если катет b = 3 см, а ∠β = 35°:
a = 3 / tg(35) ≈ 3 / 0.7 ≈ 4.28 см
См. также
Гипотенуза — сторона в прямоугольном треугольнике, находящаяся напротив прямого угла. Две других стороны — катеты. В прямоугольном треугольнике гипотенуза всегда длиннее катетов.
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов (формула: c² = a² + b², где c — гипотенуза, a и b — катеты). Очень часто для вычисления гипотенузы используется именно эта теорема.
Как найти гипотенузу?
Как найти гипотенузу, зная катеты?
Если известны оба катета (две другие стороны прямоугольного треугольника), можно применить Теорему Пифагора.
Теорема Пифагора — в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Формула: c² = a² + b² (при c — гипотенуза, a и b — катеты).
Например:
Один катет равен 3 см, другой — 4 см. Таким образом, а = 3, b = 4, подставляем в формулу:
c² = 3² + 4² <=> c² = 9 + 16 <=> c² = 25 <=> c = √25 <=> c = 5.
Ответ: длина гипотенузы 5 см (или x = 5).
Как найти катет в прямоугольном треугольнике
По той же формуле можно найти и длину одного неизвестного катета, нужно только немного её изменить:
Начальная формула: c² = a² + b² (при c — гипотенуза, a и b — катеты), и найти катет можно по этой:

Например: Один катет равен 3 см, а гипотенуза — 5 см. Нужно узнать длину второго катета.
Применяем формулу b = √c² — a² ⇔
b = √5² — 3² ⇔ b = √25 — 9 ⇔ b = √16 ⇔ b = 4.
Как найти гипотенузу, зная катет и угол?
Если есть противолежащий катет — теорема синусов
Если в условии задачи дан угол и противолежащий катет, то ищем гипотенузу по Теореме синусов: стороны треугольника пропорциональны синусам противолежащих углов.
Примечание: гипотенуза есть только в прямоугольном треугольнике, однако теорему синусов можно применять к любым треугольникам (не только к прямоугольным).
Формула:
Например:
Известна одна сторона треугольника 𝐴𝐶 = √2 и ∠β = 45º.
∠α = 90º (т.к. мы ищем гипотенузу, то второй угол в треугольнике прямой, значит имеет 90º).
Так как во всех треугольниках сумма всех углов равна 180º, то можем узнать оставшийся ∠c.
Значит: ∠c = 180º — (90º + 45º) = 45º.
Подставляем в формулу (a/sinα = b/sinβ = c/sinγ) известные:
BC/sin90º = AC/sin45º = AB/sin45º
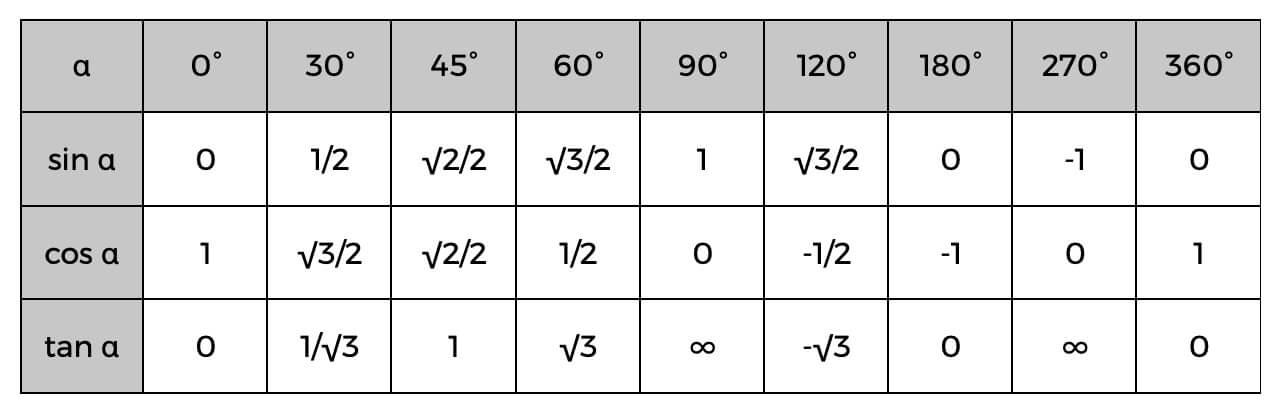
В таблице вы найдёте значения для синуса:
| sin 45º | √2/2 |
| sin 60º | √3/2 |
| sin 90º | 1 |
В условии задачи нам дано: 𝐴𝐶 = √2, значит:
BC/sin90º = √2/sin45º = AB/sin45º
Подставляем значения синуса из таблицы:
BC/1 = √2/(√2/2) = AB/(√2/2) (забудем на время про катет AB) ⇔
BC = √2/(√2/2) ⇔ BC = 2 (гипотенуза равна 2)
Если хотите вычислить катет, уже зная другой катет и гипотенузу:
AB/(√2/2) = 2 ⇔ AB = √2
Ответ: гипотенуза BC равна 2 см, а катет AB √2 см.
Если есть прилежащий катет — по косинусу
Если в условии задачи дан угол и прилежащий катет, то ищем гипотенузу по косинусу (в прямоугольном треугольнике, косинус острого угла (cos) — это отношение прилежащего катета (b) к гипотенузе(c), таким образом cos a = b/c, из этого получается c = b / cos α).
Т.е. гипотенуза (c) = прилежащий катет (b) / косинус угла или c = b / cos α.
Например:
Известна одна сторона треугольника AB = 1 и ∠β = 45º. Нужно вычислить гипотенузу (BC).
Помним, что гипотенуза (c) = прилежащий катет (b) / косинус угла или c = b / cos α. Т.е.: BC = AB / cosβ ⇔ BC = 1/ cos 45º.
Смотрим в таблице, чему равен cos 45º.
BC = 1/ (√2/2) = √2
Ответ: гипотенуза BC равна √2 см.
Как найти гипотенузу равнобедренного треугольника
В равнобедренном треугольнике есть гипотенуза только в том случае, если он одновременно и прямоугольный, т.к. гипотенуза есть только в прямоугольных треугольниках (и его основание будет гипотенузой).
Чтобы найти такую гипотенузу, нужно любой из двух одинаковых катетов возвести в квадрат, умножить на 2 и посчитать квадратный корень: b = √2a² (где b — гипотенуза, а — катет). Это следствие из теоремы Пифагора.
Например:
Катет равнобедренного треугольника равен 7см. Нужно найти гипотенузу.
Формула b = √2a². Подставляем:
b = √2*7² = √2*49 ≈ √98 ≈ 9.899
Если забудете эту формулу, можно использовать уже знакомую формулу Пифагора для гипотенузы (c² = a² + b²):
c² = a² + b²
c² = 7² + 7²
c² = 49 + 49
c² = 98
c = √98
c ≈ 9.899
Ответ: гипотенуза равна 9.899.
Узнайте больше про Теорему Пифагора, Теорему косинусов, а также, что такое Тангенс и Аксиома.
Загрузить PDF
Загрузить PDF
Все прямоугольные треугольники имеют один прямой угол (90 градусов), а противоположная ему сторона называется гипотенузой.[1]
Гипотенуза — самая длинная сторона треугольника, и найти ее можно различными способами. В этой статье мы расскажем вам, как найти гипотенузу по теореме Пифагора (когда известны длины двух других сторон треугольника), по теореме синусов (когда известны длина катета и угол) и в некоторых частных случаях (часто такие задания встречаются на контрольных и тестах).
-
1
Теорема Пифагора связывает все стороны прямоугольного треугольника.[2]
Согласно данной теореме, в любом прямоугольном треугольнике с катетами «а» и «b» и гипотенузой «с»: a2 + b2 = c2.[3]
-
2
Убедитесь, что данный вам треугольник является прямоугольным, так как теорема Пифагора применима только к прямоугольным треугольникам. В прямоугольных треугольниках один из трех углов всегда равен 90 градусам.
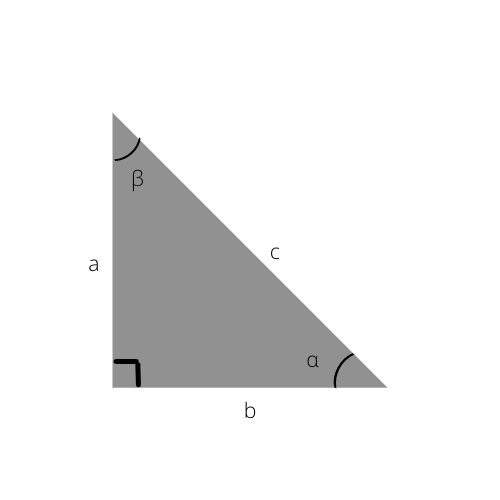
- Прямой угол в прямоугольном треугольнике обозначается значком в виде квадрата.
-
3
Обозначьте стороны треугольника. Катеты обозначьте как «а» и «b» (катеты — стороны, пересекающиеся под прямым углом), а гипотенузу — как «с» (гипотенуза — самая большая сторона прямоугольного треугольника, лежащая напротив прямого угла). Затем подставьте данные вам значения в формулу.
- Например, катеты треугольника равны 3 и 4. В этом случае а = 3, b = 4, а формула выглядит так: 32 + 42 = c2.
-
4
Возведите в квадрат значения катетов («a» и «b»). Для этого просто умножьте число само на себя:
- Если a = 3, то a2 = 3 x 3 = 9. Если b = 4, то b2 = 4 x 4 = 16.
- Подставьте эти значения в формулу: 9 + 16 = с2.
-
5
Сложите найденные квадраты катетов (a2 и b2), чтобы вычислить квадрат значения гипотенузы (с2).
- В нашем примере 9 + 16 = 25, поэтому с2 = 25.
-
6
Найдите квадратный корень с2. Используйте калькулятор, чтобы извлечь квадратный корень из найденного значения. Так вы вычислите гипотенузу треугольника.
- В нашем примере с2 = 25. Квадратный корень из 25 равен 5 (так как 5 х 5 = 25, поэтому √25 = 5). Это означает, что гипотенуза с = 5.
Реклама
-
1
Определение пифагоровой тройки. Пифагорова тройка — это три числа (длины трех сторон), которые удовлетворяют теореме Пифагора. Очень часто треугольники с такими сторонами приводятся в учебниках и на тестах. Если вы запомните первые несколько пифагоровых троек, вы сэкономите много времени на тестах или экзаменах, потому что сможете вычислить гипотенузу, просто взглянув на длины катетов.[4]
- Первая пифагорова тройка: 3-4-5 (32 + 42 = 52, 9 + 16 = 25). Если дан треугольник с катетами 3 и 4, то вы можете с уверенностью заявить, что гипотенуза равна 5 (без необходимости делать какие-либо расчеты).
- Пифагоровы тройки работают даже в том случае, когда числа умножены или разделены на один коэффициент. Например, если катеты равны 6 и 8, гипотенуза равна 10 (62 + 82 = 102, 36 + 64 = 100). То же самое верно для 9-12-15 и даже для 1,5-2-2,5.
- Вторая пифагорова тройка: 5-12-13 (52 + 122 = 132, 25 + 144 = 169). Также к этой тройке относятся, например, числа 10-24-26 и 2,5-6-6,5.
-
2
Равнобедренный прямоугольный треугольник. Это такой треугольник, углы которого равны 45,45 и 90 градусам. Соотношение между сторонами этого треугольника равно 1:1:√2. Это означает, что гипотенуза в таком треугольнике равна произведению катета и квадратного корня из 2.
- Чтобы вычислить гипотенузу такого треугольника, просто умножьте длину любого катета на √2.[5]
- Это соотношение особенно удобно, когда в задачах вместо числовых значений даются переменные.
- Чтобы вычислить гипотенузу такого треугольника, просто умножьте длину любого катета на √2.[5]
-
3
Половина равностороннего прямоугольного треугольника. Это такой треугольник, углы которого равны 30,60 и 90 градусам. Соотношение между сторонами этого треугольника равно 1:√3:2 или х:х√3:2х. Чтобы найти гипотенузу в таком треугольнике выполните одно из следующих действий:[6]
- Если вам дан короткий катет (противолежащий углу в 30 градусов), просто умножьте длину этого катета на 2, чтобы найти длину гипотенузы. Например, если короткий катет равен 4, то гипотенуза равна 8.
- Если вам дан длинный катет (противолежащий углу в 60 градусов), просто умножьте длину этого катета на 2/√3, чтобы найти длину гипотенузы. Например, если короткий катет равен 4, то гипотенуза равна 4,62.
Реклама
-
1
Поймите, что означает «синус». Синус, косинус и тангенс угла — это основные тригонометрические функции, связывающие углы и стороны в прямоугольном треугольнике. Синус угла равен отношению противолежащей стороны к гипотенузе. Обозначается синус как sin.[7]
-
2
Научитесь вычислять синус. Чтобы вычислить синус, на калькуляторе найдите клавишу sin, нажмите ее, а затем введите значение угла. В некоторых калькуляторах сначала нужно нажать клавишу перехода к работе с функциями, а затем нажать клавишу sin. Поэтому поэкспериментируйте с калькулятором или проверьте его документацию.
- Чтобы найти синус угла в 80 градусов, нажмите «sin», «8», «0», «=» или нажмите «8», «0», «sin», «=» (ответ: -0,9939).
- Вы также можете найти онлайн-калькулятор, введя в поисковой системе «вычисление синуса» (без кавычек).[8]
-
3
Запомните теорему синусов. Теорема синусов является полезным инструментом для вычисления углов и сторон любого треугольника. В частности, она поможет вам найти гипотенузу прямоугольного треугольника, если вам дан катет и угол, отличный от прямого. Согласно теореме синусов, в любом треугольнике со сторонами a, b, c и углами A, B, C верно равенство a / sin A = b / sin B = c / sin С.[9]
- Теорема синусов применяется к любым треугольникам, а не только к прямоугольным (но только в прямоугольном треугольнике есть гипотенуза).
-
4
Обозначьте стороны треугольника через «а» (известный катет), «b» (неизвестный катет), «с» (гипотенуза). Затем обозначьте углы треугольника через «А» (напротив катета «а»), «В» (напротив катета «b»), «С» (напротив гипотенузы).
-
5
Найдите третий угол. Если вам дан один из острых углов прямоугольного треугольника (А или В), а второй угол всегда равен 90 градусам (С = 90), то третий угол вычисляется по формуле 180 – (90 + А) = B (помните, что сумма углов в любом треугольнике равна 180 градусам). При необходимости уравнение можно изменить и так: 180 – (90 + B) = A.
- Например, если угол A = 40 градусам, то B = 180 – (90 + 40) = 180 – 130 = 50 градусов.
-
6
На данном этапе вам известны значения всех трех углов и длина катета «а». Теперь вы можете подставить эти значения в формулу теоремы синусов, чтобы найти две другие стороны.
- В нашем примере допустим, что катет а = 10, а углы равны C = 90˚, A = 40˚, В = 50˚.
-
7
Подставьте данные и найденные значения в теорему синусов, чтобы найти гипотенузу: катет «а»/синус угла «A» = гипотенуза «с»/синус угла «С». При этом sin 90˚ = 1. Таким образом, уравнение упрощается до: а/sinA = с/1 или с = а/sinA.
-
8
Разделите длину катета «а» на синус угла «А», чтобы найти длину гипотенузы. Для этого сначала найдите синус угла, а затем выполните деление. Или вы можете воспользоваться калькулятором, введя 10/(sin40) или 10/(40sin) (не забудьте про скобки).
- В нашем примере sin 40 = 0,64278761, а с = 10/0,64278761 = 15,6.
Реклама
Об этой статье
Эту страницу просматривали 312 249 раз.
Была ли эта статья полезной?
Гипотенуза – это самая длинная сторона прямоугольного треугольника. Она лежит напротив прямого угла. Длина гипотенузы может быть найдена различными способами.
Если известна длина обоих катетов, то ее размер вычисляется по теореме Пифагора: сумма квадратов двух катетов равняется квадрату гипотенузы.
Соответственно длина гипотенузы в прямоугольном треугольнике вычисляется по формуле:
К примеру: катет a = 3 см, катет b = 4 см.
Чтобы найти длину гипотенузы в прямоугольном треугольнике, подставим числа в формулу. 
Преобразовав эту формулу можно найти и длину одного неизвестного катета.


| Катет a= | Катет b= | |
| Ответ: Гипотенуза= 5.000 |
В случае если известна длина катета A и гипотенузы C, угол α можно определить по формуле:
Второй угол будет вычисляться так: β = 180°-90°-α. Зная, что сумма всех углов составляет 180°, вычитаем прямой угол и уже известный.
К примеру: A = 3 см, C=5 см, подставляем значения в формулу:

По таблицу синусов угол α будет приблизительно равен 36°, соответственно угол β = 54°.
Если по условиям даны параметры двух катетов, то можно найти острый угол по следующей формуле:
К примеру: A = 3 см, B = 4 см
Подставляем значения в формулу 
По таблице тангенсов угол α будет равняться 36°, соответственно угол β = 54°.
Также стороны прямоугольного треугольника можно найти по различным формулам в зависимости от количества известных переменных.
| A | B | C |
|---|---|---|
|
|
|
|
При расчете параметров прямоугольного треугольника важно обращать внимание на известные значения и решать задачу по самой простой формуле.
Гипотенуза треугольника с двух сторон
Гипотенуза треугольника по одной стороне и площади
сделано с ❤️
Оглавление
Что такое гипотенуза треугольника?
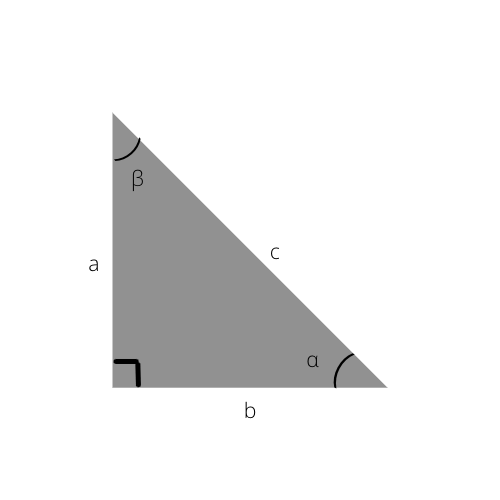
Гипотенуза – это самая длинная сторона треугольника. Это также сторона, противоположная прямому углу (90 °).
Гипотенуза в этом треугольнике равна c.
Вы также можете прочитать эту статью в Википедии:
Гипотенуза – Википедия
Почему гипотенуза – самая длинная сторона треугольника?
Изучив рисунок выше и другие прямоугольные треугольники, вы заметите, что гипотенуза всегда является самой длинной стороной всех прямоугольных треугольников. Это просто потому, что он расположен напротив самого большого угла, угла 90 °.
это также можно доказать математически с помощью теоремы Пифагора:
Как видите, результат вышеописанной операции состоит в том, что «a» (гипотенуза) больше двух других сторон.
Как рассчитать гипотенузу треугольника?
Это можно сделать 3 разными способами, в зависимости от предоставленной информации, которая может быть вариацией факторов, перечисленных ниже:
а: противоположная сторона
α: угол между соседней и гипотенузой
β: угол между противоположной стороной и гипотенузой
1) Две ножки прямоугольного треугольника
Formula: c = √(a² + b²) or c² = a² + b²
Эта формула основана на теореме Пифагора, которую можно просто использовать, извлекая квадратный корень из суммы квадратов смежных и противоположных чисел.
2) Угол и одна нога
Formula: c = a / sin(α) = b / sin(β)
Вы также можете вычислить гипотенузу, используя закон синусов, который является основой этой формулы.
3) Площадь и одна нога
Formula: c = √(a² + b²) = √(a² + (area _ 2 / a)²) = √((area _ 2 / b)² + b²)
Эта формула основана на формуле, которую мы используем для вычисления площади треугольника (a * b / 2). По сравнению с двумя другими он выглядит более сложным, однако он следует той же логике, что и два других способа вычисления гипотенузы.
Полезно знать о тригонометрических функциях
Если вы все еще хотите узнать больше о прямоугольном треугольнике, ознакомьтесь с этими тригонометрическими функциями.
Зная их, вы можете легко вычислить стороны прямоугольного треугольника или даже определить углы, используя приведенную ниже тригонометрическую таблицу.
Примером этого может быть то, что вы уже знаете значение гипотенузы и смежной; вы можете легко найти косинус угла, а затем проверить таблицу выше, чтобы найти точный угол или просто приблизительную оценку того, каким он может быть. Если косинус альфа (α) равен 0,5, то мы знаем, что угол равен 60 °.
Вы также можете прочитать эту статью в Википедии:
Тригонометрические функции – Википедия
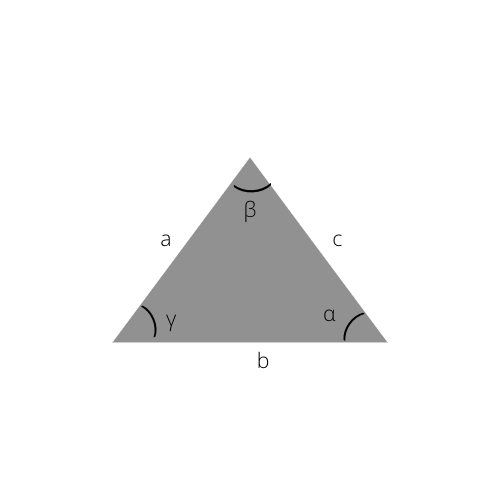
Классификация треугольников по сторонам
1) Равносторонний
У этого треугольника три равные стороны. В результате все углы составляют 60 °.
Равносторонний треугольник
2) Равнобедренная
В этом треугольнике равны только две стороны.
Равнобедренный треугольник
3) Скален
В этом треугольнике все стороны не равны.
Неравносторонний треугольник
Классификация треугольников по углам
1) острый
Все три угла в этом треугольнике меньше 90 °.
2) Право
У этого треугольника только один угол 90 °, в результате два других меньше 90 °.
α + β + γ = 180° & α = 90° → β + γ = 90° → β , γ < 90°
Прямоугольный треугольник
3) Тупой
У этого треугольника один угол больше 90 °.
Интересные факты о треугольниках
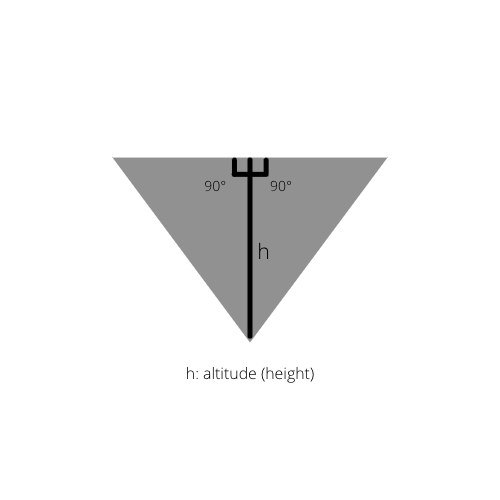
Факт 1:
Если нарисовать внутреннюю высоту треугольника, мы получим два прямоугольных треугольника в исходном треугольнике.
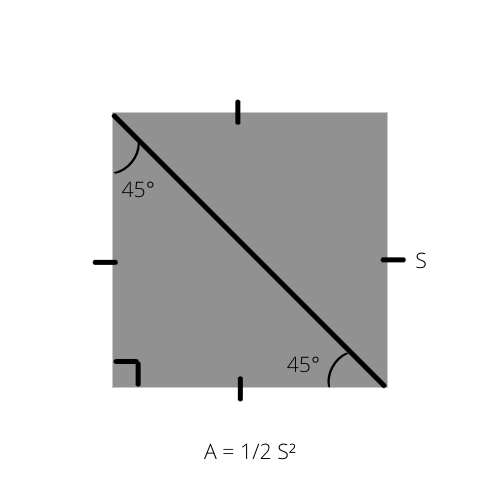
Факт 2:
Как мы знаем, площадь любого треугольника (A) равна половине высоты, умноженной на основание (A = 1/2 _ b _ h). Эта формула может быть записана особым образом для равнобедренного прямоугольного треугольника, поскольку его площадь составляет половину площади квадрата.
A – это площадь треугольника, а S – сторона квадрата.
Факт 3:
Сумма всех трех углов треугольника всегда составляет 180 °. Это верно для всех треугольников.
Автор статьи
Parmis Kazemi
Пармис – создатель контента, который любит писать и создавать новые вещи. Она также очень интересуется технологиями и любит узнавать что-то новое.
Калькулятор Гипотенузы Треугольника русский
Опубликовано: Wed Oct 27 2021
В категории Математические калькуляторы
Добавьте Калькулятор Гипотенузы Треугольника на свой сайт