Как найти гипотенузу в параллелограмме abcd

Как найти гипотенузу в параллелограмме abcd


Загрузить PDF


Загрузить PDF

Все прямоугольные треугольники имеют один прямой угол (90 градусов), а противоположная ему сторона называется гипотенузой.[1]
 Гипотенуза — самая длинная сторона треугольника, и найти ее можно различными способами. В этой статье мы расскажем вам, как найти гипотенузу по теореме Пифагора (когда известны длины двух других сторон треугольника), по теореме синусов (когда известны длина катета и угол) и в некоторых частных случаях (часто такие задания встречаются на контрольных и тестах).

  1. Изображение с названием Find the Length of the Hypotenuse Step 1

    1

    Теорема Пифагора связывает все стороны прямоугольного треугольника.[2]
     Согласно данной теореме, в любом прямоугольном треугольнике с катетами «а» и «b» и гипотенузой «с»: a2 + b2 = c2.[3]

  2. Изображение с названием Find the Length of the Hypotenuse Step 2

    2

    Убедитесь, что данный вам треугольник является прямоугольным, так как теорема Пифагора применима только к прямоугольным треугольникам. В прямоугольных треугольниках один из трех углов всегда равен 90 градусам.

    • Прямой угол в прямоугольном треугольнике обозначается значком в виде квадрата.

  3. Изображение с названием Find the Length of the Hypotenuse Step 3

    3

    Обозначьте стороны треугольника. Катеты обозначьте как «а» и «b» (катеты — стороны, пересекающиеся под прямым углом), а гипотенузу — как «с» (гипотенуза — самая большая сторона прямоугольного треугольника, лежащая напротив прямого угла). Затем подставьте данные вам значения в формулу.

    • Например, катеты треугольника равны 3 и 4. В этом случае а = 3, b = 4, а формула выглядит так: 32 + 42 = c2.

  4. Изображение с названием Find the Length of the Hypotenuse Step 4

    4

    Возведите в квадрат значения катетов («a» и «b»). Для этого просто умножьте число само на себя:

    • Если a = 3, то a2 = 3 x 3 = 9. Если b = 4, то b2 = 4 x 4 = 16.
    • Подставьте эти значения в формулу: 9 + 16 = с2.

  5. Изображение с названием Find the Length of the Hypotenuse Step 5

    5

    Сложите найденные квадраты катетов (a2 и b2), чтобы вычислить квадрат значения гипотенузы (с2).

    • В нашем примере 9 + 16 = 25, поэтому с2 = 25.

  6. Изображение с названием Find the Length of the Hypotenuse Step 6

    6

    Найдите квадратный корень с2. Используйте калькулятор, чтобы извлечь квадратный корень из найденного значения. Так вы вычислите гипотенузу треугольника.

    • В нашем примере с2 = 25. Квадратный корень из 25 равен 5 (так как 5 х 5 = 25, поэтому √25 = 5). Это означает, что гипотенуза с = 5.

    Реклама

  1. Изображение с названием Find the Length of the Hypotenuse Step 7

    1

    Определение пифагоровой тройки. Пифагорова тройка — это три числа (длины трех сторон), которые удовлетворяют теореме Пифагора. Очень часто треугольники с такими сторонами приводятся в учебниках и на тестах. Если вы запомните первые несколько пифагоровых троек, вы сэкономите много времени на тестах или экзаменах, потому что сможете вычислить гипотенузу, просто взглянув на длины катетов.[4]

    • Первая пифагорова тройка: 3-4-5 (32 + 42 = 52, 9 + 16 = 25). Если дан треугольник с катетами 3 и 4, то вы можете с уверенностью заявить, что гипотенуза равна 5 (без необходимости делать какие-либо расчеты).
    • Пифагоровы тройки работают даже в том случае, когда числа умножены или разделены на один коэффициент. Например, если катеты равны 6 и 8, гипотенуза равна 10 (62 + 82 = 102, 36 + 64 = 100). То же самое верно для 9-12-15 и даже для 1,5-2-2,5.
    • Вторая пифагорова тройка: 5-12-13 (52 + 122 = 132, 25 + 144 = 169). Также к этой тройке относятся, например, числа 10-24-26 и 2,5-6-6,5.

  2. Изображение с названием Find the Length of the Hypotenuse Step 8

    2

    Равнобедренный прямоугольный треугольник. Это такой треугольник, углы которого равны 45,45 и 90 градусам. Соотношение между сторонами этого треугольника равно 1:1:√2. Это означает, что гипотенуза в таком треугольнике равна произведению катета и квадратного корня из 2.

    • Чтобы вычислить гипотенузу такого треугольника, просто умножьте длину любого катета на √2.[5]
    • Это соотношение особенно удобно, когда в задачах вместо числовых значений даются переменные.

  3. Изображение с названием Find the Length of the Hypotenuse Step 9

    3

    Половина равностороннего прямоугольного треугольника. Это такой треугольник, углы которого равны 30,60 и 90 градусам. Соотношение между сторонами этого треугольника равно 1:√3:2 или х:х√3:2х. Чтобы найти гипотенузу в таком треугольнике выполните одно из следующих действий:[6]

    • Если вам дан короткий катет (противолежащий углу в 30 градусов), просто умножьте длину этого катета на 2, чтобы найти длину гипотенузы. Например, если короткий катет равен 4, то гипотенуза равна 8.
    • Если вам дан длинный катет (противолежащий углу в 60 градусов), просто умножьте длину этого катета на 2/√3, чтобы найти длину гипотенузы. Например, если короткий катет равен 4, то гипотенуза равна 4,62.

    Реклама

  1. Изображение с названием Find the Length of the Hypotenuse Step 10

    1

    Поймите, что означает «синус». Синус, косинус и тангенс угла — это основные тригонометрические функции, связывающие углы и стороны в прямоугольном треугольнике. Синус угла равен отношению противолежащей стороны к гипотенузе. Обозначается синус как sin.[7]

  2. Изображение с названием Find the Length of the Hypotenuse Step 11

    2

    Научитесь вычислять синус. Чтобы вычислить синус, на калькуляторе найдите клавишу sin, нажмите ее, а затем введите значение угла. В некоторых калькуляторах сначала нужно нажать клавишу перехода к работе с функциями, а затем нажать клавишу sin. Поэтому поэкспериментируйте с калькулятором или проверьте его документацию.

    • Чтобы найти синус угла в 80 градусов, нажмите «sin», «8», «0», «=» или нажмите «8», «0», «sin», «=» (ответ: -0,9939).
    • Вы также можете найти онлайн-калькулятор, введя в поисковой системе «вычисление синуса» (без кавычек).[8]

  3. Изображение с названием Find the Length of the Hypotenuse Step 12

    3

    Запомните теорему синусов. Теорема синусов является полезным инструментом для вычисления углов и сторон любого треугольника. В частности, она поможет вам найти гипотенузу прямоугольного треугольника, если вам дан катет и угол, отличный от прямого. Согласно теореме синусов, в любом треугольнике со сторонами a, b, c и углами A, B, C верно равенство a / sin A = b / sin B = c / sin С.[9]

    • Теорема синусов применяется к любым треугольникам, а не только к прямоугольным (но только в прямоугольном треугольнике есть гипотенуза).

  4. Изображение с названием Find the Length of the Hypotenuse Step 13

    4

    Обозначьте стороны треугольника через «а» (известный катет), «b» (неизвестный катет), «с» (гипотенуза). Затем обозначьте углы треугольника через «А» (напротив катета «а»), «В» (напротив катета «b»), «С» (напротив гипотенузы).

  5. Изображение с названием Find the Length of the Hypotenuse Step 14

    5

    Найдите третий угол. Если вам дан один из острых углов прямоугольного треугольника (А или В), а второй угол всегда равен 90 градусам (С = 90), то третий угол вычисляется по формуле 180 – (90 + А) = B (помните, что сумма углов в любом треугольнике равна 180 градусам). При необходимости уравнение можно изменить и так: 180 – (90 + B) = A.

    • Например, если угол A = 40 градусам, то B = 180 – (90 + 40) = 180 – 130 = 50 градусов.

  6. Изображение с названием Find the Length of the Hypotenuse Step 15

    6

    На данном этапе вам известны значения всех трех углов и длина катета «а». Теперь вы можете подставить эти значения в формулу теоремы синусов, чтобы найти две другие стороны.

    • В нашем примере допустим, что катет а = 10, а углы равны C = 90˚, A = 40˚, В = 50˚.

  7. Изображение с названием Find the Length of the Hypotenuse Step 16

    7

    Подставьте данные и найденные значения в теорему синусов, чтобы найти гипотенузу: катет «а»/синус угла «A» = гипотенуза «с»/синус угла «С». При этом sin 90˚ = 1. Таким образом, уравнение упрощается до: а/sinA = с/1 или с = а/sinA.

  8. Изображение с названием Find the Length of the Hypotenuse Step 17

    8

    Разделите длину катета «а» на синус угла «А», чтобы найти длину гипотенузы. Для этого сначала найдите синус угла, а затем выполните деление. Или вы можете воспользоваться калькулятором, введя 10/(sin40) или 10/(40sin) (не забудьте про скобки).

    • В нашем примере sin 40 = 0,64278761, а с = 10/0,64278761 = 15,6.

    Реклама

Об этой статье

Эту страницу просматривали 311 399 раз.

Была ли эта статья полезной?

Источник

3. Геометрия на плоскости (планиметрия). Часть I


1. Вспоминай формулы по каждой теме


2. Решай новые задачи каждый день


3. Вдумчиво разбирай решения

Параллелограмм и его свойства

Сумма внутренних углов любого четырехугольника равна (360^circ).

Свойства параллелограмма:

(blacktriangleright) Противоположные стороны попарно равны;

(blacktriangleright) Диагонали точкой пересечения делятся пополам;

(blacktriangleright) Противоположные углы попарно равны, а сумма соседних равна (180^circ).

Признаки параллелограмма.
Если для выпуклого четырехугольника выполнено одно из следующих условий, то это – параллелограмм:

(blacktriangleright) если противоположные стороны попарно равны;

(blacktriangleright) если две стороны равны и параллельны;

(blacktriangleright) если диагонали точкой пересечения делятся пополам;

(blacktriangleright) если противоположные углы попарно равны.

Площадь параллелограмма

Площадь параллелограмма равна произведению высоты на основание, к которому проведена эта высота.


Задание
1

#1783

Уровень задания: Легче ЕГЭ

Периметр параллелограмма равен (100), его большая сторона равна (32). Найдите меньшую сторону параллелограмма.

Так как у параллелограмма противоположные стороны равны, то его периметр равен удвоенной сумме его непараллельных сторон, тогда сумма большей и меньшей сторон равна (100 : 2 = 50), значит, меньшая сторона параллелограмма равна (50 – 32 = 18).

Ответ: 18


Задание
2

#1784

Уровень задания: Равен ЕГЭ

Периметр параллелограмма равен (15). При этом одна сторона этого параллелограмма на (5) больше другой. Найдите меньшую сторону параллелограмма.

У параллелограмма противоположные стороны равны. Пусть (BC = AB +
5), тогда периметр параллелограмма (ABCD) равен (AB + BC + CD + AD =
AB + AB + 5 + AB + AB + 5 = 4cdot AB + 10 = 15), откуда находим (AB
= 1,25). Тогда меньшая сторона параллелограмма равна (1,25).

Ответ: 1,25


Задание
3

#273

Уровень задания: Равен ЕГЭ

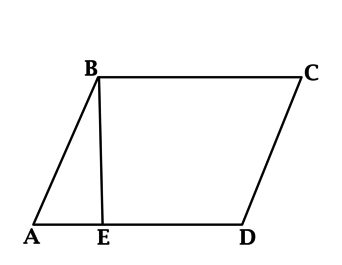
В параллелограмме (ABCD): (BE) – высота, (BE = ED = 5). Площадь параллелограмма (ABCD) равна 35. Найдите длину (AE).

Площадь параллелограмма равна произведению основания на высоту, проведённую к этому основанию, тогда (35 = BE cdot AD = 5cdot(5 + AE)), откуда находим (AE = 2).

Ответ: 2


Задание
4

#1785

Уровень задания: Равен ЕГЭ

Из точки (C) параллелограмма (ABCD) опустили перпендикуляр на продолжение стороны (AD) за точку (D). Этот перпендикуляр пересёк прямую (AD) в точке (E), причём (CE = DE). Найдите (angle B) параллелограмма (ABCD). Ответ дайте в градусах.

В равнобедренном треугольнике углы при основании равны, тогда (angle EDC = angle DCE). Так как (angle DEC = 90^{circ}), а сумма углов треугольника равна (180^{circ}), то (angle EDC =
45^{circ}), тогда (angle ADC = 180^{circ} – 45^{circ} =
135^{circ}). Так как в параллелограмме противоположные углы равны, то (angle B = angle ADC = 135^{circ}).

Ответ: 135


Задание
5

#1686

Уровень задания: Равен ЕГЭ

Диагональ (BD) параллелограмма (ABCD) перпендикулярна стороне (DC) и равна (4). Найдите площадь параллелограмма (ABCD), если (AD=5).

По теореме Пифагора находим: (AB^2=AD^2 – BD^2 = 25 – 16 = 9) (Rightarrow) (AB = 3). (S_{ABCD} = 4cdot3 = 12).

Ответ: 12


Задание
6

#1685

Уровень задания: Равен ЕГЭ

В параллелограмме (ABCD): (P_{triangle AOB} = 8), (P_{triangle AOD} = 9), а сумма смежных сторон равна (7). Найдите произведение этих сторон параллелограмма (ABCD).

(P_{triangle AOB} = AO + OB + AB), (P_{triangle AOD} = AO + OD + AD), (BO = OD) (Rightarrow) (P_{triangle AOD} – P_{triangle AOB} = AD – AB = 1), но (AD + AB = 7) (Rightarrow) (AD = 4), (AB = 3) (Rightarrow) (ADcdot AB = 12).

Ответ: 12


Задание
7

#3617

Уровень задания: Равен ЕГЭ

Стороны параллелограмма равны (9) и (15). Высота, опущенная на первую сторону, равна (10). Найдите высоту, опущенную на вторую сторону параллелограмма.

Площадь параллелограмма равна произведению высоты на сторону, к которой высота проведена. Следовательно, с одной стороны, площадь (S=9cdot 10), с другой стороны, (S=15cdot h), где (h) – высота, которую нужно найти.
Следовательно, [9cdot 10=15cdot hquadLeftrightarrowquad h=6]

Ответ: 6

Задачи из раздела «Геометрия на плоскости» являются обязательной частью аттестационного экзамена у выпускников средней школы. Теме «Параллелограмм и его свойства» в ЕГЭ традиционно отводится сразу несколько заданий. Они могут требовать от школьника как краткого, так и развернутого ответа с построением чертежа. Поэтому если одним из ваших слабых мест являются именно задачи на вычисление площадей параллелограмма или его сторон и углов, то вам непременно стоит повторить или вновь разобраться в материале.

Сделать это легко и эффективно вам поможет образовательный портал «Школково». Наши опытные специалисты подготовили необходимый теоретический материал, изложив его таким образом, чтобы школьники с любым уровнем подготовки смогли восполнить пробелы в знаниях и легко решить задачи ЕГЭ на вычисление площадей, сторон, углов или свойства биссектрисы параллелограмма. Найти базовую информацию вы можете в разделе «Теоретическая справка».

Чтобы успешно решить задачи ЕГЭ по теме «Параллелограмм и его свойства», предлагаем попрактиковаться в выполнении соответствующих упражнений. Большая подборка заданий представлена в блоке «Каталог». Специалисты портала «Школково» регулярно дополняют и обновляют данный раздел.

Последовательно выполнять упражнения учащиеся из Москвы и других городов могут в режиме онлайн. При необходимости любое задание можно сохранить в разделе «Избранное» и в дальнейшем вернуться к нему, чтобы обсудить с преподавателем.

УСТАЛ? Просто отдохни

Источник

1. Треугольник

    Сумма внутренних углов: .

    Площадь треугольника: 

    

    где p – полупериметр треугольника, .

    , где r – радиус вписанной окружности, R – радиус описанной окружности.

    Центр вписанной окружности – точка пересечения биссектрис; центр описанной окружности – точка пересечения серединных перпендикуляров.

    Теорема косинусов: a2=b2+c2-2bccosA.

    Теорема синусов: .

    Свойство медиан: AO:OM=2:1.

    Свойство биссектрис: CA:AD=CB:BD.

    Свойства средней линии: EF||AB, .

Прямоугольный треугольник

    a и b – катеты, c – гипотенуза.

    

    Теорема Пифагора: a2+b2=c2.

 Свойство высоты, опущенной на гипотенузу:

    

    Свойство медианы, опущенной на гипотенузу: .

Равнобедренный треугольник

    Медиана, высота и биссектриса, проведенные к основанию, совпадают.

    Высоты, проведенные к боковым сторонам, равны; медианы, проведенные к боковым сторонам, равны; биссектрисы углов при основании равны.

Равносторонний треугольник

    Медиана, биссектриса и высота, проведенные к каждой из сторон, совпадают.

    .

Признаки равенства треугольников

    Два треугольника равны, если выполняется одно из условий:

    1) две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника;

    2) сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны;

    3) стороны одного треугольника равны соответствующим сторонам другого треугольника.

Признаки подобия треугольников

    Два треугольника подобны, если выполняется одно из условий:

    1) две стороны одного треугольника пропорциональны двум сторонам другого треугольника, и углы, образованные этими сторонами, равны;

    2) два угла одного треугольника равны двум углам другого треугольника;

    3) стороны одного треугольника пропорциональны сторонам другого треугольника.

Пример 1. Площадь равнобедренного остроугольного треугольника равна 12, а длина высоты, опущенной на боковую сторону, . Найдите угол при основании.

    Решение:

    Пусть длина боковой стороны равна b. Тогда .

    С другой стороны, . 

    Отсюда  или . По условию задачи угол  – острый, а потому равен 300.

    Сумма углов треугольника равна . Т.о.  и .

    Ответ: 750.

Замечание. При решении задачи использован «метод площадей». Он состоит в том, что площадь треугольника выражается через разные элементы. В первом случае –  через сторону и опущенную на нее высоту, а другом – через две стороны и угол между ними.

Пример 2. Один из катетов прямоугольного треугольника в два раза больше другого. Высота, опущенная на гипотенузу, равна 12. Найдите площадь треугольника.

    Решение:

    Пусть в  угол B прямой, AB=2BC, а BH – высота.

    Треугольники ABC и AHB подобны, т.к. один из углов у каждого из них прямой, а угол A у этих треугольников общий.

    Треугольники ABC и BHC подобны, поскольку оба являются прямоугольными и имеют общий угол C.

    В каждом из перечисленных треугольников один из катетов в два раза больше другого. Следовательно,

, AH=2BH=24. Т.о. AC=AH+HC=24+6=30.

        Найдем площадь треугольника ABC: .

    Ответ: 180.

Пример 3. Гипотенуза прямоугольного треугольника равна 5, а опущенная на нее высота 2. Найдите катеты.

    Решение:

    Пусть CH – высота, опущенная на гипотенузу AB. Обозначим отрезок HB через x. Тогда AH=5-x.

Рассмотрим прямоугольные треугольники ACH и CHB. . Треугольники подобны по двум углам.

    Из подобия треугольников следует, что , откуда x2-5x+4=0. Корни полученного квадратного уравнения x1=1, x2=4. 

        Пусть HB=1, тогда AH=5-1=4. Из свойства высоты, опущенной на гипотенузу, имеем  и BC2=1•5=5, .

        Аналогично, если HB=4, то .

        Заметим, что, зная AH и BH, катеты можно также найти по теореме Пифагора.

    Ответ: .

Пример 4. В треугольнике ABC проведена медиана CM, причем треугольник BCM – равнобедренный с основанием BM. . Найдите сторону BC.

    Решение:

    Пусть BC=MC=x. .

    По теореме косинусов для : , откуда .

    По теореме косинусов для ; .

    Ответ: 6.

2. Окружность и круг

Длина окружности: 

; площадь круга: 

.

Длина дуги окружности: ;

площадь сектора:  (– центральный угол).

Углы, вписанные в окружность:

    1. углы, опирающиеся на одну хорду и лежащие по одну сторону от неё, равны;

    2. сумма углов, опирающихся на одну хорду и лежащих от нее по разные стороны, равна  ;

    3. центральный угол, опирающийся на хорду, в два раза больше острого угла, вписанного в окружность и опирающегося на ту же хорду;

    4. углы, опирающиеся на диаметр – прямые.

    Свойство хорд: AK•KB=CK•KD.

    Свойство секущих: AD•AE=AF•AG=AB2 .

    Свойство касательных: AB=AC.

    

Пример 5. В окружность вписан равносторонний треугольник ABC со стороной . Найдите площадь треугольника AOC, где O – центр окружности.

    Решение:

    Угол ABC, отпирающийся на хорду AC, равен 600. Центральный угол .

    Стороны AO и OC являются радиусами окружности. Поскольку треугольник равносторонний, то радиус описанной окружности находим как . 

    И, наконец, .

 Ответ: .

Пример 6. В равнобедренный треугольник ABC с основанием AC вписана окружность. Она касается стороны AB в точке E, причем AE составляет 3/5 боковой стороны. Найдите периметр треугольника, если его высота равна 6.

    Решение:

    Обозначим буквами F и H точки касания окружности со сторонами BC и AC. По условию задачи BH=6. Положив AB=5x, имеем AE=3x, EB=2x.

    По свойству секущих AH=AE=3x.

    Рассмотрим прямоугольный треугольник ABH. По теореме Пифагора 25x2=9x2+36, откуда 16x2=36 и  x=3/2.

    Периметр треугольника ABC равен .

    Ответ: 24.

Пример 7. Хорды AB и BC окружности радиуса 4 равны и образуют угол 600. Найти площадь части круга, лежащей внутри угла BAC. 

    Решение:

    Фигура, площадь которой требуется найти, состоит из сектора круга, соответствующего углу AOC, и двух равных треугольников AOB и AOC.

     (см. пример 4). Площадь сектора равна .

    Площадь каждого из треугольников .

        Найдем площадь заданной фигуры: .

    Ответ: .

3. Четырехугольник

Сумма внутренних углов: .

Площадь выпуклого четырехугольника: 

.

Свойство четырехугольника, описанного около окружности: a+c=b+d.

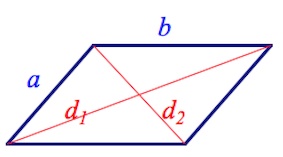
Параллелограмм – четырехугольник, у которого противолежащие стороны параллельны: AD||BC, AB||CD.

Равенство противолежащих сторон и углов: AD=BC=a, AB=CD=b; .

.

                             .

    Свойства диагоналей: .

    Площадь параллелограмма: .

Ромб – четырехугольник, у которого все стороны равны: . Ромб является параллелограммом. В любой ромб можно вписать окружность.

Свойства диагоналей: ;

,

 (диагонали взаимно перпендикулярны и являются биссектрисами углов).

    Площадь: .

Прямоугольник – четырехугольник, у которого все углы прямые: . Прямоугольник является параллелограммом. Около любого прямоугольника можно описать окружность.

Свойства диагоналей: .

    Площадь: S=a•b.

Квадрат – прямоугольник, все стороны которого равны. Квадрат также является ромбом и обладает всеми его свойствами.

Длина диагонали: . 

Площадь: .

    Около квадрата можно описать окружность радиуса . 

    В квадрат можно вписать окружность радиуса .

Трапеция – четырехугольник, у которого ровно одна пара противолежащих сторон параллельна: AD||BC.

AD=a и BC=b – основания трапеции; AB и CD – боковые стороны; CH=h – высота.

. 

Свойства средней линии: MN||AD, .

    Площадь: .

Прямоугольная трапеция – трапеция, у которой одна из боковых сторон перпендикулярна основаниям.

Равнобокая (или равнобедренная) трапеция – трапеция, у которой боковые стороны равны: AB=CD. Около равнобокой трапеции можно описать окружность.

Равенство углов при основании и диагоналей: .

Пример 8. Площадь прямоугольника равна 12, а его стороны относятся как 1 : 3. Найти периметр прямоугольника.

    Решение:

        Пусть меньшая из сторон равна x, тогда длина большей 3x. Площадь прямоугольника равна x•3x=12, откуда x=2.

        Т.о. стороны прямоугольника равны 2 и 6, а периметр 2•2 + 2•6 = 16.

    Ответ: 16.

Пример 9. Периметр прямоугольника равен 32, а площадь 48. Чему равен угол, образованный его диагоналями?

    Решение:

        Пусть стороны прямоугольника равны a и b. По условию задачи: 2a+2b=32, откуда a+b=16 и ab=48.

        Найдем длину диагонали. Для этого возведем равенство a+b=16 в квадрат.

        (a+b)2=162; a2+2ab+b2=256; a2+2•48+b2=256;

        d2=a2+b2=256-2•48=160.

        Поскольку для любого четырехугольника (в т.ч. и для параллелограмма) верно равенство , где  – угол между диагоналями, то , откуда .

    Ответ: 3/5.

Пример 10. Высоты параллелограмма, проведенные из тупого угла, равны 3 и , а угол между ними равен 450. Найти периметр параллелограмма.

    Решение:

В параллелограмме ABCD .

        Рассмотрим прямоугольный треугольник AHB. Найдем его гипотенузу: . Аналогично вычислим гипотенузу прямоугольного треугольника BFC: .

        Периметр параллелограмма равен .

    Ответ: .

Пример 11. Площадь ромба равна 24, а одна из его диагоналей равна 6. Найдите периметр ромба.

    Решение:

Пусть в ромбе ABCD диагональ BD=6. Тогда площадь ромба равна , откуда AC=8.

Найдем сторону ромба. Для этого рассмотрим треугольник AOB. Он является прямоугольным (см. свойства ромба).

Его катеты равны ,   (см. свойства параллелограмма). По теореме Пифагора найдем гипотенузу: .

        Периметр ромба равен 4•5=20.

    Ответ: 20.

Пример 12. Основания равнобокой трапеции равны 6 и 12, а высота равна 3. Чему равна диагональ трапеции?

    Решение:

В трапеции, которую обозначим ABCD, проведем высоты BE и CF. Поскольку EBCF – прямоугольник,  EF=BC=6.

Прямоугольные треугольники ABF и DCF равны, т.к.  и AB=DC. Таким образом, AE=FD. Поскольку AE+EF+FD=AD и AE+6+FD=12, то 2FD=6 и FD=3.

Рассмотрим прямоугольный треугольник DBE. Его катеты BE=3, DE=12-3=9. По теореме Пифагора найдем гипотенузу треугольника: BD2=32+92=90; .

    Ответ: .

Пример 13. В прямоугольной трапеции меньшая боковая сторона равна 8, диагонали 10 и 17. Чему равна большая боковая сторона?

    Решение:

Меньшая боковая сторона AB прямоугольной трапеции ABCD перпендикулярна основаниям и равна по длине высоте CH (т.к. ABCH – прямоугольник), т.е. AB=CH=8.

На чертеже AC=10 и BD=17.

Рассмотрим прямоугольный треугольник ABC и найдем длину его катета .

        Аналогично найдем длину катета AD в прямоугольном треугольнике .

        Поскольку ABCH – прямоугольник, то BC=AH. AD=AH+HD, 15=6+HD, откуда HD=9.

        Длину стороны CD найдем как длину гипотенузы прямоугольного треугольника .

    Ответ: .

4. Многоугольник

Сумма внутренних углов многоугольника с n вершинами (n-угольника) равна  (1).

Сумма внешних углов n-угольника равна  (2).

Число диагоналей n-угольника .

Правильный многоугольник – многоугольник, у которого равны все стороны и внутренние углы.

O – центр вписанной и описанной окружностей;

R – радиус описанной окружности – лежит на биссектрисе угла;

r – радиус вписанной окружности – лежит на серединном перпендикуляре к стороне.

Внешний угол равен центральному углу .

                           Внутренний угол .

Пример 14. Сколько сторон имеет правильный многоугольник, если наименьший угол, образованный его диагоналями, равен 400. 

    Решение:

        Наименьший угол, образованный диагоналями многоугольника – это центральный угол. Если n  – число сторон многоугольника, то:

        ; т.о. n=9.

    Ответ: 9.

Пример 15. Найти площадь правильного восьмиугольника со стороной 1.

    Решение:

Восьмиугольник можно разбить на 8 равных равнобедренных треугольников с вершиной  и основанием 1. Боковая сторона такого треугольника является радиусом описанной окружности R. Площадь каждого из треугольников равна .

        Чтобы найти R, воспользуемся теоремой косинусов. В соответствии с ней: 

        ,

        откуда .

        Т.о. . Площадь восьмиугольника .

    Ответ: .

Задачи для самостоятельного решения

    1) Углы треугольника пропорциональны числам 3, 5, 7. Найдите эти углы.

    2) Углы треугольника образуют арифметическую прогрессию. Чему равен наибольший угол, если величина наименьшего 200?

    3) Два внешних угла треугольника равны 1200 и 1600. Чему равен третий внешний угол?

    4) Медиана, проведенная к гипотенузе прямоугольного треугольника, равна 15, а один из острых углов равен 600. Чему равна длина меньшего катета?

    5) Один из углов прямоугольного треугольника равен 300, а высота, проведенная к гипотенузе, равна 9. Найдите длину гипотенузы.

    6) В треугольнике ABC проведена высота BH, причем AH=3. Найдите длину стороны BC, если .

    7) Найдите гипотенузу равнобедренного прямоугольного треугольника, если его площадь равна 18.

    8) Гипотенуза прямоугольного треугольника равна 13, а катеты относятся как 2 : 3. Чему равна площадь треугольника?

    9) Один из катетов прямоугольного треугольника равен 9, а другой относится к гипотенузе, как 4 : 5. Чему равна площадь треугольника?

    10) Катеты прямоугольного треугольника равны log49 и log316. Чему равна площадь треугольника?

    11) Высота равнобедренного треугольника, равна 15, а боковая сторона больше основания на 1. Чему равно основание?

    12) Найдите боковую сторону равнобедренного треугольника, если его основание равно 18, а площадь 108.

    13) Найдите боковую сторону равнобедренного треугольника, если  основание равно 10 см, а медиана, проведённая к основанию, равна 3 см.

    14) Величины углов треугольника относятся как 1 : 1 : 2, а большая из сторон равна 15. Чему равна высота, проведенная к этой стороне?

    15) Площадь равнобедренного треугольника равна , а углы при основании 300. Найдите высоту, опущенную на основание.

    16) В треугольнике ABC проведена медиана AM. . Чему равна сторона AC?

    17) Основание треугольника равно 22, боковые стороны 13 и 19. Чему равна медиана, опущенная на основание?

    18) Две стороны треугольника равны 11 и 7, а медиана, опущенная на третью сторону 6. Найдите длину третьей стороны.

    19) В треугольнике ABC медиана AM равна 6 и образует со стороной AC, равной 8, угол 300. Найдите площадь треугольника.

    20) В треугольнике ABC к стороне BC=12 проведена медиана AM=7 и образует с этой стороной угол 300. Найдите площадь треугольника.

    21) Площадь треугольника ABC равна 12. Из вершины B проведена медиана BD, длина которой равна 3. Найдите сторону AC, если .

    22) Площадь правильного треугольника равна 64. Найдите его периметр.

    23) В треугольнике ABC на сторонах AB и AC взяты точки M и N такие, что . Найдите площадь треугольника AMN.

    24) Площадь треугольника ABC равна 48. Точка D лежит на стороне AC, деля ее в отношении AD:DC=1:7. Найдите площадь треугольника ABD.

    25) Сторона треугольника равна 2, а прилегающие к ней углы 300 и 450. Найдите его площадь.

    26) Один из катетов прямоугольного треугольника равен 6, а противолежащий ему угол . Найдите площадь круга, описанного около треугольника.

    27) Площадь правильного треугольника равна . Чему равен радиус описанной около него окружности?

    28) Высота правильного треугольника равна 18. Найдите диаметр вписанной в него окружности.

    29) Точка касания с вписанной окружностью делит гипотенузу треугольника в отношении 2 : 3. Расстояние от прямого угла треугольника до центра окружности равно . Найдите периметр треугольника.

    30) Катеты прямоугольного треугольника равны 16 и 30. Найдите радиус описанной около него окружности.

    31) Один катет прямоугольного треугольника равен 15, проекция другого катета на гипотенузу равна 16. Чему равен радиус вписанной в треугольник окружности?

    32) Радиус вписанной в треугольник окружности равен , радиус описанной около него окружности . Чему равна площадь треугольника, если один из его углов равен .

    33) На диаметре круга построен треугольник, вписанный в этот круг. Площадь круга равна , одна из сторон треугольника 30. Чему равна площадь круга, вписанного в треугольник?

    34) Радиус окружности равен 6. Перпендикуляр, опущенный из точки окружности на диаметр, делит его в отношении 1 : 3. Найдите длину перпендикуляра.

    35) Найдите величину острого угла, который опирается на дугу, равную 2/5 окружности. Ответ дайте в градусах.

    36) Найдите величину тупого угла, который опирается на дугу, равную 1/7 окружности. Ответ дайте в радианах.

    37) Радиус окружности равен 5. Найдите длину дуги окружности, соответствующей центральному углу 1080.

    38) Радиус окружности равен 20. Найдите Величину центрального угла, которому соответствует дуга окружности длины .

    39) Хорда окружности, стягивающая дугу 900, равна . Чему равна длина окружности?

    40) Радиус окружности равен 13. На каком расстоянии от центра окружности находится хорда длины 24.

    41) Из точки окружности радиуса R проведены две хорды длины . Чему равен косинус угла между этими хордами?

    42) По разные стороны от центра окружности проведены две параллельные хорды длин 12 и 16. Чему равен радиус окружности, если расстояние между хордами равно 14?

    43) Найти площадь прямоугольника, если его диагональ равна , а одна из сторон 18.

    44) В прямоугольнике ABCD биссектриса угла BAD пересекает сторону BC в точке M и делит ее на отрезки BM=6, MC=4. Чему равна площадь прямоугольника?

    45) Площадь параллелограмма равна 120,  а его высоты  8 и 12. Найдите периметр параллелограмма.

    46) Высоты параллелограмма равны 4 и 8.   Большая высота опущена на  сторону, равную 6.  Найти другую сторону параллелограмма.

    47) Углы между стороной ромба и его диагоналями относятся как 5 : 4. Найдите тупой угол ромба.

    48) Как изменится площадь ромба, если одну из его диагоналей уменьшить на 10%, а другую увеличить на 20%?

    49) Сторона ромба равна 5, а одна из диагоналей 6. Чему равна его площадь?

    50) Разница между радиусами окружностей, описанной около квадрата и вписанной в квадрат, составляет . Чему равна сторона квадрата?

    51) Боковая сторона равнобокой трапеции равна , высота и большее из оснований, соответственно, 4 и 9. Найдите длину средней линии трапеции.

    52) Средняя линия трапеции ABCD делит ее на две трапеции со средними линиями, равными 5 и 9. Найдите большее основание ABCD.

    53) Трапеция, средняя линия которой равна ,  равновелика (т.е. равна по площади) равностороннему  треугольнику со стороной 12. Найти   высоту трапеции.

    54) В равнобокой  трапеции  тупой  угол равен  1200  и  меньшее основание  равно  боковой  стороне  и  равно  6. Найдите площадь  трапеции.

    55) В равнобедренной трапеции основания равны 4 и 6, боковая сторона равна 5. Чему равна сумма длин диагоналей?

    56) В равнобедренной трапеции разность длин оснований равна длине боковой стороны. Чему равен тупой угол трапеции?

    57) Высота равнобокой трапеции равна 40, боковая сторона 41, средняя линия 45. Чему равно большее основания трапеции?

    58) В прямоугольной трапеции боковые стороны равны 4 и 5, меньшее из оснований 5. Чему равна площадь трапеции?

    59) В прямоугольнике перпендикуляр, опущенный на диагональ, делит прямой угол на две части в отношении 3 : 1. Чему равен угол между этим перпендикуляром и другой диагональю?

    60) Периметр ромба равен 52, а сумма длин диагоналей 34. Чему равна его площадь?

    61) Диагонали ромба равны 26 и . Чему равен синус острого угла ромба?

    62) В равнобокой трапеции боковая сторона равна 7, диагональ 8, а средняя линия 4. Найдите меньшее основание.

    63) В окружность радиуса 6 вписан прямоугольник. Найдите большую сторону прямоугольника, если угол между его диагоналями составляет 600.

    64) В круг вписан прямоугольник со сторонами 2 и 6. Найдите площадь круга.

    65) Равнобедренная трапеция вписана в окружность радиуса 6. Ее диагональ составляет угол 300 с большим основанием и перпендикулярна боковой стороне. Найдите периметр трапеции.

    66) Периметр равнобедренной трапеции, описанной около окружности, равен 60. Найдите длину средней линии трапеции.

    67) Основания равнобокой трапеции равны 12 и 20. Центр описанной около окружности трапеции лежит на ее большем основании. Чему равна диагональ трапеции?

    68) В трапецию вписана окружность. Расстояние от центра этой окружности до вершины верхнего основания равно 15; до вершины нижнего 20. Чему равна площадь трапеции?

    69) Четырехугольник ABCD вписан в окружность. BC=4, CD=5, . Чему равна диагональ BD?

    70) Окружность, вписанная в ромб, разбивает его диагональ на отрезки длины 9, 16, 9. Найдите площадь ромба.

    71) Сторона вписанного в окружность правильного треугольника равна 6. Чему равна площадь квадрата, вписанного в ту же окружность?

    72) Во сколько раз площадь круга больше площади вписанного в него квадрата?

    73) Какой правильный многоугольник имеет внутренний угол 1440?

    74) Сколько диагоналей можно провести в многоугольнике, если сумма его внутренних углов равна ?

    75) Чему равна площадь круга, описанного около правильного шестиугольника со стороной 2?

    76) Дан правильный восьмиугольник ABCDEFKM. Найдите радиус описанной около него окружности, если площадь треугольника ABE равна .

    77) Найдите радиус окружности, описанной около правильного девятиугольника A1A2…A9, если периметр треугольника A1OA4 равен .

Источник

24
Июл 2013

Категория: Справочные материалы

Параллелограмм. Свойства и признаки параллелограмма

2013-07-24
2015-09-16

Определение параллелограмма

Параллелограмм – четырехугольник, у которого противоположные стороны попарно  параллельны.

вш

Частные случаи параллелограмма: ромб, прямоугольник, квадрат.

Свойства параллелограмма

свойства параллелограмма

1. Противоположные стороны параллелограмма  попарно равны

2. Противоположные углы параллелограмма попарно равны

свойства параллелограмма

3. Сумма смежных (соседних) углов параллелограмма равна 180 градусов

4. Сумма всех углов равна 360°

свойства параллелограмма5. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам

sd

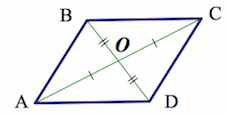
6. Точка пересечения диагоналей является центром симметрии параллелограмма

khj

7. Диагонали  d_1,;d_2 параллелограмма и стороны
a,;b связаны следующим соотношением: d_1^2+d_2^2=2(a^2+b^2)

щд

8. Биссектриса отсекает от параллелограмма равнобедренный треугольник

Признаки параллелограмма

Четырехугольник ABCD является параллелограммом, если выполняется хотя бы одно из следующих условий:

1. Противоположные стороны попарно равны: AB=CD,;BC=AD

2. Противоположные углы попарно равны: angle A=angle C,;angle B=angle D

3. Диагонали пересекаются и в точке пересечения делятся пополам

4. Противоположные стороны равны и параллельны: AB=CD,;AB||CD

5. AC^2+BD^2=AB^2+BC^2+CD^2+AD^2

Небольшой видеоролик о свойствах параллелограмма (в том числе ромба, прямоугольника, квадрата) и о том, как эти свойства  применяются в задачах:

7Формулы площади параллелограмма смотрите здесь.

Хорошую подборку задач на нахождение углов и длин в параллелограмме смотрите здесь.

Автор: egeMax |

комментариев 7

Источник

Skip to content

Home » База знаний » В па­рал­ле­ло­грам­ме АВСD про­ве­де­ны пер­пен­ди­ку­ля­ры ВЕ и DF

В па­рал­ле­ло­грам­ме АВСD про­ве­де­ны пер­пен­ди­ку­ля­ры ВЕ и DF к диа­го­на­ли АС (см. ри­су­нок). До­ка­жи­те, что ВFDЕ — па­рал­ле­ло­грамм.
В па­рал­ле­ло­грам­ме АВСD про­ве­де­ны пер­пен­ди­ку­ля­ры ВЕ и DF
Доказательство:
∆ ABE=∆CDF (треугольники прямоугольные ABE и CDFравны, так как гипотенузы AB = CD и острые углы, угол BAE и угол DCF равны)
Следовательно:
BE = DF
BE || DF, (BE паралельны DF, так как являются пер­пен­ди­ку­ля­рыами к одной пря­мой)

∆ BEF=∆DFE (BE = DF доказано выше и EF — общая сторона, угол DFE и угол BEF равны 90 градусов)
Следовательно:
BF = DE и BF || DE, (пер­пен­ди­ку­ля­ры к одной пря­мой)
В па­рал­ле­ло­грам­ме АВСD про­ве­де­ны пер­пен­ди­ку­ля­ры ВЕ и DF
Доказано:
Четырёхуголь­ни­к BFDE — параллелограмм, (про­ти­во­ле­жа­щие сто­ро­ны равны и па­рал­лель­ны.)

Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.

Реклама

Источник

Добавить комментарий