Как найти гипотенузу зная радиус вписанной окружности

Как найти гипотенузу: 4 способа поиска ответа

После изучения темы про прямоугольные треугольники ученики часто выбрасывают из головы всю информацию о них. В том числе и то, как найти гипотенузу, не говоря уже о том, что это такое.

И напрасно. Потому что в дальнейшем диагональ прямоугольника оказывается этой самой гипотенузой, и ее нужно найти. Или диаметр окружности совпадает с самой большой стороной треугольника, один из углов которого прямой. И найти ее без этого знания невозможно.

Существует несколько вариантов того, как найти гипотенузу треугольника. Выбор метода зависит от исходного набора данных в условии задачи величин.

Способ под номером 1: даны оба катета

Это самый запоминающийся метод, потому что использует теорему Пифагора. Только иногда ученики забывают, что по этой формуле находится квадрат гипотенузы. Значит, чтобы найти саму сторону, нужно будет извлечь квадратный корень. Поэтому формула для гипотенузы, которую принято обозначать буквой «с», будет выглядеть так:

с = √ (а 2 + в 2 ), где буквами «а» и «в» записаны оба катета прямоугольного треугольника.

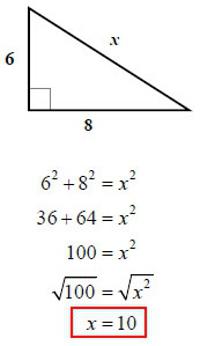
Способ под номером 2: известен катет и угол, который к нему прилежит

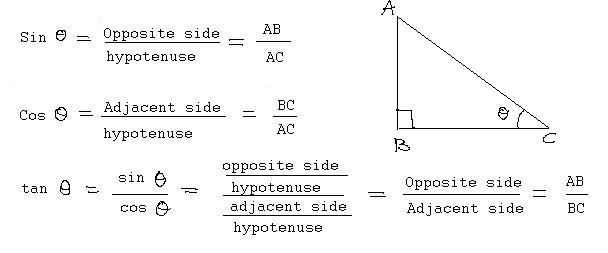
Для того чтобы узнать, как найти гипотенузу, потребуется вспомнить тригонометрические функции. А именно косинус. Для удобства будем считать, что даны катет «а» и прилежащий к нему угол α.

Теперь нужно вспомнить, что косинус угла прямоугольного треугольника равен отношению двух сторон. В числителе будет стоять значение катета, а в знаменателе — гипотенузы. Из этого следует, что последнюю можно будет сосчитать по формуле:

с = а / cos α.

Способ под номером 3: даны катет и угол, который лежит напротив него

Чтобы не запутаться в формулах, введем обозначение для этого угла — β, а сторону оставим прежнюю «а». В этом случае потребуется другая тригонометрическая функция – синус.

Как и в предыдущем примере, синус равен отношению катета к гипотенузе. Формула этого способа выглядит так:

с = а / sin β.

Для того чтобы не запутаться в тригонометрических функциях, можно запомнить простое мнемоническое привило: если в задаче идет речь о противолежащем угле, то нужно использовать синус, если — о прилежащем, то косинус. Следует обратить внимание на первые гласные в ключевых словах. Они образуют пары о-и или и-о.

Способ под номером 4: по радиусу описанной окружности

Теперь, для того чтобы узнать, как найти гипотенузу, потребуется вспомнить свойство окружности, которая описана около прямоугольного треугольника. Оно гласит следующее. Центр окружности совпадает с серединой гипотенузы. Если сказать по-другому, то самая большая сторона прямоугольного треугольника равна диагонали окружности. То есть удвоенному радиусу. Формула для этой задачи будет выглядеть так:

с = 2 * r, где буквой r обозначен известный радиус.

Это все возможные способы того, как находить гипотенузу прямоугольного треугольника. Пользоваться в каждой конкретной задаче нужно тем методом, который больше подходит по набору данных.

Пример задачи №1

Условие: в прямоугольном треугольнике проведены медианы к обоим катетам. Длина той, которая проведена к большей стороне, равна √52. Другая медиана имеет длину √73. Требуется вычислить гипотенузу.

Так как в треугольнике проведены медианы, то они делят катеты на два равных отрезка. Для удобства рассуждений и поиска того, как найти гипотенузу, нужно ввести несколько обозначений. Пусть обе половинки большего катета будут обозначены буквой «х», а другого — «у».

Теперь нужно рассмотреть два прямоугольных треугольника, гипотенузами у которых являются известные медианы. Для них нужно дважды записать формулу теоремы Пифагора:

(2у) 2 + х 2 = (√52) 2

(у) 2 + (2х) 2 = (√73) 2 .

Эти два уравнения образуют систему с двумя неизвестными. Решив их, легко можно будет найти катеты исходного треугольника и по ним его гипотенузу.

Сначала нужно все возвести во вторую степень. Получается:

Из второго уравнения видно, что у 2 = 73 – 4х 2 . Это выражение нужно подставить в первое и вычислить «х»:

4(73 – 4х 2 ) + х 2 = 52.

292 – 16 х 2 + х 2 = 52 или 15х 2 = 240.

Из последнего выражения х = √16 = 4.

Теперь можно вычислить «у»:

у 2 = 73 – 4(4) 2 = 73 – 64 = 9.

По данным условия получается, что катеты исходного треугольника равны 6 и 8. Значит, можно воспользоваться формулой из первого способа и найти гипотенузу:

√(6 2 + 8 2 ) = √(36 + 64) = √100 = 10.

Ответ: гипотенуза равна 10.

Пример задачи №2

Условие: вычислить диагональ, проведенную в прямоугольнике с меньшей стороной, равной 41. Если известно, что она делит угол на такие, которые соотносятся как 2 к 1.

В этой задаче диагональ прямоугольника является наибольшей стороной в треугольнике с углом 90º. Поэтому все сводится к тому, как найти гипотенузу.

В задаче идет речь об углах. Это значит, что нужно будет пользоваться одной из формул, в которых присутствуют тригонометрические функции. А сначала требуется определить величину одного из острых углов.

Пусть меньший из углов, о которых идет речь в условии, будет обозначен α. Тогда прямой угол, который делится диагональю, будет равен 3α. Математическая запись этого выглядит так:

Из этого уравнения просто определить α. Он будет равен 30º. Причем он будет лежать напротив меньшей стороны прямоугольника. Поэтому потребуется формула, описанная в способе №3.

Гипотенуза равна отношению катета к синусу противолежащего угла, то есть:

Узнать ещё

Знание — сила. Познавательная информация

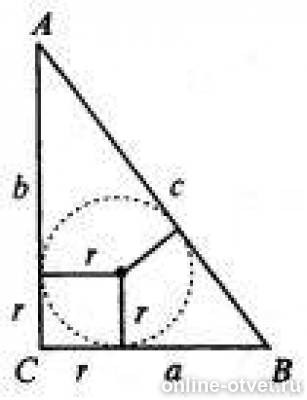
Окружность, вписанная в прямоугольный треугольник

Если в задаче дана окружность, вписанная в прямоугольный треугольник, то ее решение может быть связано со свойством отрезков касательных, проведенных из одной точки, и теоремой Пифагора.

Кроме того, следует учесть, что радиус вписанной в прямоугольный треугольник окружности вычисляется по формуле

где a и b — длины катетов, c — гипотенузы.

Рассмотрим две задачи на вписанную в прямоугольный треугольник окружность.

Точка касания окружности, вписанной в прямоугольный треугольник, делит гипотенузу на отрезки 4 см и 6 см. Найти периметр и площадь треугольника и радиус окружности.

Дано: ∆ ABC, ∠C=90º,

окружность (O, r) — вписанная,

K, M, F — точки касания со сторонами AC, AB, BC,

1) По свойству отрезков касательных, проведенных из одной точки,

AK=AM=6 см,

2) AB=AM+BM=6+4=10 см,

3) По теореме Пифагора:

Второй корень не подходит по смыслу задачи. Значит, CK+CF=2 см, AC=8 см, BC=6 см.

Ответ: 24 см, 24 см², 2 см.

Найти площадь прямоугольного треугольника, гипотенуза которого равна 26 см, а радиус вписанной окружности — 4 см.

Дано:∆ ABC, ∠C=90º,

окружность (O, r) — вписанная,

K, M, F — точки касания со сторонами AC, AB, BC,

1) Проведем отрезки OK и OF.

(как радиусы, проведенные в точки касания).

Четырехугольник OKCF — прямоугольник (так как у него все углы — прямые).

А так как OK=OF (как радиусы), то OKCF — квадрат.

2) По свойству касательных, проведенных из одной точки,

3) AC=AK+KC=(x+4) см, BC=BF+CF=26-x+4=(30-x) см.

Прямоугольный треугольник

Прямоугольный треугольник – треугольник, в котором один угол прямой (то есть равен 90˚).

Сторона, противоположная прямому углу, называется гипотенузой прямоугольного треугольника.

Стороны, прилежащие к прямому углу, называются катетами .

Признаки равенства прямоугольных треугольников

Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны ( по двум катетам ).

Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны ( по катету и острому углу ).

Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и острому углу ).

Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и катету ).

Свойства прямоугольного треугольника

1. Сумма острых углов прямоугольного треугольника равна 90˚.

2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.

И обратно, если в треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.

3. Теорема Пифагора:

, где – катеты, – гипотенуза. Видеодоказательство

4. Площадь прямоугольного треугольника с катетами :

5. Высота прямоугольного треугольника, проведенная к гипотенузе выражается через катеты и гипотенузу следующим образом:

6. Центр описанной окружности – есть середина гипотенузы.

7. Радиус описанной окружности есть половина гипотенузы :

8. Медиана, проведенная к гипотенузе, равна ее половине

9. Радиус вписанной окружности выражается через катеты и гипотенузу следующим образом:

Тригонометрические соотношения в прямоугольном треугольнике смотрите здесь.

[spoiler title=”источники:”]

[/spoiler]

Гипотенуза – это самая длинная сторона прямоугольного треугольника. Она лежит напротив прямого угла. Длина гипотенузы может быть найдена различными способами.

Если известна длина обоих катетов, то ее размер вычисляется по теореме Пифагора: сумма квадратов двух катетов равняется квадрату гипотенузы.

Соответственно длина гипотенузы в прямоугольном треугольнике вычисляется по формуле:

К примеру: катет a = 3 см, катет b = 4 см.
Чтобы найти длину гипотенузы в прямоугольном треугольнике, подставим числа в формулу. =5 см

Преобразовав эту формулу можно найти и длину одного неизвестного катета.
,

В случае если известна длина катета A и гипотенузы C, угол α можно определить по формуле:
Второй угол будет вычисляться так: β = 180°-90°-α. Зная, что сумма всех углов составляет 180°, вычитаем прямой угол и уже известный.

К примеру: A = 3 см, C=5 см, подставляем значения в формулу: =0,6
По таблицу синусов угол α будет приблизительно равен 36°, соответственно угол β = 54°.

Если по условиям даны параметры двух катетов, то можно найти острый угол по следующей формуле:

К примеру: A = 3 см, B = 4 см
Подставляем значения в формулу =0,75
По таблице тангенсов угол α будет равняться 36°, соответственно угол β = 54°.

Также стороны прямоугольного треугольника можно найти по различным формулам в зависимости от количества известных переменных.

A	B	C

При расчете параметров прямоугольного треугольника важно обращать внимание на известные значения и решать задачу по самой простой формуле.

Тренировочный вариант 399 от Ларина Задание 1 № задачи в базе 2965

Радиус окружности, вписанной в прямоугольный треугольник, равен 6. Найдите гипотенузу, если точка касания с вписанной окружностью делит ее на отрезки, длины которых относятся как 5 : 12

Ответ: 34

ФИПИ 2023 🔥 …

Примечание: Радиус окружности, вписанной в прямоугольный треугольник, равен 6 ! Тренировочный вариант 399 от Ларина Задание 1 # Тренировочный вариант 360 от Ларина Задание 3 (6)

Рейтинг сложности задачи: