Для термина «Математическая гипотеза» см. также другие значения.
Действительная (красный) и мнимая части (синий) дзета-функции Римана на критической прямой 
. Первые нетривиальные нули находятся в точках 
. Гипотеза Римана утверждает, что все нетривиальные нули дзета-функции находятся на критической линии. Этот факт позволяет сделать некоторые выводы о размещении простых чисел на действительной оси.
Гипотеза в математике — утверждение, которое на основе доступной информации представляется с высокой вероятностью верным, но для которого не удаётся получить математическое доказательство[1][2]. Математическая гипотеза является открытой математической проблемой, и каждую нерешённую математическую проблему, которая является проблемой разрешимости, можно сформулировать в форме гипотезы. Однако в виде гипотезы может быть сформулирована не всякая математическая проблема. Например, конкретное решение некоторой системы уравнений или задачи оптимизации для 2208 неизвестных предугадать невозможно, но такое решение может быть не только практическим, но и собственно математическим результатом[3].
Гипотеза Римана, Великая теорема Ферма, гипотеза Варинга и некоторые другие математические гипотезы сыграли значительную роль в математике, поскольку попытки их доказательства привели к созданию новых областей и методов исследования.
Математическая и естественнонаучная гипотеза[править | править код]
В отличие от естественнонаучной гипотезы, математическая гипотеза может быть логически доказана в некоторой системе аксиом, после чего она становится теоремой, верной при этих ограничениях, «на все времена». Характерным примером является научное наследие Ньютона, заявлявшего, что он «гипотез не измышляет», и стремившегося в физике не выходить за рамки математической модели. Математические теоремы Ньютона, как и древнейшая теорема Пифагора, по сей день остаются в силе, однако его классическая механика и теория тяготения после появления специальной и общей теорий относительности стали опровергнутыми физическими гипотезами. Если разрешимая математическая гипотеза может быть либо доказана, либо опровергнута, то для естественнонаучной гипотезы в силу относительности естественнонаучного знания свойства верифицируемости и фальсифицируемости не исключают друг друга[4]. Механика Ньютона неприменима для скоростей, близких к скорости света, но с очень большой точностью описывает движение большинства тел Солнечной системы. Поэтому в физике обычно говорят не об опровержении гипотез, а об ограничении сферы применимости теории.
Разрешение математических гипотез[править | править код]
Доказательство[править | править код]
Математика основана на формальных доказательствах. Сколь бы убедительной гипотеза ни казалась, сколько бы ни было приведено примеров в её подтверждение, гипотеза может быть опровергнута одним контрпримером. Современные математические журналы иногда публикуют результаты исследований о диапазоне, в пределах которого справедливость гипотезы проверена. Например, гипотеза Коллатца проверена для всех целых чисел вплоть до 1,2 × 1012, однако этот факт сам по себе ничего не даёт для доказательства гипотезы.
Для доказательства гипотезы должно быть предъявлено математическое доказательство, которое путём логически безупречного рассуждения на основе некоторой системы аксиом делает единственно возможным утверждение гипотезы или логически невозможным противоположное утверждение.
Когда гипотеза доказана, то в математике она становится теоремой. Теоремой может стать и опровержение явной или неявной гипотезы. В истории математики некоторые гипотезы длительное время существовали в неявной форме, и многочисленные попытки найти квадратуру круга или решение алгебраического уравнения пятой степени в радикалах исходили из опровергнутых впоследствии гипотез о том, что это возможно.
Опровержение[править | править код]
Опровержение гипотезы также осуществляется с помощью доказательства, но с учётом типичных формулировок гипотез опровержение часто является простейшим видом доказательства — контрпримером. Такое доказательство является простейшим с логической точки зрения, однако построение примера в теории графов или поиск примера в теории чисел (гипотеза Эйлера) может быть делом очень непростым. После опровержения гипотеза может стать фактом истории математики, а может трансформироваться в новую математическую гипотезу. Например, гипотеза Эйлера после опровержения трансформировалась в гипотезу Ландера — Паркина — Селфриджа. В этом случае процесс сходен с эволюцией естественнонаучных гипотез.
Неразрешимые гипотезы[править | править код]
Не для всякой гипотезы можно доказать её истинность или ложность в заданной системе аксиом. Согласно теореме Гёделя о неполноте, во всякой достаточно сложной аксиоматической теории, например в арифметике, существуют утверждения, которые нельзя ни опровергнуть, ни доказать в рамках самой теории. Поэтому всякая математическая теория, содержащая арифметику, содержит не опровергаемые и недоказуемые в её рамках гипотезы.
Например, было доказано, что континуум-гипотеза Кантора в теории множеств не зависит от общепринятой системы аксиом Цермело — Френкеля. Поэтому можно принять в качестве аксиомы это утверждение или его отрицание, не приходя к противоречию с остальными аксиомами и без каких-либо последствий для доказанных ранее теорем. В геометрии с древнейших времён сомнения математиков вызывала аксиома параллельности Евклида. Сегодня известно, что если принять противоположную аксиому, то можно построить непротиворечивую геометрию Лобачевского, включающую абсолютную геометрию, то есть с сохранением всех остальных аксиом.
Условные доказательства[править | править код]
Из справедливости некоторых недоказанных гипотез вытекают важные следствия. Если существует широко распространённое мнение, что гипотеза верна, то математики иногда доказывают теоремы, которые верны только при условии справедливости такой гипотезы, в надежде что гипотеза будет доказана. Подобные доказательства распространены, например, в связи с гипотезой Римана.
Несколько известных примеров[править | править код]
Здесь перечислены утверждения, которые оказали большое влияние на математику, находясь в статусе гипотез. Одни из них остаются гипотезами по сей день, другие были доказаны либо опровергнуты.
Великая теорема Ферма[править | править код]
В теории чисел Великая теорема Ферма утверждает, что ни для каких для трёх натуральных чисел 
равенство 
не выполняется, если целое число 
превышает 2.
Пьер Ферма записал это предположение в 1637 году на полях «Арифметики» Диофанта вместе с утверждением, что имеет доказательство, но оно слишком большое, чтобы уместиться на этих полях.[5] Первое успешное доказательство было получено Джоном Уайлсом в 1994 году и опубликовано в 1995 году, после 358 лет усилий многих математиков. Попытки решить эту проблему в XIX веке привели к развитию алгебраической теории чисел и доказательству теоремы о модулярности в XX веке.
Гипотеза Пуанкаре[править | править код]
Гипотеза Пуанкаре утверждает, что всякое односвязное компактное трёхмерное многообразие без края гомеоморфно трёхмерной сфере. Анри Пуанкаре сформулировал эту гипотезу в 1904 году. После почти вековых усилий математиков Григорий Перельман доказал эту гипотезу в трёх статьях, размещенных в 2002 и 2003 годах на сайте arXiv. Доказательство следовало предложению Ричарда Гамильтона использовать для решения поток Риччи.[6] Несколько команд математиков проверили доказательство Перельмана и подтвердили, что оно верное. Интересно, что для сфер большей размерности доказательства были получены ранее.
Гипотеза Римана[править | править код]
Гипотеза Римана, предложенная в 1859 году, утверждает, что все нетривиальные корни дзета-функции Римана имеют действительную часть, равную 1/2. Из справедливости гипотезы Римана вытекает ряд результатов о распределении простых чисел. Некоторые математики считают эту гипотезу наиболее важной нерешённой проблемой в «чистой математике». Гипотеза Римана входит в списки проблем Гильберта и задач тысячелетия.
Равенство классов P и NP[править | править код]
Вопрос о равенстве классов P и NP входит в список задач тысячелетия и является одной из главных проблем информатики. Неформально, но достаточно точно вопрос сводится к тому, можно ли любую задачу, предъявленное решение которой можно проверить за полиномиальное время, также и решить за полиномиальное время, используя полиномиальную память. Сегодня преобладает мнение, что это не так. Но если доказательство истинности этой гипотезы может быть конструктивным (надо предъявить всего лишь один алгоритм, что пытаются сделать очень многие), то как доказывать обратное — неясно. Вероятно, впервые проблема упомянута в
1956 году в письме Курта Гёделя Джону Нейману.[7] Точно проблему сформулировал в 1971 году Стивен Кук[8] и она считается многими важнейшей открытой проблемой в этой области[9].
История[править | править код]
Древнегреческие математики часто применяли в качестве метода математического доказательства мысленный эксперимент, включавший в себя выдвижение гипотез и вывод из них с помощью дедукции следствий с целью проверки правильности первоначальных догадок. Сегодня такие рассуждения называются методом доказательства от противного. Платон рассматривал гипотезы как посылки разработанного им аналитико-синтетического метода доказательства, способного обеспечить абсолютно истинный характер вывода. Однако гипотеза как метод исследования была отвергнута Аристотелем, который в качестве посылок силлогистического доказательства мыслил лишь общие, необходимые и абсолютные истины. Это обусловило последующее негативное отношение учёных к гипотезам как форме недостоверного или вероятного знания[4]. Преодолеть противопоставление гипотез и абсолютно точного знания и, как следствие, пренебрежительное отношение к гипотезам удалось лишь в XIX веке. В частности, Энгельс, рассматривая гипотезу как форму «развития естествознания»[10], выдвинул положение о взаимосвязи гипотез с законами и теориями как разными формами относительно истинного знания.
Примечания[править | править код]
- ↑ Oxford Dictionary of English (неопр.). — 2010.
- ↑ JL Schwartz. Shuttling between the particular and the general: reflections on the role of conjecture and hypothesis in the generation of knowledge in science and mathematics (англ.). — 1995. — P. 93.
- ↑ The Approximate Bilinear Algorithm of Length 46 for Multiplication of 4×4 Matrices (недоступная ссылка)
- ↑ 1 2 Гипотеза Архивная копия от 5 марта 2016 на Wayback Machine // Новая философская энциклопедия
- ↑ Ore, Oystein (1988), Number Theory and Its History, Dover, с. 203–204, ISBN 978-0-486-65620-5
- ↑ Hamilton, Richard S. Four-manifolds with positive isotropic curvature (неопр.) // Communications in Analysis and Geometry. — 1997. — Т. 5, № 1. — С. 1—92.
- ↑ Juris Hartmanis 1989, Godel, von Neumann, and the P = NP problem Архивная копия от 26 февраля 2015 на Wayback Machine, Bulletin of the European Association for Theoretical Computer Science, vol. 38, pp. 101—107
- ↑ Cook, Stephen (англ.) (рус.. The complexity of theorem proving procedures // Proceedings of the Third Annual ACM Symposium on Theory of Computing (англ.). — 1971. — P. 151—158.
- ↑ Lance Fortnow, The status of the P versus NP problem Архивировано 24 февраля 2011 года., Communications of the ACM 52 (2009), no. 9, pp. 78-86. doi:10.1145/1562164.1562186
- ↑ Маркс К. и Энгельс Ф. Соч., т. 20, с. 555
Содержание:
Теория статистической проверки гипотез
Пусть имеется выборка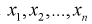 
Тогда нулевой гипотезой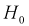 
называют основную (проверяемую) гипотезу, которая утверждает, что различие между сравниваемыми величинами отсутствует.
Альтернативной (конкурирующей, противоположной) гипотезой Н называется гипотеза, которая принимается тогда, когда отвергается нулевая.
Целью статистической проверки гипотез является выбор критерия по выборке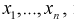 
на основании которого принимается гипотеза 
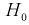или отклоняется в пользу альтернативной. При этом возможны ошибки двух видов:
- Отклонение
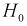, когда она на самом деле верна – ошибка первого рода. Вероятность этой ошибки обозначается а и называется уровнем значимости. - Принятие когда она на самом деле не верна – ошибка второго рода, вероятность ошибки – .
, когда она на самом деле верна – ошибка первого рода. Вероятность этой ошибки обозначается а и называется уровнем значимости. 
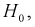когда она на самом деле не верна – ошибка второго рода, вероятность ошибки – 
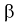.Чем серьезнее будут последствия ошибки первого рода, тем меньше надо выбирать уровень значимости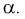 
Обычно выбирают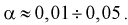 
Статистической характеристикой Z гипотезы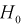 
называется некоторая случайная величина, определяемая по выборке, для которой известен закон распределения.
Областью отклонения (критической областью)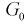 
называется область, при попадании в которую статистической характеристики Z гипотеза 
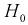отклоняется.
Дополнение области отклонения до всех возможных значений статистической характеристики Z называется областью принятия G.
При попадании статистической характеристики Z в область принятия гипотеза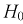 
принимается. На рис. 11.1 изображены область отклонения 
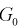и область принятия G . Разделяет их точка на числовой оси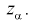 
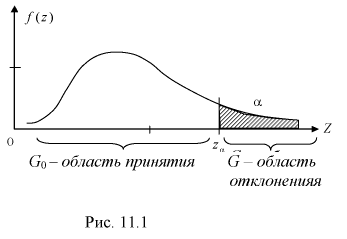
При попадании Z в область принятия гипотеза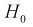 
принимается. По существу область принятия есть доверительный интервал для статистической характеристики Z с доверительной вероятностью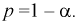 
Область отклонения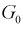 
выбирается таким образом, чтобы вероятность попадания в нее статистической характеристики Z при условии, что 
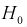верна, равнялась уровню значимости 
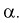То есть область отклонения удовлетворяет условию:
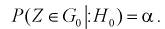(11.1)
С другой стороны, для того чтобы уменьшить вероятность ошибки второго рода при выбранном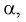 
область отклонения 
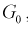, удовлетворяющую условию 1, нужно выбрать таким образом, чтобы вероятность попадания в нее статистической характеристики Z при условии, что верна альтернативная гипотеза 
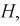была максимальной, т. е.
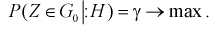
Вероятность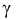 
– называется мощностью критерия проверки гипотез.
Так как события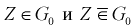 
, – противоположны, то можно написать
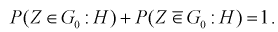
Таким образом, имеем
где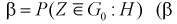 
– вероятность совершения ошибки второго рода).
Отметим, что ошибка первого рода существенней, поэтому а мы выбираем, а р – нет (принимаем полученное значение).
Из (11.2) следует, что между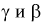 
существует простая зависимость и чтобы уменьшить 
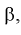надо увеличить мощность критерия 
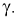Если 
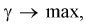то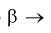 
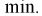
Между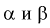 
простой функциональной связи не существует, можно только сказать, что с увеличением одной, другая уменьшается и наоборот.
На рис. 11.2 приведены две кривые плотности распределения: одна кривая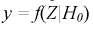 
– когда верна гипотеза 
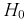, другая кривая 
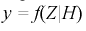– когда верна альтернативная гипотеза Н.
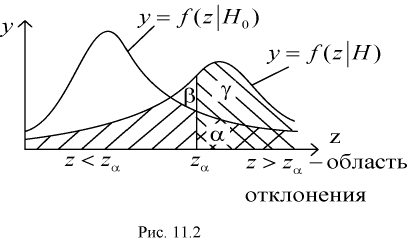
Из рис. 11.2 видно, что при уменьшении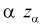 
, возрастает, область отклонения сужается и, следовательно, уменьшается вероятность отклонения гипотезы 
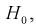если она верна. Вместе с тем при сужении области отклонения 
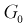расширяется область принятия G и увеличивается вероятность принятия гипотезы 
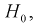если она на самом деле не верна. Поэтому нельзя брать 
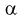слишком малой.
Гипотезы бывают двух видов – параметрические и непараметрические.
Параметрические гипотезы – это гипотезы о проверке параметров законов распределения.
Непараметрические – это гипотезы о виде закона распределения.
Проверка гипотезы равенства математических ожиданий при неизвестной дисперсии (критерий Стьюдента)
Пусть Хи У – независимые нормальные случайные величины.
Введем обозначения:
Пусть дисперсии этих случайных величин равны и неизвестны:
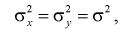
где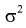 
– не предполагается известным.
Пусть даны выборки
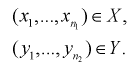
По выборкам найдем критерий проверки гипотезы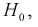 
, состоящей в том, что математические ожидания этих случайных величин одинаковы:
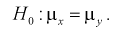
При альтернативной гипотезе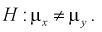 
Известно, что случайные величины
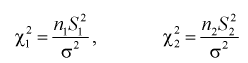
имеют распределение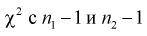 
степенями свободы, где
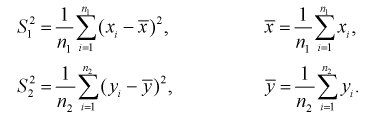
Сумма независимых случайных величин с распределением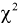 
имеет то же распределение 
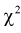с суммарным числом степеней свободы:
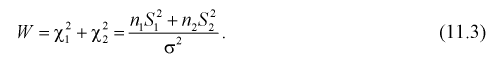
Случайная величина W имеет распределение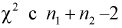 
степенями свободы, (этот факт не очевиден, но несложно показать с помощью характеристических функций).
Ранее мы показывали, что несмещенной оценкой математического ожидания является выборочное среднее. Поэтому для проверки гипотезы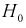 
возьмем разность между оценками математических ожиданий: 
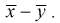Нормируем эту разность, т. е. сделаем безразмерной. Для этого разделим ее на 
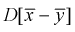и обозначим как U:
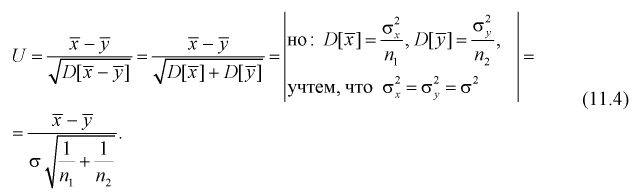
Очевидно, что случайная величина U имеет нормальное распределение, т. к. X и Y нормально распределены. Если проверяемая гипотеза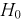 
о равенстве математических ожиданий выполняется 
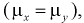то имеем:
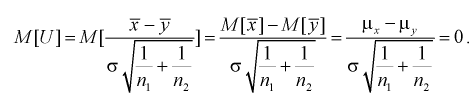
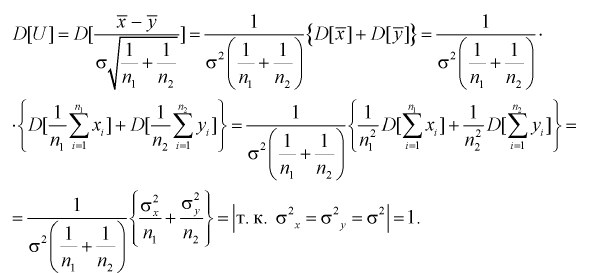
Таким образом, если гипотеза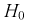 
верна, то случайная величина U имеет нормированный нормальный закон распределения.
Рассмотрим случайную величину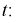 
где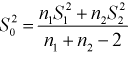 
где ; – ооъединенная выборочная дисперсия.
Случайную величину t можно представить в следующем виде через ранее введенные Un W:
Действительно:
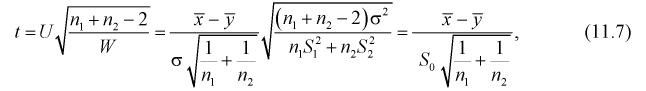
т. е. правые части (11.5) и (11.6 или 11.7) совпадают.
Но величина t (11.6) имеет распределение Стьюдента с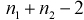 
степенями свободы. Это следует из того, что U имеет нормированное нормальное распределение при условии, что 
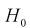– верна. W – имеет распределение 
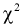с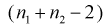 
степенями свободы, кроме того величины U и W независимы. Таким образом, величина t определяется по (11.5) и имеет распределение Стьюдента с 
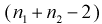степенями свободы, если верна проверяемая гипотеза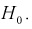 
Эту величину t (11.5) примем за статистическую характеристику Z. Проверка гипотезы о равенстве .математических ожиданий состоит в следующем.
По таблицам распределения Стьюдента для заданного уровня значимости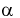 
или доверительной вероятности 
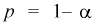и числу степеней свободы 
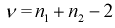находим квантиль 
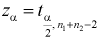, удовлетворяющий условию (на рис. 11.3 изображена кривая распределения Стьюдента и заштрихована область отклонения 
):
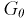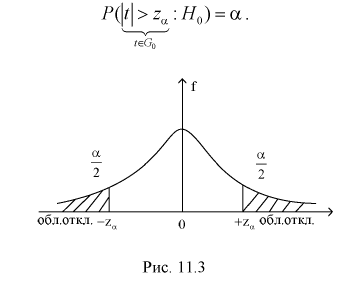
Тогда если фактически найденное по выборкам значение статистической характеристики t (11.5) удовлетворяет условию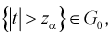 
то проверяемую гипотезу 
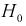о равенстве математических ожиданий отклоняем как несогласующуюся с результатами выборочных данных; при этом вероятность ошибки равна 
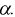Если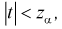 
то гипотеза 
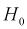принимается, математические ожидания случайных величин Х и Y одинаковы.
Проверка гипотезы о равенстве дисперсий (критерий Фишера)
Пусть Х и Y – нормальные независимые случайные величины. Обозначим их дисперсии:
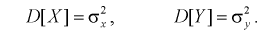
По выборкам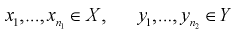 
найдем критерий проверки гипотезы 
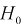состоящей в том, что дисперсии этих случайных величин равны
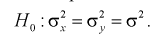
При альтернативной гипотезе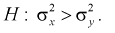 
.
Такая гипотеза выбирается, например, при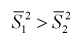 
, где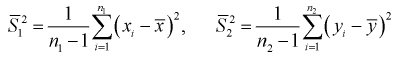 
– модифицированные выборочные дисперсии.
В качестве статистической характеристики возьмем случайную величину
Если гипотеза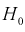 
, о равенстве дисперсии верна, то случайная величина F имеет распределение Фишера с 
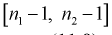степенями свободы. Покажем это, представляя числитель и знаменатель (11.8) в следующем виде:
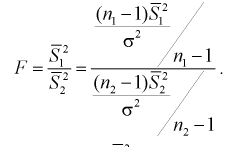
Видим, что величина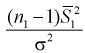 
имеет распределение 
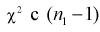степенью свободы, 
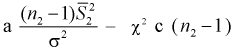степенями свободы. Следовательно, согласно определению (см. раздел 9.5, формула (9.7)), случайная величина F имеет распределение Фишера с 
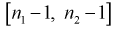степенями свободы.
Проверка гипотезы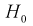 
состоит в следующем:
Из таблиц распределения Фишера по выбранному уровню значимости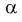 
и числу степеней свободы 
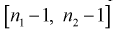находим квантиль 
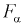, который удовлетворяет условию 
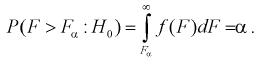Ha рис. 11.4 изображена кривая распределения Фишера с числом степеней свободы 
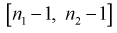и заштрихована область отклонения 
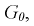площадь которой области равна 
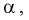отмечен квантиль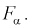 
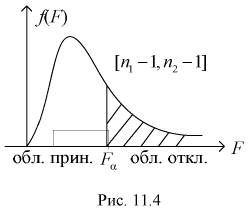
По выборкам, используя (11.8), определяем значение статистической характеристики F. Если фактически вычисленное по формуле (11.8) значение F окажется больше табличного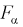 
(как видно из рис. 11.4, мы попадаем в область отклонения), то гипотезу о равенстве дисперсий отклоняем как не согласующуюся с выборкой. При этом вероятность ошибки равна 
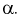В противном случае, когда 
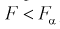, принимается гипотеза 
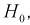т. е. дисперсии случайных величин Х и Yравны.
Пример:
Пусть X – чувствительность телевизоров марки «Горизонт», Y – чувствительность телевизоров марки «Витязь». Проведены выборочные измерения чувствительности телевизоров для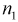 
= 7 телевизоров марки «Горизонт» и 
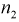= 6 телевизоров марки «Витязь». Результаты измерений чувствительности в 
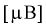представлены в таблицах.
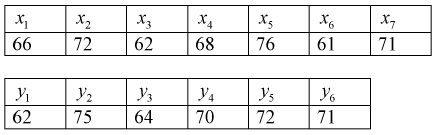
Определить лучшую марку телевизора, если лучшим будет тот, у которого чувствительность в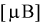 
будет меньше.
Найдем по результатам измерений средние значения чувствительности, вычисляя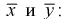 
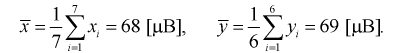
Можно ли сказать, что чувствительность телевизоров марки «Горизонт» лучше? Нет, т. к. выборки, выборочные средние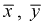 
и разность между ними – элементы случайные.
Сначала убедимся в равенстве дисперсий по критерию Фишера – гипотеза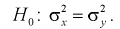 
Вычислим несмещенные оценки дисперсий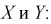 
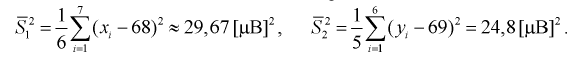
Используя (11.8), найдем значение статистической характеристики F:
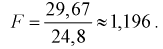
По таблицам распределения Фишера для [6;5] степеней свободы, задавая уровень значимости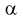 
= 0,05, найдем квантиль – 
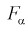= 4,95. Сравнивая 
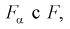видим, что 1,196 < 4,95. Значит, гипотеза 
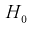принимается, т. е. дисперсии случайных величин X и Y равны.
Теперь проверим гипотезу о равенстве математических ожиданий случайных величин X и Y , применяя критерий Стьюдента.
Гипотеза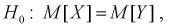 
т. е. чувствительность телевизоров марки «Горизонт» и «Витязь» одинакова.
Найдем объединенную выборочную дисперсию:
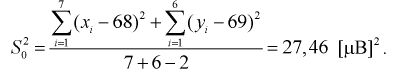
По формуле (11.5) вычислим статистическую характеристику t :
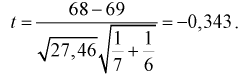
Задавая уровень значимости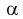 
= 0,05 для числа степеней свободы v = 7 + 6 – 2 = ll, по таблицам распределения Стьюдента находим квантиль 
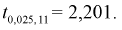Сравнивая 
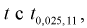видим, что |0,343| <2,201, значит, гипотезу о равенстве чувствительности телевизоров марки «Горизонт» и «Витязь» принимаем.
Проверка гипотезы о законе распределения генеральной случайной величины. Критерий Пирсона
Проверка гипотезы о законе распределения генеральной случайной величины. Критерий Пирсона. (Критерий согласия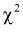 
)
Пусть задана генеральная случайная величинами выборка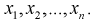 
Если по выборке построить гистограмму, то по виду гистограммы можно выдвинуть гипотезу о виде закона распределения генеральной случайной величины X. Тогда в качестве нулевой гипотезы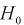 
будет предположение, что случайная величина X имеет плотность распределения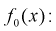
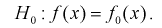
При альтернативной гипотезе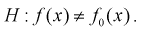 
Обычно для построения гистограммы равноинтервальным способом разбивают весь диапазон выборочных значений случайной величины X на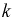 
одинаковых интервалов. Если 
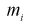– число выборочных значений, попавших в 
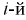интервал, то 
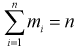– объем выборки. Введем случайную величину 
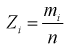относительную частоту попадания случайной величины X в 
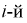интервал. Теоретическая вероятность 
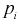попадания значений случайной величины X в 
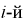интервал может быть определена как 
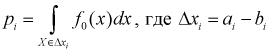– длина 
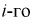интервала, 
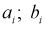– границы 
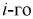интервала.
Рассмотрим событие, состоящее в том, что случайная величина X попадет в интервал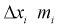 
раз. Тогда введем случайную величину Y, равную числу попаданий случайной величины в 
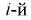интервал 
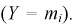Вероятности возможных ее значений определяются по формуле Бернулли, случайная величина У имеет биномиальный закон распределения, и ее числовые характеристики имеют вид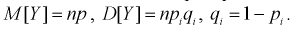 
Для введенной ранее случайной величины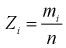 
определим числовые характеристики:
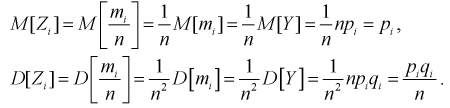
Проведем нормировку случайной величины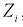 
для этого мы ее центрируем, сделаем безразмерной, разделив на 
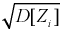и обозначим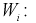 
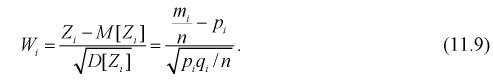
Эта величина распределена по биномиальному закону, т. к. в нее входит случайная величина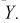 
Образуем сумму квадратов случайных величин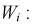 
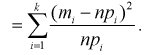
Сумма квадратов нормированных нормальных случайных величин (как было показано ранее) имеет распределение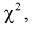 
обозначим
Эта случайная величина имеет закон распределения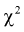 
с числом степеней свободы
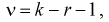(11.11)
где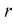 
– число параметров закона распределения, оцениваемых по выборочным данным.
Анализируя правые части формул (11.9) и (11.10), можно отметить, что в критерии согласия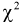 
фактически сравниваются эмпирические и теоретические частоты распределения.
Проверка гипотезы состоит в следующем. Задаем уровень значимости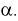 
По таблицам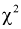 
– распределения для заданных 
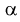и числу степеней свободы 
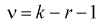находим квантиль 
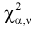, удовлетворяющий условию 
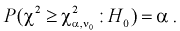По формуле (11.10) вычисляем значение 
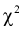. Сравнивая рассчитанное значение 
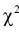с квантилем 
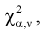, найденным по таблицам, принимаем одно из двух решений:
- Если 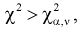то нулевая гипотеза 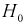отвергается в пользу альтернативной Н, т. е. 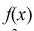не согласуется с результатами эксперимента.
- Если 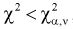, то , принимается, т. е. согласуется с экспериментальными данными, закон распределения подтверждается. При этом вероятность ошибки равна
то нулевая гипотеза 
отвергается в пользу альтернативной Н, т. е. 
не согласуется с результатами эксперимента.
, то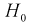 
, принимается, т. е. 
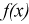согласуется с экспериментальными данными, закон распределения 
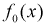подтверждается. При этом вероятность ошибки равна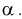 
Критерий Романовского
Рассмотрим неравенство
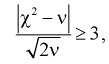(11.12)
где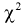 
вычисляется по формуле (11.10);
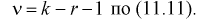
Проверка гипотезы состоит в следующем: если это неравенство выполняется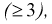 
то расхождение теоретических и экспериментальных данных неслучайно, т. е. закон распределения не подтверждается, гипотеза 
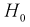отклоняется.
В противном случае гипотеза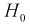 
подтверждается, действительно случайная величина X имеет плотность распределения
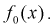Этот критерий хорош тем, что для проверки гипотезы не требуются таблицы 
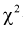– распределения.
Критерий согласия Колмогорова
В критерии согласия А. Н. Колмогорова проводится сравнение эмпирической и теоретической функций распределения. Укажем этапы проверки гипотез этим критерием.
1. По выборке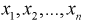 
строится вариационный ряд и график эмпирической функции распределения.
2. По виду графика функции распределения выдвигается гипотеза о виде закона распределения генеральной случайной величины X. Тогда в качестве нулевой гипотезы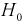 
будет предположение, что генеральная случайная величина X имеет функцию распределения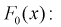 
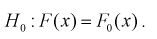
При альтернативной гипотезе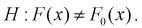 
3. По выборке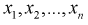 
находят точечные оценки параметров теоретической функции распределения 
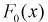, используя метод моментов или метод наибольшего правдоподобия.
4. На графике эмпирической функции распределения строится график теоретической функции распределения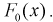 
5. Путем сравнения графиков вычисляется максимальное значение модуля отклонения значений эмпирической функции распределения от теоретической функции распределения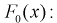 
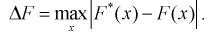
6. Рассчитывают значение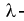 
критерия Колмогорова:
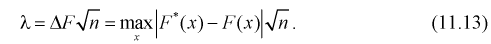
7. Задавая уровень значимости а , определяем квантиль из условия
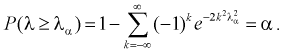
Отметим, что самостоятельно решать это уравнение не надо, поскольку составлены таблицы квантилей распределения Колмогорова, из которых по заданному уровню значимости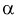 
определяем квантиль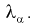 
Сравнивая значение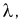 
рассчитанное по формуле (11.13) с квантилем 
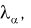делаем следующие выводы:
Следует отметить, что критерий Колмогорова применяется тогда, когда полностью известен закон распределения функции распределения F(x) и значения ее параметров. При решении практических задач это не всегда удается выполнить. Для этого прибегают к некоторым дополнительным исследованиям: применяют вероятностные бумаги, строят гистограммы и т. д. Это помогает правильно подобрать теоретический закон распределения для функции распределения F(x). Но в этом случае неизвестны ее параметры. И если их оценивать по этой же выборке, то это может привести к ошибочным выводам в отношении принятой гипотезы. В этом случае следует использовать другие критерии согласия, например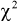 
.
Пример:
Проведено 100 измерений расстояния радиодальномером до цели. Результаты представлены в виде статистического ряда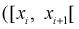 
– границы интервалов в [км], 
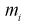– число выборочных значений, попавших в 
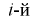интервал).
Оценить закон распределения ошибки измерения дальности радиодальномером.
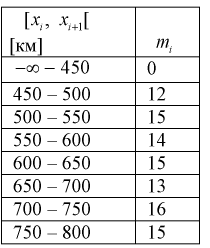
Занесем в таблицу значения относительных частот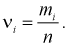 
Анализ значений относительных частот позволяет выдвинуть гипотезу о равномерном законе распределения. Теоретическая функция распределения для этого закона имеет вид
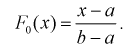
Принимаем а = 450, b = 800. Полагая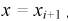 
для каждого интервала, рассчитываем 
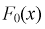в этих точках и заносим результат в таблицу. Зная 
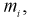рассчитаем эмпирическую функцию распределения 
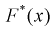в точках 
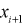для каждого интервала: 
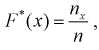где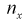 
– число значений 
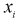меньших заданного х, 
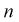– объем выборки. Рассчитаем разность: 
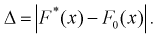Данные заносим в таблицу.
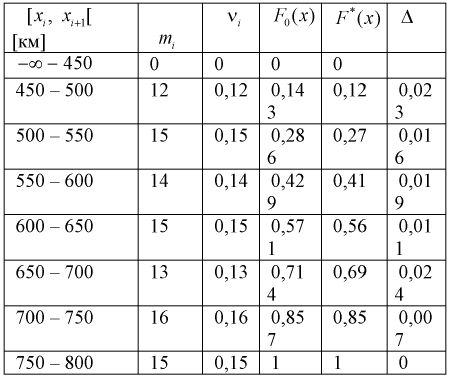
Вычисляем критерий Колмогорова по формуле (11.13), учитывая, что из таблицы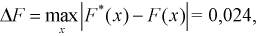 
тогда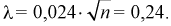 
Задавая уровень значимости 
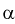– 0,05, по таблице квантилей Колмогорова находим квантиль 
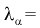1,358. Поскольку 
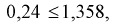то гипотеза 
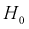принимается, т. е. действительно генеральная случайная величина X имеет функцию распределения 
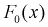c равномерным законом распределения.
- Линейный регрессионный анализ
- Вариационный ряд
- Законы распределения случайных величин
- Дисперсионный анализ
- Случайные процессы
- Выборочный метод
- Статистическая проверка гипотез
- Статистические оценки
Гипотеза в математике — утверждение, которое на основе доступной информации представляется с высокой вероятностью верным, но для которого не удаётся получить математическое доказательство. Математическая гипотеза является открытой математической проблемой, и каждую нерешённую математическую проблему, которая является проблемой разрешимости, можно сформулировать в форме гипотезы. Однако в виде гипотезы может быть сформулирована не всякая математическая проблема. Например, конкретное решение некоторой системы уравнений или задачи оптимизации для 2208 неизвестных предугадать невозможно, но такое решение может быть не только практическим, но и собственно математическим результатом.
Гипотеза Римана, Великая теорема Ферма, гипотеза Варинга и некоторые другие математические гипотезы сыграли значительную роль в математике, поскольку попытки их доказательства привели к созданию новых областей и методов исследования.
Математическая и естественнонаучная гипотеза
В отличие от естественнонаучной гипотезы, математическая гипотеза может быть логически доказана в некоторой системе аксиом, после чего она становится теоремой, верной при этих ограничениях, «на все времена». Характерным примером является научное наследие Ньютона, заявлявшего, что он «гипотез не измышляет», и стремившегося в физике не выходить за рамки математической модели. Математические теоремы Ньютона, как и древнейшая теорема Пифагора, по сей день остаются в силе, однако его классическая механика и теория тяготения после появления специальной и общей теорий относительности стали опровергнутыми физическими гипотезами. Если разрешимая математическая гипотеза может быть либо доказана, либо опровергнута, то для естественнонаучной гипотезы в силу относительности естественнонаучного знания свойства верифицируемости и фальсифицируемости не исключают друг друга. Механика Ньютона неприменима для скоростей, близких к скорости света, но с очень большой точностью описывает движение большинства тел Солнечной системы. Поэтому в физике обычно говорят не об опровержении гипотез, а об ограничении сферы применимости теории.
Разрешение математических гипотез
Доказательство
Математика основана на формальных доказательствах. Сколь бы убедительной гипотеза ни казалась, сколько бы ни было приведено примеров в её подтверждение, гипотеза может быть опровергнута одним контрпримером. Современные математические журналы иногда публикуют результаты исследований о диапазоне, в пределах которого справедливость гипотезы проверена. Например, гипотеза Коллатца проверена для всех целых чисел вплоть до 1,2 × 1012, однако этот факт сам по себе ничего не даёт для доказательства гипотезы.
Для доказательства гипотезы должно быть предъявлено математическое доказательство, которое путём логически безупречного рассуждения на основе некоторой системы аксиом делает единственно возможным утверждение гипотезы или логически невозможным противоположное утверждение.
Когда гипотеза доказана, то в математике она становится теоремой. Теоремой может стать и опровержение явной или неявной гипотезы. В истории математики некоторые гипотезы длительное время существовали в неявной форме, и многочисленные попытки найти квадратуру круга или решение алгебраического уравнения пятой степени в радикалах исходили из опровергнутых впоследствии гипотез о том, что это возможно.
Опровержение
Опровержение гипотезы также осуществляется с помощью доказательства, но с учётом типичных формулировок гипотез опровержение часто является простейшим видом доказательства — контрпримером. Такое доказательство является простейшим с логической точки зрения, однако построение примера в теории графов или поиск примера в теории чисел (гипотеза Эйлера) может быть делом очень непростым. После опровержения гипотеза может стать фактом истории математики, а может трансформироваться в новую математическую гипотезу. Например, гипотеза Эйлера после опровержения трансформировалась в гипотезу Ландера — Паркина — Селфриджа. В этом случае процесс сходен с эволюцией естественнонаучных гипотез.
Неразрешимые гипотезы
Не для всякой гипотезы можно доказать её истинность или ложность в заданной системе аксиом. Согласно теореме Гёделя о неполноте, во всякой достаточно сложной аксиоматической теории, например в арифметике, существуют утверждения, которые нельзя ни опровергнуть, ни доказать в рамках самой теории. Поэтому всякая математическая теория, содержащая арифметику, содержит не опровергаемые и недоказуемые в её рамках гипотезы.
Например, было доказано, что континуум-гипотеза Кантора в теории множеств не зависит от общепринятой системы аксиом Цермело — Френкеля. Поэтому можно принять в качестве аксиомы это утверждение или его отрицание, не приходя к противоречию с остальными аксиомами и без каких-либо последствий для доказанных ранее теорем. В геометрии с древнейших времён сомнения математиков вызывала аксиома параллельности Евклида. Сегодня известно, что если принять противоположную аксиому, то можно построить непротиворечивую геометрию Лобачевского, включающую абсолютную геометрию, то есть с сохранением всех остальных аксиом.
Условные доказательства
Из справедливости некоторых недоказанных гипотез вытекают важные следствия. Если существует широко распространённое мнение, что гипотеза верна, то математики иногда доказывают теоремы, которые верны только при условии справедливости такой гипотезы, в надежде что гипотеза будет доказана. Подобные доказательства распространены, например, в связи с гипотезой Римана.
Несколько известных примеров
Здесь перечислены утверждения, которые оказали большое влияние на математику, находясь в статусе гипотез. Одни из них остаются гипотезами по сей день, другие были доказаны либо опровергнуты.
Великая теорема Ферма
В теории чисел Великая теорема Ферма утверждает, что ни для каких для трёх натуральных чисел a , b , c {displaystyle a,b,c} равенство a n + b n = c n {displaystyle a^{n}+b^{n}=c^{n}} не выполняется, если целое число n {displaystyle n} превышает 2.
Пьер Ферма записал это предположение в 1637 году на полях «Арифметики» Диофанта вместе с утверждением, что имеет доказательство, но оно слишком большое, чтобы уместиться на этих полях. Первое успешное доказательство было получено Джоном Уайлсом в 1994 году и опубликовано в 1995 году, после 358 лет усилий многих математиков. Попытки решить эту проблему в XIX веке привели к развитию алгебраической теории чисел и доказательству теоремы о модулярности в XX веке.
Гипотеза Пуанкаре
Гипотеза Пуанкаре утверждает, что всякое односвязное компактное трёхмерное многообразие без края гомеоморфно трёхмерной сфере. Анри Пуанкаре сформулировал эту гипотезу в 1904 году. После почти вековых усилий математиков Григорий Перельман доказал эту гипотезу в трёх статьях, размещенных в 2002 и 2003 годах на сайте arXiv. Доказательство следовало предложению Ричарда Гамильтона использовать для решения поток Риччи. Несколько команд математиков проверили доказательство Перельмана и подтвердили, что оно верное. Интересно, что для сфер большей размерности доказательства были получены ранее.
Гипотеза Римана
Гипотеза Римана, предложенная в 1859 году, утверждает, что все нетривиальные корни дзета-функции Римана имеют действительную часть, равную 1/2. Из справедливости гипотезы Римана вытекает ряд результатов о распределении простых чисел. Некоторые математики считают эту гипотезу наиболее важной нерешённой проблемой в «чистой математике». Гипотеза Римана входит в списки проблем Гильберта и задач тысячелетия.
Равенство классов P и NP
Вопрос о равенстве классов P и NP входит в список задач тысячелетия и является одной из главных проблем информатики. Неформально, но достаточно точно вопрос сводится к тому, можно ли любую задачу, предъявленное решение которой можно проверить за полиномиальное время, также и решить за полиномиальное время, используя полиномиальную память. Сегодня преобладает мнение, что это не так. Но если доказательство истинности этой гипотезы может быть конструктивным (надо предъявить всего лишь один алгоритм, что пытаются сделать очень многие), то как доказывать обратное — неясно. Вероятно, впервые проблема упомянута в 1956 году в письме Курта Гёделя Джону Нейману. Точно проблему сформулировал в 1971 году Стивен Кук и она считается многими важнейшей открытой проблемой в этой области.
История
Древнегреческие математики часто применяли в качестве метода математического доказательства мысленный эксперимент, включавший в себя выдвижение гипотез и вывод из них с помощью дедукции следствий с целью проверки правильности первоначальных догадок. Сегодня такие рассуждения называются методом доказательства от противного. Платон рассматривал гипотезы как посылки разработанного им аналитико-синтетического метода доказательства, способного обеспечить абсолютно истинный характер вывода. Однако гипотеза как метод исследования была отвергнута Аристотелем, который в качестве посылок силлогистического доказательства мыслил лишь общие, необходимые и абсолютные истины. Это обусловило последующее негативное отношение учёных к гипотезам как форме недостоверного или вероятного знания. Преодолеть противопоставление гипотез и абсолютно точного знания и, как следствие, пренебрежительное отношение к гипотезам удалось лишь в XIX веке. В частности, Энгельс, рассматривая гипотезу как форму «развития естествознания», выдвинул положение о взаимосвязи гипотез с законами и теориями как разными формами относительно истинного знания.
Решения задач на проверку статистических гипотез
Проверка статистических гипотез включает в себя большой пласт задач математической статистики. Зная некоторые характеристики выборки (или имея просто выборочные данные), мы можем проверять гипотезы о виде распределении случайной величины или ее параметрах.
В учебных задачах речь обычно идет о простой гипотезе $H_0$ (ее называют нулевой), однозначно определяющей закон распределения. Вместе с ней вводят альтернативную гипотезу $H_1$ (конкурирующую) и определяют уровень значимости $alpha$, на котором будет сделан вывод о справедливости гипотезы.
Далее по выборочным данным вычисляется значение статистического критерия (формула зависит от конкретной гипотезы) и выясняется, попадает ли оно в критическую область (одностороннюю или двустороннюю). Если попадает – нулевую гипотезу следует отвергнуть. При проверке гипотез есть вероятность допустить ошибку: первого рода (верная гипотеза отклонена, $alpha$) или второго рода (неверная гипотеза принята, $beta$).
Ниже в примерах мы разберем основные учебные задачи на проверку гипотез о значении среднего, дисперсии, вероятности, о равенстве числовых характеристики. Задачи на проверку гипотез о виде распределения (с помощью критерия согласия Пирсона и других) ищите тут: Проверка гипотез о законе распределения.
Понравилось? Добавьте в закладки
Примеры решений на проверку гипотез онлайн
Гипотеза о равенстве среднего значения числу
Пример 1. Утверждается, что шарики для подшипников, изготовленные автоматическим станком, имеют средний диаметр 10 мм. Используя односторонний критерий с α=0,05, проверить эту гипотезу, если в выборке из n шариков средний диаметр оказался равным 10,3 мм, а дисперсия известна и равна 1 мм.
Пример 2. Продавец утверждает, что средний вес пачки чая составляет 100 г. Из партии извлечена выборка и взвешена. Вес каждой пачки – см. таблицу вариантов. Не противоречит ли это утверждению продавца? Доверительная вероятность 99%. Вес пачек чая распределен нормально.
Гипотеза о равенстве дисперсии числу
Пример 3. По результатам $n=7$ независимых измерений найдено, что $overline{x}=82,48$ мм, а $S=0,08$ мм. Допустив, что ошибки измерения имеют нормальное распределение проверить на уровне значимости $alpha=0,05$ гипотезу $H_0: sigma^2=0,01$ мм$^2$. против конкурирующей гипотезы $H_0: sigma^2=0,005$ мм$^2$. В ответе записать разность между фактическим и табличным значениями выборочной характеристики.
Пример 4. Компания не осуществляет инвестиционных вложений в ценные бумаги с дисперсией годовой доходности более чем 0,04. Выборка из 52 наблюдений по активу А показала, что выборочная дисперсия ее доходности равна 0,045.Выяснить, допустимы ли для данной компании инвестиционные вложения в актив А на уровне значимости: а) 0,05; б) 0,01.
Гипотеза о равенстве вероятности числу
Пример 5. Фирма рассылает рекламные каталоги возможным заказчикам. Как показал опыт, вероятность того, что организация получившая каталог, закажет рекламируемое изделие, равна 0,08. Фирма разослала 1000 каталогов новой, улучшенной, формы и получила 100 заказов. На уровне значимости 0,05 выяснить, можно ли считать, что новая форма рекламы существенно лучше прежней.
Пример 6. Обычно применяемое лекарство снимает послеоперационные боли у 80% пациентов. Новое лекарство, применяемое для тех же целей, помогло 90 пациентам из первых 100 оперированных. Можно ли на уровне значимости а = 0,05 считать, что новое лекарство лучше? А на уровне а = 0,01?
Гипотеза о равенстве средних
Пример 7. Ожидается, что добавление специальных веществ уменьшит жесткость воды. По оценке жесткости воды до после добавления специальных веществ по 40-ка и 50-ти пробам соответственно получим средние значения жесткости (в стандартных единицах), равные 4,0 и 0,8. Дисперсия измерений в обоих случаях предполагается равно 0,25. Подтверждают ли эти результаты ожидаемый эффект? Принять $alpha=0,05$. Контролируемая величина имеет нормальное распределение.
Пример 8. Производительность каждого из агрегатов А и В составила (в кг вещества за час работы)
Номер замера 1 2 3 4 5
Агрегат А 14,1 13,1 14,7 13,7 14,0
Агрегат В 14,0 14,5 13,7 12,7 14,1
Можно ли считать производительность агрегатов А и В одинаковой в предложении, что обе выборки получены из нормально распределенных генеральных совокупностей, при уровне значимости a = 0,1?
Гипотеза о равенстве дисперсий
Пример 9. До наладки станка была проверена точность изготовления 10 втулок и найдено значение оценки дисперсии диаметра $s_1^2=9,6$ мкм$^2$. После наладки подверглись контролю еще 15 втулок и получено новое значение оценки дисперсии $s_2^2=5,7$ мкм$^2$. Можно ли считать, что в результате наладки станка точность изготовления деталей увеличилась? Принять $alpha=0,05$.
Пример 10. При уровне значимости $alpha=0,1$ проверить гипотезу о равенстве дисперсий двух нормально распределенных случайных величин Х и Y на основе выборочных данных (табл. 4) при альтернативной гипотезе $H_1: sigma_x^2 ne sigma_y^2$.
Гипотеза о равенстве вероятностей
Пример 11. Из 200 задач первого раздела курса математики, предложенных для решения, абитуриенты решили 130, а из 300 задач второго раздела абитуриенты решили 120. Можно ли при α=0,01 утверждать, что первый раздел школьного курса абитуриенты усвоили лучше, чем второй.
Пример 12. Выборочная проверка надежности материнских плат 2-х производителей дала следующие результаты: в течения месяца после продажи в 15 из 200 материнских плат производителя А обнаружены дефекты, тогда как среди 400 материнских плат производителя В 8% оказались дефектами. Существенны ли различия в надежности материнских плат производителей А и В? Уровень значимости принять равным 0,01.
Нужно решить задачи на проверку статистических гипотез?
Полезные ссылки
- Проверка гипотез о законе распределения по критерию Пирсона
- Что такое проверка статистической гипотезы?
- Решение задач на заказ
- Ссылки на учебники
- Решенные контрольные
Решебник по математической статистике
Ищете решенное задание на проверку статистических гипотез? Попробуйте тут:
Проверка статистических гипотез
- Понятие о статистической гипотезе
- Уровень значимости при проверке гипотезы
- Критическая область
- Простая гипотеза и критерии согласия
- Критерий согласия (X^2) Пирсона
- Примеры
п.1. Понятие о статистической гипотезе
Статистическая гипотеза – это предположение о виде распределения и свойствах случайной величины в наблюдаемой выборке данных.
Прежде всего, мы формулируем «рабочую» гипотезу. Желательно это делать не на основе полученных данных, а исходя из природы и свойств исследуемого явления.
Затем формулируется нулевая гипотеза (H_0), отвергающая нашу рабочую гипотезу.
Наша рабочая гипотеза при этом называется альтернативной гипотезой (H_1).
Получаем, что (H_0=overline{H_1}), т.е. нулевая и альтернативная гипотеза вместе составляют полную группу несовместных событий.
Основной принцип проверки гипотезы – доказательство «от противного», т.е. опровергнуть гипотезу (H_0) и тем самым доказать гипотезу (H_1).
В результате проверки гипотезы возможны 4 исхода:
| Верная гипотеза | |||
| (H_0) | (H_1) | ||
| Принятая гипотеза | (H_0) | True Negative (H_0) принята верно |
False Negative (H_0) принята неверно Ошибка 2-го рода |
| (H_1) | False Positive (H_0) отвергнута неверно (H_1) принята неверно Ошибка 1-го рода |
True Positive (H_0) отвергнута верно (H_1) принята верно |
Ошибка 1-го рода – «ложная тревога».
Ошибка 2-го рода – «пропуск события».
Например:
К врачу обращается человек с некоторой жалобой.
Гипотеза (H_1) – человек болен, гипотеза (H_0) – человек здоров.
True Negative – здорового человека признают здоровым
True Positive – больного человека признают больным
False Positive – здорового человека признают больным – «ложная тревога»
False Negative – больного человека признают здоровым – «пропуск события»
Уровень значимости при проверке гипотезы
Статистический тест (статистический критерий) – это строгое математическое правило, по которому гипотеза принимается или отвергается.
В статистике разработано множество критериев: критерии согласия, критерии нормальности, критерии сдвига, критерии выбросов и т.д.
Уровень значимости – это пороговая (критическая) вероятность ошибки 1-го рода, т.е. непринятия гипотезы (H_0), когда она верна («ложная тревога»).
Требуемый уровень значимости α задает критическое значение для статистического теста.
Например:
Уровень значимости α=0,05 означает, что допускается не более чем 5%-ая вероятность ошибки.
В результате статистического теста на конкретных данных получают эмпирический уровень значимости p. Чем меньше значение p, тем сильнее аргументы против гипотезы (H_0).
Обобщив практический опыт, можно сформулировать следующие рекомендации для оценки p и выбора критического значения α:
| Уровень значимости (p) |
Решение о гипотезе (H_0) | Вывод для гипотезы (H_1) |
| (pgt 0,1) | (H_0) не может быть отклонена | Статистически достоверные доказательства не обнаружены |
| (0,5lt pleq 0,1) | Истинность (H_0) сомнительна, неопределенность | Доказательства обнаружены на уровне статистической тенденции |
| (0,01lt pleq 0,05) | Отклонение (H_0), значимость | Обнаружены статистически достоверные (значимые) доказательства |
| (pleq 0,01) | Отклонение (H_0), высокая значимость | Доказательства обнаружены на высоком уровне значимости |
Здесь под «доказательствами» мы понимаем результаты наблюдений, свидетельствующие в пользу гипотезы (H_1).
Традиционно уровень значимости α=0,05 выбирается для небольших выборок, в которых велика вероятность ошибки 2-го рода. Для выборок с (ngeq 100) критический уровень снижают до α=0,01.
п.3. Критическая область
Критическая область – область выборочного пространства, при попадании в которую нулевая гипотеза отклоняется.
Требуемый уровень значимости α, который задается исследователем, определяет границу попадания в критическую область при верной нулевой гипотезе.
Различают 3 вида критических областей
Критическая область на чертежах заштрихована.
(K_{кр}=chi_{f(alpha)}) определяют границы критической области в зависимости от α.
Если эмпирическое значение критерия попадает в критическую область, гипотезу (H_0) отклоняют.
Пусть (K*) – эмпирическое значение критерия. Тогда:
(|K|gt K_{кр}) – гипотеза (H_0) отклоняется
(|K|leq K_{кр}) – гипотеза (H_0) не отклоняется
п.4. Простая гипотеза и критерии согласия
Пусть (x=left{x_1,x_2,…,x_nright}) – случайная выборка n объектов из множества (X), соответствующая неизвестной функции распределения (F(t)).
Простая гипотеза состоит в предположении, что неизвестная функция (F(t)) является совершенно конкретным вероятностным распределением на множестве (X).
Например: 
Глядя на полученные данные эксперимента (синие точки), можно выдвинуть следующую простую гипотезу:
(H_0): данные являются выборкой из равномерного распределения на отрезке [-1;1]
Критерий согласия проверяет, согласуется ли заданная выборка с заданным распределением или с другой выборкой.
К критериям согласия относятся:
- Критерий Колмогорова-Смирнова;
- Критерий (X^2) Пирсона;
- Критерий (omega^2) Смирнова-Крамера-фон Мизеса
п.5. Критерий согласия (X^2) Пирсона
Пусть (left{t_1,t_2,…,t_nright}) – независимые случайные величины, подчиняющиеся стандартному нормальному распределению N(0;1) (см. §63 данного справочника)
Тогда сумма квадратов этих величин: $$ x=t_1^2+t_2^2+⋯+t_n^2 $$ является случайной величиной, которая имеет распределение (X^2) с n степенями свободы.
График плотности распределения (X^2) при разных n имеет вид: 
С увеличением n распределение (X^2) стремится к нормальному (согласно центральной предельной теореме – см. §64 данного справочника).
Если мы:
1) выдвигаем простую гипотезу (H_0) о том, что полученные данные являются выборкой из некоторого закона распределения (f(x));
2) выбираем в качестве теста проверки гипотезы (H_0) критерий Пирсона, –
тогда определение критической области будет основано на распределении (X^2).
Заметим, что выдвижение основной гипотезы в качестве (H_0) при проведении этого теста исторически сложилось.
В этом случае критическая область правосторонняя.
Мы задаем уровень значимости α и находим критическое значение
(X_{кр}^2=X^2(alpha,k-r-1)), где k – число вариант в исследуемом ряду, r – число параметров предполагаемого распределения.
Для этого есть специальные таблицы.
Или используем функцию ХИ2ОБР(α,k-r-1) в MS Excel (она сразу считает нужный нам правый хвост). Например, при r=0 (для равномерного распределения):
Пусть нам дан вариационный ряд с экспериментальными частотами (f_i, i=overline{1,k}).
Пусть наша гипотеза (H_0) –данные являются выборкой из закона распределения с известной плотностью распределения (p(x)).
Тогда соответствующие «теоретические частоты» (m_i=Ap(x_i)), где (x_i) – значения вариант данного ряда, A – коэффициент, который в общем случае зависит от ряда (дискретный или непрерывный).
Находим значение статистического теста: $$ X_e^2=sum_{j=1}^kfrac{(f_i-m_i)^2}{m_i} $$ Если эмпирическое значение (X_e^2) окажется в критической области, гипотеза (H_0) отвергается.
(X_e^2geq X_{кр}^2) – закон распределения не подходит (гипотеза (H_0) не принимается)
(X_e^2lt X_{кр}^2) – закон распределения подходит (гипотеза (H_0) принимается)
Например:
В эксперименте 60 раз подбрасывают игральный кубик и получают следующие результаты:
| Очки, (x_i) | 1 | 2 | 3 | 4 | 5 | 6 |
| Частота, (f_i) | 8 | 12 | 13 | 7 | 12 | 8 |
Не является ли кубик фальшивым?
Если кубик не фальшивый, то справедлива гипотеза (H_0) – частота выпадений очков подчиняется равномерному распределению: $$ p_i=frac16, i=overline{1,6} $$ При N=60 экспериментах каждая сторона теоретически должна выпасть: $$ m_i=p_icdot N=frac16cdot 60=10 $$ по 10 раз.
Строим расчетную таблицу:
| (x_i) | 1 | 2 | 3 | 4 | 5 | 6 | ∑ |
| (f_i) | 8 | 12 | 13 | 7 | 12 | 8 | 60 |
| (m_i) | 10 | 10 | 10 | 10 | 10 | 10 | 60 |
| (f_i-m_i) | -2 | 2 | 3 | -3 | 2 | -2 | – |
| (frac{(f_i-m_i)^2}{m_i}) | 0,4 | 0,4 | 0,9 | 0,9 | 0,4 | 0,4 | 3,4 |
Значение теста: $$ X_e^2=3,4 $$ Для уровня значимости α=0,05, k=6 и r=0 находим критическое значение:
$$ X_{кр}^2approx 11,1 $$ Получается, что: $$ X_e^2lt X_{кр}^2 $$ На уровне значимости α=0,05 принимается гипотеза (H_0) про равномерное распределение.
Значит, с вероятностью 95% кубик не фальшивый.
п.6. Примеры
Пример 1. В эксперименте 72 раза подбрасывают игральный кубик и получают следующие результаты:
| Очки, (x_i) | 1 | 2 | 3 | 4 | 5 | 6 |
| Частота, (f_i) | 8 | 12 | 13 | 7 | 10 | 22 |
Не является ли кубик фальшивым?
Если кубик не фальшивый, то справедлива гипотеза (H_0) – частота выпадений очков подчиняется равномерному распределению: $$ p_i=frac16, i=overline{1,6} $$ При N=72 экспериментах каждая сторона теоретически должна выпасть: $$ m_i=p_icdot N=frac16cdot 72=12 $$ по 12 раз.
Строим расчетную таблицу:
| (x_i) | 1 | 2 | 3 | 4 | 5 | 6 | ∑ |
| (f_i) | 8 | 12 | 13 | 7 | 10 | 22 | 72 |
| (m_i) | 12 | 12 | 12 | 12 | 12 | 12 | 72 |
| (f_i-m_i) | -4 | 0 | 1 | -5 | -2 | 10 | – |
| (frac{(f_i-m_i)^2}{m_i}) | 1,333 | 0,000 | 0,083 | 2,083 | 0,333 | 8,333 | 12,167 |
Значение теста: $$ X_e^2=12,167 $$ Для уровня значимости α=0,05, k=6 и r=0 находим критическое значение:
$$ X_{кр}^2approx 11,1 $$ Получается, что: $$ X_e^2gt X_{кр}^2 $$ На уровне значимости α=0,05 гипотеза (H_0) про равномерное распределение не принимается.
Значит, с вероятностью 95% кубик фальшивый.
Пример 2. Во время Второй мировой войны Лондон подвергался частым бомбардировкам. Чтобы улучшить организацию обороны, город разделили на 576 прямоугольных участков, 24 ряда по 24 прямоугольника.
В течение некоторого времени были получены следующие данные по количеству попаданий на участки:
| Число попаданий, (x_i) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Количество участков, (f_i) | 229 | 211 | 93 | 35 | 7 | 0 | 0 | 1 |
Проверялась гипотеза (H_0) – стрельба случайна.
Если стрельба случайна, то попадание на участок должно иметь распределение, подчиняющееся «закону редких событий» – закону Пуассона с плотностью вероятности: $$ p(k)=frac{lambda^k}{k!}e^{-lambda} $$ где (k) – число попаданий. Чтобы получить значение (lambda), нужно посчитать математическое ожидание данного распределения.
Составим расчетную таблицу:
| (x_i) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ∑ |
| (f_i) | 229 | 211 | 93 | 35 | 7 | 0 | 0 | 1 | 576 |
| (x_if_i) | 0 | 211 | 186 | 105 | 28 | 0 | 0 | 7 | 537 |
$$ lambdaapprox M(x)=frac{sum x_if_i}{N}=frac{537}{576}approx 0,932 $$ Тогда теоретические частоты будут равны: $$ m_i=Ncdot p(k) $$ Получаем:
| (x_i) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ∑ |
| (f_i) | 229 | 211 | 93 | 35 | 7 | 0 | 0 | 1 | 576 |
| (p_i) | 0,39365 | 0,36700 | 0,17107 | 0,05316 | 0,01239 | 0,00231 | 0,00036 | 0,00005 | 0,99999 |
| (m_i) | 226,7 | 211,4 | 98,5 | 30,6 | 7,1 | 1,3 | 0,2 | 0,0 | 576,0 |
| (f_i-m_i) | 2,3 | -0,4 | -5,5 | 4,4 | -0,1 | -1,3 | -0,2 | 1,0 | – |
| (frac{(f_i-m_i)^2}{m_i}) (результат) | 0,02 | 0,00 | 0,31 | 0,63 | 0,00 | 1,33 | 0,21 | 34,34 | 36,84 |
Значение теста: (X_e^2=36,84)
Поскольку в ходе исследования мы нашли оценку для λ через подсчет выборочной средней, нужно уменьшить число степеней свободы на r=1, и критическое значение статистики искать для (X_{кр}^2=X^2(alpha,k-2)).
Для уровня значимости α=0,05 и k=8, r=1 находим:
(X_{кр}^2approx 12,59)
Получается, что: (X_e^2gt X_{кр}^2)
Гипотеза (H_0) не принимается.
Стрельба не случайна.
Пример 3. В предыдущем примере объединили события x={4;5;6;7} с редким числом попаданий:
| Число попаданий, (x_i) | 0 | 1 | 2 | 3 | 4-7 |
| Количество участков, (f_i) | 229 | 211 | 93 | 35 | 8 |
Проверялась гипотеза (H_0) – стрельба случайна.
Для последней объединенной варианты находим среднюю взвешенную: $$ x_5=frac{4cdot 7+5cdot 0+6cdot 0+7cdot 1}{7+1}=4,375 $$ Найдем оценку λ.
| (x_i) | 0 | 1 | 2 | 3 | 4,375 | ∑ |
| (f_i) | 229 | 211 | 93 | 35 | 8 | 576 |
| (x_if_i) | 0 | 211 | 186 | 105 | 35 | 537 |
$$ lambdaapprox M(x)=frac{sum x_if_i}{N}=frac{537}{576}approx 0,932 $$ Оценка не изменилась, что указывает на правильное определение средней для (x_5).
Строим расчетную таблицу для подсчета статистики:
| (x_i) | 0 | 1 | 2 | 3 | 4,375 | ∑ |
| (f_i) | 229 | 211 | 93 | 35 | 8 | 576 |
| (p_i) | 0,3937 | 0,3670 | 0,1711 | 0,0532 | 0,0121 | 0,9970 |
| (m_i) | 226,7 | 211,4 | 98,5 | 30,6 | 7,0 | 574,2 |
| (f_i-m_i) | 2,3 | -0,4 | -5,5 | 4,4 | 1,0 | – |
| (frac{(f_i-m_i)^2}{m_i}) | 0,02 | 0,00 | 0,31 | 0,63 | 0,16 | 1,12 |
Значение теста: (X_e^2=1,12)
Критическое значение статистики ищем в виде (X_{кр}^2=X^2(alpha,k-2)), где α=0,05 и k=5, r=1
(X_{кр}^2approx 7,81)
Получается, что: (X_e^2lt X_{кр}^2)
Гипотеза (H_0) принимается.
Стрельба случайна.
И какой же ответ верный? Полученный в Примере 2 или в Примере 3?
Если посмотреть в расчетную таблицу для статистики (X_e^2) в Примере 2, основной вклад внесло слагаемое для (x_i=7). Оно равно 34,34 и поэтому сумма (X_e^2=36,84) в итоге велика. А в расчетной таблице Примера 3 такого выброса нет. Для объединенной варианты (x_i=4,375) слагаемое статистики равно 0,16 и сумма (X_e^2=1,12) в итоге мала.
Правильный ответ – в Примере 3.
Стрельба случайна.
