Как найти главное значение интеграла - Сайт, где вы сможете решить свои вопросы

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 30 мая 2021 года; проверки требуют 3 правки.

Главное значение интеграла по Коши — это обобщение понятия интеграла Римана, которое позволяет вычислять некоторые расходящиеся несобственные интегралы. Идея главного значения интеграла по Коши заключается в том, что при приближении интервалов интегрирования к особой точке с обеих сторон «с одинаковой скоростью» особенности нивелируют друг друга (за счёт различных знаков слева и справа), и в результате можно получить конечную границу, которая и называется главным значением интеграла по Коши. Эта концепция имеет важные применения в комплексном анализе (Теорема Сохоцкого — Племеля)^[1].

Так, например, интеграл ${displaystyle int _{-1}^{1}{frac {dx}{x}}}$ — это несобственный интеграл второго рода, не существует, однако он существует в смысле главного значения интеграла по Коши.

Определение главного значения интеграла по Коши[править | править код]

Определение (для особой точки «∞»)[править | править код]

Определение (для особой точки «∞»). Пусть f (x) определена на интервале (-∞, + ∞) и f ∈ R ([- A, A]) для всех A> 0, но несобственный интеграл I рода ${displaystyle int _{-infty }^{+infty }f(x),dx}$ расходится. Если существует конечный предел

${displaystyle lim _{Arightarrow +infty }int _{-A}^{A}f(x),dx,}$

то эта граница называется главным значением интеграла по Коши (или главным значением в смысле Коши) для функции f в области (-∞, + ∞) и обозначается символом

${displaystyle mathrm {v.p.} int _{-infty }^{+infty }f(x),dx.}$

При этом говорят, что функция f (x) интегрируема на интервале (-∞, + ∞) по Коши (или интегрируема в области (-∞, + ∞) в смысле Коши).

Пример. Рассмотрим несобственный интеграл ${displaystyle int _{-infty }^{+infty }x,dx.}$ Этот интеграл расходится, потому что расходящимся будет, например, интеграл ${displaystyle int _{0}^{+infty }x,dx,}$ но существует главное значение данного интеграла в смысле Коши:

${displaystyle mathrm {v.p.} int _{-infty }^{+infty }x,dx=lim _{Arightarrow +infty }int _{-A}^{A}x,dx=lim _{Arightarrow +infty }{frac {x^{2}}{2}}{Bigr |}_{-A}^{A}=0.}$

Теорема

Определение (для конечной особой точки)[править | править код]

Определение (для конечной особой точки). Пусть функция f : [a, b] → R удовлетворяет условиям:

существует δ> 0 такое, что f ∈ R ([a, c — ε]) и f ∈ R ([c + ε, b]) для всех ε ∈ (0, δ)
расходящимся есть несобственный интеграл второго рода ${displaystyle int _{a}^{b}f(x),dx.}$

Если существует конечный предел

${displaystyle lim _{varepsilon rightarrow +0}left(int _{a}^{c-varepsilon }f(x),dx+int _{c+varepsilon }^{b}f(x),dxright),}$

то этот предел называется главным значением интеграла по Коши (или главным значением в смысле Коши) для функции f на отрезке [a, b] и обозначается символом

${displaystyle mathrm {v.p.} int _{a}^{b}f(x),dx.}$

При этом говорят, что функция f (x) интегрируема в [a, b] по Коши (или интегрируема на отрезке [a, b] в смысле Коши).

Пример. Рассмотрим несобственный интеграл второго рода ${displaystyle int _{-2}^{2}{frac {dx}{x}}}$ (см. рисунок) Он расходится, поскольку расходится, например, интеграл ${displaystyle int _{-2}^{0}{frac {dx}{x}}.}$ При этом в понимании главного значения по Коши данный интеграл существует и равен нулю:

${displaystyle {begin{aligned}mathrm {v.p.} int _{-2}^{2}{frac {dx}{x}}&=lim _{varepsilon rightarrow +0}left(int _{-2}^{-varepsilon }{frac {dx}{x}}+int _{varepsilon }^{2}{frac {dx}{x}}right)=\&=lim _{varepsilon rightarrow +0}left(ln |x|{Bigr |}_{-2}^{-varepsilon }+ln |x|{Bigr |}_{varepsilon }^{2}right)=\&=lim _{varepsilon rightarrow +0}{big (}ln |-varepsilon |-ln |varepsilon |{big )}=\&=0.end{aligned}}}$

Случай нескольких особых точек на промежутке интегрирования[править | править код]

Пример. Рассмотрим несобственный интеграл ${displaystyle int _{-infty }^{+infty }{frac {2x}{x^{2}-1}},dx}$ (см. рисунок). Особые точки подынтегральной функции f (x) = 2 x / (x²-1) есть точки -1, 1 и ∞. Данный интеграл расходится, потому расходится, например, интеграл

${displaystyle {begin{aligned}int _{2}^{+infty }{frac {2x}{x^{2}-1}},dx&=lim _{Ato +infty }int _{2}^{A}{frac {2x}{x^{2}-1}},dx=\&=lim _{Ato +infty }ln |x^{2}-1|{Bigr |}_{x=2}^{A}=\&=lim _{Ato +infty }{big (}ln |A^{2}-1|-ln 3{big )}=\&=+infty .end{aligned}}}$

Очевидно, что f ∈ R ([-1 / ε, −1-ε]) ∩ R ([-1 + ε, 1-ε]) ∩ R ([1 + ε, 1 / ε]) для всех ε ∈ (0, 1) (так как ограничена на каждом из этих отрезков). Проверим интегрируемость функции f в смысле Коши:

${displaystyle {begin{aligned}mathrm {v.p.} int _{-infty }^{+infty }{frac {2x}{x^{2}-1}},dx&=lim _{varepsilon to 0+}left(int _{-1/varepsilon }^{-1-varepsilon }{frac {2x}{x^{2}-1}},dx+int _{-1+varepsilon }^{1-varepsilon }{frac {2x}{x^{2}-1}},dx+int _{1+varepsilon }^{1/varepsilon }{frac {2x}{x^{2}-1}},dxright)=\&=lim _{varepsilon to +0}{Big (}ln |x^{2}-1|{Bigr |}_{-1/varepsilon }^{-1-varepsilon }+ln |x^{2}-1|{Bigr |}_{-1+varepsilon }^{1-varepsilon }+ln |x^{2}-1|{Bigr |}_{1+varepsilon }^{1/varepsilon }{Big )}=\&=0.end{aligned}}}$

Следовательно, функция f интегрируема в смысле Коши на промежутке (-∞, + ∞).

Примечания[править | править код]

↑ Павлов В. П. Главное значение интеграла // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1988. — Т. 1: Ааронова — Бома эффект — Длинные линии. — 707 с. — 100 000 экз.

Источники[править | править код]

Дороговцев А. Я. Математический анализ. — Киев, Высшая школа, 1985.

Источник

Макеты страниц

Пример 1. Найдем главное значение интеграла от функции? х. Поскольку в силу нечетности х,

Точно так же заключаем, что

Справедливо следующее

Утверждение. Пусть функция интегрируема на каждом сегменте прямой Если эта функция нечетна, то она интегрируема по Коши и главное значение интеграла от нее равняется нулю.

Если функция четна, то она интегрируема по Коши тогда и только тогда, когда сходится несобственный интеграл

Первая часть этого утверждения является очевидной. Для доказательства второй части достаточно воспользоваться равенством справедливым для любой четной функции, и определением сходимости несобственного интеграла (9.1.17).

Понятие интегрируемости по Коши можно ввести и для несобственных интегралов второго рода в случае, когда особая точка, является внутренней точкой сегмента, по которому производится: интегрирование.

Определение. Пусть функция определена на сегменте кроме, быть может, точки и интегрируема на любом сегменте, принадлежащем либо , либо . Будем говорить, что функция интегрируема по Коши, если существует предел

называемый главным значением интеграла в смысле Коши.

Пример 2. Функция не интегрируема на сегменте в несобственном смысле, однако она интегрируема по Коши. При этом

Источник

Пусть интеграл

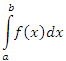имеет единственную особенность во внутренней точке

промежутка [a,b]. Составим сумму

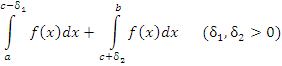
(1)

и выполним предельный переход, устремив к нулю 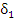и .

Если существует двойной предел выражения (1), не зависящий от способа предельного перехода, то он называется несобственным интегралом от функции f(x) по промежутку [a,b]:

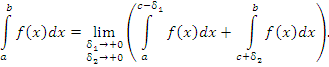
(2)

В этом случае

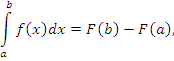
(3)

где F(x) – первообразная функции f(x).

Если предел (2) существует лишь при согласованном предельном переходе, а именно когда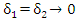, то этот предел называется главным значением несобственного интеграла 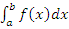и обозначается символическим выражением

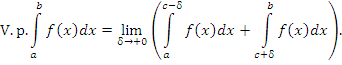
(4)

В таких случаях говорят, что интеграл 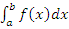сходится в смысле главного значения.

Обозначение “V.p.” введено Коши и представляет собой аббревиатуру, которая берет свое начало от слов “Valeur principale”, означающих по-французски “Главное значение”.

Любой сходящийся несобственный интеграл существует и в смысле главного значения. Обратное утверждение является неверным.

Отметим, что интегралы в смысле главного значения играют важную роль в различных приложениях. Например, интегральный логарифм определяется формулой

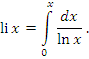
(5)

Этот несобственный интеграл сходится при 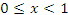. Если же x > 1, то интеграл (5) понимается в смысле главного значения.

Источник

Пример:

Полученный предел очевидно не существует. Пусть, тогда указанный интеграл:

Пусть определена на И пусть функция интегрируема на любом сегменте.

Определение: Если существует предел , то он называется главным значением несобственного интеграла в смысле Коши и обозначается следующим образом:

(V.P. = Vabeur principal).

В этом случае говорят, что функция интегрируема на прямой . Очевидно, что если несобственный интеграл сходится, то его значение совпадает с его собственным значением. Но может так быть, что несобственный интеграл расходится, но при этом имеет конечное главное значение.

Рассмотрим несобственный интеграл второго рода , где C – внутренняя особая точка интервала .

Определение: Если существует предел «конструкции» следующего вида: ,

То он называется главным значением несобственного интеграла второго рода И обозначается V.P. .

Отметим, что исходный несобственный интеграл может быть расходящимся, то есть может не существовать предел .

Пример:

не существует.

Вычислим интеграл в смысле главного значения:

V.P. .

< Предыдущая		Следующая >

Источник

К
Н. и. относятся интегралы в смысле
главного значения. Пусть функция f
определена на открытом множестве
,
кроме, быть может, точки
,
и пусть для любого
функция
f интегрируема (по Риману или по Лебегу)
на множестве
есть
-окрестность
точки х. Тогда если существует
предел

то
его наз. интегралом в смысле главного
значения и обозначают

Если
интеграл

существует
как Н. и., то он существует и в смысле
главного значения. Обратное, вообще
говоря, неверно. Напр., Н. и.
расходится,
а

Аналогично
определяют интегралы в смысле главного
значения в бесконечно удаленной точке.

19. Двойной интеграл. Вычисление двойного интеграла

Пусть
обл-ть D задана неравенствами

т.е. изображается прямоугольником.
Тогда двойной интеграл вычисляется по
одной из формул

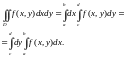
В
1-й формуле сначала вычисляется внутренний
интеграл

.
В процессе этого интегрирования x
рассм-ся как постоянная величина. Но
результат интегрирования рассм-ся как
ф-ция от х, и второе интегрирование (в
пределах от a до b) выполняется по
аргументу x. Во 2-й формуле порядок
действий обратный.

1.
Если контур области D встречается со
всякой пересекающей его вертикальной
прямой не более чем в двух точках
(М1,М2), то обл-ть D задаётся неравенствами

.
[a, b – крайние абсциссы обл-ти, φ1(x), φ2(x)
– ф-ции, выражающие ординаты нижней и
верхней граничных линий AM1B1, AM2B2]. В этом
случае двойной интеграл вычисляется
по формуле (если ф-ция f(x,y) непрерывна
на элементарном множестве D):

(1) 2. Если контур области встречается
не более чем в двух точках со всякой
пересекающей его горизонтальной прямой,
имеем аналогично (при обозначениях
чертежа 2).

(2) 3. Если область интегрирования не
является элементарной, т.е. не подходит
ни под первый, ни под второй случай, то
область D разбивают на несколько частей
(D1, D2, D3 на чертеже 3) так, чтобы к кажой
части была применима формула (1) или
(2).

20. Двойной интеграл. Замена переменных в двойном интеграле

Замена
переменных в двойном интеграле
описывается формулой

где
выражение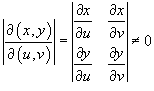
представляет
собой так называемый якобиан преобразования
,
а S − образ области
интегрирования R, который можно найти
с помощью подстановки
в
определение области R. Отметим, что
в приведенной выше формуле
означает
абсолютное значение соответствующего
определителя.

Предполагая,
что преобразование координат
является
взаимно-однозначным, обратное соотношение
описывается якобианом

при
условии, что знаменатель нигде не равен
0.

Итак, замена переменных в
двойном интеграле производится с
помощью следующих трех шагов:

Найти
образ S в новой системе координат
для
исходной области интегрирования R;

Вычислить
якобиан преобразования
и
записать дифференциал в новых переменных
;

Заменить
в подынтегральном выражении исходные
переменные x и y, выполнив,
соответственно, подстановки
и
.

21. Тройной интеграл. Вычисление тройного интеграла

Пусть
ф-ция u=f(x,y,z) непрерывна внутри замкнутой
пространственной области V и на её
границе. Разобьём область V сеткой
поверхностей на части, которые пронумеруем
индексами i, j, k:

– длины сторон при

Т.е. можно утверждать, что Vчаст→V.
Выберем в каждой части произвольную
точку (ζi, ηi, θi). Составим интегральную
сумму

для ф-ции f(x,y,z) по обл-ти V. Если предел
интегральной суммы существует при
неограниченном увеличении числа n таким
образом, что каждая «элементарная
область» Vi стягивается в точку, т.е.
диаметр области стремится к нулю, т.е.
di→0), то его называют тройным интегралом
от ф-ции u=f(x,y,z) по области V и обозначают

Вычисление.
Пусть областью интегрирования
является тело, ограниченное снизу
поверхностью z=z1(x,y), сверху – поверхностью
z=z2(x,y), причем f(x,y) и g(x,y) – непрерывные
ф-ции в замкнутой области D, являющейся
проекцией тела на плоскость Oxy. Будем
считать область V – правильной в
направлении оси Oz: любая прямая
параллельная оси Oz, пересекает границу
области не более чем в двух точках.
Тогда для любой непрерывной в области
V ф-ции f(x,y,z) имеет место формула

.
В процессе вычисления интеграла

величины
x, y являются постоянными. Результат
вычисления рассматривается как ф-ция
аргументов x,y. После того как интегрирование
по переменной z выполнено, правая часть
превращается в двойной интеграл. Поэтому
в итоге тройной интеграл сводится к
повторному: