Как найти главную часть функции онлайн

Определение 1. Функция называется Малой более высокого Порядка по сравнению с функцией при , если и и обозначается .

Примеры. 1. при , т. к. . Заметим, что при : ~, . Число назы-вается Порядком малости функции .

Определение 2. Функция называется Большой более высокого Порядка по сравнению с функцией при , если и .

2. при , т. к. .

Определение 3. Функция называется Главной частью функции при , если она представима при в виде .

При этом, функции и называются Эквивалент-ными при и обозначаются ~ .

Теорема 1. Для того чтобы функции и были экви-валентными при необходимо и достаточно, чтобы

=1.

Теорема 2. Следующие функции эквивалентными между собой при

~ ~ ~ ~ ~ .

Первые три соотношения следуют из 1-го замечательного предела и его следствий, а четвертое и пятое – из следствий 2-го замечательного предела.

Теорема 3. ~ при .

Применим первый замечательный предел и формулу бинома Ньютона к тождеству

~ ~ при .

Выделение главной части функции значительно упрощает вычисление пределов.

Примеры.

1.

Поскольку ~ , ~ , ~ , ~ ~ , ~ , то . Наконец, ~ , ~ при , то

2.

Т. к. ~, ~ 3, то .

3. .

Здесь нельзя использовать эквивалентные функции: ~, т. к. получим неопределенность. Преобразуем основание степени

.

Тогда,

.

Замечание. Последний пример продемонстрировал, что методом выделения главной части функции следует обращаться осторожно. Может оказаться, что решающую роль играет не главная часть функции, а другие ее части.

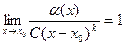
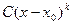
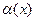
Определение. Если то функция называется ГЛАВНОЙ ЧАСТЬЮ бесконечно-малой .

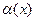
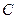
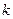
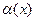
Фактически, это степенная функция, эквивалентная данной . Если найти коэффициент и степень , то мы найдём такую степенную функцию, график которой наилучшим образом (среди всех степенных) похож на график функции в окрестности точки.

Пример. Найти главную часть бесконечно-малой 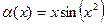в точке 0.

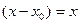
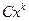
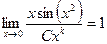
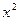
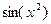
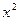
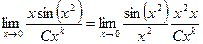
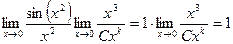
Решение. Так как точка 0, то , то есть главная часть имеет вид . Запишем отношение данной бесконечно-малой и «эталонной» степенной. Нужно потребовать, чтобы этот предел был 1, ведь мы ищем именно эквивалентную бесконечно-малую.

. Преобразуем выражение с целью его упростить. Домножим и поделим на , этим мы фактически можем заменить на . Параметры C и k пока просто переписываем, не меняя их в процессе преобразований.

= .

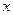
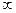
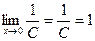
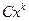
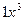
Полное сокращение всех будет лишь в случае k=3, а иначе предел 0 или , и не будет равен 1.

, тогда С = 1. Итак, = .

Ответ. .

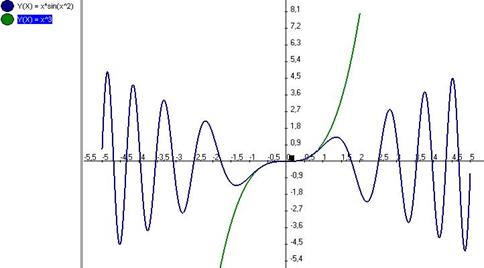
Ниже изображены графики бесконечно-малой и её главной части:

как видно, вблизи (0,0) они практически неотличимы.

Задачи на поиск главной части по методам и сложности похожи на вычисление lim, но фактически это обратная задача: при вычислении предела внутри нет параметров, а предел неизвестен, здесь же наоборот, известно, что предел равен 1, но внутри выражения неизвестные параметры C, k, которые надо найти, так, чтобы предел был равен 1.

Если учесть не только одну степенную функцию, но добавить ещё и последующие степени, то можно построить ещё более точное приближение. Это будет изучено позже, тема «формула Тейлора».

Дата добавления: 2016-12-26 ; просмотров: 817 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

аР(х) иногда называют асимптотическим равенством функций а(х) и 0(х) в окрестности точки а. Данное асимптотическое равенство можно читать слева направо и справа налево. Но обычно слева записывают изучаемую функцию, а справа эквивалентную ей более простую или более изученную функцию, и в этом случае говорят, что установлена асимптотика изучаемой функции в окрестности данной точки. Теорема 10.2. Для того чтобы две б.м. при х а функции а(х) и 0(х) были эквивалентными при а, необходимо и достаточно, чтобы их разность а(х) — 0(х) была б.м. более высокого порядка по сравнению с каждой из них, т.е. Пусть а(х) Х

Q х. (10.12) 4. Из непрерывности в точке t = 0 функции x(t) = arctg£ (см. 9.5) следует lira arctgt = arctgO = 0. Тогда из (10.11) и t^o теоремы 10.3 t = tg(arctgt), или, обозначая аргумент через х, имеем 5. Исходя из второго замечательного предела, заключаем, что lim(l-f х). В силу непрерывности функции In у в точке с учетом (9.12) получим ИЛИ Поскольку loge(l + x) = (ln(l + x))/lna, согласно (10.14) имеем 6. В силу непрерывности функции Согласно (10.14) можно записать — 1. Возвращаясь к обозначению аргумента через х, получим Эквивалентные бесконечно малые функции. Главная часть бесконечно малой функции. Сравнение бесконечно больших функций 7. С учетом (10.16) вычислим Следовательно, (1 -f x)* — или при s £ R <0>В частности, при Из полученных соотношений (10.10)^(10.17) с учетом транзитивности свойства эквивалентности (10.9) следует Еще раз отметим, что, согласно теореме 10.3, в этой цепочке эквивалентных при х —> 0 б.м. функций аргумент х сам может быть функцией, которая отлична от нуля в некоторой о проколотей окрестности U(r) точки г и timx(t) = 0. В частности, при а > 0 будем иметь Полагая, например, в (10.14) х = t — 1, при t —t 1 получим ln(l + t-l)£lt-l. Итак, Учитывая (10.14), (10.16) и (10.20), можно, например, записать ln(l+sinx)x

0tgx, ec08X-lr_^y2cosx, Incosx^^cosx-1. Теорема 10.4. Пусть a(x) и /(х) — некоторая функция, определенная в проколотой окрестности точки а. Тогда, если существует предел при х а произведения (или частного f(x)/a(x)), он не изменится при замене а(х) на эквивалентную при х-ча б.м. функцию /?(х), или Действительно, с учетом Из этой теоремы следует удобное для использования (10.18) правило: предел отношения б.м. при i-4a функций равен пределу отношения эквивалентных им при х -»а б.м. функций. Пример 10.4. Вычислим с учетом (10.18) Главная часть бесконечно малой функции Согласно утверждению 7.4 сумма конечного числа функций, б.м. при х а, есть снова б.м. при х а функция. Пусть an(x), n=l, N> — б.м. при х-ta функции и а(х) —их сумма. Если для n = 2, N orn(x)x=eo(ai(x)), то ai(x) называют главной частью суммы б.м. при х а функций. Инаг че, главная часть суммы б.м. — это слагаемое более низкого порядка малости по сравнению с каждым из остальных слагаемых. Ясно, что если в сумме есть несравнимые слагаемые (см. определение 10.3), то выделить главную часть не удается. Пример 10.6. Для суммы sins + ln(l + ж2) + ^/х б.м. при х 0 функций главной частью будет f/xy поскольку с учетом (10.18) и теоремы 10.4 согласно определению Когда для каждого слагаемого в сумме б.м. при х а функций можно указать порядок к относительно х — а, главной частью такой суммы будет слагаемое (если оно единственное) низшего порядка. В сумме б.м. при х -> оо функций главной частью будет слагаемое низшего порядка относительно 1/х при условии, что оно единственное, и для каждого слагаемого можно указать порядок малости. Теорема 10.6. Сумма конечного числа б.м. при х а функций эквивалентна своей главной части, или 4 Если ai(s) — главная часть суммы a(x), то с учетом свойства (7.22) суммы функций, имеющих конечные пределы) и определения 10.2 найдем I что, согласно (10.8), означает эквивалентность при х а суммы б.м. функций и ее главной части. Следствие 10.1. В некоторой проколотой окрестности о U (а) точки а сумма конечного числа б.м. при х а функций сохраняет знак своей главной части, или В ходе доказательства теоремы 10.5 установлено, что при х а а(х)/а(х) 1. Из свойства функции, имеющей в точке а отличный от нуля конечный предел, сохранять в некоторой проколотой окрестности этой точки знак предела, следует (10.23). Пример Ю.в. а. Вычислим то в силу Главной частью числителя дроби под знаком предела будет б.м. при х 0 функция которая, согласно теореме 10.5, эквивалентна при х 0 всему числителю. Из (10.18) и теоремы 10.3 sin yfx^^ Ух. Таким образом, и числитель, и знаменатель эквивалентны одной и той же б.м. при х 0 функции т.е. в силу (10.9) они эквивалентны при х 0 между собой, и искомый предел равен, по определению 10.5, единице. Найдем Числитель дроби под знаком предела является суммой двух б.м. при х О функций 7.x и 1 -cosx = 2sin2(x/2). Главной частью этой суммы будет 2х, так как из примера 10.2.а следует, что 2sin2(x/2)r=0o(2x). В силу (10.18) arcsins^o*’ Заменив числитель и знаменатель дроби на эквивалентные им при х 0 б.м. функции соответственно 2х и х, получим, что данный предел равен 2. в. Вычислим Числитель дроби под знаком предела является алгебраической суммой трех б.м. при х 0 функций, причем х4а?=()о(х), и согласно (10.5), (10.8), (10.18) sinxx=Q0 а функций, но и произвольной по структуре функции а(х), эквивалентной при х а степенной функции Л(х — а)*. Тогда, согласно теореме 10.2, а(х) = Л(х-а)Ч7(х), Аф 0, к > 0, где х=ао((х-а)к) —б.м. функция более высокого порядка по сравнению с (х — а)к при х а. Степенная функция А(х — а)к будет главной частью б.м. при х а функции а(х). Покажем, что представление функции а(х) в виде (10.24) единственное. В самом деле, если бы наряду с ним было возможно представление a(g) = = В(х — a)m + 6(х), где Вф 0, т> 0 и S(x)^ao((x-a)m), то, согласно теореме 10.2, что возможно в силу (10.8) лишь при В = А и т = к. Процедура выделения главной части в виде А(х — а)к для б.м. при х-ьа, функции а(х) связана с рассмотрением предела и подбором значений А: и Л, так, чтобы этот предел оказался равным единице. После выделения главной части ее можно использовать для приближенного вычисления значений функции ог(х) при значениях х в некоторой окрестности точки а. Возникающая при этом абсолютная |7(х)| и относительная |7(я)/а(х)| погрешности будут стремиться к нулю при х -4 а. Если требуется более высокая точность вычисления значений или представления функции в окрестности точки а, то следует попытаться выделить главную часть из б.м. при х а функции 7(ж). Эту процедуру можно продолжить. Такую процедуру уточнения называют построением асимптотического разложения функции в окрестности данной точки. Пример 10.7. Пусть точность замены по (10.17) при s = = 1/2 и х->0 функции Л + х -1 на функцию х/2 недостаг точна. Выделим из функции 7(х) = у/1 + х — 1 — х/2 главную часть в виде Ахк, подобрав А и к из условия у(х) x

QAxk. Для этого преобразуем: 24-644 Нетрудно заметить, что у(х)х

0-х2/8. Отсюда А =-1/8 и к = 2. Тогда Эквивалентные бесконечно малые функции. Главная часть бесконечно малой функции. Сравнение бесконечно больших функций где £(x)r=^o(x2). Если потребуется еще более высокая точность, то наступит очередь выделять главную часть из б.м. при х-» О функции £(х) и т.д. # Если для двух б.м. при х а функций а(х) и /3(х) известны их главные части, соответственно А(х-а)к и J9(x-a)m, то что можно сказать о главной части суммы а(х) 4-/?(х) ? При к ф т главной частью суммы будет то из слагаемых А(х — а)* и В(х — а)т, в котором показатель степени меньше. Если же к = т, то главная часть суммы есть (Л-f В)(х — а)* при условии, что А + В ф 0. В противном случае главные части слагаемых взаимно уничтожаются, и сумма а(х) + 0(х) оказывается при х а б.м. функцией более высокого порядка, чем каждое из слагаемых. В этом случае приходится выделять из нее б.м. функцию вида С (х- а)4 при q > к. Пример 10.8. а. Функции а(х) = у/1 + х — 1 и (3(х) = = у/1-х -1 являются б.м. при х 0. Из примера 10.7 следует, что при х —> 0 2. Отсюда где , и главной частью суммы заданных функций при х 0 будет -х2/4. б. Рассмотрим теперь функции а(х) = 1п(1 + Зх + х2) и /?(х) = 1п(1 — Зх + х2), являющиеся б.м. при х 0. Из (10.18) с учетом теоремы 10.3 получим Теперь, казалось бы, можно сказать, что главной частью суммы а(х) + /3(х) при х 0 будет 2х2. Но такой вывод является поспешным и поверхностным, а потому, как часто бывает, неверным. Дело в том, что из (10.18) непосредственно следует лишь эквивалентность ln(l + z) т.е., согласно теореме 10.2, справедлива запись . На основании теоремы 10.3 полагаем z равным либо Зх + х2,либо —Зх + х2, и тогда После сложе- ния заданных б.м. функций получим но два последних слагаемых в правой части сами могут содержать слагаемые вида Ах2, которые обязаны войти в главную часть суммы ot(x)+0(x) при х 0. Поэтому для выделения главной части суммы исходных б.м. функций преобразуем эту сумму к виду где е(х)x=qo(-7×2 + х4). Вот теперь вполне определенно и обоснованно можно сказать, что при х 0 главная часть этой суммы равна -7х2. Сравнение бесконечно больших функций Для 6.6. функций можно ввести классификацию, аналогичную классификации б.м. функций (см. 10.1), также связанную с пределом их частного. Пусть v(s) и w(x) — функции, б.б. при х а (см. определение 7.11), где а — конечная или бесконечная точка расширенной числовой прямой. Если существует lim v(x)/w(x) = с6 R <0>, то в этом х—¥а случае v(x) и w(x) называют б.б. функциями одного порядка при х а и записывают v(x)x=aO(u;(a;)) или t0(s)r=aO(v(a:)). При с = 0 v(x) называют б.б. функцией более низкого порядка роста по сравнению с w(x) при х а и записывают а в случае бесконечного предела отношения v(x)/w(x) — б.б. функцией более высокого порядка роста по сравнению с w(x) при х а и записывают w(x)x=eo(t;(a;)) (слово „роста” часто опускают). Наконец, если не существует ни бесконечного, ни конечного предела этого отношения, то и(х) и ги(х) называют несравнимыми при х а б.б. функциями. Пример 10.9. а. Функции 2х2 и х2 + х являются б.б. одного порядка при , так как б. Функция ах (а > 1) является б.б. более высокого порядка роста по сравнению с хк <к>0) при х +оо, так как согласно (7.32) в. Функции x(2 + sinx) и х являются несравнимыми б.б. при х оо, поскольку при х —> оо не существует предела отношения z(2 + sina:)/x = 2 +sin а: (ни конечного, ни бесконечного). является суммой б.б. при х оо функций, причем порядок роста к относительно х каждого слагаемого совпадает с соответствующим показателем степени. Поэтому слагаемое а$хп высшего порядка роста (к = п), поскольку оно единственно, и будет главной частью этой суммы при х оо. Аналогично, если в сумме конечного числа б.б. функций при х а можно указать для каждого слагаемого порядок роста к относительно 1/(х — а), слагаемое высшего порядка будет также главной частью такой суммы при хча, если это слагаемое единственное. Например, в сумме l/sin2g+ctgz двух б.б. функций при х 0 согласно (10.18) первое слагаемое имеет второй порядок относительно 1/х, а второе — первый порядок. Поэтому главной частью этой суммы при х —>0 будет l/sin2x. Утверждение 10.2. Сумма конечного числа б.б. функций эквивалентна своей главной части. В общем случае можно говорить о главной части не только алгебраической суммы конечного числа б.б. при х а (или при х оо) функций, но и произвольной по структуре функции f(x)y эквивалентной при х а степенной функции А/(х — а)* (при х оо —степенной функции Ахк), Аф 0, к > 0. Эта степенная функция и будет главной частью б.б. функции соответственно при х —у а или при х оо. Путь нахождения коэффициента А и показателя степени к основан на использовании определения 10.7 и утверждения 10.2 и подобен процедуре выделения главной части б.м. функции. Пример 10.10. Функция /(ж) = yj 1/х — 1 определена в полуинтервале (0, 1] и как элементарная функция — непрерывна в этом промежутке (см. 3.6 и 9.5). Так как при х +0 эта функция является б.б., а прямая х = 0 будет вертикальной асимптотой графика . Найдем главную часть f(x) при х->+0 в виде А/хк из условия (10.27) эквивалентности б.б. функции и ее главной части: limQf+0 будет 1/у/х (рис. 10.1). Поскольку lim fix) = lim — 1 = 0, г-И-0 v ‘ г-fl-O V х при х 1 — 0 , f(x) является б.м. функцией. Найдем главную часть >(х) при z-4 1-О в виде А(1-х)к Рис. 10.1 из условия (10.8) эквивалентности б.м. функции и ее главной части: lim q f(x)/(A(l — х)*) = 1. Отсюда Эквивалентные бесконечно малые функции. Главная часть бесконечно малой функции. Сравнение бесконечно больших функций (1 — х)к Предел в правой части этого равенства будет конечным и отличным от нуля, если А: = 1/2. Тогда А = 1, и главной частью f(x) при х-» 1-0 будет у/1 -х (см. рис. 10.1).

Информация расположенная на данном сайте несет информационный характер и используется для учебных целей.
© Брильёнова Наталья Валерьевна

пусть a(х)®0, b(х)®0 при х®а и пусть $ .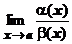

Опр.Если 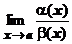— конечное число, отличное от нуля, то БМ функции a(х) и b(х) называются бесконечно малыми одного порядка.

Опр.Если 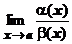=0, то БМ a(х) называется бесконечно малой более высокого порядка по сравнению с b(х) (b(х) называется бесконечно малой низшего порядка по сравнению с a(х)). Обозначение: a(х) = о(a(х)).

Опр.Если 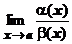=1, то БМ a(х) и b(х) называются эквивалентными. Обозначение: a(х)

b(х); если a(х)

b(х), то b(х)

Теор. (Необходимое и достаточное условие эквивалентности ББ). Для того, чтобы ББ функции F(х) и G(х) были эквивалентными, необходимо и достаточно, чтобы выполнялось условие F(х) — G(х) = о(F(х)) (или F(х) — G(х) = о(G(х)).

Основная цель выделения главной части — получение более простой функции, которая в окрестности предельной точки ведёт себя также, как исходная.

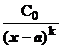
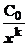
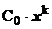
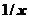
При выделении главных частей указывается их вид; при решении задач на вычисление пределов при х®а обычно это С₀(х—а) k для бесконечно малых и для бесконечно больших, при х®¥ — это для бесконечно малых и для бесконечно больших, где С₀ = const¹0, k =const>0 – порядок малости или роста функции f(x) относительно функции (х—а) (или относительно при х®¥). Для главных частей такого вида бесконечно малых при х®а функций равносильны следующие утверждения:

1) ;

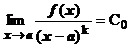
2) , где a(х) – БМ при х®а;

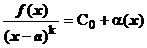
3) ;

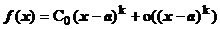
4) , где ;

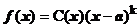
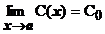
5) f(x)

.

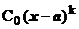
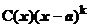
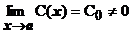
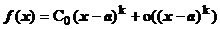
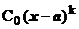
Таким образом, в простейших случаях рецепт для выделения главной части вида С₀(х—а) k БМ при х®а функции f(x) состоит в следующем: f(x) надо представить в виде f(x)= , где . Тогда , и — главная часть функции f(x) при х®а. Аналогично с заменой (х—а) k

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Как то на паре, один преподаватель сказал, когда лекция заканчивалась — это был конец пары: “Что-то тут концом пахнет”. 8404 — | 8021 — или читать все.

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Если выбрана основная бесконечно малая а, то простейшими бесконечно малыми естественно считать величины вида где с – постоянный коэффициент и . Пусть бесконечно малая будет порядка относительно а, т. е.

где с – конечное и отличное от нуля число. Тогда

и бесконечно малые оказываются эквивалентными:

Эта простейшая бесконечно малая эквивалентная данной бесконечно малой , называется ее главной частью (или главным членом).

Пользуясь установленными выше результатами, кроме уже указанных простых примеров, легко выделить главные части выражений:

Здесь и именно является основной бесконечно малой.

Наконец, если и за основную принята бесконечно малая то имеем также

Все эти результаты снова приводят к приближенным формулам.

Пусть где Можно представить себе, что из бесконечно малой у снова выделен главный член: где к

Например, если положить (считая ):

то, как мы уже имели [56, 4)],

так что главная часть у есть . Отсюда

В частности,

Этот процесс последовательного выделения из бесконечно малой простейших бесконечно малых все возрастающих порядков можно продолжать и дальше.

Мы ограничиваемся в настоящем параграфе установлением общих понятий, иллюстрируя их лишь немногими примерами. В последующем мы укажем систематический прием как для построения главной части данной бесконечно малой величины, так и для дальнейшего выделения из нее простейших бесконечно малых, о котором только что шла речь [см. 104, 124].

В заключение, остановимся еще на таком вопросе: если для двух бесконечно малых и у известны их главные члены что можно сказать о главном члене их суммы

При главным членом ее, очевидно, будет тот из членов в котором показатель меньше. Пусть теперь тогда главной частью для явится сумма – в предположении, однако, что . В случае же, когда оба главных члена взаимно уничтожаются, сумма оказывается бесконечно малой высшего порядка, чем каждое из слагаемых.

Так будет, например, при для бесконечно малых

Если выделить в них еще следующие члены:

то ясно, что

так что будет бесконечно малой второго порядка, а ее главный член равен