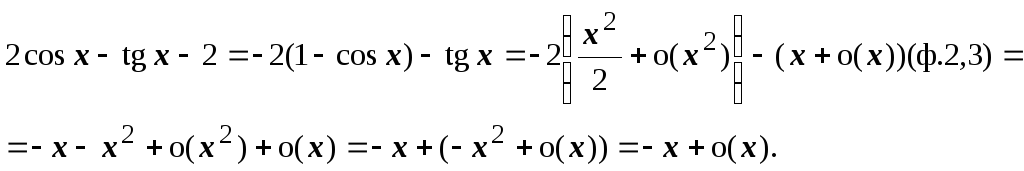Определение 1. Функция 
называется Малой более высокого Порядка по сравнению с функцией 
при 
, если 
и 
и обозначается 
.
Примеры. 1. 
при 
, т. к. 
. Заметим, что при : 
~
, 
. Число 
назы-вается Порядком малости функции 
.
Определение 2. Функция 
называется Большой более высокого Порядка по сравнению с функцией 
при , если 
и 
.
2. 
при 
, т. к. 
.
Определение 3. Функция называется Главной частью функции при , если она представима при в виде 
.
При этом, функции и 
называются Эквивалент-ными при и обозначаются ~ 
.
Теорема 1. Для того чтобы функции и были экви-валентными при необходимо и достаточно, чтобы
=1.
Теорема 2. Следующие функции эквивалентными между собой при 
~ 
~ 
~ 
~ 
~ 
.
Первые три соотношения следуют из 1-го замечательного предела и его следствий, а четвертое и пятое – из следствий 2-го замечательного предела.
Теорема 3. 
~ 
при .
Применим первый замечательный предел и формулу бинома Ньютона к тождеству
~ 
~ при 
.
Выделение главной части функции значительно упрощает вычисление пределов.
Примеры.
1. 
Поскольку 
~ , 
~ 
, 
~ 
, 
~ ~ 
, 
~ , то 
. Наконец, 
~ 
, 
~ при , то 
2. 
Т. к. 
~
, 
~ 3, то 
.
3. 
.
Здесь нельзя использовать эквивалентные функции: ~, т. к. получим неопределенность. Преобразуем основание степени
.
Тогда,
.
Замечание. Последний пример продемонстрировал, что методом выделения главной части функции следует обращаться осторожно. Может оказаться, что решающую роль играет не главная часть функции, а другие ее части.
| < Предыдущая | Следующая > |
|---|
4.5.1. Непосредственное вычисление пределов.
1.
В простейших случаях нахождение предела
сводится к подстановке предельного
значения аргумента в функцию: если f(x)
– элементарная функция, определённая в
точке а,
то
,
например
;
2.
,
если f(х)0
при ха;
3.
,
если f(х)
при ха;
4.
,
если g(х)0,
f(х)
при ха,
например 
и т.д.
Найдём ряд пределов,
которые понадобятся впоследствии:
-
Докажем,
что
.
При х
+
и числитель, и знаменатель стремятся
к бесконечности, поэтому пределы такого
типа называются неопределённостями
.
А).При
справедливо неравенство
(оно
справедливо при n=2,
далее, по индукции: пусть оно верно при
произвольном n,
тогда n
+1< n
+ n
= 2n
<2
,
т.е. оно верно и при n
+1). Следствие:
,
т.е. последовательность
ограничена. Б). Рассмотрим последовательность
.
.
.
(оно
,
,
.
(как
предел произведения ограниченной и
бесконечно малой последовательностей).
В). Пусть х
– произвольное вещественное число, x>0.
Тогда
,
где Е(х)
– целая часть числа х.
Обозначим Е(х)=n.
.
Устремим х
+,
тогда и n
.
Предел постоянной 0 равен этой постоянной,
предел правой части 
.
По теореме
4.4.6 о пределе
промежуточной функции 
,
что и требовалось доказать. Легко видеть,
что это доказательство с небольшими
изменениями воспроизводится, если
заменить число 4 любым числом а>1,
поэтому будем считать доказанным, что
при а>1.
-
при
а>1
легко сводится к предыдущему. Пусть
,
тогда
,
у
+
при х
+,
и
.
при
,
,
.
7.
Как следствие 
при а>1,
b>1.
8.
(неопределённость 
)
также сводится к первому из рассмотренных
пределов. Пусть у=1/х.
Тогда х=1/у,
у
+
при х
+0,
ln
x=ln(1/y)=-ln
y,
поэтому
.
4.5.2. Выделение главной части функции.
Выделение
главной части функции – мощный приём
при решении задач на вычисление пределов.
Основная цель выделения главной части
– получение более простой функции,
которая в окрестности предельной точки
ведёт себя также, как исходная громоздкая
(тогда по теореме 4.4.9.2
о замене бесконечно малых на эквивалентные
мы можем заменить громоздкие функции
в числителе и знаменателе на эквивалентные
простые); основной инструмент при
выделении главных частей – табл.
4.4.10 эквивалентных бесконечно малых.
Как
следует из определений разделов
4.4.8-4.4.11,
утверждения “при ха
1. f(x)g(x);
2. f(x)-g(x)=o(g(x))
=o(f(x));
3. g(x)
есть главная часть f(x)”
эквивалентны. Так как для f(x)
может существовать бесконечно много
главных частей при ха
(например, при х0
…..), при выделении главных частей
указывается их вид; при решении задач
на вычисление пределов при ха
обычно это С0(х–а)k
для бесконечно
малых и
для бесконечно больших, прих
– это
для бесконечно малых и
для бесконечно больших, где С0
= const0,
k
=const>0
– порядок малости или роста функции
f(x)
относительно функции (х–а)
(или относительно
прих).
Для главных частей такого вида бесконечно
малых при ха
функций равносильны следующие
утверждения:
1.
;
2.
,
где(х)
– БМ при ха;
3.
;
4.
,
где
;
-
f(x)
.
.
Таким
образом, в простейших случаях рецепт
для выделения главной части вида С0(х–а)k
БМ при ха
функции f(x)
состоит в следующем: f(x)
надо представить в виде f(x)=
,
где
.
Тогда
,
и
– главная часть функцииf(x)
при ха.
Аналогично
изложенному выше, с заменой (х–а)k
на
,
формулируются утверждения и правило
для выделения главной части функции,
бесконечно малой прих.
Рассмотрим
ряд примеров на выделение главной части
и определение порядка малости функций
(в скобках указываются применённые
формулы табл.
4.4.10):
1.
.
Представимf(x)
в виде
.
Если
,
то
,
поэтому
,k=1
– порядок малости f(x)
при х0.
2.
.
Представимf(x)
в виде
.
Если
,
то
,
поэтому
,k=2
– порядок малости f(x)
при х
по сравнению с
.
3.
.
С помощью формул 4,6таблицы
4.4.10 представим
f(x)
в виде
.
Здесь
,
,
поэтому
,k=1
– порядок малости f(x)
при х0.
4.
.
Так какf(-2)
= 0, то
,
и многочлен
делится нах
+ 2 без остатка. Произведя деление, получим
.
Так как иf1(-2)
= 0, то
,
поэтому
,
где
.
Результат:
,
– главная частьf(x),
k=2
– порядок малости f(x)
при х-2.
5.
.
,
где
.
Поэтому
,
– главная часть
,k=5/6
(относительно БМ
)
при
.
В следующих задачах
решение излагается более кратко.
6.
7.
.
8.
.
9.
Неаккуратность
при решении последнего примера даст
результат
верный,
но бесполезный.
10.
Пусть х
+0.
Тогда
Если
рассматривается случай ха
0, часто полезно сделать замену переменной
у=
х–а.
Пример:
11.
Пусть х2.
Найти главную часть БМ функции 
(убедитесь, что f(x)
0
при х2).
Перейдём к переменной у=
х-2
х=
у+2; у0
при х2.
Меняем в функции х
на у+2:
Так
как у0,
мы пришли к задаче, рассмотренной в
примере 2. Ответ: 
,
при х2.
12.
Для функции, представляющей собой
линейную комбинацию степенных выражений
легко показать, что при х0
f(x)
эквивалентна своему слагаемому с
минимальной степенью: f(x)
:
и все слагаемые, кроме последнего,
стремятся к нулю при х0,
так как 
при i=1,2,…,k-1.
При
х
f(x)
эквивалентна своему слагаемому с
максимальной степенью f(x)
:
и все слагаемые, кроме первого, стремятся
к нулю при х,
так как 
при i=2,…,k.
Соседние файлы в папке lec1
- #
- #
- #
- #
Если выбрана основная бесконечно малая а, то простейшими бесконечно малыми естественно считать величины вида 
где с – постоянный коэффициент и 
. Пусть бесконечно малая 
будет 
порядка относительно а, т. е.
где с – конечное и отличное от нуля число. Тогда
и бесконечно малые 
оказываются эквивалентными: 
Эта простейшая бесконечно малая 
эквивалентная данной бесконечно малой 
, называется ее главной частью (или главным членом).
Пользуясь установленными выше результатами, кроме уже указанных простых примеров, легко выделить главные части выражений:
Здесь 
и именно 
является основной бесконечно малой.
Наконец, если 
и за основную принята бесконечно малая 
то имеем также
Все эти результаты снова приводят к приближенным формулам.
Пусть 
где 
Можно представить себе, что из бесконечно малой у снова выделен главный член: 
где к 
Например, если положить (считая 
):
то, как мы уже имели [56, 4)],
так что главная часть у есть 
. Отсюда
В частности,
Этот процесс последовательного выделения из бесконечно малой простейших бесконечно малых все возрастающих порядков можно продолжать и дальше.
Мы ограничиваемся в настоящем параграфе установлением общих понятий, иллюстрируя их лишь немногими примерами. В последующем мы укажем систематический прием как для построения главной части данной бесконечно малой величины, так и для дальнейшего выделения из нее простейших бесконечно малых, о котором только что шла речь [см. 104, 124].
В заключение, остановимся еще на таком вопросе: если для двух бесконечно малых 
и у известны их главные члены 
что можно сказать о главном члене их суммы 
При 
главным членом ее, очевидно, будет тот из членов 
в котором показатель меньше. Пусть теперь 
тогда главной частью для 
явится сумма 
– в предположении, однако, что 
. В случае же, когда оба главных члена взаимно уничтожаются, сумма 
оказывается бесконечно малой высшего порядка, чем каждое из слагаемых.
Так будет, например, при 
для бесконечно малых
Если выделить в них еще следующие члены:
то ясно, что
так что 
будет бесконечно малой второго порядка, а ее главный член равен 
Метод выделения главной части функции и его применение к вычислению пределов
Метод выделения главной части функции и его применение к вычислению пределов. Дадим функции. Если функция P всех x∈X может быть выражена в виде Р(х)= а (Х)+ О(а(Х)), Х> Х、 В свою очередь, функция a называется основной частью функции при x> x0. Образцы. 1. поскольку x ^8m x = x + o(x), функция 8m x из x ^равна X. 2. Пн (х)= apxn + … + а х + а apΦ, функция apnnn является главной частью многочлена РП (х) в Х>. потому что Pn (x)= apnn + o (xn) для x>^. 267. Функция P. учитывая X ^ K, основная часть x ^ x не определена однозначно. Согласно теореме 1, p-эквивалентная функция X> X0, a, является основной частью x> X0.
Однако, если вы запросите определенный тип основной детали, этот разумный выбор может гарантировать, что основная часть указанного типа определена однозначно.
Людмила Фирмаль
- Например, P = x + x2 + x3.С другой стороны, x2 + x3 = o (x) для x^, P = x + o (x) для x^ и xP = o (x + x2) для x^, поэтому、 P = х + Х2 + о (Х + Х2). В первом случае основную часть можно считать a = x. 2-й а = х + Х2. В частности, справедлива следующая Лемма. Лемма 5. X K, x∈K, x как предельная точка множества X. / Для функции P X ^ K для x ^ ^ x имеет основную часть вида a (X-x) Й, AΦ.Здесь A и V являются константами, которые определяются однозначно среди всех основных частей этой формы. Это справедливо только если A = A и V = ви. Я не уверен.
Понятие основной части функции полезно для изучения бесконечно малых и бесконечно малых чисел, оно используется при решении различных математических задач. analysis. In во многих случаях бесконечно сложная аналитическая форма в окрестности данной точки может быть заменена более простой (в некотором смысле) функцией с бесконечно малым высшим порядком. Например, P (x)=P (x) = A (x-x) d + o ((x-x) d), что является максимумом в случае x> x0, бесконечно малая бесконечность, бесконечно малая бесконечность (x), выше, чем (x-Xo) d, работает в окрестности Укажите на x как функцию, которая должна быть A (x-xo) d.
- В качестве примера мы покажем, как метод разделения основной части десятичной дроби применяется для расчета пределов function. In кроме того, широко используется полученное соотношение эквивалентности (8.26). Так что вам нужно найти предел(и таким образом доказать, что он существует). Используя вышеизложенное (см. отношения(8.26)）、 Валентность 1N (1 + u)〜и u ^имеют 1n (1 + x + x)—x + x в x^, поэтому (см. теорему 1) 1n (1 + x + x)= = х + Х2 + о(Х + Х2).Однако o (x + x2)= o(x) (почему?) И быть X>x2 = o (x)、 Кроме того, агентство работает от 3 до 3 раз、 agszx 3х = 3х + о(Х3)= Х3 + о(Х). Также ясно, что это 5x = o (x).Из асимптотического уравнения получаем 8W 2x-2×8 Вт Х2 = Х2 + о (Х2)= 2х + о(Х).
Двадцать два от Х-Х a ^ 2 x = x2 + o (x2)= o (x), и(ex-1)5〜x5, аналогично、 (Пример-1) 5 = x5 + o(x5)= o(x). Все эти отношения справедливы для x^. Теперь у нас есть 1П(1 + х + х2)+ х3 ags81n-5×3 = = Х + О (х)+ 3х + о(Х) О (х)= 4х + о(Х）、 81n 2x + 1 ^ 2 x +(ex-1) 5 = 2x + o (x)+ o (x)= 2x + o (x), следовательно Однако по теореме 4 ^ + o (x)〜4x, а x ^2x + o (x) 2x Итак, предел искомого существует и равен 2. При вычислении пределов функции с использованием метода разделения основной части следует отметить, что если она не учитывается в разделе 8.3, то, в общем случае, заменить десятичную дробь эквивалентной не представляется возможным.
Метод расчета лимитов путем выделения основной части функции очень удобен, прост и в то же время очень популярен.
Людмила Фирмаль
- Например 。 S1P в Х-Х При нахождении предела формулы 11t p-это х<sup class=»reg»>®</sup>х Ошибочно замените функцию 81n x эквивалентной функцией x из x^. Естественный способ решения такой задачи описан в разделе 13.4. чтобы найти предел выражения в виде н (х) г (х), рекомендуется найти предел логарифма. Рассмотреть 1 / Х2 Хороший пример. Найти предел 11T сои 2x. равенства Некоторые сложности в работе приложения связаны с тем, что до сих пор не существует достаточно популярного способа выделения основной части функции. Эта проблема будет устранена в будущем (см.§ 13). Поскольку экспонента непрерывна, из(8.38).
Смотрите также:
Предмет математический анализ
