Как найти главную диагональ матрицы в матлаб

Как найти главную диагональ матрицы в матлаб

Main Content

diag

Create diagonal matrix or get diagonal elements of matrix

Syntax

Description

example

D = diag(v) returns
a square diagonal matrix with the elements of vector v on
the main diagonal.

example

D = diag(v,k) places
the elements of vector v on the kth
diagonal. k=0 represents the main diagonal, k>0 is
above the main diagonal, and k<0 is below the
main diagonal.

example

x = diag(A) returns
a column vector of the main diagonal elements of A.

example

x = diag(A,k) returns
a column vector of the elements on the kth diagonal
of A.

Examples

collapse all

Create Diagonal Matrices

Create a 1-by-5 vector.

Use diag to create a matrix with the elements of v on the main diagonal.

D = 5×5

     2     0     0     0     0
     0     1     0     0     0
     0     0    -1     0     0
     0     0     0    -2     0
     0     0     0     0    -5

Create a matrix with the elements of v on the first super diagonal (k=1).

D1 = 6×6

     0     2     0     0     0     0
     0     0     1     0     0     0
     0     0     0    -1     0     0
     0     0     0     0    -2     0
     0     0     0     0     0    -5
     0     0     0     0     0     0

The result is a 6-by-6 matrix. When you specify a vector of length n as an input, diag returns a square matrix of size n+abs(k).

Get Diagonal Elements

Get the elements on the main diagonal of a random 6-by-6 matrix. 

A = 6×6

     9     3    10     8     7     8
    10     6     5    10     8     1
     2    10     9     7     8     3
    10    10     2     1     4     1
     7     2     5     9     7     1
     1    10    10    10     2     9

Get the elements on the first subdiagonal (k=-1) of A. The result has one fewer element than the main diagonal.

Calling diag twice returns a diagonal matrix composed of the diagonal elements of the original matrix.

A1 = 6×6

     9     0     0     0     0     0
     0     6     0     0     0     0
     0     0     9     0     0     0
     0     0     0     1     0     0
     0     0     0     0     7     0
     0     0     0     0     0     9

Input Arguments

collapse all

v — Diagonal elements
vector

Diagonal elements, specified as a vector. If v is
a vector with N elements, then diag(v,k) is
a square matrix of order N+abs(k).

diag([]) returns an empty matrix, [].

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical | char
Complex Number Support: Yes

A — Input matrix
matrix

Input matrix. diag returns an error if ndims(A)
> 2.

diag([]) returns an empty matrix, [].

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical | char
Complex Number Support: Yes

k — Diagonal number
integer

Diagonal number, specified as an integer. k=0 represents
the main diagonal, k>0 is above the main diagonal,
and k<0 is below the main diagonal.

For an m-by-n matrix, k is in the
range (−m+1)≤k≤(n−1). For example, for matrices with n greater than
m, the k=0 main diagonal consists of the elements with
indices (1,1), (2,2), …, (m,m).
The k=1 above the main diagonal consists of the elements with indices
(1,2), (2,3), …, (m,m+1). The
k=-1 below the main diagonal consists of the elements with indices
(2,1), (3,2), …, (m,m-1).

Diagonal numbers k=0, k>0, and k<0

Tips

  • The trace of
    a matrix is equal to sum(diag(A)).

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

Usage notes and limitations:

  • If you supply k, then it must be
    a real and scalar integer value.

  • For variable-size inputs that are variable-length
    vectors (1-by-: or :-by-1), diag:

    • Treats the input as a vector

    • Returns a matrix with the input vector along the specified diagonal

  • For variable-size inputs that are not variable-length
    vectors, diag:

    • Treats the input as a matrix

    • Does not support inputs that are vectors at run time

    • Returns a variable-length vector

    If the input is variable-size (:m-by-:n) and has shape 0-by-0 at run time, then the output is
    0-by-1, not 0-by-0. However, if the input is a constant size 0-by-0, then the output is
    [].

  • For variable-size inputs that are not variable-length
    vectors (1-by-: or :-by-1), diag treats the input
    as a matrix from which to extract a diagonal vector. This behavior
    occurs even if the input array is a vector at run time. To force diag to
    build a matrix from variable-size inputs that are not 1-by-: or :-by-1,
    use:

    • diag(x(:)) instead of diag(x)

    • diag(x(:),k) instead of diag(x,k)

  • See Variable-Sizing Restrictions for Code Generation of Toolbox Functions (MATLAB Coder).

GPU Code Generation
Generate CUDA® code for NVIDIA® GPUs using GPU Coder™.

Usage notes and limitations:

  • If you supply k, then it must be a real and scalar integer
    value.

  • For variable-size inputs that are variable-length vectors (1-by-: or :-by-1),
    diag:

    • Treats the input as a vector

    • Returns a matrix with the input vector along the specified diagonal

  • For variable-size inputs that are not variable-length vectors, diag:

    • Treats the input as a matrix

    • Does not support inputs that are vectors at run time

    • Returns a variable-length vector

    If the input is variable-size (:m-by-:n) and has shape 0-by-0 at run time, then the
    output is 0-by-1, not 0-by-0. However, if the input is a constant size 0-by-0, then the output
    is [].

  • For variable-size inputs that are not variable-length vectors (1-by-: or :-by-1),
    diag treats the input as a matrix from which to extract a diagonal
    vector. This behavior occurs even if the input array is a vector at run time. To force
    diag to build a matrix from variable-size inputs that are not 1-by-: or
    :-by-1, use:

    • diag(x(:)) instead of diag(x)

    • diag(x(:),k) instead of diag(x,k)

Thread-Based Environment
Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.

This function fully supports thread-based environments. For
more information, see Run MATLAB Functions in Thread-Based Environment.

GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

This function fully supports GPU arrays. For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).

Distributed Arrays
Partition large arrays across the combined memory of your cluster using Parallel Computing Toolbox™.

This function fully supports distributed arrays. For more
information, see Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox).

Version History

Introduced before R2006a

Источник

Main Content

diag

Create diagonal matrix or get diagonals from symbolic matrices

Syntax

Description

example

D = diag(v) returns a square diagonal matrix
with vector v as the main diagonal.

example

D = diag(v,k) places vector
v on the kth diagonal. k = 0
represents the main diagonal, k > 0 is above the main diagonal, and
k < 0 is below the main diagonal.

example

x = diag(A) returns the main diagonal of
A.

example

x = diag(A,k) returns the
kth diagonal of A.

Examples

collapse all

Create Matrix with Diagonal as Vector

Create a symbolic matrix with the main diagonal specified by the vector
v.

syms a b c
v = [a b c];
diag(v)
ans =
[ a, 0, 0]
[ 0, b, 0]
[ 0, 0, c]

Create Matrix with Subdiagonal as Vector

Create a symbolic matrix with the second diagonal below the main diagonal
specified by the vector v.

syms a b c
v = [a b c];
diag(v,-2)
ans =
[ 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0]
[ a, 0, 0, 0, 0]
[ 0, b, 0, 0, 0]
[ 0, 0, c, 0, 0]

Extract Diagonal from Matrix

Extract the main diagonal from a square matrix.

syms x y z
A = magic(3).*[x, y, z];
diag(A)

Extract Superdiagonal from Matrix

Extract the first diagonal above the main diagonal.

syms x y z
A = magic(3).*[x, y, z];
diag(A,1)

Input Arguments

collapse all

v — Diagonal elements
symbolic vector

Diagonal elements, specified as a symbolic vector. If v is a vector
with N elements, then diag(v,k) is a square matrix of
order N + abs(k).

A — Input matrix
symbolic matrix

Input matrix, specified as a symbolic matrix.

k — Diagonal number
integer

Diagonal number, specified as an integer. k = 0 represents the main
diagonal, k > 0 is above the main diagonal, and k < 0
is below the main diagonal.

Tips

  • The trace of a matrix is equal to
    sum(diag(A)).

Version History

Introduced before R2006a

Источник

Создайте диагональную матрицу или получите диагональные элементы матрицы

Синтаксис

Описание

пример

D = diag(v) возвращает квадратную диагональную матрицу с элементами векторного v на основной диагонали.

пример

D = diag(v,k) помещает элементы векторного v на kдиагональ th. k=0 представляет основную диагональ, k>0 выше основной диагонали и k<0 ниже основной диагонали.

пример

x = diag(A) возвращает вектор-столбец основных диагональных элементов A.

пример

x = diag(A,k) возвращает вектор-столбец элементов на kдиагональ th A.

Примеры

свернуть все

Создание диагональных матриц

Создайте вектор 1 на 5.

Используйте diag создать матрицу с элементами v на основной диагонали.

D = 5×5

     2     0     0     0     0
     0     1     0     0     0
     0     0    -1     0     0
     0     0     0    -2     0
     0     0     0     0    -5

Создайте матрицу с элементами v на первой супер диагонали (k=1).

D1 = 6×6

     0     2     0     0     0     0
     0     0     1     0     0     0
     0     0     0    -1     0     0
     0     0     0     0    -2     0
     0     0     0     0     0    -5
     0     0     0     0     0     0

Результат 6 6 матрица. Когда вы задаете вектор из длины n как вход, diag возвращает квадратную матрицу размера n+abs(k).

Получение диагональных элементов

Получите элементы на основной диагонали случайного 6 6 матрица. 

A = 6×6

     9     3    10     8     7     8
    10     6     5    10     8     1
     2    10     9     7     8     3
    10    10     2     1     4     1
     7     2     5     9     7     1
     1    10    10    10     2     9

Получите элементы на первой поддиагонали (k=-1) из A. Результат имеет тот меньше элемента, чем основная диагональ.

Вызов diag дважды возвращает диагональную матрицу, состоявшую из диагональных элементов исходной матрицы.

A1 = 6×6

     9     0     0     0     0     0
     0     6     0     0     0     0
     0     0     9     0     0     0
     0     0     0     1     0     0
     0     0     0     0     7     0
     0     0     0     0     0     9

Входные параметры

свернуть все

v — Диагональные элементы
вектор

Диагональные элементы в виде вектора. Если v вектор с N элементы, затем diag(v,k) квадратная матрица порядка N+abs(k).

diag([]) возвращает пустую матрицу, [].

Типы данных: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical | char
Поддержка комплексного числа: Да

A — Введите матрицу
матрица

Введите матрицу. diag возвращает ошибку если ndims(A) > 2.

diag([]) возвращает пустую матрицу, [].

Типы данных: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical | char
Поддержка комплексного числа: Да

k — Диагональный номер
целое число

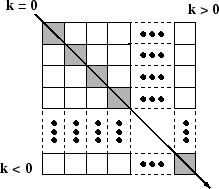
Диагональный номер в виде целого числа. k=0 представляет основную диагональ, k>0 выше основной диагонали и k<0 ниже основной диагонали.

Для m-by-n матрица, k находится в области значений (−m+1)≤k≤(n−1)  .

Советы

  • trace из матрицы равно sum(diag(A)).

Расширенные возможности

Генерация кода C/C++
Генерация кода C и C++ с помощью MATLAB® Coder™.

Указания и ограничения по применению:

  • Если вы предоставляете k, затем это должно быть действительное и скалярное целочисленное значение.

  • Для входных параметров переменного размера, которые являются векторами переменной длины (1 на: или:-1), diag:

    • Обрабатывает вход как вектор

    • Возвращает матрицу с входным вектором по заданной диагонали

  • Для входных параметров переменного размера, которые не являются векторами переменной длины, diag:

    • Обрабатывает вход как матрицу

    • Не поддерживает входные параметры, которые являются векторами во время выполнения

    • Возвращает вектор переменной длины

    Если вход является переменным размером (: m-by-:n), и имеет форму 0 на 0 во время выполнения, затем выход 0 1, не 0 на 0. Однако, если вход является постоянным размером 0 на 0, то выходом является [].

  • Для входных параметров переменного размера, которые не являются векторами переменной длины (1 на: или:-1), diag обрабатывает вход как матрицу, из которой можно извлечь диагональный вектор. Это поведение происходит, даже если входной массив является вектором во время выполнения. Обеспечивать diag чтобы создать матрицу из входных параметров переменного размера, которые не являются 1 на: или:-1, используйте:

    • diag(x(:)) вместо diag(x)

    • diag(x(:),k) вместо diag(x,k)

  • “Смотрите информацию о генерации кода функций Toolbox (MATLAB Coder) в разделе “”Ограничения переменных размеров””.”.

Генерация кода графического процессора
Сгенерируйте код CUDA® для NVIDIA® графические процессоры с помощью GPU Coder™.

Указания и ограничения по применению:

  • Если вы предоставляете k, затем это должно быть действительное и скалярное целочисленное значение.

  • Для входных параметров переменного размера, которые являются векторами переменной длины (1 на: или:-1), diag:

    • Обрабатывает вход как вектор

    • Возвращает матрицу с входным вектором по заданной диагонали

  • Для входных параметров переменного размера, которые не являются векторами переменной длины, diag:

    • Обрабатывает вход как матрицу

    • Не поддерживает входные параметры, которые являются векторами во время выполнения

    • Возвращает вектор переменной длины

    Если вход является переменным размером (: m-by-:n), и имеет форму 0 на 0 во время выполнения, затем выход 0 1, не 0 на 0. Однако, если вход является постоянным размером 0 на 0, то выходом является [].

  • Для входных параметров переменного размера, которые не являются векторами переменной длины (1 на: или:-1), diag обрабатывает вход как матрицу, из которой можно извлечь диагональный вектор. Это поведение происходит, даже если входной массив является вектором во время выполнения. Обеспечивать diag чтобы создать матрицу из входных параметров переменного размера, которые не являются 1 на: или:-1, используйте:

    • diag(x(:)) вместо diag(x)

    • diag(x(:),k) вместо diag(x,k)

Основанная на потоке среда
Запустите код в фоновом режиме с помощью MATLAB® backgroundPool или ускорьте код с Parallel Computing Toolbox™ ThreadPool.

Эта функция полностью поддерживает основанные на потоке среды. Для получения дополнительной информации смотрите функции MATLAB Запуска в Основанной на потоке Среде.

Массивы графического процессора
Ускорьте код путем работы графического процессора (GPU) с помощью Parallel Computing Toolbox™.

Эта функция полностью поддерживает массивы графического процессора. Для получения дополнительной информации смотрите функции MATLAB Запуска на графическом процессоре (Parallel Computing Toolbox).

Распределенные массивы
Большие массивы раздела через объединенную память о вашем кластере с помощью Parallel Computing Toolbox™.

Эта функция полностью поддерживает распределенные массивы. Для получения дополнительной информации смотрите функции MATLAB Запуска с Распределенными Массивами (Parallel Computing Toolbox).

Представлено до R2006a

Источник

diag

Diagonal matrices and diagonals of a matrix

Syntax 

  • X = diag(v,k)
X = diag(v)
v = diag(X,k)
v = diag(X)

Description

X = diag(v,k)
 when v is a vector of n components, returns a square matrix X of order n+abs(k), with the elements of v on the kth diagonal. k = 0 represents the main diagonal, k > 0 above the main diagonal, and k < 0 below the main diagonal.

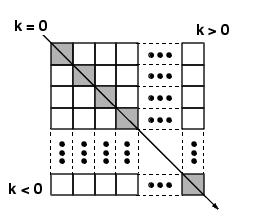
X = diag(v)
 puts v on the main diagonal, same as above with k = 0.

v = diag(X,k)
 for matrix X, returns a column vector v formed from the elements of the kth diagonal of X.

v = diag(X)
 returns the main diagonal of X, same as above with k = 0.

Examples

diag(diag(X)) is a diagonal matrix.

sum(diag(X)) is the trace of X.

The statement

  • diag(-m:m)+diag(ones(2*m,1),1)+diag(ones(2*m,1),-1)

produces a tridiagonal matrix of order 2*m+1.

See Also

spdiags, tril, triu

   deval   dialog 

Источник

I tried to use matlab to find the upper and lower diagonal matrix in matlab

here is the idea

if I have matrix 4×4

 1  2  3  4 
 5  6  7  8
 9 10 11 12 
13 14 15 16

the main diagonal is 

1 6 11 16

but the second upper diagonal is 

2 7 12

and the lower is

5 10 15

so there is triu and tril but to to write it or use any other function in matlab to find this upper and lower diagonal in matrix.

Shai's user avatar

Shai

110k38 gold badges236 silver badges367 bronze badges

asked Nov 16, 2013 at 21:04

Haider Ali's user avatar

just use diag , for example

 diag(A,0)   % main diagonal, also diag(A)
 diag(A,-1)  % lower diagonal
 diag(A,1)   % upper ...

answered Nov 16, 2013 at 21:17

bla's user avatar

blabla

25.8k10 gold badges70 silver badges101 bronze badges

0

You can use simple linear indexing to get any diagonal of a matrix. All you need to know is the linear index of the first element and the number of rows in the matrix:

 >> [m n] = size(A);

Get the main diagonal on the matrix (first element index is 1):

 >> A( 1 : ( m+1 ) : end )

Get the lower diagonal (first index is 2):

 >> A( 2 : ( m+1 ) : end )

Get the upper diagonal (first index is m+1):

>> A( (m+1) : (m+1) : end )

answered Nov 16, 2013 at 21:12

Shai's user avatar

ShaiShai

110k38 gold badges236 silver badges367 bronze badges

0

Источник

Добавить комментарий