Как найти главную диагональ в квадрате - Сайт, где вы сможете решить свои вопросы

На занятии будет рассмотрен двумерный массив в Pascal и примеры работы с ним. Кроме того, предстоит знакомство с понятиями побочная диагональ матрицы в Паскаль и главная диагональ

Содержание:

Двумерный массив в Pascal
Описание, ввод и вывод элементов двумерного массива
Главная и побочная диагональ при работе с двумерными матрицами в Pascal

Матрица или двумерный массив – это прямоугольная таблица чисел (или других элементов одного типа). Каждый элемент матрицы имеет два индекса (номер строки и номер столбца).

Исходные данные для решения многих задач можно представить в табличной форме:

Таблица результатов производственной деятельности нескольких филиалов фирмы может быть представлена так:

zavod1: array [1..4] of integer;
zavod2: array [1..4] of integer; 
zavod3: array [1..4] of integer;

Или в виде двумерного массива так:

Объявление двумерного массива:

var A: array[1..3,1..4] of integer;
begin
{...}

begin
  var  a := new integer[3,4];
  {...}
end.

Описание, ввод и вывод элементов двумерного массива

Варианты описания двумерного массива (традиционный pascal)

Описание массива в разделе переменных:

const N = 3;
      M = 4;
var A: array[1..N,1..M] of integer;

Описание массива через раздел type:

const
  M=10;
  N=5;
type
  matrix=array [1..M, 1..N] of integer;
var A: matrix;

Ввод двумерного массива m x n с клавиатуры:

for i:=1 to N do
  for j:=1 to M do begin
    write('A[',i,',',j,']=');
    read ( A[i,j] );
  end;

for var i:=0 to a.RowCount-1 do
  for var j:=0 to a.ColCount-1 do
     a[i,j]:=readinteger;

Заполнение случайными числами:

var a := MatrRandomInteger(3,4,0,10); // целые числа в диапазоне от 0 до 10
var a1 := MatrRandomReal(3,4,1,9) // веществ. числа в диапазоне от 1 до 9

«Красивый» вывод элементов двумерного массива m x n:

Следующий фрагмент программы выводит на экран значения элементов массива по строкам:

for i:=1 to N do begin
  for j:=1 to M do
     write ( A[i,j]:5 );
  writeln;
end;

begin
  var a := MatrRandomInteger(3,4,0,10);
  var a1 := MatrRandomReal(3,4,1,9);
  a.Println;
  a1.Println(6,1) // 6 позиций всего на вывод, 1 знак после десят. запятой
end.

Результат:

   8   2   1   3
   5   8   0   8
   6   3   9   3
   3.3   4.7   3.7   5.4
   2.9   1.7   2.3   4.0
   8.3   3.7   8.4   1.4

Рассмотрим следующую задачу: Получены значения температуры воздуха за 4 дня с трех метеостанций, расположенных в разных регионах страны:

Номер станции	1-й день	2-й день	3-й день	4-й день
1	-8	-14	-19	-18
2	25	28	26	20
3	11	18	20	25

Т.е. запись показаний в двумерном массиве выглядела бы так:

t[1,1]:=-8;	t[1,2]:=-14;	t[1,3]:=-19;	t[1,4]:=-18;
t[2,1]:=25;	t[2,2]:=28;	t[2,3]:=26;	t[2,4]:=20;
t[3,1]:=11;	t[3,2]:=18;	t[3,3]:=20;	t[3,4]:=25;

Или в pascalabc.NET:

var t := Matr(3,4,-8,-14,-19,-18,25,28,26,20,11,18,20,25);  
t.Println;

Объявление двумерного массива:

var t: array [1..3, 1..4] of integer;

Задание array 1: Необходимо:

Распечатать температуру на 2-й метеостанции за 4-й день и на 3-й метеостанции за 1-й день.
Распечатать показания термометров всех метеостанций за 2-й день.
Определить среднюю температуру на 3-й метеостанции.
Распечатать, в какие дни и на каких метеостанциях температура была в диапазоне 24-26 градусов тепла.

Дополните код:

Показать решение:

var t: array [1..3, 1..4] of integer;
s,i,j:integer;
begin
t[1,1]:=-8; 	t[1,2]:=-14; 	t[1,3]:=-19; 	t[1,4]:=-18;
t[2,1]:=25; 	t[2,2]:=28; 	t[2,3]:=26; 	t[2,4]:=20;
t[3,1]:=11; 	t[3,2]:=18; 	t[3,3]:=20; 	t[3,4]:=25;
{1. Распечатать показания термометров на 2-й метеостанции за 4-й день и на 3-й метеостанции за 1-й день}
writeln('1-е задание: ',t[2,4] , ' и ',t[...,...]);
 
{2. Показания термометров всех метеостанций за 2-й день}
for i:=1 to ... do 
   writeln ('2-е задание: ',t[...,...]);
 
{3. Определим среднее значение температуры на 3-й метеостанции:}
i:=3;
s:=0;
for j:=1 to 4 do 
   s:=...; {сумматор}
writeln('3-е задание: ', s/4);
{распечатаем всю таблицу}
for i:=1 to 3 do
    for j:=1 to 4 do
        writeln(t[i,j]);
{4. Распечатаем станции и дни с температурой 24-26 гр}
writeln('4-е задание: ');
for i:=1 to 3 do
    for ... ... do
        if (...) and (...) then
           writeln('станция ', i, ' день ', j)
end.

Самостоятельно подумайте, как находится сумма элементов массива pascal.

Задание array 2. Найти сумму элементов массива (прямоугольной таблицы) размером [m x n]

Задание array 4.
Найти сумму всех элементов массива (переменная sum) 5 x 4, а также сумму элементов, составляющих столбцы таблицы (двумерного массива). Для хранения сумм столбцов чисел использовать одномерный массив (s). Дополните код.

Показать решение:

const  m = 5;
       n = 4;
var
    a: array[1..m,1..n] of byte;
    s: array[1..n] of byte;
    i,j, sum: byte;
begin
    randomize;
    for i := 1 to m do begin
        for j := 1 to n do begin
            ... {инициализация элементов массива случайными числами}
            ... {вывод элементов массива}
        end;
        writeln
    end;
    writeln ('------------'); {для оформления}
    {обнуление значений массива суммы s[]:}
    ...
    {поиск сумм элементов по столбцам:}
    for i := 1 to n do begin
         for j := 1 to m do begin
           s[i]:=...;
        end;
     write(...)  ; 
    end;
    {поиск общей суммы:}
    sum:=0;
    ...
    {вычисление суммы элементов массива значений сумм по столбцам:}
    for ...
        ...
    write (' | sum = ', sum);
readln
end.

Задание array 4_1.
Найти сумму элементов двумерного массива [m x n] по строкам:

2 8 1 9  : sum = 20
3 1 7 2  : sum = 13
4 5 6 2  : sum = 17

Методы матриц для работы со строками и столбцами:

begin
  var a := MatrRandomInteger(3,4);  
  a.Println;
 
  a.Row(0).Sum.Println();
  a.Row(1).Average.Println;
  a.Row(2).Product.Println;
 
  a.Col(0).Min.Println;
  a.Col(1).Max.Println;
end.

Результат:

  86  62  80  33
  51   4  36  65
  78  30   5  16
261 
39 
187200 
51 
62

Главная и побочная диагональ при работе с двумерными матрицами в Pascal

Главная диагональ квадратной матрицы n x n (т.е. той, у которой количество строк равно количеству столбцов) проходит с верхнего левого угла матрицы (элемент 1,1) до правого нижнего угла матрицы (элемент n,n).

Побочная диагональ квадратной матрицы n x n проходит с нижнего левого угла матрицы (элемент n,1) до правого верхнего угла матрицы (элемент 1,n).

Формулу поиска элементов диагоналей проще всего искать, нарисовав элементы матрицы:
Если индексы начинаются с единицы (традиционный Паскаль):

1,1	1,2	1,3	1,4
2,1	2,2	2,3	2,4
3,1	3,2	3,3	3,4
4,1	4,2	4,3	4,4

Если индексы начинаются с нуля (pascalAbc.NET):

0,0	0,1	0,2	0,3
1,0	1,1	1,2	1,3
2,0	2,1	2,2	2,3
3,0	3,1	3,2	3,3

Учитывая, что первая цифра в программе будет соответствовать счетчику i, а вторая — счетчику j, то из таблицы можно вывести формулы:

Главная диагональ матрицы в Паскаль имеет формулу:
i=j
Побочная диагональ матрицы в Паскале традиционном имеет формулу:
n=i+j-1 (или j=n-i+1)

где n — размерность квадратной матрицы

Побочная диагональ матрицы в pascalAbc.Net имеет формулу:
n=i+j+1

где n — размерность квадратной матрицы

Пример: Вывести на экран сначала главную диагональ квадратной матрицы из N строк и N столбцов, а затем ее побочную диагональ.

Решение:

Пример: Заменить элементы главной и побочной диагонали квадратной матрицы нулями

Показать решение:

Паскаль:

var i,j,n:integer;
a: array[1..100,1..100]of integer;
begin
   randomize;
   writeln ('введите размерность матрицы:');
   readln(n);
   for i:=1 to n do begin
        for j:=1 to n do  begin
            a[i,j]:=random(10);
            write(a[i,j]:3);
        end;
        writeln;
   end;
   writeln;
   for i:=1 to n do begin
        for j:=1 to n do  begin
            if (i=j) or (n=i+j-1) then a[i,j]:=0;
            write(a[i,j]:3)
        end;
        writeln;
   end;
end.

PascalAbc.Net

begin
  var n := readinteger('введите размерность матрицы:');
  var a := matrRandomInteger(n, n, -10, 10);
  a.Println(6);
  for var i := 0 to n - 1 do
  begin
    a[i, i] := 0;
    a[i, n - i - 1] := 0;
  end;
  writeln();
  a.Println(6);
end.

Задание array 5:
Найти отдельно сумму элементов главной и побочной диагонали квадратной матрицы

1 7 3 7
2 1 8 3
5 7 6 4
8 2 3 1
-------
sum1 = 9
sum2 = 30

Пример:
Дана матрица 5х5. Найти сумму элементов, стоящих на двух соседних диагоналях с главной и параллельных ей.

Для решения задачи воспользуйтесь таблицей

Показать решение:

var
A:array[1..5,1..5] of integer;
i,j:integer;
sum,sum1,sum2:integer;
begin
randomize;
for i:=1 to 5 do
for j:=1 to 5 do
    A[i,j]:=random(10);
write ('Исходный массив A: ');
for i:=1 to 5 do begin
    writeln;
    for j:=1 to 5 do
        write (A[i,j]:2,' ');
    end;
sum1:=0;
for i:=1 to 5 do
    for j:=1 to 5 do
        if (i-j=1) then
            sum1:=sum1+A[i,j];
sum2:=0;
for i:=1 to 5 do
    for j:=1 to 5 do
        if (j-i=1) then
           sum2:=sum2+A[i,j];
sum:=sum1+sum2;
writeln;
writeln('Сумма = ',sum);
end.

Задание array 6: Сформировать матрицу размерностью n. Вывести ее на экран. Затем преобразовать ее, заменив необходимые элементы на 0:

Задание array 7: Сформировать матрицу размерностью n. Вывести ее на экран. Затем преобразовать ее, заменив необходимые элементы на 0:

Задание array 8: Сформировать матрицу размерностью n. Вывести ее на экран. Затем преобразовать ее, заменив необходимые элементы на 0:

Задание array 9: Составить программу, позволяющую с помощью датчика случайных чисел сформировать матрицу размерностью N. Определить:

минимальный элемент, лежащий ниже побочной диагонали;

произведение ненулевых элементов последней строки.

Рассмотрим еще один пример работы с двумерным массивом.

Пример: В двумерном массиве размером N х M определить среднее значение элементов. Найти индекс элемента массива, наиболее близкого к среднему значению.

var index1,index2,i,j,N,M:integer;
s,min,f:real;
a:array[1..300,1..300] of real;
begin
N:=10;
M:=5;
for i:=1 to N do begin
  for j:=1 to M do begin
    a[i,j]:=random(20);
    s:=s+a[i,j];
    write(a[i,j]:3);
   end;
   writeln;
end;
 
f:=s/(N*M);
writeln('srednee znachenie ',f);
min:=abs(a[1,1]-f);
for i:=1 to N do begin
  for j:=1 to M do begin
    if abs(a[i,j]-f)<min then begin
      min:=abs(a[i,j]-f);
      index1:=i;
      index2:=j;
    end;
  end;
end;
writeln('naibolee blizkiy ',index1,' ',index2);
end.

Потренируйтесь в решении задач по теме, щелкнув по пиктограмме:

Источник

Диагональ квадрата

Диагональ

Четырехугольник, у которого все углы прямые, а стороны равны, называется квадратом. Проведенная внутри квадрата диагональ делит его на два одинаковых равнобедренных прямоугольных треугольника, у которых гипотенузой будет диагональ, а катетами — стороны квадрата. Отсюда, диагональ d как гипотенузу прямоугольного треугольника с равными сторонами а, можно вычислить по теореме Пифагора:

a² + a² = d²

2a² = d²

где d — диагональ квадрата, а — сторона квадрата
Диагональ квадрата равна стороне квадрата, умноженной на корень из двух.

Калькулятор расчета диагонали квадрата

Источник

Квадрат принадлежит к рангу правильных многоугольников, то есть это равносторонний четырехугольник. Являясь синтезом ромба и прямоугольника, каждый из которых в свою очередь представляет собой производную фигуру от, параллелограмма, квадрат объединяет в себе все свойства вышеперечисленных фигур.

Как это поможет найти диагональ квадрата? Рассмотрим два его основных свойства:
– Все стороны квадрата равны (от ромба)
– Все углы квадрата являются прямыми, то есть равны 90 градусам (от прямоугольника)

Если провести диагональ квадрата, то она образует с его сторонами не просто прямоугольный треугольник (как в прямоугольнике), но равнобедренный прямоугольный треугольник, который по теореме Пифагора будет связывать всего два параметра – диагональ квадрата и его сторону. Стороны квадрата будут катетами для треугольника, а диагональ гипотенузой.

a²+b²=c²
a²+b²=d²
2a²=d²

Чтобы из данного тождества вывести формулу диагонали, нужно поместить удвоенный квадрат стороны под квадратный корень, и так как сторона квадрата также возведена во вторую степень, ее можно будет сразу вынести из под корня. В итоге формула диагонали квадрата через сторону будет выглядеть как сторона квадрата, умноженная на корень из двух:

d=√(2a²)
d=a√2

Данная формула применима ко всем случаям, когда необходимо найти диагональ квадрата. При этом в задаче может быть дан не сам квадрат, а форма квадрата как осевое сечение цилиндра, например, тогда длина диагонали квадрата равна диагонали сечения.

Следует также учитывать, что точка пересечения диагоналей делит их на две равные части (свойство параллелограмма), соответственно каждый отрезок, полученный в результате пересечения диагоналей, будет равен половине диагонали квадрата.

Формулы диагонали квадрата через площадь, периметр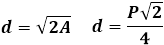

Источник

Квадрат — определение и свойства

Квадрат — это прямоугольник, у которого все стороны равны.
Можно дать и другое определение квадрата:
квадрат — это ромб, у которого все углы прямые.

Получается, что квадрат обладает всеми свойствами параллелограмма, прямоугольника и ромба.

Квадрат относится к правильным многоугольникам. У правильного многоугольника все стороны равны и все углы равны.

Перечислим свойства квадрата:

Все углы квадрата — прямые, все стороны квадрата — равны.

$angle A= angle B=angle C=angle D=90^{circ }.$
Диагонали квадрата равны и пересекаются под прямым углом.
Диагонали квадрата делятся точкой пересечения пополам.
Диагонали квадрата являются биссектрисами его углов (делят его углы пополам).
Диагонали квадрата делят его на 4 равных прямоугольных равнобедренных треугольника:

Периметр квадрата P в 4 раза больше его стороны и равен: P=4a.

Площадь квадрата равна квадрату его стороны: S=a^2 .

Теорема 1. Диагональ квадрата равна произведению его стороны на sqrt{2} , то есть
.

Доказательство:

Рассмотрим квадрат ABCD. Проведем диагональ квадрата AC.

Треугольник АВС – прямоугольный с гипотенузой АС. Запишем для треугольника АВС теорему Пифагора:

$AC^{2}=AB^{2}+BC^{2};$

$AC^{2}=a^{2}+a^{2}=2a^{2}, AC=asqrt{2},$ что и требовалось доказать.

Теорема 2. Радиус вписанной в квадрат окружности равен половине его стороны:

$displaystyle r=frac{1}{2}cdot a$

Доказательство:

Пусть окружность с центром в точке О и радиусом r вписана в квадрат АВСD и касается его сторон в точках
P, M, N, K.

Тогда поскольку AB параллельно CD. Через точку О можно провести только одну прямую, перпендикулярную АВ, поэтому точки Р, О и N лежат на одной прямой. Значит, PN – диаметр окружности. Поскольку АРND – прямоугольник, то PN = AD, то есть

, что и требовалось доказать.

Теорема 3. Радиус описанной около квадрата окружности равен половине его диагонали:

$R=frac{sqrt{2}}{2}cdot a.$

Доказательство:

Диагонали квадрата АС и BD равны, пересекаются в точке О и делятся точкой пересечения пополам. Поэтому OA=OB=OC=OD, т.е. точки A, B, C и D лежат на одной окружности, радиус которой R = d/2 (d=AC=BD). Это и есть описанная около квадрата АВСD окружность.

По теореме

Тогда $R=afrac{sqrt{2}}{2}$ , что и требовалось доказать.

Заметим, что периметр квадрата тоже можно связать с радиусами вписанной и описанной окружностей:

Четырехугольник является квадратом, если выполняется хотя бы одно из условий:

Все стороны равны и среди внутренних углов есть прямой угол.
Диагонали равны, перпендикулярны и, пересекаясь, делятся пополам.

Разберем несколько простых задач на тему «Квадрат». Все они взяты из Банка заданий ФИПИ.

Задача 1. Найдите сторону квадрата, диагональ которого равна sqrt{8} .

Решение:

Мы знаем, что . Тогда $a=genfrac{}{}{}{0}{displaystyle d}{displaystyle sqrt{2}}= 2$ .

Ответ: 2.

Задача 2. Найдите площадь квадрата, если его диагональ равна 1.

Первый способ решения:

Зная связь между стороной и диагональю квадрата (теорема 1), выразим сторону квадрата через его диагональ:

$displaystyle d=sqrt{2}cdot a Rightarrow a=frac{d}{sqrt{2}}Rightarrow a=frac{1}{sqrt{2}}.$

Тогда по формуле площади квадрата:

$displaystyle S=a^{2}=left (frac{1}{sqrt{2}} right )^{2}=frac{1}{2}=0,5.$

Второй способ решения:

Воспользуемся формулой для площади ромба:

$displaystyle S=frac{1}{2}d_{1}d_{2}=frac{1}{2}d^{2}=0,5.$

Ответ: 0,5

Задача 3. Найдите радиус окружности, описанной около квадрата со стороной, равной sqrt{8} .

Решение:

Радиус описанной окружности равен половине диагонали квадрата, поэтому

$displaystyle R=frac{d}{2}=afrac{sqrt{2}}{2}=sqrt{8}cdot frac{sqrt{2}}{2}=2.$

Ответ: 2.

Задача 4. Найдите сторону квадрата, описанного около окружности радиуса .

Решение:

Диаметр окружности равен стороне квадрата: a=2r=8 .

Ответ: 8.

Задача 5. Радиус вписанной в квадрат окружности равен . Найдите диагональ этого квадрата.

Решение:

Сторона квадрата в два раза больше радиуса вписанной окружности:

Диагональ найдем, зная сторону квадрата:

Ответ: 56.

Задача 6. Радиус вписанной в квадрат окружности равен . Найдите радиус окружности, описанной около этого квадрата.

Решение:

Радиус окружности, вписанной в квадрат, равен половине стороны квадрата, а радиус описанной окружности равен половине диагонали квадрата:

$displaystyle r=frac{a}{2}; R=frac{d}{2}; d=asqrt{2}.$

Поэтому

Ответ: 22.

Задача 7. Найдите периметр квадрата, если его площадь равна 9.

Решение:

Найдем сторону квадрата:

Периметр квадрата со стороной 3 равен:

Ответ: 12.

Задача 8. Найдите площадь квадрата, в который вписан круг площадью 4pi .

Решение:

Площадь круга $S_{kp}=pi r^{2}=4pi ,$ откуда радиус круга равен 2.

Сторона квадрата в два раза больше радиуса вписанного круга и равна 4. Площадь квадрата равна 16.

Ответ: 16.

Задача 9. Найдите радиус окружности, вписанной в квадрат ABCD, считая стороны квадратных клеток равными sqrt{2} .

Решение:

Сторону квадрата найдем как диагональ другого квадрата со стороной 2 клеточки. Поскольку длина одной клеточки равна sqrt{2} ., то сторона малого квадрата равна . А сторона квадрата ABCD равна

Радиус вписанной окружности в два раза меньше стороны квадрата и равен 2.

Ответ: 2.

Задача 10. Найдите радиус r окружности, вписанной в четырехугольник ABCD. В ответе укажите .

Решение:

Считаем стороны клеток равными единице. Четырехугольник ABCD — квадрат. Все его стороны равны, все углы — прямые. Как и в предыдущей задаче, радиус окружности, вписанной в квадрат, равен половине его стороны.

Найдем на чертеже прямоугольный треугольник. По теореме Пифагора найдем сторону, например, AB.

Она равна . Тогда радиус вписанной окружности равен $genfrac{}{}{}{0}{displaystyle sqrt{10}}{displaystyle 2}$ . В ответ запишем .

Ответ: 5.

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Квадратu0026nbsp;u0026mdash; определение иu0026nbsp;свойства» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Как понятно из вышеизложенного, у квадрата только две диагонали. Поскольку квадрат является прямоугольником и сохраняет его свойства, то они равны между собой. Рассмотрим различные методы нахождения её длины.

Ещё один способ, который на само деле очень простой. Радиус описанной окружности будем обозначать латинской буквой R, радиус вписанной окружности будем обозначать латинской буквой r.

Сначала разберёмся с описанной окружностью. В данной ситуации её радиус составляет ровно половину диагонали (это нетрудно убедиться с использованием построения), таким образом: R = 1/2*d. отсюда имеем: d = два*R. Снова поясним наши рассуждения на примере. Пусть R = 45 километров. Получим, d = два*45 = 90 километров.

И, наконец, рассмотрим метод, связанный с радиусом вписанной окружности. Опять-таки из построения чётко видно, что диаметр вписанной окружности равняется стороне квадрата. Таким образом, её радиус вдвое меньше стороны. Запишем это в виде формулы: r = 1/2*a. Отсюда следует, a = 2*r. Снова воспользуемся формулой из первого метода, подставим вместо стороны её выражение через радиус вписанной окружности. Выражение примет вид: d = rad2*a = rad2*2*r.

Ещё раз воспользуемся помощью примера. Пусть r = 98 метров. Тогда имеем, d = rad2*2*98 = 196*rad2.

bezdelnik

7 лет назад

Длину d диагонали квадрата по отношению к длине b его стороны находят по теореме Пифагора на основании того, что все стороны квадрата равны и все углы, образованные сторонами квадрата, прямые. Поэтому сумма квадратов двух сторон равна квадрату диагонали, являющейся гипотенузой прямоугольного треугольника: 2b^2=d^2, d= b√2. Если принять сторону квадрата за единицу, то d= √2=1,414… .

автор вопроса выбрал этот ответ лучшим

Степан-16

4 года назад

Диагональ (с) — это гипотенуза треугольника, у которого катеты (а и а, поскольку они равны) — это две стороны квадрата.

Два способа решения.

По теореме Пифагора: диагональ равна квадратному корню из суммы квадратов сторон.
Через формулы тригонометрии. Диагональ квадрата (гипотенуза треугольника) равна отношению стороны квадрата (или треугольника) к величине 0.707, что есть синус (или косинус, который для 45 град равен синусу) угла в 45град. 45 град — это угол между стороной квадрата и его диагональю.

Алиса в Стране

4 года назад

Если поделить квадрат диагональю, то мы увидим перед собой два одинаковых прямоугольных треугольника, а диагональ квадрата будет для любого из этих треугольников гипотенузой. А как рассчитывать длину гипотенузы, зная длину катетов, мы все знаем. Для этого у нас имеется теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов. Катеты у нас равны друг другу (потому что у нас квадрат), значит, обозначив длину катета латинской буквой «а», а длину гипотенузы латинской буквой «с», получаем формулу:

c² = a² + a² = 2 a²

с = √2a.

Ответ: диагональ квадрата равна квадратному корню из суммы квадратов его сторон.

Ксарфакс

4 года назад

Диагональ квадрата представляет собой отрезок, соединяющий две противоположные вершины.

В то же время диагональ разбивает квадрат на 2 равных прямоугольных треугольника.

Таким образом, чтобы найти диагональ квадрата, следует воспользоваться теоремой Пифагора.

a² + b² = c².

Пусть c — это диагональ, a и b — стороны квадрата, которые по определению равны между собой.

Перепишем формулу в виде:

2a² = c².

Выразим диагональ c:

c = √2 * a.

Таким образом, диагональ квадрата равна произведению его стороны на квадратный корень из числа 2.

Пример

Сторона квадрата равна 10 см.

Диагональ будет равна 10 * √2 см ≈ 14 см.

terli4eno4ka

4 года назад

Под диагональю квадрата понимается отрезок, соединяющий противоположные углы квадрата. Для того, чтобы найти диагональ квадрата, можно воспользоваться следующими формулами, для которых нужно знать, чему равна сторона квадрата, площадь или периметр:

К примеру, если у нас есть квадрат со сторонами 100 см, то его диагональ будет по формуле

√2*a = √2*100 = 1,4142*100 = 141,42 см.

Zolotynka

4 года назад

Исходя из того, что, согласно теореме Пифагора, диагональ делит квадрат на два конгруэнтных прямоугольных треугольника, мы можем использовать длину стороны квадрата, чтобы найти длину диагонали (которая будет являться гипотенузой треугольника). Следовательно, d=b√2, где d — длина диагонали, а b — длина одной из сторон.

Например, если длина стороны квадрата 5 сантиметров, то, согласно нашей формуле, длина диагонали будет: d=5√2, или d=5*1,414=7,07.

Длину диагонали можно узнать, если известны, например, площадь или периметр квадрата. В этом случае придется использовать сразу несколько формул.

Так же как и найти гипотенузу у равнобедренного треугольника.

Квадрат это правильная геометрическая фигура, имеющая четыре равных стороны.

Имея в условии слово «квадрат» можно вообще найти его диагональ по одной стороне, ибо все остальные будут равные ёй.

Длину одной из сторон, умножить её на два и возвести в квадрат. Результатом и будет квадрат диагонали.

Alexgroovy

4 года назад

Диагональ квадрата принято рассчитывать, оперируя понятиями сторона, площадь и периметр. Имея эти данные легко воспользоваться формулами для расчета диагонали квадрата.

d = √2 * a,

где a — длина стороны квадрата.

d = √2S,

здесь S — площадь квадрата.

d = P / 2√2,

где P — периметр.

Татьяна-Татьяна

7 лет назад

На основании теоремы Пифагора — сумма квадратов катетов равна квадрату гипотенузы. То есть, если сторона квадрата равна «а», то диагональ его («в») равна корню квадратному из выражения (2a^2).

То есть вот так:

а^2=b^2+b^2

а^2= 2b^2

a=√2b^2

a=b√2

gematogen

6 лет назад

Если взять любой квадрат и принять его сторону за букву — a, то диагональ будет равна √2а.

Это можно вычислить так же по теореме Пифагора, при которой сторона a*a+a*a=2a*a, из этого извлекаем корень и получаем √2а.

Знаете ответ?

Таким образом, мы рассмотрели в статье пять принципиально различных методов вычисления диагонали квадрата. Если, на первый взгляд, задача казалась сложной, то после проведённых нами рассуждений стало очевидно, что особых проблем здесь нет. Сведём все полученные нами формулы в одну таблицу.

Хочется ещё отметить, что с помощью первой из наших формул очень легко построить отрезок, равный корню квадратному из двух. Для этого строим квадрат со стороной единица, его диагональ и будет равняться искомому отрезку.

Если на полученной диагонали мы построим прямоугольник, используя её как длину, а ширину возьмём равной единице, то получим отрезок равный ещё одному иррациональному числу корень квадратный из трёх.

Продолжая нашу цепочку и далее, мы научимся строить отрезки равные любому иррациональному числу.

Источник

Описание, ввод и вывод элементов двумерного массива

Главная и побочная диагональ при работе с двумерными матрицами в Pascal

Диагональ квадрата

Калькулятор расчета диагонали квадрата

Квадрат — определение и свойства

Вам также может понравиться

Как найти дату регистрации самозанятого

Как по фото найти человека или профиль

Как можно найти девушку отдыхать

Добавить комментарий Отменить ответ