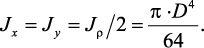Главные оси и главные
моменты инерции
Оси,
относительно
которых центробежный момент инерции
равен нулю, называют главными
осями (иногда
их называют главными
осями инерции). Через
любую точку, взятую в плоскости сечения,
можно провести в общем случае пару
главных осей (в некоторых частных случаях
их может быть бесчисленное множество).
Для того чтобы убедиться в справедливости
этого утверждения, рассмотрим, как
изменяется центробежный момент инерции
при повороте осей на 90′ (рис. б.7). Для
произвольной площадки dA, взятой в первом
квадранте системы осей хОу, обе координаты,
а следовательно, и их произведение
положительны. В новой системе координат
х,Оу„ повернутой относительно
первоначальной на 90′, произведение
координат рассматриваемой площадки
отрицательно. Абсолютное
значение этого
произведения не изменяется, т. е. ху= —
х1у,. Очевидно,
то
же самое имеет место и для любой другой
элементарной площадки. Значит, и знак
суммы dAxy, представляющий собой центробежный
момент инерции сечения, при повороте
осей на 90′ меняется на противоположный,
т. е. J = = — J.
В
процессе поворота осей центробежный
момент инерции изменяется непрерывно,
следовательно,
при некотором положении осей он становится
равным нулю. Эти оси и являются главными.
Хотя
мы и установили, что главные оси можно
провести через любую точку сечения, но
практический интерес представляют
только те из них, которые проходят через
центр тяжести сечения — главные
центральные оси.
В
дальнейшем,
как правило,
для краткости будем называть их просто
главными
осями, опуская
слово «центральные».
В
общем случае сечения произвольной формы
для определения положения главных осей
необходимо провести специальное
исследование. Здесь ограничимся
рассмотрением частных случаев сечений,
имеющих по меньшей мере одну ось симметрии
(рис. 6.8).
П
роведем
через. центр тяжести сечения ось Ох,
перпендикулярную оси симметрии Оу, и
определим центробежный момент инерции
J. Воспользуемся известным из курса
математики свойством определенного
интеграла (интеграл суммы равен сумме
интегралов) и представим J s виде двух
слагаемых:
так
как, для любой элементарной площадки,
расположенной справа от оси симметрии,
есть соответствующая слева, для которой
произведение координат отличается лишь
знаком.
Таким
образом, центробежный момент инерции
относительно осей Ох и Оу оказался
равным нулю, т. е. это главные
оси. Итак,
для
нахождения главных осей симметричного
сечения достаточно найти положение его
центра тяжести. Одной из главных
центральных осей является ось симметрии,
вторая ось ей перпендикулярна. Конечно,
приведенное доказательство остается
в силе, если ось, перпендикулярная оси
симметрии, проходит и не через центр
тяжести сечения, т. е. ось
симметрии и любая, ей перпендикулярная,
образуют систему главных осей.
Нецентральные
главные оси, как уже указывалось, интереса
не представляют.
Осевые
моменты инерции относительно главных
центральных осей называют главными
центральными (или
сокращенно главными) моментами
инерции. Относительно
одной из главных осей момент инерции
максимален, относительно другой —
минимален. Например, для сечения,
изображенного на рис. 6.8, максимальным
является момент инерции J
(относительно
оси Ox). Конечно, говоря об экстремальности
главных моментов инерции, имеют в виду
лишь их сравнение с другими моментами
инерции, вычисленными относительно
осей, проходящих через ту же
точку сечения. Таким
образом, то обстоятельство, что один из
главных моментов инерции максимален,
а другой — минимален, можно рассматривать
как объяснение того, что они (н
соответствующие оси) называются главными.
Равенство же нулю центробежного момента
инерции относительно главных осей —
удобный признак для нх нахождения.
Некоторые типы сечений, например круг,
квадрат, правильный шестиугольник и
др. (рис. 6.9), имеют бесчисленное множество
главных центральных осей. Для этих
сечений любая центральная ось является
главной.
Не
приводя доказательства, укажем, что, в
случае если два главных центральных
момента инерции сечения равны между
собой, у этого сечения любая центральная
ось главная и все главные центральные
моменты инерции одинаковы.
Соседние файлы в папке sopromat_teory_www.baumanka.ru
- #
11.02.2014401 б43readme.htm
- #
11.02.20142.53 Кб52Sopromat.html
- #
- #
- #
- #
- #
- #
Определить главные центральные моменты инерции, осевые моменты сопротивления сечения, составленного из стандартных профилей проката.
Сечение состоит из двух неравнополочных уголков 75×50х5 (маркировка в мм) и швеллера № 16 (№ швеллера говорит о его высоте в см).

- Определим положение центра тяжести сечения.
Сечение симметрично относительно оси у, проводим её как ось – главную и центральную. Координата хС=0. Для нахождения уС проводим случайную ось х′ (выбранную случайным образом). Обозначим центры тяжести всех профилей и выпишем необходимые характеристики профилей из сортамента прокатной стали.
Фигуры 1,2 – уголки 75×50х5

А1=А2=6,11 см2
Iх1= Iх2=34,8 см4
Iу1= Iу2=12,5 см4
Фигура 3 – швеллер №16

А3=18,1 см2,
Iх3=747 см4,
Iу3=63,3 см4.
Покажем на схеме и определим координаты у для профилей
у1 = у2 = у0 =2,39 см,
у1= –z0 =-1,8 см.
Определим координату уС по формуле
 ,
,
где Аi – площадь каждого профиля,
уi – координата.

Проводим главную центральную ось х вниз от оси х′ на 0,11 см, наносим т.С – центр тяжести всего сечения.
2. Определяем главные центральные моменты инерции по формулам перехода:
 ,
,
где Ixi , Iyi — моменты инерции каждой фигуры;
Аi – площадь сечения каждой фигуры;
аi – расстояние от центра тяжести каждой фигуры до главной центральной оси х;
bi – расстояние от центра тяжести каждой фигуры до главной центральной оси у.
Определяем аi (смотрим схему)
а1 = а2 = у1+|уС|= 2,39 + 0,11 = 2,5см,
а3= — (|у3|-|уС|) = -1,69см.
Определяем Iх. Следует обратить внимание на то, что фигура 3 – швеллер – повернут, поэтому, для определения Iх следует из сортамента взять Iу швеллера.
Iх3=63,3см4

Определяем Iу. Для швеллера (повернут) Iу3 = Iх = 747см4.
Определим размеры bi, показываем на схеме.
b1= –х0 = -1,17см,
b2= х0 = 1,17см,
b3=0, т.к. центр тяжести швеллера лежит на оси у.
 3. Определим осевые моменты сопротивления сечения по формулам:
3. Определим осевые моменты сопротивления сечения по формулам:

Из схемы видно ,что

Тогда

Определить главные центральные моменты инерции сечения геометрической формы.

- Определим положение центра тяжести сечения.
Сечение симметрично относительно оси у, поэтому нанесем ось у – ось, на которой находится центр тяжести всего сечения. Координата хС=0, значит, следует определить координату уС.
Выберем случайную ось х′ — внизу сечения.
Разобьем сечение на простые фигуры:
фигура 1 – прямоугольник с основанием 8 см и высотой 6 см, отмечаем центр тяжести прямоугольника – т. С1
фигура 2 – равнобедренный треугольник с основанием 8 см и высотой 3 см, отмечаем его центр тяжести – т. С2.
Теперь вычислим площади каждой фигуры и определим координаты у каждой фигуры, затем координаты нанесем на схему
Прямоугольник

Треугольник

Теперь определим координату центра тяжести всего сечения по формуле:

Тогда

Отмечаем уС на схеме, центр тяжести всего сечения – т.С — и проводим через эту точку главную центральную ось х.
По формулам перехода определяем главные центральные моменты инерции сечения:
 ,
,
где Ixi , Iyi — моменты инерции каждой фигуры;
Аi – площадь сечения каждой фигуры;
аi – расстояние от центра тяжести каждой фигуры до главной центральной оси х;
bi – расстояние от центра тяжести каждой фигуры до главной центральной оси у.
Фигура 1 – прямоугольник

Расстояние а1 от С1 до оси х покажем на схеме. Из схемы видно, что а1=- ( уС – у1 )= -0,8 см. Так как С1 находится на оси у, то b1=0.
Фигура 2 – треугольник

Находим а2 = у2 – уС = 7 — 3,8= 3,2 см, отмечаем на схеме.
b2=0, т.к. С2 находится на оси у.
Подставляем значения в формулы перехода и определяем:
— главный центральный момент инерции сечения относительно оси х
![]()
— главный центральный момент инерции сечения относительно оси у
![]()
Таким образом,

Для заданного поперечного сечения, состоящего из швеллера и равнобокого (равнополочного) уголка требуется определить главные центральные моменты инерции

1) Вычерчиваем сечение в масштабе.
2) Разбиваем на простейшие фигуры:
1. Швеллер №30 (пользуемся сортаментом прокатных профилей):
![]()
2. Уголок ![]() :
:

3) В каждой фигуре найти собственный центр тяжести С1 и С2 ,провести собственные оси.
4) Выбрать вспомогательные оси ![]() .
.
5) Относительно вспомогательных осей определить центр тяжести всей фигуры:

Через найденный центр тяжести проводим центральные оси.
6) Находим моменты инерции всей фигуры относительно центральных осей, используя формулы перехода между параллельными осями
При определении центробежного момента инерции следует помнить ,что если фигура имеет хотя бы одну ось симметрии, то эта ось является главной, вторая ось, перпендикулярная ей, тоже главная. Центробежный момент относительно главных осей равен 0. Таким образом, для швеллера ![]()
Для уголка ![]() см4, знак зависит от расположения уголка (см. Таблицы «Знак центробежного момента для уголков»). В нашем случае он положительный.
см4, знак зависит от расположения уголка (см. Таблицы «Знак центробежного момента для уголков»). В нашем случае он положительный.

Здесь: аi – расстояния между центральной осью Х и собственным центром тяжести каждой фигуры,
bi – расстояние между центральной осью Y и собственным центром тяжести каждой фигуры
Как видим из вычислений, центробежный момент инерции сечения ![]() значит, центральные оси Х;Y не являются главными!
значит, центральные оси Х;Y не являются главными!
7) Определим положение главных осeй через угол α0:

Знак «-» означает, что надо повернуть оси Х, У по часовой стрелке.
8) Определим главные моменты инерции сечения
 9) Проверка: Сумма моментов инерции относительно любых двух взаимно перпендикулярных осей есть величина постоянная:
9) Проверка: Сумма моментов инерции относительно любых двух взаимно перпендикулярных осей есть величина постоянная:

Проверка выполняется.
Найти главные центральные моменты инерции.

- Подготовка исходных данных.
Из сортамента выписываем:
— для двутавра №10:

— для швеллера №20:

Нумеруем составные части, показываем их центры тяжести (С1, С2, С3) и собственные центральные оси каждой из них (х1,у1; х2,у2; х3,у3).
2. Поскольку сечение имеет одну ось симметрии, то она – одна из главных центральных (у0). Найдем положение центра тяжести на этой оси. Для этого выберем вспомогательную ось х‘, перпендикулярную оси симметрии, и реализуем формулу:
которая и определит расстояние от оси х‘ до искомого центра тяжести.
Тогда А=А1+А2+А3=2×20+14,3+28,83=83,15 см2,

тогда

Показываем на схеме центр тяжести «С» и проводим вторую главную центральную ось х0.
Ординаты собственных центров тяжести простых фигур в системе главных центральных осей:

3. Вычисляем главные центральные моменты инерции![]()

Итак,

Определить главные центральные моменты инерции сечения.
Составные простые части сечения: прямоугольник 100×60см (I), полукруг r=30см (IIи III), треугольник 100×30см (IV).

Вертикальная ось симметрии у0 является одной из главных центральных осей.
- Найдем положение центра тяжести сечения на оси симметрии. Для этого выберем вспомогательную ось х‘, перпендикулярную оси симметрии. Пусть она совпадает с осями: х1, х2, х3
.
Общая площадь А = А1 — А2 — А3 + А4 = 6000 – 1415 – 1415 + 1500 = 4670см2.
Статический момент относительно вспомогательной оси х‘:

Тогда
значит, центр тяжести сечения располагается на 12,8см выше вспомогательной оси х‘.
2. Вычисляем осевые моменты инерции ![]()
Они и будут главными центральными моментами инерции сечения.

Здесь применялись формулы:

Найти главные центральные моменты инерции сечения, состоящего из листа 40×2см и двух уголков №14/9.

Исходные данные из сортамента для неравнобокого уголка №14/9.

Сечение имеет одну ось симметрии. Она – одна из главных центральных. Обозначаем её х0. Чтобы показать вторую главную центральную ось, надо найти положение центра тяжести на оси симметрии:

Выбираем вспомогательную ось у‘, перпендикулярную к оси симметрии и вычисляем статический момент сложного сечения относительно этой оси:

Проводим главную центральную ось у0 через найденный центр тяжести.
Вычисляем непосредственно главные центральные моменты инерции:

Таким образом,

Требуется найти главные центральные моменты инерции.

Сечение имеет две оси симметрии. Следовательно, центр тяжести совпадает с точкой пересечения этих осей, а сами они оказываются главными центральными осями.
Остается лишь вычислить осевые моменты инерции относительно осей х0 и у0.
«Разбиваем» сечение на простые фигуры: прямоугольник 6×8см и два круга r=1см. Тогда:

Итак
,
Требуется определить величины главных центральных моментов инерции.
Сечение имеет одну ось симметрии.

На основании первого признака главных осей для симметричных сечений можно утверждать, что ось симметрии является одной из главных центральных осей. Обозначаем ее «у0». Значит, вторая главная центральная ось, перпендикулярная оси симметрии, должна проходить через центр тяжести сечения.
Следовательно, нам достаточно только найти положение центра тяжести на оси симметрии, а для этого необходимо вычислить одну лишь координату его по формуле:
С этой целью выбираем вспомогательную ось х‘, «разбиваем» сложное сечение на прямоугольник со сторонами 10 и 4см и треугольник с основанием 4см и высотой 3см.
Тогда:
Проводим через найденный центр тяжести вторую главную центральную ось х0.
Расстояние между осями х1 и х0: а1=5 — 4,3 =0,7см, а расстояние между осями х2 и х0: а2=10 – 1 — 4,3 = 4,7см.
Таким образом, положение главных центральных осей найдено, осталось вычислить величины главных центральных моментов инерции:

х‘, у‘ – вспомогательные оси при определении положения центра тяжести сечения,
Sх’, Sу’ – статические моменты относительно вспомогательных осей,
хс, ус – координаты центра тяжести сечения, а также и обозначение случайных (т.е. не главных) центральных осей,
х0, у0 – главные центральные оси,
α0 – угол поворота главных центральных осей от случайных центральных осей хс и ус,
![]() , — главные центральные моменты инерции,
, — главные центральные моменты инерции,
сi – центры тяжести отдельных фигур, из которых состоит сечение сложной формы,
хi, уi – собственные центральные оси отдельных фигур, а также и координаты центров тяжести отдельных фигур в системе вспомогательных осей х‘, у‘,
аi, вi – расстояния между собственными центральными осями отдельных фигур хi, уi и случайными центральными осями всего сечения хс, ус.
Требуется определить положение главных центральных осей и величины главных центральных моментов инерции.
Сечение имеет сложную форму, состоит их 4х простых фигур:
I – швеллера №30а,
II – прямоугольника 2×40см,
III – двутавра №20а,
IV – равнобокого уголка №12 (d=10мм).
Всё начинается с подготовки исходных данных. С этой целью необходимо сделать выписки из таблиц Сортамента прокатных сечений (см. рубрику «Таблицы»).

Этап 0. Подготовительный
Фигура I. Швеллер №30а

Фигура II – прямоугольник 2×40см, В сортаменте прокатной стали этой фигуры нет, поскольку все геометрические характеристики ее свободно вычисляются
Фигура III. Двутавр №20а.

Фигура IV. Равнобокий уголок №12 (d=10мм).

Пользуясь данными сортамента, на схеме сечения, вычерченной в достаточно крупном масштабе, показываем положение центров тяжести каждой из фигур и собственные центральные оси хi, уi.
Этап 1. Определение положения центра тяжести сечения. Сечение не имеет осей симметрии. Поэтому придётся определять две координаты центра тяжести, используя формулы:

Для реализации этих формул выбираем вспомогательные оси х‘ и у‘ (см.схему сечения).
Площади отдельных фигур: А1=43,89см2, А2=2×40=80см2,
А3=35,5см2, А4=23,3см2.
Координаты центров тяжести отдельных фигур:
Площадь всего сечения А=182,7см2.

Тогда координаты собственных центров тяжести отдельных фигур в системе случайных центральных осей хс, усбудут:
а1=2,66см, b1=-7,5см
а2=-2,34см, b2=-1,93см
а3=-7,34см, b3=9,07см
а4=14,33см, b4=2,4см.
Этап 2. Определение моментов инерции относительно случайных центральных осей хс, ус.

Справочные сведения о знаке собственного центробежного момента инерции уголка (равнобокого и неравнобокого):

Справочные сведения для определения собственного центробежного момента инерции неравнобокого уголка:

Этап 3. Определение положения главных центральных осей

Положительный угол α0 соответствует повороту против часовой стрелки главных осей относительно случайных (см.схему).
Этап 4. Определение величин главных центральных моментов инерции

Правило: Ось с максимальным главным моментом инерции «тяготеет» к более тяжелой случайной оси. Поэтому в нашем случае:
![]()
тогда ![]()
Проверки.
- Выполнение закона суммы осевых моментов инерции.
Для этого сравним
.
получаем:
![]()
Разница в последней цифре дает незначительную погрешность <<5%, что вполне допустимо в инженерных расчетах.
2. Проверка правильности вычислений.
Суть ее в том, что если все сделано правильно, то центробежный момент инерции сечения относительно найденных нами главных осей должен равняться нулю.

Подставляя сюда ![]() и sin13˚20’=0,2306, cos13˚20’=0,9730,имеем
и sin13˚20’=0,2306, cos13˚20’=0,9730,имеем

погрешность составляет:

И эта проверка выполняется.
Лекция 4. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ СТЕРЖНЯ
Математические определения геометрических характеристик плоских
фигур: статические моменты, осевые моменты инерции и центробежный,
полярный момент инерции. Центральные оси. Главные оси. Определение
положения центра тяжести элементарных сечений и составленного из
элементарных фигур. Нахождение геометрических характеристик сечений
относительно центральных осей.
Различают следующие характеристики сечений: площадь А, статические
моменты площади, моменты инерции площади, центробежный момент инерции
площади.
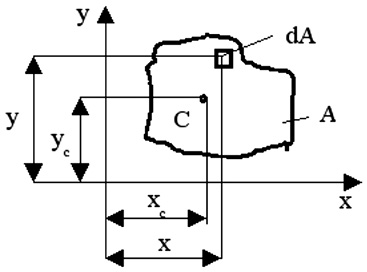
Рис. 10. Площадь А в системе координат х, у
Под статическим моментом площади относительно некоторой оси
понимается сумма произведений площадей элементарных площадок на
расстояния от их центра тяжести до соответствующей оси:
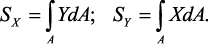
Определение центра тяжести сечения. Статические моменты сечения
относительно осей проходящих через центр тяжести равны нулю, поэтому их
используют для определения координат центров тяжести сечения. Для этого
проводят вспомогательные оси x и y и координаты центра тяжести сечения
определяют по зависимостям:
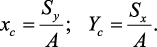 (3)
(3)
Моменты инерции сечения. Осевым моментом инерции сечения I
называется интеграл по площади произведения элементарной площадки на
квадрат расстояния до оси. Осевые моменты инерции сечения относительно
осей x и y будут соответственно равны
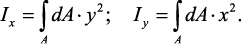 (4)
(4)
Полярным моментом инерции сечения Iρ называется интеграл по
площади произведения элементарной площадки на квадрат расстояния до
начало координат.
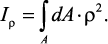 (5)
(5)
Учитывая, что ρ2 = x2 + y2, получаем Iρ = Ix + Iy.
Полярный момент инерции сечения равен сумме осевых моментов инерции сечения.
Оси, относительно которых центробежный момент инерции равен нулю,
называются главными центральными осями, осевые моменты инерции
относительно их принимают свои экстремальные значения (максимум
и минимум).
Полярный момент инерции
Jρ = Jx + Jy;, (6)
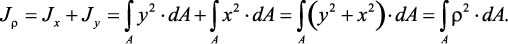
Полярный момент инерции относительно данной точки – сумма
произведений элементарных площадей dA на квадраты их расстояний
(ρ2 = y2 + z2) до этой точки, взятая по всей площади сечения А.
Моменты сопротивления. Осевой момент сопротивления относительно
рассматриваемой оси – величина равная моменту инерции относительно той
же оси отнесенному к расстоянию до наиболее удаленной от этой оси точки
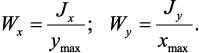
Полярный момент сопротивления
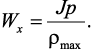
Осевой и полярный моменты сопротивления имеют размерность м3.
Радиус инерции
Радиусом инерции сечения относительно некоторой оси, называется величина, определяемая из соотношения:
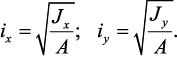
Вычисление геометрических характеристик простых фигур.
Прямоугольное сечение.
Определим осевой момент инерции прямоугольника относительно оси х.
Разобьем площадь прямоугольника на элементарные площадки
с размерами b (ширина) и dy (высота) (рис. 11). Тогда площадь такого
элементарного прямоугольника (заштрихована)равна dA = b•dy. Подставляя
значение dA в формулу для определения осевого момента инерции, получим:
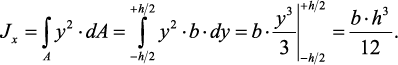
По аналогии запишем
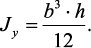
Круглое сечение
Вначале целесообразно найти полярный момент инерции. Затем,
учитывая, что для круга Jx = Jy, а Jρ = Jx + Jy, найдем Jx = Jy = Jρ/2.
Разобьем круг на бесконечно малые кольца толщиной dρ и радиусом ρ
(рис. 12); площадь такого кольца 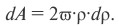 . Подставляя выражение для
. Подставляя выражение для
площади кольца в выражение для Jρ и интегрируя, получим:
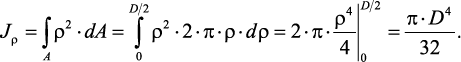
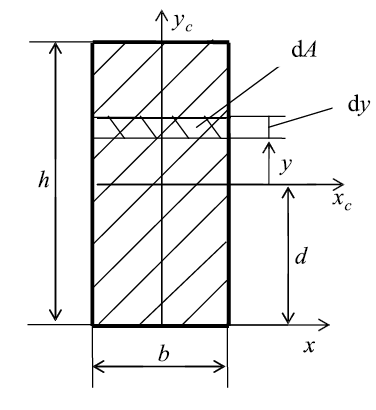
Рис. 11. Прямоугольник
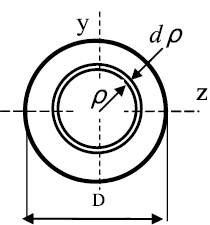
Рис. 12. Круг
Тогда