Как найти главный диаметр

Как найти главный диаметр

Определение
14.1. Направление
ненулевого вектора 

 называется
сопряженным с направлением ненулевого
вектора 

 относительно
кривой второго порядка, заданной
уравнением 

,
если выполняется равенство

или
в эквивалентной форме

Так
как 

,
то понятие сопряженности направлений
является взаимным (т.е. если
направление вектора 

сопряжено
с направлением вектора 

, то
направление вектора 

 сопряжено
с направлением вектора 

 ).

Отметим
далее, что сопряженные диаметры
центральной кривой второго порядка
имеют сопряженные направления.

Заметим
также, что асимптотическое направление
является самосопряженным
направлением.

Определение
14.2. Направление
ненулевого вектора 

 называется
особым относительно кривой второго
порядка, заданной уравнением 

,
если оно сопряжено с направлением любого
вектора 

.

Ясно,
что для того чтобы направление
вектора 

 было
особым, необходимо и достаточно, чтобы
одновременно выполнялись равенства

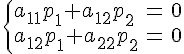
Поскольку
система двух однородных уравнений с
двумя неизвестными имеет нетривиальное
решение тогда и только тогда, когда ее
определитель 

,
то особые направления могут быть только
у кривых параболического типа
(нецентральные кривые). Далее при 

 уравнения
системы пропорциональны, и поэтому
определяют единственное (с точностью
до пропорциональности) нетривиальное
решение 

.
Поскольку отношение 

 характеризует
(см. главу 10) асимптотическое направление
параболической кривой, то тем самым
доказано, что любая кривая параболического
типа имеет единственное особое
направление, совпадающее с ее
асимптотическим направлением.

Определение
14.3. Направление
называется главным относительно данной
кривой второго порядка, если оно сопряжено
с перпендикулярным направлением.

Так
как понятие сопряженности является
взаимным, то если данное направление
является главным, то и перпендикулярное
к нему — главное. Отметим также, что для
любой нецентральной линии особое
направление является главным, а значит
и перпендикулярное к нему — главное.

По
определению ненулевой вектор 

 является
вектором главного направления относительно
кривой второго порядка, заданной
относительно ПДСК, тогда и только тогда,
когда векторы 

 и 

 сопряжены.
Используя 

,
получаем равенство, позволяющее найти
главные направления:

Выясним,
сколько главных направлений имеется
относительно той или иной кривой второго
порядка. Рассмотрим следующие случаи.

1. 

.
В этом случае 

.
Поэтому если положить 

,
то уравнение 

 запишется
так:

Это
квадратное уравнение имеет два различных
действительных корня:

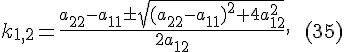
причем 

.
Отсюда следует, что в этом случае
относительно данной кривой имеется два
и только два главных направления.

Замечание
14.1. Используя
равенство 

,
можно находить угловые коэффициенты
главных направлений относительно кривой
второго порядка, в случае если в
уравнении 

 коэффициент 

.

2. 

.
Уравнение 

 принимает
вид

 или 

.

И
в этом случае имеется два главных
направления, совпадающих с направлением
координатных осей.

3. 

.
Ясно, что координаты любого
вектора 

 удовлетворяют
равенству 

,
поэтому любое направление является
главным (в этом случае данная кривая
является окружностью).

Итак
доказана

ТЕОРЕМА
14.1. Относительно
любой линии второго порядка, отличной
от окружности, существует два и только
два главных направления. Относительно
окружности любое направление является
главным.

Определение
14.4. Диаметр
называется главным, если он сопряженным
с перпендикулярным ему направлением,
т. е. если он перпендикулярен некоторому
главному направлению.

Так
как любой диаметр проходит через середины
хорд сопряженного направления, то любой
главный диаметр кривой второго порядка
является ее осью симметрии.

Обратное
вообще говоря неверно (например, две
взаимно перпендикулярные прямые).

Далее,
ясно, что направление
любого главного диаметра является
главным.

Обратное
также, вообще говоря, неверно. Действительно
для параболических линий все диаметры
имеют особое

(асимптотическое)
направление, но существует главное
направление, которое неасимптотично,
а потому не может быть направлением
никакого диаметра.

Для
вырожденных параболических линий (пара
параллельных прямых) существует только
один диаметр (прямая центров) и поскольку
перпендикулярное к нему направление
является главным, он является главным
диаметром. Для парабол также существует
только один главный диаметр, а именно,
диаметр сопряженный с главным
неасимптотическим направлением.

Для
центральных кривых, отличных от
окружности, существует два главных
диаметра, каждый из которых сопряжен с
направлением другого (и потому ему
перпендикулярен).

Таким образом,
справедлива

ТЕОРЕМА
14.2. Центральная
кривая второго порядка, отличная от
окружности, имеет два и только два
главных диаметра.

Нецентральная
кривая второго порядка имеет только
один главный диаметр.

Мы
знаем, что для нецентральных кривых
второго порядка главный диаметр сопряжен
с направлением, перпендикулярным
единственному асимптотическому
направлению (см. выше), т.е. характеризующимся
отношением

Следовательно,
чтобы получить уравнение главного
диаметра, следует в уравнении 

 положить
либо 

,
либо 

 .
Получим либо

либо

Таким
образом, уравнение главного диаметра
параболической линии может быть записано
либо в виде 

,
либо в виде 

.

Замечание
14.2. Уравнением 

 пользуемся
если 

,
а уравнением 

,
если 

.
Когда оба уравнения имеют смысл, они
равносильны. В случае, когда рассматриваемая
линия является параболой, ее главный
диаметр является ее осью. Следовательно,
для параболы уравнения 

 и 

 являются
уравнениями ее оси. В случае вырожденной
параболической линии из условий 

 легко
вытекает, что уравнения 

 и 

 приобретают
вид

соответственно.
Каждое из этих уравнений является прямой
центров.

Теперь
можно без труда охарактеризовать
прямоугольную систему координат, в
которой уравнение данной линии имеет
канонический вид:

Осью
абсцисс этой системы является главный
диаметр (единственный главный диаметр
для нецентральных кривых

и
любой из двух главных диаметров для
центральных кривых).

Осью
ординат этой системы является для
центральных кривых другой главный
диаметр, а для нецентральных кривых —
прямая, перпендикулярная главному
диаметру и проходящая (в случае параболы)
через точку пересечения кривой с главным
диаметром, а в случае вырожденной кривой
произвольная.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Рассмотрим все прямые, имеющие одно и то же неасимптотическое направление на каждой из этих прямых возьмем в качестве точки середину хорды, высекаемой из этой прямой кривой

Эти точки (координаты теперь уже переменные!) удовлетворяют уравнению (§ )

т. е.

которое, группируя по-новому его члены, переписываем в виде

Это уравнение есть уравнение некоторой прямой d, на которой и лежат середины всех хорд данного неасимптотического направления (рис. 173). Прямая d называется диаметром кривой (1), сопряженным направлению

Центр (или центры, если их много) кривой (1), очевидно, удовлетворяет уравнению (2), каково бы ни было направление и поэтому лежит на любом диаметре кривой (1).

Только что данное определение диаметра имеет силу для любой кривой второго порядка (как центральной, так и параболической).

При этом направляющим вектором диаметра, сопряженного направлению является вектор где .

Пусть теперь (1) – центральная кривая. Возьмем какую-нибудь прямую d неасимптотического направления, проходящую через единственный центр ) кривой (1); уравнение прямой d записывается в виде

где удовлетворяют уравнениям центра, т. е. уравнениям (6) предыдущего параграфа.

Рис. 173.

Мы ищем направление для которого прямая d была бы сопряженным диаметром, и решаем для этого уравнения

Уравнения эти решаются однозначно (так как по предположению ) и позволяют переписать (3) в виде

что представляет лишь другую запись уравнения (2).

В самом деле, переписываем (4) в виде

Но ввиду уравнений центра, которым удовлетворяют числа правая часть равенства (4) есть т. е. (4) принимает вид (2).

Итак, всякая прямая d неасимптотического направления, проходящая через (единственный) центр центральной кривой второго порядка, есть диаметр, сопряженный некоторому вполне определенному направлению

Посмотрим, что дает уравнение (2) в случае, когда направление асимптотическое. Тогда уравнение (2), тождественное уравнению (2), есть уравнение асимптоты (см. § 5, замечание). Таким образом, естественно считать асимптоту диаметром, сопряженным своему собственному направлению (хотя при этом первоначальный, наглядно геометрический смысл диаметра, сопряженного данному направлению, утрачивается, так как хорд асимптотического направления не существует).

Теперь диаметры центральной кривой второго порядка могут быть определены просто как прямые, проходящие через центр данной кривой.

Замечание. Из сказанного выше следует, что если направление данного диаметра неасимптотическое, то и направление, ему сопряженное, также неасимптотическое.

Источник
643 Составить уравнение диаметра
эллипса , проходящего через
середину его хорды, отсекаемой на прямой . 644 Составить
уравнение хорды эллипса , проходящей
через точку А(1; -2) и делящейся ею пополам. 645 Составить
уравнения двух взаимно сопряженных диаметров
эллипса , из которых один образует
с осью Ох угол 450. 646 Составить
уравнения двух взаимно двух взаимно сопряженных
диаметров эллипса , из которых один
параллелен прямой . 647 Составить
уравнения двух взаимно сопряженных диаметров
эллипса , из которых один
перпендикулярен к прямой . 648 На чертеже
изображен эллипс. Пользуясь циркулем и линейкой,
построить его центр. 649 Доказать, что оси
эллипса являются единственной парой его главных
диаметров. 650 Пользуясь
свойствами сопряженных диаметров, доказать, что
каждый диаметр окружности является главным.
651 а). В эллипс вписан
равнобедренный треугольник так, что его вершина
совпадает с одной из вершин эллипса. Доказать,
что основание этого треугольника параллельно
одной из осей эллипса; б). Доказать, что стороны
прямоугольника вписанного в эллипс,параллельны
осям этого эллипса; в). На чертеже изображен
эллипс. Пользуясь циркулем и линейкой, построить
его главные диаметры.
652 Доказать, что хорды
эллипса, соединяющие его произвольную
произвольную точку с концами любого диаметра
этого эллипса, праллельны паре его сопряженных
диаметров.
653 а). Доказать, что
сумма квадратов двух сопряженных полудиаметров
эллипса есть величина постоянная (равная сумме
квадратов его полуосей), б). Доказать, что площадь
параллелограмма, построенного на двух
сопряженных полудиаметрах эллипса, есть
величина постоянная (равная площади
прямоугольника, построенного на его полуосях).
654 Составить
уравнение диаметра гиперболы , походящего
через середину ее хорды, отсекаемой на прямой .
655 Дана гипербола . Составить уравнение ее хорды,
которая проходит через точку А(3; -1) и делится
точкой А пополам.
656 Составить
уравнениядвух сопряженных диаметров гиперболы , из которых один проходит через точку
А(8; 1).
657 Составить
уравнения сопряженных диаметров гиперболы , угол между которыми равен 450.
658 На чертеже
изображена гипербола. Пользуясь циркулем и
линейкой, построить ее центр.
659 Доказать, что оси
гиперболы являются единственной парой ее
главных диаметров.
660 На чертеже
изображена гипербола. Пользуясь циркулем и
линейкой, построить ее главные диаметры.
661 Составить
уравнение диаметра параболы , проходящего
через середину ее хорды, отсекаемой на прямой .
662 Дана парабола . Составить уравнение ее хорды,
которая проходит через точку А(2; 5) и делится
точкой А пополам.
663 Доказать, что ось
параболы является единственной ее главным
диаметром.
664 На чертеже
изображена парабола. Пользуясь циркулем и
линейкой, построить ее главный диаметр.
Источник

Общая теория линий второго порядка

Подобный материал:

  • Дифференциальные эллиптические уравнения второго порядка. Слабое решение. Обобщенное, 106.04kb.
  • Календарный план лекций по курсу «методы математической физики» Число недель, 26.17kb.
  • Б. Д. Плющенков 1/2 года I. Общая теория дифференциального уравнения (нелинейного), 16.96kb.
  • § 23. Центр линии второго порядка, 35.02kb.
  • Векторы. Линейные операции над векторами. Скалярное произведение векторов. Векторное, 8.22kb.
  • Решение дифференциального уравнения первого и второго порядка методом Рунге-Кутта 4-го, 55.71kb.
  • Лекция №5 «Боровская теория водородоподобного атома», 181.56kb.
  • Программа Курса «Высшая математика» для специальности 033300 Безопасность жизнедеятельности, 53.79kb.
  • Метод прогонки решения краевой задачи для обыкновенного дифференциального уравнения, 49.69kb.
  • Институт философии ра н постоянный семинар исследовательской группы по прикладной философии, 303.41kb.

^ ГЛАВНЫЕ НАПРАВЛЕНИЯ. ГЛАВНЫЕ ДИАМЕТРЫ.

Определение

. Направление называется главным относительно линии второго порядка, если оно сопряжено с перпендикулярным направлением.

Раз речь идёт о перпендикулярности, то линия должна быть задана своим уравнением вида (1) в ПДСК!

Критерий главного направления относительно линии второго порядка:

Ненулевой вектор () задаёт главное направление относительно линии второго порядка, заданной в уравнением (1),

(9).

Такое аналитическое условие получается исходя из двух фактов:

1) ()(-); 2) условие сопряжённости двух направлений.

Ясно, что если задаёт главное направление относительно линии второго порядка, то и перпендикулярный ему вектор также задаёт главное направление относительно этой линии.

Теорема.

Относительно любой линии второго порядка, отличной от окружности, существует два и только два главных направления. Относительно окружности любое направление является главным.

Определение

. Диаметр линии второго порядка называется главным, если он перпендикулярен сопряженным хордам.

Обсудить

:

1. Для эллипса, гиперболы и параболы, заданных каноническими уравнениями, найдите главные направления.

(Оси координат имеют главные направления!)

2. Может ли асимптотическое направление совпадать с главным?

(Да, для нецентральных линий это так: легко показать, используя критерий асимптотического направления нецентральной линии.)

3. . Если d – главный диаметр, какому направлению он сопряжён?

(Главному, но не асимптотическому.)

4. Верно ли, что главный диаметр является осью симметрии линии второго порядка?

(Верно, это следует из определения).

Верно ли, что ось симметрии всегда является главным диаметром?

(Нет, для пары параллельных прямых это не так.)

Почему любая линия второго порядка имеет хотя бы одну ось симметрии?

5. Как написать уравнение главного диаметра?

(Найти главные, но не асимптотические направления; записать уравнения диаметров, сопряжённых этим направлениям.)

Заполняем таблицу!

ЗАДАЧИ

.

1.(946) Для линии определите, сколько существует главных диаметров. Напишите уравнения главных диаметров.

(Линия параболического типа, поэтому существует один главный диаметр с уравнением 2х – 4у – 5 = 0)

2.Найдите ось и вершину параболы .

(4х + 4у + 3 = 0, А())

Домашнее задание

.

[1] №№ 946 (в, г), 947 (в, г), 949, 952, 954; Шпаргалка

^ ВОПРОСЫ ДЛЯ ПРОВЕДЕНИЯ ОТЧЁТА (ЗАЧЁТА)

ПО ОБЩЕЙ ТЕОРИИ ЛИНИЙ ВТОРОГО ПОРЯДКА.

  1. Приведите примеры линий второго порядка, которые:

а) не имеют асимптотических направлений;

б) имеют одно асимптотическое направление;

в) имеют два асимптотических направления;

г) имеют более двух асимптотических направлений.

  1. Приведите примеры линий второго порядка, которые имеют прямые асимптотического направления:

а) пересекающие линию только в одной точке;

б) пересекающие линию только в двух точках;

в) содержащиеся в линии;

г) не пересекающие линию.

  1. Сформулируйте критерий того, что является вектором асимптотического направления относительно линии второго порядка.
  2. Как по общему уравнению линии второго порядка определить, сколько асимптотических направлений существует относительно этой линии?
  3. Может ли не иметь асимптотических направлений линия второго порядка, для коэффициентов из общего уравнения которой выполняется условие:

а) ; б) и ?

  1. Сколько асимптотических направлений существует относительно линии второго порядка, если члены второй степени xy+ из её общего уравнения образуют полный квадрат?
  2. Какой вид имеет общее уравнение линии второго порядка, для которой

а) ось Ох имеет асимптотическое направление;

б) ось Оу имеет асимптотическое направление;

в) Ох и Оу – прямые асимптотического направления?

  1. Может ли линия второго порядка: а) иметь асимптоты и не иметь асимптотических направлений; б) иметь асимптотические направления и не иметь асимптоты?
  2. Как, зная общее уравнение линии второго порядка, определить координаты центра этой линии?
  3. Сколько центров может иметь линия второго порядка? Приведите примеры линий второго порядка:

а) имеющих только один центр;

б) имеющих только два центра;

в) имеющих бесконечно много центров;

г) не имеющих центров.

  1. Центром линии второго порядка является начало координат. Как это отражается на коэффициентах в уравнении этой линии?
  2. Может ли не иметь центров линия второго порядка, относительно которой:

а) не существует асимптотических направлений;

б) существует два асимптотических направления?

  1. Может ли центр линии второго порядка принадлежать этой линии?
  2. Существуют ли линии второго порядка, у которых:

а) нет центра и имеются две взаимно перпендикулярные оси симметрии;

б) есть три центра, не лежащие на одной прямой;

в) каждая точка линии является её центром?

  1. Докажите, что если линия второго порядка имеет две непараллельные асимптоты, то точка их пересечения есть центр этой линии.
  2. Существует ли параллелограмм, все вершины которого лежат на некоторой параболе?
  3. Дано общее уравнение линии второго порядка, имеющей вещественные точки. Как определить вид этой линии?
  4. Назовите все линии второго порядка, которые:

а) не имеют особых точек;

б) имеют только одну особую точку;

в) имеют только две особые точки;

г) имеют более двух особых точек.

  1. Как по общему уравнению линии второго порядка определить координаты особой точки этой линии?
  2. Почему касательную к линии второго порядка не определяют в особой точке?
  3. Запишите уравнение касательной к линии второго порядка в обыкновенной точке ).
  4. Существуют ли линии второго порядка, у которых касательная имеет асимптотическое направление?
  5. Почему в определении диаметра линии второго порядка рассматривается вектор не асимптотического направления?
  6. Запишите уравнение диаметра линии второго порядка, заданной общим уравнением. Объясните, почему это уравнение является уравнением прямой.
  7. Любая ли линия второго порядка имеет хотя бы один диаметр? Почему?
  1. Что можно сказать о диаметрах:

а) линий второго порядка, имеющих прямую центров;

б) центральных линий второго порядка;

в) нецентральных линий второго порядка?

  1. У каждой ли линии второго порядка есть сопряженные диаметры? Почему?
  2. Верно ли, что сопряженные диаметры линии второго порядка имеют сопряженные направления?
  3. Сколько направлений сопряжено направлению вектора , если

а) задаёт не асимптотическое направление;

б) – вектор асимптотического направления относительно центральной линии;

в) – вектор асимптотического направления относительно нецентральной линии второго порядка?

  1. Сколько общих диаметров могут иметь:

а) эллипс и гипербола;

б) эллипс и парабола;

в) две параболы;

г) парабола и пара параллельных прямых?

  1. В тех случаях, когда возможно, постройте общий диаметр двух линий второго порядка и :

а)

..

б)

в)

г)

д)

е)

ж)

  1. Изобразите прямую, содержащую ту хорду, для которой точка М является серединой:

М

  1. Направления осей координат сопряжены относительно линии второго порядка. Как это скажется на общем уравнении этой линии?
  2. Сколько главных направлений может существовать относительно линии второго порядка?
  3. Что можно сказать о главных направлениях линии второго порядка, заданной каноническим уравнением?
  4. Может ли главное направление линии второго порядка совпадать с её асимптотическим направлением?
  5. Почему главный диаметр является осью симметрии линии второго порядка? Верно ли, что ось симметрии линии второго порядка является главным диаметром этой линии?
  6. Сколько главных диаметров может иметь линия второго порядка?
  7. Почему любая линия второго порядка имеет хотя бы одну ось симметрии?
  8. Как, зная общее уравнение линии второго порядка, написать уравнение главного диаметра этой линии?
  9. Дано изображение линии второго порядка γ. В каждом из случаев а)-в) изобразите такую ПДСК ,чтобы в этой системе координат линия γ задавалась общим уравнением, в котором:

а) ;

б) ;

в) =

а) б) в)

^ КОНТРОЛЬНАЯ РАБОТА ПО ТЕОРИИ ЛИНИЙ ВТОРОГО ПОРЯДКА

(Задачи повторяются!)

ВАРИАНТ 1

    1. Напишите уравнение множества всех точек плоскости (в ПДСК), для каждой из которых абсолютное значение разности расстояний до точек А(0, -2) и В(0, 2) равно 3.
    2. Напишите уравнение общего диаметра линий второго порядка, заданных уравнениями х2 + 2ху + у2 – 11=0 и (х – 2)2 – 2(у + 2)2 = 13.
    3. При каких значениях к прямые у = kх + b пересекают линию

4х2 – 4ху + у2 + 6х + 1 = 0 не более чем в одной точке?

    1. Через точку А(2, 0) проведена касательная к линии ху = 1. Составьте уравнение этой касательной.
    2. Может ли линия второго порядка, заданная уравнением а11х2+2а12ху+а22у2+а00=0 не иметь центров? Ответ объясните.

ВАРИАНТ 2

  1. Найдите угол между асимптотами гиперболы, у которой расстояние между фокусами вдвое больше расстояния между директрисами (ПДСК).
  2. Для линии 3х2 – 5ху + у2 + 8х = 0 напишите уравнение множества середин хорд, принадлежащих прямым с угловым коэффициентом к = – 2/3.
  3. Найдите ось симметрии и вершину параболы

х2 + 4у2 + 4ху – 6х – 2у + 1=0 (ПДСК).

  1. Определите вид линии второго порядка у2 – 6у + 4х + 5=0.
  2. Почему любая линия второго порядка имеет хотя бы одну ось симметрии?

ВАРИАНТ 3

  1. Напишите уравнение параболы, которая проходит через точки А(0,0), В(1, 4) и симметрична относительно оси абсцисс. Найдите координаты фокуса и уравнение директрисы этой параболы (ПДСК).
  2. Напишите уравнение гиперболы, проходящей через точку А(-5, 0) и имеющей асимптоты у – 1 = 0 и х – 2у – 1 = 0.
  3. Напишите уравнение какой-нибудь оси симметрии линии, заданной в ПДСК уравнением х2 + 2х –у + 1=0.
  4. Определите вид линии второго порядка: 4х2 + у2 – 4ху – 15=0.
  5. Направления осей координат сопряжены относительно линии второго порядка. Как это скажется на общем уравнении этой линии?

ВАРИАНТ 4

  1. Напишите уравнение гиперболы в ПДСК, если её асимптоты имеют уравнения 4у+3х=0 и 4у – 3х=0, а директрисы – уравнения 5х+16=0,

5х – 16=0.

  1. Напишите уравнение линии второго порядка, если С(0,1) – её центр симметрии, линия проходит через точку А(3,0) и пересекает каждую из прямых 2х – 3у + 1 = 0 и х + у – 5=0 лишь в одной точке.
  2. Найдите середину хорды, отсекаемой линией

2х2 + 3у2 + 4ху – 3х – 3у = 0 на прямой х+3у – 12=0.

  1. Определите вид линии второго порядка: 2ху – 4х + 2у – 3 = 0.
  2. Любая ли линия второго порядка имеет хотя бы один диаметр? Ответ объясните.

ВАРИАНТ 5

      1. Напишите уравнение гиперболы в ПДСК, если её асимптоты имеют уравнения 4у+3х=0 и 4у – 3х=0, а директрисы – уравнения 5х+16=0, 5х – 16=0.
      2. Найдите ось симметрии и вершину параболы

х2 + 4у2 + 4ху – 6х – 2у + 1 = 0 (ПДСК).

      1. Две пары прямых 2х – 3у = 0, х + 2у = 0 и х – у=0, 3х – 5у = 0 служат сопряженными диаметрами линии второго порядка. Составьте уравнение этой линии, зная, что она проходит через точку В(1, 1).
      2. При каких значениях к прямая у = kх + b имеет асимптотическое направление относительно линии 4х2 + у2 – 4ху + 6х + 1 = 0?
      3. Почему любая линия второго порядка имеет хотя бы один диаметр?

ВАРИАНТ 6

  1. Напишите уравнение параболы, которая проходит через точки А(0,0), В(1, 4) и симметрична относительно оси абсцисс. Найдите координаты фокуса и уравнение директрисы этой параболы (ПДСК).
  2. Напишите уравнение прямой, проходящей через середины хорд, отсекаемых линией 2х2-3у2+5ху+3х+16у=0 на прямых 4х+5у=0 и 4х+5у+2008=0.
  3. Напишите уравнения тех касательных к линии

х2 + у2 + ху + 2х + 3у – 3 = 0, которые параллельны оси абсцисс.

  1. Напишите уравнение какой-нибудь оси симметрии линии, заданной в ПДСК уравнением х2+2х – у + 1 = 0.
  2. Может ли не иметь центров линия второго порядка, если в её общем уравнении а) а12=0 и а11а22=0; б) а12=0 и а11а22=0; в) а12=0 и а11а22=0? Ответ объясните!

ВАРИАНТ 7

  1. Напишите каноническое уравнение гиперболы, если угол между её асимптотами равен 60о и гипербола проходит через точку А(6, 3) (ПДСК).
  2. Напишите уравнение общего диаметра линий второго порядка:

4х2 + у2 – 4ху – 6х + 8у + 13 = 0 и 4х2 + у2 – 4ху – 1=0.

  1. Для линии второго порядка у2 = 8х напишите уравнение касательной, параллельной прямой 2х + 2у – 13 = 0.
  2. Найдите оси симметрии линии второго порядка, заданной в ПДСК уравнением 2ху – 4х + 2у – 3 = 0.
  3. Может ли не иметь асимптотических направлений линия второго порядка, для коэффициентов общего уравнения которой выполняется условие: а) а11а22=0; б) а12=0 и а11а22<0? Ответ объясните!

ВАРИАНТ 1

1. Напишите уравнение множества всех точек плоскости (в ПДСК), для каждой из которых абсолютное значение разности расстояний до точек А(0, -2) и В(0, 2) равно 3.

  1. Напишите уравнение общего диаметра линий второго порядка, заданных уравнениями х2+2ху+у2-11=0 и (х-2)2-2(у+2)2=13.
  2. При каких значениях к прямые у=kх+b пересекают линию 4х2-4ху+у2+6х+1=0 не более чем в одной точке?
  3. Через точку А(2,0) проведена касательная к линии ху=1. Составьте уравнение этой касательной.
  4. Может ли линия второго порядка, заданная уравнением а11х2+2а12ху+а22у2+а00=0 не иметь центров?

ВАРИАНТ 2

      1. Найдите угол между асимптотами гиперболы, у которой расстояние между фокусами вдвое больше расстояния между директрисами (ПДСК).
      2. Для линии 3х2-5ху+у2+8х=0 напишите уравнение множества середин хорд, принадлежащих прямым с угловым коэффициентом к= – 2/3.
      3. Найдите ось симметрии и вершину параболы х2+4у2+4ху-6х-2у+1=0 (ПДСК).
      4. Определите вид линии второго порядка у2-6у+4х+5=0.
  1. Почему любая линия второго порядка имеет хотя бы одну ось симметрии?
Источник

Диа́метр (фр. diamètre из лат. diametrus из др.-греч. διάμετρος — поперечник[1]) — отрезок, соединяющий две точки на окружности и проходящий через центр окружности, а также длина этого отрезка. Диаметр равен двум радиусам.

Обобщённо диаметром фигуры (множества) называется максимальное расстояние между точками этой фигуры (множества), или точная верхняя грань всевозможных расстояний, если максимальное не существует.

Диаметр геометрических фигур[править | править код]

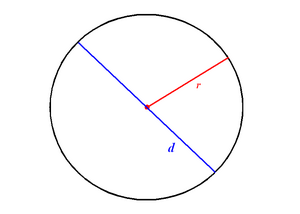
Радиус (r) и диаметр (d) окружности

Диаметр — это хорда (отрезок, соединяющий две точки) на окружности (сфере, поверхности шара), проходящая через центр этой окружности (сферы). Также диаметром называют длину этого отрезка. Диаметр окружности является хордой, проходящей через её центр; такая хорда имеет наибольшую длину. По величине диаметр равен двум радиусам.

Символ диаметра[править | править код]

Символы со сходным начертанием: Ø · ø · ∅

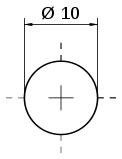
В инженерной графике и технических спецификациях диаметр принято обозначать символом Boundy diameter symbol.png[2].
Символ диаметра представлен в Юникоде (U+2300 ⌀ diameter sign)[3] и, хотя он отсутствует в стандартных раскладках клавиатуры, может быть введён с клавиатуры:

  • в HTML как ⌀ или ⌀
  • в LaTeX для его отображения предназначена команда diameter из пакета wasysym
  • в Microsoft Word символ можно получить, введя 2300 и нажав Alt+X
  • в Windows с помощью Alt-кода Alt+8960 (в английской раскладке)
  • в системах, использующих X Window System (Unix/Linux/ChromeOS и др.), с помощью комбинации Ctrl+⇧ Shift+u 2300Пробел или с использованием клавиши Compose, нажав поочерёдно Composedi[4].

Также, символ можно найти и скопировать в приложениях и инструментах типа «таблица символов», например:

  • в Windows — Таблица символов[en]
  • в программах из пакета Microsoft Office — меню «Вставка» → «Символ…»
  • в macOS — Character Palette/Viewer (вызывается комбинацией ⌥ Opt+⌘ Cmd+T)
  • в GNOME — Таблица символов GNOME (ранее — gucharmap).

Во многих случаях символ диаметра может не отображаться, так как его редко включают в шрифты (он присутствует, например, в Arial Unicode MS (поставляется с Microsoft Office, при установке именуется «Универсальный шрифт»), DejaVu (свободный), Code2000 (условно-бесплатный) и некоторых других), в связи с чем вместо него часто используются другие символы со схожим начертанием. К примеру, в САПР AutoCAD вместо символа диаметра используется символ пустого множества (U+2205 ∅ empty set), вводящийся сочетанием %%c (буква c — латинская) или U+2205 в текстовой строке. Взаимозаменяемость этих символов отражена и в стандартах консорциума W3C[5]. Также, для замены часто используется буква Ø датско-норвежского алфавита.

Сопряжённые диаметры эллипса и гиперболы[править | править код]

Сопряжённые диаметры эллипса[править | править код]

Пара сопряжённых диаметров эллипса. Если в точках касания диаметра с эллипсом провести прямую, параллельную сопряжённому диаметру, то прямая будет касательной к эллипсу и четыре таких касательных ко всем четырём концам пары сопряжённых диаметров эллипса образуют описанный около эллипса параллелограмм

  • Диаметром эллипса называют произвольную хорду, проходящую через его центр. Сопряжёнными диаметрами эллипса называют пару его диаметров, обладающих следующим свойством: середины хорд, параллельных первому диаметру, лежат на втором диаметре. В этом случае и середины хорд, параллельных второму диаметру, лежат на первом диаметре.

На рисунке представлена пара сопряжённых диаметров (красный и синий). Если в точках пересечения диаметра с эллипсом провести прямую, параллельную сопряжённому диаметру, то прямая будет касательной к эллипсу, и четыре таких касательных ко всем четырём концам пары сопряжённых диаметров эллипса образуют описанный около эллипса параллелограмм (зелёные линии на рисунке).

Сопряжённые диаметры гиперболы[править | править код]

kcdot k_{1}=varepsilon ^{2}-1={frac {b^{2}}{a^{2}}}

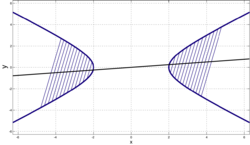
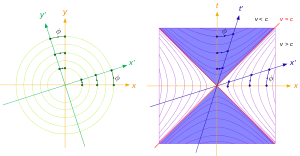
Для произвольного угла φ показаны диаметры и сопряжённые им диаметры для окружностей и равнобочных гипербол.

  • Если диаметр гипербол a делит пополам хорды, параллельные диаметру b, то диаметр b делит пополам хорды, параллельные диаметру a. Такие диаметры называются взаимно сопряжёнными.
  • Главными диаметрами гипербол называются взаимно сопряжённые и взаимно перпендикулярные диаметры. У гиперболы есть только одна пара главных диаметров — действительная и мнимая оси.
  • В случае гипербол с асимптотами, образующими прямой угол, её сопряжённые гиперболы получатся при её зеркальном отражении относительно одной из асимптот. При таком зеркальном отражении её диаметр перейдет в сопряжённый диаметр, который будет просто диаметром сопряжённой гиперболы (см. рис.). Также. как наблюдается перпендикулярность сопряжённых диаметров на окружности (на рис. слева), аналогичная ортогональность наблюдается для сопряжённых диаметров гиперболы со взаимно перпендикулярными асимптотами (на рис. справа).

Вариации и обобщения[править | править код]

Понятие диаметра допускает естественные обобщения на некоторые другие геометрические и математические объекты. Если во множестве некоторых объектов определена метрика пространства, то для подмножества этих объектов может быть введено понятие диаметра множества.

Диаметром множества M, лежащего в метрическом пространстве с метрикой rho , называется величина (sup_{x,y in M}rho(x, y)).

Под диаметром метрического пространства понимается точная верхняя грань расстояний между парой любых его точек.

  • В частности:

Например, диаметр n-размерного гиперкуба со стороной s равен

d = scdot sqrt{n}.

Некоторые окружности, построенные в треугольнике на одном отрезке, как на диаметре[править | править код]

  • Окружность Фурмана построена на одном отрезке, как на диаметре
  • Окружность Брокара построена на одном отрезке, как на диаметре

См. также[править | править код]

  • Радиус
  • Пи
  • При делении фигур на части меньшего диаметра возникла гипотеза Борсука, опровергнутая в 1993 году
  • Изодиаметрическое неравенство
  • Угловой диаметр астрономических объектов.
  • Диаметр циркуляции
  • Гидравлический диаметр

Примечания[править | править код]

  1. ↑ диаметр // Этимологический словарь русского языка = Russisches etymologisches Wörterbuch : в 4 т. / авт.-сост. М. Фасмер ; пер. с нем. и доп. чл.‑кор. АН СССР О. Н. Трубачёва, под ред. и с предисл. проф. Б. А. Ларина [т. I]. — Изд. 2-е, стер. — М. : Прогресс, 1986—1987.
  2. ↑
    Большаков В. П., Тозик В. Т., Чагина А. В. Инженерная и компьютерная графика. — СПб.: БХВ-Петербург, 2013. — 288 с. — ISBN 978-5-9775-0422-5. — С. 90.
  3. ↑ The Unicode Standard, Version 13.0. Miscellaneous Technical, Range: 2300–23FF (англ.) (PDF). Unicode Inc[en] (2020). Дата обращения: 6 сентября 2020. Архивировано 30 декабря 2019 года.
  4. ↑ Monniaux, David UTF-8 (Unicode) compose sequence (англ.). — Файл конфигурации вводимых с помощью клавиши Compose символов. Дата обращения: 6 сентября 2020. Архивировано 3 августа 2020 года.
  5. ↑ SYMBOL Characters and Glyphs. Дата обращения: 6 сентября 2020. Архивировано 6 августа 2020 года.

Литература[править | править код]

  • Диаметр // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
Источник

Добавить комментарий