К решению задачи
рекомендуется приступить после
выполнения самостоятельной работы
5 (гл. 1). Порядок решения задачи остается
таким же.
Пример
29. Определить
моменты инерции сечения, составленного
из прокатных профилей, относительно
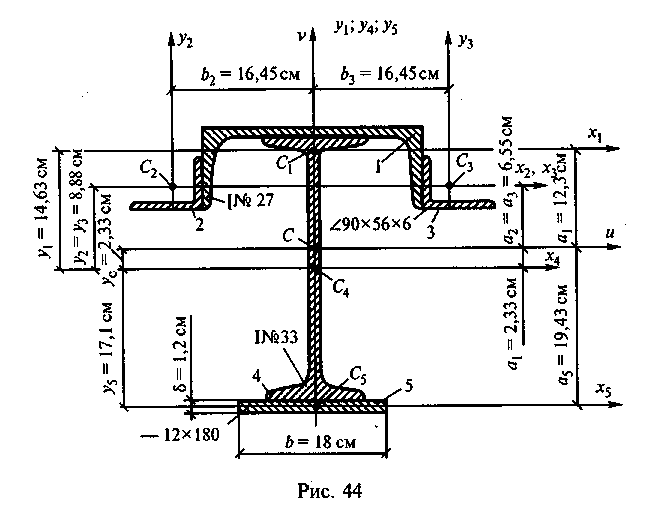
главных центральных осей (рис. 44).
Сечение состоит из двутавра № 33, швеллера
№ 27, двух уголков 90 х 56 х 6 и листа сечением
12 х 180 мм.
Решение.
1.
Положение центра тяжести определено в
примере 25: ус
= 2,33
см, если ось проходит через центр тяжести
двутавра.
2.
Проводим
центральные оси для каждого профиля
проката х1
ъ
x
2
, x3,
x4
и х5.
3.
Проводим
главные центральные оси. Вертикальную
ось v
совмещаем с осью симметрии, а
горизонтальную и
проводим
через центр тяжести сечения С
перпендикулярно
оси v.
4.
Определим
момент инерции сечения относительно
оси «:
![]()
Учитывая,
что уголки одинаковые и расположены на
одинаковом расстоянии от оси и,
получим:
![]()
Определим
величину каждого слагаемого. Момент
инерции швеллера № 27 относительно оси
и
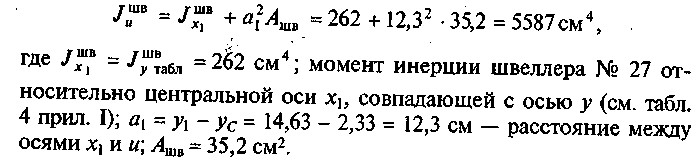
Момент инерции
уголка 90 х 56 х 6 относительно оси «
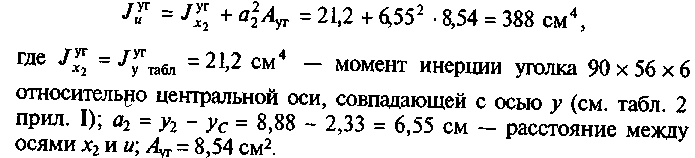
Момент
инерции двутавра № 33 относительно оси
и:
![]()
140

Момент
инерции листа 12×180 мм относительно оси
и:
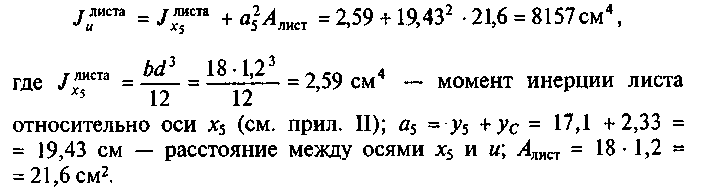
Подставим полученное
значение в формулу (а):
![]()
5.
Определим
момент инерции сечения относительно
оси v:
![]()
Момент
инерции швеллера № 27 относительно оси
v:
![]()
141
Момент
инерции уголка 90 х 56 х 6 относительно
оси v:
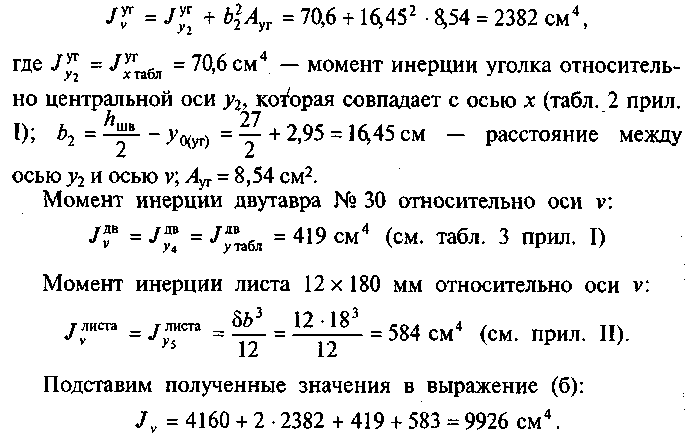
Ответ:
Ju
= 24652 см4;
Jv
= 9926
см4.
Пример
30. Определить
моменты инерции сечения, составленного
из простых геометрических фигур,
относительно главных центральных
осей по условию примера 25 (см. рис. 37).
Решение.
1.
Положение центра тяжести определено:
ус
= = 9,84
см.
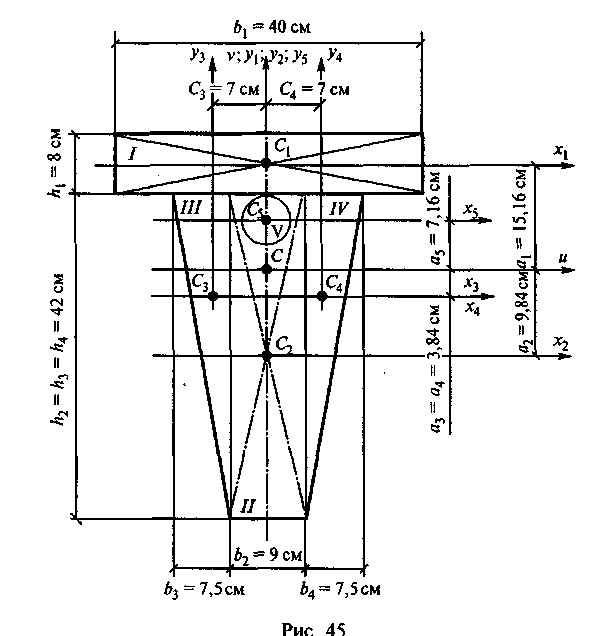
2. Для
каждой фигуры проводим центральные оси
х{,
х2,
х3,
х4
и
х5,
причем
оси х3
и x4
совпали (рис. 45).
3.
Проводим
главные центральные оси. Вертикальную
ось v
совместим с осью симметрии, а
горизонтальную ось и
проведем
через центр тяжести сечения С
перпендикулярно оси v.
4.
Момент
инерции сечения относительно оси и
![]()
Определим значение
каждого слагаемого. Момент инерции;’
первого прямоугольника
![]()
Момент инерции
второго прямоугольника
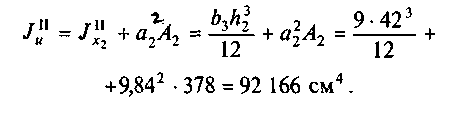
142
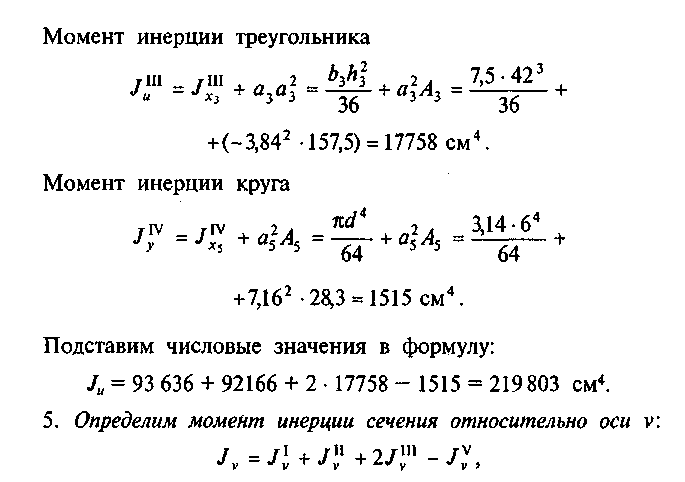
143
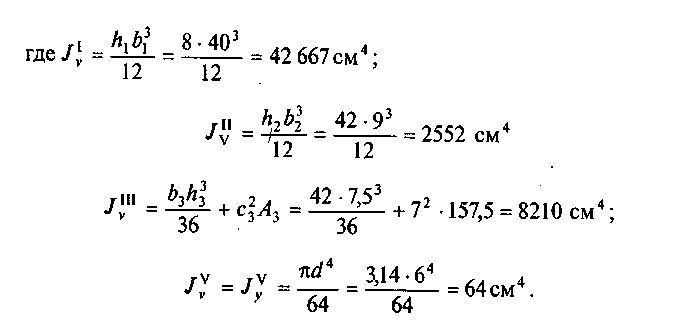
Подставим
числовые значения в формулу для
определения /v:
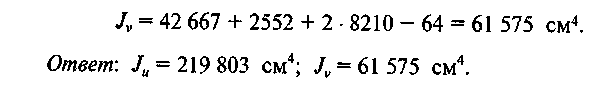
Задание для
расчетно-графической работы 5.
Задача
1. Определить
моменты инерции сечения, составленного
из профилей прокатной стали, относительно
главных центральных осей по данным
одного из вариантов, приведенных на
рис. 38.
Задача
2.
Определить моменты инерции сечения,
составленного из простых геометрических
фигур, относительно главных центральных
осей по данным одного из вариантов,
приведенных на рис. 39.
5.3. Подбор сечения балки из прокатного двутавра
1.
Строят
эпюры Qx
и Мх
(см.
самостоятельную работу 6, гл. I).
2.
Подбирают
сечение стальной балки в
следующем порядке: а) определяют
требуемый момент сопротивления
сечения балки:
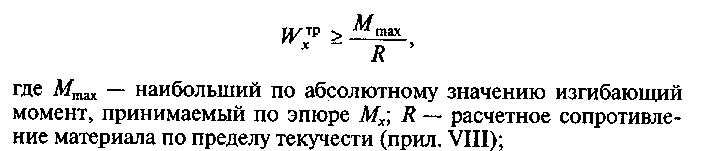
б) по
ГОСТам прил. I
подбираем номер двутавровой стальной
балки, которая должна иметь момент
сопротивления Wx,
наиболее
близкий по значению к требуемому моменту
сопротивления Wxтр
3.
Проверяют
прочность принятой двутавровой балки
по
нормальным напряжениям. Такую проверку
выполняют для сечения с наибольшим
изгибающим моментом:
144
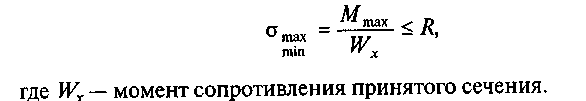
Если условие
удовлетворено, прочность балки по
нормальным сечениям считается
обеспеченной, и наоборот.
4.
Строят
эпюру нормальных напряжений о.
Для этого вычерчивают крупно поперечное
сечение балки и проводят на отдельном
рисунке нулевую линию перпендикулярно
нейтральной оси. Затем на уровне крайних
точек сечения (верхней и нижней)
откладывают найденные ранее значения
Qтах
и Qmin
и соединяют эти значения прямой линией.
Полученный график называется эпюрой
а. Значения Qтах
и Qmin
откладывают по разные стороны от нулевой
линии.
5.
Проверяют
прочность принятой двутавровой балки
по касательным, напряжениям. Наибольшие
касательные напряжения возникают в том
сечении по длине балки, в котором
действует наибольшая поперечная сила
(по абсолютному значению), а по высоте
сечения — на уровне нейтрального слоя.
Для
определения этих напряжений действительное
сечение двутавровой балки упрощают:
полка и стенка принимаются прямоугольными:
полка с размерами b
и
/, а стенка — d
и
(h
— 2f).
Размеры
b,
t
и
h
берутся
по ГОСТу (прил. I).
Таким образом, сечение двутавровой
балки теперь состоит из трех
прямоугольников.
Касательные
напряжения на уровне нейтрального слоя
определяют по формуле Журавского:
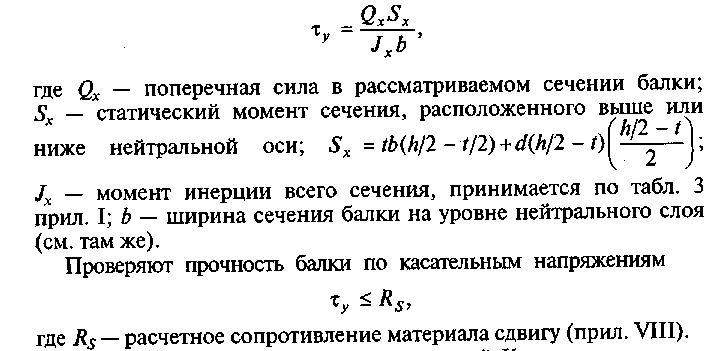
6.
Строим
эпюру касательных напряжении, касательные
напряжения изменяются по высоте
балки по криволинейному закону и имеют
скачок в месте соединения полки и стенки.
Поэтому эпюру т строят по значениям,
найденным в пяти точках сечения:
145
крайних точках,
на уровне нейтральной оси и на уровне
сопряжения стенки и полки — чуть
ниже и чуть выше этого сопряжения.
Напряжение
в этих точках определяется по формуле
Журав-ского. При этом статический момент
Sx
и
ширина сечения Ь
определяются
для каждой точки сечения. Касательные
напряжения в крайних точках сечения
равны нулю.
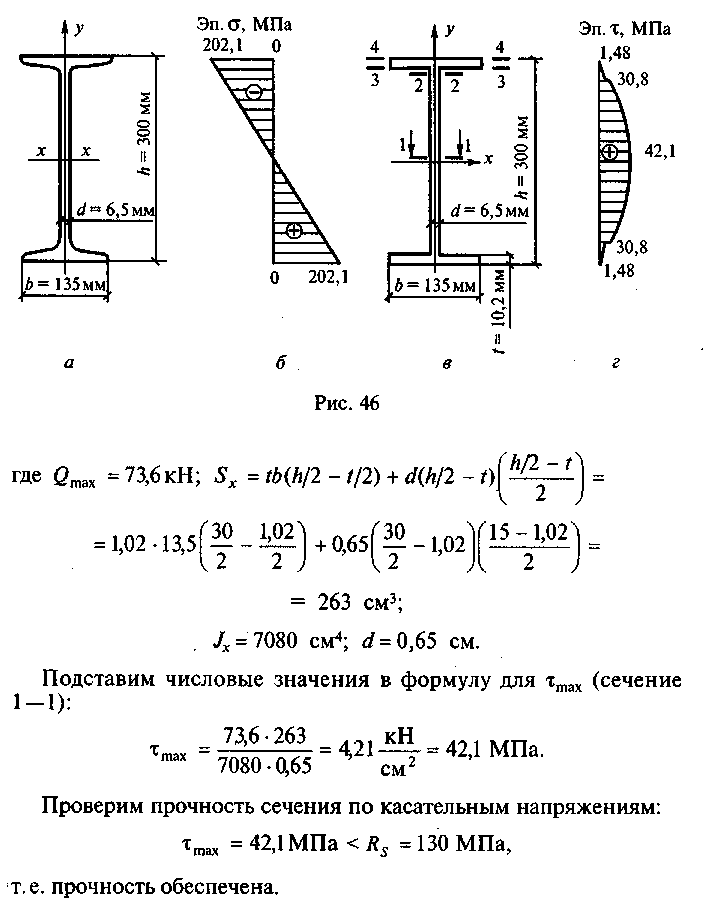
Пример
31.
По условию примера 11 подобрать сечение
стальной двутавровой балки (рис. 46,
а). Проверить прочность принятого
сечения по нормальным напряжениям в
сечении с наибольшим изгибающим
моментом и по касательным напряжениям
в сечении с наибольшей поперечной силой.
Материал — сталь марки С-235.
Решение.
1.
Строим
эпюры Qx
и
Мх
(см.
пример 11). Наибольшее значение
поперечной силы Qmax
= 73,6
кН, изгибающего момента Mтах
=95,4кН-м (см. рис. 15).
2.
Подберем
сечение стальной двутавровой балки по
наибольшему изгибающему моменту
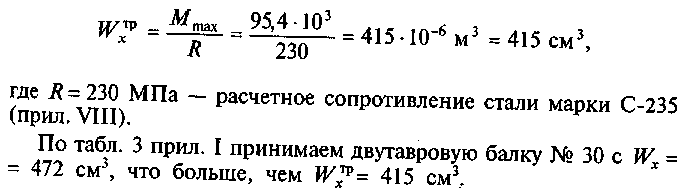
3.
Проверим
прочность принятого сечения:
![]()
Прочность сечения
по нормальным напряжениям обеспечена.
4.
Строим
эпюру нормальных напряжений. Отложим
от нулевой линии 0—0 (рис. 46, б)
значение
qтах
=
202,1 МПа и c
qmin
= = 202,1 МПа и соединим полученные точки.
Верхняя часть испытывает сжатие,
нижняя — растяжение, так как по эпюре
Мх
видно,
что балка прогибается (обращена
выпуклостью) вниз.
5.
Проверим
прочность балки по касательным
напряжениям. Заменим
действительное сечение упрощенным
(рис. 46, в).
Размеры
d=
6,5
мм; t=
10,2
мм; b
=
135 мм приняты по табл. 3 прил. I.
Определим наибольшее
касательное напряжение
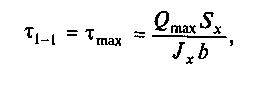
146
В прокатных балках,
которые не несут больших сосредоточенных
сил в приопорных участках, это условие
обычно соблюдается с большим запасом.
6.
Построим
эпюру т.
Напряжение в сечении 2 — 2
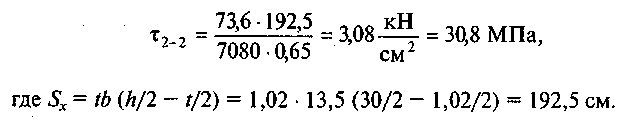
147
Напряжение в
сечении 3 — 3
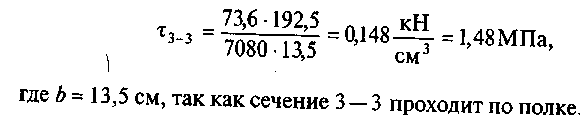
Напряжение
в сечении 4 — 4 равно нулю, так как Sx
= 0. По
найденным значениям строим эпюру r
y
(рис.
46, г).
Задание
для расчетно-графической работы 6.
Подобрать
сечение стальной двутавровой балки,
проверить принятое сечение по нормальным
(для сечения с наибольшим изгибающим
моментом) и по касательным (для сечения
с наибольшей поперечной силой) напряжениям
и построить эпюры q
и r
для соответствующих сечений. Материал
— сталь С-245. Остальные данные принять
по одному из вариантов, показанных на
рис. 7.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

Рассмотрим формулы для определения геометрических характеристик плоских сечений: статического момента площади фигуры, осевых моментов инерции и радиуса инерции сечения.
При расчете элементов конструкций на прочность, жесткость и устойчивость приходится кроме общеизвестной характеристики – площади поперечного сечения A, оперировать такими геометрическими характеристиками сечений, как статический момент площади, момент инерции, момент сопротивления, радиус инерции.
Статический момент площади
Интегралы вида:

называются статическими моментами площади сечения A относительно осей X и Y соответственно.
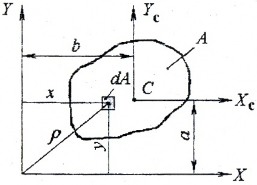
В тех случаях, когда сечение может быть разделено на простейшие фигуры площади Ai и координаты центров тяжести xi и yi которых известны, статические моменты площади сложной фигуры определяются через суммирование

Статические моменты площади имеют размерность [м3] и могут принимать любые числовые значения. Для осей XC, YC, проходящих через центр тяжести сечения C (центральные оси), статические моменты равны нулю:

Координаты центров тяжести сечения определяются относительно так называемых вспомогательных осей по формулам:
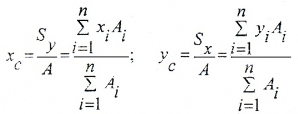
Если сечение имеет ось симметрии, то центр тяжести находится на этой оси и его положение определяется одной координатой.
При наличии двух и более осей симметрии центр тяжести совпадает с точкой пересечения этих осей.
Моменты инерции
Моментами инерции площади сечения называют интегралы вида:
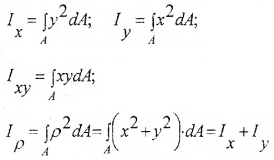
где:
Ix, Iy — осевые моменты инерции площади сечения относительно осей OX, OY соответственно;
Ixy — центробежный момент инерции;
Iρ — полярный момент инерции.
Размерность момента инерции [м4], Ix, Iy, I ρ всегда положительны, Ixy может принимать любые значения, при этом, если хотя бы одна из осей является осью симметрии, Ixy=0.
Зависимости между моментами инерции относительно параллельных осей выражаются формулами:

где a, b – расстояния между осями X, XC и Y, YC.
Оси, относительно которых Ixy=0, называют главными, а осевые моменты инерции относительно них – главными моментами инерции.
Главные оси, проходящие через центр тяжести сечения, называют главными центральными осями, а соответствующие им моменты инерции – главными центральными моментами инерции.
Главные оси характерны тем, что их моменты инерции принимают экстремальные значения (Imax, Imin).
Момент инерции сложного сечения относительно какой-либо оси находится суммированием моментов инерции составляющих его частей относительно той же оси:

Радиусы инерции
Величины

называют радиусами инерции сечения относительно осей OX и OY соответственно.
Эллипс, построенный в главных осях, с полуосями, равными главным радиусам инерции

называют эллипсом инерции.
Лекции по сопромату >
Примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее



6.6. ГЛАВНЫЕ ОСИ ИНЕРЦИИ И ГЛАВНЫЕ МОМЕНТЫ ИНЕРЦИИ
При изменении угла α значения Iz1, Iy1, Iz1y1 (6.13) изменяются, и при некотором значении угла α0 они принимают экстремальные значения. Взяв первую производную по углу α от формул (6.13) и приравняв ее нулю, получим: Эта формула определяет положение двух осей, относительно одной из которых осевой момент максимален, а относительно другой – минимален. Такие оси называют главными. Моменты инерции относительно главных осей называют главными моментами инерции. Их вычисляют следующим образом: Главные оси обладают следующими свойствами: центробежный момент инерции относительно них равен нулю; моменты инерции относительно главных осей экстремальны; для симметричных сечений оси симметрии являются главными. Главные оси, проходящие через центр тяжести фигуры, называют главными центральными осями инерции. Пример 6.4. Определить, каким образом изменяется момент инерции квадратного сечения при его повороте. Решение. Момент инерции относительно повернутой оси: Поскольку оси z, y квадрата являются осями симметрии, то есть главными, то центробежный момент инерции относительно них Izy = 0: Выводы. 1. Моменты инерции квадратного сечения с изменением положения центральных осей остаются постоянными. 2. В квадрате и других правильных многоугольниках (треугольниках, пятиугольниках) любая центральная ось является и главной. Такие фигуры называют фигурами равного сопротивления. Пример 6.5. Для фигуры, представленной в примере 6.1, определить главные центральные моменты инерции. Решение. Расстояния между центральной осью составной фигуры и собственными центральными осями элементов Моменты инерции относительно центральных осей, параллельных основанию и высоте a1= y1 – yC = 5 – 3,5 = 1,5 см; a2= y2 – yC = 1 – 3,5 = –2,5 см; b1= z1 – zC = 1 – 2,5 = –1,5 см; b2= z2 – zC = 5 – 2,5 = 2,5 см. Центробежный момент инерции Направления главных осей инерции Угол α0 (положительный) откладываем против хода часовой стрелки от оси с большим моментом инерции, то есть zC . Величины главных центральных моментов инерции
Главные центральные и главные моменты инерции
При повороте центральных осей и приближении их к главным центральным осям, больший из собственных осевых моментов инерции становится еще больше, стремясь максимальному значению (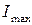 ), а меньший – меньше, приближаясь к минимальному значению (
), а меньший – меньше, приближаясь к минимальному значению (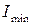 ).
).
Главные центральные моменты инерции – моменты инерции фигуры относительно главных центральных осей 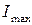 и
и 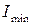 . Формулы главных центральных моментов инерции, вытекающих из формул моментов инерции при повороте осей координат:
. Формулы главных центральных моментов инерции, вытекающих из формул моментов инерции при повороте осей координат:
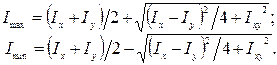
Если в частном случае 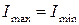 , то осевые моменты инерции при повороте координатных осей вообще не изменяются, и тогда любые две взаимно перпендикулярные оси, проходящие через центр тяжести поперечного сечения, являются главными центральными осями.
, то осевые моменты инерции при повороте координатных осей вообще не изменяются, и тогда любые две взаимно перпендикулярные оси, проходящие через центр тяжести поперечного сечения, являются главными центральными осями.
