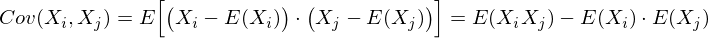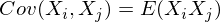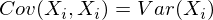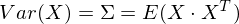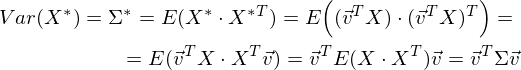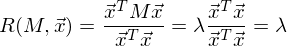В этой статье я бы хотел рассказать о том, как именно работает метод анализа главных компонент (PCA – principal component analysis) с точки зрения интуиции, стоящей за ее математическим аппаратом. Максимально просто, но подробно.
Математика вообще очень красивая и изящная наука, но порой ее красота скрывается за кучей слоев абстракции. Показать эту красоту лучше всего на простых примерах, которые, так сказать, можно покрутить, поиграть и пощупать, потому что в конце концов все оказывается гораздо проще, чем кажется на первый взгляд – самое главное понять и представить.
В анализе данных, как и в любом другом анализе, порой бывает нелишним создать упрощенную модель, максимально точно описывающую реальное положение дел. Часто бывает так, что признаки довольно сильно зависят друг от друга и их одновременное наличие избыточно.
К примеру, расход топлива у нас меряется в литрах на 100 км, а в США в милях на галлон. На первый взгляд, величины разные, но на самом деле они строго зависят друг от друга. В миле 1600м, а в галлоне 3.8л. Один признак строго зависит от другого, зная один, знаем и другой.
Но гораздо чаще бывает так, что признаки зависят друг от друга не так строго и (что важно!) не так явно. Объем двигателя в целом положительно влияет на разгон до 100 км/ч, но это верно не всегда. А еще может оказаться, что с учетом не видимых на первый взгляд факторов (типа улучшения качества топлива, использования более легких материалов и прочих современных достижений), год автомобиля не сильно, но тоже влияет на его разгон.
Зная зависимости и их силу, мы можем выразить несколько признаков через один, слить воедино, так сказать, и работать уже с более простой моделью. Конечно, избежать потерь информации, скорее всего не удастся, но минимизировать ее нам поможет как раз метод PCA.
Выражаясь более строго, данный метод аппроксимирует n-размерное облако наблюдений до эллипсоида (тоже n-мерного), полуоси которого и будут являться будущими главными компонентами. И при проекции на такие оси (снижении размерности) сохраняется наибольшее количество информации.
Шаг 1. Подготовка данных
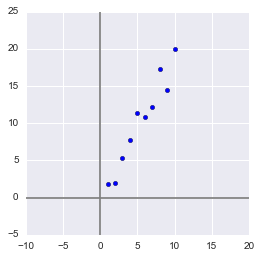
Здесь для простоты примера я не буду брать реальные обучающие датасеты на десятки признаков и сотни наблюдений, а сделаю свой, максимально простой игрушечный пример. 2 признака и 10 наблюдений будет вполне достаточно для описания того, что, а главное – зачем, происходит в недрах алгоритма.
Сгенерируем выборку:
x = np.arange(1,11)
y = 2 * x + np.random.randn(10)*2
X = np.vstack((x,y))
print X
OUT:
[[ 1. 2. 3. 4. 5.
6. 7. 8. 9. 10. ]
[ 2.73446908 4.35122722 7.21132988 11.24872601 9.58103444
12.09865079 13.78706794 13.85301221 15.29003911 18.0998018 ]]
В данной выборке у нас имеются два признака, сильно коррелирующие друг с другом. С помощью алгоритма PCA мы сможем легко найти признак-комбинацию и, ценой части информации, выразить оба этих признака одним новым. Итак, давайте разбираться!
Для начала немного статистики. Вспомним, что для описания случайной величины используются моменты. Нужные нам – мат. ожидание и дисперсия. Можно сказать, что мат. ожидание – это «центр тяжести» величины, а дисперсия – это ее «размеры». Грубо говоря, мат. ожидание задает положение случайной величины, а дисперсия – ее размер (точнее, разброс).
Сам процесс проецирования на вектор никак не влияет на значения средних, так как для минимизации потерь информации наш вектор должен проходить через центр нашей выборки. Поэтому нет ничего страшного, если мы отцентрируем нашу выборку – линейно сдвинем ее так, чтобы средние значения признаков были равны 0. Это очень сильно упростит наши дальнейшие вычисления (хотя, стоит отметить, что можно обойтись и без центрирования).
Оператор, обратный сдвигу будет равен вектору изначальных средних значений – он понадобится для восстановления выборки в исходной размерности.
Xcentered = (X[0] - x.mean(), X[1] - y.mean())
m = (x.mean(), y.mean())
print Xcentered
print "Mean vector: ", m
OUT:
(array([-4.5, -3.5, -2.5, -1.5, -0.5, 0.5, 1.5, 2.5, 3.5, 4.5]),
array([-8.44644233, -8.32845585, -4.93314426, -2.56723136, 1.01013247,
0.58413394, 1.86599939, 7.00558491, 4.21440647, 9.59501658]))
Mean vector: (5.5, 10.314393916)
Дисперсия же сильно зависит от порядков значений случайной величины, т.е. чувствительна к масштабированию. Поэтому если единицы измерения признаков сильно различаются своими порядками, крайне рекомендуется стандартизировать их. В нашем случае значения не сильно разнятся в порядках, так что для простоты примера мы не будем выполнять эту операцию.
Шаг 2. Ковариационная матрица
В случае с многомерной случайной величиной (случайным вектором) положение центра все так же будет являться мат. ожиданиями ее проекций на оси. А вот для описания ее формы уже недостаточно толькое ее дисперсий по осям. Посмотрите на эти графики, у всех трех случайных величин одинаковые мат.ожидания и дисперсии, а их проекции на оси в целом окажутся одинаковы!
Для описания формы случайного вектора необходима ковариационная матрица.
Это матрица, у которой (i,j)-элемент является корреляцией признаков (Xi, Xj). Вспомним формулу ковариации:
В нашем случае она упрощается, так как
E(Xi) = E(Xj) = 0:
Заметим, что когда Xi = Xj:
и это справедливо для любых случайных величин.
Таким образом, в нашей матрице по диагонали будут дисперсии признаков (т.к. i = j), а в остальных ячейках – ковариации соответствующих пар признаков. А в силу симметричности ковариации матрица тоже будет симметрична.
Замечание: Ковариационная матрица является обобщением дисперсии на случай многомерных случайных величин – она так же описывает форму (разброс) случайной величины, как и дисперсия.
И действительно, дисперсия одномерной случайной величины – это ковариационная матрица размера 1×1, в которой ее единственный член задан формулой Cov(X,X) = Var(X).
Итак, сформируем ковариационную матрицу Σ для нашей выборки. Для этого посчитаем дисперсии Xi и Xj, а также их ковариацию. Можно воспользоваться вышенаписанной формулой, но раз уж мы вооружились Python’ом, то грех не воспользоваться функцией numpy.cov(X). Она принимает на вход список всех признаков случайной величины и возвращает ее ковариационную матрицу и где X – n-мерный случайный вектор (n-количество строк). Функция отлично подходит и для расчета несмещенной дисперсии, и для ковариации двух величин, и для составления ковариационной матрицы.
(Напомню, что в Python матрица представляется массивом-столбцом массивов-строк.)
covmat = np.cov(Xcentered)
print covmat, "n"
print "Variance of X: ", np.cov(Xcentered)[0,0]
print "Variance of Y: ", np.cov(Xcentered)[1,1]
print "Covariance X and Y: ", np.cov(Xcentered)[0,1]
OUT:
[[ 9.16666667 17.93002811]
[ 17.93002811 37.26438587]]
Variance of X: 9.16666666667
Variance of Y: 37.2643858743
Covariance X and Y: 17.9300281124
Шаг 3. Собственные вектора и значения (айгенпары)
О’кей, мы получили матрицу, описывающую форму нашей случайной величины, из которой мы можем получить ее размеры по x и y (т.е. X1 и X2), а также примерную форму на плоскости. Теперь надо найти такой вектор (в нашем случае только один), при котором максимизировался бы размер (дисперсия) проекции нашей выборки на него.
Замечание: Обобщение дисперсии на высшие размерности — ковариационная матрица, и эти два понятия эквивалентны. При проекции на вектор максимизируется дисперсия проекции, при проекции на пространства больших порядков – вся ее ковариационная матрица.
Итак, возьмем единичный вектор на который будем проецировать наш случайный вектор X. Тогда проекция на него будет равна vTX. Дисперсия проекции на вектор будет соответственно равна Var(vTX). В общем виде в векторной форме (для центрированных величин) дисперсия выражается так:
Соответственно, дисперсия проекции:
Легко заметить, что дисперсия максимизируется при максимальном значении vT Σv. Здесь нам поможет отношение Рэлея. Не вдаваясь слишком глубоко в математику, просто скажу, что у отношения Рэлея есть специальный случай для ковариационных матриц:
и
Последняя формула должна быть знакома по теме разложения матрицы на собственные вектора и значения. x является собственным вектором, а λ – собственным значением. Количество собственных векторов и значений равны размеру матрицы (и значения могут повторяться).
Кстати, в английском языке собственные значения и векторы именуются eigenvalues и eigenvectors соответственно.
Мне кажется, это звучит намного более красиво (и кратко), чем наши термины.
Таким образом, направление максимальной дисперсии у проекции всегда совпадает с айгенвектором, имеющим максимальное собственное значение, равное величине этой дисперсии.
И это справедливо также для проекций на большее количество измерений – дисперсия (ковариационная матрица) проекции на m-мерное пространство будет максимальна в направлении m айгенвекторов, имеющих максимальные собственные значения.
Размерность нашей выборки равна двум и количество айгенвекторов у нее, соответственно, 2. Найдем их.
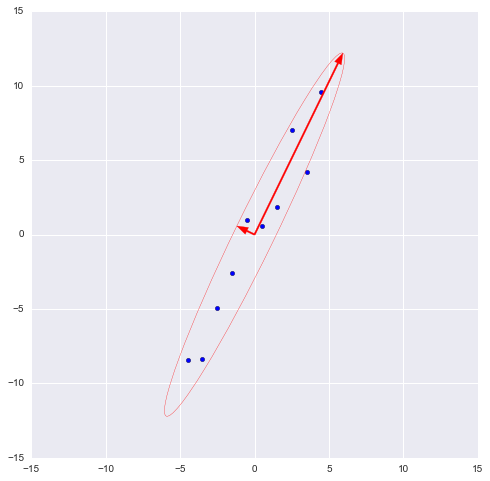
В библиотеке numpy реализована функция numpy.linalg.eig(X), где X – квадратная матрица. Она возвращает 2 массива – массив айгензначений и массив айгенвекторов (векторы-столбцы). И векторы нормированы — их длина равна 1. Как раз то, что надо. Эти 2 вектора задают новый базис для выборки, такой что его оси совпадают с полуосями аппроксимирующего эллипса нашей выборки.
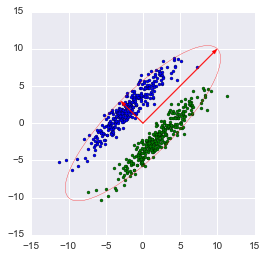
На этом графике мы апроксимировали нашу выборку эллипсом с радиусами в 2 сигмы (т.е. он должен содержать в себе 95% всех наблюдений – что в принципе мы здесь и наблюдаем). Я инвертировал больший вектор (функция eig(X) направляла его в обратную сторону) – нам важно направление, а не ориентация вектора.
Шаг 4. Снижение размерности (проекция)
Наибольший вектор имеет направление, схожее с линией регрессии и, спроецировав на него нашу выборку, мы потеряем информацию, сравнимую с суммой остаточных членов регрессии (только расстояние теперь евклидово, а не дельта по Y). В нашем случае зависимость между признаками очень сильная, так что потеря информации будет минимальна. «Цена» проекции — дисперсия по меньшему айгенвектору — как видно из предыдущего графика, очень невелика.
Замечание: диагональные элементы ковариационной матрицы показывают дисперсии по изначальному базису, а ее собственные значения – по новому (по главным компонентам).
Часто требуется оценить объем потерянной (и сохраненной) информации. Удобнее всего представить в процентах. Мы берем дисперсии по каждой из осей и делим на общую сумму дисперсий по осям (т.е. сумму всех собственных чисел ковариационной матрицы).
Таким образом, наш больший вектор описывает 45.994 / 46.431 * 100% = 99.06%, а меньший, соответственно, примерно 0.94%. Отбросив меньший вектор и спроецировав данные на больший, мы потеряем меньше 1% информации! Отличный результат!
Замечание: На практике, в большинстве случаев, если суммарная потеря информации составляет не более 10-20%, то можно спокойно снижать размерность.
Для проведения проекции, как уже упоминалось ранее на шаге 3, надо провести операцию vTX (вектор должен быть длины 1). Или, если у нас не один вектор, а гиперплоскость, то вместо вектора vT берем матрицу базисных векторов VT. Полученный вектор (или матрица) будет являться массивом проекций наших наблюдений.
_, vecs = np.linalg.eig(covmat)
v = -vecs[:,1])
Xnew = dot(v,Xcentered)
print Xnew
OUT:
[ -9.56404107 -9.02021624 -5.52974822 -2.96481262 0.68933859
0.74406645 2.33433492 7.39307974 5.3212742 10.59672425]
dot(X,Y) — почленное произведение (так мы перемножаем векторы и матрицы в Python)
Нетрудно заметить, что значения проекций соответствуют картине на предыдущем графике.
Шаг 5. Восстановление данных
С проекцией удобно работать, строить на ее основе гипотезы и разрабатывать модели. Но не всегда полученные главные компоненты будут иметь явный, понятный постороннему человеку, смысл. Иногда полезно раскодировать, к примеру, обнаруженные выбросы, чтобы посмотреть, что за наблюдения за ними стоят.
Это очень просто. У нас есть вся необходимая информация, а именно координаты базисных векторов в исходном базисе (векторы, на которые мы проецировали) и вектор средних (для отмены центровки). Возьмем, к примеру, наибольшее значение: 10.596… и раскодируем его. Для этого умножим его справа на транспонированный вектор и прибавим вектор средних, или в общем виде для всей выборки: XTvT+m
n = 9 #номер элемента случайной величины
Xrestored = dot(Xnew[n],v) + m
print 'Restored: ', Xrestored
print 'Original: ', X[:,n]
OUT:
Restored: [ 10.13864361 19.84190935]
Original: [ 10. 19.9094105]
Разница небольшая, но она есть. Ведь потерянная информация не восстанавливается. Тем не менее, если простота важнее точности, восстановленное значение отлично аппроксимирует исходное.
Вместо заключения – проверка алгоритма
Итак, мы разобрали алгоритм, показали как он работает на игрушечном примере, теперь осталось только сравнить его с PCA, реализованным в sklearn – ведь пользоваться будем именно им.
from sklearn.decomposition import PCA
pca = PCA(n_components = 1)
XPCAreduced = pca.fit_transform(transpose(X))
Параметр n_components указывает на количество измерений, на которые будет производиться проекция, то есть до скольки измерений мы хотим снизить наш датасет. Другими словами – это n айгенвекторов с самыми большими собственными числами. Проверим результат снижения размерности:
print 'Our reduced X: n', Xnew
print 'Sklearn reduced X: n', XPCAreduced
OUT:
Our reduced X:
[ -9.56404106 -9.02021625 -5.52974822 -2.96481262 0.68933859
0.74406645 2.33433492 7.39307974 5.3212742 10.59672425]
Sklearn reduced X:
[[ -9.56404106]
[ -9.02021625]
[ -5.52974822]
[ -2.96481262]
[ 0.68933859]
[ 0.74406645]
[ 2.33433492]
[ 7.39307974]
[ 5.3212742 ]
[ 10.59672425]]
Мы возвращали результат как матрицу вектор-столбцов наблюдений (это более канонический вид с точки зрения линейной алгебры), PCA в sklearn же возвращает вертикальный массив.
В принципе, это не критично, просто стоит отметить, что в линейной алгебре канонично записывать матрицы через вектор-столбцы, а в анализе данных (и прочих связанных с БД областях) наблюдения (транзакции, записи) обычно записываются строками.
Проверим и прочие параметры модели – функция имеет ряд атрибутов, позволяющих получить доступ к промежуточным переменным:
— Вектор средних: mean_
— Вектор(матрица) проекции: components_
— Дисперсии осей проекции (выборочная): explained_variance_
— Доля информации (доля от общей дисперсии): explained_variance_ratio_
Замечание: explained_variance_ показывает выборочную дисперсию, тогда как функция cov() для построения ковариационной матрицы рассчитывает несмещенные дисперсии!
Сравним полученные нами значения со значениями библиотечной функции.
print 'Mean vector: ', pca.mean_, m
print 'Projection: ', pca.components_, v
print 'Explained variance ratio: ', pca.explained_variance_ratio_, l[1]/sum(l)
OUT:
Mean vector: [ 5.5 10.31439392] (5.5, 10.314393916)
Projection: [[ 0.43774316 0.89910006]] (0.43774316434772387, 0.89910006232167594)
Explained variance: [ 41.39455058] 45.9939450918
Explained variance ratio: [ 0.99058588] 0.990585881238
Единственное различие – в дисперсиях, но как уже упоминалось, мы использовали функцию cov(), которая использует несмещенную дисперсию, тогда как атрибут explained_variance_ возвращает выборочную. Они отличаются только тем, что первая для получения мат.ожидания делит на (n-1), а вторая – на n. Легко проверить, что 45.99 ∙ (10 — 1) / 10 = 41.39.
Все остальные значения совпадают, что означает, что наши алгоритмы эквивалентны. И напоследок замечу, что атрибуты библиотечного алгоритма имеют меньшую точность, поскольку он наверняка оптимизирован под быстродействие, либо просто для удобства округляет значения (либо у меня какие-то глюки).
Замечание: библиотечный метод автоматически проецирует на оси, максимизирующие дисперсию. Это не всегда рационально. К примеру, на данном рисунке неаккуратное снижение размерности приведет к тому, что классификация станет невозможна. Тем не менее, проекция на меньший вектор успешно снизит размерность и сохранит классификатор.
Итак, мы рассмотрели принципы работы алгоритма PCA и его реализации в sklearn. Я надеюсь, эта статья была достаточно понятна тем, кто только начинает знакомство с анализом данных, а также хоть немного информативна для тех, кто хорошо знает данный алгоритм. Интуитивное представление крайне полезно для понимания того, как работает метод, а понимание очень важно для правильной настройки выбранной модели. Спасибо за внимание!
P.S.: Просьба не ругать автора за возможные неточности. Автор сам в процессе знакомства с дата-анализом и хочет помочь таким же как он в процессе освоения этой удивительной области знаний! Но конструктивная критика и разнообразный опыт всячески приветствуются!
Узнаем, какие признаки текста позволяют назвать информативный отрезок письменной речи термином «текст».
Чтобы понять, какие признаки текста связывают несколько предложений в единое целое, прежде вспомним, что такое текст.
Определение
Текст — это несколько предложений, которые объединены темой и основной мыслью.
Все предложения и части текста (абзацы, параграфы, главы) должны раскрывать его тему и основную мысль.
Определение
Тема — это то, что о чем говорится в тексте (предмет речи). Тема может быть определена в заголовке текста.
Пример:
«Осенью в лесу», «Удачная рыбалка», «Поход за грибами», «Счастливый случай» и пр.
Определение
Основная мысль — это та идея, которую автор хочет объяснить читателю или в чем-то убедить его. Это то главное, ради чего создается текст.
В каждом тексте можно указать ряд основных признаков, в соответствии с которыми его можно назвать этим термином.
В раскрытии авторского замысла используются такие основные признаки текста, как тематическое единство, развернутость, последовательность, связность, законченность и цельность.
Рассмотрим более детально признаки текста, которые обеспечивают единство внешней и внутренней формы — его цельность.
Основные признаки текста
1. Тематическое единство. Все предложения в тексте или его части (абзацы) раскрывают его тему и основную мысль.
2. Развёрнутость. Тема текста раскрывается через подтемы или микротемы. Целостный подбор подтем обеспечивает более полное раскрытие темы. В большом по объему тексте подтемы могут уточняться микротемами. Подтемы и микротемы обеспечивают глубину текста и определяют способ развития основной мысли текста.
3. Членимость — это признак, который обозначает, что текст делится на структурные смысловые отрезки:
- предложения
- абзацы
- сложные синтаксические целые;
- параграфы
- главы.
Учтем, что одно предложение, даже очень распространенное и занимающее несколько строк в письменной речи, не является текстом.
4. Последовательность — это признак, который реализуется тогда, когда каждое последующее предложение содержит новую информацию для развертывания содержания текста. В каждом тексте прослеживается логическая последовательность развития мысли.
5. Связность — признак текста, который обеспечивает единство текста как смыслового целого. Набор разрозненных предложений не является текстом. Предложения в тексте последовательно связаны по смыслу и грамматически. Для связи предложений в тексте используются как лексические, так и грамматические средства (повторы, синонимы, местоимения, союзы, параллелизм синтаксических конструкций и пр.).
6. Цельность — это признак, который не допускает вставку языковых средств (лексических, грамматических или стилистических), противоречащих авторскому замыслу.
7. Законченность — это признак текста, который выражает завершенность текста. Небольшие тексты состоят в основном из трех частей: зачина (начала), средней части и концовки. Законченным, или завершенным, считается тот текст, в котором имеются три указанные части, а тема раскрыта полностью с точки зрения замысла автора.
8. Стилистическое единство текста предполагает использование лексических, грамматических средств в соответствии со стилем, к которому принадлежит текст (научный, официально-деловой, художественный, публицистический, разговорный стиль).
Вывод
Итак, тематическое единство, последовательность, связность, развернутость, завершенность и пр. признаки текста позволят определить, что рассматриваемый фрагмент письменной речи является текстом.
Средняя оценка: 4.6.
Проголосовало: 193
Признак предмета

4.6
Средняя оценка: 4.6
Всего получено оценок: 58.
Обновлено 28 Января, 2022
4.6
Средняя оценка: 4.6
Всего получено оценок: 58.
Обновлено 28 Января, 2022
Существующие в реальности предметы или явления можно описать, перечислить их признаки. Ученики 2 класса уже знают, что лексика русского языка содержит много слов со значением признака. Эти слова помогают при чтении «увидеть» в своём воображении предмет: большой дом или маленький домишко, лёгкое белое облако или чёрная грозовая туча, лопоухий щенок или лохматый пёс.
Что такое признак предмета
В грамматике признак предмета — это характеристика его свойств, качеств, внешнего вида о пр. Слово, которое обозначает признак предмета, непременно должно относиться к существительному и отвечать на вопрос «Какой?»
Прилагательное
Значение признака предмета — общее значение прилагательного как части речи. Прилагательное, называя признак объекта или явления, согласно правилам, должно полностью совпадать с существительным в формах числа, рода и падежа.
Примеры: Ваза (какая?) хрустальная — един. ч., жен. р., именит. пад.
Пледом (каким?) тёплым — един. ч., муж. р., творит. пад.
Дней (каких?) пасмурных — множ. ч., родит. пад.
Если прилагательное стоит в форме множественного числа, его род в ходе морфологического разбора определять не нужно.
Прилагательные могут называть самые разные признаки:
- по форме: круглый, треугольный, шарообразный;
- по размеру: огромный, крохотный, микроскопичный;
- по цвету: бурый, ярко-розовый, васильковый;
- по материалу: бумажный, железный, стеклянный;
- по способности к каким-то действиям: морозоустойчивый, кипучий, крикливый;
- по качествам материала или конструкции: хрупкий, жёсткий;
- по месту: городской, европейский, лесной;
- по принадлежности: охотничий, дедушкин, верблюжий;
- по вызываемым ощущениям: приятный, ненавистный, обаятельный.
В простой форме сравнительной степени прилагательное не изменяется ни по числам, ни по падежам. Эта сумка больше. Бабушкин сундук больше. В куртке карманы больше.
Причастия
Причастия обозначают признак предмета по действию, которое он совершает или которое совершают с ним. Поющий
человек (человек, который поёт). Спетая песня (её спели). Бригада, строившая дом (бригада, которая строила). Выстроенное здание (его выстроили).
Местоимения
Отдельные разряды местоимений указывают на признак предмета. Какой-то человек, который час, своя игра, такие слова.
Числительные
Порядковые числительные обозначают признак предмета по порядку счёта. Второй этаж, сто двадцать пятый член команды.
Существительные
Существительные могут обозначать признак предмета, выступая в роли несогласованного определения. Избушка, (какая?) с рухнувшей трубой и сломанным крыльцом, выглядела необитаемой. Иван Кузьмич, (какой?) в валенках и телогрейке, вовсе не был похож на бухгалтера.
Приложения — определения, выраженные существительными. В дверях стояла Анна Петровна, глава фирмы. Это было в городе Коломна. Его стихи напечатали в журнале «Мурзилка». На крыльцо школы выбежали девочки-старшеклассницы.
Глагол
Кратко скажем о редких случаях, когда признак предмета обозначает глагол. Такая способность у глагола есть только в неопределённой форме (инфинитиве). В этом случае глагол зависит от существительного Желание (какое?) петь. Умение (какое?) трудиться. Возможность (какая?) высказаться.
Что мы узнали?
Признак предмета — его свойство, качество. В русском языке, словами, называющими признак предмета, чаще всего являются прилагательные, причастия, порядковые числительные, местоимения. Реже значение признака выражают существительные и инфинитив глагола.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка статьи
4.6
Средняя оценка: 4.6
Всего получено оценок: 58.
А какая ваша оценка?
Уважаемые студенты!
Заказать решение задач по 200+ предметам можно здесь всего за 10 минут.
Исследовать на сходимость числовой ряд
Числовой ряд в общем виде задаётся следующей формулой: $$sum_{n=1}^infty a_n.$$ Разберем из чего состоит ряд. $a_n$ – это общий член ряда. $n$ – это переменная суммирования, которая может начинаться с нуля или любого натурального числа. Таким образом ряд расписывается следующим образом: $$sum_{n=1}^infty a_n = a_1+a_2+a_3+…$$ Слагаемые $a_1,a_2,a_3,…$ называются членами ряда. Если они неотрицательные, то ряд называется положительными числовым рядом.
Ряд расходится, если сумма его членов равна бесконечности: $$sum_{n=1}^infty n^2+1 = 2+5+10+…$$Ряд сходится, если сумма его членов равна конечному числу. Например, бесконечно убывающая геометрическая прогрессия: $$sum_{n=0}^infty frac{1}{2^n} = 1+frac{1}{2} + frac{1}{4}+frac{1}{8}+…$$ Её сумма вычисляется по следующей формуле $S = frac{A}{1-q}$, где $A$ – первый член прогрессии, а $q$ – основание. В данном случае сумма равна $S = frac{1}{1 – frac{1}{2}} = 2$.
Стоит заметить, что вычислить сумму ряда в большинстве случаев просто так не получится. Поэтому используют признаки сходимости, выполнение которых достаточно для установления сходимости ряда. Например, признаки Коши и Даламбера. Зависит это от общего члена ряда.
Необходимый признак сходимости ряда
Необходимый признак сходимости ряда нужно применять мысленно перед тем, как использовать достаточные признаки. Именно благодаря ему, можно заранее установить, что ряд расходится и не тратить время на проверку достаточными признаками. Для этого, нужно найти предел общего члена ряда и в зависимости от его значения сделать вывод.
- Если ряд сходится, то $limlimits_{nto infty} a_n = 0$
- Если $limlimits_{nto infty} a_n neq 0$ или не существует, то ряд расходится
ЗАМЕЧАНИЕ ! Первый пункт не работает в обратную сторону и нужно использовать достаточный признак сходимости. То есть, если предел общего члена ряда равен нулю, то это ещё не значит, что ряд сходится! Требуется использовать один из достаточных признаков сходимости.
| Пример 1 |
| Проверить сходимость числового ряда $sum_{nto 1}^infty n^2 + 1$ |
| Решение |
| Применяем необходимый признак сходимости ряда $$lim_{ntoinfty} n^2+1 = infty$$Так как получили бесконечность, то значит ряд расходится и на этом исследование заканчивается. Если бы предел равнялся нулю, то действовали бы дальше применяя достаточные признаки. |
| Ответ |
| Ряд расходится |
| Пример 2 |
| Проверить сходимость $sum_{nto 1}^infty frac{1}{n^2+1}$ |
| Решение |
| Ищем предел общего члена ряда $$lim_{xtoinfty} frac{1}{n^2+1} = 0$$Так как предел получился равным нулю, то нельзя сказать сходится или расходится ряд. Нужно применить один из достаточных признаков сходимости. |
| Ответ |
| Требуется дополнительное исследование |
Признаки сравнения
Обобщенный гармонический ряд записывается следующим образом $ sum_{n=1} ^infty frac{1}{n^p} $.
- Если $ p = 1 $, то ряд $ sum_{n=1} ^infty frac{1}{n} $ расходится
- Если $ p leqslant 1 $, то ряд расходится. Пример,$ sum_{n=1} ^infty frac{1}{sqrt{n}} $, в котором $ p = frac{1}{2} $
- Если $ p > 1 $, то ряд сходится. Пример, $ sum_{n=1} ^infty frac{1}{sqrt{n^3}} $, в котором $ p = frac{3}{2} > 1 $
Этот ряд пригодится нам при использовании признаков сравнения, о которых пойдет речь дальше.
Признак сравнения
Пусть даны два знакоположительных числовых ряда $sum_{n=1}^infty a_n$ и $sum_{n=1}^infty b_n$, причем второй ряд сходящийся. Тогда, если начиная с некоторого номера $n$ выполнено неравенство $a_n le b_n$, то ряд $sum_{n=1}^infty a_n$ сходится вместе с $sum_{n=1}^infty b_n$.
Предельный признак сравнения
Если предел отношения общих членов двух рядов $sum_{n=1}^infty a_n$ и $sum_{n=1}^infty b_n$ равен конечному числу и отличается от нуля $$lim_{ntoinfty} frac{a_n}{b_n} = A,$$то оба ряда сходятся или расходятся одновременно.
ЗАМЕЧАНИЕ. Предельный признак удобно применять когда хотя бы один из общих членов ряда представляет собой многочлен.
| Пример 3 |
| Исследовать сходимость ряда с помощью признака сравнения $$sum_{n=1}^infty frac{1}{n^3+n^2+1}$$ |
| Решение |
|
Проверяем ряд на необходимый признак сходимости и убеждаемся в его выполнении $$lim_{ntoinfty} frac{1}{n^3+n^2+1} = 0.$$ Теперь данный ряд нужно сравнить с одним из гармонических рядов. В данном случае видим, что в знаменателе старшая степень $n^3$, значит подойдет гармонический ряд $frac{1}{n^3}$, а он как известно сходится. Но нужно дополнительно мысленно проверить, что выполняется неравенство $n^3 le n^3+n^2+1$. Убедившись в этом получаем, что $$frac{1}{n^3+n^2+1} le frac{1}{n^3}.$$Это означает, что $sum_{n=1}^infty frac{1}{n^3+n^2+1}$ сходится. |
| Ответ |
| Ряд сходится |
| Пример 4 |
| Исследовать сходимость ряда с помощью признака сравнения $$sum_{n=1}^infty frac{1}{n^2-2n}$$ |
| Решение |
| Воспользуемся предельным признаком сравнения. Сравним данный ряд со сходящимся рядом $sum_{n=1}^infty frac{1}{n^2}$. Найти предел отношения общих членов двух рядов $$lim_{ntoinfty} frac{frac{1}{n^2}}{frac{1}{n^2-2n}} = lim_{ntoinfty} frac{n^2-2n}{n^2} =$$Выносим за скобку $n^2$ и сокращаем на него числитель и знаменатель $$lim_{ntoinfty} frac{n^2(1-frac{2}{n})}{n^2} = lim_{ntoinfty} (1-frac{2}{n}) = 1.$$ Итак, получили конечное число отличное от нуля, значит оба ряда сходятся одновременно. |
| Ответ |
| Ряд сходится |
Признак Даламбера
Признак рекомендуется использовать, если в общем члене ряда есть:
- Число в степени. Например, $2^n, 3^{n+1}$
- Присутствует факториал. Например, $(n+1)!,(2n-3)!$
Для исследования сходимости ряда по признаку Даламбера нужно найти предел отношения двух членов ряда: $$lim_{ntoinfty} frac{a_{n+1}}{a_n} = L$$
В зависимости от значения предела делается вывод о сходимости или расходимости ряда:
- При $0 le L le 1$ ряд сходится
- При $L > 1$ или $L = infty$ ряд расходится
- При $L = 1$ признак не даёт ответа и нужно пробовать другой
| Пример 5 |
| Исследовать ряд на сходимость по признаку Даламбера $$sum_{n=1}^infty frac{2^{n+1}}{n!}$$ |
| Решение |
|
Общий член ряда $a_n = frac{2^{n+1}}{n!}$, тогда следующий член ряда будет $$a_{n+1} = frac{2^{(n+1)+1}}{(n+1)!} = frac{2^{n+2}}{(n+1)!}$$ Теперь находим предел предыдущего и последующего членов ряда $$L=lim_{ntoinfty} frac{a_{n+1}}{a_n} = lim_{ntoinfty} frac{frac{2^{n+2}}{(n+1)!}}{frac{2^{n+1}}{n!}} = lim_{ntoinfty} frac{2^{n+2} n!}{(n+1)! 2^{n+1}}$$ Выполняем сокращение на $2^{n+1}$ и $n!$ и находим значение предела $$L=lim_{ntoinfty} frac{2}{n+1} = 0$$ Так как предел равен нулю ($L=0$), то ряд сходится по признаку Даламбера. |
| Ответ |
| Числовой ряд сходится |
| Пример 6 |
| Исследовать сходимость ряда по признаку Даламбера $$sum_{n=1}^infty frac{3^{n+1}}{sqrt{2n+5}}$$ |
| Решение |
|
Начинаем с того, что выписываем общий член ряда $$a_n = frac{3^{n+1}}{sqrt{2n+5}}.$$ Подставляем в него $n = n + 1$ и раскрываем скобки $$a_{n+1} = frac{3^{(n+1)+1}}{sqrt{2(n+1)+5}} = frac{3^{n+2}}{sqrt{2n+7}}.$$ Находим отношение следующего общего члена к предыдущему и упрощаем $$frac{a_{n+1}}{a_n} = frac{frac{3^{n+2}}{sqrt{2n+7}}}{frac{3^{n+1}}{sqrt{2n+5}}} = frac{(3^{n+2})sqrt{2n+5}}{sqrt{2n+7}(3^{n+1})} = frac{3sqrt{2n+5}}{sqrt{2n+7}}$$ Теперь вычисляем предел последней дроби, чтобы проверить признаком Даламбера сходимость. Для этого сократим числитель и знаменатель на $n$ $$L = limlimits_{ntoinfty} frac{3sqrt{2n+5}}{sqrt{2n+7}} = 3limlimits_{ntoinfty} frac{sqrt{2+frac{5}{n}}}{sqrt{2+frac{7}{n}}} = 3frac{sqrt{2}}{sqrt{2}} = 3.$$ Так как получился $L > 0$, то по признаку Даламбера представленный ряд расходится. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| Ряд расходится |
Радикальный признак Коши
Для установления сходимости ряда по радикальному признаку Коши нужно вычислить предел корня $n$ степени из общего члена ряда $$L = limlimits_{ntoinfty} sqrt[n]{a_n}.$$
- Если $L<1$, то ряд сходится,
- если $L>1$, то ряд расходится,
- если $L=1$, то признак не даёт ответа о сходимости.
Применяется данный признак в случаях, когда общий член ряда находится в степени содержащей $n$.
| Пример 7 |
| Исследовать ряд на сходимость $$sum_{n=1}^infty bigg(frac{3n+1}{2n+7}bigg)^{3n}.$$ |
| Решение |
|
Так как у общего члена есть тепень, в составе которой, присутствует $n$, то есть смысл попробовать применить радикальный признак сходимости Коши. Для этого, извлекаем корень $n$ степени из общего члена. $$sqrt[n]{bigg(frac{3n+1}{2n+7}bigg)^{3n}} = bigg(frac{3n+1}{2n+7}bigg)^3.$$ Теперь вычисляем предел полученного выражения. $$L = limlimits_{ntoinfty} bigg(frac{3n+1}{2n+7}bigg)^3 = limlimits_{ntoinfty}frac{(3n+1)^3}{(2n+7)^3}$$ Осталось вынести за скобки $n^3$ одновременно в числетеле и знаменателе. $$L=limlimits_{ntoinfty} frac{n^3(3+frac{1}{n})^3}{n^3(2+frac{7}{n})^3} = limlimits_{ntoinfty} frac{(3+frac{1}{n})^3}{2+frac{7}{n}} = frac{3}{2}.$$ Делаем вывод: так как $L > 1$, то представленный ряд расходится. |
| Ответ |
| Ряд расходится |
| Пример 8 |
| Исследовать сходимость ряда $$sum_{n=1}^infty frac{1}{3^n} bigg(frac{n}{n+1}bigg)^n.$$ |
| Решение |
|
Выписываем общий член ряда и извлекаем из него корень $n$ степени. $$sqrt[n]{frac{1}{3^n} bigg(frac{n}{n+1}bigg)^n} = frac{1}{3}frac{n}{n+1}$$ Вычисляем предел $$L = limlimits_{ntoinfty} frac{1}{3}frac{n}{n+1} = frac{1}{3} cdot 1 = frac{1}{3}.$$ Так как предел меньше единицы $L = frac{1}{3} < 1$, то данный ряд сходится. |
| Ответ |
| Ряд сходится |