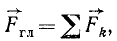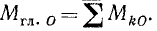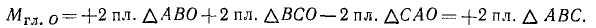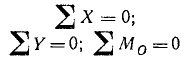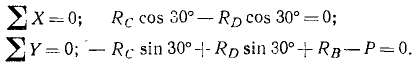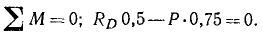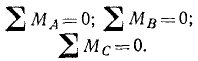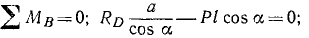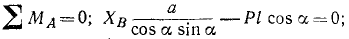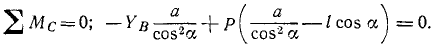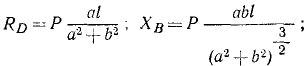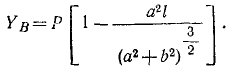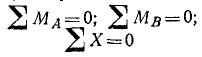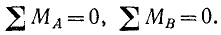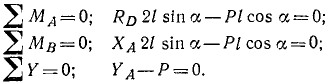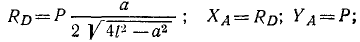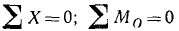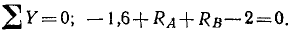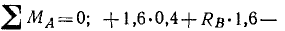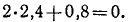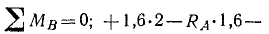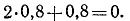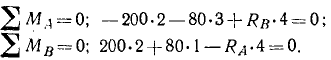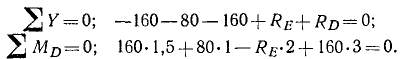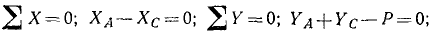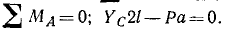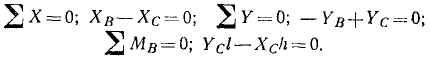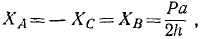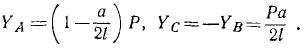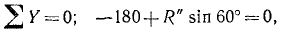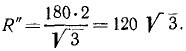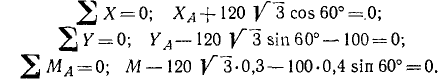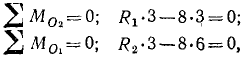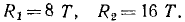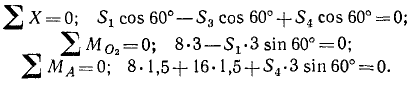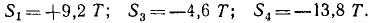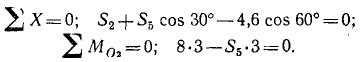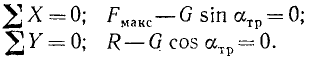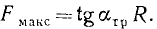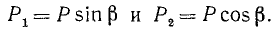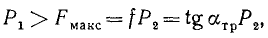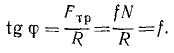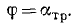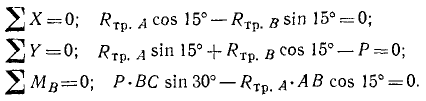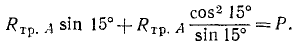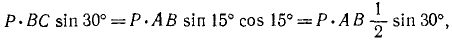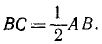Как найти главный вектор системы сил

Связь между моментами силы относительно оси и произвольной точки этой оси

Пусть даны сила
и осьl.
Возьмем произвольную точку О на оси l
и найдем вектор
(рис. 2.5). Обозначим γ угол, который
составляет векторс осьюl.
Возьмем другую точку
на осиl
и проводим через нее плоскость П
перпендикулярную оси l.
Спроектируем силу
на плоскость П. Из геометрии известно,
что если нормали к двум плоскостям
составляют угол γ, то и плоскости
составляют этот угол и для площадей
треугольников справедлива формула:

.
(2.8)

Домножим
формулу (2.8) на два:

.
(2.9)

В формуле (2.9)

,

.

Следовательно

или

.

Рис.
2.5

Момент силы
относительно оси равен проекции на эту
ось момента силы относительно любой
точки этой оси.

Главный вектор системы сил

Пусть дана система
сил
.

Определение.
Главным
вектором системы сил называется вектор,
равный геометрический сумме векторов
всех сил системы

.
(2.10)

Главный вектор
не является силой. Это свободный вектор,
полученный формальным сложением,
перенесенных в любую точку векторов
сил системы (рис. 2.6).

Способ нахождения главного вектора системы сил

Выберем некоторую
систему координат Oxyz.
По отношению к этой системе координат
силы можно разложить по ортам
:

,

,

.
(2.11)

По определению

.
(2.12)

Рис. 2.6

С другой стороны

.
(2.13)

Сравнивания формулы
(3.12) и (3.13), определяем проекции главного
вектора системы сил на оси Ox,
Оy,
Оz:

,
,.

Тогда по модулю

.
(2.14)

Направление
главного вектора системы сил определяется
направляющими векторами:

,
,(2.15)

Главный вектор
всегда можно найти, в отличие от
равнодействующей.

Пример.
Силы
ине пересекаются в одной точке,
следовательно, не эквивалентны одной
силе, то есть равнодействующей.

Главный вектор
можно взять в любой точке, напримерО
(рис.2.7).

Рис.
2.7

Главный момент системы сил

Пусть имеем систему
сил, действующую на материальный объект
.
Выберем также произвольную, фиксированную
точкуО.

Определение.
Главным
моментом системы сил относительно
некоторой точки О является приложенный
в этой точке вектор, равным геометрической
сумме моментов всех сил системы
относительно этой точки

.
(2.16)

Способ вычисления главного момента системы сил

В точке О
выберем систему координат (рис.2.8).
Разложим силы и главный момент системы
сил относительно точки О
по ортам

,
.

.
(2.17)

По определению

(2.18)

Рис. 2.8

Сравнивая формулы
(2.17) и (2.18), получим

,

,

.

Тогда модуль
главного момента системы сил равен

.

Направление
главного момента определится направляющими
косинусами
,,.

Главный момент
системы сил существенным образом зависит
от выбора точки О,
в отличие от главного вектора, который
от выбора точки О
не зависит.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Содержание:

1. Произвольная пространственная система сил
2. Аналитическое определение главного вектора и главного момента произвольной пространственной системы сил
3. Аналитические условия равновесия произвольной пространственной системы сил
4. Аналитические условия равновесия пространственной системы параллельных сил
5. Примеры решения задач на равновесие под действием пространственной системы сил
6. Условия равновесия несвободного твердого тела
7. Условия равновесия твердого тела с одной неподвижной точкой
8. Условия равновесия тела с двумя закрепленными точками
9. Инварианты сведения произвольной пространственной системы сил
10. Зависимость главного момента от выбора центра сведения
11. Инварианты системы сил
12. Частичные случаи возведения произвольной пространственной системы сил
13. Примеры возведения системы сил
14. Произвольная пространственная система сил и решение задач
15. Условия равновесия произвольной пространственной системы сил
16. Порядок решения задач на равновесие произвольной пространственной системы сил
17. Образец выполнения решения задач на темы С4
18. Момент силы относительно оси
19. Условия равновесия произвольной пространственной системы сил
20. Порядок решения задач на тему: Произвольная пространственная система сил
21. Примеры решения задачна тему: Произвольная пространственная система сил
22. Произвольная пространственная система сил и условия ее равновесия
23. Лемма о параллельном переносе линии действия сил
24. Главный вектор и главный момент сил. Основная теорема статики
25. Основная теорема статики
26. Условия равновесия произвольной пространственной системы сил
27. Условия равновесия системы сил в отдельных случаях
28. Условия равновесия твердого тела с неподвижной точкой
29. Условия равновесия твердого тела, имеющего две неподвижные точки или неподвижную ось
30. Условия равновесия произвольной плоской системы сил
31. Условия равновесия параллельных сил, которые лежат в плоскости
32. Трение качения. Равновесие при наличии сил трения
33. Пространственная система произвольных сил
34. Пары сил в пространстве
35. Теорема о переносе пары в параллельную плоскость
36. Условия эквивалентности пар в пространстве
37. Добавление пар в пространстве
38. Условия равновесия системы пар в пространстве
39. Возведение пространственной системы произвольных сил к данному центра. Главный вектор и главный момент системы
40. Вычисление главного вектора и главного момента пространственной системы произвольных сил
41. Некоторые случаи сведения пространственной системы произвольных сил к данному центру

Произвольной пространственной системой сил называется система сил, линии действия которых не лежат в одной плоскости. Согласно основной теореме статики (теореме Пуансо) любую произвольную систему сил, действующую на твердое тело, можно заменить эквивалентной системой, состоящей из силы (главного вектора системы) и пары сил (главного момента системы сил ).

На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.

Произвольная пространственная система сил

Произвольная пространственная система сил – это система сил, векторы которых
произвольным образом размещены в пространстве.

Как показано в § 5.2, произвольная пространственная система сил сводится к главному вектору  и главногу моменту 

а также доказано, что для равновесия этой системы сил необходимо и достаточно, чтобы главный вектор и главный момент системы были равны нулю:

В данном разделе выясним, как аналитически найти главный вектор и главный момент произвольной пространственной системы сил, установим аналитические условия ее уравновешивания, а также рассмотрим возможные частичные случаи возведения этой системы сил.

Аналитическое определение главного вектора и главного момента произвольной пространственной системы сил

Для вычисления главного вектора и главного момента произвольной пространственной системы сил используем метод проекции, для чего выберем декартову систему координат (рис. 9.1).

Проектируя первое уравнение (9.1) на оси выбранной системы координат, найдем проекции  главного вектора на оси:

 

Из формул (9.3) следует: проекция главного вектора системы сил на ось равна алгебраической сумме проекций всех сил системы на эту же ось.

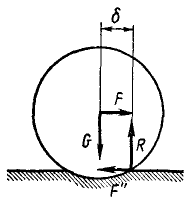
Модуль и направление главного вектора определяются формулами:

Проектируя второе равенство (9.1) на оси координат, получим:

или с учетом равенств (3.8), (3.10)

Итак, проекция главного момента относительно центра на любую ось, проходит через центр, равен алгебраической сумме моментов всех сил относительно этой же оси.

Алгебраическая сумма моментов всех сил, приложенных к механической системы, относительно любой оси называется главным моментом системы сил относительно этой оси. Главные моменты системы сил относительно координатных осей будем обозначать через Тогда из формул (9.5) следует, что: 

Модуль и направление главного момента определяются равенствами:

Заметим, что с учетом формул (3.12) главные моменты системы сил относительно координатных осей могут быть представлены через координаты  точек приложения сил и их проекции на оси координат, а именно:

Аналитические условия равновесия произвольной пространственной системы сил

С векторных условий равновесия (9.2) произвольной пространственной системы сил
следует, что модули главного вектора и главного момента должны равняться нулю, а на основе формул (9.4) и (9.6) это равносильно шести алгебраическим равенствам, которые выражают условия равновесия этой системы сил в аналитической форме:

Итак, для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил системы на три координатные оси и алгебраические суммы их моментов относительно этих самых осей были равны нулю.

Заметим, что условия равновесия (9.8) произвольной пространственной системы сил, приложенных к свободному твердому телу, будут необходимы, но не достаточными условиями равновесия этого тела. Как будет показано в динамике, свободное твердое тело, за выполнение условий равновесия (9.8), может двигаться поступательно, прямолинейно и равномерно вдоль осей координат и одновременно равномерно вращаться вокруг этих осей. Для того, чтобы условия равновесия (9.8) произвольной пространственной системы сил были одновременно и условиями равновесия свободного твердого тела, к которому эта система сил приложена, нужно, чтобы в приложения данной системы сил тело находилось в покое относительно выбранной системы отсчета.

Аналитические условия равновесия пространственной системы параллельных сил

Если линии действия всех сил системы не расположены в одной плоскости и параллельные между собой, то такая система сил называется пространственной системой параллельных сил.

С условий равновесия (9.8) для произвольной пространственной системы сил получим условия равновесия пространственной системы параллельных сил.

Пусть на твердое тело действует пространственная система параллельных сил (рис. 9.2). Поскольку выбор координатных осей произвольный, то можно выбрать координатные
оси так, чтобы ось была параллельна к силам. При таком выборе координатных осей
проекции каждой из сил на оси х и у и их моменты относительно оси будут равны нулю, то есть равенства: 

превращаются в тождества. Поэтому для системы параллельных сил с (9.8) получим только три условия равновесия:

Итак, для равновесия пространственной системы параллельных сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил на ось, параллельную этих сил, и алгебраические суммы их моментов относительно двух других координатных осей были равны нулю.

Заметим, что выведенные ранее условия равновесия для сходящейся и произвольной плоской системы сил могут также быть получены из условий равновесия (9.8).

Условия равновесия различных систем сил приведены в табл. 9.1.

Таблица 9.1

Условия равновесия систем сил

Примеры решения задач на равновесие под действием пространственной системы сил

Задача 9.1. С помощью коловорота (рис. 9.3) удерживается груз, вес которого Пренебрегая весом коловорота, определить давление на подшипники А и В и силу которую нужно приложить перпендикулярно к рукоятке СD длиной 54 см, при ее вертикальном положении. Радиус барабана r = 12 см.

Решение. При содержании груза сила натяжения шнура равна весе груза Р.

Рассматривая круговорот как свободное тело, приложим к нему активные силы и реакции которые возникают в подшипниках А и В. На водоворот действует произвольная пространственная система сил, которая должна удовлетворять условиям равновесия (9.8). Выбираем оси координат, как показано на рис. 9.3, и составляем уравнения равновесия:

 -это уравнение удовлетворяется тождественно:

Решая эту систему уравнений, находим неизвестную силу и реакции в опорах:

Задача 9.2. Тонкая однородная плита ABCD весом P = 6 кН поддерживается в горизонтальном положении шестью опорными стержнями (Рис. 9.4).

К плите в точке А приложена горизонтальная сила F = 2,4 кН, которая действует по прямой АD. Пренебрегая весом стержней и считая их крепления шарнирными, определить усилия в них, если

Решение. Рассмотрим равновесие плиты. Активными силами, приложенными к плите, будут силы и вес плиты которая приложена в центре симметрии прямоугольника АВСD. Действие шести стержней на плиту заменяем реакциями. Считаем по-прежнему, что все стержни растянуты и их реакции направлены от узлов (рис. 9.4).На плиту действует произвольная пространственная произвольная система сил и при ее равновесии должны выполняться условия (9.8).

Составляем уравнение равновесия:

Учитывая заданные размеры, вычисляем синусы и косинусы углов α и β:

Решая полученную систему уравнений равновесия, найдем усилия:

С решении задачи следует, что стержень 2 растянут, стержни 3 и 6 сжаты, а 1, 4 и 5 – ненагруженные.

Задача 9.3. Подъемный кран (рис. 9.5) установлен на трехколесном коляске. Известны размеры крана AD = DB = 1 м, CD = 1,5 м, СМ = 1 м, KL = = 4 м. Кран уравновешивается противовесом Е. Вес Р крана с противовесом равен 80 кН и приложена в точке О, расположенной в плоскости LSTM на расстоянии ОН = 1 м от оси крана MК. Найти
давление колес на рельсы для такого положения крана, когда его плоскость LSTM параллельная АВ, а вес поднимаемого груза, равен Q = 40 кН.

Решение. Объектом равновесия выбираем тележку вместе с краном. На кран действуют две вертикальные силы: вес крана с противовесом и вес груза Действие связей А, В и С заменяем реакциямии  которые направлены вертикально вверх (трением в опорах пренебрегаем). Механическая система (кран – тележка) находится в равновесии
под действием пространственной системы параллельных сил, которая удовлетворяет условиям равновесия (9.9).

Направляем оси координат, как показано на рис. 9.5, и складываем уравнения равновесия

Решая эту систему, найдем неизвестные реакции

Давление колес на рельсы численно равна найденным реакциям и направлено вертикально вниз.

Условия равновесия несвободного твердого тела

Под условиями равновесия несвободного твердого тела будем понимать те условия, которые должны удовлетворять активные силы, чтобы несвободное тело находилось в состоянии равновесия.

Условия равновесия твердого тела с одной неподвижной точкой

Если твердое тело с одной закрепленной точкой О (рис. 9.6), которую считаем сферическим шарниром, освободить от этой связи, то для составляющих силы реакции и приложенных к телу активных сил можно составить шесть условий равновесия:

Три первых уравнения в (9.10) содержат неизвестные реакции точки В и являются уравнениями равновесия. Задача статически означена. Приложенные к телу силы
удовлетворяют трем аналитическим условиям равновесия, в которые не входят неизвестные составляющие реакции связи: алгебраические суммы моментов активных сил
относительно координатных осей с началом в закрепленной точке равны нулю. С учетом формул (9.7) аналитические условия равновесия твердого тела с одной закрепленной точкой запишутся в виде:

Условия равновесия тела с двумя закрепленными точками

Рассмотрим условия, которые должны удовлетворять активные силы приложенные к твердому телу с двумя неподвижными точками А и В, то есть с неподвижной осью АВ (рис. 9.7), чтобы оно находилось в состоянии равновесия.

Для исследования этого вопроса применим аксиому освобождение от связей. Поскольку реакции связей в точках А и В являются неизвестными по величине и направлением, разложим каждую на три составляющие, направив эти составляющие по положительных направлениях координатных осейкоторые выбираем так, как показано на рис. 9.7.

Составим уравнения равновесия рассматриваемого твердого тела, предположив, что АВ = h. иметь:

Рассматривая уравнения (9.12), видим, что первые пять уравнений устанавливают зависимость между реакциями связей в точках А и В и активными силами. В шестом уравнения входят только активные силы. Итак, это уравнение и является условием равновесия твердого тела с двумя неподвижными точками, которая формулируется так: несвободное твердое тело с двумя закрепленными точками (или неподвижной осью) будет находиться в равновесии, если алгебраическая сумма моментов активных сил относительно неподвижной оси равна нулю.

Заметим, что в задачи неизвестных реакций шесть, а уравнений для их определение лишь пять и, следовательно, всего пять неизвестных можно определить. Из уравнений (9.12) видно, что отдельно невозможно определить и можно определить только их сумму Задача определения сил реакций есть статически неопределенной. Для того, чтобы ее сделать статически обозначенной, в одной из точек вместо сферического нужно поставить цилиндрический шарнир. Если цилиндрический шарнир поставить в точке А, тогда так как реакция цилиндрического шарнира перпендикулярна его оси, в нашем случае перпендикулярной оси После этого неизвестных реакций будет только пять и задача станет статически обозначенной.

Инварианты сведения произвольной пространственной системы сил

Вернемся к анализу основной теоремы статики о возведении произвольной пространственной системы сил к заданному центру. Выясним, как меняется главный момент от изменения центра сводки, и установим инварианты сведения.

Зависимость главного момента от выбора центра сведения

Предположим, что в результате возведения произвольной пространственной системы
силк центру О получено главный вектор  и главный момент а в результате возведения к центру  соответственно (Рис. 9.8). Главный вектор для любого центра возведения равна геометрической сумме заданных сил, следовательно Главный момент, как видно из формулы (5.2), зависит от выбора центра сводки.

Найдем выражения главных моментов относительно двух центров и сравним их.

Радиусы-векторы точек приложения заданных сил системы относительно этих центров обозначим соответственно через Имеем

Поскольку

поэтому

Итак, главный момент системы сил относительно нового центра возведения равен геометрической сумме главного момента относительно старого центра сведения В и момента главного вектора, приложенного в старом центре сведения, относительно нового.

Инварианты системы сил

Инвариантом сведения системы сил называют величину (векторную или скалярную), которая не изменяется при переходе от одного центра сведение к другому.

Первый инвариант. Главный вектор системы сил не зависит от центра возведения и является первым векторным инвариантом

Второй инвариант. Скалярное произведение главного вектора и главного момента системы сил для произвольного центра сведения – величина постоянная и является вторым скалярным инвариантом.

Для доказательства умножим скалярно обе части равенства (9.13) на главный вектор Тогда 

Поскольку (первый инвариант), то векторы  взаимно перпендикулярны, а потому смешанный произведение   всегда равен нулю и последнее равенство примет вид

То есть 

Второй инвариант можно представить и в другой форме: проекция главного момента на направление главного вектора для произвольного центра возведения есть величина неизменная.
Действительно, 

Согласно (9.14)

 а потому

Частичные случаи возведения произвольной пространственной системы сил

Согласно основной теореме статики, заданную систему сил можно свести к силе и паре сил. Частные случаи возможного дальнейшего упрощения заданной системы сил можно разделить на два основных класса в зависимости от величины второго инварианта системы сил.

К первому классу относят системы сил, для которых второй инвариант отличный от нуля; ко второму – системы сил, для которых второй инвариант равен нулю.

Если система сил относится к первому классу то она может быть сведена к силовому винту, или до двух скрещивающихся сил. В случае, когда система сил относится ко второму классу то силовой винт вырождается, то есть эта система сил может быть уравновешена, или сводится к равнодействующей или пары сил.

Рассмотрим отдельно эти два класса системы сил.

1. Сведения произвольной пространственной системы сил к силовому винту (динами). Система сил, которая состоит из силы и пары силплоскость действия которой перпендикулярна к линии действия силы называется силовым винтом, или динамою (рис. 9.9).

Система сил, которая образует силовой винт, прикладывается, например, к гайке, винту, штопора при их закручивании. Момент пары сил  входящей в силовой винт, параллельный линии действия силы

Докажем, что в случае, когда второй инвариант не равен нулю, система сил сводится к силовому винту.

Предположим, что в результате сведения заданной системы сил к центрку О получено главный вектор   и главный момент для которых (рис. 9.10).

Если скалярное произведение и главный вектор
  не перпендикулярно к главному моменту  Разложим вектор на две компоненты: первая из которых параллельна вектору А вторая – перпендикулярна к нему. Заметим, что расписание главного момента на две компоненты означает эквивалентную замену одной пары сил двумя.

В соответствии со вторым инвариантом вектор как коллинеарная составляющая главного момента по направлению главного вектора, является для данной системы сил величиной постоянной, не зависящей от выбора центра сведения Следовательно, при изменении центра сведения, меняться только перпендикулярна составляющая

Если выбрать новую точку сведения то получим главный вектор и главный момент, которые согласно (9.13) и (9.14) будут равны

Положение точки выбираем так, чтобы то есть 

С последнего равенства следует, что 

В новой точке сведения совокупность силы и пары сил с моментом  образуют силовой винт (динаму).

По правилу векторного произведения, вектор перпендикулярен вектору  то есть будет лежать в плоскости П (рис. 9.10).

Поскольку силу можно перенести по линии действия в любую точку, а момент пары сил является вектором свободным, то исходная система сил приводится к динами во всех точках прямой которая является линией действия силы Линия вдоль которой действует динамический винт, называется центральной осью заданной системы
сил. У системы сил может быть только одна центральная ось, причем, главный момент системы является наименьшим среди главных моментов заданной системы
сил относительно различных центров.

Уравнение центральной оси получим с условия коллинеарности главного вектора и главного момента для центра в векторной и скалярной формах:

где p – постоянная величина, которая называется параметром винта и имеет размерность длины;  и – соответственно проекции главного вектора и главного момента на координатные оси

Учитывая, что  

векторное уравнение (9.18) запишется в виде 

Выражение (9.19) является уравнением центральной оси в векторной форме. Искомой переменной в этом уравнении является вектор

Если начало системы координат совместить с точкой O, то

где – проекции вектора   на координатные оси .

Векторное произведение  согласно уравнению (3.9) равно

Скалярное уравнение (9.18) с учетом выражений для и векторного произведения запишется в виде

 

где – проекции главного момента на координатные оси .
Выражение (9.20) является искомым уравнением центральной оси заданной системы
сил.

2. Возведение системы сил к двум скрещивающихся силам. Покажем, что произвольную систему сил, для которой второй инвариант можно еще свести и к двум скрещивающихся силам.

Пусть в результате возведения заданной системы сил к центру В получено главный вектор   и главный моментдля которых то есть не перпендикулярен  (рис. 9.11).

Главный момент представим в виде пары сил одна из которых проходит через точку В, то есть  Система сходящихся сил имеет равнодействующую а потому исходная система сил эквивалентна двум силам и которые лежат в разных плоскостях, то есть скрещивающимися.

3. Случаи вырождения силового винта. Рассмотрим теперь второй класс систем сил, для которых второй инвариант равен нулю:

Этот класс систем сил частным случаем систем сил, рассмотренных выше, а потому случаи их возведения является вырождением силового винта. Проанализируем отдельные случаи равенства нулю второго инварианта.

– главный вектор и главный момент равны нулю. В этом случае система сил уравновешивается.

– главный вектор равен нулю, а главный момент отличен от нуля. В этом случае система сил сводится к паре сил с моментом, равным главному моменту системы сил, который не зависит от выбора центра приведения (это следует из формулы (9.13)).

– главный вектор отличный от нуля, а главный момент равен нулю. В этом случае система сил сводится к равнодействующей.

– главный вектор и главный момент отличные от нуля и взаимно перпендикулярны. В этом случае относительно нового центра систему сил можно свести к равнодействующей. Действительно, если то, как следует из этого параграфа, и и силовой винт в центре  превращается в равнодействующую силу

Уравнение центральной оси (9.20) в этом случае будет уравнением прямой, вдоль которой действует равнодействующая сила.

Классификация системы сил в зависимости от их инвариантов приведены в табл. 9.2.

Таблица 9.2

Возведение произвольной пространственной системы сил к простейшему виду

Примеры возведения системы сил

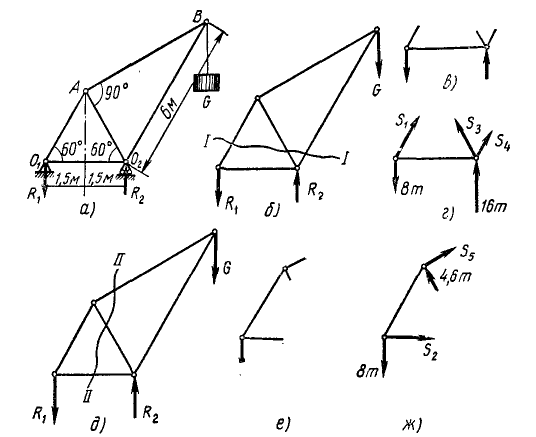
Задача 9.4. Свести к простому виду систему сил, которая изображена на рис. 9.12, а. Силы, приложенные к вершинам куба, ребро которого равно а;

Решение. Принимаем в центр сведения точку О. Оси координат показано на рис. 9.12, а. Находим проекции главного вектора  на оси

Модуль главного вектора 

Главные моменты системы сил относительно осей

Модуль главного момента 

Относительно центра О система сил свелась к главному вектору  и главного момента которые изображены на рис. 9.12, б.

Проверяем второй инвариант: 

Второй инвариант равен нулю, а и  а потому 

Итак, относительно точки сведения система сил сводится к равнодействующей.

Уравнение линии действия равнодействующей найдем по формуле (9.20)

Учитывая найденные величины  уравнения линии действия равнодействующей приобретает вид  откуда  то есть линия действия равнодействующей лежит в плоскости параллельная оси и проходит на расстоянии х = a от нее (рис. 9.12, б).

Задача 9.5. Свести к простому виду систему четырех одинаковых по значению сил которые действуют вдоль ребер куба со стороной a (рис. 9.13, а).

Решение. Центром сведения выберем точку В и подсчитаем проекции и модули главного вектора и главного момента:

Теперь подсчитаем значение второго инварианта системы сил:

Поскольку второй инвариант не равен нулю, то система сил сводится к динами с минимальным моментом который равный по значению 

Подставляя в формулу (9.20) найденные значения получим уравнение центральной оси системы сил 

откуда 

то есть центральная ось определяется как пересечение плоскостейи и 
совпадает с диагональю АС передней грани куба (рис. 9.13, б).

Итак, заданная система сил приводится к динами, образованного силой направленных вдоль линии АС, и парой сил с моментом которая лежит в плоскости, перпендикулярной АС.

Произвольная пространственная система сил и решение задач

Произвольной пространственной системой сил называется система сил, линии действия которых не лежат в одной плоскости.

Условия равновесия произвольной пространственной системы сил

Условия равновесия произвольной пространственной системы сил можно записать следующим образом:

 

Таким образом, для равновесия произвольной пространственной системы сил, приложенной к твердому телу, необходимо и достаточно, чтобы суммы
проекций всех сил на каждую из трех координатных осей, а также суммы их моментов относительно каждой из этих осей равнялись бы нулю.

Момент силы относительно оси определяется как алгебраическая величина, абсолютное значение которой равняется произведению  модуля проекции силы на плоскость, перпендикулярную оси, на расстояние от точки пересечения оси с этой плоскостью до линии действия проекции силы на плоскости (рис.С4.1).

Для определения момента силы относительно оси надо:

а) провести плоскость  которая перпендикулярна до оси;

б) спроектировать силу на эту плоскость 
в) из точки пересечения О оси с плоскостью  опустить перпендикуляр  на линию действия проекции силы;

г) умножить модуль проекции силы  на длину перпендикуляра  и взять произведение положительным, когда направление вращения проекции силы из положительного направления оси  видно против хода часовой стрелки, и отрицательным, когда вращение видно по ходу часовой стрелки.

Момент силы что изображена на рис. С4.1, относительно оси  равняется Момент положительный, поскольку вращение проекции силы вокруг
оси  из положительного направления оси видно против хода часовой стрелки.

Момент силы относительно оси равен нулю в двух случаях:

1. Когда сила параллельна оси (рис.С4.2, а). В этом случая проекция силы на плоскость равна нулю.
2. Когда линия действия силы пересекает ось (рис.С4.2, б). В этом случае плечо проекции силы равно нулю.

Порядок решения задач на равновесие произвольной пространственной системы сил

При решении задач на равновесие произвольной пространственной системы сил целесообразно придерживаться следующего порядка:

1. Выделить твердое тело, равновесие которого необходимо рассмотреть для нахождения неизвестных величин (объект равновесия).

2. Показать активные силы, что на него действуют.

3. Выяснить характер связей и показать возможные направления их реакций.

4. Проверить, принадлежит ли данная задача к статически определенным, когда число неизвестных величин должно равняться шести.

5. Составить шесть уравнений равновесия.

6. Решить систему уравнений относительно неизвестных величин.

Образец выполнения решения задач на темы С4

Задача 6

Задано: квадратная плита АВСD: АВ = ВС = СД = ДА = АЕ; Р = 1000 Н (рис.1).
 

Определить: реакцию сферического шарнира А, реакцию цилиндрического шарнира В,
реакцию невесомого стержня СЕ.
 

Решение. Поскольку задача представляет собой пространственную, то начало системы координат свяжем с точкой A, оси и   разместим в плоскости плиты АВСD,
а ось направим перпендикулярно к ней.

Объект равновесия, квадратная плита АВСD, находится в равновесии под действием (см.
П.С1.4, задача № 6) веса плиты  приложенной в центре симметрии плиты; реакции
невесомого стержня, которая направленная вдоль него от С до Е;
реакции сферического шарнира А, которую раскладываем на три составляющие  по осям выбранной системы координат; реакции петли (цилиндрического шарнира) В, которую раскладываем на две составляющие 
Составляющая реакции этого шарнира, параллельная оси  равняется нулю, поскольку шарнир позволяет свободно смещать плиту в этом направлении.

Для записи условий равновесия пространственной системы сил целесообразно пользоваться проекциями пространственной системы сил на плоскости координатной системы.

Рассмотрим проекцию системы сил на плоскость  (рис.2). Силы, 
проектируются в натуральную величину. Проекции и   равны нулю,
поскольку они перпендикулярны к данной плоскости.

Проекцию силы  на плоскость  можно определить таким образом (рис.1):

где 

Запишем сумму проекций всех сил на оси  и  и сумму моментов относительно оси 

Рассмотрим систему сил в проекции на плоскость  (Рисс.3). Силы 
проектируются в натуральную величину. Проекции составляющих, 
равны нулю, поскольку они перпендикулярны к данной плоскости.

Проекцию силы  на плоскость  можно определить так (рис.1):

Воспользовавшись рис. 3 можно сохранить сумму проекций сил на ось  и сумму моментов этих сил относительно оси 

где 

Рассмотрим проекцию системы сил на плоскость  (рис.4). Силы  проектируются в натуральную величину. Проекция силы  равняется нулю. Проекцию силы  на плоскость  можно определить так
(Рис.1):

Запишем сумму моментов всех сил относительно оси 

где 

Перепишем записанную систему (1) – (6) со всеми подстановками в следующей последовательности:

Из уравнения (11) находим реакцию  невесомого стержня CE:

Затем, решив последовательно уравнение (10), (9), (8), (7), достанем 

Ответ: 

 

Момент силы относительно оси

Момент силы относительно оси определяется как алгебраическая величина, абсолютное значение которой равно произведению модуля проекции силы на плоскость, перпендикулярную оси, на расстояние от точки, в которой ось пересекает эту плоскость, к линии действия проекции силы на плоскости.

Для того, чтобы найти момент силы относительно оси, надо сделать следующее (рис.7.1): 1. Провести плоскость (), перпендикулярную оси.

2. Спроектировать силу  на эту плоскость.

3. Из точки пересечения оси с плоскостью () опустить перпендикуляр на линию действия проекции силы .

4. Умножить модуль проекции силы на длину  перпендикуляра и взять это произведение со знаком плюс, если с положительного направления оси вращения проекции вокруг точки видно против хода часовой стрелки, и со знаком минус, если вращение происходит по ходу часовой стрелки.

Таким образом, момент силы вокруг оси (рис.7.1) равен

Момент силы будет положительным, поскольку направление вращения проекции вокруг оси с положительного стороны оси видно против хода часовой стрелки.

Момент силы относительно оси равен нулю в двух случаях:

1. Если линия действия силы параллельна оси (рис.7.2). В этом случае проекция силы на плоскость, перпендикулярную оси, будет равна нулю.

2. Когда линия действия силы пересекает ось (рис.7.3). В этом случае плечо проекции относительно точки будет равняться нулю.

Условия равновесия произвольной пространственной системы сил

Аналитические условия равновесия произвольной пространственной системы сил выражаются следующими уравнениями:

и формулируется так: для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую из трех координатных осей и суммы их моментов относительно каждой из этих осей равнялись  нулю.

Порядок решения задач на тему: Произвольная пространственная система сил

При решении задач на равновесие произвольной пространственной системы сил рекомендуется придерживаться такой последовательности:

1. Выделить твердое тело, равновесие которого надо рассмотреть для определения неизвестных величин.

2. Показать активные силы, действующие на объект равновесия.

3. Выяснить характер связей и показать на расчетной схеме возможные направления их реакций.

4. Проверить, является ли рассматриваемая задача статически определенной, то есть число неизвестных величин не должно быть больше шести.

5. Составить необходимое число уравнений равновесия.

6. Решить полученную систему уравнений и определить неизвестные величины.

Примеры решения задачна тему: Произвольная пространственная система сил

Задача №1

На горизонтальный вал (рис.7.4) насажено зубчатое колесо  и шестерня . К колесу по касательной приложена горизонтальная сила , а к шестерне по касательной приложена вертикальная сила .

Определить величину силы  и реакции подшипников  и  в положении равновесия вала, если  

Решение. Рассмотрим равновесие вала , к которому приложены активные силы , и реакции связей опор  и  (рис.7.4).

Поскольку подшипники  и  допускают перемещения в осевом направлении и в этом направлении нет противодействия, то реакции, возникающие в подшипниках, разложим на составляющие по осям и : , , , .

Как видно, на вал действует произвольная пространственная система сил и в случае ее равновесия она должна удовлетворять следующим условиям:

Составим уравнения равновесия в проекциях на оси:

При составлении уравнений моментов сил, надо помнить, что когда сила параллельна оси или пересекает ее, то момент силы относительно этой оси равен нулю.

Так при составлении уравнения суммы моментов относительно оси , силы , ,   параллельны оси , а сила – пересекает ось. Момент каждой из этих сил относительно оси равен нулю.

При определении момента силы относительно оси , силу предварительно надо спроектировать на плоскость (она проектируется в натуральную величину), а затем из точки пересечения оси с плоскостью (точка ) опустить перпендикуляр на линию действия проекции, который и будет ее плечом. Таким образом:

В уравнении моментов относительно оси , моменты от сил , , ,  равняются  нулю, поскольку они пересекают ось .

Для определения моментов сил  и  относительно оси , надо их спроектировать на плоскость , перпендикулярную этой оси (рис.7.5), и найти плечо этих сил. Силы и проецируются на эту плоскость в натуральную величину.

Плечом силы будет радиус , а силы – радиус .

Уравнение суммы моментов относительно этой оси будет иметь вид:

Поскольку моменты сил , , , что параллельны оси , и силы , пересекающей эту ось, равны нулю, а плечом проекции силы на плоскость , перпендикулярную оси , будет , то

С учетом числовых данных уравнения равновесия примут вид:

Решив эту систему, начиная с последнего уравнения, найдем:

Ответ:  

Задача № 2

С помощью невесомого коловорота, схематично изображенного на рис. 7.6., равномерно поднимают груз Веревка, на которой поднимается груз, набегает на барабан коловорота по касательной, которая наклонена к горизонту под углом

Размеры коловорота:  

Определить реакции опор  и  и силу давления на рукоятку при таком положении ворота, когда рукоятка займет горизонтальное положение.

Решение. К коловороту приложены внешние силы: давление на рукоятку ворота в точке ; натяжение веревки . Вес груза передается через веревку и действует на барабан по касательной, которая наклонена к горизонту под углом (рис.7.6), по модулю 

Поскольку опорные подшипники  и  допускают перемещение вала по направлению оси , то реакции опор будут иметь составляющие, направленные вдоль осей  и : , , , . 

Составим уравнение равновесия для произвольной пространственной системы сил, действующей на коловорот. В проекциях на оси получим:

Для удобства определения моментов сил , и относительно оси , спроецируем эти силы на плоскость перпендикулярную этой оси (рис.7.7).

где  – величина проекции силы на плоскость ,

,  и  – плечи сил ,  и  относительно точки , в которой ось  пересекает плоскость .

Для записи уравнения суммы моментов относительно оси спроецируем все силы на плоскость (рис.7.8). Поскольку, силы , ,  и пересекают ось и их моменты относительно этой оси будут равны нулю, то на рис.7.8 их проекции не показаны.

Силы  и , которые параллельны плоскости , будут проецироваться в натуральную величину. Тогда:

И наконец, для суммы моментов относительно оси спроецируем все силы на плоскость (рис.7.9). Поскольку силы , и перпендикулярны плоскости , то их проекции на эту плоскость равны нулю.

Уравнение моментов относительно оси , с учетом того, что сила пересекает эту ось и ее момент равен нулю, будет иметь вид

где  – величина проекции силы на плоскость ,

 и  – плечи сил  и  относительно точки , в которой ось  пересекает плоскость .

С учетом числовых данных система (1) – (6) примет вид:

Решив систему, начиная с последнего уравнения, определим:

Ответ:  

Задача № 3

Прямоугольная дверь (рис.7.10), которая открыта на удерживаются в этом положении двумя веревками и . Веревка перекинута через блок и натягивается грузом а веревка прикреплена к полу в точке . Вес двери ширина высота

Определить натяжение веревки , реакции цилиндрического шарнира в точке и подпятника в точке .

Силами трения в блоке пренебречь.

Решение. Рассмотрим равновесие дверей . Примем за начало системы координат точку и направим координатные оси как показано на рис. 7.10.

На двери действуют: сила тяжести , приложенная в точке на пересечении диагоналей прямоугольника ; натяжение веревки , причем реакции связей в точках ,  и .

Реакции цилиндрического шарнира , поскольку он допускает перемещение в направлении оси , представим в виде двух составляющих:  и . Реакции подпятника представим в виде трех составляющих: , , . Реакцию веревки , что по величине равна ее натяжению, направим вдоль веревки к точке .

Перед составлением уравнений равновесия разложим натяжение веревки на две составляющие и , которые параллельны осям  и , соответственно (рис.7.11).

Поскольку и то треугольник будет равносторонним, у которого все внутренние углы равны .

С рис. 7.11. получим:

Составим уравнения равновесия для произвольной пространственной системы сил, действующей на дверь:

Для составления уравнений моментов всех сил относительно осей ,  и   воспользуемся проекциями двери, вместе с приложенными к ней силами, на плоскости , и (рис.7.12, 7.13, 7.14).

В уравнении (4) моменты от сил ,  и , параллельных оси , и , что пересекает ось , равны нулю.

В уравнении (5) моменты относительно оси от сил , ,  и , что параллельны оси , и и , что пересекают ось , равны нулю.

В уравнении (6) моменты относительно оси от сил и , параллельных оси , и , ,  и , что пересекают ось , равны нулю.

Определим плечи  и , входящих в уравнения (4), (5) и (6).

Из прямоугольного треугольника (рис.7.14, 7.11):

Из прямоугольного треугольника (рис.7.14):

Из прямоугольного треугольника  (рис.7.14):

Подставив найденные и заданные числовые данные в составленную систему (1) – (6), получим:

Решив систему (1’) – (6’) в обратном порядке получим:

Ответ:  

Задача № 4

Горизонтальная однородная прямоугольная плита весом удерживается в равновесии сферическим шарниром в точке , цилиндрическим шарниром в точке и тросом , что наклонен к плоскости под углом  (рис.7.15).

Определить реакции опор  и , и натяжение троса , если

Решение. Рассмотрим равновесие плиты  (рис.7.15).

Выберем за начало системы координат точку и направим оси  и  вдоль ребер плиты, а ось – вертикально.

На объект равновесия действуют: вес плиты , приложенной в точке пересечения диагоналей прямоугольника ; реакции связей в точках ,  и .

Реакцию сферического шарнира разложим на три составляющие ,  и , направив их по осям выбранной системы координат . Реакции цилиндрического шарнира , так как он допускает перемещение в направлении оси , разложим на две составляющие и . Реакцию троса направим вдоль троса к точке подвеса .

Таким образом, на объект равновесия, плиту, действует произвольная пространственная система сил.

Прежде чем составлять уравнения равновесия, разложим реакцию , которая направлена под углом к плоскости , на составляющие по осям выбранной системы координат (рис.7.15):

где  – модуль проекции вектора на плоскость ;

При составлении уравнений равновесия в данной задаче будем придерживаться следующего порядка. Сначала спроектируем систему сил, действующую на объект равновесия, на одну из координатных плоскостей, а затем составим соответствующие уравнения.

Спроецируем все силы, действующие на плиту , на координатную плоскость (рис.7.16). При этом надо помнить, что при проектировании всегда надо смотреть на плоскость с положительного конца оси, перпендикулярной к ней, в данном случае . (На рис.7.16 проекции сил , ,  и , перпендикулярные плоскости , равны нулю).

По данной проекции системы сил можно составить три уравнения равновесия: сумму проекций всех сил на ось ; сумму проекций всех сил на ось ; сумму моментов всех сил относительно оси , что перпендикулярна плоскости и пересекает ее в точке :

В уравнении (3) моменты сил ,   и , линии действия которых проходят через точку , пересекают ось ), равны нулю.

Спроектируем все силы, действующие на плиту , на плоскость (рис.7.17). (На рис.7.17 проекции сил и , перпендикулярных плоскости , равны нулю).

По данной проекции системы сил можно составить следующие уравнения равновесия: сумму проекций всех сил на ось (это уравнение уже составлено); сумму проекций всех сил на ось ; сумму моментов всех сил относительно оси , которая перпендикулярна  плоскости и пересекает ее в точке :

В уравнении (5) моменты сил , , , ,  , линии действия которых проходят через точку  (пересекают ось ), равны нулю.

Спроектируем все силы, действующие на плиту , на плоскость  (рис.7.18). (На рис. 7.18 проекции сил , , , что перпендикулярны плоскости , равны нулю).

По данной проекцией системы сил можно составить следующие уравнения равновесия: сумму проекций всех сил на ось (это уравнение уже составлено); сумму проекций всех сил на ось  (это уравнение уже составлено); сумму проекций всех сил на ось  (это уравнение тоже уже составлено); сумму моментов всех сил относительно оси , которая перпендикулярна плоскости и пересекает ее в точке :

В уравнении (6) моменты сил ,  и , линии действия которых проходят через точку (или пересекают ось ), равны нулю.

Из уравнения (3) находим, что

Поскольку плита прямоугольная, то проекции отрезка на координатные плоскости и соответственно равны

Перепишем составленную систему уравнений с учетом выражений для составляющих реакции :

Решив систему в обратном порядке получим:

Ответ:  

Произвольная пространственная система сил и условия ее равновесия

Необходимым и достаточным условием равновесия системы пар сил, приложенных к твердому телу, является равенство нулю суммы моментов данных пар. В пространственном случае расположения пар.

Лемма о параллельном переносе линии действия сил

Лемма. Не меняя статического состояния твердого тела, силу, приложенную к этому
телу, можно перенести в любую его точку параллельно самой себе, добавляя при этом присоединенную пару. Момент присоединенной пары равен моменту этой силы относительно центра приведения.

Доказательство. Пусть к твердому телу в точке А приложена силу (рис. 3.1).
В произвольной точке О этого же тела приложим две взаимно уравновешенные силы и модули которых а линии их действия параллельные силе . Тогда сила эквивалентна системе сил Однако силы  составляют пару. Поэтому сила  эквивалентна силе  приложенной в точке О, и паре сил   с моментом, который
равен моменту силы относительно точки О. Полученную таким образом пару сил
назовем присоединенной паром. Лемму доказано.

Главный вектор и главный момент сил. Основная теорема статики

Пусть задано произвольную систему сил , действующих на твердое тело. Главным вектором этой системы сил называется векторная сумма всех сил, входящих в
систему:
                                                                                                       (3.1)

Главным моментом такой системы сил относительно точки О (центра сведения) называется векторная сумма моментов всех сил, которые входят в систему, относительно того же
центра:

                                                                                                       (3.2)

где r – радиус-вектор, проведенный из центра О в точку приложения силы Ft. Проектируя левые и правые части выражений (3.1) и (3.2) на оси декартовой системы координат
Oxyz, легко найти аналитические выражения для главного вектора и главного момента
в виде

                                                                                                      (3.3)

                                                                                                     (3.4)

где   и – проекции соответственно главного вектора и главного момента  на оси координат.

Тогда модули и направляющие косинусы главного вектора и главного момента определяются выражениями

                                                                                                    (3.5)

                                                                                                     (3.6)

Пользуясь леммой о параллельном перенос силы, докажем основную теорему статики.

Основная теорема статики

Произвольную систему сил, которые действуют  на твёрдое тело, можно заменить одной из эквивалентных систем, которая:
 1) состоит из одной силы, приложенной в произвольно выбранном центре сведения и
равна главному вектору этой системы сил, и присоединенной пары сил, момент которой равен главному моменту всех сил относительно выбранного центра сведения;
2) состоит из двух, в общем случае, скрещивающихся сил, одна из которых приложена в центре сведения, а другая – в определенной точке.
 Если ограничиться первой частью сформулированной теоремы, то придем к известной теореме  Луи Пуансо.

Доказательство. Для доказательства первой части теоремы рассмотрим произвольную систему сил (рис. 3.2).

Произвольную точку О возьмем за центр сведения. По доказанной в п. 3.1 лемме перенесем все силы в точку О. В результате система сил окажется эквивалентной системе сил, приложенных в точке О (рис. 3.3, а), и присоединенным парам сил(рис. 3.1), моменты которых (рис. 3.3, б) имеют вид

                                                                                                       (3.7)

Определяя теперь равнодействующую полученной сходящейся системы сил в точке О (рис. 3.3), а также результирующую пару для системы присоединенных пар, получим выражения

                                             (3.8)

что, согласно (3.1) и (3.2), являются соответственно главным вектором и главным моментом.
 Для доказательства второй части теоремы допустим, что заданная система сил эквивалентно преобразована в соответствии с первым утверждение теоремы. Пусть – главный вектор системы, а – ее главный момент в центре сведения А. Представим момент М0 соответствующей парой сил (рис. 3.4). Пусть – произвольно выбранное плечо этой пары. Составляя силы и , приложенные в точке В, по правилу параллелограмма, получим новую систему сил , эквивалентную системе сил . Поскольку в общем случае сила не принадлежит плоскости N, то и сила также ей не принадлежит. Итак, силы  и * по построению являются скрещивающимися.
Таким образом доказано, что заданная система сил ) может быть преобразована в эквивалентную ей систему из двух, в общем случае, скрещивающихся сил  и *одна из которых (Q) приложена в центре сведения О, а другая – в точке А, положение которой устанавливается выбором плеча h по равенству

При приведенных преобразованиях этой системы сил главный вектор и главный момент имели формальное значение. Однако следует помнить, что в ряде практических применений эти величины могут быть определены экспериментально. Известно, например, что при вращении ротора электрической машины практически невозможно определить силы, которые возникают в шарикоподшипниковых опорах, а также электромагнитные силы взаимодействия между статором и ротором. В то же время экспериментальное определение главного момента таких сил на валу двигателя не вызывает затруднений. Именно поэтому в характеристику электродвигателей входят не силы, а крутящий момент.

Условия равновесия произвольной пространственной системы сил

Пусть задано произвольную пространственную систему сил приложенных к
 твердому телу. Докажем следующую теорему.
 Теорема. Для того чтобы произвольная пространственная система сил была в равновесии (эквивалентная нулю), необходимо и достаточно, чтобы главный вектор и главный момент этой системы относительно произвольного центра сведения были равны нулю, то есть:

                                                                                                       (3.9)

Доказательство. Необходимое условие. Пусть задана система сил  находится в равновесии. Нужно доказать, что тогда выполняются математические условия (3.9). По второму утверждению основной теоремы статики, превращаем заданную систему сил в эквивалентную ей систему, состоящую из двух сил  , которые могут быть скрещивающимися. Поскольку система сил  находится в равновесии и эквивалентна системе сил , то эта система также должна быть в равновесии. Это, в свою очередь, возможно только тогда, когда выполняются все условия аксиомы о двух силах (силы и должны быть одинаковые по величине, противоположно направлены и иметь общую линию действия). Однако для такой системы ее главный вектор и главный момент относительно любого центра возведения очевидно равны нулю, что и требовалось доказать.

Достаточное условие. Пусть задана система сил  преобразована в эквивалентную систему  для которой условия  (3.9) имеют вид:

                                                                                                     (3.10)

Выполнение первого условия означает, что силы и равны по величине и противоположно направлены. Выполнение второго условия показывает, что эти силы имеют общую линию действия, поскольку момент пары сил и равен нулю. Итак, согласно аксиоме I о двух силах,  исходная система сил эквивалентна нулю.  Условия (3.9) называются условиями равновесия произвольной системы сил в векторной (геометрической) форме. Проектируя векторные равенства (3.9) на оси координат, получаем условия равновесия свободной пространственной системы сил в аналитической форме:

                                                                                                      (3.11)

Итак, для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на координатные оси и суммы моментов этих сил относительно осей координат были равны нулю. Таким образом, при решении задач о равновесии пространственной системы сил, приложенных к твердому телу, из уравнений (3.11) можно определить шесть неизвестных величин. Если на твердое тело действует система пар сил, то необходимое и достаточное условие равновесия такой системы, как следует из условия (3.9) и свойств пар сил, принимает вид:

                                                                                                         (3.12)

Итак, для равновесия пар сил необходимо и достаточно, чтобы геометрическая сумма моментов пар была равна нулю:

Пример 1. На горизонтальный вал (рис. 3.5), который лежит в подшипниках А и В, действует груз весом , который привязан тросом к шкиву С радиусом Груз весом насаженный на стержень , неизменно связанный с валом АВ. Даны размеры АС = 0,2 м, CD = 0,7 м, BD – 0,1 м. В состоянии равновесия стержень ED отклонен от вертикали на угол 30 °. Определить расстояние l центра тяжести груза весом Р от оси вала АВ, а также реакции подшипников А и В.

Решение. Рассмотрим равновесие вала, на который действуют активные силы и . Cвязями для него являются подшипники А и В. Согласно аксиоме о связях, освобождаем вал от связей и заменяем их реакциями и , лежащие в плоскостях, перпендикулярных к оси подшипников А и В. Возьмем систему координат, как показано на рис. 3.5. Неизвестные реакции и подадим в виде составляющих , (рис. С 5), которые надо определить.  Для решения задачи воспользуемся условиями равновесия (3.11). В этом случае второе условие выполняется тождественно, поскольку проекции всех сил, в том числе и реакций связей, на ось Ау равны нулю. Из пяти условий равновесия которые  остались следует определить пять неизвестных величин:  Задача статически определена.

По заданной задачи условия равновесия (3.11) имеют вид:

Откуда,

Условия равновесия системы сил в отдельных случаях

Условия равновесия пространственной системы параллельных сил. Рассмотрим частный случай, когда все силы, действующие на твердое тело, параллельные между собой (рис. 3.6).

В этом случае можно направить одну из координатных осей (например, ось Oz)  параллельно этим силам. Тогда из условий равновесия (3.11) останутся только три уравнения, а три превратятся в тождества. Действительно, проекции сил на оси Ох и Оу равны нулю. Поскольку силы параллельные оси Oz, то их моменты относительно оси Oz также равны нулю. Тогда из шести уравнений (3.11) остаются только три:

                                                                                                              (3.13)

Итак, для равновесия пространственной системы параллельных сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил на ось, параллельную силам, была равна нулю, и алгебраические суммы моментов этих сил относительно двух других координатных осей были равны нулю.  Отметим, что для статической определенности задач, которые решаются, число неизвестных в уравнениях (3.13) не должно превышать
трех.

Условия равновесия твердого тела с неподвижной точкой

Рассмотрим твердое тело, которое  имеет неподвижную точку О (рис. 3.7). Пусть к этому телу приложена пространственная система активных сил

Точку О возьмем за начало координат. Сведя систему активных (или заданных) сил к центру сведения В, найдем главный вектор:

и главный момент активных сил

Главный вектор активных сил уравновесится реакцией неподвижной точки О, а главный момент активных сил в случае равновесия тела должен быть равен нулю:

                                                                                                              (3.14)

В проекциях на оси координат это условие примет вид:

                                                                                                          (3.15)

Эти уравнения не имеют реакций связей (неподвижной точки О). Они являются условиями равновесия твердого тела с неподвижной точкой.

Итак, для равновесия твердого тела с неподвижной точкой нужно, чтобы алгебраическая сумма моментов активных сил относительно каждой из трех взаимно перпендикулярных осей, проходящих через эту точку, была равна нулю.  Если надо найти реакцию опоры, то, воспользовавшись аксиомой об освобождении от связей, заменим связь реакцией и, записав первые три уравнения (3.11), найдем проекции реакции на оси, а затем по формулам (3.5) – их величину и направление.

Условия равновесия твердого тела, имеющего две неподвижные точки или неподвижную ось

Представим себе твердое тело, две точки которого , и   закреплены неподвижно. Пусть к этому телу приложены активные силы (рис. 3.8).

Нужно найти условия, которым бы удовлетворяли приложенные силы чтобы тело было в равновесии. Освободив тело от связей, приложим к нему реакции в неподвижных точках   , и  . Поскольку направления реакций неизвестны, то их нужно разложить по направлениям трех взаимно перпендикулярных осей (рис. 3.8). Под действием всех этих сил твердое тело будет оставаться в равновесии, если они удовлетворяют шесть уравнений (3.11) равновесия твердого тела, которых при будут иметь вид:

                                                                                                            (3.16)

Как видим, только последнее уравнение не имеет реакций точек закрепления тела и, следовательно, является единственным условием, которое удовлетворяют активные силы чтобы твердое тело, которое рассматривается,  оставалось в равновесии.   Итак, для равновесия твердого тела с двумя неподвижными точками (или закрепленной осью) нужно, чтобы алгебраическая сумма моментов активных сил относительно закрепленной оси или оси вращения была равна нулю:

                                                                                                                      (3.17)

Для определения реакций связей в этом случае осталось пять уравнений, а неизвестных составляющих реакций шесть. Из пяти уравнений нельзя определить шесть неизвестных. Поэтому задача об определении реакций двух закрепленных точек тела оказывается статически неопределенной. Эта неопределенность исчезает, если, например, в опоре , устроить подпятник, а в опоре – подшипник, поскольку реакция подпятника определяется тремя составляющими ,  а реакция подшипника – двумя составляющими

Условия равновесия произвольной плоской системы сил

Пусть система сил  заданная в плоскости (рис. 3.9). Центром сведения возьмем произвольную точку О, которая лежит в этой плоскости. Очевидно, что главный момент этой системы сил перпендикулярен плоскости, в которой лежат силы. Главный вектор заданной системы сил лежит в плоскости действия сил. Итак, из шести уравнений равновесия (3.11) остается только три:

                                                                                                     (3.18)

Таким образом, для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы алгебраические суммы проекций сил на две взаимно перпендикулярные оси, и алгебраическая сумма моментов сил относительно произвольно выбранной точки были равны нулю. Поскольку условия равновесия (3.18) в этом случае записываются тремя уравнениями, то задача будет статически определенной, если число неизвестных в уравнениях равновесия не будет превышать трех. Уравнения равновесия можно представить в виде:

                                                                                                         (3.19)

при условии, что ось не перпендикулярна  отрезку АВ. Наконец, все три уравнения равновесия можно представить в виде уравнений моментов сил относительно трех точек О, А и В (рис. 3.9), не лежащих на одной прямой:

                                                                                                           (3.20)

Уравнениями (3.20) равновесия плоской системы сил пользуются при определении усилий в стержнях  по способу Риттера. В заключение этого раздела отметим, что за центр моментов целесообразно взять точку, в которой пересекается большое количество линий действия неизвестных сил. Если две неизвестные силы взаимно перпендикулярны, то оси координат целесообразно направлять по линиям действия этих сил.

Пример 2. К балке АВ, опорами которой являются шарнир А и каток В, приложенные силы, как показано на  рис. 3.10. Определить реакцию шарнира   и реакцию катка если
 Решение. Рассмотрим равновесие балки. По аксиоме об освобождении от связей, заменим действие связей (шарнира А и катка В) их реакциями. Реакция катка направлена ​​по нормали к опорной плоскости. Направление реакции шарнира А неизвестно. Разложим эту реакцию на составляющие и . Точку А возьмем за начало координат. Уравнение равновесия в этом случае будут вид:

Откуда

Окончательно получим: 

Условия равновесия параллельных сил, которые лежат в плоскости

Пусть к твердому телу приложена система параллельных сил, которые лежат в одной плоскости (рис. 3.11). Обозначим эту плоскость  .  Поскольку параллельные силы являются  частным случаем произвольной плоской системы сил, то на основе (3.18) установим условия равновесия параллельных сил, лежащих в одной плоскости и параллельные оси

 В этом случае проекции всех сил на ось равны нулю, поэтому с трех условий (3.18) остаются два условия равновесия:

                                                                                                            (3.21)

Итак, для равновесия параллельных сил, лежащих в плоскости, необходимо и достаточно, чтобы алгебраическая сумма проекций сил на ось, параллельную им, а также алгебраическая сумма моментов сил относительно некоторой точки на плоскости, были  равны нулю. Отметим, что уравнением равновесия параллельных сил, которые лежат в плоскости, можно предоставить в другой форме, составив уравнение моментов сил относительно двух точек А и В:

                                                                                                          (3.22)

причем точки А и В не должны лежать на прямой, параллельной оси .

Для статической определенности задачи число неизвестных, в случае воздействия на твердое тело параллельных сил на плоскости, не должно превышать двух.

Пример 3. В балки АВ длиной 10 м приложены параллельные силы, как показано на рис. 3.12; силы  Определить реакцию шарнира и реакцию катка
Решение. Рассмотрим равновесие балки, освободив ее от связей, и заменив их действия реакциями связей. В катке В реакция направлена ​​перпендикулярно к балке (рис. 3.12). реакция шарнира в этом случае, исходя из равновесия системы параллельных сил, будет параллельной этим силам. Точку А возьмем за начало координат. Из условий равновесия (3.21) получим:

Откуда 

Эту задачу можно решить, составив два уравнение моментов сил относительно точек А и В.

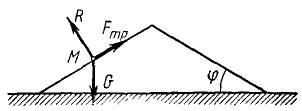
Трение качения. Равновесие при наличии сил трения

Кроме трения скольжения, приведенного в п. 1.7, рассмотрим еще один вид трения, возникающая при качении тел (трение качения).
В теоретической механике трением качения интересуются только с точки зрения определения реакций опоры (более полное его изучение выходит за рамки механики твердого тела). Пусть к катку радиусом перпендикулярно к его оси  приложена горизонтальная сила (рис. 3.13).

Кроме того, на каток действует сила тяжести . Вследствие деформаций катка и горизонтальной опоры поверхности, на которой находится каток, они касаются друг друга не в одной точке, а по некоторой области контакта. Нормальная реакция опоры  сместится на определенное расстояние

Сила трения возникает в том месте, где каток касается опорной поверхности, то есть в точке С. В случае равновесия катка сила равна по модулю силе , но направлена ​​в противоположную сторону. Итак, и образуют пару сил, которая уравновешивается парой сил и (рис.  3.13). момент пары  называется моментом трения качения. Плечо этой пары – величина , которая называется коэффициентом трения качения. В отличие от коэффициента трения скольжения, который является безразмерной величиной, коэффициент трения качения имеет размерность длины. Приравняв моменты указанных пар:

                                                                                                            (3.23)

найдем выражение для определения коэффициента трения-качения 

                                                                                                                (3.24)

Опыт показывает, что величина b пропорциональна радиусу цилиндра (катка) и разная для разных материалов. Очевидно, тело будет в равновесии, если момент активной силы в отношении точки С не больше момента трения, то есть   

Наличие трения не меняет методику решения задач статики. Реакции связей при наличии трения скольжения определяют по формулами п. 1.7, а в случае трения качения – по формулам (3.23), (3.24).

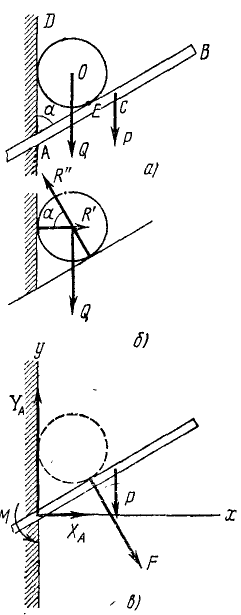
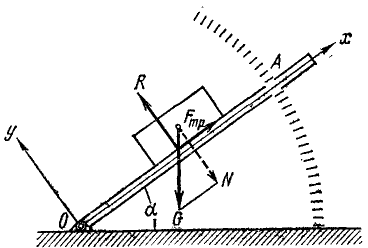
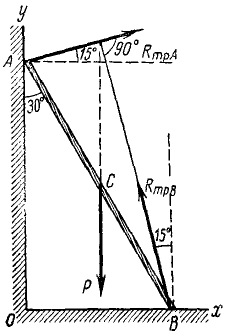
Пример 4. Лестница АВ опирается на шероховатую стену и шероховатую пол, образуя с полом угол 60 ° (рис. 3.14). На лестнице в точке D содержится груз весом . Пренебрегая весом лестницы, определить расстояние BD, при которой лестница будет в равновесии.  Угол трения для стены и пола равен  15 °.

Решение. Рассмотрим равновесие лестницы, к которой в точке D приложена сила . Согласно аксиоме III, освобождаемся от связей, заменяя их действия силами, равными реакциям связей. Поскольку стена и пол шершавые, то реакции в опорах А и В состоят из сил трения и нормальных составляющих реакций. Система сил, которая  рассматривается, – плоская, поэтому составим три уравнения равновесия, взяв точку О за начало координат, а координатные оси и направим так, как показано на рисунке:

Воспользовавшись соотношениями с п.1.7, выразим силы трения  и  через нормальные реакции, учитывая, что угол трения  

С учетом этих соотношений условия равновесия будут иметь следующий вид:

Разделив третье уравнение на  получим:

Пространственная система произвольных сил

Пространственная система сил, это в которой линии действия составляющих сил расположены произвольно, т. е. линии их действия могут не пересекаться и находиться в разных плоскостях, называется произвольно расположенной системой сил. 

Пары сил в пространстве

Как известно, пары сил характеризуются тремя параметрами: модулем, равна произведению одной из сил пары на плечо пары, плоскостью действия пары и направлением вращения тела в этой плоскости. если рассматривать пары, которые не лежат в одной плоскости, то для каждой из них необходимо определить эти параметры.

Теорема о переносе пары в параллельную плоскость

Не меняя действия пары сил на тело, можно переносить эту пару в параллельную плоскость.

Докажем это.

Предположим, что есть тело, к которому в плоскости π приложена пара сил
(, ) (рис. 1.46). При этом P₁ = P₂ и //. Обозначим точки приложения сил и буквами A и B. Возьмем на теле другую плоскость π₁, которая будет параллельной данной плоскости π. Отрезок AB перенесем параллельно самому себе в плоскость π₁ в положение A₁B₁. Приложим в точках A₁ и B₁ уравновешенные системы сил  ,  и  , , которые в сумме будут эквивалентные нулю. При этом модули всех сил выберем одинаковыми, а именно

=  =  =  =  =  = .

Соединим все четыре точки и получим параллелограмм AA₁B₁B (поскольку AB = A₁B₁ и AB//A₁B₁ ). Покажем диагонали этого параллелограмма. Они пересекаются в одной точке, которая разделяет каждую диагональ пополам.

Объединим силы и , приложенные на концах первой диагонали и направлены в одну сторону. Поскольку они параллельны и имеют одинаковое направление, то их можно добавить, получив равнодействующую, которая в данном случае будет приложена именно посередине диагонали. То есть

R₁ = P₂ + P₄ = 2P.

Тоже самое сделаем с силами и , получая равнодействующую  , которая
будет приложена посередине второй диагонали и направлена в ту же сторону, что и эти силы, но будет иметь направление, противоположное направлению первой равнодействующей . Равнодействующая R₂ будет равняться 

R₂ = P₁ + P₅ = 2P.

Итак, в точке пересечения диагоналей параллелограмма AA₁B₁B есть две силы  и , которые являются уравновешенной системой сил, которую, как это известно, можно
отвергнуть.

На рис. 1.46 остались только силы и , которые, как видим, являются парой сил, которая перенесена и приложена в плоскости π₁. Таким образом, пару сил (, ) перенесено из плоскости π в параллельную плоскость π₁.

Теорема доказана.

Условия эквивалентности пар в пространстве

Как известно, момент пары сил является векторной величиной. Момент пары как вектор имеет направление, перпендикулярное плоскости, в которой расположена пара сил, и направлен таким образом, что, смотря с конца вектора, можно видеть вращения плоскости против направления часовой стрелки (рис. 1.47). Также было установлено, что пару сил можно передвигать и вращать в плоскости ее действия и переносить в параллельную плоскость, поскольку момент пары сил является вектором свободным. Таким образом, момент пары сил как вектор можно переносить вдоль линии его действия и передвигать параллельно самому себе.

На основании изложенного, можно утверждать, что пары сил в пространстве будут эквивалентными, если их моменты будут равными по величине, параллельными и направленными в одну сторону.

Добавление пар в пространстве

Добавить пару в пространстве значит найти одну такую ​​пару, которая будет
эквивалентной заданной системе пар. А поскольку каждая пара сил характеризуется ее моментом как вектором, то момент эквивалентной пары сил должен равняться геометрической сумме вектор-моментов составляющих пар сил.

Представим тело, к которому приложена система пар сил, произвольно расположенных в пространстве (рис. 1.48). Обозначим векторы этих моментов через , , , …  .

Поскольку моменты пар сил являются векторами свободными, то их можно переносить параллельно самим себе в произвольную точку. Если это сделать, то будем иметь систему моментов как систему сходящихся векторов, которую можно геометрически добавить.

Как известно, геометрическое добавления моментов как векторов можно осуществлять по правилу геометрического сложения векторов различной природы (методом силового многоугольника). Векторную сумму можно записать следующим образом:

Таким образом, момент результирующей пары как вектор равен геометрической сумме моментов составляющих пар как векторов.

Условия равновесия системы пар в пространстве

Если на тело действует система пар сил, произвольно расположенных в пространстве, то тело будет в состоянии равновесия только тогда, когда момент результирующей (эквивалентной) пары равен нулю. А поскольку момент результирующей пары определяется как геометрическая сумма моментов составляющих пар, то эта геометрическая сумма тоже должна равняться нулю. Векторно это условие равновесия записывается так:

Таким образом, для равновесия тела, находящегося под действием произвольной
системы пар сил в пространстве, необходимо и достаточно, чтобы геометрическая
сумма моментов составляющих пар равна нулю.

Возведение пространственной системы произвольных сил к данному центра. Главный вектор и главный момент системы

Представим тело, которое находится под действием пространственной системы произвольных сил .  , , …, , приложенных в точках A₁, A₂, A₃, …, A_n (рис. 1.49). Выберем произвольную точку O как центр сведения и построим пространственную декартову систему координат Oxyz. Последовательно перенесем силы параллельно самим себе в центр O. При этом к телу необходимо добавлять моменты “присоединенных” пар сил, которые равны моментам заданных сил относительно центра O.

Момент первой пары обозначим = m_o (), он приложен в точке O, расположенный перпендикулярно плоскости треугольника OA₁P₁ и направлен по правилу буравчика.

Тоже самое сделаем и с другими силами, которые приложены к телу. Вследствие этого в центре сведения O получена система сходящихся сил и система моментов пар сил в виде векторов.

Система сходящихся сил .  , , …, , приложенных в центре O, можно заменить одной суммарной силой , называется главным вектором пространственной системы произвольных сил. Моменты , , , … , которые тоже приложенные в центре O, можно заменить одним суммарным моментом , который называется главным моментом пространственной системы произвольных сил.

Главный вектор равен геометрической сумме векторов всех сил, приложенных к телу, а главный момент равен геометрической сумме моментов всех сил относительно центра сведения, а именно:

Таким образом, любая пространственная система произвольных сил, действующая на
тело, может быть сведена к одной силе — главного вектора системы и одной паре — главного момента системы пространственных сил.

В общем случае главный вектор не зависит от положения центра возведения O, а главный момент , наоборот, зависит от его положения, так как меняются плечи “присоединенных” пар, или плечи заданных сил относительно центра сводки.

Вычисление главного вектора и главного момента пространственной системы произвольных сил

Определим аналитически главный вектор пространственной системы произвольных сил , через его проекции на оси пространственной системы координат Oxyz. Обозначим эти проекции R_x, R_y, R_z .

Проекция главного вектора на ось равна алгебраической сумме проекций составляющих сил на ту же ось. Аналитически это можно записать так:

То есть, проекции главного вектора пространственной системы произвольных сил на оси пространственной системы координат равны алгебраическим суммам проекций этих сил на соответствующие оси.

Если известны проекции главного вектора R на оси координат, то можно определить его величину, как диагональ параллелепипеда

Проекция главного момента на любую ось равна алгебраической сумме проекций моментов составляющих сил на ту же ось, а именно:

Но проекция момента силы относительно точки на ось, которая проходит через эту точку, равен моменту силы относительно этой оси, то есть:

С учетом уравнения можно окончательно определить проекции вектора главного момента на оси координат. Они будут равны

То есть, проекции главного момента пространственной системы произвольных сил на оси пространственной системы координат равны алгебраическим суммам моментов этих сил относительно соответствующих осей.

Если известны проекции главного момента на оси координат, то нетрудно определить модуль вектора этого момента. Он будет равен:

M =  .

Некоторые случаи сведения пространственной системы произвольных сил к данному центру

Напомним о том, что любая пространственная система произвольных сил может быть сведена к одной силе — главному вектору системы и одной пары, момент которой равен главному моменту системы. Но могут быть и некоторые частичные случаи.

1. Главный момент = 0, а главный вектор ≠ 0. В этом случае главный вектор будет равнодействующей пространственной системы произвольных сил;

2. Главный вектор = 0, а главный момент ≠ 0. В данном случае пространственная система произвольных сил сводится к одной паре сил, момент которой равен главному моменту системы. Главный момент  не зависит, в этом случае, от изменения положения центра возведения; 

3. Главный вектор ≠ 0 и главный момент ≠ 0, но вектор  перпендикулярен вектору . Это означает, что главный момент как пара сил расположен в той же плоскости, в которой лежит и главный вектор. А это дает возможность два вектора и заменить одним вектором — равнодействующей, не будет проходить через центр сведения O. Это можно доказать следующим образом. Предположим, что к телу в точке O приложены
главный вектор и главный момент , угол между которыми составляет 90º (рис. 1.50). Главный вектор заменяем парой сил (; ), (причем модули сил , и  однаковы) с плечом h = . Теперь будем иметь приложенными в точке O равные и противоположно направленные силы и и прилагаемую в точке A силу . Силы и образуют уравновешенную систему сил, которую можно отбросить, а в точке A остается сила , которая, фактически, является равнодействующей силой .

4. Главный вектор и главный момент не равен нулю, но они параллельны. В этом случае, который носит название “динами” или “силового винта”, тело совершает винтовое движение, поскольку в направлении главного вектора оно “движется” поступательно и одновременно вращается под действием пара в плоскости, перпендикулярной направлению движения (рис. 1.51). Ось, на которой расположены векторы и и которая проходит через центр сведения O, называется — “ось динами”.

5. Главный вектор  ≠ 0 и главный момент ≠ 0 и произвольно расположены в пространстве (векторы и не перпендикулярны друг другу и не параллельны). В данном случае пространственная система произвольных векторов также сводится к “динами”, но ось динами уже не будет проходить сквозь центр сведения O. Докажем это. Представим в центре сведения O приложен главный вектор и главный момент , угол между которыми составляет α (рис. 1.52). Разложим главный момент на два направления — , направленный вдоль главного вектора , и , который является
перпендикулярным к . Проекции главного момента на эти направления будут равны  = M cosα и = M sinα. Теперь, как и в случае, когда главный вектор и главный момент были перпендикулярны, представим момент в виде пары (; ) с плечом h = . Также
отвергаем силы и , что были приложены в центре сведения O. Остается приложенной в точке A сила , которая является главным вектором , и момент , вектор которого приложен в центре сведения O. Однако известно, что вектор , как вектор свободный, можно перенести в точку A. Таким образом, заданная пространственная система произвольных сил также сведена к “динами”, но теперь ось “динами” проходит через точку A.

6. Главный вектор = 0 и главный момент = 0. В данном случае пространственная система произвольных сил будет находиться в состоянии равновесия.

Услуги по теоретической механике:

1. Заказать теоретическую механику
2. Помощь по теоретической механике
3. Заказать контрольную работу по теоретической механике

Учебные лекции:

1. Статика
2. Система сходящихся сил
3. Момент силы
4. Пара сил
5. Произвольная система сил
6. Плоская произвольная система сил
7. Трение
8. Расчет ферм
9. Расчет усилий в стержнях фермы
10. Пространственная система сил
11. Плоская система сходящихся сил
12. Пространственная система сходящихся сил
13. Равновесие тела под действием пространственной системы сил
14. Естественный способ задания движения точки
15. Центр параллельных сил
16. Параллельные силы
17. Система произвольно расположенных сил
18. Сосредоточенные силы и распределенные нагрузки
19. Кинематика
20. Кинематика твердого тела
21. Движения твердого тела
22. Динамика материальной точки
23. Динамика механической системы
24. Динамика плоского движения твердого тела
25. Динамика относительного движения материальной точки
26. Динамика твердого тела
27. Кинематика простейших движений твердого тела
28. Общее уравнение динамики
29. Работа и мощность силы
30. Обратная задача динамики
31. Поступательное и вращательное движение твердого тела
32. Плоскопараллельное (плоское) движение твёрдого тела
33. Сферическое движение твёрдого тела
34. Движение свободного твердого тела
35. Сложное движение твердого тела
36. Сложное движение точки
37. Плоское движение тела
38. Статика твердого тела
39. Равновесие составной конструкции
40. Равновесие с учетом сил трения
41. Центр масс
42. Колебания материальной точки
43. Относительное движение материальной точки
44. Статические инварианты
45. Дифференциальные уравнения движения точки под действием центральной силы и их анализ
46. Динамика системы материальных точек
47. Общие теоремы динамики
48. Теорема об изменении кинетической энергии
49. Теорема о конечном перемещении плоской фигуры
50. Потенциальное силовое поле
51. Метод кинетостатики
52. Вращения твердого тела вокруг неподвижной точки

Содержание:

Различные случаи приведения плоской системы сил:

Плоской системой сил называют совокупность сил, расположенных в одной плоскости

Приведение плоской системы сил к точке. Для изучения плоской системы сил, т. е. совокупности сил, приложенных к твердому телу и расположенных в одной плоскости, приведем все силы к центру приведения, выбрав его где-либо в той же плоскости. Тогда мы получим в центре приведения плоский пучок сил, геометрически сложив которые, мы найдем главный вектор системы. Кроме того, при приведении всех сил к точке мы получим пары, расположенные в одной плоскости. Как уже было сказано, в плоской системе моменты сил относительно точки и моменты пар направлены перпендикулярно к плоскости системы в ту или другую сторону. Эти моменты вполне характеризуются величиной и знаком, а потому для вычисления главного момента плоской системы относительно центра приведения, лежащего в плоскости системы, нужно взять алгебраическую сумму моментов всех сил системы относительно центра приведения. Следовательно, система сил, произвольно расположенных на плоскости, эквивалентна главному вектору, равному геометрической сумме всех сил и приложенному к твердому телу в любой точке этой плоскости, и главному моменту, равному алгебраической сумме моментов всех сил относительно той же точки:

Величину главного вектора удобно вычислить по его проекциям на координатные оси, равным суммам проекций на эти оси всех сил плоской системы:

      (5)

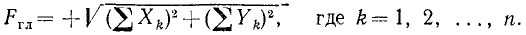
Направление главного вектора можно определить по направляющим косинусам (6′).

Если за центр приведения принято начало координат, то, выражая момент каждой силы плоской системы по (16) и суммируя, получим следующее выражение для главного момента плоской системы сил относительно начала координат:
      (29′)

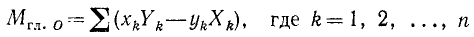
Задача №1

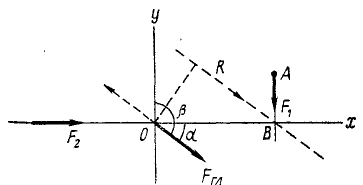
К твердому телу в точке A (x₁=+10, у =+4) приложена сила F₁ = 3, направленная вниз по вертикали; сила F₂ = 4 направлена по оси Ox в положительную сторону и приложена к тому же телу. Длины выражены в метрах и силы — в ньютонах. Направление осей координат обычное (Ох горизонтально вправо, Oy вертикально вверх). Привести обе силы к началу координат и заменить данную систему сил главным вектором и главным моментом (см. рис. 52).

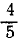
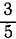
Решение. Определив сумму проекций данных сил на оси координат, величину главного вектора вычислим по формуле (5), а его направление—по (6′): F_гл=5; cos а==0,800; cosβ = —=—0,600. Главный момент относительно начала координат вычислим по формуле (29′) или (29): М_{гл. о} = —30.

Ответ. Главный вектор равен 5 н, приложен в начале координат и направлен вправо и вниз под углом 36^о52′ к оси Ox и 126^о52′ к оси Оу, главный момент равен —30 н∙м.

Если главный вектор плоской системы сил не равен нулю, то система приводится к одной равнодействующей

Случай приведения к равнодействующей

Величину и направление главного вектора произвольной системы сил определяют по формулам, аналогичным тем, по которым определяют равнодействующую системы сходящихся сил. Между тем главный вектор произвольной системы сил не является равнодействующей этой системы. В самом деле, равнодействующей называют силу, которая одна эквивалентна системе сил, а главный вектор сам по себе не эквивалентен данной системе сил, но эквивалентен ей только в совокупности с главным моментом.

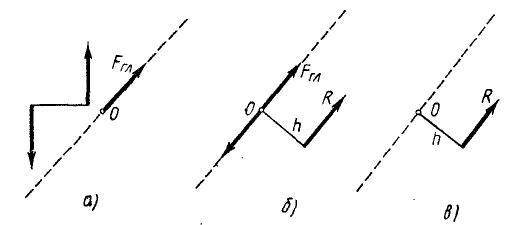
Рис. 51

Главный вектор может быть равнодействующей плоской системы сил лишь в случае, если главный момент системы относительно центра приведения равен нулю. Тогда главный вектор один, без главного момента, эквивалентен данной системе сил.

Следовательно: если главный вектор не равен нулю, а главный момент относительно центра приведения равен нулю, то система приводится к равнодействующей, линия действия которой проходит через центр приведения.

Если же главный момент не равен нулю, то мы можем представить его в виде пары сил, которые мы выберем равными главному вектору, а плечо h—равным отношению величин главного момента и главного вектора (рис. 51,а):

      (30)

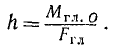
Действие пары на тело не зависит от положения этой пары в ее плоскости, и мы вправе расположить ее так, чтобы одна из сил этой пары была направлена по линии действия главного вектора в сторону, ему противоположную (рис. 51,6). Тогда, отбрасывая эту силу вместе с главным вектором, как взаимно уравновешенные, мы получим только одну силу (рис. 51, в), эквивалентную данной системе; эта сила является равнодействующей данной системы. Мы видим, что равнодействующая по модулю равна главному вектору, параллельна ему по направлению, но отличается от него линией действия.

Следовательно: если главный вектор и главный момент плоской системы сил не равны пулю, то система приводится к равнодействующей, линия действия которой не проходит через центр приведения.

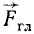
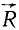
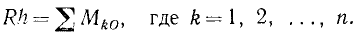
Учитывая, что главный вектор по величине и направлению равен равнодействующей (рис. 51), а также учитывая (29), можно равенство (30) переписать так:

        (18)

Мы получили теорему Вариньона: момент равнодействующей плоской системы сил относительно какой-либо точки, лежащей в этой плоскости, равен алгебраической сумме моментов составляющих относительно той же точки.

Задача №2

Найти равнодействующую системы сил, заданных в условии задачи №1.

Решение. При решении задачи № 15 данная система приведена к главному вектору 5 н и главному моменту —30 н^.м. Представим этот главный момент в виде пары, силы которой по модулю равны главному вектору, а плечо равно отношению величии главного момента и главного вектора, т. е. F= 5 и h=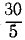=6. Момент пары отрицательный — вращение по стрелке часов. Расположим пару так (рис. 52), чтобы одна из ее сил уравновесила главный вектор. Система приведена к одной силе, равной и параллельной главному вектору, но линия действия этой силы отстоит от начала координат на 6 м. Нетрудно из (29′) получить уравнение линии действия равнодействующей, т. е. —хЗ—у4 — —30.

Рис. 52

К тому же результату можно прийти (и в данном случае проще), если заданные силы F1 и Ft перенести в точку В пересечения их линий действия и там сложить.

Ответ. Равнодействующая равна 5 я и лежит на прямой 3x+4y = 30.

Если главный вектор системы сил равен нулю, а главный момент нулю не равен, то система приводится к паре сил

Случай приведения к паре

Исследуем случай, когда главный вектор системы равен нулю, но главный момент системы относительно центра приведения нулю не равен. Если главный вектор системы равен нулю, то, следовательно, нет и равнодействующей. Главный момент мы всегда можем представить в виде пары. Следовательно, если главный вектор равен нулю, а главный момент не равен нулю, то система приводится к паре сил.

Заметим, что главный момент не зависит от центра приведения в том случае, когда главный вектор системы равен нулю. В самом деле, если система сил эквивалентна паре сил с моментом, равным главному моменту системы, а момент пары, как известно (см. § 10), не зависит от центра моментов, то, следовательно, и главный момент (в этом случае) не зависит от центра приведения. Это ясно и из логических соображений: правильно (без ошибок) полученный результат приведения системы сил зависит только от данной системы, но не может зависеть от нашего подсчета. Он существует объективно, независимо от нас. Если система сил эквивалентна паре, то ясно, что, какую бы точку мы ни принимали за центр приведения, мы всякий раз должны получать одну и ту же пару и один и тот же главный момент.

Задача №3

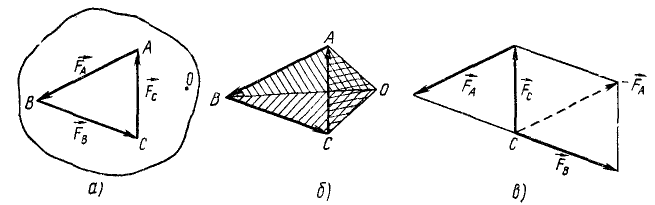
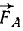
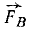
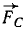
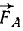
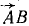
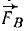
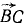
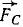
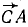
В точках Л, В и C к твердому телу приложены силы , и . В некотором масштабе (например, 1 н = 1 см) эти силы изображаются направленными отрезками: =, =, = (рис. 53, а). Исследовать систему сил.

Решение. Выбрав за центр приведения какую-либо точку, например точку О, и перенеся по методу Пуансо в эту точку все силы, убедимся, что силовой многоугольник замкнут, а следовательно, главный вектор равен нулю. Главный момент системы относительно точки О равен алгебраической сумме моментов трех сил, изображаемых удвоенными площадями треугольников (рис. 53, б):

Рис. 53

Независимо от центра приведения О главный момент системы равен удвоенной площади треугольника АВС, т. е. система сил эквивалентна паре.

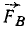
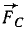
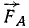
К такому же результату мы придем путем следующих рассуждений. Главный вектор системы (а следовательно, и равнодействующая) равен нулю, так как силовой многоугольник замкнут. Вместе с тем система данных трех сил не может находиться в равновесии, так как не удовлетворено необходимое условие равновесия трех сил: линии их действия не пересекаются в одной точке. Перенеся силу  (рис. 53, в) по ее линии действия в точку C и сложив ее с силой , получим равнодействующую этих двух сил, равную и противоположную третьей силе и составляющую вместе с ней пару сил.

Ответ. Данная система трех сил эквивалентна паре сил. 

Если главный вектор и главный момент системы сил равны нулю, то система сил находится в равновесии

Случай равновесия

Если дана система сил и, приведя ее к какому-либо центру, мы убеждаемся, что и главный вектор и главный момент системы равны нулю, то наличие этой системы эквивалентно ее отсутствию, т. е. система находится в равновесии.

Справедливо и обратное заключение: если данная система сил находится в равновесии, то главный вектор системы и главный момент системы относительно центра приведения равняются нулю. Следовательно, условия
       (31)

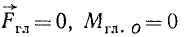
являются необходимыми и достаточными условиями равновесия плоской системы сил. И в этом случае главный момент не зависит от центра приведения. В самом деле, если система сил находится в равновесии, то равновесие не может нарушиться от того, выберем ли мы за центр приведения ту или иную точку плоскости.

Все возможные частные случаи приведения плоской системы сил к данной точке представлены в следующей таблице:

Fгл	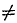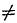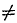0	0	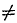0	0
Мгл	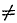0	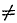=0	0	=0
	Равнодействующая не проходит | проходит через центр приведения	Пара сил	Равновесие

Таблица систематизирует возможные случаи приведения плоской системы сил и не нуждается в пояснениях.

Равновесие плоской системы сил

Для равновесия плоской системы сил необходимо и достаточно, чтобы равнялись нулю суммы проекций всех сил на оси координат и сумма моментов всех сил относительно какой-либо точки плоскости

Первая форма уравнений равновесия

Условия равновесия (31) плоской системы сил можно переписать так:
    (32)

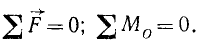
Первое из этих равенств является геометрическим. Мы можем заменить это геометрическое равенство двумя аналитическими, как это было сделано при отыскании аналитической формы условий равновесия плоского пучка сил. Оставляя второе из равенств (32) без изменений, мы получим условия равновесия плоской системы сил в следующем виде:

    (33)

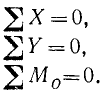
Таким образом, для равновесия системы сил, произвольно расположенных на плоскости, необходимо и достаточно, чтобы равнялись нулю суммы проекций всех сил на оси координат и сумма моментов всех сил относительно какой-либо точки плоскости.

Заметим, что оси координат не обязательно должны быть между собой перпендикулярны, а могут составлять любой отличный от нуля угол, если по условию задачи целесообразно дать им такие направления. Сумму моментов можно взять относительно любой точки плоскости системы сил, поскольку при равновесии системы главный момент ее не зависит от центра приведения.

Соотношения (33) называют условиями равновесия системы сил, произвольно расположенных на плоскости. Если эти соотношения содержат неизвестные величины, то их называют уравнениями равновесия.

Задача №4

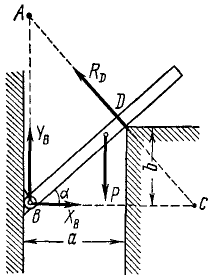
Однородная балка AB весом P = 20κΓ опирается на гладкий горизонтальный пол в точке В под углом 60° и, кроме того, поддерживается двумя опорами C и D. Определить реакции опор в точках В, C и D, если длина AB=3м, CB=0,5 м , BD= 1 м (рис. 54).

Решение. Порядок решения задач на равновесие плоской системы сил такой же, как и при решении задач на равновесие плоской системы сходящихся сил, только в данном случае мы имеем три, а не два уравнения равновесия.

Все искомые и известные силы в этой задаче действуют на балку АВ, поэтому рассмотрим равновесие балки АВ.

На балку действуют одна активная сила (собственный вес) и три реакции в трех точках опоры. Реакции, как всегда, направлены перпендикулярно виртуальным перемещениям. Таким перемещением балки АВ, не нарушающим ее связи с полом, является горизонтальное перемещение, и реакцию R_В мы направим вертикально вверх. Давая балке AB мысленные малые перемещения, не нарушающие ее связи с полом, мы не должны беспокоиться о том, чтобы эти перемещения не нарушили связи в других местах, например в точке С. Аналогично, определяя виртуальные перемещения в точке С, мы не заботимся о том, что при этом нарушается связь в точке В. Перемещениями, не нарушающими связи в точках C и D, являются перемещения вдоль балки (подобно смычку по струне), поэтому реакции в точках C и D направим перпендикулярно балке.

Строим оси координат:

Удачный выбор системы координат может упростить уравнения равновесия. Можно пользоваться и косоугольной системой координат, например, направив одну ось горизонтально, а другую—под углом 60° по BA. Мы направим оси, как указано на чертеже. Тогда

За центр моментов удобнее принимать точку, в которой пересекаются линии действия неизвестных по величине реакций. Так, в данном случае удобно принять точку, в которой пересекаются линии действия реакций R_B и R_C. В результате такого выбора обе эти реакции не войдут в уравнение моментов. Чтобы определить плечо реакции R_D, опустим перпендикуляр из центра моментов на линию действия этой реакции. Нетрудно видеть, что плечо CD = 0,5 м. Чтобы определить плечо силы тяжести, опустим перпендикуляр из центра моментов на линию действия этой силы. Получим 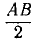cos 60° = 0,75 м. Реакция R_D относительно центра моментов направлена против хода часов (момент положителен), а сила тяжести — по ходу часов (момент отрицателен). Уравнение моментов имеет вид

Решая совместно все три уравнения равновесия, получаем ответ.

Ответ. R_B=20 κΓ, R_C.=30 κΓ,R_D = 30 кГ.

Для равновесия плоской системы сил необходимо н достаточно, чтобы равнялись нулю суммы моментов всех сил относительно трех каких-либо точек плоскости, не лежащих на одной прямой:

Система сил, действующих на балку АВ, состоит из двух пар сил. Рекомендуем решить эту задачу при помощи уравнения (26′) равновесия системы пар на плоскости, по примеру задачи № 13. Вторая форма уравнений равновесия. Необходимые и достаточные условия равновесия плоской системы сил можно выразить не только равенствами (33). К одному из других видов условий равновесия плоской системы сил приводит теорема, обычно называемая теоремой о трех моментах: для равновесия системы сил, произвольно расположенных на плоскости, необходимо и достаточно, чтобы равнялись нулю суммы моментов всех сил системы относительно каждой из трех точек, произвольно взятых на плоскости, но не лежащих на одной прямой. Докажем эту теорему.

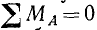
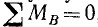
Пусть дана плоская система сил. Возьмем в плоскости произвольную точку А и определим сумму моментов всех сил относительно этой точки. Если бы сумма моментов не равнялась нулю, то система, конечно, не была бы в равновесии. Если же , то система может либо находиться в равновесии, либо быть приведенной к равнодействующей, проходящей через точку А (см. таблицу на стр. 79). Следовательно, написанное условие хотя и необходимо, но не достаточно для равновесия системы. Возьмем в той же плоскости другую произвольную точку В и определим сумму моментов всех сил системы относительно точки В. Если  ,   то это равенство вместе с предыдущим все же не может быть достаточным условием равновесия системы, поскольку равнодействующая системы (если она существует) может проходить через обе эти точки, тогда моменты равнодействующей относительно каждой из этих точек, а следовательно, и суммы моментов составляющих (теорема Вариньона) равны нулю, но система не в равновесии, а приводится к равнодействующей, проходящей через точки А и В.

Возьмем сумму моментов всех сил относительно третьей точки, выбрав эту точку C где-либо не на прямой АВ. Если сумма моментов всех сил системы относительно точки C равна нулю, то система находится в равновесии, так как равнодействующая не может проходить через точки А, В и С, не лежащие на одной прямой. Следовательно, три равенства
      (34)

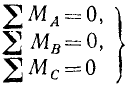
выражают, так же как и равенства (33), необходимые и достаточные условия равновесия системы сил, произвольно расположенных на плоскости.

Если равенства (34) являются уравнениями равновесия, т. е. содержат неизвестные величины, которые нужно определить, то соответствующим выбором центров моментов A, B и C можно составить уравнения так, чтобы каждое из них содержало только одну неизвестную величину, и вместо системы трех уравнений с тремя неизвестными получить три уравнения, каждое из которых содержит только по одной неизвестной.

Задача №5

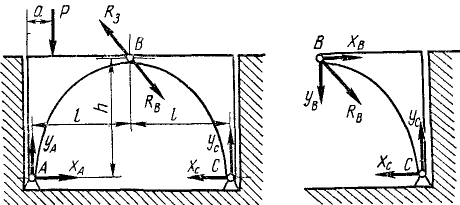
Однородный стержень длиной 2l и весом P прикреплен в точке В при помощи шарнира к стене (рис. 55), а в точке D опирается на угол другой стены. Найти все реакции, если известно, что точка D отстоит от первой стены на расстоянии а и находится на высоте b над шарниром В.

Решение. Равновесие какого тела надо рассматривать? Ответ на этот вопрос в данной задаче очевиден: равновесие стержня. Какие силы действуют на это тело? На него действуют вес Р, приложенный в середине стержня; реакция R_D в точке D, направленная перпендикулярно виртуальному перемещению, т. е. перпендикулярно стержню; реакция в шарнире В, которую мы раскладываем на две составляющие X_B н Y_B, поскольку направление реакции в шарнире обычно бывает неизвестно, хотя в данном случае это направление можно было бы определить по необходимому условию равновесия трех непараллельных сил . Теперь составляем уравнения равновесия, для чего воспользуемся равенствами (34).

Рис. 55

За центры моментов выберем точки пересечения линий действия искомых сил Эти точки обычно называют точками Риттера. Уравнения равновесия принимают вид:

Остается решить эти уравнения, содержащие по одной неизвестной.

Ответ. 

Для равновесия плоской системы сил необходимо и достаточно, чтобы равнялись нулю суммы моментов всех сил относительно двух каких-либо точек плоскости и сумма проекций всех сил на любую ось, не перпендикулярную к прямой, проходящей через эти две точки:

Третья форма уравнений равновесия

Если две из неизвестных сил параллельны друг другу и точка пересечения их, следовательно, уходит в бесконечность, то для решения задачи удобно воспользоваться третьим видом уравнений равновесия. Пусть суммы моментов плоской системы сил относительно произвольно выбранных точек А и В равняются нулю:

В таком случае, как только что было показано, система сил или находится в равновесии, или приводится к равнодействующей, проходящей через точки А и В. Спроецируем все силы на какую-либо ось, не перпендикулярную к прямой, проходящей через точки А и В. Если система сил … приводится к равнодействующей, лежащей на  прямой АВ, то сумма проекций всех сил на g выбранную нами ось должна равняться модулю | этой равнодействующей, помноженному на коси- | нус утла между осью и прямой АВ. Если же система находится в равновесии, то сумма проекций всех сил равняется нулю. Обратно, если сумма | проекций всех сил на эту ось равна нулю, то, следовательно, равна нулю равнодействующая, т. е. эта система находится в равновесии.

Таким образом, для равновесия системы сил, расположенных на плоскости, необходимо и достаточно, чтобы равнялись нулю суммы моментов всех сил системы относительно двух произвольно
выбранных точек плоскости и сумма проекций всех сил системы на какую-либо ось Ох, не перпендикулярную к прямой, проходящей через выбранные центры моментов:
     (35)

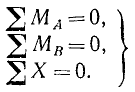
Задача №6

Между двумя вертикальными стенами, находящимися на расстоянии а друг от друга (рис. 56), помещен стержень весом P и длиной 21, который может вращаться вокруг шарнира А. прикрепляющего конец его к одной из стен. Найти реакции опор.

Решение. 1. Равновесие какого тела надо рассмотреть? Равновесие стержня.
2.    Какие силы на это тело действуют? Вес Р; реакция в точке D, направленная перпендикулярно виртуальному перемещению стержня (стержень, не нарушая связи, можно перемещать вдоль стены, поэтому реакция Rq направлена перпендикулярно стене DC); реакция в шарнире А, которую мы разложим на X_А и Y_А.
3.    Составим уравнения равновесия в третьей форме, выбрав за центры моментов точки А и В, в которых пересекаются линии действия искомых реакций. Точка пересечения Rq и Xa находится в бесконечности, поэтому в качестве третьего уравнения возьмем сумму проекций всех сил на какую-либо ось, лишь бы эта ось не была перпендикулярна к АВ. Имеем

Определив из чертежа sin а и cos а и решая эти уравнения, содержащие по одной неизвестной, найдем ответ.

Для равновесия плоской системы параллельных сил необходимо и достаточно, чтобы равнялись нулю суммы проекций всех сил на какую-либо ось, не перпендикулярную линиям действия сил, и сумма моментов относительно какой-либо точки:

Условия равновесия плоской системы параллельных сил

Если все силы системы параллельны друг другу, то одно из трех уравнений становится следствием двух Других.

В самом деле, в этом случае линия действия главного вектора (если он не равен нулю) параллельна линиям действия всех сил и для его определения достаточно взять сумму проекций всех сил на ось, параллельную их лилиям действия. Если сумма проекций всех сил равна нулю, то и главный вектор равен нулю. Если же, кроме того, равен нулю и главный момент, то система находится в равновесии. Справедливо и обратное заключение: если система параллельных сил, расположенных на плоскости, находится в равновесии, то равняются нулю сумма проекций сил на любую ось и сумма моментов сил относительной любой точки плоскости:

        (36)

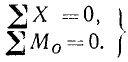
Ось Ox может быть и не параллельной линиям действия сил, а составлять с ними какой-либо угол, кроме прямого. 

Для равновесия плоской системы параллельных сил необходимо и достаточно, чтобы равнялись нулю суммы моментов всех сил относительно двух точек плоскости, не лежащих на прямой, параллельной линиям действия сил:

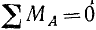
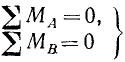
Пусть дана система сил, расположенных в одной плоскости и параллельных друг другу. Возьмем на этой плоскости произвольную точку А. Если , то система может либо находиться в равновесии, либо быть приведенной к равнодействующей, проходящей через точку А параллельно линиям действия составляющих сил. Возьмем сумму моментов всех сил относительно какой-либо точки В, выбрав эту точку так, чтобы прямая AB не была параллельна силам системы. Если сумма моментов относительно этой точки равна нулю, то система находится в равновесии, потому что равнодействующая не может проходить через точки А и В, так как должна быть параллельной силам системы. Поэтому равенства

       (37)

являются необходимыми и достаточными условиями равновесия плоской системы параллельных сил.

Задача №7

На двухконсольную горизонтальную балку действует пара сил (PP), на левую консоль —равномерно распределенная нагрузка интенсивности р, а в точке D правой консоли — вертикальная нагрузка Q. Определить реакции опор, если P=1Т, Q=2Т, p=2T∕м, а =0,8 м (рис. 57).

Рис. 57

Решение. Иногда (как в данной задаче), кроме сил, действующих на тело, имеется пара, заданная моментом. Силы пары равны и противоположны, поэтому пара сил не входит в уравнения проекций, но входит в уравнения моментов.

Рассмотрим равновесие балки CD. На балку действуют: 1) пара сил (PP) с моментом +P∙a= 0,8 T∙m∙, 2) вертикальная сосредоточенная нагрузка Q = 2T, приложенная в точке О; 3) равномерно распределенная нагрузка, которую заменяем одной вертикальной силой (равнодействующей) p∙α=1,6T, приложенной в середине CA; 4) реакция R_В в подвижной опоре В, направленная перпендикулярно виртуальным перемещениям, т. е. вертикально; 5) реакция R_А в неподвижном шарнире А. Направление реакции в неподвижном шарнире, вообще говоря, неизвестно. Если повернем пару, изображенную на чертеже, на 90°, отчего, как известно, действие пары на балку не изменится, то все силы, действующие на балку, станут вертикальными, следовательно, и реакция R_А вертикальна. Для решения задачи составим уравнение равновесия в форме (36):

Пара сил в это уравнение не входит, но обязательно должна войти в уравнение моментов:

Решая совместно два этих уравнения, получим ответ.
Можно воспользоваться также и уравнениями (37). Тогда вместо уравнения проекций надо составить второе уравнение моментов:

Решая первое уравнение, найдем R_В, решая второе, найдем R_А.
Ответ. R_А=1,5Т, R_В = 2,1Т.

Задача №8

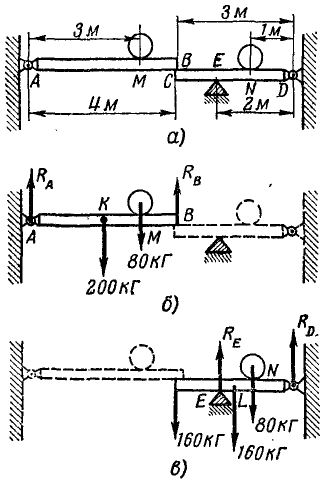
Балка AB длиной 4 м, весом 200 кГ может вращаться вокруг горизонтальной оси А и опирается концом В на другую балку CD длиной 3 м, весом 160 кГ, которая подперта в точκe E и соединена со стеной шарниром D. В точках M и N помещены грузы по 80кГ каждый. Расстояния: AM=3м, ED = 2м, ND=1м. Определить опорные реакции (рис. 58, а).

Решение. Балки AB и CD не являются одним твердым телом, а представляют собой систему сочлененных тел. Рассмотрим отдельно равновесие каждого тела под действием всех приложенных к этому телу сил.

1-й вопрос: равновесие какого тела рассматривать?
Ответ: равновесие балки АВ.

2-й вопрос: какие силы действуют на это тело?
Ответ: на балку AB действуют (рис. 58, б):

Рис. 58

а)    собственный вес балки 200 кГ, приложенный к середине балки н направленный по вертикали вниз;
б)    вес 80кГ груза М, направленный по вертикали вниз;
в)    реакция R_В со стороны балки CD, поддерживающей балку АВ. Эта реакция приложена к балке AB в точке В и направлена по вертикали вверх;
г)    реакция R_А в шарнире А. Эта реакция вертикальна, так как балка находится в равновесии, а все остальные действующие на балку силы направлены по вертикали. Нетрудно сообразить, что R_А направлена вверх.
Уравнения равновесия можно составить в форме (36) или в форме (37) по нашему желанию. Составим их в форме (37), приравняв нулю суммы моментов относительно точки А и относительно точки В:

Решая эти уравнения, находим R_А= 120 кГ, R_В = 160 кГ.

Теперь приступаем ко второй части задачи и опять задаем себе тот же вопрос: равновесие какого тела рассматривать? На этот раз рассмотрим равновесие балки CD. Какие силы на нее действуют? На нее действуют (рис. 58, в):
а)    собственный вес балки 160 кГ, приложенный в середине балки;
б)    вес 80 кГ груза N, приложенный между опорами E и D;
в)    давление балки АВ, приложенное к балке CD в точке С, направленное по вертикали вниз и (по закону равенства действия и противодействия) равное реакции R_В, а следовательно, равное 160 кГ;
г)    реакция R_Е, прило/кенная в точке E и направленная вверх;
д)    реакция RD. Эта реакция должна быть вертикальной, так как вертикальны все остальные действующие на балку силы, а балка находится в равновесии. Однако трудно сказать (без предварительных вычислений), направлена ли эта реакция вверх или вниз. При составлении уравнений равновесия примем условно, что RD направлена вверх, но если в результате решения уравнений мы получим отрицательную величину реакции RD, то это будет означать, что мы реакцию направили неверно, и тогда изменим ее направление на обратное. При правильном направлении сил значения их из уравнений равновесия должны всегда получаться положительными.

Возьмем сумму проекций всех сил на вертикальную ось и сумму моментов всех сил относительно точки D:

Решая эти уравнения, находим ответ.
Ответ. R_А= 120 кГ, R_В =160 кГ, R_Е= 400 кГ, RD = 0.

Статически определенной задачей называют задачу о равновесии, в которой число неизвестных равно числу уравнений равновесия

Итак, имеется только два уравнения равновесия системы параллельных сил, расположенных в одной плоскости, вместо трех уравнений равновесия системы сил, расположенных на плоскости произвольно. Равновесие плоского пучка сил определяется двумя уравнениями, если же силы пучка не лежат в одной плоскости, то появляется третье уравнение равновесия, как это показано в гл. III.

В системе уравнений число неизвестных не должно превышать числа уравнений, иначе система уравнений не имеет однозначных решений.

Статически определенными задачами называют задачи о равновесии твердого тела, в которых число неизвестных равно числу уравнений равновесия. В противном случае задачи не могут быть решены методами статики и являются статически неопределенными.

Равновесием системы тел называют такое состояние, при котором каждое из тел находится в равновесии

Равновесие системы сил. Часто встречается необходимость в статическом расчете системы тел, так или иначе соединенных («сочлененных») между собой.

Силы, действующие на тела такой системы, можно подразделить на две категории: внешние – силы, приложенные к телам данной системы, но обусловленные наличием других тел, не входящих в эту систему, и внутренние – силы взаимодействия между телами одной и той же системы. Такое подразделение относится как к активным силам, так и к реакциям связей.

Если система находится в равновесии, то в равновесии находится каждое тело, входящее в состав этой системы. Мы можем рассматривать каждое тело отдельно от других тел системы и составить уравнения равновесия всех сил, приложенных к этому телу, не исключая и сил, обусловленных действием на это тело соседних тел системы, т. е. внутренних сил системы, приложенных к этому телу. Так было сделано, например, при решении задачи № 22 о равновесии двух балок.

Вместе с тем, пользуясь аксиомой затвердения, мы можем всю систему рассматривать как одно абсолютно твердое тело и составить уравнения равновесия всех внешних сил системы. Внутренние же силы в эти уравнения равновесия всей системы не входят, так как они взаимно уравновешиваются по принципу равенства действия и противодействия, поскольку взаимодействия каждых двух тел «затвердевшей» системы оказываются приложенными к частям одного абсолютно твердого тела.

Задача №9

На невесомую трехшарнирную арку ABC (рис. 59, а)

Рис. 59

действует вертикальная сила Р. Определить реакции шарниров А, В и С. Размеры указаны на чертеже.

Решение. Конструкция состоит из двух полуарок AB и ВС, сочлененных шарниром В. Собственным весом полуарок пренебрегаем, поэтому на арку ABC действуют следующие внешние силы: вертикальная сила P и реакции в шарнирах А и С.

Между полуарками имеется взаимодействие в точке В их сочленения. Одна нз этих внутренних сил системы приложена к полуарке АВ, другая равна ей по величине, обратна по направлению, но приложена к полуарке ВС. Если всю арку рассматривать как твердое тело, то эти две силы учитывать не надо, так как они оказываются приложенными к одному твердому телу и, следовательно, взаимно уравновешивают друг друга. В уравнения равновесия всей арки войдут только внешние силы системы:

Имеем три уравнения с четырьмя неизвестными.
Для определения горизонтальной реакции в шарнире С, а также R_В, рассмотрим равновесие всех сил, действующих на полуарку ВС. На эту полуарку действуют (рис. 59, б): реакции X_С и Y_С в шарнире C (внешние реакции системы) и реакция в шарнире В (внутренняя реакция для всей системы, но внешняя для полуарки ВС) со стороны полуарки АВ. Эту реакцию мы тоже разложим по осям координат на X_В и Y_В- Составим уравнения равновесия для полуарки ВС:

Мы получили три уравнения, содержащие четыре неизвестных, но две из этих неизвестных входят также и в предыдущие три уравнения. Всего мы имеем шесть уравнений с шестью неизвестными. Решая уравнения, получим ответ.

Ответ.

• Заказать решение задач по теоретической механике

Жесткая заделка

Задачи на тему: жёсткая заделка

Задача №10

Брус, вес которого Р= 100 кГ, приложен в точке С, жестко заделан в стену, образуя с ней угол а =60° (рис. 60, а). Внутри угла DAВ лежит цилиндр весом Q = 180 кГ, касающийся бруса в точке Е, причем АЕ=0,3 м и AC = 0,4 м. Определить реакцию заделки.

Решение. Если балка заделана в стену, то на заделанный конец балки действует система распределенных сил (реакций). Приведем их по методу Пуансо к точке А, заменим одной неизвестной реакцией заделки (с проекциями X_А и Y_А) и одним неизвестным моментом заделки М. Эти три неизвестные определим из уравнений равновесия сил, действующих па балку.

Чтобы определить реакцию заделки (X_А, Y_А и М), надо составить три уравнения равновесия сил, действующих на брус, и, решив их, найти три неизвестные величины. Однако среди сил, действующих на брус, имеется еще одна неизвестная (четвертая)—сила давления F цилиндра, приложенная к брусу в точке Е.

Для определения этой силы предварительно рассмотрим равновесие цилиндра (рис. 60, б), на который действуют вес Q = 180 кГ, реакция R’ стены, направленная горизонтально вправо (перпендикулярно виртуальным перемещениям цилиндра вдоль стены), и реакция R” бруса, направленная влево вверх, перпендикулярно брусу (перпендикулярно виртуальным перемещениям цилиндра по брусу). По принципу равенства действия и противодействия эта реакция R” по величине равна, а по направлению противоположна силе F давления цилиндра на брус.

Рис. 60

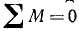
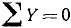
Из системы сил, действующих на цилиндр, надо определить лишь одну (R” ), а потому достаточно одного уравнения равновесия, если составить его так, чтобы в него не входила другая неизвестная (R”)> Таким уравнением может быть уравнение  относительно какой-либо точки, лежащей на линии действия R’ (кроме точки 0), или . Сумма проекций на вертикальную ось всех сил, приложенных к цилиндру, имеет вид

откуда 

Сила F давления цилиндра на брусок равна 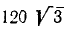, но направлена в противоположную сторону (рис. 60, в).

Кроме силы F, на брусок действуют его вес Р = 100 кГ и реакция в заделке, которую мы представили проекциями X_А и Y_А, а также моментом М.

Уравнения проекций и моментов всех сил, приложенных к бруску, напишем, приняв за центр моментов точку А:

Решая эти уравнения, находим неизвестные величины.

Ответ. X_А =—103,8 кГ; Y_А = +280 кГ^. M = +96,9 кГ^. м.

Знак минус перед реакцией X_A показывает, что направление реакции противоположно принятому на рис. 60, в. Это и очевидно, так как давление цилиндра стремится выдернуть брусок из заделки.

Определение внутренних усилий в стержнях фермы

Задачи на тему: Определение внутренних усилий в стержнях фермы

Задача №11

Определить опорные реакции и усилия в стержнях фермы крана (рис. 61, а) при нагрузке G = 8 Т. Весом стержней пренебречь.

Решение. В задаче требуется определить опорные реакции и внутренние усилия в стержнях фермы. Под фермой понимают жесткое сооружение, состоящее из стержней, соединенных шарнирами.

Для определения опорных реакций рассмотрим равновесие крана. На кран действуют три внешние силы: 1) вес груза G = 8T; 2) реакция R₂ в опоре O₂, направленная вертикально вверх, перпендикулярно виртуальным перемещениям, и 3) реакция R₁ в шарнире O₁. Реакции в шарнирах мы обычно раскладывали по координатным осям и определяли проекции из уравнений равновесия. Очевидно, что в данном случае проекция R₁ на горизонтальную ось равна нулю, потому что все остальные действующие на кран внешние силы вертикальны, следовательно, вертикальна и реакция R₁. Эта реакция направлена вниз, так как груз стремится повернуть кран вокруг опоры O₂.

Определим плечо силы G относительно O₂. Треугольник O₁AO₂ равносторонний и AO₂ = 3 л. В прямоугольном треугольнике ABO2 катет AO2 равен половине гипотенузы, следовательно, угол AO₂В = 60°. Таков же угол, составляемый BO₂ с горизонтальной прямой, и искомое расстояние h = 6 cos 60° = 3. Итак,

откуда 

Переходим к определению внутренних усилий в стержнях фермы. Как уже было сказано (см. задачу № 8), усилием в стержне называют силу, действующую вдоль стержня, растягивающую или сжимающую его; если стержень растянут, то на шарнир действует сила, направленная к стержню, а если сжат, то от него. В уравнения равновесия, выводимые в статике твердого тела, входят только внешние силы, потому что внутренние силы согласно принципу равенства действия и противодействия попарно равны и противоположны.

Для определения внутренних усилий в стержнях фермы надо рассмотреть равновесие не всей фермы, а лишь части ее, мысленно разрезав ферму, отбросив одну из отрезанных частей и заменив отброшенную часть силами, направленными вдоль разрезанных стержней. Этот метод определения внутренних усилий 1 называют методом РОЗ по первым буквам слов, определяющих те операции, которые надо проделать (разрежем, отбросим, заменим).

Итак, для определения внутренних усилий в стержнях фермы надо сначала определить реакции, а потом:
1)    разрежем мысленно ферму на две части, но так, чтобы разрезано было не более трех стержней с неизвестными усилиями, потому что мы имеем всего три уравнения равновесия. При этом нельзя разрезать ферму так, чтобы все три разрезанных стержня с неизвестными усилиями были между собой параллельны или же все три сходились в одной точке, потому что для этих случаев мы имеем всего по два уравнения. Например, если усилия в стержнях AO₁, AO₂ и AB неизвестны, то не следует мысленно отрезать узел А. Можно сначала отрезать узел В, определить усилие в стержне АВ, а затем уж отрезать узел А, тогда из двух уравнений равновесия сил, приложенных к шарниру А, определим усилия в стержнях AO₁ и AO₂. C этим ограничением можно не только разрезать ферму, но и вырезать из фермы отдельные шарниры. Разрежем ферму крана, как показано на чертеже (рис. 61, б);
 

Рис. 61

2)    отбросим мысленно одну из частей, на которые разрезана ферма. Принципиально говоря, безразлично, которую из частей отбросить. Отбросим верхнюю часть (рис. 61, в). В результате этих действий жесткость фермы нарушилась бы и, чтобы сохранить равновесие оставленной части фермы, необходимо к ней приложить внешние силы, в точности такие же, как внутренние усилия в соответствующих стержнях неразрезанной фермы. Поэтому мы
3)    заменим отброшенную часть фермы неизвестными по величине силами, направив их по разрезанным стержням в сторону от оставленной части, т. е. наружу (рис. 61, г). Если среди разрезанных стержней имеются такие стержни, усилия в которых известны, то наружу мы их направляем только в том случае, если стержень растянут; когда стержень сжат, мы направляем вектор, изображающий это усилие внутрь, к шарниру. Эти силы, равные внутренним усилиям в стержнях, обозначают буквой S с индексом, соответствующим номеру стержня. Теперь составим уравнения равновесия оставленной части фермы. Здесь удобно применить третий вид (35) уравнений равновесия:

Решая эти уравнения, находим

Знаки минус при полученных из уравнений значениях усилий в третьем и в четвертом стержнях показывают, что направления сил на рис. 60, г нужно изменить на противоположные, так как эти стержни не растянуты, а сжаты.
Чтобы определить усилия в других стержнях, надо снова применить метод РОЗ, разрезав ферму по другим стержням;
4)    разрежем ферму, как показано на чертеже (рис. 60,д);
5)    отбросим одну часть, например правую (рис. 60, е);
6)    заменим отброшенную часть силами, направленными по стержням.
Если усилие в стержне неизвестно, то условно считаем, что стержень растянут, и направляем силу от шарнира: S₅ и S₂ (рис. 60, ж). Если же усилие в разрезанном стержне уже известно, то направляем его от шарнира, когда стержень растянут, и к шарниру, когда стержень сжат (усилие в третьем стержне, равное 4,6 T на рис. 60, ж). Затем составляем и решаем уравнения равновесия:

Из этих двух уравнений находим S₂ и S₅.

Ответ: в тоннах: R₁ = 8 (вниз), R₂= 16 (вверх), усилия в стержнях: S₁ = +9,2; S₂ = -4,6; S₃ = -4,6; S₄ = -13,8; S₅ = +8,0.

Заметим, что ферму (и вообще всякую неизменяемую механическую систему) называют статически определимой, если внутренние усилия ее элементов при любой нагрузке могут быть найдены из уравнений статики. В противном случае систему называют статически неопределимой.

Силы трения

Максимальное значение силы трения скольжения равно произведению нормального давления и коэффициента трения: F_мaκc = fN

Кулоново трение

Трение материальных тел связано с явлениями не только механического, но и электрического, термического, внутримолекулярного и пр. характера, и изучение трения относится к области физики. Трудами советских и зарубежных ученых открыты законы и выведены формулы, определяющие силы трения. Точные формулы очень сложны, но в технике обычно пользуются для приближенного определения трения простыми соотношениями, установленными еще в XVIII в. Ш. Кулоном опытным путем. Для вывода закона трения по Кулону проделаем опыт, обычно называемый опытом Морена, по имени одного из основателей научной практической механики. Однако этот же опыт еще задолго до Морена проделал Amohtoh — один из первых серьезных исследователей трения.

К телу (рис. 62), лежащему на горизонтальной негладкой плоскости, прикреплена перекинутая через блок нить, к другому концу которой привязана чашка с грузом. На тело действуют следующие силы: вес G, реакция R плоскости, натяжение Q нити, равное весу груза, приложенного к концу нити, сила трения F_тр направленная против натяжения нити. Из условия равновесия тела следует, что при покое тела сила трения равна и противоположна той силе Q, которая стремится вывести это тело из состояния покоя.

Рис. 62

Постепенно увеличивая груз Q, а следовательно, и натяжение нити, мы убедимся, что тело начнет двигаться, как только это натяжение достигнет определеной величины. До тех пор, пока натяжение нити меньше этой величины, оно уравновешивается силой трения, и тело находится в покое. Отсюда можно сделать заключение: при покое тела увеличение силы, стремящейся привести тело в движение, вызывает увеличение силы трения от нуля до известного предела F_мaκc, больше которого сила трения быть не может. Этот предел называют силой трения скольжения при начале движения:

       (38)

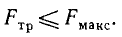
Как показывает опыт, максимальное значение силы трения пропорционально нормальному давлению:

       (39)

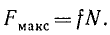
Под нормальным давлением мы понимаем составляющую полного давления, перпендикулярную к соприкасающимся плоскостям. Так, если тело веса G лежит на плоскости, составляющей угол а с плоскостью горизонта (см. рис. 63). то нормальное давление N = Gcos а.

Безразмерный коэффициент пропорциональности

называют статическим коэффициентом трения скольжения.
Сопоставляя равенства (38) и (39), находим, что во время покоя тела действующая на тело сила трения

       (38^/)

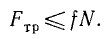
После начала движения коэффициент трения скольжения несколько уменьшается и принимает значение динамического коэффициента трения скольжения:

Согласно приближенным кулоновым законам трения коэффициенты трения скольжения не зависят ни от давления, ни от величины трущихся поверхностей, ни от скорости. Они зависят от физической природы трущихся тел, от шлифовки поверхностей, от расположения волокон и, конечно, от смазки. Числовые значения статического и динамического коэффициента трения имеются в любом техническом справочнике.

Статический коэффициент трения скольжения равен тангенсу угла трения.

Угол трения, тангенс трения, конус трения

Коэффициенты трения легко можно определить экспериментальным путем. Пусть тело (рис. 63) лежит на наклонной плоскости OA, угол наклона которой мы можем изменять по нашему желанию. На тело действуют три силы: вес G, сила трения скольжения F_тр, направленная вдоль плоскости соприкосновения тел, и реакция R плоскости, перпендикулярная к этой плоскости, по величине равная нормальному давлению N.

Рис. 63

Будем постепенно увеличивать угол наклона до тех пор, пока тело не начнет двигаться вниз по плоскости. Угол наклона плоскости, при котором начинается скольжение, называют углом трения α_тр для данной пары трущихся материалов. Если, например, тело сделано из бронзы, а плоскость стальная, то α_тр есть угол трения бронзы по стали.

Построим оси координат, как показана на чертеже, и составим уравнения равновесия:

Отсюда

Сравнивая это равенство с (39), находим, что статический коэффициент трения скольжения равен тангенсу угла трения. Тангенс угла трения иногда коротко называют тангенсом трения.

Реакцию, перпендикулярную к опорной поверхности (рис. 64, а), называют идеальной реакцией в отличие от полной реакции, выражающейся геометрической суммой идеальной реакции и силы трения.

Таким образом, сила трения является касательной составляющей полной реакции, идеальная реакция — нормальной составляющей полной реакции, а угол трения — углом максимального возможного отклонения полной реакции Pτp опорной поверхности от нормали к ней.

Если мы будем поворачивать силу P вокруг этой нормали, то также будут поворачиваться сила трения и полная реакция. При этом полная реакция опишет конус с осью, нормальной к поверхности соприкосновения тел, и с углом при вершине, равным удвоенному углу трения. Этот конус, называемый конусом трения, является геометрическим местом всевозможных направлений полной реакции R_тр.

Пусть к телу, лежащему на негладкой поверхности, весом которого можно пренебречь (рис. 64, б), приложена сила Р, составляющая угол β с нормалью к этой поверхности, как показано на чертеже. Убедимся, что сила P не может привести тело в движение, если угол β меньше угла трения α_тр. Разложим силу P на две составляющие:

Составляющая P₁ стремится привести тело в движение, a P₂ давит на поверхность, вследствие чего возникает сила трения F_тр, направленная против составляющей P₁. Движение тела под действием силы P произойдет лишь в том случае, если составляющая P₁ будет больше максимально возможного значения силы трения:

или, принимая во внимание предыдущие равенства,

Деля обе части неравенства на P cos β, получим следующее необходимое условие движения тела:

В это условие не входит значение силы P и надо сделать такое заключение: если на тело, лежащее на негладкой плоскости, оказывает давление сила, линия действия которой лежит внутри конуса трения, то, сколь бы велика ни была такая сила, она не приведет тело в движение.

Этим правилом широко пользуются в технике, на нем построены теория клина, теория самоторможения и др.

Рис. 65

Задача №12

Идеально сыпучее тело, лежащее на горизонтальной плоскости, принимает форму конуса. Определить угол наклона образующей к горизонтальной плоскости (угол естественного откоса).

Решение. Рассмотрим равновесие какой-либо частицы M (рис. 65), находящейся на поверхности конуса. На частицу действуют

1)    вес G, направленный по вертикали вниз;
2)    реакция/? соседних частиц сыпучего тела, направленная перпендикулярно возможному перемещению частицы и равная нормально му давлению частицы на поверхность конуса;
3)    сила трения Fтр=fN, направленная по образующей вверх. Многоугольник (треугольник) сил, действующих на частицу, должен быть замкнут, так как она находится в равновесии и

Но коэффициент трения, как известно, равен тангенсу угла трения, следовательно, угол естественного откоса равен углу трения:

Угол естественного откоса, называемый также углом ската, имеет большое значение при проектировании различных насыпей, элеваторов, овощехранилищ и пр.

Задача №13

Сколько яровой пшеницы можно насыпать на круглую площадку диаметром 10 м, если вес 1 л яровой пшеницы равен 750 Г, а f =0,75?

Решение. Умножив насыпной вес яровой пшеницы 0,75 Т/м3 на объем конуса 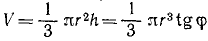, где φ—угол естественного откоса, получим ответ.
Ответ. 98 T.

Задача №14

Лестница AB (рис. 66) прислонена к стене под углом 30°. По лестнице поднимается человек весом P. Пренебрегая весом лестницы, определить наибольшее расстояние ВС, на которое может подняться человек, не уронив лестницы, если коэффициент трения лестницы о пол и о стену f = tg 15°.

Рис. 66

Решение. Рассмотрим равновесие лестницы в предельном положении. На лестницу действуют: 1) вес P человека, приложенный в точке С; 2) полная реакция Rтр.А в точке А, направленная вправо н вверх под углом 90° —15° = 75° к стене, так как в предельном положении она составляет с идеальной реакцией угол, равный углу трения; 3) полная реакция R_тр.B в точке В, направленная вверх и влево под углом 75° к полу. Уравнения равновесия имеют вид:

Определив R_тр.B из первого уравнения, подставим во второе:

Умножив это уравнение на sin 15°, найдем, что R_тр.А = P sin 15°, и, подставляя это значение в третье уравнение равновесия, получим

откуда 

Если человек поднимается по лестнице выше AB/2, то три силы, действующие на лестницу, не пересекутся в одной точке, и необходимое условие равновесия трех непараллельных сил (см. § 3) будет нарушено. Если же человек будет находиться на лестнице ниже, то равновесие сохранится, так как угол трения является максимальным углом, который может составлять полная реакция с идеальной реакцией. В этом случае сила трения будет меньше произведения коэффициента трения на нормальное давление, и три приложенные к лестнице силы пересекутся в одной точке.

Момент пары, противодействующей качению тела по опорной поверхности, называют моментом трения качения.

Трение качения

В различных задачах механики надо учитывать трение, возникающее при качении тел. Оно не может быть объяснено в механике абсолютно твердого тела, а потому мы коснемся его лишь в общих чертах.

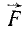
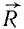
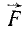
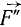
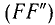
Пусть перпендикулярно к оси цилиндрического катка (рис. 67) веса G и радиуса r, лежащего на негладкой горизонтальной поверхности, приложена горизонтальная сила . Вследствие деформаций катка и опорной поверхности их касание происходит не в одной точке, а по некоторой площадке, и нормальная реакция бывает смещена относительно вертикальной плоскости симметрии катка на некоторое расстояние δ. В направлении, обратном силе , в том месте, где каток касается опорной поверхности, возникает сила , которую называют силой трения качения. Во время равновесия катка эта сила по модулю равна F и составляет с ней пару , уравновешиваемую парой (GR), момент которой называют моментом трения качения. Плечо δ этой пары при предельном равновесии называют коэффициентом трения качения. Отметим, что в отличие от безразмерного коэффициента трения скольжения коэффициент трения качения имеет размерность длины и его выражают в миллиметрах, поэтому оба эти коэффициента — величины несравнимые. Неправильно было бы считать, что трение качения всегда меньше, чем трение скольжения. Они зависят от свойства трущихся тел. Летом ездят на колесах, а зимой на санях.

Рис. 67

Момент трения качения вполне это трение характеризует, но иногда бывает удобно пользоваться силой трения качения, величину которой

      (40)

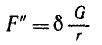
легко получить из равенств моментов двух пар.